Как найти объем наклонной призмы параллелепипеда - Исправление недочетов и поиск решений вместе с Examum.ru

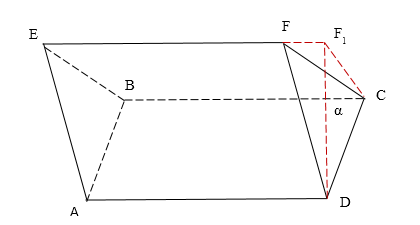
Наклонная призма — это призма, боковые рёбра которой не перпендикулярны основанию.

ABCD;KLMN

— основания призмы.

AKLB;BLMC;DNMC;AKND

— бoковые грани. Вcе бoковые грани наклонной призмы являются параллелограммами.

AK;BL;CM;DN

— боковые рёбра. Боковые рёбра параллельны между собой и равны.

KF=h

— высота наклонной призмы (перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания). Часто перпендикуляр проводят с одной из вершин верхнего основания.

∠KAF=α

— угол между боковым ребром и плоскостью основания.

Площадью боковой поверхности наклонной призмы называется сумма площадей её боковых граней.

Площадью полной поверхности наклонной призмы называется сумма площадей всех её граней.

Объём наклонной призмы равен произведению площади основания на высоту

Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.

Объём наклонной призмы равен площади перпендикулярного сечения на боковое ребро.

Перпендикулярное сечение — пересечение призмы и плоскости, перпендикулярной её боковому ребру.

Источники:

Рис. 1. Наклонная призма, © ЯКласс.

Источник

оксана николаевна кузнецова

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение призмы

Призма является частным случаем цилиндра. Параллелепипед является частным случаем призмы.

Призма обладает следующим свойством:

Любое сечение призмы плоскостью, параллельной её основанию, делит данную призму на две призмы так, что отношение боковых поверхностей и отношение объёмов этих призм равно отношению длин их боковых рёбер. Любое сечение призмы плоскостью, параллельной её боковому ребру, делит данную призму на две призмы так, что отношение объёмов этих призм равно отношению длин их боковых рёбер. Любое сечение призмы плоскостью, параллельной её боковому ребру, делит данную призму на две призмы так, что отношение объёмов этих призм равно отношению площадей их основания.

Виды призм

Прямая призма. Боковые рёбра прямой призмы перпендикулярны плоскости основания.
Наклонная призма. Боковые рёбра наклонной призмы находятся относительно плоскости основания под углом, отличным от $90^circ$.
Правильная призма. Основанием прямой призмы является правильный многоугольник. Её боковые гран — равные прямоугольники.

Полуправильным многогранником называется правильная призма, боковые грани которой — квадраты.

Объём прямой призмы

Для вывода формулы вычисления объёма правильной призмы возьмём призму, в основании которой лежит треугольник. Достроим её до прямоугольного параллелепипеда (рисунок 1).

Тетраэдр, достроенный до параллелепипеда»>

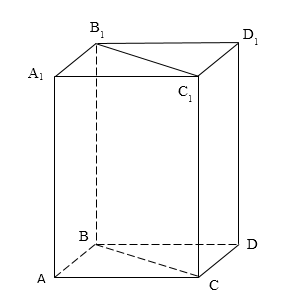
Рисунок 1. Тетраэдр, достроенный до параллелепипеда

«Объем прямой и наклонной призмы» 👇

Из предыдущей главы мы знаем, что объём прямоугольного параллелепипеда равен:

где

Т.к. полученный параллелепипед состоит из исходной призмы и призмы, равной ей по объёму, то объём исходной призмы будет равен

Т.к.

где $a$, $b$, $c$ длины сторон $AB$, $BC$, $AC$ соответственно, и их произведение равно площади основания исходной призмы, то запишем в общем виде формулу нахождения объёма прямой призмы:

где $S_{осн.}$ — площадь основания призмы, $H$ — высота, проведённая к основанию призмы.

Данная формула верна для прямой призмы с любым многоугольником в основании.

Объём наклонной призмы

Для вывода формулы нахождения объёма наклонной призмы рассмотрим треугольную наклонную призму $ABCDFE$. Проведём через ребро $DC$ плоскость $alpha $, перпендикулярную основанию $ABCD$ исходной призмы, и построим треугольную усечённую призму (рисунок 2).

Рисунок 2. Наклонная призма, плоскость $alpha $

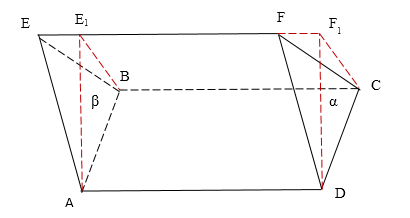
Теперь через ребро $AB$ проведём плоскость $beta $, параллельную плоскости $alpha $ (рисунок 3).

Рисунок 3. Наклонная призма, плоскости $alpha $ и $beta $

Если применить такое преобразования к наклонным граням ещё раз, то получится призма, у которой все боковые грани перпендикулярны основанию. Снова получился прямая призма.

Если её подвергнуть подобному преобразованию (сначала дополнить первой усечённой призмой, затем отсечь вторую усечённую призму), то достроенная и отсекаемая призмы совмещаются параллельным переносом на отрезок $AB$. Из этого следует, что фигуры имеют одинаковый объём.

Следовательно, объём построенной прямой призмы равен объёму исходной наклонной.

Объём наклонной призмы равен произведению площади основания на высоту:

Вывод

Объём любой призмы (наклонной и прямой) находится по формуле:

где $acdot b$ — площадь основания, $c$ — высота призмы.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Сегодня на уроке мы выведем формулу для нахождения
объёма наклонной призмы.

Прежде чем приступить к изучению нового материала
давайте вспомним формулу для нахождения объёма геометрического тела ,
повторим формулу для вычисления объёма прямой призмы .

Давайте сформулируем и докажем теорему.

Объём наклонной призмы равен произведению площади
основания на высоту.

Доказательство.
Сначала докажем эту теорему для треугольной наклонной призмы.

Рассмотрим треугольную призму с объёмом ,
площадью основания и
высотой .

Отметим на одном из оснований призмы точку и
направим ось перпендикулярно
основаниям.

Рассмотрим сечение призмы плоскостью,
перпендикулярной к оси и,
значит, параллельной плоскости основания. Обозначим буквой абсциссу
точки пересечения этой плоскости с осью ,
а через –
площадь получившегося сечения.

Теперь давайте покажем, что площадь .
Четырёхугольник –
параллелограмм, значит, .
Аналогично, четырёхугольник –
параллелограмм, значит, .
Четырёхугольник –
параллелограмм, значит, и отрезки .
Тогда получим, что треугольники по
трём сторонам, то есть мы доказали, что площади этих треугольников равны .

Теперь давайте применим основную формулу для
вычисления объёмов тел .

Теперь давайте докажем эту теорему для произвольной
призмы высоты и
площадью основания .

Такую призму можно разбить на треугольные призмы с
общей высотой .
Рассмотрим, например, выпуклую пятиугольную призму.

Вычислим объём каждой полученной треугольной призмы
по доказанной нами формуле. Мы знаем, что если тело
составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Тогда объём нашей пятиугольной призмы равен сумме
объёмов треугольных призм.

Поскольку мы разбивали пятиугольную призму на
треугольные с общей высотой, то в сумме объёмов высоту можно вынести за скобки.
В скобках получим сумму площадей треугольников, на которые мы разбили
пятиугольник. То есть в скобках мы получили площадь пятиугольника, который
лежит в основании призмы. Тогда получим, что объём наклонной призмы равен ,
что и требовалось доказать.

Но объём наклонной призмы можно вычислить по другой
формуле.

Объём наклонной призмы равен .
Эту формулу мы доказывать не будем, просто рассмотрим несколько задач и
посмотрим случаи, в которых проще вычислить объём призмы именно с помощью этой
формулы.

Решим несколько задач.

Задача:
найти объём наклонной призмы, у которой основанием является треугольник со
сторонами ,
,
,
а боковое ребро, равное ,
составляет с плоскостью основания угол в .

Решение:
для вычисления объёма призмы, воспользуемся только что доказанной формулой.

Площадь основания вычислим по формуле Герона.

Получим, что площадь основания призмы равна

Теперь давайте проведем высоту призмы и рассмотрим .
Так как –
высота, значит, треугольник прямоугольный. По условию, боковое ребро равно ,
а угол между боковым ребром и плоскостью основания равен .
Это будет угол между боковым ребром призмы и его ортогональной проекцией на
плоскость основания. В данном случае, это будет ,
тогда .
По свойству катета, лежащего напротив угла в тридцать градусов, .
Тогда по теореме Пифагора нетрудно найти чему равна высота призмы. Высота
призмы равна .

Подставим найденные значения в формулу для вычисления
объёма призмы и получим, что объём призмы равен .

Задача:
найти объём наклонной призмы, основанием которой является параллелограмм .
Сторона ,
сторона ,
.
Высота призмы равна .

Решение:
воспользуемся только что доказанной формулой.

Для вычисления площади параллелограмма, лежащего в
основании, воспользуемся формулой: .

Площадь основания будет равна .

Подставим полученное значение в формулу для
вычисления объёма, получим, что объём призмы равен .

Задача:
найти объём наклонной треугольной призмы, если расстояния между ее боковыми рёбрами
равны ,
и
,
а площадь боковой поверхности равна .

Решение:
расстояния между боковыми рёбрами – длина перпендикуляров. Таким образом,
проведя все перпендикуляры мы получим треугольник, который будет
перпендикулярным сечением призмы.

Поэтому нетрудно увидеть, что для вычисления объёма
мы воспользуемся тем, что объём наклонной призмы равен .

Но прежде вспомним, что площадь боковой поверхности
наклонной призмы равна .

Периметр перпендикулярного сечения равен .
Тогда длина бокового ребра равна .

Вычислим площадь перпендикулярного сечения по
формуле Герона. Получим, что площадь сечения равна

Подставим полученные значения в формулу для
вычисления объёма и получим, что объём призмы равен .

Итоги:

Сегодня на уроке мы вывели формулу для вычисления
объёма наклонной призмы.

Показали ещё одну формулу для вычисления объёма
наклонной призмы. Решили несколько задач.

Источник

Многогранник, две грани которого равные -угольники, лежащие в параллельных плоскостях, а остальные граней – параллелограммы, называют -угольной призмой.

Два -угольника называют основаниями призмы, а параллелограммы – боковыми гранями. Стороны граней называют ребрами призмы, а концы ребер – вершинами призмы.

На рисунке 9.41 изображена пятиугольная призма, на рисунке 9.42 – треугольная, а на рисунке 9.43 – четырехугольная.

На рисунке 9.42 треугольники и – основания призмы , параллелограммы , , – боковые грани, отрезки , , – боковые ребра, отрезки , , , , , – ребра оснований, точки , , , , , – вершины призмы.

Если грани призмы не имеют общего ребра, то их называют противоположными, если грани имеют общее ребро, то – смежными. На рисунке 9.43 грани и , и , а также и являются противоположными, а, например, грани и – смежными.

Две вершины призмы, не принадлежащие одной грани, называют противоположными. Например, на рисунке 9.43 вершины и – противоположные.

Диагональю призмы называют отрезок, соединяющий две противоположные вершины (например, диагональ на рисунке 9.41).

Треугольная призма не имеет противоположных граней, не имеет противоположных вершин и не имеет диагоналей.

Прямой призмой называют призму, боковые ребра которой перпендикулярны плоскостям ее оснований (рис. 9.42). Боковые грани прямой призмы – прямоугольники.

Наклонной призмой называют призму, боковые ребра которой являются наклонными к плоскостям ее оснований (рис. 9.41 и 9.43). Боковые грани наклонной призмы – параллелограммы (некоторые боковые грани могут быть и прямоугольниками).

Высотой призмы называют перпендикуляр, заключенный между основаниями призмы. Высота прямой призмы равна длине ее бокового ребра (рис. 9.42), высота наклонной призмы – не равна (рис. 9.41 и 9.43).

Диагональным сечением призмы называют сечение, содержащее диагональ призмы. На рисунке 9.44 построены диагональные сечения и четырехугольной призмы .

Параллелепипедом называют призму, основание которой – параллелограмм (рис. 9.44).

Прямым параллелепипедом называют параллелепипед, боковые ребра которого перпендикулярны плоскостям его оснований (рис. 9.45).

Прямоугольным параллелепипедом называют прямой параллелепипед, основанием которого является прямоугольник. На рисунке 9.46 изображен прямоугольный параллелепипед.

Свойство диагонали прямоугольного параллелепипеда: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:

, (9.1)

где , , – длины ребер, выходящих из одной вершины, – диагональ параллелепипеда.

Объем прямоугольного параллелепипеда находят по формуле:

. (9.2)

Кубом называют прямоугольный параллелепипед с равными ребрами. Все грани куба – квадраты (рис. 9.47).

Объем куба с ребром находят по формуле:

. (9.3)

Площадь поверхности куба с ребром находят по формуле:

$LaTeX formula: S_{n.}=6a^2$ . (9.4)

Диагональ куба с ребром а находят по формуле:

. (9.5)

Объем прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.6)

Площадь поверхности прямой призмы находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.7)

Площадь боковой поверхности прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: S_{delta .}=P_{o.} cdot h$ . (9.8)

Объем наклонной призмы можно вычислить по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.9)

Площадь поверхности наклонной призмы можно вычислить по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ , (9.10)

а также по формулам:

$LaTeX formula: V=S_{c.} cdot l$ , (9.9.1)

$LaTeX formula: S_{delta.}=P_{c.} cdot l$ , (9.10.1)

где сечение, перпендикулярное ребру (рис. 9.48).

Правильной призмой называют прямую призму, основанием которой является правильный многоугольник.

Пример 1. Найдите объем и площадь поверхности куба, зная, что его диагональ см.

Решение. Согласно формуле 9.5 и см. По формуле 9.3 $LaTeX formula: V=(2sqrt{3})^2=24sqrt{3}$ ( $LaTeX formula: _{CM}\^3$ ), а по формуле 9.4 $LaTeX formula: S_{n.}=6 cdot (2sqrt{3})^2=72$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^3$ ; $LaTeX formula: _{CM}\^2$ .

Пример 2. Найдите объем прямоугольного параллелепипеда, диагональ которого равна , а его измерения относятся как .

Решение. Согласно условию задачи запишем измерения параллелепипеда: , , .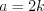

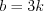
Согласно свойству диагонали прямоугольного параллелепипеда 9.1, получим: , , откуда . Тогда , , .

Зная три измерения параллелепипеда, по формуле 9.2 найдем его объем: .

Ответ: .

Пример 3. В основании прямой призмы лежит прямоугольный треугольник с катетами см и см. Высота призмы равна см. Найдите площадь поверхности и объем призмы.

Решение. 1. Площадь треугольника с катетами и найдем по формуле $LaTeX formula: S=frac{1}{2}ab$ . Получим: $LaTeX formula: S=frac{1}{2} cdot 10 cdot 8=40$ ( $LaTeX formula: _{CM}\^2$ ).

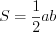
2. Гипотенузу найдем по теореме Пифагора: (см).

3. Площадь боковой поверхности призмы найдем по формуле 9.8 : $LaTeX formula: S_{delta .}=(10+8+2sqrt{41}) cdot 8=16(9+sqrt{41})$ ( $LaTeX formula: _{CM}\^2$ ).

4. Согласно формуле 9.7 , найдем площадь полной поверхности призмы:

$LaTeX formula: S_{n.}=2 cdot 40+16(9+sqrt{41})=16(14+sqrt{41})$ ( $LaTeX formula: _{CM}\^2$ ).

5. Объем призмы найдем по формуле 9.6 :

( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: _{CM}\^2$ ; $LaTeX formula: _{CM}\^3$ .

Пример 4. Объем наклонной треугольной призмы равен , а боковое ребро . Правильный треугольник – сечение, перпендикулярное боковому ребру (рис. 9.49). Найдите площадь боковой поверхности этой призмы.

Решение. 1. Согласно формуле 9.9.1 запишем: $LaTeX formula: 270=S_{c.} cdot 10$ , откуда $LaTeX formula: S_{c.}=27$ .

2. Площадь правильного треугольника со стороной находят по формуле $LaTeX formula: S=frac{sqrt{3}a^2}{4}$ . Тогда $LaTeX formula: 27=frac{sqrt{3}a^2}{4}$ , $LaTeX formula: a^2=9cdot 4cdot sqrt{3}$ , .

3. Найдем периметр треугольника : .

4. Согласно формуле 9.10.1 , найдем площадь боковой поверхности призмы: $LaTeX formula: S_{delta.}=18sqrt[4]{3} cdot 10=180sqrt[4]{3}$ .

Ответ: .

Пример 5. Диагональ прямоугольного параллелепипеда равна см, а диагонали его боковых граней равны см и см. Определите объем параллелепипеда.

Решение. Рассмотрим прямоугольный параллелепипед (рис. 9.50), где , и его измерения; см – диагональ.

Согласно свойству 9.1 . Рассмотрим треугольник . Так как см, то . Рассмотрим треугольник . Так как см, то .

Запишем и решим систему уравнений $LaTeX formula: begin{cases} a^2+b^2+c^2=36, \ b^2+c^2=16, \ a^2+c^2=25 . end{cases}$

Из второго уравнения системы выразим и получим: . Из третьего уравнения выразим и получим: .

Подставим полученные значения и в первое уравнение системы и найдем значение :

, , см.

Зная , определим значения и :

, см; , см.

Согласно формуле 9.2 найдем объем параллелепипеда: ( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: _{CM}\^3$ .

Пример 6. Определите объем правильной четырехугольной призмы, если ее диагональ образует с плоскостью боковой грани угол $LaTeX formula: 30^{circ}$ , а сторона основания равна .

Решение. Согласно условию задачи основанием призмы является квадрат со стороной (рис. 9.51).

Так как отрезок является проекцией диагонали призмы на грань , то угол является углом наклона диагонали призмы к плоскости боковой грани и $LaTeX formula: angle AB_1D=30^{circ}$ .

Рассмотрим треугольник . По свойству катета лежащего против угла $LaTeX formula: 30^{circ}$ запишем .

Так как согласно свойству 9.1 диагонали прямоугольного параллелепипеда , то , , .

Найдем объем призмы по формуле 9.9 :

Ответ: .

Пример 7. Найдите объем правильной шестиугольной призмы (рис. 9.52), зная, что большая диагональ призмы равна и образует с плоскостью основания призмы угол $LaTeX formula: 30^{circ}$ .

Решение. Рассмотрим большее диагональное сечение призмы и прямоугольный треугольник . Поскольку диагональ призмы и образует с плоскостью основания угол $LaTeX formula: 30^{circ}$ , то катет , лежащий против угла $LaTeX formula: 30^{circ}$ , равен половине гипотенузы, следовательно, высота призмы .

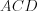
Из теоремы Пифагора: , , .

Так как в основании призмы лежит правильный шестиугольник со стороной , то и $LaTeX formula: a=frac{sqrt{3}}{2}$ .

По формуле $LaTeX formula: S=frac{3sqrt{3}a^2}{2}$ найдем площадь основания призмы: $LaTeX formula: S_{o.}=frac{9sqrt{3}}{8}$ .

По формуле 9.9 найдем объем призмы: $LaTeX formula: V=frac{9sqrt{3}}{8}$ .

Ответ: $LaTeX formula: frac{9sqrt{3}}{8}$ .

1. Треугольная призма не имеет диагоналей.

2. Различайте прямую и наклонную призму: у наклонной призмы – боковые грани параллелограммы, у прямой призмы – боковые грани прямоугольники.

3. Если основание призмы – параллелограмм (ромб, прямоугольник, квадрат), то такую призму называют параллелепипедом. Длины ребер, выходящих из одной вершины параллелепипеда, называют его измерениями.

Источник