|
Как рассчитать объем жидкости в цилиндре?В Рокотов 4 года назад
Какая формула? Приведите примеры, чтобы было понятно. Как найти объем жидкости в цилиндре, бочке в литрах? bezdelnik 4 года назад Полный объём ёмкости цилиндрической формы определяется по формуле V=S*H, где V -объём ёмкости в литрах, S — внутренняя площадь круглого основания ёмкости в квадратных дм, H -высота или длина цилиндра в дм. S=Пи*D^2/4, где Пи= 3,14… , D -внутренний диаметр цилиндра в дм. Поскольку Пи трансцендентное число то вычислить объём цилиндра можно только с некоторой погрешностью. Например, при D=10 дм и Н=10 дм V=Пи*100*10/4=Пи*1000/4= 3,14*250…=785… литров. Если полностью наполненную ёмкость наклонить, то чтобы найти объём Vо оставшейся в ней жидкости надо измерить расстояние h от верха ёмкости до оставшейся жидкости. Например, если в выше приведённой ёмкости расстояние h=H/2=5 дм, то Vо = V/2+V/4=3*V/4= 3*785/4= 588,75… литров. автор вопроса выбрал этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить Aitur Kabylbek 4 года назад Для измерения объема жидкости в емкости цилиндрической формы необходимо произвести расчеты по следующей формуле: Объем = Площадь (S) * Высоту (L). Площадь, в свою очередь, равна = число Пи * диаметр * диаметр / 4 = (3.14 * d^2) / 4. Теперь, нужно определить уровень жидкости в цилиндре. К примеру, мы положили туда тонкую палочку и определили высоту (L), до которой жидкость поднялась в цилиндре. Итоговая формула будет выглядеть следующим образом: V = ((3.14 * d^2) / 4) * L.
в избранное
ссылка
отблагодарить Грустный Роджер A если это цилиндр, лежащий на боку? ТОгда формула совсем другая будет…
il63 И тогда нужно задать длину цилиндра, его диаметр и высоту уровня воды от низшнй точки. Для ее решения без интегрирования можно обойтись? А если цилиндр лежит не горизонтально, а наклонен под углом альфа? Хорошая задача для вступительных экзаменов на физтех или в СПГУ.
spin Если на боку, то тоже не так сложно. Надо только знать формулу площади сегмента окружности. И без всякого интегрирования задача решается.
Знаете ответ? |
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Загрузить PDF
Загрузить PDF
Объем – это количество занимаемого телом пространства, а плотность равна массе тела, поделенной на его объем.[1]
Прежде чем вычислить плотность тела, необходимо найти его объем. Если тело имеет правильную геометрическую форму, его объем можно рассчитать при помощи простой формулы. Объем измеряется обычно в кубических сантиметрах (см3) или кубических метрах (м3). Используя найденный объем тела, легко рассчитать его плотность. Для измерения плотности служат граммы на кубический сантиметр (г/см3) или граммы на миллилитр (г/мл).
-
1
Определите форму тела. Знание формы позволит вам выбрать правильную формулу и провести измерения, необходимые для расчета объема.
-
Сфера представляет собой идеально круглый трехмерный объект, все точки поверхности которого отстоят на равном расстоянии от центра. Иными словами, сферическое тело похоже на круглый мяч.[2]
-
Конус – это трехмерная фигура, в основании которой лежит круг, а вершину составляет единственная точка, называемая вершиной конуса. Конус можно представить также в виде пирамиды с круглым основанием.[3]
-
Куб представляет собой трехмерную фигуру, составленную из шести одинаковых квадратных граней.[4]
-
Прямоугольный параллелепипед, называемый также прямоугольной призмой, похож на куб: он также имеет шесть граней, однако в этом случае они представляют собой прямоугольники, а не квадраты.[5]
-
Цилиндр – это трехмерная фигура, состоящая из одинаковых круглых концов, края которых соединены округлой поверхностью.[6]
-
Пирамида является трехмерной фигурой, в основании которой лежит многоугольник, который соединен с вершиной боковыми гранями.[7]
Правильной пирамидой называется такая пирамида, в основании которой лежит правильный многоугольник, все стороны и углы которого равны между собой.[8]
- Если тело имеет неправильную форму, его объем можно найти, полностью погрузив его в воду.
-
Сфера представляет собой идеально круглый трехмерный объект, все точки поверхности которого отстоят на равном расстоянии от центра. Иными словами, сферическое тело похоже на круглый мяч.[2]
-
2
Выберите для вычисления объема правильное уравнение. Для тела каждого типа существует своя формула, позволяющая рассчитать занимаемый им объем. Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье Как находить объем.
- Сфера: V = (4/3) π r3, где r – радиус сферы, а π – константа, равная примерно 3,14.
- Конус: V = (1/3) π r2h, где r – радиус круглого основания, h – высота конуса, π – константа, равная приблизительно 3,14.
- Куб: V = s3, где s – длина ребра куба (стороны любой из его квадратных граней).
- Прямоугольный параллелепипед: V = l x w x h, где l – длина прямоугольной грани, w – ее ширина, h – высота параллелепипеда (призмы).
- Цилиндр: V= π r2h , где r – радиус круглого основания, h – высота цилиндра, π – константа, составляющая примерно 3,14.
- Пирамида: V= (1/3) b x h, где b – площадь основания пирамиды (l x w), h – высота пирамиды.
-
3
Произведите необходимые измерения. Они будут зависеть от того, с телом какого вида вы имеете дело. Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.
- Радиус круга равен половине его диаметра. Измерьте диаметр, приложив к середине круга линейку, после чего поделите полученный результат на 2.
- Радиус сферы измерить немного сложнее, однако и это не составит труда, если вы воспользуетесь методами, подробно изложенными в статье Как найти радиус шара.
- Длину, ширину и высоту тела можно определить, приложив к нему линейку в соответствующих местах и записав результаты измерений.
-
4
Вычислите объем. Выяснив форму тела, выберите подходящую формулу и измерьте входящие в нее величины. Подставьте в формулу измеренные значения и выполните необходимые математические действия. В результате вы получите объем тела.
- Помните о том, что ответ должен выражаться в кубических единицах независимо от того, какой системой единиц вы пользуетесь (метрической либо другой). После полученной величины обязательно напишите единицы, в которых она измеряется.
Реклама
-
1
Определите объем тела по количеству вытесняемой им воды. Тело может иметь неправильную форму, что затрудняет измерение его размеров и ведет к неточному определению объема. В этом случае прекрасно работает метод, заключающийся в определении объема воды, вытесняемой телом при полном погружении.[9]
- Данный метод можно применить и для нахождения объема тел правильной формы, чтобы избежать вычислений.
-
2
Наполните водой мерный цилиндр (мензурку). Это лабораторная емкость с метками на боковой поверхности, позволяющая измерять объем жидкостей. Выберите достаточно большой цилиндр, чтобы в него полностью поместился измеряемый объект. Необходимо наполнить цилиндр водой так, чтобы в нее можно было полностью погрузить объект, но при этом она не выливалась. Запишите начальный объем воды без измеряемого тела.
- Наблюдая первоначальный объем воды, наклонитесь так, чтобы ваши глаза находились на одном уровне с поверхностью жидкости, после чего запишите высоту, на которой расположено дно мениска. Мениск – это внешняя поверхность воды, которая искривляется при контакте с другими поверхностями (в нашем случае это стенки сосуда).[10]
- Наблюдая первоначальный объем воды, наклонитесь так, чтобы ваши глаза находились на одном уровне с поверхностью жидкости, после чего запишите высоту, на которой расположено дно мениска. Мениск – это внешняя поверхность воды, которая искривляется при контакте с другими поверхностями (в нашем случае это стенки сосуда).[10]
-
3
Аккуратно поместите в емкость измеряемое тело. Делайте это плавно, чтобы не уронить объект, поскольку в этом случае часть воды может выплеснуться из мерного цилиндра. Убедитесь в том, что тело полностью погрузилось в воду. Запишите новые показания уровня воды в емкости, вновь расположившись так, чтобы ваши глаза находились на одном уровне с мениском.
- Если при погружении тела часть воды выплеснулась, попробуйте повторить с самого начала, налив меньше воды или взяв больший мерный цилиндр.
-
4
Вычтите из окончательного уровня воды его первоначальное значение. Количество вытесненной предметом воды будет равняться его объему в кубических сантиметрах. Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.[11]
- Например, если сначала уровень воды был 35 мл, а после опускания в нее предмета поднялся до 65 мл, объем этого предмета составляет 65 – 35 = 30 мл, или 30 см3.
Реклама
-
1
Определите массу предмета. Масса объекта соответствует количеству материи, из которой он состоит.[12]
Массу находят путем прямого взвешивания на весах, она измеряется в граммах или килограммах.- Возьмите точные измерительные весы и поместите на них предмет. Запишите показания весов в свой блокнот.
- Массу тела можно определить и при помощи чашечных весов. Положив объект на одну чашу, на вторую поместите гирьки с известными массами так, чтобы обе чаши уравновесили друг друга, расположившись на одинаковой высоте. В этом случае искомая масса предмета будет равна сумме масс использованных гирек.
- Перед взвешиванием проследите, чтобы предмет не был влажным, иначе погрешность измерений возрастет.
-
2
Определите объем тела. Если предмет имеет правильную форму, для определения его объема используйте одну из формул, приведенных выше. Если форма тела неправильна, измерьте объем, погрузив его в воду, как описано выше.
-
3
Вычислите плотность. Согласно определению, плотность равна массе, деленной на объем. Таким образом, поделите измеренную массу на вычисленный объем. В результате вы получите плотность тела, измеренную в г/см3.
- Например, вычислим плотность предмета объемом 8 см3 и массой 24 г.
- плотность = масса / объем
- d = 24 г / 8 см3
- d = 3 г/см3
Реклама
Советы
- Нередко предметы состоят из нескольких частей, имеющих правильные геометрические формы. В этом случае разделите составляющие элементы на группы, относящиеся к той или иной правильной форме, найдите объем каждого элемента, а затем сложите их вместе, определив тем самым общий объем всего предмета.
- Можно определить объем какого-либо предмета как путем вычислений, так и погружением в воду, после чего сравнить полученные результаты.
Реклама
Предупреждения
- Будьте внимательны: прежде чем приступать к вычислениям, обязательно переведите все измеренные величины в метрическую систему (систему единиц СИ).
Реклама
Об этой статье
Эту страницу просматривали 43 264 раза.
Была ли эта статья полезной?
Калькулятор объема цилиндра
Рассчитайте онлайн объем любого цилиндрического объекта: трубы, бочки, банки.
Что известно
Размерность
Радиус основания
см
Диаметр основания
см
Площадь основания
см2
Высота
см
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🛢️ Когда требуется знать объем цилиндра?
Знание объема цилиндра может потребоваться в различных ситуациях, к примеру:
- Расчет объема бака или резервуара: если вы планируете хранить жидкость или газ в баке или резервуаре, то может быть важно знать его объем, чтобы знать, сколько материала вы можете в него поместить.
- Расчет объема емкости для транспортировки: если вы занимаетесь перевозкой жидкостей или газов, то может потребоваться знать объем емкости, чтобы убедиться, что вы можете перевезти нужное количество материала.
- Расчет объема цилиндрических труб: если вы занимаетесь установкой трубопроводов или работой с другими цилиндрическими объектами, то может быть полезно знать их объем, чтобы правильно рассчитать количество материала, необходимого для работы.
- Расчет объема бутылки или бочки: если вы хотите знать, сколько жидкости вы можете вместить в определенную бутылку или бочку, то калькулятор объема цилиндра может помочь рассчитать объем емкости.
- Определение объема цилиндрических объектов, используемых в декоративных целях, например, колонн, скульптур и других элементов архитектуры и дизайна.
Также умение рассчитывать объем цилиндра пригодится в строительстве, химии и фармацевтике, механике и технике, производстве, учебе и творчестве.
📏 Как рассчитывается объем цилиндра?
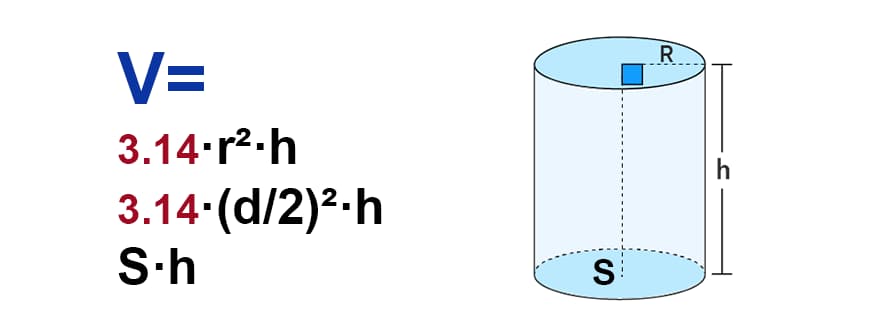
Объем цилиндра можно рассчитать по формуле:
V = πr²h
где V – объем цилиндра, r – радиус основания цилиндра, h – высота цилиндра, π (пи) – математическая константа, приблизительно равная 3,14.
Чтобы использовать эту формулу, необходимо знать значения радиуса основания и высоты цилиндра. Радиус основания – это расстояние от центра основания до края, высота цилиндра – это расстояние между основаниями цилиндра.
Например, если радиус основания цилиндра равен 5 см, а высота цилиндра составляет 10 см, то объем цилиндра можно рассчитать следующим образом:
V = 3,14 x 5² x 10 = 785 см3
Обратите внимание, что единицы измерения должны быть одинаковыми, чтобы получить правильный ответ. Если радиус основания и высота цилиндра измеряются в сантиметрах, то и объем цилиндра должен быть выражен в кубических сантиметрах.
🧮 Что такое калькулятор объема цилиндра?
Калькулятор объема цилиндра – это инструмент, который позволяет автоматически рассчитывать объем цилиндра по его размерам. Обычно калькулятор объема цилиндра предоставляет пользователю простую форму, где нужно ввести значение радиуса основания и высоты цилиндра, а затем нажать кнопку «Рассчитать». Калькулятор объема цилиндра может быть представлен в виде программы на компьютере или мобильном устройстве, а также в виде онлайн-сервиса на веб-сайте, как у нас.
Использование калькулятора объема цилиндра упрощает и ускоряет процесс расчета объема цилиндра, особенно если нужно рассчитать объем нескольких цилиндров или если значения радиуса и высоты цилиндра имеют сложные числовые значения. Калькулятор объема цилиндра может быть полезен в различных областях, включая науку, технику, строительство, производство, учебу и домашнее хозяйство.
📏 Как работает калькулятор объема цилиндра?
Калькулятор объема цилиндра работает на основе математической формулы для расчета объема цилиндра, рассмотренной выше.
Чтобы рассчитать объем цилиндра, пользователь должен ввести значения радиуса основания и высоты цилиндра в соответствующие поля калькулятора и нажать кнопку «Рассчитать». Калькулятор использует введенные значения, выполняет математическую операцию по формуле и выводит результат в соответствующем поле на экране.
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения (например, сантиметры или дюймы) и возможность рассчитать объем цилиндра, используя диаметр основания вместо радиуса.
🛢 Как использовать калькулятор объема цилиндра?
Для использования калькулятора объема цилиндра следуйте этим простым шагам:
- Откройте калькулятор объема цилиндра, который находится на компьютере, мобильном устройстве или на веб-сайте.
- Введите значение радиуса основания цилиндра в соответствующее поле калькулятора. Если вы используете калькулятор, который принимает во внимание диаметр, убедитесь, что вы выбрали правильную единицу измерения.
- Введите значение высоты цилиндра в соответствующее поле калькулятора. Убедитесь, что вы выбрали правильную единицу измерения.
- Нажмите кнопку «Рассчитать» или «Получить результат». Калькулятор выполнит расчеты и выведет объем цилиндра в соответствующем поле.
- Проверьте результаты и убедитесь, что все значения введены правильно и выбраны правильные единицы измерения.
- Если нужно рассчитать объем нескольких цилиндров, повторите шаги 2-5 для каждого цилиндра.
- Сохраните результаты или скопируйте их в буфер обмена, если нужно использовать их в другой программе или приложении.
В зависимости от функционала калькулятор может иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
В чем измеряется объем цилиндра?
Объем цилиндра измеряется в кубических единицах длины. Например, если размеры цилиндра измеряются в метрах, то его объем будет выражаться в кубических метрах (м³). Если размеры измеряются в сантиметрах, то объем будет выражаться в кубических сантиметрах (см³). Также можно использовать другие единицы измерения, такие как литры или галлоны, которые также выражают объем жидкости или газа, но они не являются кубическими единицами длины.
Несколько лайфхаков
Если вы хотите упростить расчет объема цилиндра, есть несколько лайфхаков, которые могут пригодиться:
- Используйте формулу площади основания цилиндра. Объем цилиндра можно вычислить, умножив площадь основания на высоту. Если вы знаете формулу площади основания цилиндра, то можете сначала вычислить ее, а затем умножить на высоту, чтобы найти объем.
- Используйте приближенное значение числа Пи. Число Пи является бесконечной десятичной дробью, но для большинства расчетов достаточно использовать его приближенное значение. Например, можно использовать значение 3,14 или 22/7 вместо точного значения числа Пи, которое равно примерно 3,14159265359.
- Используйте онлайн калькулятор. Наш онлайн калькулятор объема цилиндра поможет быстро выполнить расчеты за вас. Просто введите значения радиуса и высоты, и калькулятор автоматически вычислит объем.
- Используйте замены единиц измерения. Если вы хотите перевести объем из одной единицы измерения в другую, например, из кубических сантиметров в литры, можете также воспользоваться калькулятором на нашем сайте.
❓ Вопросы и ответы
Сейчас мы представим ответы на вопросы, которые часто возникают по данной теме.
Что такое цилиндр?
Цилиндр — это геометрическая фигура, которая имеет два плоских основания, обычно круглой формы, и боковую поверхность, которая состоит из параллельных прямых линий.
Как вычислить объем цилиндра?
Объем цилиндра можно вычислить, используя формулу:
V = πr²h
где V — объем цилиндра, π — число Пи (приблизительно равно 3.14), r — радиус основания цилиндра и h — высота цилиндра.
Можно ли использовать формулу объема цилиндра для вычисления объема других фигур?
Нет, формула объема цилиндра может использоваться только для вычисления объема цилиндра. Для других фигур существуют свои собственные формулы для расчета объема.
Как найти радиус или диаметр цилиндра, если они неизвестны?
Если известна площадь основания цилиндра, можно найти радиус, используя формулу:
r = √(A/π)
где A — площадь основания цилиндра.
Если известен объем цилиндра, можно найти радиус, используя формулу:
r = √(V/πh)
где V — объем цилиндра, h — высота цилиндра.
Диаметр можно найти, удваивая радиус.
Как найти объем трубы или канала?
Для трубы или канала формула для вычисления объема имеет немного другой вид:
V = πr²h
где V — объем, r — радиус, h — длина (высота) трубы или канала.
Например, если радиус трубы равен 10 см, а длина трубы составляет 2 м, то объем трубы будет:
V = 3.14 * 10² * 200 = 62,800 см³, что равно 62.8 литрам.
Как узнать, сколько литров вмещает бочка?
Чтобы узнать, сколько литров вмещает бочка, нужно знать ее объем. Если известны диаметр и высота бочки, то можно использовать формулу для объема цилиндра. Например, если диаметр бочки составляет 1 метр, а высота — 1,5 метра, то ее объем будет:
V = πr²h = 3.14 * (1/2)² * 1.5 = 1.18 кубических метров, что равно 1180 литрам. Таким образом, бочка вмещает 1180 литров жидкости.
Как узнать, сколько литров вмещает труба?
Для расчета объема трубы нужно знать ее длину и радиус. Если известны диаметр и длина трубы, то радиус можно найти, разделив диаметр на 2. Например, если диаметр трубы составляет 10 см, а длина трубы — 2 метра, то радиус будет 5 см. Тогда объем трубы можно найти, используя формулу:
V = πr²h = 3.14 * (5/100)² * 200 = 15.7 литров. Таким образом, труба вмещает 15.7 литров жидкости.
Какой тип калькулятора нужен для расчета объема цилиндра?
Для расчета объема цилиндра нужен специальный калькулятор, который может выполнить математические операции с использованием формулы для объема цилиндра.
Какие значения нужно ввести в калькулятор объема цилиндра?
Для расчета объема цилиндра необходимо ввести значение радиуса основания цилиндра и высоты цилиндра.
Какие единицы измерения могут использоваться при вводе значений в калькулятор объема цилиндра?
Единицы измерения, которые могут использоваться при вводе значений в калькулятор объема цилиндра, это сантиметры, метры, дюймы и т.д.
Какие дополнительные функции могут быть включены в калькулятор объема цилиндра?
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
Где можно найти калькулятор объема цилиндра?
Калькулятор объема цилиндра можно найти в Интернете на специализированных сайтах, в приложениях для мобильных устройств и на компьютерах, а также в других программных приложениях, связанных с инженерными и научными расчетами.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку.
И это не праздности ради, а дела для.
Цитирую запрос пользователя объем сегмента цилиндра (2):
Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности. Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре?
Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем 
Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним.
Объем жидкости в цилиндрической таре
Точность вычисления
Знаков после запятой: 2
Процентов от общего объема
Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. рисунок). Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. всегда сводим к случаю, изображенному на рисунке.
Формула объема всего цилиндра известна — площадь основания, помноженная на высоту.
А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника.
Площадь сектора находится как
, где альфа — это угол дуги в радианах.
Угол дуги нам неизвестен. Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника. Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом,
соответственно
и ответ нам Javascript даст как раз в радианах, то что нам нужно.
Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. Найдем его.
А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен
Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона — Расчет площади треугольника по формуле Герона.
где
Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника. Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.