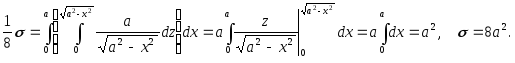Как найти объем области

Вычисление объёмов

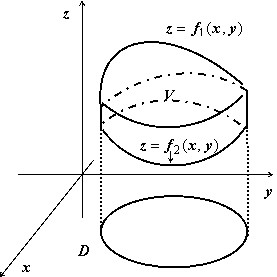
Объём тела, ограниченного сверху и снизу поверхностями $mathbf { textit { z } } =mathbf { textit { f } } _ { 1 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $mathbf { textit { z } } =mathbf { textit { f } } _ { 2 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $(x,y)in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $mathbf { textit { Oz } } $, равен $v=iintlimits_D { left[ { f_1 (x,y)-f_2 (x,y) }right]dxdy } $; эта формула очевидно следует из геометрического смысла двойного интеграла.

Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.

Пример 1

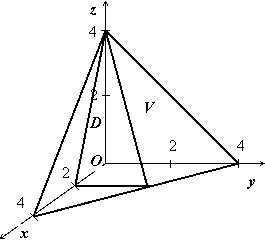
Найти объём тела $V:left[{ begin{array} { l } y=0,;z=0, \ x+y+z=4,; \ 2x+z=4. \ end{array} }right.$

Решение:

Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $mathbf { textit { Oxz } } $:

$V:left[{ begin{array} { l } (x,z)in D, \ 0leqslant yleqslant 4-x-z. \ end{array} }right.$

Область $mathbf { textit { D } } $ — треугольник, ограниченный прямыми $mathbf { textit { x } } $ = 0, $mathbf { textit { z } } $ = 0, 2$mathbf { textit { x } } +mathbf { textit { z } } $ = 4, поэтому

$V=iintlimits_D { (4-x-z)dxdz } =intlimits_0^2 { dxintlimits_0^ { 4-2x } { (4-x-z)dz } } = intlimits_0^2 { dxleft. { left( { 4z-xz-z^2/2 }right) }right|_0^ { 4-2x } } = intlimits_0^2 { left[ { 16-8x-4x+2x^2-(4-2x)^2/2 }right]dx } = \ = intlimits_0^2 { left( { 8-4x }right)dx } = left. { left( { 8x-2x^2 }right) }right|_0^2 =16-8=8$

Пример 2

Найти объём области, ограниченной поверхностями $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { R } } ^ { 2 } $,

$(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$.

Решение:

Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $mathbf { textit { Oz } } $ { в уравнении нет $mathbf { textit { z } } $ в явной форме). Построить в плоскости $mathbf { textit { Oxy } } $ кривую шестого порядка, заданную уравнением $(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей { чётные степени } и точка $mathbf { textit { О } } (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(cos ^4varphi +sin ^4varphi );r^2=R^2((cos ^2varphi +sin ^2varphi )^2-2cos ^2varphi sin ^2varphi )=R^2(1-frac { sin ^22varphi } { 2 } )=$

$=R^2(1-frac { 1-cos 4varphi } { 4 } )=R^2frac { 3+cos 4varphi } { 4 } ;r=Rfrac { sqrt { 3+cos 4varphi } } { 2 } .$ Эту кривую построить уже можно. $r(varphi )$ максимально, когда $cos 4varphi =1;(varphi =0,frac { 2pi } { 4 } =frac { pi } { 2 } ,frac { 4pi } { 4 } =pi ,frac { 6pi } { 4 } =frac { 3pi } { 2 } )$, минимально, когда

$cos 4varphi =-1;(varphi =frac { pi } { 4 } ,frac { 3pi } { 4 } ,frac { 5pi } { 4 } ,frac { 7pi } { 4 } ),$ и гладко меняется между этими пределами { точка $mathbf { textit { О } } (0,0)$ не принадлежит этой кривой, где мы её потеряли? } .

Пользуясь симметрией, получаем $ V=16iintlimits_D { sqrt { R^2-x^2-y^2 } dxdy= } 16iintlimits_D { sqrt { R^2-r^2 } rdrdvarphi = } =16intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } rdr } = $ $ =-8intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } d(R^2-r^2) } =-8frac { 2 } { 3 } intlimits_0^ { frac { pi } { 4 } } { left. { (R^2-r^2)^ { frac { 3 } { 2 } } }right|_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } dvarphi } =-frac { 16 } { 3 } R^3intlimits_0^ { frac { pi } { 4 } } { left. { left[ { left( { frac { sin ^22varphi } { 2 } }right)^ { frac { 3 } { 2 } } -1 }right] }right|dvarphi } = $ и т.д.

Пример 3

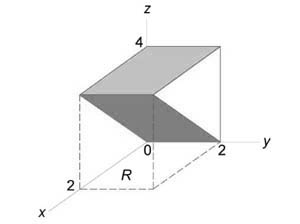
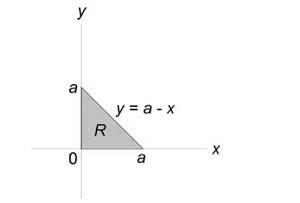
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)

Решение:

Данное тело показано на рисунке.

Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ { V = iintlimits_R { left[ { left( { 4 — x }right) — x }right]dxdy } } = { intlimits_0^2 { left[ { intlimits_0^2 { left( { 4 — 2x }right)dy } }right]dx } } = { intlimits_0^2 { left[ { left. { left( { 4y — 2xy }right) }right|_ { y = 0 } ^2 }right]dx } } = { intlimits_0^2 { left( { 8 — 4x }right)dx } } = { left. { left( { 8x — 2 { x^2 } }right) }right|_0^2 } = { 16 — 8 = 8. } $

Пример 4

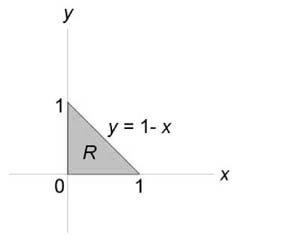
Описать тело, объем которого определяется интегралом (V = intlimits_0^1 { dx } intlimits_0^ { 1 — x } { left( { { x^2 } + { y^2 } }right)dy } .)

Решение:

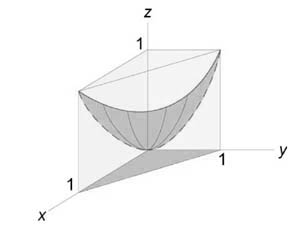
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = { x^2 } + { y^2 } .) Объем тела равен $ { V = intlimits_0^1 { dx } intlimits_0^ { 1 — x } { left( { { x^2 } + { y^2 } }right)dy } } = { intlimits_0^1 { left[ { left. { left( { { x^2 } y + frac { { { y^3 } } } { 3 } }right) }right|_ { y = 0 } ^ { 1 — x } }right]dx } } = { intlimits_0^1 { left[ { { x^2 } left( { 1 — x }right) + frac { { { { left( { 1 — x }right) } ^3 } } } { 3 } }right]dx } } = \ = { intlimits_0^1 { left( { { x^2 } — { x^3 } + frac { { 1 — 3x + 3 { x^2 } — { x^3 } } } { 3 } }right)dx } } = { intlimits_0^1 { left( { 2 { x^2 } — frac { { 4 { x^3 } } } { 3 } — x + frac { 1 } { 3 } }right)dx } } = { left. { left( { frac { { 2 { x^3 } } } { 3 } — frac { 4 } { 3 } cdot frac { { { x^4 } } } { 4 } — frac { { { x^2 } } } { 2 } + frac { x } { 3 } }right) }right|_0^1 } = { frac { 2 } { 3 } — frac { 1 } { 3 } — frac { 1 } { 2 } + frac { 1 } { 3 } = frac { 1 } { 6 } . } $

Пример 5

Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)

Решение:

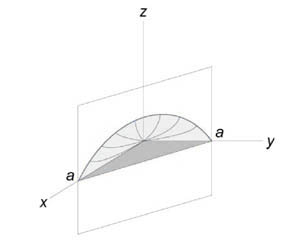
Данное тело лежит над треугольником (R) в плоскости (Oxy) ниже поверхности (z = xy.) Объем тела равен $ { V = iintlimits_R { xydxdy } } = { intlimits_0^a { left[ { intlimits_0^ { a — x } { xydy } }right]dx } } = { intlimits_0^a { left[ { left. { left( { frac { { x { y^2 } } } { 2 } }right) }right|_ { y = 0 } ^ { a — x } }right]dx } } = { frac { 1 } { 2 } intlimits_0^a { x { { left( { a — x }right) } ^2 } dx } } = { frac { 1 } { 2 } intlimits_0^a { xleft( { { a^2 } — 2ax + { x^2 } }right)dx } } = \ = { frac { 1 } { 2 } intlimits_0^a { left( { { a^2 } x — 2a { x^2 } + { x^3 } }right)dx } } = { frac { 1 } { 2 } left. { left( { { a^2 } cdot frac { { { x^2 } } } { 2 } — 2a cdot frac { { { x^3 } } } { 3 } + frac { { { x^4 } } } { 4 } }right) }right|_0^a } = { frac { 1 } { 2 } left( { frac { { { a^2 } } } { 2 } — frac { { 2 { a^4 } } } { 3 } + frac { { { a^4 } } } { 4 } }right) } = { frac { { { a^4 } } } { { 24 } } . } $

Пример 6

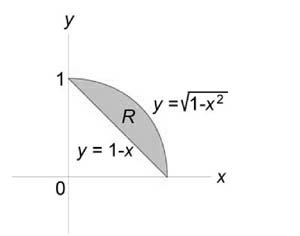
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( { x^2 } + { y^2 } = 1,) (z = 1 — x.)

Решение:

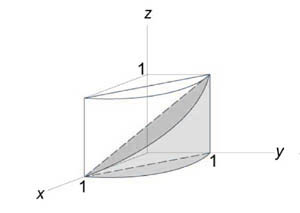
Как видно из рисунков, в области интегрирования (R) при (0 le x le 1) значения (y) изменяются от (1 — x) до (sqrt { 1 — { x^2 } } .)

Сверху тело ограничено плоскостью (z = 1 — x.) Следовательно, объем данного тела равен $ { V = iintlimits_R { left( { 1 — x }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_ { 1 — x } ^ { sqrt { 1 — { x^2 } } } { left( { 1 — x }right)dy } }right]dx } } = { intlimits_0^1 { left[ { left( { 1 — x }right)left. y right|_ { 1 — x } ^ { sqrt { 1 — { x^2 } } } }right]dx } } = { intlimits_0^1 { left( { 1 — x }right)left( { sqrt { 1 — { x^2 } } — 1 + x }right)dx } } = \ = { intlimits_0^1 { left( { sqrt { 1 — { x^2 } } — xsqrt { 1 — { x^2 } } — 1 + 2x — { x^2 } }right)dx } } = { intlimits_0^1 { sqrt { 1 — { x^2 } } dx } } — { intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } } — { intlimits_0^1 { left( { 1 + 2x — { x^2 } }right)dx } . } $

Вычислим полученные три интеграла отдельно. $ { I_1 } = intlimits_0^1 { sqrt { 1 — { x^2 } } dx } .$ Сделаем замену: (x = sin t.) Тогда (dx = cos tdt.) Видно, что (t = 0) при (x = 0) и (t = largefrac { pi } { 2 } normalsize) при (x = 1.) Следовательно, $ { { I_1 } = intlimits_0^1 { sqrt { 1 — { x^2 } } dx } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { sqrt { 1 — { { sin } ^2 } t } cos tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { cos } ^2 } tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { frac { { 1 + cos 2t } } { 2 } dt } } = { frac { 1 } { 2 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { left( { 1 + cos 2t }right)dt } } = { frac { 1 } { 2 } left. { left( { t + frac { { sin 2t } } { 2 } }right) }right|_0^ { largefrac { pi } { 2 } normalsize } } = { frac { 1 } { 2 } left( { frac { pi } { 2 } + frac { { sin pi } } { 2 } }right) = frac { pi } { 4 } . } $ { Сравните с площадью сектора единичного круга в первом квадранте).

Вычислим второй интеграл ( { I_2 } = intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } ,) используя замену переменной. Полагаем (1 — { x^2 } = w.) Тогда (-2xdx = dw) или (xdx = largefrac { { — dw } } { 2 } normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ { { I_2 } = intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } } = { intlimits_1^0 { sqrt w left( { — frac { { dw } } { 2 } }right) } } = { — frac { 1 } { 2 } intlimits_1^0 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { { w^ { largefrac { 1 } { 2 } normalsize } } dw } } = { frac { 1 } { 2 } left. { left( { frac { { 2 { w^ { largefrac { 3 } { 2 } normalsize } } } } { 3 } }right) }right|_0^1 = frac { 1 } { 3 } . } $ Наконец, вычислим третий интеграл. $require { cancel } { { I_3 } = intlimits_0^1 { left( { 1 — 2x + { x^2 } }right)dx } } = { left. { left( { x — { x^2 } + frac { { { x^3 } } } { 3 } }right) }right|_0^1 } = { cancel { 1 } — cancel { 1 } + frac { 1 } { 3 } = frac { 1 } { 3 } . } $ Таким образом, объем тела равен $ { V = { I_1 } — { I_2 } — { I_3 } } = { frac { pi } { 4 } — frac { 1 } { 3 } — frac { 1 } { 3 } = frac { pi } { 4 } — frac { 2 } { 3 } approx 0,12. } $

Пример 7

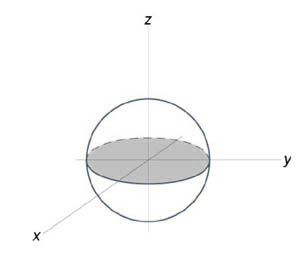
Вычислить объем единичного шара.

Решение:

Уравнение сферы радиусом (1) имеет вид ( { x^2 } + { y^2 } + { z^2 } = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = sqrt { 1 — left( { { x^2 } + { y^2 } }right) } .$ Преобразуя это уравнение в полярные координаты, получаем $zleft( { r,theta }right) = sqrt { 1 — { r^2 } } .$ В полярных координатах область интегрирования (R) описывается множеством (R = left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].) Следовательно, объем верхнего полушара выражается формулой $ { { V_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 — { r^2 } } rdrdtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } } = { 2pi intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } . } $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — { r^2 } = t.) Тогда (-2rdr = dt) или (rdr = — largefrac { { dt } } { 2 } normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ { { V_ { largefrac { 1 } { 2 } normalsize } } = 2pi intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } } = { 2pi intlimits_1^0 { sqrt t left( { — frac { { dt } } { 2 } }right) } } = { — pi intlimits_1^0 { sqrt t dt } } = { pi intlimits_0^1 { { t^ { largefrac { 1 } { 2 } normalsize } } dt } } = { pi left. { left( { frac { { { t^ { largefrac { 3 } { 2 } normalsize } } } } { { frac { 3 } { 2 } } } }right) }right|_0^1 } = { frac { { 2pi } } { 3 } . } $ Таким образом, объем единичного шара равен $V = 2 { V_ { largefrac { 1 } { 2 } normalsize } } = frac { { 4pi } } { 3 } .$

Пример 8

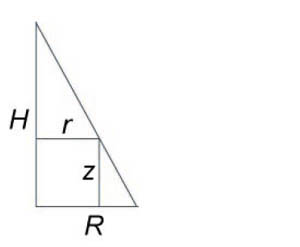
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).

Решение:

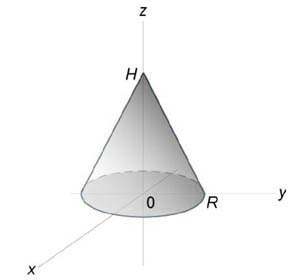
Сначала получим уравнение поверхности конуса. Используя подобные треугольники, можно записать $ { frac { r } { R } = frac { { H — z } } { H } , } ;; { text { где } ;;r = sqrt { { x^2 } + { y^2 } } . } $ Следовательно, $ { H — z = frac { { Hr } } { R } } ;; { text { или } ;;zleft( { x,y }right) } = { H — frac { { Hr } } { R } } = { frac { H } { R } left( { R — r }right) } = { frac { H } { R } left( { R — sqrt { { x^2 } + { y^2 } } }right). } $ Тогда объем конуса равен $ { V = iintlimits_R { zleft( { x,y }right)dxdy } } = { iintlimits_R { frac { H } { R } left( { R — sqrt { { x^2 } + { y^2 } } }right)dxdy } } = { frac { H } { R } iintlimits_R { left( { R — r }right)rdrdtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { left[ { intlimits_0^R { left( { R — r }right)drd } }right]dtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { dtheta } intlimits_0^R { left( { Rr — { r^2 } }right)dr } } = { frac { { 2pi H } } { R } intlimits_0^R { left( { Rr — { r^2 } }right)dr } } = \ = { frac { { 2pi H } } { R } left. { left( { frac { { R { r^2 } } } { 2 } — frac { { { r^3 } } } { 3 } }right) }right|_ { r = 0 } ^R } = { frac { { 2pi H } } { R } left( { frac { { { R^3 } } } { 2 } — frac { { { R^3 } } } { 3 } }right) } = { frac { { 2pi H } } { R } cdot frac { { { R^3 } } } { 6 } = frac { { pi { R^2 } H } } { 3 } . } $

(схема 42)

1. Вычисление объема тела

Пусть функция f(x;y) ≥ 0.
Рассмотрим тело, ограниченное    
поверхностью z = f(x;y), плоскостью z=0 и цилиндрической поверхно­стью, образующие которой
па­раллельны оси 0z, а направ­ляющей
служит граница об­ласти D. Как было показано 
выше, согласно формуле (6.3) объем данного тела равен     

                                                                                                                                                   (6.18)

Пример 6.9. Вычислить объём тела, ограниченного параболоидом z= x²+y²+1,
плоскостью x+y
–3=0 и координатными плоскостями.

Решение. Основанием тела служит треугольник ОАВ. Область D в данном
случае определяется неравенствами:

. Заметим, что тело, заданное по условию, аналогично телу,
изображенному на рисунке 6.6 (пример 6.5). Следовательно, используя формулу
(6.18), получим:

2.
Вычисление площади плоской фигуры

Если положить в формуле (6.18) f(x,y)=1, то цилиндрическое тело «превратится»  в  прямой  цилиндр  с  высотой  h=1. Объем такого цилиндра,

как
известно, численно равен площади S основания D. Получаем формулу для вычисления площади  S области D:

                                                                                                                                                                                       (6.19)

или,  в полярных
координатах,

                                                                                                                                                                    (6.20)

Пример
6.10. Вычислить площадь фигуры,
ограниченной прямой y=2x+1 и параболой y=x²+1.

Решение. Решая совместно систему

, находим точки пересечения этих линий: A(0;1)
и  B(2;5).

Применяя формулу (6.19), будем иметь:

Пример 6.11. Вычислить площадь фигуры ограниченной лемнискатой  

 (рис. 6.9).

Решение. Переходим к полярной системе координат, полагая x=r cosφ  и y=r sinφ; тогда получаем

 . В силу симметрии кривой относительно координатных осей
можно вычислить сначала ту часть, которая расположена  первой четверти. В этом случае угол φ будет изменяться от 0 до, а радиус r от 0 до . По формуле (6.20) получим:

3.
Вычисление массы плоской фигуры (пластины)

Масса плоской пластинки D с
переменной плотностью γ=γ(x,y) находится
по формуле

.                                                                                                                                                                         (6.21)

4.
Определение статических моментов и координат центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей 0x и 0y могут быть вычислены по формулам

        ;                                                                                                   (6.22)

а
координаты центра масс фигуры – по формулам

    .                                                                                                                                                       (6.23)

Статические моменты широко используются в
сопротивлении материалов и других технических науках.

5.
Определение моментов  инерции плоской
фигуры

Моментом инерции материальной точки массы m относительно оси l называется произведение массы m  на
квадрат расстояния d точки до оси, т.е. . Моменты инерции плоской фигуры относительно 0x и 0y могут быть
вычислены по формулам:

                                                                                                  (6.24)

Момент
инерции фигуры относительно начала координат – по формуле

.                                                                                                                                                                      (6.25)

Пример
6.12. Найти массу, статические
моменты и координаты центра тяжести фигуры, лежащей в первой четверти,
ограниченной эллипсом  и координатными осями.
Поверхностная плотность в каждой точке фигуры пропорциональна произведению
координат точки.

Решение. По
формуле (6.21) находим массу пластины. По условию, γ=γ(x,y)=k∙xy, где k –
коэффициент пропорциональности.Тогда

.

Находим
статические моменты пластинки по формулам (6.22):

Находим
координаты центра тяжести пластинки, используя формулы (6.23):

  6. Поверхностный интеграл I рода

Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве Оxyz в точках некоторой поверхности площади S определена непрерывная функция u = f (x;y;z). Разобьем поверхность на конечное число n частей S_i, площади которых равны ∆S_i, а диаметры – d_i, . Выберем в каждой части S_i  произвольную точку M_i(x_i;y_i;z_i)
и составим сумму произведений вида

.                                                                                                                                                                   (6.26)

Она
называется интегральной суммой для функции f(x;y;z) по поверхности S. Если при интегральная
сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек M_i(x_i;y_i;z_i), то он называется поверхностным интегралом I рода от
функции f(x;y;z) по поверхности S и обозначается . Следовательно, 

 .                                                                                                                                (6.27)

Теорема 6.3
(о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная
плоскость, которая непрерывно меняется с перемещением точки по поверхности), а
функция f(x;y;z) непрерывна на этой поверхности, то поверхностный
интеграл существует

Формула                                                                                            (6.28)

выражает интеграл по поверхности
S
через двойной интеграл по проекции S на плоскость x0y. Отметим, что если поверхность S задана
уравнением вида  y=y(x;z) или x=x(y;z), то аналогично получим:

 и                                                                                                       (6.29)

,                                                                                                          (6.30)

где
D₁ и D₂ –
проекции  поверхности S на
координатные плоскости xОz и   yОz
соответственно.

Пример 6.13. Вычислить , где S – часть цилиндрической поверхности , отсеченной плоскостями z = 0 и z = 3.

Решение. Из уравнения заданной
цилиндрической поверхности выразим  и учтём, что
при x = 0 в плоскости xОy: . Так как частные производные равны , то согласно формуле (6.30),
имеем 

         Приведем некоторые примеры применения
поверхностного интеграла I рода.

6.1. Площадь
поверхности

Если поверхность S задана уравнением z = f(x;y), a ее проекция на
плоскость x0y есть область D, в которой  z = f(x;y), z_x(x;y) и z_y(x;y) –
непрерывные  функции, то ее площадь S
вычисляется по формуле:

        .                                                                                                                                                     (6.31)

Пример 6.14. Вычислить площадь части плоскости x+y+z=4,
вырезаемой цилиндром x²+y² =4 (рис. 6.10).

Решение. Применим формулу (6.31). Область интегрирования D есть круг
радиуса r=2. Находим частные производные и  заданной
функции z=4 – x – y:

 . Тогда .

Чтобы вычислить этот интеграл, введём полярные
координаты. Область D определяется: . Следовательно,

 Кроме того, поверхностный интеграл применяют для
вычисления массы, координат центра масс, моментов инерции материальных
поверхностей с известной поверхностной плотностью распределения массы  γ=γ(x;y;z). Все эти величины
определяются одним и тем же способом:

– данную область разбивают на конечное число мелких частей;

– делают для каждой такой части  предположения, упрощающие задачу;

– находят приближенное значение  искомой величины;

– переходят к пределу при неограниченном измельчении разбиения
области.

Проиллюстрируем описанный способ на примере
определения массы материальной поверхности.

6.2. Масса
поверхности

Пусть плотность распределения массы материальной
поверхности есть γ=γ(x;y;z). Для нахождения
массы поверхности:

1.     Разбиваем поверхность S на n частей S_i, , площадь которых обозначим ∆S_i.

2.     Выберем произвольную точку M_i(x_i;y_i;z_i) в каждой области S_i. Предполагаем, что 
в переделах области  S_i
плотность постоянна  и  равна её

значению  в
точке M_i.

3.     Масса m_i области  S_i  мало отличается от
массы γ(x_i;y_i;z_i)∙∆S_i   однородной области с постоянной полностью γ= γ(x_i;y_i;z_i).

4.     Суммируя  m_i
по всей области, получаем:.

5.     За точное значение массы материальной поверхности S
принимается предел, к которому стремится полученное приближенное значение при
стремлении к нулю диаметров областей S_i, то есть

 .                                                                                                               (6.32)

6.3. Моменты
и центр тяжести поверхности. Статические
моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по
соответствующим формулам:

Пример 6.15.
Вычислить координаты центра тяжести
однородной поверхности параболоида z=x²+y², ограниченной плоскостью z=1.

Решение. Вершина заданного параболоида совпадает с началом
координат. Так как поверхность однородная (постоянная плотность массы), то,
основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен
на оси 0z. Тогда x_c=0, y_c=0
и по формуле (6.36)  аппликата. Пересечем параболоид поверхностью z=1,
спроектируем линию пересечения на плоскость x0y – получим окружность x²+y²=1 в
качестве области D. Вычислим элемент поверхности параболоида z=x²+y² по
формуле (6.31), учитывая, что:

.

Аналогично, переходя к полярным координатам на
плоскости x0y, получим:

.

Таким образом,, то есть центр тяжести заданного параболоида, ограниченного плоскостью z=1, находится в точке (0;0;1) и совпадает с точкой
пересечения поверхности с плоскостью

а) Объём.

Как мы знаем, объем
V
тела, ограничен­ного поверхностью
,
где
—
неотрицательная функ­ция, плоскостьюи цилиндрической поверхностью,
направ­ляющей для которой служит
граница областиD,
а образующие параллельны оси Oz,
равен двойному интегралу от функции
по областиD
:

Пример 1. Вычислить
объем тела, ограниченного поверхностями
x=0,
у=0, х+у+z=1,
z=0
(рис. 17).

Рис.17
Рис.18

Решение.
D
— заштрихованная на рис. 17 треугольная
область в плоскости Оху,
ограниченная прямыми x=0,
у=0, x+y=1.
Расставляя пределы в двойном интеграле,
вычислим объем:

Итак,
куб. единиц.

Замечание 1.
Если тело, объем которого ищется,
ограни­чено сверху поверхностью
а снизу—поверхностью,
причем проекцией обеих поверхностей
на пло­скостьОху
является область D,
то объем V
этого тела равен разности объемов двух
«цилиндрических» тел; первое из этих
цилиндрических тел имеет нижним
основанием область D,
а верх­ним — поверхность
второе тело имеет нижним осно­ванием
также областьD,
а верхним — поверхность
(рис.18).

Поэтому объём V
равен разности двух двойных интегралов
:

или

(1)

Легко, далее,
доказать, что формула (1) верна не только
в том случае, когда
инеотрицательны, но и тогда, когдаи—
любые непрерывные функции, удовлетворяющие
соотношению

Замечание 2.
Если в области D
функция
меняет
знак, то разбиваем область на две части:
1) областьD₁
где
2) областьD₂
,где
.
Предположим, что областиD₁
и D₂
таковы, что двойные интегралы по этим
обла­стям существуют. Тогда интеграл
по области D₁
будет положи­телен и будет равен
объему тела, лежащего выше плоскости
Оху. Интеграл
по D₂
будет отрицателен и по абсолютной
величине равен объему тела, лежащего
ниже плоскости Оху,
Следовательно, интеграл по D
будет выражать раз­ность соответствующих
объемов.

б) Вычисление
площади плоской области.

Если мы со­ставим
интегральную сумму для функции
по областиD,
то эта сумма будет равна площа­ди S,

при любом способе
разбиения. Пере­ходя к пределу в правой
части равен­ства, получим

Если область D
правильная , то площадь выразится
двукратным интегралом

Производя
интегрирование в скобках, имеем,
очевидно,

Пример 2. Вычислить
площадь области, ограниченной кривыми

Рис.19

Решение. Определим
точки пересечения данных кривых
(Рис.19). В точке пересечения ординаты
равны, т.е.
,
отсюдаМы
получили две точки пересечения

Следовательно,
искомая площадь

5. Вычисление площади поверхности.

Пусть требуется
вычислить площадь поверхности,
ограниченной линией Г (рис.20); поверхность
задана уравнением
где функциянепрерывна и имеет непрерывные частные
производные. Обозначим проекцию линии
Г на плоскостьOxy
через L.
Область на плоскости Oxy,
ограниченную линией L,
обозначим D.

Разобьём произвольным
образом область D
на n
элементарных площадок
В
каждой площадкевозьмём точкуТочкеP_i
будет соответствовать на поверхности
точка
Через точкуM_i
проведём касательную плоскость к
поверхности. Уравнение её примет вид

(1)

На этой плоскости
выделим такую пло­щадку
,
которая проектируется на плоскостьОху
в виде площадки
.
Рассмотрим сумму всех площадок

Предел
этой суммы, когда наибольший из диаметров
пло­щадок—
стремится к нулю, мы будем называтьплощадью
по­верхности,
т. е. по определению положим

(2)

Займемся теперь
вычислением площади поверхности.
Обозна­чим через

угол между
касательной плоскостью и плоскостью
Оху.

Рис.20
Рис.21

На основании
известной формулы аналитической
геометрии можно написать (рис.21)

или

(3)

Угол
есть в то же время угол между осьюOz
и перпендикуляром к плоскости (1). Поэтому
на основании уравнения (1) и формулы
аналитической геометрии имеем

Следовательно,

Подставляя это
выражение в формулу (2), получим

Так как предел
интегральной суммы, стоящей в правой
части последнего равенства, по определению
представляет собой двойной интеграл
то окончательно получаем

(4)

Это и есть формула,
по которой вычисляется площадь поверхности

Если уравнение
поверхности дано в виде
или в видето соответствующие формулы для вычисления
поверхности имеют вид

(3^’)

(3^’’)

где D^’
и D^’’
— области на плоскостях Oyz
и Oxz,
в которые проектируется данная
поверхность.

а) Примеры.

Пример 1. Вычислить
поверхность
сферы

Решение. Вычислим
поверхность верхней половины сферы
(рис.22). В этом случае

Следовательно,
подынтегральная функция примет вид

Область интегрирования
определяется условием
.
Таким образом, на основании формулы (4)
будем иметь

Для вычисления
полученного двойного интеграла перейдём
к полярным координатам. В полярных
координатах граница области интегрирования
определяется уравнением
Следовательно,

Пример2. Найти
площадь той части поверхности цилиндра
которая вырезается цилиндром

Рис.22
Рис.23

Решение. На рис.23
изображена
часть искомой поверхности. Уравнение
поверхности имеет вид;
поэтому

Область интегрирования
представляет собой четверть круга, т.е.
определяется условиями

Следовательно,

Список использованной
литературы.

1. А.Ф. Бермант ,И.Г.
   Араманович

Краткий курс
математического анализа для втузов:
Учебное пособие для втузов: — М.: Наука,
Главная редакция физико-математической
литературы , 1971 г.,736с.

1. Н.С. Пискунов

Дифференциальное
и интегральное исчисления для втузов,
Том 2:

Учебное пособие
для втузов.-13-е изд. -М. :Наука, Главная
редакция физико-математической
литературы, 1985.-560с.

1. В.С. Шипачёв

Высшая
математика: Учебное пособие для втузов:
— М: Наука,

Главная редакция
физико-математической литературы.

Соседние файлы в предмете Алгебра и геометрия

• #
• #
• #

Содержание:

1. Двойной интеграл
2. Двойной интеграл в прямоугольных декартовых координатах
3. Двойной интеграл в полярных координатах
4. Двойной интеграл в декартовых координатах. Определение, теорема существования
5. Геометрический смысл двойного интеграла
6. Свойства двойного интеграла
7. Вычисление двойного интеграла в декартовых координатах
8. Двойной интеграл в полярных координатах
9. Вычисление площади плоской фигуры с помощью двойного интеграла
10. Вычисление объема тела с помощью двойного интеграла

Двойной интеграл

В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл

На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным интегралом.

Задача.

Найти объем тела, ограниченного сверху непрерывной поверхностью снизу конечной замкнутой областью плоскости и с боков прямой цилиндрической поверхностью, построенной на границе области и имеющей образующие, перпендикулярные плоскости (рис. 245).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Тело указанного вида для краткости называется цилиндроидом. В частном случае, когда верхнее основание цилиндроида есть плоскость, параллельная нижнему основанию его, то цилиндроид называется цилиндром.

Примером цилиндра служит круговой цилиндр, рассматриваемый в средней школе.

Обобщая рассуждение, обычно применяемое для нахождения объема кругового цилиндра, нетрудно доказать, что объем цилиндра с площадью основания и высотой равен

Для вычисления объема данного цилиндроида разобьем основание его на конечное число элементарных ячеек (вообще говоря, криволинейных). В каждой из этих ячеек выберем точку и построим прямой цилиндрический столбик с основанием и высотой равной аппликате поверхности в выбранной точке.

Объем такого столбика на основании формулы объема цилиндра, очевидно, равен

где — площадь соответствующей ячейки. Сумма объемов этих цилиндрических столбиков представляет собой объем ступенчатого тела, приближенно заменяющего данное криволинейное тело, причем аппроксимация является, вообще говоря, тем более точной, чем меньше диаметры ячеекПоэтому объем нашего цилиндроида приближенно выразится суммой

Формула (2) дает возможность найти объем с любой степенью точности, если число ячеек достаточно велико и линейные размеры их весьма малы. Обозначим через диаметр ячейки , т. е. наибольший линейный размер ее. Точнее говоря, под диаметром ограниченной замкнутой (т. е. с присоединенной границей) фигуры (дуги, площадки и т. п.) понимается длина наибольшей ее хорды где (рис. 246)2)

Из данного определения следует, что фигура имеющая диаметр целиком помещается внутри круга радиуса описанного из любой ее точки как из центра. Поэтому если то фигура «стягивается в точку». Аналогично определяется диаметр пространственного тела.

Пусть — наибольший из диаметров ячеек Предполагая, что в формуле (2) число ячеек неограниченно возрастает причем диаметр наибольшей из них становится сколь угодно малым в пределе получаем точную формулу для объема цилиндроида

Выражение, стоящее в правой части формулы (3), называется двойным интегралом от функции распространенным на область и обозначается следующим образом:

Поэтому для объема цилиндроида окончательно имеем

Обобщая конструкцию, примененную для вычисления объема цилиндроида, приходим к следующим определениям.

Возможно вам будут полезны данные страницы:

Опрелеление 1. Двумерной интегральной суммой (2) от данной функции распространенной на данную область называется сумма парных произведений площадей элементарных ячеек области назначения функции в выделенных точках этих ячеек (рис. 247).

Опрелеление 2. Двойным интегралом (4) от функции распространенным на данную область называется предел соответствующей двумерной интегральной суммы (2) при неограниченном возрастании числа элементарных ячеек и стремлении к нулю их наибольшего диаметра при условии, что этот предел существует и не зависит от способа дробления области на элементарные ячейки и выбора точек в них. В формуле (4) называется подынтегральной функцией, — областью интегрирования, а — элементом площади.

Справедлива следующая теорема:

ТЕОРЕМА. Если область с кусочно-гладкой границей ограничена и замкнута а функция непрерывна в области то двойной интеграл существует, т. е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа дробления области на элементарные ячейки и выбора точек в них.

В дальнейшем мы будем предполагать, что условия этой теоремы выполнены.

В формуле (6) нет необходимости указывать, что так как из очевидно, следует

Если то двойной интеграл (6) представляет собой объем прямого цилиндроида, построенного на области как на основании и ограниченного сверху поверхностью (геометрический смысл двойного интеграла).

Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем при решении задач мы будем использовать это обстоятельство, выбирая наиболее подходящие сетки. Весьма часто удобной оказывается прямоугольная сетка, образованная пересечением двух систем прямых, параллельных соответственно координатным осям и (рис. 248).

В этом случае элементарными ячейками являются прямоугольники со сторонами, равными и за исключением, возможно, ячеек, примыкающих к границе Чтобы подчеркнуть использование прямоугольной сетки, в обозначении интеграла (4) полагают (двумерный элемент площади в прямоугольных координатах), причем где и сумма (8) распространяется на все значения и для которых (можно показать, что непрямоугольные ячейки, примыкающие к кусочно-гладкой границе не влияют на значение предела (8)).

В следующих параграфах мы рассмотрим основные способы вычисления двойного интеграла.

Примеры с решением

Пример 1.

Найти

где — квадрат

Расставляя пределы интегрирования, будем иметь Геометрически представляет собой объем цилиндроида с квадратным нижним основанием, ограниченного сверху параболоидом вращения (рис. 254).

Пример 2.

Вычислить двойной интеграл

где — прямоугольник

Расставляя пределы интегрирования и разделяя переменные, будем иметь

Пример 3.

Вычислить где — треугольник с вершинами (рис. 255).

Область ограничена прямыми 2 и является стандартной как относительно оси так и оси

Для вертикали точка входа в область есть «точка выхода» — Таким образом, при фиксированном переменная для точек области меняется от до Поэтому, интегрируя в двойном интеграле (10) сначала по при а затем по согласно формуле (5) будем иметь

Аналогично, для горизонтали «точка входа» в область есть и «точка выхода» — Следовательно, при фиксированном переменная для точек области меняется от до Произведя в двойном интеграле (10) интегрирование сначала по при а затем по на основании формулы (9) получаем

Мы пришли, как и следовало ожидать, к тому же самому результату, причем второй способ вычисления оказался несколько более сложным.

Пример 4.

Изменить порядок интегрирования в повторном интеграле

Область интегрирования ограничена кривыми (рис. 256). Отсюда, изменяя роли осей координат, получаем

Следовательно,

Пример 5.

Расставить пределы интегрирования в двойном интеграле если область интегрирования есть круговое кольцо, ограниченное окружностями (рис. 257). Область не является стандартной. Для расстановки пределов интегрирования в интервале (13) разбиваем область на четыре стандартные относительно оси области как указано на рисунке. Используя уравнение окружностей

имеем

Аналогичная формула получится, если мы будем расставлять пределы интегрирования в другом порядке.

Двойной интеграл в прямоугольных декартовых координатах

Предположим для определенности, что область интегрирования представляет собой криволинейную трапецию (рис. 249)

где — однозначные непрерывные функции на отрезке Такую область будем называть стандартной относительно оси Заметим, что вертикаль, проходящая через точку оси при пересекает границу области только в двух точках («точка входа») и («точка выхода»).

Пусть — функция, непрерывная в области и = — ее двойной интеграл.

1) Предположим сначала, что в области Тогда двойной интеграл представляет собой объем цилиндроида (рис. 250), ограниченного снизу областью сверху поверхностью и с боков прямой цилиндрической поверхностью

Для вычисления объема применим метод сечений (гл. XV, § 5). А именно, пусть — площадь сечения цилиндроида плоскостью перпендикулярной оси в точке ее (рис. 250).

Тогда имеем

Но представляет собой площадь криволинейной трапеции, ограниченной снизу отрезком и сверху кривой

Поэтому

Можно доказать, что при наших условиях непрерывна при

Подставляя выражение (4) в формулу (3), получим окончательно

Таким образом, двойной интеграл равен соответствующему повторному интегралу (5), т. е. вычисление двойного интеграла сводится к двум квадратурам. Заметим, что при вычислении внутреннего интеграла в формуле (5) рассматривается как постоянная величина.

2) В случае знакопеременной функции например, если при и при двойной интеграл (2) равен алгебраической сумме объемов цилиндроидов, построенных соответственно на основаниях (pиc. 251),

т. е. Можно доказать, что формула (5) справедлива и в этом случае.

Отметим один важный случай: пусть — прямоугольник (рис. 252) и где — функция, непрерывная на и зависящая только от и — функция, непрерывная на и зависящая только от

В силу формулы (5) имеем

Но внутренний интеграл в формуле (7) есть постоянное число, поэтому его можно вынести за знак внешнего интеграла и мы получим

т. е. двойной интеграл (8) равен произведению двух однократных интегралов.

Замечание 1. Если область — стандартная относительно оси (рис. 253) то по аналогии с формулой (5) получаем

В частности, если область есть прямоугольник: a есть прямоугольник: a то имеем

Отсюда получаем

т е. если пределы интегрирования в повторном интеграле от непрерывной функции конечны и постоянны, то результат интегрирования не зависит от порядка интегрирования.

Двойной интеграл в полярных координатах

Пусть в двойном интеграле

при обычных предположениях мы желаем перейти к полярным координатам и , полагая

Область интегрирования разобьем на элементарные ячейки с помощью координатных линий (окружности) и = (лучи) (рис. 258).

Введем обозначения Так как окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями поэтому площадь каждой такой ячейки будет равна

Что касается ячеек неправильной формы, примыкающих к границе области интегрирования то эти ячейки не повлияют на значение двойного интеграла (ср. § 1, формула (8)) и мы их будем игнорировать.

В качестве точки для простоты выберем вершину ячейки с полярными координатами и Тогда декартовы координаты точки равны

и, следовательно,

Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, причем можно показать, что на значение этого предела не влияют добавки к слагаемым интегральной суммы, являющиеся бесконечно малыми высшего порядка малости. Поэтому, учитывая формулы (3) и (3′)» получаем

где — максимальный диаметр ячеек и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области

С другой стороны, величины и суть числа и их можно рассматривать как прямоугольные декартовы координаты некоторых точек плоскости Таким образом, сумма (4) является интегральной суммой для функции

соответствующая прямоугольной сетке с линейными элементами и Следовательно,

Выравнивая формулы (4) и (5), получаем окончательно

Выражение называется двумерным элементом площади в полярных координатах (ср. гл. XV, § 2).

Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты и заменить по формулам (2), а вместо элемента площади и подставить выражение (7).

Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования определяется неравенствами

где — однозначные непрерывные функции на отрезке (рис. 259) Тогда по аналогии с прямоугольными координатами (см. § 2) имеем

где

Пример 6.

Переходя к полярным координатам и вычислить двойной интеграл где первая четверть круга радиуса с центром в точке (рис. 260). Так как то , применяя формулу (6), получаем

Область определяется неравенствами Поэтому на основании формулы (8) имеем

Пример 7.

В интеграле

перейти к полярным координатам.

Область интегрирования здесь есть треугольник. ограниченный прямыми (рис. 261).

В полярных координатах уравнения этих прямых записываются следующим образом: и, следовательно, область определяется неравенствами Отсюда на основании формул (6) и (8), учитывая, что имеем

Двойной интеграл в декартовых координатах. Определение, теорема существования

Понятие «двойной интеграл» является естественным обобщением понятия «определенный интеграл» на случай функции двух переменных. Поэтому его определение принципиально не отличается от определения определенного интеграла и вводится аналогичным образом.

Пусть функция или где определена и непрерывна в замкнутой области плоскости то есть на множестве точек координатной плоскости, ограниченная сомкнуты линией (или линиями) , с учетом точек линии — пределы области.

Выполним такую (стандартную) процедуру:

1) разобьем область произвольным образом какими-либо линиями на n частичных областей с площадями (или просто — на плоскостей (рис. 26.1) и самую большую из расстояний между двумя точками границы плоскости назовем диаметром плоскости  а максимальный среди них — диаметром разбиения области
2) выберем на каждой из плоскостей произвольным образом по точке вычислим и найдем произведения
3) составим сумму всех таких произведений

которую назовем интегральной суммой для функции в области
4) вычислим границу (если она существует) интегральной суммы (26.1) при условии, что диаметр разбиения стремится к нулю при неограниченном росте то есть вместе с

Рис. 26.1

Конечна граница интегральной суммы когда диаметр разбиения стремится к нулю а называется двойным интегралом (от) функции по области и обозначается так:

 или 

где — знак (символ) двойного интеграла;

— область интегрирования;

— подынтегральная функция;

— подынтегральное выражение;

— переменные интегрирования;

— элемент площади, или дифференциал площади.

Следовательно, по определению

Теорема 26.1 (существование двойного интеграла). Если задана функция двух переменных непрерывна в рассматриваемой замкнутой области, то существует конечное предел интегральной суммы (то есть двойной интеграл), и она не зависит ни от способа разбиения области на плоскости, ни от выбора точек в них для составления интегральной суммы.

Теорему приводим без доказательства.
Функция для которой существует двойной интеграл по области называется интегрируемой на этой области.

Согласно теореме 26.1 разбиения области можно осуществлять простым из возможных способов (рис. 26.2), а именно: в декартовой системе координат — прямыми, параллельными координатным осям.

Рис. 26.2

В этом случае плоскость — прямоугольник со сторонами который образуется при переходе от точки к точке где Поэтому потому приросты независимых переменных  равны их дифференциалам:

Таким образом, можно записать:

Геометрический смысл двойного интеграла

В дальнейшем тело, ограниченное поверхностью плоскостью и цилиндрической поверхностью, образующая которой параллельна оси а направляющей предел области (рис. 26.3), коротко будем называть цилиндрическим телом для функции на (области)

Анализируя с геометрической точки зрения процедуру, которая предшествовала определению двойного интеграла для неотъемлемой в области функции приходим к выводу: каждое слагаемое интегральной суммы численно равен объему прямой призмы с площадью основания и высотой (рис. 26.3), а интегральная сумма численно дает приближенное значение объема цилиндрического тела для функции  на области

Рис. 26.3

Свойства двойного интеграла

Сравнивая определение двойного интеграла и определение определенного интеграла функции одной переменной, можно сделать вывод, что по структуре эти определения аналогичны. Поэтому свойства двойного интеграла, а также их доведения почти повторяют соответствующие свойства определенного интеграла. Приведем эти свойства.

1. Двойной интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме двойных интегралов от слагаемых:

2. Постоянный множитель можно выносить за знак двойного интеграла:

3. Если область разбить на две области и которые не имеют общих внутренних точек, и функция непрерывна в области то

4. Если в области то

5. Если в каждой точке области функции и непрерывны и удовлетворяют условию то

6. Если функция непрерывна в области и удовлетворяет двойное неравенство где и — наименьшее и наибольшее значение функции в области , то

где — площадь области

7. Если функция   непрерывна в области то в этой области существует такая точка что

где — площадь области

Значение называется средним значением функции в области

Вычисление двойного интеграла в декартовых координатах

Установим формулы для вычисления двойного интеграла  опираясь на его геометрический смысл (26.3) и формулу вычисления объема тела с помощью определенного интеграла: (26.11) где — площадь поперечного сечения тела плоскостью, перпендикулярной к оси а и = — уравнение плоскостей, ограничивающих данное тело.

Область плоскости называется правильной, или простой, в направлении оси если она ограничена прямыми  и двумя непрерывными кривыми и  а любая прямая параллельная оси пересекает каждую из этих кривых только в одной точке (рис. 26.4 а, б).

Рис. 26.4

Рассмотрим цилиндрическое тело для функции на правильной в направлении оси области (рис. 26.5). Проведем произвольную плоскость, параллельную плоскости В сечении цилиндрического тела этой плоскостью получаем криволинейную трапецию, площадь которой выражается интегралом от функции где фиксировано, а меняется от Таким образом, площадь сечения равна:

Согласно формуле (26.11) объем данного цилиндрического тела равна:

Рис. 26.5

С другой стороны, на основании геометрического смысла двойного интеграла имеем:

Сопоставляя последние две формулы, окончательно получаем:

или в более удобной (для использования) форме:

Правую часть формулы (26.12) как определенный интеграл от определенного интеграла называют двукратным или повторным интегралом от функции по области В нем интеграл по переменной y называют внутренним, а по переменной — внешним интегралом

Согласно формуле (26.12) сначала проводят интегрирования по переменной то есть находят внутренний интеграл (при этом переменная считается постоянной), после чего полученную функцию от интегрируют в пределах от до с переменной то есть вычисляют внешний интеграл.

Аналогично область плоскости называется правильной, или простой, в направлении оси если она ограничена прямыми и  и двумя непрерывными кривыми и а любая прямая , параллельная оси пересекает каждую из этих кривых только в одной точке (рис.26.6 а, б).

Рис. 26.6

Для правильной в направлении оси области вычисления двойного интеграла сводится к вычислению двукратного или повторного, интеграла по формуле:

Как итог рассматриваемого наведем порядок нахождения двойного интеграла:

1) строим область интегрирования ограниченную заданными линиями;
2) анализируем ее с целью установления того, является ли она правильной в направлении хотя бы одной из осей координат, и определяем границы интегрирования;
3) применяем одну из формул, (26.12) или (26.13), и находим сначала внутренний интеграл (как правило, со сменными пределами интегрирования), а затем — внешний (с постоянными пределами интегрирования).

Рис. 26.7

Если область не является правильной, то ее подают в виде объединения правильных областей, осуществив ее разбиение на части прямыми, параллельными координатным осям, и применяют свойство 3 двойного интеграла, а именно:

Формулы приведения двойного интеграла к повторным (26.12) и (26.13) существенно упрощаются, если область является прямоугольником со сторонами, параллельными осям координат (рис. 26.7).

В этом случае пределы интегрирования являются постоянными не только для внешнего, но и для внутреннего интеграла:

и в каком порядке интегрировать сначала по переменной а затем по переменной или наоборот, не имеет значения.

Вычислим если область — прямоугольник:  

По формуле (26.15) имеем:

Если подынтегральная функция является произведением функции от с функцией от и пределы интегрирования постоянные, то двойной интеграл равен произведению определенных интегралов по каждой переменной.

Вычислим  если область ограничена линиями: и

Построим область интегрирования (рис. 26.8). Она является правильным в направлении оси поэтому внутреннее интегрирование проводим по переменной а внешнее — по

Рис. 26.8

Вычислим если область  ограничена линиями:
и

Построим область (рис. 26.9).

Рис. 26.9

Она является правильной в направлении оси поэтому внутреннее интегрирование проводим по переменной  а внешнее — по

Вычислим если область ограничена линиями:
и

Построим область (рис. 26.10).
Находим точки взаимного пересечения каждой пары линий, ограничивающих .
Линии — пересекаются в начале координат

Рис. 26.10

Область не является правильным ни в направлении оси ни в направлении оси Разобьем ее прямой на две правильные в направлении оси области и По формуле (26.14) имеем:

Двойной интеграл в полярных координатах

При переходе в двойном интеграле от декартовых координат и  к полярным и используют связь между координатами и (24.4):

и выражение для дифференциала площади в полярных координатах:

Соответствующая формула перехода имеет вид:

где  и — полярные координаты точек области

Вычисление двойного интеграла в полярных координатах сводится к вычислению двукратного (повторного) интеграла по переменными и .

Если область является разностью двух криволинейных секторов (рис. 26.11), то есть фигурой, ограниченной лучами, которые образуют с полярной осью углы и и кривыми и где то

Рис. 26.11

Если область ограничена сомкнутой линией и начало координат лежит внутри области, то

Переход к полярным координатам в двойном интеграле целесообразно делать, если область интегрирования представляет собой круг, кольцо или их частями, то есть граница области содержит дуги кругов и отрезки лучей, исходящих из полюса

Вычислим  где — круг 

Пределом области является окружность радиуса 2 с центром в точке

Применим формулы перехода от декартовых координат к полярным:

В координатах уравнение границы области примет вид:

Построим в декартовых координатах круг или  (рис. 26.12). В полярных координатах соответствующая область интегрирования — криволинейный сектор, ограниченный лучами а полярный радиус меняется от до

Рис. 26.12

По формуле (26.17) имеем:

Вычислим с помощью двойного интеграла в полярных координатах несобственный интеграл Эйлера-Пуассона:

Для этого рассмотрим двойной интеграл  где — четверть круга некоторого радиуса расположенного в первом квадранте декартовой системы координат: Для вычисления перейдем к полярным координатам: тогда

Если теперь неограниченно увеличивать радиус то получим несобственный интеграл по всей первой четверти (рис. 26.13), так как при область

Рис. 26.13

расширяется так, что любая точка первой четверти попадет в и останется в ней, а направляться в

С другой стороны, при и и поэтому можно записать:

поскольку определенный интеграл (а с ним и несобственный) не зависит от обозначения переменной интегрирования.

Таким образом, откуда: 

Вычисление площади плоской фигуры с помощью двойного интеграла

Если в формуле (26.3): положить то интегральная сумма для функции в области давать приближенно площадь этой области

а за ее точное значение принимается значение интеграла:

Если область — разность двух криволинейных секторов (рис. 26.11) — заданная в полярной системе координат неровностями то

Найдем площадь фигуры, ограниченной линиями: 

Построим плоскую фигуру (рис. 26.14) и определим точки пересечения заданных линий — гиперболы и прямой, — решив систему их уравнений:

Рис. 26.14

Решим первое уравнение: откуда  тогда Следующим образом: . (Вторая ветвь гиперболы не показаны, поскольку она не имеет общих точек с прямой

Заданная фигура является областью, правильной и в направлении оси и в направлении оси Для вычисления ее площади воспользуемся формулой (26.19). В соответствующем повторном интеграле внешний интеграл берем по переменной от до а внутренний — по переменной от к

Вычислим площадь плоской области ограниченной кругом  и прямыми

Построим область для чего предварительно сведем уравнение окружности к каноническому виду (рис. 26.15).

Площадь заданной области целесообразно вычислить в полярных координатах: Запишем уравнение окружности в координатах или По уравнениям заданных прямых устанавливаем, что угол изменяется от до Таким образом, согласно формуле (26.20) имеем:

Вычисление объема тела с помощью двойного интеграла

По определению двойного интеграла и его геометрическим смыслом было доказано, что двойной интеграл равен объему тела, ограниченного поверхностью областью плоскости и цилиндрической поверхностью, направляющей которой является граница области и образующими, параллельными оси а именно:

Найдем объем тела, ограниченного поверхностями:

Проанализируем уравнение поверхностей и построим область интегрирования Заданное пространственное тело ограничено: сверху — плоскостью боков — двумя параболическими цилиндрами и с образующими, параллельными оси снизу — областью которая «вырезается» на плоскости цилиндрическими поверхностями и плоскостью (рис. 26.16).

Рис. 26.16

По формуле (26.3) получаем:

Найдем объем тела, ограниченного параболоидом и плоскостями (в I октанте).

Построим область интегрирования согласно условию задачи (рис. 26.17).
Вычислим объем осуществив в двойном интеграле переход к полярным координатам, при этом уравнение окружности запишется как а прямые и образуют с осью углы и в соответствии.

Рис. 26.17
Итак, по формуле (26.17) получим:

Рассмотрим две задачи, в которых двойной интеграл применяется для вычислений в сфере экономики.

1. Пусть — областьь посевов некоторой сельскохозяйственной культуры. В каждой точке известна урожайность этой культуры (например, по наблюдениям из космоса). Тогда величина численно равна урожая, который можно собрать с области  при отсутствии потерь.

2. Аналогично, если функция описывает плотность населения в точке некоторого региона-области то величина численно равна численности населения этого региона.

В обоих задачах аналитическое выражение подынтегральной функции устанавливается как эмпирическая формула.

Подводя итоги темы «двойной интеграл», отметим, что рядом с двойными существуют также и многомерные (-мерные, ) интегралы. Определение соответствующих интегралов вводятся аналогично тому, как это было сделано при определении двойного интеграла, а их вычисления сводится к вычислению -кратных определенных интегралов. Наиболее распространенными являются тройные интегралы от функции по пространственной (трехмерной) области ограниченной некоторой замкнутой поверхностью. Взятие тройного интеграла сводится к последовательному вычисления трех определенных интегралов.