Объём шара
Онлайн калькулятор

Чему равен объём шара, если:
Площадь поверхности шара Sпов =
Теория
Объём шара через радиус
Чему равен объём шара Vшара, если его радиус r?
Формула
Пример
Для примера посчитаем чему равен объём шара в кубических сантиметрах, если его радиус r = 2 см:
Vшара = 4/3 ⋅ 3.14 ⋅ 2³ = 4/3 ⋅ 3.14 ⋅ 8 = 100.48/3 ≈ 33.493 см³
Объём шара через диаметр
Чему равен объём шара Vшара, если его диаметр d?
Формула
Пример
Для примера посчитаем чему равен объём шара в кубических метрах, если его диаметр d = 0.5 м:
Vшара = 1/6 ⋅ π ⋅ 0.5³ = (3.14 ⋅ 0.125) / 6 ≈ 0.0654 м³
Объём шара через длину окружности
Чему равен объём шара Vшара, если длина его окружности L?
Формула
Пример
Для примера посчитаем чему равен объём шара в кубических миллиметрах, если длина окружности у него L = 50 мм:
Vшара = 50³ ⁄ 6 ⋅ 3.14² = 125000 / 59.1576 ≈ 2113 мм³
Объём шара через площадь поверхности шара
Чему равен объём шара Vшара, если площадь его поверхности Sпов?
Формула
Пример
Для примера посчитаем чему равен объём шара в кубических сантиметрах, если площадь поверхности у него Sпов = 225 см²:
Объем шара
На этой странице вы можете рассчитать объем шара. Предлагаем вам 3 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр или длину окружности. Просто введите значение в калькулятор и получите мгновенный результат.
Шар — это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.
Объем шара через радиус
Формула для нахождения объема шара через радиус: <3>pi r^3> , где r — радиус шара.
Объем шара через диаметр
Формула для нахождения объема шара через диаметр: <6>pi D^3> , где D — диаметр шара.
Объем шара через длину окружности
Формула для нахождения объема шара через длину окружности: <6pi^3>> , где L — длина окружности шара.
Эта формула легко выводится формулы объема шара через его радиус и формулы для нахождения длины окружности
Пример расчета
Найдем объем шара, радиус которого 1 метр. Подставим это значение в первую формулу и произведем вычисления:
<3>pi r^3 = dfrac<4><3>pi cdot 1^3 = dfrac<4><3>pi cdot 1 = 4,19 м^3>
Также на нашем сайте вы можете найти объем параллелепипеда.
Объемы фигур
Что такое шар?
Шар или сфера представляет собой объемное тело, которое образовано вращением окружности вдоль оси. Ось вращения окружности также является ее осью симметрии и совпадает с диаметром. Поскольку все параметры шара, как и окружности, неразрывно связаны с числом π, то и его объем не является исключением. Интегрируя по трем углам в сферической плоскости, получаем объем равный четырем третям числа π , умноженным на радиус в третьей степени.
Введите радиус шара:
Шар – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние называется радиусом шара.
Формула объема шара: 
где R – радиус шара
- Если дана только площадь поверхности сферы, вычислите радиус так: площадь поверхности разделите на 4π, а затем из полученного значения извлеките квадратный корень. Таким образом: r = √(S/4π), где S — площадь поверхности сферы. [5]
- Если радиус равен 5 см, то кубический радиус равен 5 3 = 5 * 5 * 5 = 125.
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара , заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя .
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс , у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента .
По той же причине всю сферу можно рассматривать как сферический пояс , у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Высотой шарового сектора называют высоту его сферического сегмента .
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы .
Молярный объём
Vm — величина, равная отношению объёма V системы (тела) к её количеству вещества n:
Молярный объем для газов при нормальных условиях: Vm = 22,4 л/моль
Формула вычисления объема шара
1. Через радиус
Объем (V) шара равняется трем четвертым произведения его радиуса в кубе и числа π .
Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
Диаметр шара равняется двум его радиусам: d = 2R. А значит, формула вычисления объема может выглядеть следующим образом:
Формула расчёта объёма шара
Объем шара можно вычислить по формуле:
Как найти объем трехмерных объектов
Начнем с расчета для прямоугольных и квадратных фигур. Придерживайтесь инструкции и постарайтесь рассчитать самостоятельно, чтобы закрепить знания. Числа, указанные в описании, берутся в качестве примера. Вы можете производить другие расчеты.
- Измеряем длину предмета в сантиметрах – 9. Сантиметры приходят на помощь, когда невозможно получить целое число в метрах .
- Замеряем ширину в сантиметрах – 17.
- Умножаем между собой длину и ширину 9 * 17 = 152 см 2 – получили площадь основания
- Производим замер высоты – 28 см.
- Умножаем площадь основания на высоту 152 см 2 * 28 см = 4256.
Полученное число необходимо перевести в кубические метры. Для этого конечный результат делим на 1.000.000. Пример будет выглядеть следующим образом – 4256 м 3 /1000000 = 0,004256 м 3
Площади сферы и ее частей. Объемы шара и его частей
В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.
где
r – радиус сферы.
где
r – радиус шара.
где
r – радиус сферы,
h – высота сферического пояса .
Площадь сферического пояса не зависит от радиусов r1 и r2 !
где
r1 , r2 – радиусы оснований шарового слоя,
h – высота шарового слоя .
где
r – радиус сферы,
h – высота сферического сегмента .
где
r – радиус шара,
h – высота шарового сегмента .
| Фигура | Рисунок | Формула | Описание |
| Сфера |  |
Площадь сферы | |
| Шар | Объем шара | ||
| Сферический пояс |  |
Площадь сферического пояса | |
| Шаровой слой | Объем шарового слоя | ||
| Сферический сегмент |  |
Площадь сферического сегмента | |
| Шаровой сегмент | Объем шарового сегмента | ||
| Шаровой сектор |  |
где |
Объем шарового сектора |
| Сфера |
 |
где
r – радиус сферы.
Шар
где
r – радиус шара.
Сферический пояс
Площадь сферического пояса:
где
r – радиус сферы,
h – высота сферического пояса .
Площадь сферического пояса не зависит от радиусов r1 и r2 !
Шаровой слой
Объем шарового слоя:
где
r1 , r2 – радиусы оснований шарового слоя,
h – высота шарового слоя .
Сферический сегмент
Площадь сферического сегмента:
где
r – радиус сферы,
h – высота сферического сегмента .
Шаровой сегмент
Объем шарового сегмента:
где
r – радиус шара,
h – высота шарового сегмента .
Шаровой сектор
Объем шарового сектора:
где
r – радиус шара,
h – высота шарового сектора .
Прочие единицы измерения
- 1 дюйм кубический = 1,63871·10 −5 м³
- 1 литр = 1·10 −3 м³
- Лямбда 1 λ = 1·10 −9 м³
- 1 унция = 2,841·10 −5 м³ (анг.)
- 1 унция = 2,957·10 −5 м³ (амер.)
- 1 фут кубический = 2,83168·10 −2 м³
- 1 ярд кубический = 0,76455 м³
- 1 стер = 1 м³
- 1 ае кубическая =3,348071936e+40 км³
- 1 км кубический = 1 000 000 000 м³
- 1 световой год кубический = 8,46590536e+38 км³
- 1 пк кубический = 2,9379989989648103256576e+40 км³
- 1 мпк кубический =1 000 000 000 пк³=2,9379989989648103256576e+49 км³
Пример нахождения объёма шара
Найти объем шара радиусом 10 сантиметров.
Для того чтобы вычислить объем шара формула используется следующая:
где V – искомый объем шара, π – 3,14 , R – радиус.
Таким образом, при радиусе 10 сантиметров объем шара равен:
3,14 × 10 3
= 4186,7
В геометрии шар определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара. Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.
С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара. Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары. С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.
В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение. Следует заметить, что при их расчете конструкторам требуется найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки. Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.
Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений. В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.
Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы. Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные). Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.
Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка. Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий. Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.
Как найти объем для фигур цилиндрической формы
Цилиндр – это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Одним из видов цилиндра является призма.
Чтобы произвести вычисления нужно найти диаметр тела (ширина) одного круглого основания и полученное число поделить на 2. Допустим, диаметр основания равен 30 см.
- Производим расчеты: 30 см / 2 = 15 см. Половина диаметра круга ‒ радиус.
- Возводим полученный радиус в квадрат или умножаем самого на себя: 15 * 15 = 225 см 2 .
- Полученное число 225 см 2 – это квадрат радиуса. Эту цифру умножаем на число ПИ — 3,14. Например: 225 см 2 * 3,14 = 706,5 см 2 .
- Проводим новый замер, чтобы узнать расстояние между круглыми основаниями, допустим, оно равно 12 см.
- Это число умножаем на площадь круглого основания: 706,5 см 2 * 12 см = 8 478 см 3
- Полученное значение и будет искомым объемом. Для перевода в кубические метры необходимо конечное число поделить на один миллион. Как мы делали в предыдущем примере.
Объем шарового сегмента
Шаровой сегмент – часть шара, отсекаемая какой нибудь плоскостью. Объем шарового сегмента вычисляется по формуле:
[ LARGE V = <1 over 3>cdot pi cdot h^2 cdot (3 cdot R – h) ]
где:
V – объем шарового сегмента
h – высота шарового сегмента
R – радиус шарового сегмента
π – число пи (3.1415)
Советы
- Используйте кубические единицы измерения (например, 113 см³).
- Убедитесь, что все значения представлены в одной единице измерения. В противном случае преобразуйте единицы измерения.
- Обратите внимание, что символ «*» используется как знак умножения, чтобы избежать путаницы с переменной «x».
- Если нужно найти объем некоторой части сферы, например, ее половины или четверти, сначала вычислите объем всей сферы, а затем полученное значение разделите на число, на которое поделена сфера. Например, чтобы найти объем полусферы, когда объем всей сферы равен 8, разделите 8 на 2 и получите 4.
Примеры задач
Задание 1
Вычислите объем шара, если его радиус равняется 3 см.
Решение:
Применив первую формулу (через радиус) получаем:
Задание 2
Найдите объем шара, если известно, что его диаметр равен 12 см.
Решение:
Используем вторую формулу, в которой задействован диаметр:
http://mnogoformul.ru/obem-shara-formula-i-raschet-onlayn
http://exceltut.ru/obemy-figur/
Перейти к содержанию
Калькуляторы объёма и площади круга, цилиндра, куба, шара (сферы), конуса
На чтение 1 мин Просмотров 29.9к.
Обновлено 10.01.2022
Содержание
- Калькулятор площади и периметра (длины окружности) круга
- Калькулятор расчета площади и объёма шара (сферы)
- Калькулятор расчета объёма цилиндра
- Калькулятор расчета объёма параллелепипеда
- Калькулятор куба-объём, площадь поверхности

Калькулятор площади и периметра (длины окружности) круга
Калькулятор расчета площади и объёма шара (сферы)
Калькулятор расчета объёма цилиндра
Калькулятор расчета объёма параллелепипеда

Калькулятор куба-объём, площадь поверхности
Enter the radius of the circle (in) and the height of the circle (in) into the Circle Volume Calculator. The calculator will evaluate and display the Circle Volume.
- All Volume Calculators
- Area of a semi circle calculator
- Area of an Oval Calculator
- Aquarium Volume Calculator
Circle Volume Formula
The following formula is used to calculate the Circle Volume.
- Where CV is the Circle Volume (in^3)
- R is the radius of the circle (in)
- H is the height of the circle (in)
To calculate circle volume, square the radius, then multiply by pi times the height.
How to Calculate Circle Volume?
The following example problems outline how to calculate Circle Volume.
Example Problem #1:
- First, determine the radius of the circle (in).
- The radius of the circle (in) is given as: 4.
- Next, determine the height of the circle (in).
- The height of the circle (in) is provided as: 20.
- Finally, calculate the Circle Volume using the equation above:
CV = pi*R^2*H
The values given above are inserted into the equation below:
CV = 3.14159*4^2*20 = 10005.308 (in^3)
Example Problem #2:
The variables needed for this problem are provided below:
radius of the circle (in) = 6
height of the circle (in) = 3
Entering these values and solving gives:
CV = 3.14159*6^2*3 = 339.29 (in^3)
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
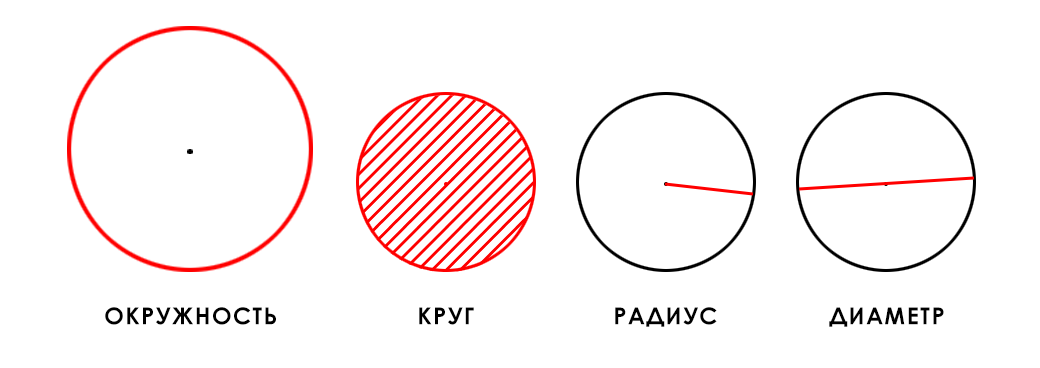
Что такое окружность?
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
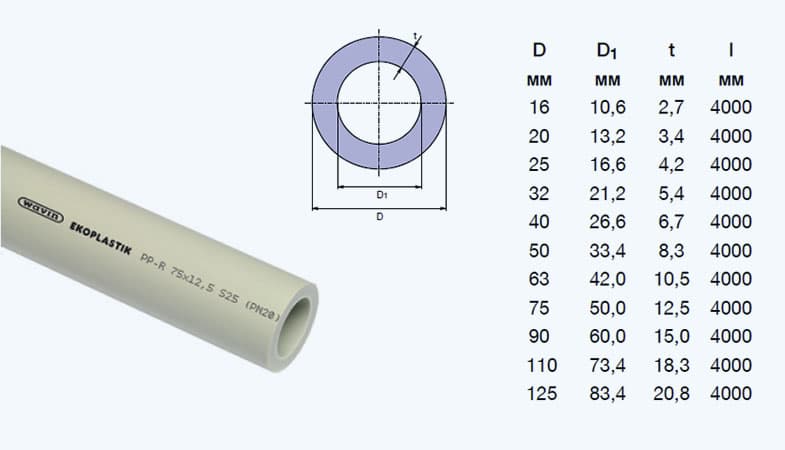
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.
Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Информация по назначению калькулятора
В евклидовой геометрии круг — это множество всех точек на плоскости на фиксированном расстоянии, называемом радиусом, от заданной точки, центра. Длина круга называется его окружностью, а любая непрерывная часть окружности называется дугой.
Окружность — это простая замкнутая кривая, которая делит плоскость на внутреннюю и внешнюю. Внутренняя часть круга называется диском. Математически круг можно понимать и несколькими другими способами. Например, это частный случай эллипса, в котором два фокуса совпадают (то есть они являются одной и той же точкой). Альтернативно, окружность можно рассматривать как коническое сечение, достигаемое, когда прямой круговой конус пересекается плоскостью, перпендикулярной оси конуса.
Число π (ПИ) равно 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375…
Все круги обладают одинаковыми свойствами. Некоторые из них отмечены далее:
⇒ Для любого круга заключенная площадь и квадрат его радиуса находятся в фиксированной пропорции, равной математической константе π (ПИ).
⇒ Для любого круга длина окружности и радиус находятся в фиксированной пропорции, равной 2π.
⇒ Круг — это фигура с наибольшей площадью для заданной длины периметра.
⇒ Круг имеет очень симметричную форму. Каждая линия, проходящая через центр, образует линию симметрии отражения. Кроме того, существует вращательная симметрия вокруг центра для каждого угла.
⇒ Окружность с центром в начале координат радиусом 1 называется единичной окружностью.
Онлайн калькулятор поможет найти параметры круга, такие как:
- Диаметр
- Радиус
- Длина окружности
- Площадь
— равен двум радиусам или длине окружности поделенной на число π (d=r*2=P/π)
— равен половине диаметра или длине окружности поделенной на 2π (r=d/2=P/2π)
— (или периметр круга) равна диаметру умноженному на число π (P=d*π=2π*r)
— равна радиусу в квадрате умноженному на число π (S=πr2=¼πd2)