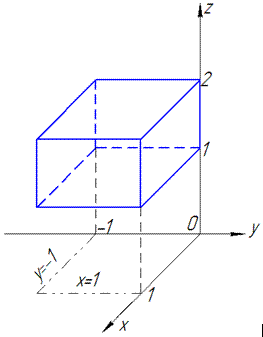
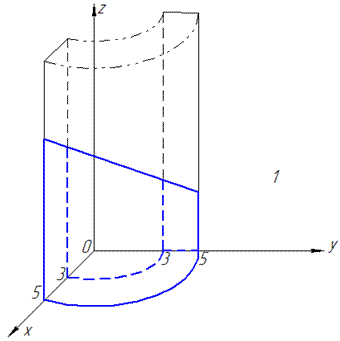
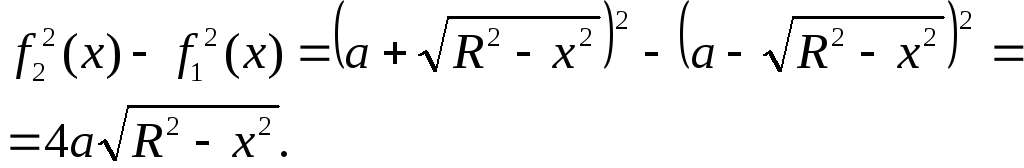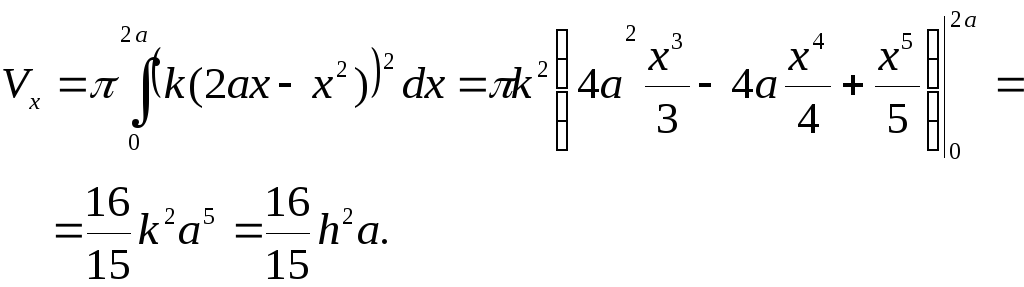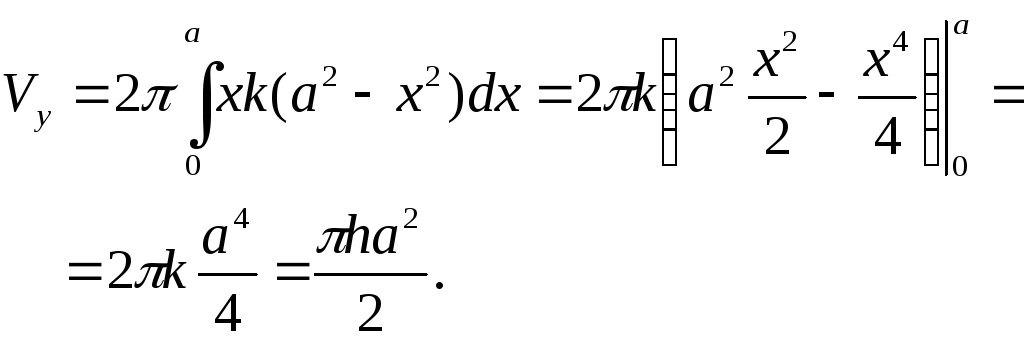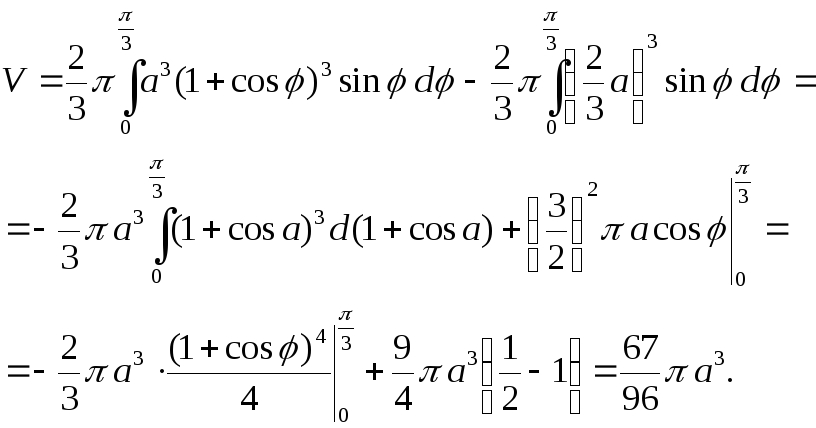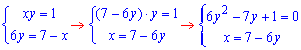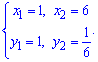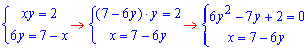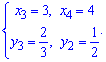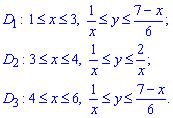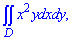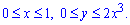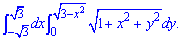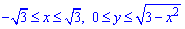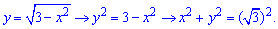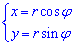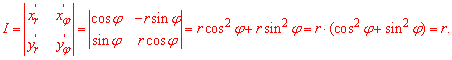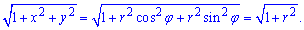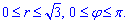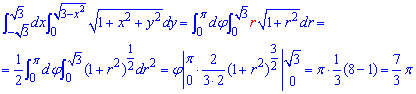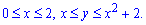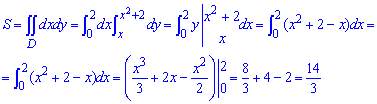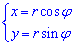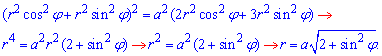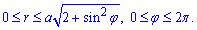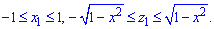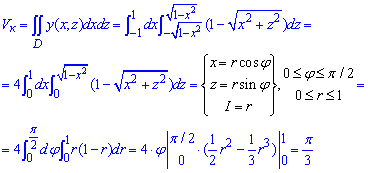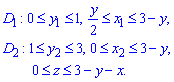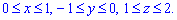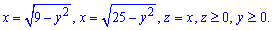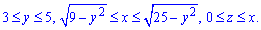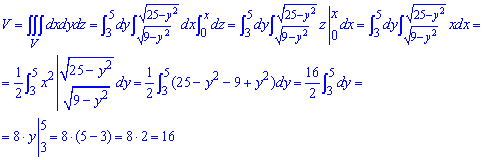Определение
3. Тело
вращения – это тело, полученное вращением
плоской фигуры вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.
Ось вращения может
и пересекать фигуру, если это ось
симметрии фигуры.
Теорема
2. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямых
и
вращается вокруг оси
.
Тогда объём получающегося тела вращения
можно вычислить по формуле
(2)
Доказательство.
Для такого тела сечение с абсциссой
– это круг радиуса
,
значити формула (1) даёт требуемый результат.
Если фигура
ограничена графиками двух непрерывных
функций
и
,
и отрезками прямыхи
,
причёми
,
то при вращении вокруг оси абсцисс
получим тело, объём которого
Пример
3. Вычислить
объём тора, полученного вращением круга,
ограниченного окружностью вокруг оси абсцисс.
Р
Указанный круг снизу ограничен графиком
функции
,
а сверху –.
Разность квадратов этих функций:
Искомый объём
(графиком
подынтегральной функции является
верхняя полуокружность, поэтому
написанный выше интеграл – это площадь
полукруга).
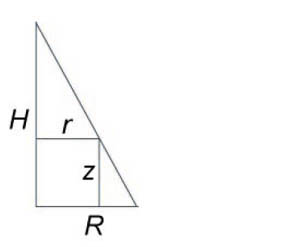
Пример 4.
Параболический сегмент с основанием
,
и высотой,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).
Р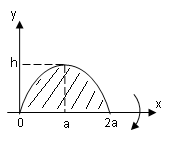
Параболу расположим как показано на
рисунке. Тогда её уравнение
,
причем.
Найдём значение параметра:
.
Итак, искомый объём:
Теорема
3. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямых
и
,
причём,
вращается вокруг оси.
Тогда объём получающегося тела вращения
может быть найден по формуле
(3)

доказательства.
Разбиваем отрезок
точками
,
на части и проводим прямые.
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основаниеми высотой
.
Получающийся при
вращении такого прямоугольника цилиндр
разрежем по образующей и развернём.
Получим «почти» параллелепипед с
размерами:
,
и
.
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство
Для получения
точного равенства надо перейти к пределу
при .
Написанная выше сумма есть интегральная
сумма для функции ,
следовательно, в пределе получим интеграл
из формулы (3). Теорема доказана.
Замечание
1. В теоремах
2 и 3 условие
можно опустить: формула (2) вообще
нечувствительна к знаку,
а в формуле (3) достаточнозаменить на
.
Пример
5.
Параболический сегмент (основание
,
высота)
вращается вокруг высоты. Найти объём
получающегося тела.
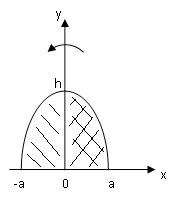
Расположим
параболу как показано на рисунке. И хотя
ось вращения пересекает фигуру, она –
ось – является осью симметрии. Поэтому
надо рассматривать лишь правую половину
сегмента. Уравнение параболы
,
причем,
значит.
Имеем для объёма:
Замечание
2. Если
криволинейная граница криволинейной
трапеции задана параметрическими
уравнениями
,
,
и
,
то можно использовать формулы (2) и (3) с
заменойна
и
на
при измененииt
от
до
.
Пример
6. Фигура
ограничена первой аркой циклоиды
,
,
,
и осью абсцисс. Найти объём тела,
полученного вращением этой фигуры
вокруг: 1) оси;
2) оси.
Решение.
1) Общая формула
В нашем случае:
2) Общая формула
Для нашей фигуры:
Предлагаем
студентам самостоятельно провести все
вычисления.
Замечание
3. Пусть
криволинейный сектор, ограниченный
непре-рывной линией
и лучами
,
,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.
Пример
7. Часть
фигуры, ограниченной кардиоидой
,
лежащая вне окружности,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.
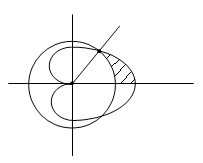
Обе линии, а значит и фигура, которую
они ограничивают, симметричны относительно
полярной оси. Поэтому необходимо
рассматривать лишь ту часть, для которой
.
Кривые пересекаются прии
при
.
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:
Задачи
для самостоятельного решения.
1. Круговой сегмент,
основание которого ,
высота
,
вращается вокруг основания. Найти объём
тела вращения.
2. Найти объём
параболоида вращения, основание которого
,
а высота равна.
3. Фигура, ограниченная
астроидой
,
вращает-ся вокруг оси абсцисс. Найти
объём тела, которое получается при этом.
4. Фигура, ограниченная
линиями
и
вращается вокруг оси абсцисс. Найти
объём тела вращения.
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
- #
(схема 42)
1. Вычисление объема тела
Пусть функция f(x;y) ≥ 0.
Рассмотрим тело, ограниченное
поверхностью z = f(x;y), плоскостью z=0 и цилиндрической поверхностью, образующие которой
параллельны оси 0z, а направляющей
служит граница области D. Как было показано
выше, согласно формуле (6.3) объем данного тела равен

Пример 6.9. Вычислить объём тела, ограниченного параболоидом z= x2+y2+1,
плоскостью x+y
–3=0 и координатными плоскостями.
Решение. Основанием тела служит треугольник ОАВ. Область D в данном
случае определяется неравенствами:

изображенному на рисунке 6.6 (пример 6.5). Следовательно, используя формулу
(6.18), получим:
2.
Вычисление площади плоской фигуры
Если положить в формуле (6.18) f(x,y)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h=1. Объем такого цилиндра,
как
известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:

или, в полярных
координатах,

Пример
6.10. Вычислить площадь фигуры,
ограниченной прямой y=2x+1 и параболой y=x2+1.
Решение. Решая совместно систему

и B(2;5).
Применяя формулу (6.19), будем иметь:
Пример 6.11. Вычислить площадь фигуры ограниченной лемнискатой

Решение. Переходим к полярной системе координат, полагая x=r cosφ и y=r sinφ; тогда получаем

можно вычислить сначала ту часть, которая расположена первой четверти. В этом случае угол φ будет изменяться от 0 до

3.
Вычисление массы плоской фигуры (пластины)
Масса плоской пластинки D с
переменной плотностью γ=γ(x,y) находится
по формуле

4.
Определение статических моментов и координат центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей 0x и 0y могут быть вычислены по формулам

а
координаты центра масс фигуры – по формулам

Статические моменты широко используются в
сопротивлении материалов и других технических науках.
5.
Определение моментов инерции плоской
фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на
квадрат расстояния d точки до оси, т.е. 
вычислены по формулам:

Момент
инерции фигуры относительно начала координат – по формуле

Пример
6.12. Найти массу, статические
моменты и координаты центра тяжести фигуры, лежащей в первой четверти,
ограниченной эллипсом 
Поверхностная плотность в каждой точке фигуры пропорциональна произведению
координат точки.
Решение. По
формуле (6.21) находим массу пластины. По условию, γ=γ(x,y)=k∙xy, где k –
коэффициент пропорциональности.Тогда

Находим
статические моменты пластинки по формулам (6.22):
Находим
координаты центра тяжести пластинки, используя формулы (6.23):
6. Поверхностный интеграл I рода
Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве Оxyz в точках некоторой поверхности площади S определена непрерывная функция u = f (x;y;z). Разобьем поверхность на конечное число n частей Si, площади которых равны ∆Si, а диаметры – di, 
и составим сумму произведений вида

Она
называется интегральной суммой для функции f(x;y;z) по поверхности S. Если при 
сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек Mi(xi;yi;zi), то он называется поверхностным интегралом I рода от
функции f(x;y;z) по поверхности S и обозначается 

Теорема 6.3
(о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная
плоскость, которая непрерывно меняется с перемещением точки по поверхности), а
функция f(x;y;z) непрерывна на этой поверхности, то поверхностный
интеграл существует
Формула 
выражает интеграл по поверхности
S
через двойной интеграл по проекции S на плоскость x0y. Отметим, что если поверхность S задана
уравнением вида y=y(x;z) или x=x(y;z), то аналогично получим:


где
D1 и D2 –
проекции поверхности S на
координатные плоскости xОz и yОz
соответственно.
Пример 6.13. Вычислить 

Решение. Из уравнения заданной
цилиндрической поверхности выразим 
при x = 0 в плоскости xОy: 

имеем
Приведем некоторые примеры применения
поверхностного интеграла I рода.
6.1. Площадь
поверхности
Если поверхность S задана уравнением z = f(x;y), a ее проекция на
плоскость x0y есть область D, в которой z = f(x;y), zx(x;y) и zy(x;y) –
непрерывные функции, то ее площадь S
вычисляется по формуле:

Пример 6.14. Вычислить площадь части плоскости x+y+z=4,
вырезаемой цилиндром x2+y2 =4 (рис. 6.10).
Решение. Применим формулу (6.31). Область интегрирования D есть круг
радиуса r=2. Находим частные производные

функции z=4 – x – y:


Чтобы вычислить этот интеграл, введём полярные
координаты. Область D определяется: 
Кроме того, поверхностный интеграл применяют для
вычисления массы, координат центра масс, моментов инерции материальных
поверхностей с известной поверхностной плотностью распределения массы γ=γ(x;y;z). Все эти величины
определяются одним и тем же способом:
– данную область разбивают на конечное число мелких частей;
– делают для каждой такой части предположения, упрощающие задачу;
– находят приближенное значение искомой величины;
– переходят к пределу при неограниченном измельчении разбиения
области.
Проиллюстрируем описанный способ на примере
определения массы материальной поверхности.
6.2. Масса
поверхности
Пусть плотность распределения массы материальной
поверхности есть γ=γ(x;y;z). Для нахождения
массы поверхности:
1. Разбиваем поверхность S на n частей Si, 
2. Выберем произвольную точку Mi(xi;yi;zi) в каждой области Si. Предполагаем, что
в переделах области Si
плотность постоянна и равна её
значению в
точке Mi.
3. Масса mi области Si мало отличается от
массы γ(xi;yi;zi)∙∆Si однородной области с постоянной полностью γ= γ(xi;yi;zi).
4. Суммируя mi
по всей области, получаем:
5. За точное значение массы материальной поверхности S
принимается предел, к которому стремится полученное приближенное значение при
стремлении к нулю диаметров областей Si, то есть

6.3. Моменты
и центр тяжести поверхности. Статические
моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по
соответствующим формулам:
Пример 6.15.
Вычислить координаты центра тяжести
однородной поверхности параболоида z=x2+y2, ограниченной плоскостью z=1.
Решение. Вершина заданного параболоида совпадает с началом
координат. Так как поверхность однородная (постоянная плотность массы), то,
основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен
на оси 0z. Тогда xc=0, yc=0
и по формуле (6.36) аппликата
спроектируем линию пересечения на плоскость x0y – получим окружность x2+y2=1 в
качестве области D. Вычислим элемент поверхности параболоида z=x2+y2 по
формуле (6.31), учитывая, что

Аналогично, переходя к полярным координатам на
плоскости x0y, получим:

Таким образом,
пересечения поверхности с плоскостью
Двойные и тройные интегралы даются трудно всем студентам. Одна из причин — это отсутствие возможности качественно строить области интегрирования.
Из воображения их брать удается не многим специалистам. Что касается нахождения объемов, образованных пересечением плоскостей, то здесь эта проблема становится еще большей.
Другое дело, что часто кратные интегралы начинают изучать когда студенты только что научились находить определенные интегралы.
Всем Вам помогут в учебе готовые ответы индивидуальной работы.
Приведенные ниже 10 примеров научат Вас решать задание разной сложности.
ВАРИАНТ — 19
Двойной интеграл
ЗАДАНИЕ 2.13 Найти площадь плоской фигуры, заданной следующими условиями, : xy=1, xy=2, 6y=7-x.
Решение: Сначала выполняем построение кривых, чтобы понять площадь какой фигуры ищем
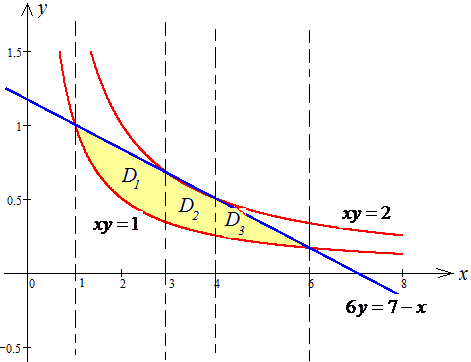
Дальше видим, что область интегрирования нужно разбивать на три части.
Есть другой вариант, более легкий с точки зрения практической реализации.
Можно найти площадь между двумя красными кривыми и от нее отнять площадь в области D2 между красной и синей кривыми. В результате получим разницу двух двойных интегралов.
Но здесь пойдем более длинным по пути, описанный попробуйте реализовать самостоятельно.
Первое, что нам нужно — это определить в каких точках графика кривые пересекают друг друга.
Найдем точки пересечения графиков 1 и 3 функций:
складываем систему из двух уравнений
и находим решение
Пересечение второй и третьей функций дают систему уравнений
для определения двух точек
Заданную область будем разбивать на три области: D=D1+D2+D3.
Расставим пределы интегрирования в каждой области:
Через двойной интеграл вычисляем площадь фигуры, ограниченной заданными кривыми:
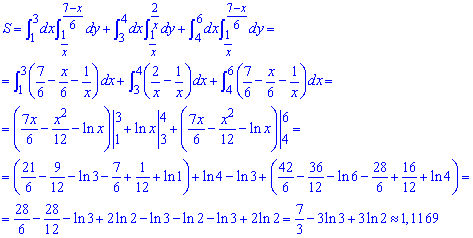
Приближенно площадь поверхности равна 1,12 единиц квадратных.
ЗАДАНИЕ 3.12 Вычислить двойной интеграл по области D, ограниченной указанными линиями:
D: y=2x3, y=0, x=1.
Решение: Найдем точки пересечения графиков заданных функций : 2x3=0, x=0.
Изобразим графически область интегрирования
Расставим пределы в заданной области D:
Вычислим двойной интеграл по области D, ограниченной указанными линиями: 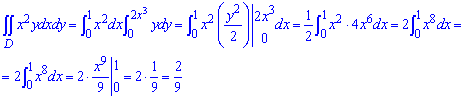
Площадь имеет место лишь в тех случаях, когда функция интегрирования равна единице.
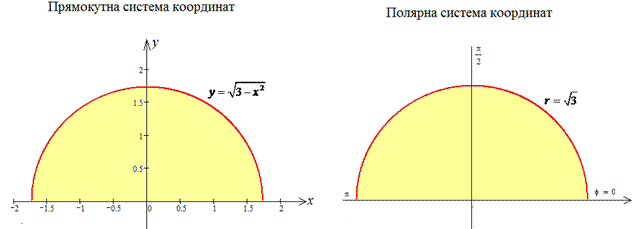
ЗАДАНИЕ 4.11 Вычислить двойной интеграл, используя полярные координаты:
Решение: Запишем область интегрирования, которая ограничена кривыми
где
Получили круг с центром в точке O (0;0) и радиусом ровным ругаю из трех 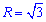
Изобразим полукруг в декартовой и полярной системе координат
Перейдем к полярной системе координат (СК), используя следующую замену переменных :
Следует помнить, что дополнительно нужно вычислить якобиан перехода от декартовой к полярной СК:
Он важен, поскольку на него нужно домножити подинтегральную функцию, выраженную в новых координатах
Найдем вид подинтегральной функции в полярной системе координат :
Запишем пределы интегрирования в полярной СК:
Осталось вычислить двойной интеграл:
Интеграл равен I=7*Pi/3.
То, что интеграл содержит число Pi лишь подтверждает правильность вычислений, ведь для круговых форм это распространено.
ЗАДАНИЕ 5.10 Вычислить площадь области D, ограниченной указанными линиями:
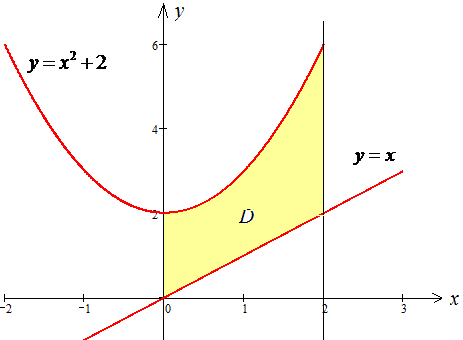
D: y=x2+2, x=2, y=x
Решение: Расставим пределы в заданной области D:
Построим кривые, чтобы представить фигуру площадь которой мы ищем.
Здесь есть два варианта: сложный — когда внутренний интеграл за переменной x предусматривает нахождение площади, через сумму двойных интегралов по 2 или 3 областям.
Мы же пойдем легким по пути и определим площадь заштрихованной фигуры с помощью одного двойного интеграла.
Вычислим площадь криволинейной трапеции, ограниченной указанными линиями:
Площадь равна S=14/3 единиц квадратных.
Как видите — выбор порядка интегрирования может существенно сэкономить время при написании контрольной работы, на экзамене или практических заданиях. Для сравнения попробуйте вычислить первым временем и сравнить масштаб выполненных работ.
ЗАДАНИЕ 6.9 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x2+y2)2=a2(2x2+3y2).
Решение: Один из предыдущих примеров содержал переход к полярной системе координат :
и был найден якобиан переходу I=r.
Определим пределы интегрирования :
Пределы интегрирования:
Их легко определить в полярной СК — радиус изменяется от нуля к кривой, которая ограничивает площадь, а угол изменяется от 0 до 360 градусов.
Это Вы должны знать при вычислении подобных заданий.
Вычислим площадь плоской фигуры:
Под интегралом пришлось понижать степень синуса за известной тригонометрической формулой. На пратиці Вы такие случаи рассматривали, то же здесь мы Вам ничего нового не открываем.
ЗАДАНИЕ 7.8 Найти объем тела, заданного поверхностями, что его ограничивают:
y=7-x2-z2, 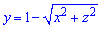
Решение: Половину 3d рисунка тела изобразим графически — это хорошая подсказка, которая развивает воображение.
Вычислим объем тела, которое ограничивает эти две поверхности (то есть рисунок разрезали пополам для наглядного отражения)+ снизу плоскостью y=0.
Чтобы упростить интегралы объем тела найдем как разницу объемов параболоида и конуса (см. рис.).
Расставим пределы в заданной области D1 (круг радиусом 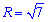
Найдем объем параболоида:
При нахождении двойного интегралу целесообразно перейти к полярной СК, поскольку обе фигуры образованы вращением кривой вокруг оси Oy.
Расставим пределы в области D2 (круг радиусом R=1):
Вычислим объем конуса:
Он равен V=Pi/3 единиц кубических.
Здесь также во время интегрирования перешли к полярной СК.
Последним шагом найдем объем тела, которое находится между параболоидом и конусом, :
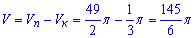
Тройной интеграл
ЗАДАНИЕ 8.7 Расставить пределы интегрирования в тройном интеграле 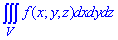
V: 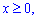
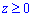
Нарисовать область интегрирования.
Решение: В плоскости Oxy уравнение прямых запишем следующим образом: y=1, x=y/2, x=3-y.
Уравнение плоскости в пространстве запишем в виде: z=3-y-x.
Построим пространственный рисунок тела и его проекцию в декартовую плоскость
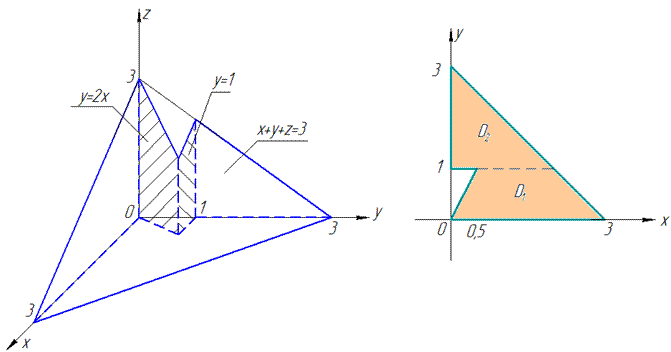
D=D1+D2, поэтому пределы интегрирования расставляем следующим образом:
На основе проведенного анализа записываем пределы в тройной интеграл
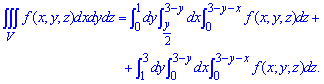
Легко убедиться, что получим сумму из трех тройных интегралов.
ЗАДАНИЕ 9.6 Вычислить тройные интегралы: 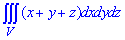
Решение: Область являет собой параллелепипед, который изображен ниже
Это значительно упрощает интегрирование
ЗАДАНИЕ 10.5 Используя тройной интеграл, вычислить объем тела, ограниченного поверхностями:
Нарисовать область интегрирования.
Решение: Прежде всего выполняем построение к условию, в крайнем случае старайтесь схематически нарисовать область интегрирования
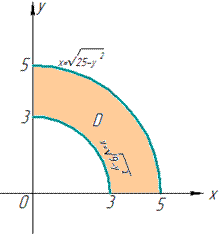
Дальше записываем пределы интегрирования, учитывая выполненный рисунок:
Через тройной интеграл находим объем тела:
Превращения не сложны и их разберите самостоятельно.
Объем ровный 16 куб. од.
На этом индивидуальная работа из повторных интегралов выполнена.
Больше примеров на двойные и тройные интегралы Вы можете найти в следующих материалах.
Конев В.В. Определенные интегралы
Объемы тел (примеры)
***
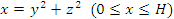 .
.
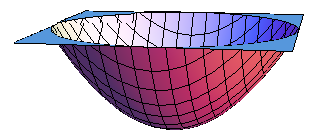
Решение. Такой параболоид может быть получен вращением дуги параболы 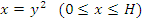
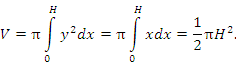
Вычисление объёмов
Объём тела, ограниченного сверху и снизу поверхностями $mathbf { textit { z } } =mathbf { textit { f } } _ { 1 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $mathbf { textit { z } } =mathbf { textit { f } } _ { 2 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $(x,y)in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $mathbf { textit { Oz } } $, равен $v=iintlimits_D { left[ { f_1 (x,y)-f_2 (x,y) }right]dxdy } $; эта формула очевидно следует из геометрического смысла двойного интеграла.
Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.
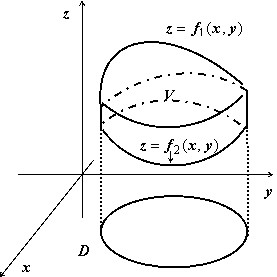
Пример 1
Найти объём тела $V:left[{ begin{array} { l } y=0,;z=0, \ x+y+z=4,; \ 2x+z=4. \ end{array} }right.$
Решение:
Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $mathbf { textit { Oxz } } $:
$V:left[{ begin{array} { l } (x,z)in D, \ 0leqslant yleqslant 4-x-z. \ end{array} }right.$
Область $mathbf { textit { D } } $ — треугольник, ограниченный прямыми $mathbf { textit { x } } $ = 0, $mathbf { textit { z } } $ = 0, 2$mathbf { textit { x } } +mathbf { textit { z } } $ = 4, поэтому
$V=iintlimits_D { (4-x-z)dxdz } =intlimits_0^2 { dxintlimits_0^ { 4-2x } { (4-x-z)dz } } = intlimits_0^2 { dxleft. { left( { 4z-xz-z^2/2 }right) }right|_0^ { 4-2x } } = intlimits_0^2 { left[ { 16-8x-4x+2x^2-(4-2x)^2/2 }right]dx } = \ = intlimits_0^2 { left( { 8-4x }right)dx } = left. { left( { 8x-2x^2 }right) }right|_0^2 =16-8=8$
Пример 2
Найти объём области, ограниченной поверхностями $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { R } } ^ { 2 } $,
$(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$.
Решение:
Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $mathbf { textit { Oz } } $ { в уравнении нет $mathbf { textit { z } } $ в явной форме). Построить в плоскости $mathbf { textit { Oxy } } $ кривую шестого порядка, заданную уравнением $(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей { чётные степени } и точка $mathbf { textit { О } } (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(cos ^4varphi +sin ^4varphi );r^2=R^2((cos ^2varphi +sin ^2varphi )^2-2cos ^2varphi sin ^2varphi )=R^2(1-frac { sin ^22varphi } { 2 } )=$
$=R^2(1-frac { 1-cos 4varphi } { 4 } )=R^2frac { 3+cos 4varphi } { 4 } ;r=Rfrac { sqrt { 3+cos 4varphi } } { 2 } .$ Эту кривую построить уже можно. $r(varphi )$ максимально, когда $cos 4varphi =1;(varphi =0,frac { 2pi } { 4 } =frac { pi } { 2 } ,frac { 4pi } { 4 } =pi ,frac { 6pi } { 4 } =frac { 3pi } { 2 } )$, минимально, когда
$cos 4varphi =-1;(varphi =frac { pi } { 4 } ,frac { 3pi } { 4 } ,frac { 5pi } { 4 } ,frac { 7pi } { 4 } ),$ и гладко меняется между этими пределами { точка $mathbf { textit { О } } (0,0)$ не принадлежит этой кривой, где мы её потеряли? } .
Пользуясь симметрией, получаем $ V=16iintlimits_D { sqrt { R^2-x^2-y^2 } dxdy= } 16iintlimits_D { sqrt { R^2-r^2 } rdrdvarphi = } =16intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } rdr } = $ $ =-8intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } d(R^2-r^2) } =-8frac { 2 } { 3 } intlimits_0^ { frac { pi } { 4 } } { left. { (R^2-r^2)^ { frac { 3 } { 2 } } }right|_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } dvarphi } =-frac { 16 } { 3 } R^3intlimits_0^ { frac { pi } { 4 } } { left. { left[ { left( { frac { sin ^22varphi } { 2 } }right)^ { frac { 3 } { 2 } } -1 }right] }right|dvarphi } = $ и т.д.
Пример 3
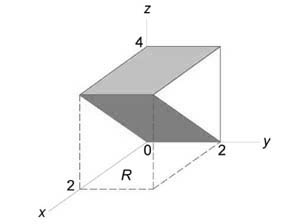
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)
Решение:
Данное тело показано на рисунке.
Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ { V = iintlimits_R { left[ { left( { 4 — x }right) — x }right]dxdy } } = { intlimits_0^2 { left[ { intlimits_0^2 { left( { 4 — 2x }right)dy } }right]dx } } = { intlimits_0^2 { left[ { left. { left( { 4y — 2xy }right) }right|_ { y = 0 } ^2 }right]dx } } = { intlimits_0^2 { left( { 8 — 4x }right)dx } } = { left. { left( { 8x — 2 { x^2 } }right) }right|_0^2 } = { 16 — 8 = 8. } $
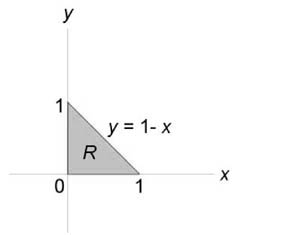
Пример 4
Описать тело, объем которого определяется интегралом (V = intlimits_0^1 { dx } intlimits_0^ { 1 — x } { left( { { x^2 } + { y^2 } }right)dy } .)
Решение:
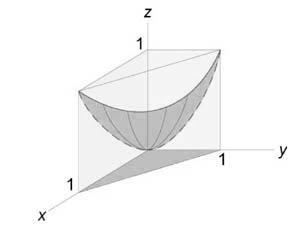
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = { x^2 } + { y^2 } .) Объем тела равен $ { V = intlimits_0^1 { dx } intlimits_0^ { 1 — x } { left( { { x^2 } + { y^2 } }right)dy } } = { intlimits_0^1 { left[ { left. { left( { { x^2 } y + frac { { { y^3 } } } { 3 } }right) }right|_ { y = 0 } ^ { 1 — x } }right]dx } } = { intlimits_0^1 { left[ { { x^2 } left( { 1 — x }right) + frac { { { { left( { 1 — x }right) } ^3 } } } { 3 } }right]dx } } = \ = { intlimits_0^1 { left( { { x^2 } — { x^3 } + frac { { 1 — 3x + 3 { x^2 } — { x^3 } } } { 3 } }right)dx } } = { intlimits_0^1 { left( { 2 { x^2 } — frac { { 4 { x^3 } } } { 3 } — x + frac { 1 } { 3 } }right)dx } } = { left. { left( { frac { { 2 { x^3 } } } { 3 } — frac { 4 } { 3 } cdot frac { { { x^4 } } } { 4 } — frac { { { x^2 } } } { 2 } + frac { x } { 3 } }right) }right|_0^1 } = { frac { 2 } { 3 } — frac { 1 } { 3 } — frac { 1 } { 2 } + frac { 1 } { 3 } = frac { 1 } { 6 } . } $
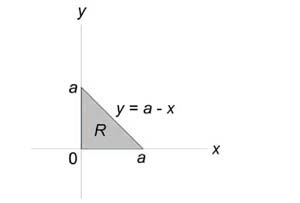
Пример 5
Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)
Решение:
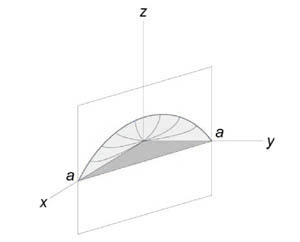
Данное тело лежит над треугольником (R) в плоскости (Oxy) ниже поверхности (z = xy.) Объем тела равен $ { V = iintlimits_R { xydxdy } } = { intlimits_0^a { left[ { intlimits_0^ { a — x } { xydy } }right]dx } } = { intlimits_0^a { left[ { left. { left( { frac { { x { y^2 } } } { 2 } }right) }right|_ { y = 0 } ^ { a — x } }right]dx } } = { frac { 1 } { 2 } intlimits_0^a { x { { left( { a — x }right) } ^2 } dx } } = { frac { 1 } { 2 } intlimits_0^a { xleft( { { a^2 } — 2ax + { x^2 } }right)dx } } = \ = { frac { 1 } { 2 } intlimits_0^a { left( { { a^2 } x — 2a { x^2 } + { x^3 } }right)dx } } = { frac { 1 } { 2 } left. { left( { { a^2 } cdot frac { { { x^2 } } } { 2 } — 2a cdot frac { { { x^3 } } } { 3 } + frac { { { x^4 } } } { 4 } }right) }right|_0^a } = { frac { 1 } { 2 } left( { frac { { { a^2 } } } { 2 } — frac { { 2 { a^4 } } } { 3 } + frac { { { a^4 } } } { 4 } }right) } = { frac { { { a^4 } } } { { 24 } } . } $
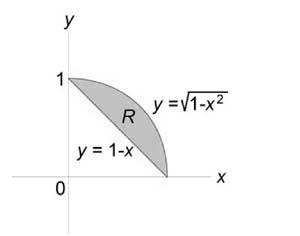
Пример 6
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( { x^2 } + { y^2 } = 1,) (z = 1 — x.)
Решение:
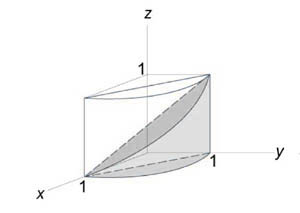
Как видно из рисунков, в области интегрирования (R) при (0 le x le 1) значения (y) изменяются от (1 — x) до (sqrt { 1 — { x^2 } } .)
Сверху тело ограничено плоскостью (z = 1 — x.) Следовательно, объем данного тела равен $ { V = iintlimits_R { left( { 1 — x }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_ { 1 — x } ^ { sqrt { 1 — { x^2 } } } { left( { 1 — x }right)dy } }right]dx } } = { intlimits_0^1 { left[ { left( { 1 — x }right)left. y right|_ { 1 — x } ^ { sqrt { 1 — { x^2 } } } }right]dx } } = { intlimits_0^1 { left( { 1 — x }right)left( { sqrt { 1 — { x^2 } } — 1 + x }right)dx } } = \ = { intlimits_0^1 { left( { sqrt { 1 — { x^2 } } — xsqrt { 1 — { x^2 } } — 1 + 2x — { x^2 } }right)dx } } = { intlimits_0^1 { sqrt { 1 — { x^2 } } dx } } — { intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } } — { intlimits_0^1 { left( { 1 + 2x — { x^2 } }right)dx } . } $
Вычислим полученные три интеграла отдельно. $ { I_1 } = intlimits_0^1 { sqrt { 1 — { x^2 } } dx } .$ Сделаем замену: (x = sin t.) Тогда (dx = cos tdt.) Видно, что (t = 0) при (x = 0) и (t = largefrac { pi } { 2 } normalsize) при (x = 1.) Следовательно, $ { { I_1 } = intlimits_0^1 { sqrt { 1 — { x^2 } } dx } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { sqrt { 1 — { { sin } ^2 } t } cos tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { cos } ^2 } tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { frac { { 1 + cos 2t } } { 2 } dt } } = { frac { 1 } { 2 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { left( { 1 + cos 2t }right)dt } } = { frac { 1 } { 2 } left. { left( { t + frac { { sin 2t } } { 2 } }right) }right|_0^ { largefrac { pi } { 2 } normalsize } } = { frac { 1 } { 2 } left( { frac { pi } { 2 } + frac { { sin pi } } { 2 } }right) = frac { pi } { 4 } . } $ { Сравните с площадью сектора единичного круга в первом квадранте).
Вычислим второй интеграл ( { I_2 } = intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } ,) используя замену переменной. Полагаем (1 — { x^2 } = w.) Тогда (-2xdx = dw) или (xdx = largefrac { { — dw } } { 2 } normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ { { I_2 } = intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } } = { intlimits_1^0 { sqrt w left( { — frac { { dw } } { 2 } }right) } } = { — frac { 1 } { 2 } intlimits_1^0 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { { w^ { largefrac { 1 } { 2 } normalsize } } dw } } = { frac { 1 } { 2 } left. { left( { frac { { 2 { w^ { largefrac { 3 } { 2 } normalsize } } } } { 3 } }right) }right|_0^1 = frac { 1 } { 3 } . } $ Наконец, вычислим третий интеграл. $require { cancel } { { I_3 } = intlimits_0^1 { left( { 1 — 2x + { x^2 } }right)dx } } = { left. { left( { x — { x^2 } + frac { { { x^3 } } } { 3 } }right) }right|_0^1 } = { cancel { 1 } — cancel { 1 } + frac { 1 } { 3 } = frac { 1 } { 3 } . } $ Таким образом, объем тела равен $ { V = { I_1 } — { I_2 } — { I_3 } } = { frac { pi } { 4 } — frac { 1 } { 3 } — frac { 1 } { 3 } = frac { pi } { 4 } — frac { 2 } { 3 } approx 0,12. } $
Пример 7
Вычислить объем единичного шара.
Решение:
Уравнение сферы радиусом (1) имеет вид ( { x^2 } + { y^2 } + { z^2 } = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = sqrt { 1 — left( { { x^2 } + { y^2 } }right) } .$ Преобразуя это уравнение в полярные координаты, получаем $zleft( { r,theta }right) = sqrt { 1 — { r^2 } } .$ В полярных координатах область интегрирования (R) описывается множеством (R = left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].) Следовательно, объем верхнего полушара выражается формулой $ { { V_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 — { r^2 } } rdrdtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } } = { 2pi intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } . } $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — { r^2 } = t.) Тогда (-2rdr = dt) или (rdr = — largefrac { { dt } } { 2 } normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ { { V_ { largefrac { 1 } { 2 } normalsize } } = 2pi intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } } = { 2pi intlimits_1^0 { sqrt t left( { — frac { { dt } } { 2 } }right) } } = { — pi intlimits_1^0 { sqrt t dt } } = { pi intlimits_0^1 { { t^ { largefrac { 1 } { 2 } normalsize } } dt } } = { pi left. { left( { frac { { { t^ { largefrac { 3 } { 2 } normalsize } } } } { { frac { 3 } { 2 } } } }right) }right|_0^1 } = { frac { { 2pi } } { 3 } . } $ Таким образом, объем единичного шара равен $V = 2 { V_ { largefrac { 1 } { 2 } normalsize } } = frac { { 4pi } } { 3 } .$
Пример 8
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).
Решение:
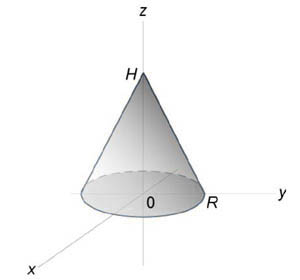
Сначала получим уравнение поверхности конуса. Используя подобные треугольники, можно записать $ { frac { r } { R } = frac { { H — z } } { H } , } ;; { text { где } ;;r = sqrt { { x^2 } + { y^2 } } . } $ Следовательно, $ { H — z = frac { { Hr } } { R } } ;; { text { или } ;;zleft( { x,y }right) } = { H — frac { { Hr } } { R } } = { frac { H } { R } left( { R — r }right) } = { frac { H } { R } left( { R — sqrt { { x^2 } + { y^2 } } }right). } $ Тогда объем конуса равен $ { V = iintlimits_R { zleft( { x,y }right)dxdy } } = { iintlimits_R { frac { H } { R } left( { R — sqrt { { x^2 } + { y^2 } } }right)dxdy } } = { frac { H } { R } iintlimits_R { left( { R — r }right)rdrdtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { left[ { intlimits_0^R { left( { R — r }right)drd } }right]dtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { dtheta } intlimits_0^R { left( { Rr — { r^2 } }right)dr } } = { frac { { 2pi H } } { R } intlimits_0^R { left( { Rr — { r^2 } }right)dr } } = \ = { frac { { 2pi H } } { R } left. { left( { frac { { R { r^2 } } } { 2 } — frac { { { r^3 } } } { 3 } }right) }right|_ { r = 0 } ^R } = { frac { { 2pi H } } { R } left( { frac { { { R^3 } } } { 2 } — frac { { { R^3 } } } { 3 } }right) } = { frac { { 2pi H } } { R } cdot frac { { { R^3 } } } { 6 } = frac { { pi { R^2 } H } } { 3 } . } $