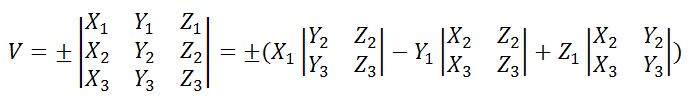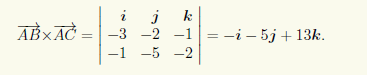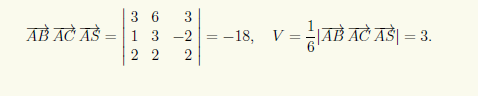Как найти объем параллелепипеда по координатам векторов

Объём параллелепипеда
равен
смешанному произведению векторов
на которых он построен:

Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:

Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.

Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.

Объём параллелепипеда

Объём параллелепипеда, построенного на трех векторах

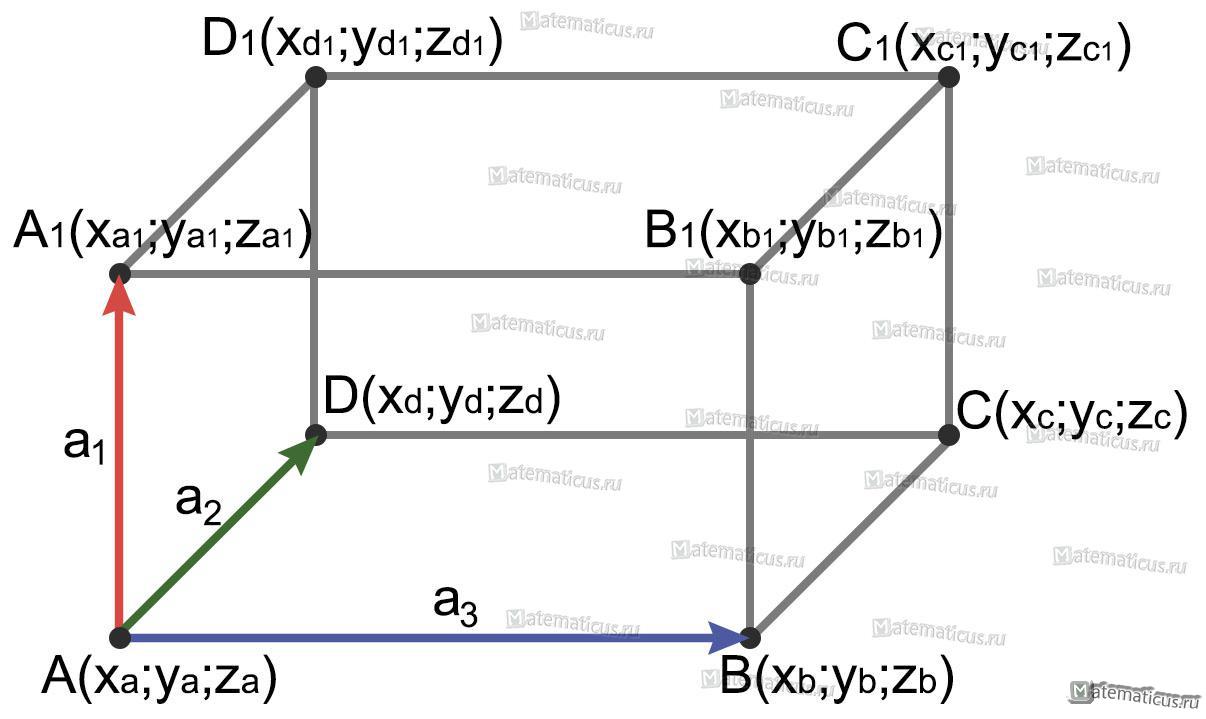
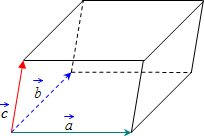
где координаты векторов в соответствии с рисунком

вычисляются следующим образом

Знак плюс берется, когда определитель третьего порядка положителен, а минус наоборот – знак отрицателен.

Найти объём параллелепипеда, построенного на векторах a₁=<2;3;2>, a₂= <-1;-4;3>и a₃=

$ = pm left( <2cdotleft( <left( < — 4>right)cdot2 — 1cdot3> right) — 3left( <left( < — 1>right)cdot2 — 3cdot3> right) + 2left( <left( < — 1>right)cdot1 — 3cdotleft( < — 4>right)> right)> right) = -33$

Так как определитель отрицателен, берем перед ним знак « − ».

Тогда объём параллелепипеда построенного на векторах равен V=33

Объем параллелепипеда, построенного на векторах онлайн

Объём параллелепипеда равен смешанному произведению векторов на которых он построен:

Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:

Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.

Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.

Вектор. Смешанное произведение векторов.

Также его называют тройным скалярным произведением векторов, скорее всего это связано с тем,

что результат — это скаляр (точнее — псевдоскаляр).

Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и .

Или другими словами:

Смешанным произведением векторов является число , состоящее из скалярного произведения вектора на векторное произведение векторов и . Смешанное произведение

векторов записывается следующим образом:

Геометрический смысл смешанного произведения векторов.

Геометрический смысл смешанного произведения векторов: если три вектора правые, то их

смешанное произведение равно объему параллелепипеда построенного на них:

.

В случае левой тройки , смешанное произведение указанных векторов равно объему

параллелепипеда со знаком “–“:

.

Если , и компланарны, то их смешанное произведение = 0.

Вывод: объем параллелепипеда, построенного на векторах , и равен модулю смешанного

произведения этих векторов:

Объем пирамиды, построенной на этой тройке этих векторов, находим по формуле:

Геометрические свойства смешанного произведения векторов.

1. Модуль смешанного произведения некомпланарных векторов равен объему

параллелепипеда, построенного на этих векторах. Произведение будет со знаком плюс, если

тройка векторов — правая, и будем иметь отрицательный знак, если тройка — левая,

2. Смешанное произведение =0 тогда и только тогда, когда векторы компланарны:

векторы компланарны.

Алгебраические свойства смешанного произведения векторов.

1. При перемене мест двух множителей смешанное произведение меняет знак на противоположный:

При циклической (круговой) перестановке множителей смешанное произведение остается без изменений:

2. Смешанное произведение линейно по любому множителю.

Первое свойство следует из первого геометрического свойства и свойств ориентации троек векторов, так

как от перестановки двух множителей местами, модуль смешанного произведения остается прежним, а

изменяется только ориентация тройки. При циклической перестановке векторов ориентация тройки

остается без изменений.

Второе свойство следует из линейности скалярного произведения и первого свойства.

Формула вычисления смешанного произведения векторов.

Теорема (формула вычисления смешанного произведения векторов):

Если у векторов в правом ортонормированном базисе координаты, ,

соответственно, то смешанное произведение их вычисляется по следующей формуле:

Из определения следует:

что и требовалось доказать.

Еще некоторые свойства смешанного произведения векторов.

1.

2.

3 .Три вектора компланарны в том случае, если

4. Тройка векторов будет правой только если . Ежели , то векторы, и

создают левую тройку векторов.

5.

6.

7.

8.

9.

10. Тождество Якоби:

Если векторы , и заданы своими координатами, то их

смешанное произведение можно найти по формуле, приведенной ниже:

Skip to content

Объём параллелепипеда, построенного на трех векторах

a₁={X₁;Y₁;Z₁}, a₂={X₂;Y₂;Z₂} и a₃={X₃;Y₃;Z₃} равен модулю смешанного произведения векторов и  находится по формуле:

где координаты векторов в соответствии с рисунком

вычисляются следующим образом

a₁=$overrightarrow {AA_1} $={X₁=X_a1-X_a; Y₁=Y_a1-Y_a; Z₁=Z_a1-Z_a; }

a₂=$overrightarrow {AD} $={X₂=X_d-X_a; Y₂=Y_d-Y_a; Z₂=Z_d-Z_a; }

a₃=$overrightarrow {AB} $={X₃=X_b-X_a; Y₃=Y_b-Y_a; Z₃=Z_b-Z_a; }

  Знак плюс берется, когда определитель третьего порядка положителен, а минус наоборот – знак отрицателен.

---

Пример

  Найти объём параллелепипеда, построенного на векторах a₁={2;3;2}, a₂={-1;-4;3} и a₃={3;1;2}

Решение

$V =  pm left| {begin{array}{*{20}{c}}2&3&2 \  { — 1}&{ — 4}&3 \ 3&1&2 end{array}} right| =  pm left( {2left| {begin{array}{*{20}{c}} { — 4}&3 \ 1&2 end{array}} right| — 3left| {begin{array}{*{20}{c}}{ — 1}&3 \ 3&2 end{array}} right| + 2left| {begin{array}{*{20}{c}}{ — 1}&{ — 4} \ 3&1 end{array}} right|} right) = $

$ =  pm left( {2cdotleft( {left( { — 4} right)cdot2 — 1cdot3} right) — 3left( {left( { — 1} right)cdot2 — 3cdot3} right) + 2left( {left( { — 1} right)cdot1 — 3cdotleft( { — 4} right)} right)} right) = -33$

  Так как определитель отрицателен, берем перед ним знак «−».

Тогда объём параллелепипеда построенного на векторах равен  V=33

16878

Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.

Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.

Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3; —1;2).

Для определения площади ΔABC с помощью (4.10) найдем координаты векторов AB и AC: AB = {1 — 4; 2 — 4; 3 — 4} = { — 3; —2; —1}, —1 = {3 — 4; —1 — 4; 2 — 4} = { — 1; —5; —2}.

Затем по (3.2) вычислим их векторное произведение:

Модуль этого векторного произведения равен |AB×AC| = √((—1)² + (—5)² + 13²) = √195, и следовательно, S ΔABC = |AB×AC|/2 = √195/2 #

Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах AB, AC и AS. Таким образом, объем этой пирамиды равен VSABC = |ABACAS|/6.

Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; —1;1), B(5; 5; 4), C(3; 2; —1), S(4;1;3).

Используя (4.10), вычисляем координаты векторов, направленных по ребрам пирамиды: AB = {5 — 2; 5 — (—1);4 — 1} = {3; 6; 3}, AC = {3 — 2; 2 — (—1); —1 — 1} = {1;3; —2},= AS {4 — 2;1 — (—1); 3 — 1} = {2;2;2}, и определяем объем с помощью смешанного произведения найденных векторов:

Ошибка в том, что произведение длин векторов и произведение векторов это разные вещи. Произведение векторов дает на плоскости площадь параллелограмма, то есть произведение длин векторов на синус угла между ними. А в пространстве Ваше решение было бы верным, если бы углы между векторами были прямыми, то есть синус был бы равен 1.

При решении задачи нужно было определить по координатам точек координаты векторов

вектор АВ(1,-4,-2)

вектор АD(1,2,-4)

вектор АА1(-4,-1,1)

и перемножить вектора, удобно матрицей

| 1 -4 -2|

V= | 1 2 -4|= 2+4-4-16+64-2=48

|-4 -1 1|