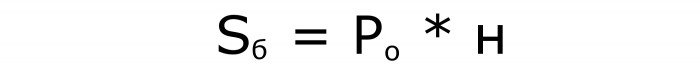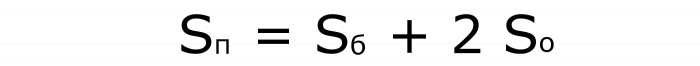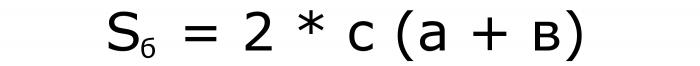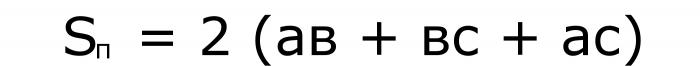ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
Гранью параллелепипеда является ромб
Дата: 2022-06-08
462
Категория: Стерео Куб Парал-ед
Метка: ЕГЭ-№2
27104. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60 градусов. Одно из ребер параллелепипеда составляет с этой гранью угол в 60 градусов и равно 2. Найдите объем параллелепипеда.
Покажем на эскизе заданные размеры:
Где S – площадь основания параллелепипеда
h – высота параллелепипеда
Площадь ромба (основание параллелепипеда) с острым углом в 60° равна двум площадям равносторонних треугольников:
*Использовали формулу: площадь треугольника равна половине произведения соседних сторон на синус угла межу ними.
Высоту можем найти из прямоугольного треугольника, в котором нам известна гипотенуза равная двум и острый угол 60°. По определению синуса в прямоугольном треугольнике:Вычислим объем:
Ответ: 1,5
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok
Часто ученики возмущенно спрашивают: «Как мне в жизни это пригодится?». На любую тему каждого предмета. Не становится исключением и тема про объем параллелепипеда. И вот здесь как раз можно сказать: «Пригодится».
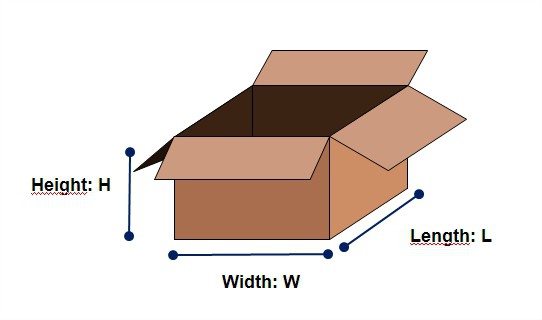
Как, например, узнать, поместится ли в почтовую коробку посылка? Конечно, можно методом проб и ошибок выбрать подходящую. А если такой возможности нет? Тогда на выручку придут вычисления. Зная вместимость коробки, можно рассчитать объем посылки (хотя бы приблизительно) и ответить на поставленный вопрос.
Параллелепипед и его виды
Если дословно перевести его название с древнегреческого, то получится, что это фигура, состоящая из параллельных плоскостей. Существуют такие равносильные определения параллелепипеда:
- призма с основанием в виде параллелограмма;
- многогранник, каждая грань которого — параллелограмм.
Его виды выделяются в зависимости от того, какая фигура лежит в его основании и как направлены боковые ребра. В общем случае говорят о наклонном параллелепипеде, у которого основание и все грани — параллелограммы. Если у предыдущего вида боковые грани станут прямоугольниками, то его нужно будет называть уже прямым. А у прямоугольного и основание тоже имеет углы по 90º.
Причем последний в геометрии стараются изображать так, чтобы было заметно, что все ребра параллельны. Здесь, кстати, наблюдается основное отличие математиков от художников. Последним важно передать тело с соблюдением закона перспективы. И в этом случае параллельность ребер совсем незаметна.
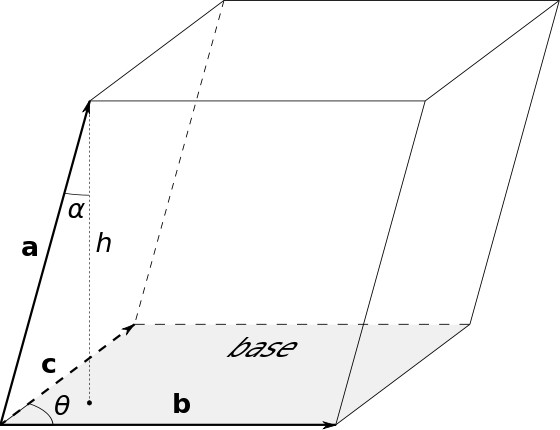
О введенных обозначениях
В приведенных ниже формулах справедливы обозначения, указанные в таблице.
| Величина | Ее обозначение |
| длины ребер основания | а, в |
| длина бокового ребра | с |
| высота | н |
| площадь основания | Sо |
| площадь боковой поверхности | Sб |
| площадь всей поверхности | Sп |
| периметр основания | Ро |
| объем | V |
Формулы для наклонного параллелепипеда
Первая и вторая для площадей:
Третья для того, чтобы вычислить объем параллелепипеда:
Так как основание — параллелограмм, то для расчета его площади нужно будет воспользоваться соответствующими выражениями.
Формулы для прямоугольного параллелепипеда
Аналогично первому пункту — две формулы для площадей:
И еще одна для объема:
Первая задача
Условие. Дан прямоугольный параллелепипед, объем которого требуется найти. Известна диагональ — 18 см — и то, что она образует углы в 30 и 45 градусов с плоскостью боковой грани и боковым ребром соответственно.
Решение. Чтобы ответить на вопрос задачи, потребуется узнать все стороны в трех прямоугольных треугольниках. Они дадут необходимые значения ребер, по которым нужно сосчитать объем.
Сначала нужно выяснить, где находится угол в 30º. Для этого нужно провести диагональ боковой грани из той же вершины, откуда чертилась главная диагональ параллелограмма. Угол между ними и будет тем, что нужен.
Первый треугольник, который даст одно из значений сторон основания, будет следующим. В нем содержатся искомая сторона и две проведенные диагонали. Он прямоугольный. Теперь потребуется воспользоваться отношением противолежащего катета (стороны основания) и гипотенузы (диагонали). Оно равно синусу 30º. То есть неизвестная сторона основания будет определяться как диагональ, умноженная на синус 30º или ½. Пусть она будет обозначена буквой «а».
Это легко сосчитать: а = 18 * ½ = 9 (см).
Вторым будет треугольник, содержащий известную диагональ и ребро, с которым она образует 45º. Он тоже прямоугольный, и можно опять воспользоваться отношением катета к гипотенузе. Другими словами, бокового ребра к диагонали. Оно равно косинусу 45º. То есть «с» вычисляется как произведение диагонали на косинус 45º.
с = 18 * 1/√2 = 9 √2 (см).
В этом же треугольнике требуется найти другой катет. Это необходимо для того, чтобы потом сосчитать третью неизвестную — «в». Пусть она будет обозначена буквой «х». Ее легко вычислить по теореме Пифагора:
х = √(182 — (9√2)2) = 9√2 (см).
Теперь нужно рассмотреть еще один прямоугольный треугольник. Он содержит уже известные стороны «с», «х» и ту, что нужно сосчитать, «в»:
в = √((9√2)2 — 92 = 9 (см).
Все три величины известны. Можно воспользоваться формулой для объема и сосчитать его:
V = 9 * 9 * 9√2 = 729√2 (см3).
Ответ: объем параллелепипеда равен 729√2 см3.
Вторая задача
Условие. Требуется найти объем параллелепипеда. В нем известны стороны параллелограмма, который лежит в основании, 3 и 6 см, а также его острый угол — 45º. Боковое ребро имеет наклон к основанию в 30º и равно 4 см.
Решение. Для ответа на вопрос задачи нужно взять формулу, которая была записана для объема наклонного параллелепипеда. Но в ней неизвестны обе величины.
Площадь основания, то есть параллелограмма, будет определена по формуле, в которой нужно перемножить известные стороны и синус острого угла между ними.
Sо = 3 * 6 sin 45º = 18 * (√2)/2 = 9 √2 (см2).
Вторая неизвестная величина — это высота. Ее можно провести из любой из четырех вершин над основанием. Ее найти можно из прямоугольного треугольника, в котором высота является катетом, а боковое ребро — гипотенузой. При этом угол в 30º лежит напротив неизвестной высоты. Значит, можно воспользоваться отношением катета к гипотенузе.
н = 4 * sin 30º = 4 * 1/2 = 2.
Теперь все значения известны и можно вычислить объем:
V = 9 √2 * 2 = 18 √2 (см3).
Ответ: объем равен 18 √2 см3.
Третья задача
Условие. Найти объем параллелепипеда, если известно, что он прямой. Стороны его основания образуют параллелограмм и равны 2 и 3 см. Острый угол между ними 60º. Меньшая диагональ параллелепипеда равна большей диагонали основания.
Решение. Для того чтобы узнать объем параллелепипеда, воспользуемся формулой с площадью основания и высотой. Обе величины неизвестны, но их несложно вычислить. Первая из них высота.
Поскольку меньшая диагональ параллелепипеда совпадает по размеру с большей основания, то их можно обозначить одной буквой d. Больший угол параллелограмма равен 120º, поскольку с острым он образует 180º. Пусть вторая диагональ основания будет обозначена буквой «х». Теперь для двух диагоналей основания можно записать теоремы косинусов:
d2 = а2 + в2 — 2ав cos 120º,
х2 = а2 + в2 — 2ав cos 60º.
Находить значения без квадратов не имеет смысла, так как потом они будут снова возведены во вторую степень. После подстановки данных получается:
d2 = 22 + 32 — 2 * 2 * 3 cos 120º = 4 + 9 + 12 * ½ = 19,
х2 = а2 + в2 — 2ав cos 60º = 4 + 9 — 12 * ½ = 7.
Теперь высота, она же боковое ребро параллелепипеда, окажется катетом в треугольнике. Гипотенузой будет известная диагональ тела, а вторым катетом — «х». Можно записать Теорему Пифагора:
н2 = d2 — х2 = 19 — 7 = 12.
Отсюда: н = √12 = 2√3 (см).
Теперь вторая неизвестная величина — площадь основания. Ее можно сосчитать по формуле, упомянутой во второй задаче.
Sо = 2 * 3 sin 60º = 6 * √3/2 = 3√3 (см2).
Объединив все в формулу объема, получаем:
V = 3√3 * 2√3 = 18 (см3).
Ответ: V = 18 см3.
Четвертая задача
Условие. Требуется узнать объем параллелепипеда, отвечающего таким условиям: основание — квадрат со стороной 5 см; боковые грани являются ромбами; одна из вершин, находящихся над основанием, равноудалена от всех вершин, лежащих в основании.
Решение. Сначала нужно разобраться с условием. С первым пунктом про квадрат вопросов нет. Второй, про ромбы, дает понять, что параллелепипед наклонный. Причем все его ребра равны 5 см, поскольку стороны у ромба одинаковые. А из третьего становится ясно, что три диагонали, проведенные из нее, равны. Это две, которые лежат на боковых гранях, а последняя внутри параллелепипеда. И эти диагонали равны ребру, то есть тоже имеют длину 5 см.
Для определения объема будет нужна формула, записанная для наклонного параллелепипеда. В ней опять нет известных величин. Однако площадь основания вычислить легко, потому что это квадрат.
Sо = 52 = 25 (см2).
Немного сложнее обстоит дело с высотой. Она будет таковой в трех фигурах: параллелепипеде, четырехугольной пирамиде и равнобедренном треугольнике. Последним обстоятельством и нужно воспользоваться.
Поскольку она высота, то является катетом в прямоугольном треугольнике. Гипотенузой в нем будет известное ребро, а второй катет равен половине диагонали квадрата (высота — она же и медиана). А диагональ основания найти просто:
d = √(2 * 52) = 5√2 (см).
Высоту нужно будет сосчитать как разность второй степени ребра и квадрата половины диагонали и не забыть потом извлечь квадратный корень:
н = √ (52 — (5/2 * √2)2) = √(25 — 25/2) = √(25/2) = 2,5 √2 (см).
Осталось сосчитать объем:
V = 25 * 2,5 √2 = 62,5 √2 (см3).
Ответ: 62,5 √2 (см3).

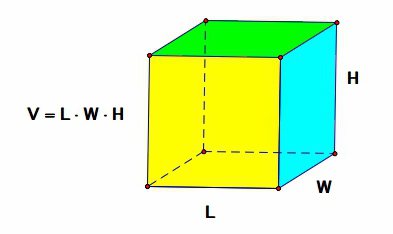
{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
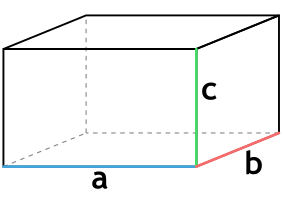
Формула объема прямоугольного параллелепипеда через три стороны
{V= a cdot b cdot c}
a — длина параллелепипеда
b — ширина параллелепипеда
c — высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab — это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
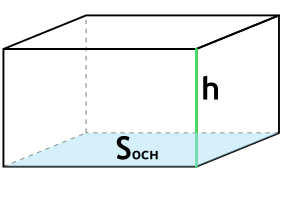
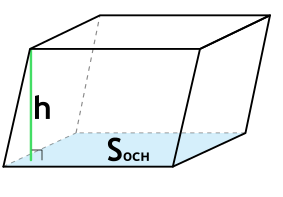
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн — площадь основания параллелепипеда
h — высота параллелепипеда
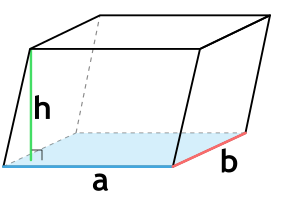
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
{V= a cdot b cdot h}
a — длина основания параллелепипеда
b — ширина основания параллелепипеда
h — высота параллелепипеда
Формула объема наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн — площадь основания параллелепипеда
h — высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Грани параллелепипеда — равные ромбы со стороной а и острым углом 60°. Найдите объем параллелепипеда.
Задача из пособия: Погорелов А.В. 11 класс
22. Объемы многогранников
Решение
Далее
Смотрите также: