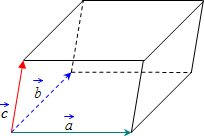
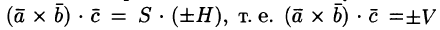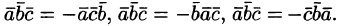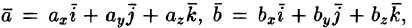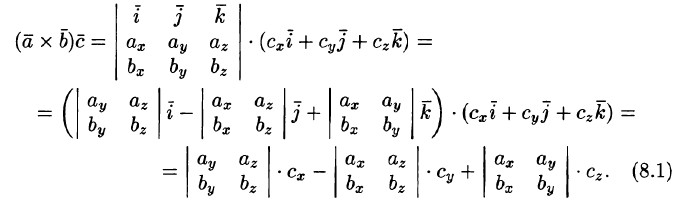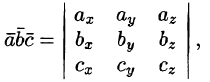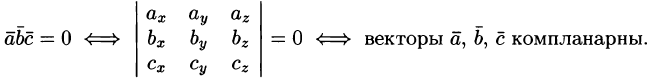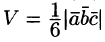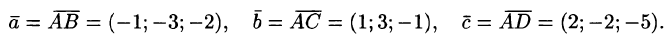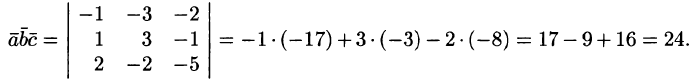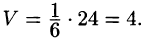Параллелепипед — это призма, основанием которой является параллелограмм.
Онлайн-калькулятор объема параллелепипеда
Как и у куба, у этого многогранного тела есть двенадцать ребер, шесть граней и восемь вершин. Вид параллелепипеда зависит от геометрической фигуры, лежащей в основании, и от угла, образованного им при пересечении с гранями.
Если его гранями являются прямоугольники, то он называется прямоугольным.
Если такие прямоугольники имеют отношение только к боковым граням, то он называется прямым.
Иногда бывают случаи, когда эти грани образуют не прямой угол с основанием. Тогда в данном случае параллелепипед является наклонным.
Если он состоит исключительно из равных ромбов, то он называется ромбоэдром.
Если все грани параллелепипеда являются одинаковыми квадратами, то получаем куб. Таким образом, куб — это частный случай параллелепипеда.
Формула объема прямоугольного параллелепипеда
Объемом такого параллелепипеда называется произведение всех его трех измерений: длины, ширины, высоты. Вычисляется он так:
V=a⋅b⋅cV=acdot bcdot c
a,b,ca, b, c — длина, ширина и высота прямоугольного параллелепипеда.
Рассмотрим несколько примеров.
Найти объем прямоугольного параллелепипеда, если известны его длина, равная 5 см.5text{ см.}, ширина, имеющая длину 10 см.10text{ см.} и высота длиной в 7 см.7text{ см.}
Решение
a=5a=5
b=10b=10
c=7c=7
Сразу подставляем в формулу численные значения:
V=a⋅b⋅c=5⋅10⋅7=350 см3V=acdot bcdot c=5cdot 10cdot 7=350text{ см}^3
Ответ
350 см3.350text{ см}^3.
Формула объема наклонного параллелепипеда
V=Sосн⋅hV=S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания наклонного параллелепипеда;
hh — его высота.
Вычислить объем наклонного параллелепипеда, если в его основании лежит прямоугольник со сторонами в 4 см.4text{ см.} и 5 см.5text{ см.}, а высота его равна 10 см.10text{ см.}
Решение
a=4a=4
b=5b=5
h=10h=10
Находим площадь основания, то есть площадь прямоугольника:
Sосн=a⋅b=4⋅5=20S_{text{осн}}=acdot b=4cdot 5=20
Сам объем равен:
V=Sосн⋅h=20⋅10=200 см3V=S_{text{осн}}cdot h=20cdot 10=200text{ см}^3
Ответ
200 см3.200text{ см}^3.
Формула объема параллелепипеда через определитель
Альтернативным способом нахождения объема параллелепипеда является вычисление смешанного произведения векторов, на которых построен данный параллелепипед.
Пусть параллелепипед построен на векторах a⃗vec{a}, b⃗vec{b} и c⃗vec{c} с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующего параллелепипеда это определитель, составленный из этих координат:
V=∣axayazbxbybzcxcycz∣V=begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем параллелепипеда через смешанное произведение векторов, координаты которых таковы: a⃗=(2,3,5)vec{a}=(2, 3, 5), b⃗=(1,4,4)vec{b}=(1, 4, 4), c⃗=(3,5,7)vec{c}=(3, 5, 7).
Решение
a⃗=(2,3,5)vec{a}=(2, 3, 5)
b⃗=(1,4,4)vec{b}=(1, 4, 4)
c⃗=(3,5,7)vec{c}=(3, 5, 7)
По формуле:
V=∣235144357∣=2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7=56+36+25−60−40−21=−4V=begin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 — 5cdot4cdot3 — 2cdot4cdot5 — 3cdot1cdot7 = 56 + 36 + 25 — 60 — 40 — 21 = -4
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=4 см3V=4text{ см}^3
Ответ
4 см3.4text{ см}^3.
У вас не получается решить задачу по геометрии? Наши эксперты помогут вам!
Тест по теме «Объем параллелепипеда»
Решение
По
формуле (2.33)
.
,
так как соединяет точку
с началом координат. По условию
.
По
формуле
Т.о.,
.
Смешанное произведение трех векторов
Определение
Смешанным произведением трех векторов
и
называется число, полученное, если
перемножить векторыи
векторно,
а потом полученный вектор умножить
скалярно на вектор.
Поэтому это произведение еще называется
векторно-скалярным произведением.
Смешанное произведение записывается
таким образом:,
т.е..
С
геометрической точки зрения смешанное
произведение некомпланарных векторов
и
по модулю равно объему параллелепипеда,
построенного на векторах.
Если
векторы
и
заданы координатами в прямоугольной
системе координат
то
можно показать, что

Если
,
то это означает, что параллелепипед на
этих векторах построить нельзя, то есть
векторыи
лежат в одной плоскости, ведь

условие компланарности векторов
и
.
Смешанное
произведение имеет такие свойства:
1)
— операции скалярного и векторного
произведений можно менять местами,
поэтому смешанное произведение записывают
еще в виде;
2)
круговая перестановка множителей не
изменяет величины смешанного произведения
;
3)
перестановка двух соседних множителей
изменяет знак произведения на
противоположный
.
Пример.
Найти объем пирамиды с вершинами
и
Решение
Как
известно из элементарной геометрии,
объем пирамиды
равен
одной шестой объема параллелепипеда,
построенного на векторах
та
.
Поэтому найдем координаты этих векторов
Вычислим
объем параллелепипеда, то есть за
формулой (2.34) найдем смешанное произведение
векторов
и
:
Отсюда
=
84 куб. ед.
Пример
Показать, что точки
и
лежат в одной плоскости.
Решение
Точки
и
будут лежать в одной плоскости, если
векторыи
компланарны. Найдем координаты этих
векторов:Вычислим смешанное произведение этих
векторов
Равенство
нулю смешанного произведения есть
необходимым и достаточным условием
компланарности векторов
и
,
а значит, точкии
принадлежат одной плоскости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Объём параллелепипеда
равен
смешанному произведению векторов
на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Объем параллелепипеда, построенного на векторах онлайн
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Вектор. Смешанное произведение векторов.
Также его называют тройным скалярным произведением векторов, скорее всего это связано с тем,
что результат — это скаляр (точнее — псевдоскаляр).
Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и .
Или другими словами:
Смешанным произведением векторов является число , состоящее из скалярного произведения вектора на векторное произведение векторов и . Смешанное произведение
векторов записывается следующим образом:
Геометрический смысл смешанного произведения векторов.
Геометрический смысл смешанного произведения векторов: если три вектора правые, то их
смешанное произведение равно объему параллелепипеда построенного на них:
.
В случае левой тройки , смешанное произведение указанных векторов равно объему
параллелепипеда со знаком “–“:
.
Если , и компланарны, то их смешанное произведение = 0.
Вывод: объем параллелепипеда, построенного на векторах , и равен модулю смешанного
произведения этих векторов:
Объем пирамиды, построенной на этой тройке этих векторов, находим по формуле:
Геометрические свойства смешанного произведения векторов.
1. Модуль смешанного произведения некомпланарных векторов равен объему
параллелепипеда, построенного на этих векторах. Произведение будет со знаком плюс, если
тройка векторов — правая, и будем иметь отрицательный знак, если тройка — левая,
2. Смешанное произведение =0 тогда и только тогда, когда векторы компланарны:
векторы компланарны.
Алгебраические свойства смешанного произведения векторов.
1. При перемене мест двух множителей смешанное произведение меняет знак на противоположный:
При циклической (круговой) перестановке множителей смешанное произведение остается без изменений:
2. Смешанное произведение линейно по любому множителю.
Первое свойство следует из первого геометрического свойства и свойств ориентации троек векторов, так
как от перестановки двух множителей местами, модуль смешанного произведения остается прежним, а
изменяется только ориентация тройки. При циклической перестановке векторов ориентация тройки
остается без изменений.
Второе свойство следует из линейности скалярного произведения и первого свойства.
Формула вычисления смешанного произведения векторов.
Теорема (формула вычисления смешанного произведения векторов):
Если у векторов в правом ортонормированном базисе координаты, ,
соответственно, то смешанное произведение их вычисляется по следующей формуле:
Из определения следует:
что и требовалось доказать.
Еще некоторые свойства смешанного произведения векторов.
1.
2.
3 .Три вектора компланарны в том случае, если
4. Тройка векторов будет правой только если . Ежели , то векторы, и
создают левую тройку векторов.
5.
6.
7.
8.
9.
10. Тождество Якоби:
Если векторы , и заданы своими координатами, то их
смешанное произведение можно найти по формуле, приведенной ниже:
Правило параллелепипеда. Разложение вектора
Вы будете перенаправлены на Автор24
Правило параллелепипеда
Для правила сложения трех векторов рассмотрим следующую задачу.
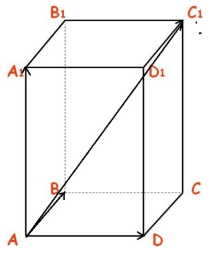
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Доказательство.
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$
Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.
Разложение вектора по двум неколлинеарным векторам
Вспомним сначала, какие векторы называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Произвольный вектор $overrightarrow
$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.
Математически это можно записать следующим образом
Доказательство.
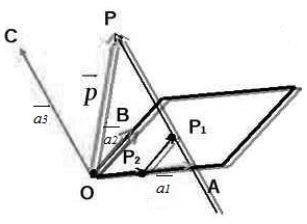
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:
[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow
=overrightarrow]
Рассмотрим следующий рисунок:
Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Тогда, получаем, что
Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow
$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:
Вычтем эти разложения друг из друга
Из этого получаем
Теорема доказана.
http://www.calc.ru/Vektor-Smeshannoye-Proizvedeniye-Vektorov.html
http://spravochnick.ru/matematika/dekartovy_koordinaty_i_vektory_v_prostranstve/pravilo_parallelepipeda_razlozhenie_vektora/
Определение смешанного произведения, его геометрический смысл:
Рассмотрим произведение векторов 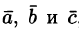
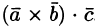
Выясним геометрический смысл выражения 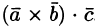
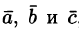
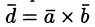
Имеем: 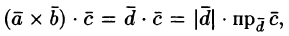
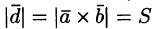
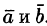
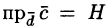
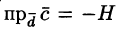
где V — объем параллелепипеда, образованного векторами 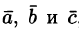
Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
Свойства смешанного произведения
1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е.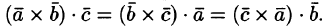
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. 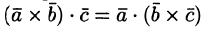
Действительно, 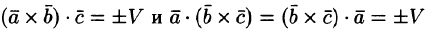
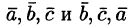
Следовательно, 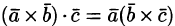
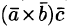
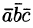
3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е.
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4. Смешанное произведение ненулевых векторов 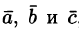
Если 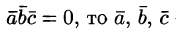
Допустим, что это не так. Можно было бы построить параллелепипед с объемом 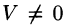
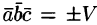
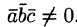
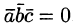
Обратно, пусть векторы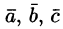
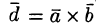
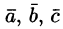
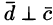
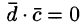
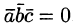
Выражение смешанного произведения через координаты
Пусть заданы векторы 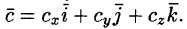
Полученную формулу можно записать короче:
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки. Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов 
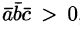
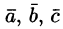
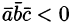
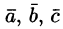
Установление компланарности векторов
Векторы 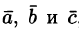
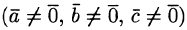
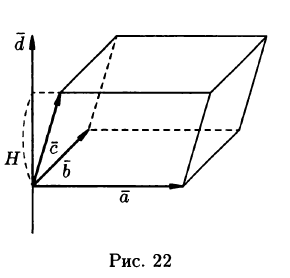
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах 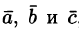
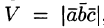
Пример:
Вершинами пирамиды служат точки A(1; 2;3), B(0; -1; 1), С(2;5;2) и D(3;0; -2). Найти объем пирамиды.
Решение:
Находим векторы 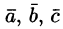
Находим 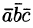
Следовательно,
Определение смешанного произведения, его геометрический смысл
Рассмотрим произведение векторов 

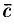
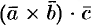
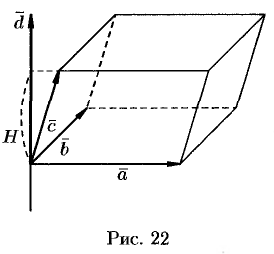
Выясним геометрический смысл выражения 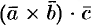


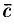
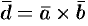
Имеем: 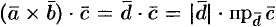
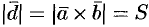
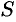
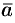

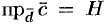
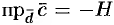
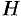
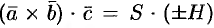
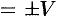


Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. 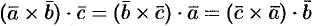
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. 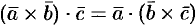
Действительно, 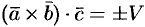
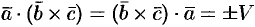


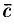

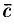

Следовательно, 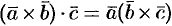
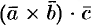
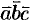
3.Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. 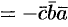
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4. Смешанное произведение ненулевых векторов 

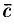
Если 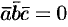


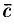
Допустим, что это не так. Можно было бы построить параллелепипед с объемом 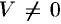
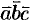
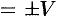
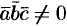
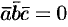
Обратно, пусть векторы 

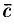


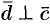
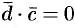
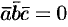
Другие темы по высшей математике возможно вам они будут полезны:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат