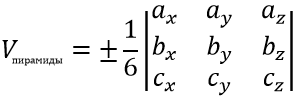© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Пирамида (др.-греч. πυραμίς, πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.
Лемма
Две пирамиды, имеющие равные высоты и равновеликие основания, имеют равные объемы.
Теорема
Объем пирамиды равен одной трети произведения площади основания на высоту: (V={1over3}S*H) , где S – площадь основания, H – высота пирамиды.
Теорема
Объем V усеченной пирамиды может быть найден по формуле (V={1over3}H(S1+{{sqrt {S1S2}}}+S2)), где H – высота усеченной пирамиды, S1 и S2 – площади ее оснований.
Часто даны координаты вершин пирамиды ABCD и требуется найти ее объем. Даная задача может быть решена методами аналитической геометрии. Покажем ее решение на примере.
Пусть даны координаты вершин пирамиды ABCD и требуется найти ее объем: A(10;6;6), B(-2;8;2), C(6;8;9), D(7;10;3).
Решение
Объем пирамиды равен (1over6) объема параллелепипеда, построенного на векторах AB, AC, AD. Найдем координаты этих векторов, для этого из соответствующей координаты конца вектора вычтем координату его начала:
AB=(-12;2;-4), AC=(-4;2:3), AD=(-3;4;-3).
Тогда объем параллелепипеда равен значению детерминанта (определителя) матрицы, составленной из координат векторов (строка матрицы – координаты вектора). Определитель третьего порядка находим по правилу треугольников.
Автор — Дмитрий Айстраханов
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Аналитическая геометрия — задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное — разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
Skip to content
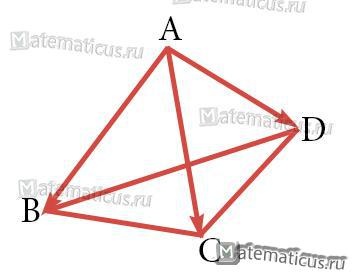
Объём треугольной пирамиды, построенной на векторах
Рисунок — Треугольная пирамида, построенная на векторах
Объём треугольной пирамиды (см. рисунок выше), построенной на векторах вычисляется по формуле:
Пример
Найти объём треугольной пирамиды, построенной на векторах ABCD c вершинами
А(2; -1; 1), B(5;5;4), C(3;2;-1), D(4;1;3).
Решение
Находим координаты векторов
$overrightarrow {AB} = left{ {left( {5 — 2} right);left( {5 — left( { — 1} right)} right);left( {4 — 1} right)} right} = left{ {3;6;3} right}$
$overrightarrow {AC} = left{ {left( {3 — 2} right);left( {2 — left( { — 1} right)} right);left( { — 1 — 1} right)} right} = left{ {1;3; — 2} right}$
$overrightarrow {AD} = left{ {left( {4 — 2} right);left( {1 — left( { — 1} right)} right);left( {2 — 1} right)} right} = left{ {2;2;2} right}$
Искомый объём равен $frac{1}{6}$ объём параллелепипеда, построенного на рёбрах,
$overrightarrow {AB} $, $overrightarrow {AС} $, $overrightarrow {AD} $, следовательно объем равен:
$V = pm frac{1}{6}left| {begin{array}{*{20}{c}}3&6&3 \ 1&3&{ — 2} \ 2&2&2 end{array}} right|=$
$ = pm frac{1}{6}cdotleft( {3cdotleft( {3cdot2 — left( { — 2} right)cdot2} right) — 6cdotleft( {1cdot2 — left( { — 2} right)cdot2} right) + 3cdotleft( {1cdot2 — 3cdot2} right)} right) = 3$
Решая, находим определитель матрицы третьего порядка и получаем искомый объём треугольной пирамиды V=3
17773
Расчет объема пирамиды
(по значениям координат 4-ех вершин)
На данной странице представлен онлайн калькулятор для расчета объема пирамиды по значениям
координат 4-ех вершин. Объем пирамиды Вы можете найти в режиме реального времени, просто введя свои данные!
На нашем сайте Вы найдете много программ для решения задач по геометрии.
См. также Вычисление объема пирамиды через площадь ее основания и высоту.
Введите координаты 4-ех вершин пирамиды:
| А: | ( | , | , | ) | Координаты точки А, 1-ой вершины. |
| В: | ( | , | , | ) | Координаты точки В, 2-ой вершины. |
| С: | ( | , | , | ) | Координаты точки С, 3-ей вершины. |
| D: | ( | , | , | ) | Координаты точки D, 4-ой вершины. |
Примеры нахождения объема пирамиды: Пример № 1,
Пример № 2
- Расчет объема шара
- Расчет объема куба
Если после использования данного онлайн калькулятора
(Расчет объема пирамиды) у Вас возникли какие-то вопросы по работе сервиса или вопросы
образовательного характера, то Вы всегда можете задать их на нашем
форуме.
Вы поняли, как решать? Нет?
Рассчитайте цену решения ваших задач


Калькулятор
стоимости
Решение контрольной
от 300 рублей
*
* Точная стоимость будет определена после загрузки задания для исполнителя
+Загрузить файл
Файлы doc, pdf, xls, jpg, png не более 5 МБ.