Как найти объем пирамиды хеопса

Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим формулы объема пирамиды как полной, так и усеченной.

Пирамида как объемная фигура

Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.

Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.

Вам будет интересно:Балбес – это кто? Сказка и реальность

Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:

2*n = (n+1) + (n+1) — 2.

Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.

Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.

Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.

Формула объема пирамиды

Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.

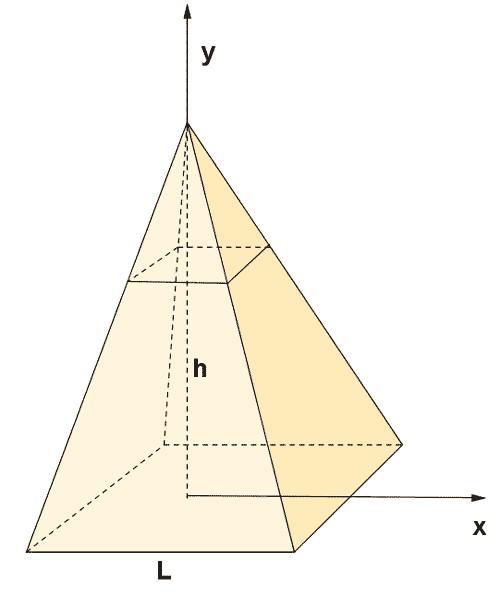
Площадь каждого такого слоя можно вычислить по формуле:

A(z) = A0*(h-z)2/h2.

Здесь A0 — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A0.

Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:

V = ∫h0(A(z)*dz).

Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:

V = -A0*(h-z)3/(3*h2)|h0 = 1/3*A0*h.

Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.

Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.

Правильная пирамида и ее объем

Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:

A0 = n/4*L2*ctg(pi/n).

Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.

Подставляя выражение для A0 в общую формулу, получаем объем правильной пирамиды:

Vn = 1/3*n/4*L2*h*ctg(pi/n) = n/12*L2*h*ctg(pi/n).

Например, для треугольной пирамиды эта формула приводит к следующему выражению:

V3 = 3/12*L2*h*ctg(60o) = √3/12*L2*h.

Для правильной четырехугольной пирамиды формула объема приобретает вид:

V4 = 4/12*L2*h*ctg(45o) = 1/3*L2*h.

Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.

Пирамида усеченная

Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.

Рисунок выше демонстрирует усеченную правильную шестиугольную пирамиду. Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.

Формула объема усеченной пирамиды, которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:

V = 1/3*h*(A0 + A1 + √(A0*A1)).

Где A0 и A1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.

Объем пирамиды Хеопса

Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.

В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.

Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:

V4 = 1/3*L2*h.

Подставляем цифры, получаем:

V4 = 1/3*(230,363)2*146,5 ≈ 2591444 м3.

Объем пирамиды Хеопса равен практически 2,6 млн м3. Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м3. То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!

Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим формулы объема пирамиды как полной, так и усеченной.

Пирамида как объемная фигура

Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.

Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.

Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:

2*n = (n+1) + (n+1) — 2.

Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.

Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.

Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.

Формула объема пирамиды

Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.

Площадь каждого такого слоя можно вычислить по формуле:

A(z) = A₀*(h-z)²/h².

Здесь A₀ — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A₀.

Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:

V = ∫^h₀(A(z)*dz).

Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:

V = -A₀*(h-z)³/(3*h²)|^h₀ = 1/3*A₀*h.

Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.

Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.

Правильная пирамида и ее объем

Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:

A₀ = n/ L²*ctg(pi/n).

Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.

Подставляя выражение для A₀ в общую формулу, получаем объем правильной пирамиды:

V_n = 1/3*n/ L²*h*ctg(pi/n) = n/12*L²*h*ctg(pi/n).

Например, для треугольной пирамиды эта формула приводит к следующему выражению:

V₃ = 3/12*L²*h*ctg(60^o) = √3/12*L²*h.

Для правильной четырехугольной пирамиды формула объема приобретает вид:

V₄ = 4/12*L²*h*ctg(45^o) = 1/3*L²*h.

Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.

Пирамида усеченная

Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.

Рисунок выше демонстрирует усеченную правильную шестиугольную пирамиду. Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.

Формула объема усеченной пирамиды, которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:

V = 1/3*h*(A₀ + A₁ + √(A₀*A₁)).

Где A₀ и A₁ — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.

Объем пирамиды Хеопса

Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.

В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.

Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:

V₄ = 1/3*L²*h.

Подставляем цифры, получаем:

V₄ = 1/3*(230,363)²*146,5 ≈ 2591444 м³.

Объем пирамиды Хеопса равен практически 2,6 млн м³. Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м³. То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!

Объем пирамиды – это характеристика объемного геометрического тела, указывающая на то, сколько внутри фигуры может вместиться единичных кубических элементов. Если вычисляется объем пирамиды Хеопса, единицей объема могут быть кубические метры.

Если рассматривается небольшая оптическая деталь того или иного проектируемого прибора, имеющая форму пирамиды, единицей измерения объема пирамиды могут быть кубические миллиметры. Калькулятор осуществляет вычисление объема пирамиды, основываясь на формуле, в которой исходными данными является высота и площадь основания: V = (1/3) х S х h. Исходные данные нужно задавать в одинаковых единицах меры длины.