© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Объем пирамиды
Если заданы координаты точек вершин пирамиды, то координаты векторов находятся по формуле:
X = xj — xi; Y = yj — yi; Z = zj — zi
где xi, yi, zi — координаты точки Аi; xj, yj, zj — координаты точки Аj;
Пример №2 . Найти объем пирамиды, отсекаемой от угла плоскостью, проходящей через точки А(0,2,-1), В(3,4,2), С(-3,0,4).
Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи
Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу — ответит приведенная ниже статья.
Что представляет собой пирамида?
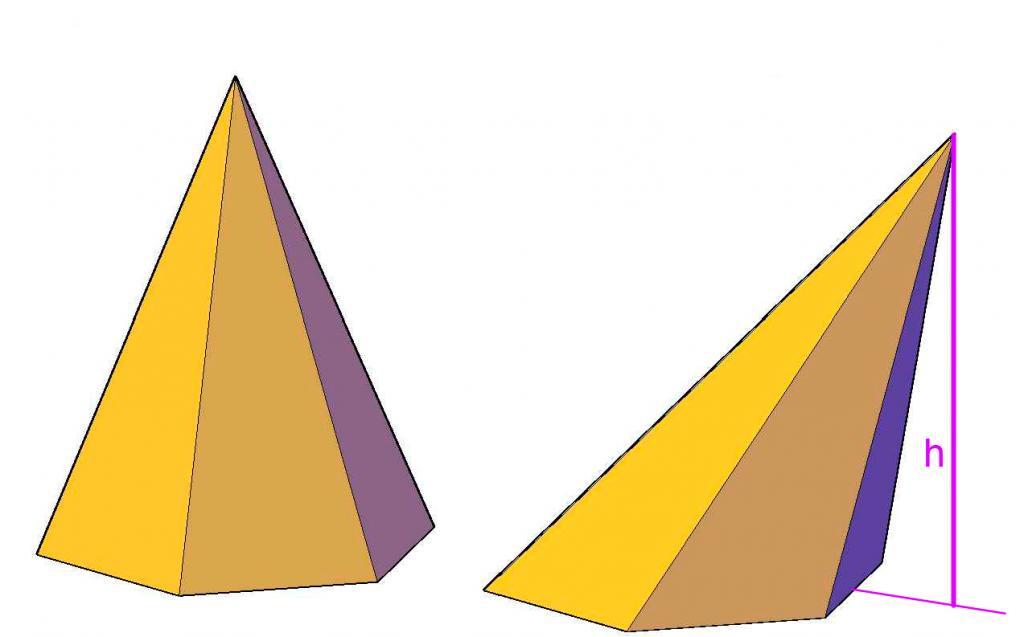
Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.
Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания — это высота фигуры.
Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.
Как рассчитывается объем пирамиды?
Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:
Здесь So — это основания площадь, h — расстояние от главной вершины до основания, то есть высота пирамиды.
Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.
Как найти объем пирамиды по координатам вершин: методика
Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.
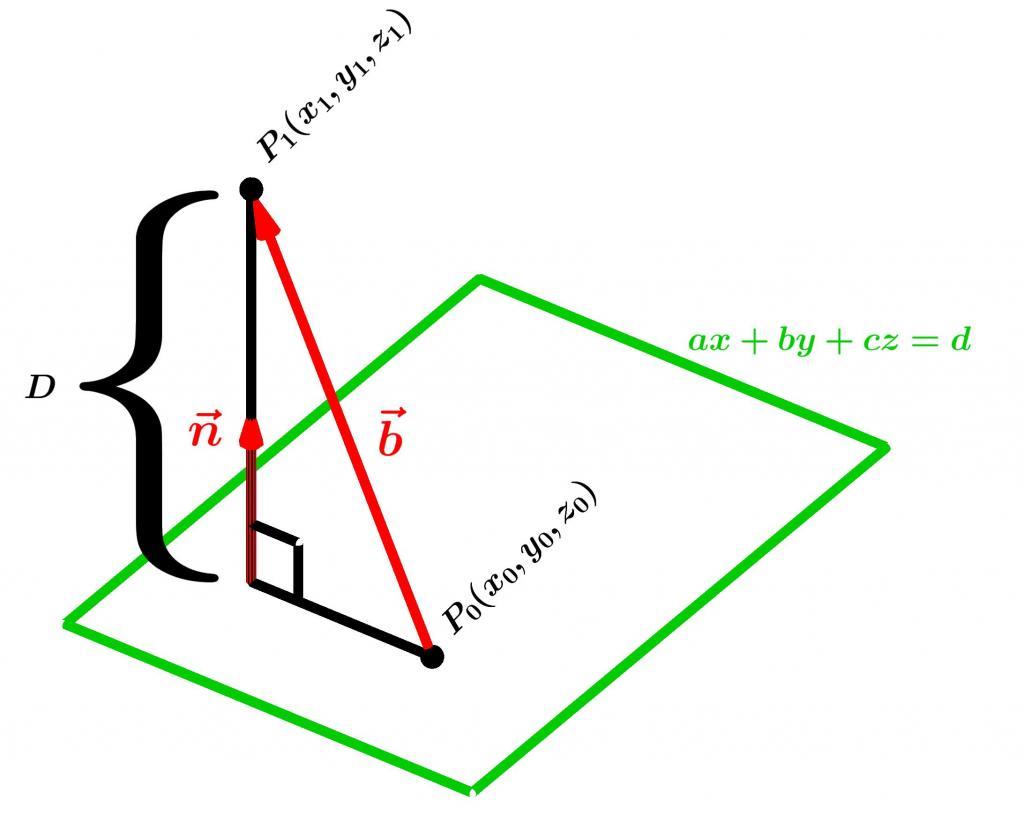
Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:
d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).
Здесь (x1; y1; z1) — координаты точки.
Уравнение плоскости имеет вид:
A * x + B * y + C * z + D = 0.
Задача с треугольной пирамидой
Решим задачу на примере самой простой пирамиды — треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:
Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:
Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:
n¯ = [AB¯ * AC¯] = (8; -10; -7).
Площадь треугольного основания равна полудлине вектора n¯, то есть:
So = √(82 + 102 + 72) / 2 = 7,3.
Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:
D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.
Тогда уравнение плоскости основания пирамиды принимает форму:
8 * x — 10 * y — 7 * z + 13 = 0.
Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:
d = |(8 * 4 — 10 * 3 — 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.
Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:
V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.
Полученное значение объема выражено в кубических единицах выбранной координатной системы.
Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.
Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.
Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Выберите каким образом задается пирамида (тетраэдр):
Введите значения векторов: Введите координаты вершин пирамиды:
Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Объем пирамиды (объем тетраэдра) построенной на векторах
Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://1ku.ru/obrazovanie/51574-kak-rasschitat-obem-piramidy-po-koordinatam-vershin-metodika-i-primer-zadachi/
http://ru.onlinemschool.com/math/assistance/vector/pyramid_volume/
Skip to content
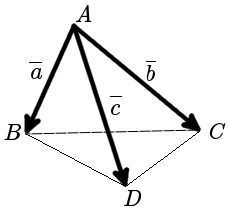
Объём треугольной пирамиды, построенной на векторах
Рисунок — Треугольная пирамида, построенная на векторах
Объём треугольной пирамиды (см. рисунок выше), построенной на векторах вычисляется по формуле:
Пример
Найти объём треугольной пирамиды, построенной на векторах ABCD c вершинами
А(2; -1; 1), B(5;5;4), C(3;2;-1), D(4;1;3).
Решение
Находим координаты векторов
$overrightarrow {AB} = left{ {left( {5 — 2} right);left( {5 — left( { — 1} right)} right);left( {4 — 1} right)} right} = left{ {3;6;3} right}$
$overrightarrow {AC} = left{ {left( {3 — 2} right);left( {2 — left( { — 1} right)} right);left( { — 1 — 1} right)} right} = left{ {1;3; — 2} right}$
$overrightarrow {AD} = left{ {left( {4 — 2} right);left( {1 — left( { — 1} right)} right);left( {2 — 1} right)} right} = left{ {2;2;2} right}$
Искомый объём равен $frac{1}{6}$ объём параллелепипеда, построенного на рёбрах,
$overrightarrow {AB} $, $overrightarrow {AС} $, $overrightarrow {AD} $, следовательно объем равен:
$V = pm frac{1}{6}left| {begin{array}{*{20}{c}}3&6&3 \ 1&3&{ — 2} \ 2&2&2 end{array}} right|=$
$ = pm frac{1}{6}cdotleft( {3cdotleft( {3cdot2 — left( { — 2} right)cdot2} right) — 6cdotleft( {1cdot2 — left( { — 2} right)cdot2} right) + 3cdotleft( {1cdot2 — 3cdot2} right)} right) = 3$
Решая, находим определитель матрицы третьего порядка и получаем искомый объём треугольной пирамиды V=3
17817
Пирамида – это многогранник, основанием которого является многоугольник, а грани его являются треугольниками.
Онлайн-калькулятор объема пирамиды
У пирамиды есть ребра. Можно сказать, что они тянутся к точке, называемой вершиной данной пирамиды. Ее основанием может быть произвольный многоугольник. Грань — это фигура, которая образуется в результате объединения двух ближайших ребер со стороной основания. Гранью пирамиды является треугольник. Расстояние от вершины пирамиды до середины стороны основания называется апофемой. Высотой пирамиды называется длина перпендикуляра, опущенного из вершины к центру ее основания.
Типы пирамид
Различают следующие типы пирамид.
- Прямоугольная — у нее ребро образует угол в 90 градусов с основанием.
- Правильная — ее основание — какой-либо правильный многоугольник, а вершина проецируется в центр этого основания.
- Тетраэдр — пирамида, у которой в основании лежит треугольник.
Формулы объема пирамиды
Объем пирамиды находится несколькими способами.
По площади основания и высоте пирамиды
Простое умножение одной трети площади основания на высоту пирамиды и является ее объемом.
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания пирамиды;
hh — высота данной пирамиды.
Площадь основания пирамиды равна 100 см2100text{ см}^2, а высота ее равна 30 см30text{ см}. Найдите объем тела.
Решение
Sосн=100S_{text{осн}}=100
h=30h=30
Все величины нам известны, подставляем их численные значения в формулу и находим:
V=13⋅Sосн⋅h=13⋅100⋅30=1000 см3V=frac{1}{3}cdot S_{text{осн}}cdot h=frac{1}{3}cdot 100cdot 30=1000text{ см}^3
Ответ
1000 см3.1000text{ см}^3.
Формула объема правильной треугольной пирамиды
Этот способ подходит, если пирамида правильная и треугольная.
V=h⋅a243V=frac{hcdot a^2}{4sqrt{3}}
hh — высота пирамиды;
aa — сторона основания пирамиды.
Вычислите объем правильной треугольной пирамиды, если в ее основании лежит равносторонний треугольник, в котором сторона равна 5 см5text{ см}, а высота пирамиды равна – 19 см19text{ см}.
Решение
a=5a=5
h=19h=19
Просто подставляем данные величины в формулу для объема:
V=h⋅a243=19⋅5243≈68.6 см3V=frac{hcdot a^2}{4sqrt{3}}=frac{19cdot 5^2}{4sqrt{3}}approx68.6text{ см}^3
Ответ
68.6 см3.68.6text{ см}^3.
Формула объема правильной четырехугольной пирамиды
V=13⋅h⋅a2V=frac{1}{3}cdot hcdot a^2
hh — высота пирамиды;
aa — сторона основания пирамиды.
Дана правильная четырехугольная пирамида. Вычислите ее объем, если ее высота равна 7 см7text{ см}, a сторона основания составляет – 2 см2text{ см}.
Решение
a=2a=2
h=7h=7
По формуле вычисляем:
V=13⋅h⋅a2=13⋅7⋅22≈9.3 см3V=frac{1}{3}cdot hcdot a^2=frac{1}{3}cdot 7cdot 2^2approx9.3text{ см}^3
Ответ
9.3 см3.9.3text{ см}^3.
Формула объема тетраэдра
V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}
aa — длина ребра тетраэдра.
Длина ребра тетраэдра равна 13 см13text{ см}. Найдите его объем.
Решение
a=13a=13
Подставляем aa в формулу для объема тетраэдра:
V=2⋅a312=2⋅13312≈259 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 13^3}{12}approx259text{ см}^3
Ответ
259 см3.259text{ см}^3.
Формула объема пирамиды как определитель
Наверное, самый экзотический способ вычисления объема данного тела.
Пусть даны векторы, на которых построена пирамида как на сторонах. Тогда ее объем будет равен одной шестой смешанного произведения векторов. Последний в свою очередь равен определителю составленному из координат этих векторов. Итак, если пирамида построена на трех векторах:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующей пирамиды это такой определитель:
V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем пирамиды через смешанное произведение векторов, координаты которых такие: a⃗=(2,3,5)vec{a}=(2,3,5) , b⃗=(1,4,4)vec{b}=(1,4,4), c⃗=(3,5,7)vec{c}=(3,5,7).
Решение
a⃗=(2,3,5)vec{a}=(2,3,5)
b⃗=(1,4,4)vec{b}=(1,4,4)
c⃗=(3,5,7)vec{c}=(3,5,7)
По формуле:
V=16⋅∣235144357∣=16⋅(2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7)=16⋅(56+36+25−60−40−21)=16⋅(−4)=−23≈−0.7V=frac{1}{6}cdotbegin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=frac{1}{6}cdot(2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 — 5cdot4cdot3 — 2cdot4cdot5 — 3cdot1cdot7) =frac{1}{6}cdot( 56 + 36 + 25 — 60 — 40 — 21)=frac{1}{6}cdot(-4)=-frac{2}{3}approx-0.7
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=0.7 см3V=0.7text{ см}^3
Ответ
0.7 см3.0.7text{ см}^3.
Не знаете, где можно оформить заказ контрольных работ недорого? Наши эксперты помогут вам с решением работ по объемам фигур!
Тест по теме “Объем пирамиды”
Коллинеарные векторы
Коллинеарными называются векторы, лежащие на параллельных прямых (или на одной и той же прямой).
Коллинеарные векторы могут иметь одно и то же направление (равнонаправленные векторы) или противоположные направления.
Два ненулевых вектора равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными.
Условие коллинеарности векторов
Если векторы a(x1,y1,z1) и b(x2,y2,z2) коллинеарны, то их соответствующие координаты пропорциональны:
x2/x1 = y2/y1 = z2/z1
И обратно: если соответствующие координаты векторов пропорциональны, то векторы эти — коллинеарны.
Если коэффициент пропорциональности λ = x2/x1 = y2/y1 = z2/z1 положителен, то векторы a и b равнонаправлены, а если отрицателен — то противоположно направлены.
Например:
- векторы АВ(3, 5,
и CD(6, 10, 16) коллинеарны;
- векторы АВ(-12, -8, -22) и CD(6, 4, 11) коллинеарны;
- векторы АВ(-10, -8, -21) и CD(6, 5, 11) не коллинеарны
Компланарные векторы
Три вектора (или большее их число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.
Если хотя бы один из трёх векторов — нулевой, то три вектора также считаются компланарными.
Компланарность векторов, доказательство их компланарности
Необходимым и достаточным условием компланарности трёх векторов a, b, c является равенство нулю их смешанного произведения.
Например:
- векторы AB(2, 1, 3), CD(-2, 8, 12), EF(3, 15, 27) компланарны;
- векторы AB(-4, 2, -6), CD(-1, -4, 6), EF(-2, 10, -18) компланарны.
Смешанное произведение векторов
Смешанным (или векторно-скалярным) произведением трёх векторов a, b, c называется скалярное произведение вектора а на векторное произведение b×c, т.е. число а(b×c), или, что то же, (b×c)а.
Для того, чтобы найти смешанное произведение трёх векторов a, b и c, заданных своими координатами a(ax,ay,az), b(bx,by,bz), c(cx,cy,cz), нужно определенным образом составить определитель третьего порядка. В первой строке определителя записываем координаты первого вектора, во второй строке — второго, в третьей — третьего:
ax ay az
bx by bz
cx cy cz
и вычисляем определитель. Результат вычислений и есть искомое смешанное произведение трёх векторов.
Например, смешанное произведение векторов a(-2, 5, -3), b(1, -4, 6), c(1, 5, 9) равно 90.
Смешанное произведение abc трех некомпланарных векторов a, b, c равно объёму параллелепипеда, построенного на векторах a, b, c, взятому со знаком «плюс», если система a, b, c — правая, и со знаком «минус», если эта система левая.
Иногда вопрос задают так: «Чему равен объём параллелепипеда, построенного на векторах a, b и c?». Как уже известно, равен он смешанному произведению векторов a, b и c. Если результат окажется со знаком «минус», то результат, конечно же, нужно взять по модулю.
Например, объём параллелепипеда, построенного на векторах a(-2, 5, -3), b(1, -4, 6), c(1, 5, 9), равен 90 кубических единиц.
Объём пирамиды, построенной на векторах
Объём пирамиды, построенной на векторах a, b и c, равен 1/6 объёма параллелепипеда, построенного на векторах a, b и c.
Если известны координаты вершин A, B, C, D пирамиды, то последовательность действий для нахождения её объёма следующая:
- находим координаты векторов AB, AC и AD;
- находим 1/6 смешанного произведения векторов AB, AC и AD (результат вычислений берём со знаком «плюс»).
Например, даны вершины пирамиды ABCD:
- A(5, 0, 14);
- B(-7, 16, 9);
- C(14, -5, 17);
- D(15, 11, -2).
Находим координаты векторов AB, AC и AD:
- AB = (-7-5, 16-0, 9-14) = (-12, 16, -5);
- AC = (14-5, -5-0, 17-14) = (9, -5, 3);
- AD = (15-5, 11-0, -2-14) = (10, 11, -16).
Вычисляем 1/6 смешанного произведения векторов AB, AC и AD.
V = 1/6 · 1475 = 245,83 кубических единиц.
Источники:
- М.Я. Выгодский. Справочник по высшей математике.
- В.Д. Черненко. Высшая математика в примерах и задачах. В 3 томах. Том 1.
Дополнительно на Геноне:
- Что такое определитель матрицы?
- Как найти определитель матрицы?
- Какими свойствами обладает определитель матрицы?

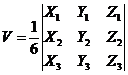
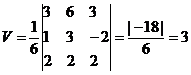

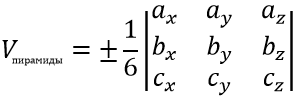
 и CD(6, 10, 16) коллинеарны;
и CD(6, 10, 16) коллинеарны;