Как найти объем пирамиды решение задач

Видео по теме

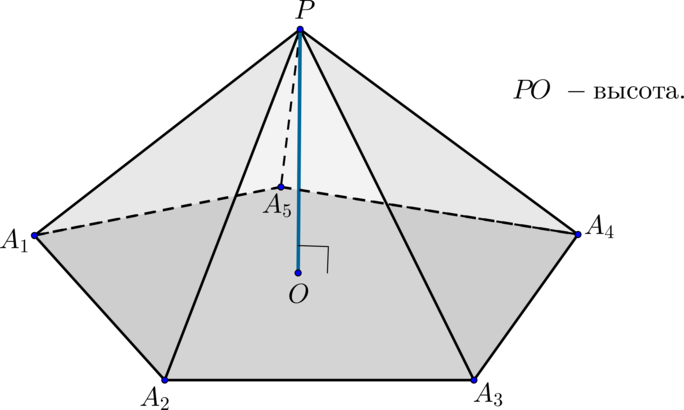
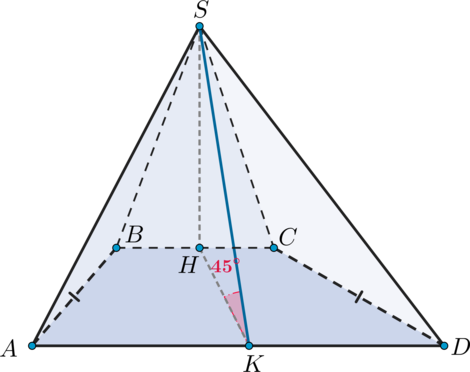
Задача 1. В правильной четырехугольной пирамиде SABCD  точка  O – центр основания, S  – вершина,  SB=13,;BD=24. Найдите длину отрезка SO.

fgk

Решение: + показать

Задача 2.  В правильной четырехугольной пирамиде SABCD  точка O – центр основания, S – вершина, SO=8, BD=30.  Найдите боковое ребро SC.

Решение: + показать

Задача 3. Стороны основания правильной четырехугольной пирамиды равны 60, боковые ребра равны 78. Найдите площадь поверхности этой пирамиды.

Решение: + показать

Задача 4.  В правильной четырёхугольной пирамиде SABCD  точка O  —  центр основания, S — вершина, SO=48, SD=60.  Найдите длину отрезка AC.

Решение: + показать

Задача 5. Основанием пирамиды является прямоугольник со сторонами 5 и 6. Ее объем равен 40. Найдите высоту этой пирамиды.

Решение: + показать

Задача 6. В правильной четырёхугольной пирамиде SABCD  с основанием ABCD боковое ребро SA равно 39, сторона основания равна 15sqrt2. Найдите объём пирамиды.

Решение: + показать

Задача 7. В правильной четырёхугольной пирамиде все рёбра равны 7. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

Решение: + показать

Задача 8.  Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 9. У второй пирамиды высота в 1,5 раза больше, а сторона основания в 2 раза больше, чем у первой. Найдите объём второй пирамиды.

Решение: + показать

Задача 9.  В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс угла между боковой гранью и плоскостью основания равен sqrt{14}. Найти сторону основания пирамиды.

Решение: + показать

Задача 10. Основанием пирамиды является прямоугольник со сторонами 4 и 6. Ее объем равен 48. Найдите высоту этой пирамиды.

18f3561bdbae5ca26a77784787b7d0bc

Решение: + показать

Задача 11. Стороны основания правильной четырехугольной пирамиды равны 42, боковые ребра равны 75. Найдите площадь поверхности этой пирамиды.

8913063b078b7196c5a3071ca02c523b

Решение: + показать

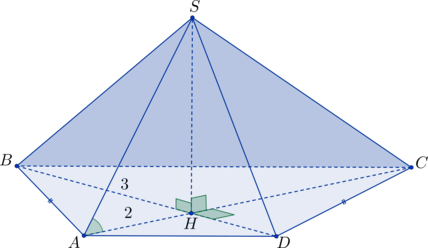
Задача 12. В правильной треугольной пирамиде SABC  медианы основания ABC пересекаются в точке O. Площадь треугольника ABC  равна 9, объем пирамиды равен 6. Найдите длину отрезка OS.

u

Решение: + показать

Задача 13.  В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.

ts

Решение: + показать

Задача 14. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 11, а высота равна 4sqrt3. 

u

Решение: + показать

Задача 15.  Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 5, а объем равен 6sqrt3.

u

Решение: + показать

Задача 16. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

н

Решение: + показать

Задача 17. Объем правильной шестиугольной пирамиды 324. Сторона основания равна 6. Найдите боковое ребро.

н

Решение: + показать

Задача 18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?

1694cdf5de68632ee14aa0c5c5fefad1

Решение: + показать

Задача 19. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 5 раз?

d5e28b2cf1aaba18d4a7a6a87f80215a

Решение: + показать

Задача 20.  Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в пять раз?

п

Решение: + показать

Задача 21. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 12. Найдите объем пирамиды.

8fb4942644d6aea0ba85825e7c81c610

Решение: + показать

Задача 22. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 12. Найдите объем пирамиды.

a8a2781d4cd5ed8f62d05cbf4f061676

Решение: + показать

Задача 23. От треугольной призмы, объем которой равен 129, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

g

Решение: + показать

Задача 24. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды. Видео по теме 1 2 

efc4238b7e0c4ff80662906a06e27364

Решение: + показать

Задача 25.  Сторона основания правильной шестиугольной пирамиды равна 8, боковое ребро равно 16. Найдите объём пирамиды.

1694cdf5de68632ee14aa0c5c5fefad1

Решение: + показать

Задача 26. Сторона основания правильной шестиугольной пирамиды равна 11, а угол между боковой гранью и основанием равен 45^{circ}. Найдите объем пирамиды.

Решение: + показать

Задача 27. Найдите объём правильной шестиугольной пирамиды SABCDEF, если объём треугольной пирамиды SABD равен 34.

Решение: + показать

Задача 28.  Объем параллелепипеда ABCDA_1B_1C_1D_1 равен 9. Найдите объем треугольной пирамиды ABCA_1. 

Решение: + показать

Задача 29. Объем куба равен 123. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение: + показать

Задача 30. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

Решение: + показать

Задача 31. Объем правильной четырехугольной пирамиды SABCD равен 120. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

рб

Решение: + показать

Задача 32. От треугольной пирамиды, объем которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

ор

Решение: + показать

Задача 33.  Ребра тетраэдра равны 16. Найдите площадь сечения, проходящего через середины четырех его ребер.

ь

Решение: + показать

  Вы можете пройти тест

Источник

8. Геометрия в пространстве (стереометрия)


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Задачи по теме «Пирамида»

Пирамида (PA_1A_2…A_n):

(blacktriangleright) Многоугольник (A_1…A_n) – основание;

треугольники (PA_1A_2, PA_2A_3) и т.д. – боковые грани;

точка (P) – вершина;

отрезки (PA_1, PA_2, …, A_1A_2) и т.д. – ребра.

(blacktriangleright) Если в основании пирамиды лежит треугольник, то она называется тетраэдром.

(blacktriangleright) Высота пирамиды – перпендикуляр, опущенный из вершины (P) к основанию.

(blacktriangleright) Объем пирамиды ({Large{V=dfrac{1}{3}S_{text{осн}}h}}) , где (S_{text{осн}}) – площадь основания, (h) – высота.

(blacktriangleright) Площадь боковой поверхности – сумма площадей всех боковых граней.
Площадь полной поверхности – сумма площади боковой поверхности и площади основания.

Заметим, что принято записывать название пирамиды, начиная с вершины.


Задание
1

#2878

Уровень задания: Равен ЕГЭ

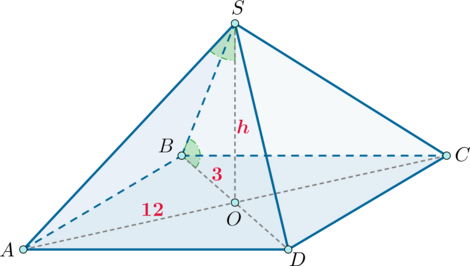
Дана пирамида (SABCD), вершиной которой является точка (S), в основании лежит ромб, а высота (SO) пирамиды падает в точку пересечения диагоналей ромба. Найдите объем пирамиды, если известно, что угол (ASO) равен углу (SBO), а диагонали основания равны (6) и (24).

Так как диагонали ромба точкой пересечения делятся пополам, то (AO=12), (BO=3).
Заметим, что так как (SO) – высота пирамиды, то (triangle ASO) и (triangle BSO) – прямоугольные. Так как у них есть равные острые углы, то они подобны. Пусть (SO=h), тогда из подобия имеем: [dfrac{BO}{h}=dfrac{h}{AO} quadRightarrowquad h=6.] Так как площадь ромба равна полупроизведению диагоналей, то объем пирамиды равен [V=dfrac13cdot hcdot dfrac12cdot 24cdot 6=144.]

Ответ: 144


Задание
2

#2879

Уровень задания: Равен ЕГЭ

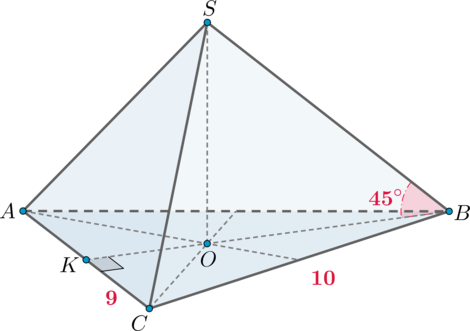
В пирамиде (SABC) высота (SO) падает в точку пересечения медиан основания. Треугольник (ABC) равнобедренный, боковые стороны равны (10), а основание (AC=18). Найдите объем пирамиды, если известно, что угол между боковым ребром (SB) и плоскостью основания равен (45^circ).

Пусть (BK) – высота в (triangle ABC), а значит и медиана. Тогда из прямоугольного (triangle BKC): [BK=sqrt{BC^2-KC^2}=sqrt{10^2-9^2}=sqrt{19}.] Тогда площадь основания равна [S_{ABC}=dfrac12cdot ACcdot
BK=9sqrt{19}.] Так как (O) – точка пересечения медиан, то (O) лежит на (BK). Так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то [BO=dfrac23BK=dfrac23sqrt{19}.] Заметим, что угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость, следовательно, (angle SBO=45^circ) и есть угол между (SB) и основанием (так как (BO) – проекция (SB) на плоскость (ABC)). Так как к тому же (triangle SBO) прямоугольный, то он равнобедренный, следовательно, [SO=BO=dfrac23sqrt{19}.] Тогда объем пирамиды равен [V=dfrac13cdot SOcdot S_{ABC}=38.]

Ответ: 38


Задание
3

#2880

Уровень задания: Равен ЕГЭ

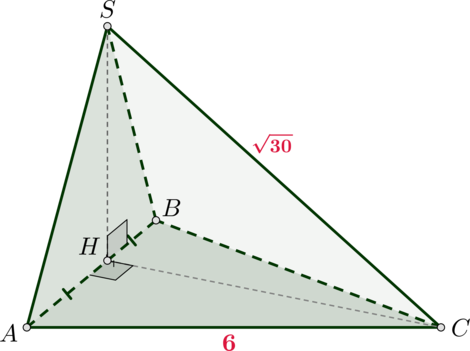
Высота (SH) треугольной пирамиды (SABC) падает на середину стороны (AB), (ABC) – правильный треугольник со стороной (6). Найдите объем пирамиды, если (SC=sqrt{30}).

Так как (H) – середина (AB) и треугольник правильный, то (CH) – высота. Следовательно, [CH=dfrac{sqrt3}2AB=3sqrt3.] Так как (SH) – высота пирамиды, то (triangle SHC) – прямоугольный, следовательно, [SH=sqrt{SC^2-CH^2}=sqrt{30-27}=sqrt3.] Следовательно, объем равен [V=dfrac13cdot SHcdot S_{ABC}=
dfrac13cdot SHcdot dfrac12cdot CHcdot AB=9.]

Ответ: 9


Задание
4

#2881

Уровень задания: Сложнее ЕГЭ

В основании пирамиды (SABCD) лежит равнобедренная трапеция (ABCD), (AD) – большее основание. Высота пирамиды падает на отрезок (BC). Апофема грани (ASD) равна (10) и образует угол (45^circ) с плоскостью трапеции. Найдите объем пирамиды, если средняя линия трапеции равна (9).

Пусть (SH) – высота пирамиды. Проведем (HKperp AD). Следовательно, по теореме о трех перпендикулярах (SK) (наклонная) также перпендикулярна (AD) (так как (HK) – ее проекция на плоскость (ABC)). Следовательно, (SK) и есть апофема грани (ASD). Также отсюда следует, что (angle SKH=45^circ) (так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость). Следовательно, (triangle SHK) прямоугольный и равнобедренный, значит, [SH=HK=SKdiv sqrt2=dfrac{10}{sqrt2}] По определению получается, что (HK) также высота трапеции. Так как площадь трапеции равна полусумме оснований, умноженной на высоту, а полусумма оснований в свою очередь равна средней линии, то [S_{ABCD}=9cdot dfrac{10}{sqrt2}] А значит объем пирамиды равен [V=dfrac13cdotdfrac{10}{sqrt2}cdot9cdot dfrac{10}{sqrt2}=150.]

Ответ: 150


Задание
5

#1857

Уровень задания: Сложнее ЕГЭ

В основании пирамиды (SABCD) лежит равнобедренная трапеция с основаниями (AD) и (BC). (H) – точка пересечения диагоналей трапеции, а (SH) – высота пирамиды. Диагонали трапеции перпендикулярны, (mathrm{tg}, angle SAC = 3), (BH = 3), (AH = 2). Найдите объем пирамиды.

(triangle AHD) и (triangle BHC) – равнобедренные треугольники, т.к. трапеция (ABCD) равнобедренная (Rightarrow) (AH = HD), (BH = HC) (Rightarrow) (AC = BD = 2 + 3 = 5) (Rightarrow)

[S_{ABCD} = S_{ABC} + S_{ADC} = frac{1}{2}cdot ACcdot BH + frac{1}{2}cdot ACcdot HD = frac{1}{2}cdot ACcdot(BH + HD) = frac{1}{2}cdot ACcdot BD.]

В (triangle SAH): (SH = AHcdot mathrm{tg}, angle SAC = 6), т.к. (triangle SAH) – прямоугольный. Тогда объем пирамиды можно найти следующим образом: [V_{text{пир.}} = frac{1}{3}cdot S_{ABCD}cdot SH = frac{1}{3}cdotfrac{1}{2}cdot5cdot5cdot6 = 25].

Ответ: 25


Задание
6

#1858

Уровень задания: Сложнее ЕГЭ

В основании пирамиды (SABC) лежит прямоугольный треугольник с прямым углом (angle A). Точка (H) – центр описанной вокруг треугольника (triangle ABC) окружности, (SH) – высота пирамиды. Найдите объем пирамиды, если известно, что (AB = 6), (AC = 8) , (SA = 5sqrt5).

Центр описанной вокруг прямоугольного треугольника окружности лежит на гипотенузе и делит ее пополам (Rightarrow) (BH = AH = CH) – радиусы описанной окружности. В прямоугольном треугольнике (triangle BAC) по теореме Пифагора: (BC^2 = AB^2 + AC^2 = 6^2 + 8^2 = 100) (Rightarrow) (BC = 10) (Rightarrow) (AH = frac{BC}{2} = frac{10}{2} = 5). Треугольник (triangle AHS) – прямоугольный, т.к. (SH perp ABC) ((SH) – высота), тогда по теореме Пифагора можно найти (SH): (SH^2 = AS^2 — AH^2 = (5sqrt5)^2 — 5^2 = 100) (Rightarrow) (SH = 10). Теперь найдем объем пирамиды: [V_{text{пир.}} = frac{1}{3}cdot SHcdot S_{triangle BAC} = frac{1}{3}cdot SHcdotfrac{1}{2}cdot ABcdot AC = frac{1}{3}cdot10cdotfrac{1}{2}cdot6cdot8 = 80.]

Ответ: 80


Задание
7

#2769

Уровень задания: Сложнее ЕГЭ

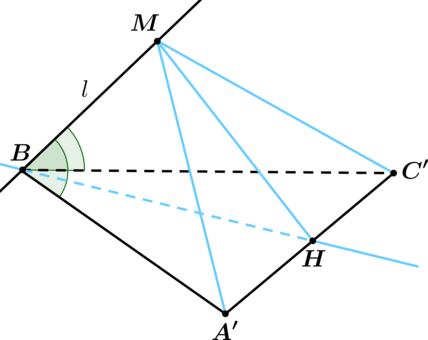
Точки (A), (B) и (C) лежат в плоскости (pi). Прямая (l) образует с плоскостью (pi) угол в (45^circ) и проходит через точку (B) так, что (angle(l; AB) = angle(l; BC)). Через (l’) обозначим проекцию (l) на (pi). Найдите (angle(l’; AB)), если (angle ABC = 80^circ). Ответ дайте в градусах.

Докажем, что (l’) содержит биссектрису угла (ABC). Выберем на (AB) точку (A’), а на (BC) точку (C’) так, чтобы (A’B = BC’). Построим прямую, проходящую через точку (B) и точку (H) – середину (A’C’).

Отметим на (l) точку (M). Треугольник (A’BC’) – равнобедренный, тогда (BH) – высота.

Рассмотрим треугольники (A’BM) и (C’BM): они равны по двум сторонам и углу между ними, тогда (MA’ = MC’) и треугольник (A’MC’) – равнобедренный, тогда (MH) – его высота.

В итоге (A’C’perp BH) и (A’C’perp MH), следовательно, (A’C’perp (MBH)). Если предположить, что (M’) – проекция точки (M) на ((A’BC’)), не попадает на прямую, содержащую (BH), то получим, что (A’C’perp M’M) и (A’C’perp MH), откуда следует, что (A’C’perp (MM’H)). Но тогда плоскости ((MM’H)) и ((MBH)) перпендикулярны к одной прямой, пересекаются, но не совпадают, чего быть не может.

Таким образом, (M’) лежит на прямой, содержащей (BH), но тогда (l’) совпадает с прямой, содержащей (BH). В итоге, (angle(l’; AB) = 0,5angle ABC = 40^circ).

Ответ: 40

При подготовке к ЕГЭ по математике старшеклассникам следует особое внимание уделить теме «Пирамида», так как задачи, связанные с расчетом объема и площади данного многогранника, непременно встретятся на финальной аттестации. Весь необходимый для повторного изучения материал вы найдете в данном разделе. Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию и элементарные упражнения, а затем постепенно переходим к заданиям экспертного уровня.

Базовая информация

Пирамида — многогранник, образованный благодаря соединению всех точек плоского многоугольника с точкой, выходящей за пределы плоскости данного многоугольника.

Пирамиду называют n-угольной по количеству углов в основании. Если последним является правильный многоугольник, а основание высоты совпадает с его центром, фигуру называют правильной.

Все боковые грани пирамиды — треугольники.

Подробная теоретическая часть приведена в начале страницы. Вы также можете сразу приступить к практике. Задачи, представленные в данном разделе, помогут вам найти объем пирамиды, длину ее определенных отрезков и т. д. Каждое упражнение содержит подробный алгоритм решения и правильный ответ. Таким образом, разобраться в теме вы сможете самостоятельно, без помощи репетитора.

Как часто следует тренироваться?

Чтобы на ЕГЭ ребенок смог легко решить задачи по стереометрии (а определение площади и других параметров пирамиды относятся к данному разделу геометрии), мы рекомендуем выполнять по 2—3 упражнения каждый день. Таким образом, знания будут лучше усваиваться и вам будет проще переходить от простого к сложному.

Проверьте, легко ли вы рассчитаете площадь пирамиды, прямо сейчас. Разберите любое задание онлайн. Если решение дастся вам легко, значит, шансы на высокие экзаменационные баллы по математике достаточно велики. А при возникновении затруднений планируйте свой день таким образом, чтобы в ежедневное расписание был включен дистанционный образовательный проект «Школково». Мы поможем вам восполнить пробелы в знаниях!

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Введение

Вспомним, что объем пирамиды, как и объем конуса, находятся по формуле , где  – площадь основания,  – высота. Разумеется, в случае конуса площадь основания можно подставить: . Теперь перейдем непосредственно к задачам.

Пример 1

В правильной треугольной пирамиде с вершиной  биссектрисы  пересекаются в точке , , . Найдите длину отрезка . (См. Рис. 1.)

Иллюстрация к условию задачи

Рис. 1. Иллюстрация к условию задачи

Решение. Так как пирамида правильная, то точка  будет проектироваться в центр треугольника , то есть в точку  (точка пересечения биссектрис равностороннего треугольника и есть его центр). Значит, найти надо высоту пирамиды. Мы знаем, что , откуда

Ответ: .

Пример 2

От треугольной пирамиды  отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды  и среднюю линию основания . Найдите объем отсеченной треугольной пирамиды , если . (См. Рис. 2.)

Иллюстрация к условию задачи 2

Рис. 2. Иллюстрация к условию задачи 2

Решение. Проблема здесь в том, что найти площадь основания и высоту нельзя. Но это и не нужно. Запишем два равенства  и  . Заметим, что раз вершина и плоскость основания у новой пирамиды те же, то и высота та же. (См. Рис. 3.)

Высота у новой пирамиды и старой одна и та же

Рис. 3. Высота у новой пирамиды и старой одна и та же

То есть чтобы посчитать объем необходимо знать, во сколько раз площадь основания новой пирамиды меньше площади основания исходной. , т. к.  с коэффициентом подобия . Тогда .

Ответ: .

Пример 3

Во сколько раз увеличится объем правильного тетраэдра , если все его ребра увеличить в два раза ? (См. Рис. 4.)

Исходный и увеличенный тетраэдры

Рис. 4. Исходный и увеличенный тетраэдры

Решение. Заметим, что в этом случае площадь основания увеличится в  раза, т. к. исходную сторону  увеличили в  раза и получили треугольник со стороной . (См. Рис. 5.). То есть .

основание исходного и увеличенного тетраэдра

Рис. 5. Основание исходного и увеличенного тетраэдра

Высота тетраэдра также увеличится в  раза. Доказать это можно так: опустим высоту и рассмотрим прямоугольный : в нем гипотенуза увеличилась вдвое и катет тоже как радиус описанной окружности около основания. Значит, треугольник перейдет в подобный с коэффициентом . (См. Рис. 6.) То есть .

Треугольник с коэффициентом подобия

Рис. 6. Треугольник  с коэффициентом подобия

. Раз площадь увеличилась в  раза, а высота – в , то объем увеличится в  раз .

Ответ: в  раз.

Пример 4

В сосуде, имеющем форму конуса, уровень жидкости достигает половины высоты . Объем налитой жидкости  мл. Сколько миллилитров жидкости  нужно долить, чтобы полностью наполнить сосуд? (См. Рис. 7.)

Иллюстрация к условию задачи 4

Рис. 7. Иллюстрация к условию задачи 4

Решение. Сначала найдем объем всего сосуда  (в миллилитрах). . Объем маленького конуса , тогда искомый объем .

Заметим, что  с коэффициентом подобия , т. к. , значит,  и .

Получаем, что  и , то есть объем большого конуса в  раз больше объема маленького, заполненного жидкостью.

Тогда объем всего сосуда  мл, а значит, долить надо  мл.

Ответ:  мл.

Замечание. Из двух последних примеров можно сделать вывод, что если мы пропорционально увеличим фигуру в  раз, то объем увеличится в  раз.

Пример 5

Найдите объем  конуса (См. Рис. 8.), если образующая  и наклонена к плоскости основания под углом . В ответе укажите .

Иллюстрация к условию задачи 5

Рис. 8. Иллюстрация к условию задачи 5

Решение. Рассмотрим осевое сечение конуса . Нам известно, что ; . Тогда из прямоугольного  : ;  (как катет, лежащий напротив угла ). (См. Рис. 9.)

Выносной рисунок осевого сечения

Рис. 9. Выносной рисунок осевого сечения

Тогда .

Для записи в ответ .

Ответ: .

Метод объемов в пространстве

Этот метод похож на метод площадей на плоскости. Кратко о сути метода площадей: считаем площадь двумя способами и приравниваем. Например, как найти высоту прямоугольного треугольника со сторонами ,  и , опущенную на гипотенузу? (См. Рис. 10.)

Иллюстрация к примеру

Рис. 10. Иллюстрация к примеру

Считаем площадь. С одной стороны , а с другой стороны . Отсюда

То же самое и с объемами: считаем объем двумя способами и находим неизвестную величину.

Пример. Дана правильная треугольная пирамида , сторона основания , а боковое ребро . (См. Рис. 11.) Найти расстояние  от точки  до плоскости .

Треугольная пирамида

Рис. 11. Треугольная пирамида

Решение. Эту задачу можно решить и «в лоб». Но мы решим так. Заметим, что . Найдем площадь основания . Теперь найдем высоту . Рассмотрим прямоугольный .  – радиус описанной около основания окружности, он равен . (См. Рис. 12.)

Длины сторон

Рис. 12. Длины сторон в прямоугольном

Тогда по теореме Пифагора .

Получаем, что .

С другой стороны, . (См. Рис. 13.)

Интересующая грань

Рис. 13. Интересующая грань

Тогда . Найдем . Рассмотрим равнобедренный . Опускаем в нем перпендикуляр на основание и получаем два прямоугольных треугольника с катетом  и гипотенузой . Тогда из египетского треугольника получаем, что высота равна . (См. Рис. 14.)

Выносной рисунок грани

Рис. 14. Выносной рисунок грани

Тогда

Окончательно: .

Ответ: .

Заключение

Сегодня был решен ряд задач на объемы пирамиды и конуса, мы посмотрели, как работают формулы, выведенные на предыдущем уроке.

Список литературы

  1. Геометрия. Учебник для 10–11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
  2. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
  3. Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия. 11 класс. Рабочая тетрадь. 8-е изд. – М.: Просвещение, 2013. – 78 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. Matematikalegko.ru (Источник).
  2. Matematikalegko.ru (Источник).
  3. Matematikalegko.ru (Источник).

Домашнее задание

  1. В основании конуса проведена хорда, которая равна радиусу основания и удалена от центра основания конуса на  см. Через вершину конуса и эту хорду проведена плоскость, образующая с плоскостью основания угол . Найдите объем конуса.
  2. Найдите объем правильной треугольной пирамиды, если сторона основания равна  см, а боковое ребро образует с плоскостью основания угол .
  3. Стороны оснований правильной усеченной треугольной пирамиды равны  см и  см, а острый угол боковой грани равен . Найдите объем усеченной пирамиды.
Источник

В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.

  • Формула вычисления объема пирамиды

    • 1. Общая формула

    • 2. Объем правильной треугольной пирамиды

    • 3. Объем правильной четырехугольной пирамиды

    • 4. Объем правильной шестиугольной пирамиды

  • Примеры задач

Формула вычисления объема пирамиды

1. Общая формула

Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.

Формула объема пирамиды

Объем пирамиды

  • ABCD – основание;
  • E – вершина;
  • h – высота, перпендикулярная основанию.

2. Объем правильной треугольной пирамиды

Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Формула площади равностороннего треугольника

Подставляем данное выражение в формулу расчета объема фигуры и получаем:

Формула объема правильной треугольной пирамиды

3. Объем правильной четырехугольной пирамиды

Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны.

Следовательно, формулу объема можно представить в виде:

Формула объема правильной четырехугольной пирамиды

4. Объем правильной шестиугольной пирамиды

Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):

Формула площади основания правильного шестиугольника

С учетом этого, объем фигуры считается так:

Формула объема правильного шестиугольника

Примеры задач

Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Формула расчета объема правильной треугольной пирамиды

Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.

Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:
Формула расчета объема правильной четырехугольной пирамиды

Источник

1.  В правильной треугольной пирамиде SABC с
вершиной S биссектрисы треугольника ABC пересекаются
в точке O. Площадь треугольника ABC равна 2; объем
пирамиды равен 6. Найдите длину отрезка OS.

Решение.

Отрезок OS высота
треугольной пирамиды SABC, ее объем выражается формулой

V= дробь, числитель — 1, знаменатель — 3 S_ABC умножить на SO.Таким
образом, SO= дробь, числитель — 3V, знаменатель — S _{ABC}= дробь, числитель — 3 умножить на 6, знаменатель — 2 =9.Ответ: 9.

https://mathb-ege.sdamgia.ru/get_file?id=565&png=1

2.  В правильной четырехугольной пирамиде SABCD точка O –
центр основания, S – вершина, SO=15, BD=16. Найдите
боковое ребро SA.

Решение.

В правильной пирамиде вершина проецируется в центр основания,
следовательно, SO является высотой пирамиды. тогда
по теореме Пифагора

SA=SB= корень из S{O в степени 2 плюс BO в степени 2 }= корень из S{O в степени 2 плюс левая круглая скобка дробь, числитель — BD, знаменатель — 2 правая круглая скобка в степени 2 }= корень из 225 плюс 64=17.Ответ: 17.

https://mathb-ege.sdamgia.ru/get_file?id=575&png=1

3.  В правильной четырехугольной пирамиде SABCD точка O –
центр основания, S – вершина, SB=13, AC=24. Найдите
длину отрезка SO.

Решение.

в правильной пирамиде вершина проецируется в центр основания,
следовательно, SO является высотой пирамиды. тогда
по теореме Пифагора

SO= корень из S{B в степени 2 минус BO в степени 2 }= корень из S{B в степени 2 минус левая круглая скобка дробь, числитель — AC, знаменатель — 2 правая круглая скобка в степени 2 }= корень из 169 минус 144=5.Ответ: 5.

https://mathb-ege.sdamgia.ru/get_file?id=576&png=1

4.  В правильной треугольной пирамиде SABC точка M –
середина ребра AB, S – вершина. Известно,
что BC = 3, а площадь боковой поверхности пирамиды равна 45.
Найдите длину отрезка SM.

Решение.

Найдем площадь грани SAB:

S_SAB= дробь, числитель — S_бок, знаменатель — 3 = дробь, числитель — 45, знаменатель — 3 =15. Отрезок SM является
медианой равнобедренного треугольника SAB, а значит, его
высотой. Тогда

SM= дробь, числитель — 2S_SAB, знаменатель — AB = дробь, числитель — 2S_SAB, знаменатель — BC = дробь, числитель — 2 умножить на 15, знаменатель — 3 =10.Ответ: 10.

https://mathb-ege.sdamgia.ru/get_file?id=627&png=1

5.  В правильной треугольной пирамиде SABC точка L —
середина ребра AC, S — вершина. Известно, что BC = 6,
а SL = 5. Найдите площадь боковой поверхности пирамиды.

Решение.

Отрезок SL является медианой правильного
треугольника SAC, а значит, и его высотой. Боковые грани пирамиды
равны, поэтому

S_бок=3S_SAC=3 умножить на дробь, числитель — 1, знаменатель — 2 AC умножить на SL= дробь, числитель — 3, знаменатель — 2 BC умножить на SL= дробь, числитель — 3, знаменатель — 2 умножить на 6 умножить на 5=45.Ответ: 45.

https://mathb-ege.sdamgia.ru/get_file?id=628&png=1

6.  Во сколько раз увеличится объем правильного тетраэдра, если все
его ребра увеличить в два раза?

Решение.

Объёмы подобных тел относятся как куб коэффициента подобия.
Поэтому если все ребра увеличить в 2 раза, объём увеличится в 8 раз.

Это же следует из формулы для объёма правильного тетраэдра V= дробь, числитель — корень из 2, знаменатель — 12 a в степени 3 , где a —
длина его ребра.         Ответ:
8.

https://mathb-ege.sdamgia.ru/get_file?id=791&png=1

7.  Во сколько раз увеличится объем пирамиды, если ее высоту
увеличить в четыре раза?

Решение.

Объем
пирамиды равен V= дробь, числитель — 1, знаменатель — 3 Sh,где  S – площадь
основания, а  h – высота пирамиды. При увеличении
высоты в 4 раза объем пирамиды также увеличится в 4 раза.

Ответ: 4.

https://mathb-ege.sdamgia.ru/get_file?id=795&png=1

8.  Объем треугольной пирамиды SABC, являющейся
частью правильной шестиугольной пирамиды SABCDEF, равен 1.
Найдите объем шестиугольной пирамиды.

Решение.

Данные пирамиды имеют общую высоту, поэтому их объемы
соотносятся как площади их оснований. Площадь правильного шестиугольника со
стороной a равна S= дробь, числитель — 3 корень из 3, знаменатель — 2 a в степени 2 . Площадь
же равнобедренного треугольника ACB с боковой стороной a и
углах при основании 30 в степени circ  равна S_Delta =a в степени 2 дробь, числитель — корень из 3, знаменатель — 4 . Получаем,
что площадь шестиугольника больше площади треугольника  ACB  в   дробь, числитель — S, знаменатель — S _{Delta }=6 раз и равна
6. Ответ: 6.

https://mathb-ege.sdamgia.ru/get_file?id=831&png=1

9.  Объем правильной четырехугольной пирамиды SABCD равен
12. Точка E – середина ребра SB. Найдите
объем треугольной пирамиды EABC.

Решение.

Площадь основания пирамиды EABC по условию в 2
раза меньше площади основания пирамиды SABCD. Также высота
данной треугольной пирамиды в 2 раза меньше высоты пирамиды SABCD (т.к.
точка E – середина ребра SB).
Поскольку объем пирамиды равен V= дробь, числитель — 1, знаменатель — 3 Sh, то объем данной
треугольной пирамиды в 4 раза меньше объема пирамиды SABCD и
равен 3.

 Ответ: 3.

https://mathb-ege.sdamgia.ru/get_file?id=832&png=1

10.  От треугольной пирамиды, объем которой равен 12, отсечена
треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю
линию основания. Найдите объем отсеченной треугольной пирамиды.

Решение.

Объем пирамиды V= дробь, числитель — 1, знаменатель — 3 Sh. Площадь основания
отсеченной части меньше в 4 раза (так как высота и сторона треугольника в
основании меньше исходных в 2 раза), поэтому и объем оставшейся части меньше
в 4 раза. Тем самым, он равен 3. 

Ответ: 3.

https://mathb-ege.sdamgia.ru/get_file?id=6967&png=1

11.  Во сколько раз увеличится площадь поверхности правильного
тетраэдра, если все его ребра увеличить в два раза?

Решение.

Площадь поверхности тетраэдра равна сумме площадей его граней,
которые равны S= дробь, числитель — корень из 3, знаменатель — 4 a в степени 2 . Поэтому
при увеличении ребер вдвое, площадь поверхности увеличится в 4 раза.

 Ответ: 4.

https://mathb-ege.sdamgia.ru/get_file?id=846&png=1

12.  Во сколько раз увеличится площадь поверхности октаэдра, если
все его ребра увеличить в 3 раза?

Решение.

При увеличении ребер в 3 раза площади треугольников, образующих
грани октаэдра, увеличатся в 9 раз, поэтому суммарная площадь поверхности
также увеличится в 9 раз.

 Ответ: 9.

https://mathb-ege.sdamgia.ru/get_file?id=861&png=1

13.  Во сколько раз увеличится площадь поверхности пирамиды, если
все ее ребра увеличить в 2 раза?

Решение.

Площади подобных тел относятся как квадрат коэффициента подобия.
Поэтому, если все ребра увеличены в 2 раза, площадь поверхности увеличится в
4 раза.                         

 Ответ:
4.

https://mathb-ege.sdamgia.ru/get_file?id=876&png=1

14.  Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего
через середины четырех его ребер.

Решение.

В правильном тетраэдре скрещивающиеся ребра перпендикулярны.
Каждая сторона сечения является средней линией соответствующей грани,
которая, как известно, в 2 раза меньше параллельной ей стороны и равна
поэтому 0,5. Значит, сечением является квадрат со стороной 0,5. Тогда площадь
сечения S=a в степени 2 =0,25.

 Ответ: 0,25

https://mathb-ege.sdamgia.ru/get_file?id=879&png=1

15.  Объем параллелепипеда ABCDA_1B_1C_1D_1 равен
12. Найдите объем треугольной пирамиды B_1ABC.

Решение.

Объем параллелепипеда равен V_пар=S_парH_пар, а
объем пирамиды равен V_пир= дробь, числитель — 1, знаменатель — 3 S_пирH_пир. Высота
пирамиды равна высоте параллелепипеда, а ее основание вдвое меньше, поэтому

V_пир= дробь, числитель — 1, знаменатель — 3 S_пирH_пир= дробь, числитель — 1, знаменатель — 3 дробь, числитель — S_пар, знаменатель — 2H_пар= дробь, числитель — 1, знаменатель — 6 S_парH_пар= дробь, числитель — 1, знаменатель — 6 умножить на 12 = 2.

Ответ: 2.

https://mathb-ege.sdamgia.ru/get_file?id=885&png=1

16.  Объем куба равен 12. Найдите объем четырехугольной пирамиды,
основанием которой является грань куба, а вершиной — центр куба.

Решение.

Объем пирамиды равен

V= дробь, числитель — 1, знаменатель — 3 Sh= дробь, числитель — 1, знаменатель — 3 a в степени 2 дробь, числитель — a, знаменатель — 2 = дробь, числитель — 1, знаменатель — 6 a в степени 3 = дробь, числитель — 1, знаменатель — 6 V_куба=2.

Ответ: 2. 

Примечание.

Куб состоит из 6 таких пирамид, объем каждой из них равен 2.

https://mathb-ege.sdamgia.ru/get_file?id=886&png=1

17.  Найдите объем параллелепипеда ABCDA_1B_1C_1D_1, если
объем треугольной пирамиды ABDA_1 равен 3.

Решение.

Объем параллелепипеда равен V=Sh, где S –
площадь основания, h – высота. Объем пирамиды
равен V= дробь, числитель — 1, знаменатель — 3 S_Delta h, где S_Delta  – площадь основания пирамиды, равная половине площади
основания параллелепипеда. Тогда объем параллелепипеда в 6 раз больше объема
пирамиды ABDA_1. 

Ответ: 18.

https://mathb-ege.sdamgia.ru/get_file?id=919&png=1

18. В правильной треугольной пирамиде SABC R — середина
ребра BC, S — вершина. Известно,
что AB=1, а SR=2. Найдите
площадь боковой поверхности.

Решение.

Площадь боковой поверхности правильной треугольной пирамиды
равна половине произведения периметра основания на апофему:

S_бок= дробь, числитель — 1, знаменатель — 2 P_ABC умножить на SR= дробь, числитель — 1, знаменатель — 2 умножить на 3AB умножить на SR= дробь, числитель — 3, знаменатель — 2 умножить на 2=3.Ответ:3.

https://mathb-ege.sdamgia.ru/get_file?id=705&png=1

19. В правильной треугольной пирамиде SABC N — середина
ребра BC, S — вершина. Известно,
что AB=1, а площадь боковой поверхности
равна 3. Найдите длину отрезка SN.

Решение.

Площадь боковой поверхности правильной треугольной пирамиды
равна половине произведения периметра основания на апофему: S_бок= дробь, числитель — 1, знаменатель — 2 P_ABC умножить на SN. Тогда SN= дробь, числитель — 2S_бок, знаменатель — P _{ABC}= дробь, числитель — 2S_бок, знаменатель — 3AB = дробь, числитель — 2 умножить на 3, знаменатель — 3 =2.

О т в е т: 2.

https://mathb-ege.sdamgia.ru/get_file?id=11216&png=1

20. В правильной треугольной пирамиде SABC точка L —
середина ребра BC, S — вершина. Известно,
что SL=2, а площадь боковой поверхности
равна 3. Найдите длину отрезка AB.

Решение.

Площадь боковой поверхности правильной пирамиды равна
произведению апофемы на полупериметр основания. Поэтому

SL умножить на дробь, числитель — AB плюс BC плюс AC, знаменатель — 2 = 3 равносильно 2 умножить на дробь, числитель — 3AB, знаменатель — 2 =3 равносильно AB=1.

Ответ: 1.

https://mathb-ege.sdamgia.ru/get_file?id=707&png=1

21. В правильной треугольной пирамиде SABC медианы
основания пересекаются в точке M. Площадь треугольника ABC равна
3, объем пирамиды равен 1. Найдите длину отрезка MS.

Решение.

Основание пирамиды — равносторонний треугольник, поэтому,
точка M является центром основания, а MS —
высотой пирамиды SABC. Ее объем вычисляется по
формуле V_SABC= дробь, числитель — 1, знаменатель — 3 S_осн умножить на MS. ТогдаMS= дробь, числитель — 3V_SABC, знаменатель — S _{осн}= дробь, числитель — 3, знаменатель — 3 =1.

Ответ: 1.

https://mathb-ege.sdamgia.ru/get_file?id=708&png=1

22. В правильной треугольной пирамиде SABC медианы
основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS=1. Найдите
объем пирамиды.

Решение.

Основание пирамиды — равносторонний треугольник, поэтому, M является
центром основания, а MS — высотой пирамиды SABC. Тогда
V_SABC= дробь, числитель — 1, знаменатель — 3 S_осн умножить на MS= дробь, числитель — 1, знаменатель — 3 умножить на 3=1.

Ответ: 1.

https://mathb-ege.sdamgia.ru/get_file?id=709&png=1

23. В правильной треугольной пирамиде SABC медианы
основания пересекаются в точке P. Объем пирамиды равен 1, PS=1. Найдите
площадь треугольника ABC.

Решение.

Основание пирамиды — равносторонний треугольник, поэтому, P является
центром основания, а SP — высотой пирамиды SABC. Ее
объем вычисляется по формуле V_SABC= дробь, числитель — 1, знаменатель — 3 S_осн умножить на PS. Тогда
S_осн= дробь, числитель — 3V_SABC, знаменатель — PS =3.

Ответ: 3.

https://mathb-ege.sdamgia.ru/get_file?id=11217&png=1

.

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти школу в агенте
  • Корел как найти rgb объекты
  • Как найти человека по одному тел номеру
  • Как найти шанс выпадения
  • Как найти биологического отца ребенка