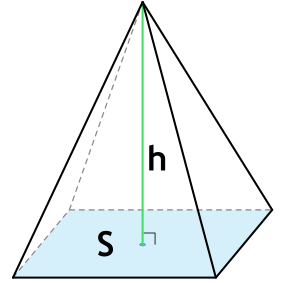
Как найти объем пирамиды зная все ребра - Исправление недочетов и поиск решений вместе с Examum.ru

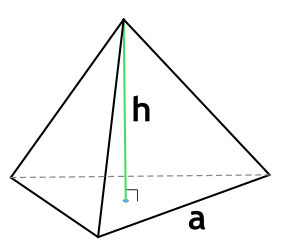
{V= S cdot h}

На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.

Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.

Содержание:

калькулятор объема пирамиды
формула объема пирамиды
объем правильной треугольной пирамиды
объем правильной четырехугольной пирамиды
объем правильной шестиугольной пирамиды
объем правильной n-угольной пирамиды
объем тетраэдра
примеры задач

Формула объема пирамиды

{V= dfrac{1}{3} S cdot h}

S — площадь основания пирамиды

h — высота пирамиды

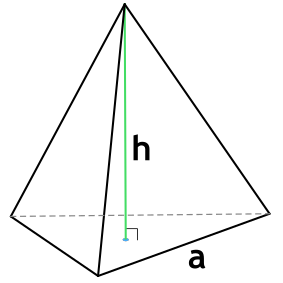
Формула объема правильной треугольной пирамиды

Правильная треугольная пирамида — пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.

{V= dfrac{h cdot a^2}{4 sqrt{3}}}

a — длина стороны основания пирамиды

h — высота пирамиды

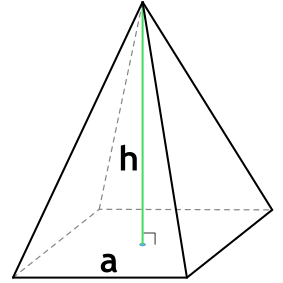
Формула объема правильной четырехугольной пирамиды

Правильная четырехугольная пирамида — пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.

{V= dfrac{1}{3} cdot h cdot a^2}

a — длина стороны основания пирамиды

h — высота пирамиды

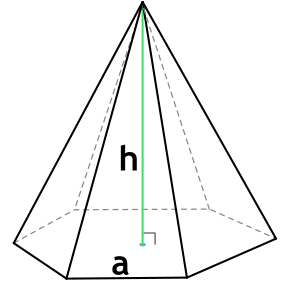
Формула объема правильной шестиугольной пирамиды

Правильная шестиугольная пирамида — пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.

{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}

a — длина стороны основания пирамиды

h — высота пирамиды

Формула объема правильной n-угольной пирамиды

Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.

{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}

a — длина стороны основания пирамиды

h — высота пирамиды

n — число сторон многоугольника в основании пирамиды

Формула объема тетраэдра

Тетраэдр — правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.

{V= dfrac{sqrt{2} a^3}{12}}

a — длина стороны тетраэдра

Примеры задач на нахождение объема пирамиды

Задача 1

Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.

Решение

Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.

V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3

Ответ: 6 м³

Используем калькулятор для проверки полученного ответа.

Задача 2

Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.

Решение

Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.

V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3

Ответ: 0.25 см³

Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.

Источник

Определение пирамиды

Пирамида – это многогранник, основанием которого является многоугольник, а грани его являются треугольниками.

Онлайн-калькулятор объема пирамиды

У пирамиды есть ребра. Можно сказать, что они тянутся к точке, называемой вершиной данной пирамиды. Ее основанием может быть произвольный многоугольник. Грань — это фигура, которая образуется в результате объединения двух ближайших ребер со стороной основания. Гранью пирамиды является треугольник. Расстояние от вершины пирамиды до середины стороны основания называется апофемой. Высотой пирамиды называется длина перпендикуляра, опущенного из вершины к центру ее основания.

Типы пирамид

Различают следующие типы пирамид.

Прямоугольная — у нее ребро образует угол в 90 градусов с основанием.
Правильная — ее основание — какой-либо правильный многоугольник, а вершина проецируется в центр этого основания.
Тетраэдр — пирамида, у которой в основании лежит треугольник.

Формулы объема пирамиды

Объем пирамиды находится несколькими способами.

По площади основания и высоте пирамиды

Простое умножение одной трети площади основания на высоту пирамиды и является ее объемом.

Объем пирамиды по площади основания и высоте

V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h

SоснS_{text{осн}} — площадь основания пирамиды;
hh — высота данной пирамиды.

Задача 1

Площадь основания пирамиды равна 100 см2100text{ см}^2, а высота ее равна 30 см30text{ см}. Найдите объем тела.

Решение

Sосн=100S_{text{осн}}=100
h=30h=30

Все величины нам известны, подставляем их численные значения в формулу и находим:

V=13⋅Sосн⋅h=13⋅100⋅30=1000 см3V=frac{1}{3}cdot S_{text{осн}}cdot h=frac{1}{3}cdot 100cdot 30=1000text{ см}^3

Ответ

1000 см3.1000text{ см}^3.

Формула объема правильной треугольной пирамиды

Этот способ подходит, если пирамида правильная и треугольная.

Объем правильной треугольной пирамиды

V=h⋅a243V=frac{hcdot a^2}{4sqrt{3}}

hh — высота пирамиды;
aa — сторона основания пирамиды.

Задача 2

Вычислите объем правильной треугольной пирамиды, если в ее основании лежит равносторонний треугольник, в котором сторона равна 5 см5text{ см}, а высота пирамиды равна – 19 см19text{ см}.

Решение

a=5a=5
h=19h=19

Просто подставляем данные величины в формулу для объема:

V=h⋅a243=19⋅5243≈68.6 см3V=frac{hcdot a^2}{4sqrt{3}}=frac{19cdot 5^2}{4sqrt{3}}approx68.6text{ см}^3

Ответ

68.6 см3.68.6text{ см}^3.

Формула объема правильной четырехугольной пирамиды

Объем правильной четырехугольной пирамиды

V=13⋅h⋅a2V=frac{1}{3}cdot hcdot a^2

hh — высота пирамиды;
aa — сторона основания пирамиды.

Задача 3

Дана правильная четырехугольная пирамида. Вычислите ее объем, если ее высота равна 7 см7text{ см}, a сторона основания составляет – 2 см2text{ см}.

Решение

a=2a=2
h=7h=7

По формуле вычисляем:

V=13⋅h⋅a2=13⋅7⋅22≈9.3 см3V=frac{1}{3}cdot hcdot a^2=frac{1}{3}cdot 7cdot 2^2approx9.3text{ см}^3

Ответ

9.3 см3.9.3text{ см}^3.

Формула объема тетраэдра

Объем тетраэдра

V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}

aa — длина ребра тетраэдра.

Задача 4

Длина ребра тетраэдра равна 13 см13text{ см}. Найдите его объем.

Решение

a=13a=13

Подставляем aa в формулу для объема тетраэдра:

V=2⋅a312=2⋅13312≈259 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 13^3}{12}approx259text{ см}^3

Ответ

259 см3.259text{ см}^3.

Формула объема пирамиды как определитель

Наверное, самый экзотический способ вычисления объема данного тела.

Пусть даны векторы, на которых построена пирамида как на сторонах. Тогда ее объем будет равен одной шестой смешанного произведения векторов. Последний в свою очередь равен определителю составленному из координат этих векторов. Итак, если пирамида построена на трех векторах:

a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),

тогда объем соответствующей пирамиды это такой определитель:

Объем пирамиды через определитель

V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}

Задача 5

Найти объем пирамиды через смешанное произведение векторов, координаты которых такие: a⃗=(2,3,5)vec{a}=(2,3,5) , b⃗=(1,4,4)vec{b}=(1,4,4), c⃗=(3,5,7)vec{c}=(3,5,7).

Решение

a⃗=(2,3,5)vec{a}=(2,3,5)
b⃗=(1,4,4)vec{b}=(1,4,4)
c⃗=(3,5,7)vec{c}=(3,5,7)

По формуле:

V=16⋅∣235144357∣=16⋅(2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7)=16⋅(56+36+25−60−40−21)=16⋅(−4)=−23≈−0.7V=frac{1}{6}cdotbegin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=frac{1}{6}cdot(2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 — 5cdot4cdot3 — 2cdot4cdot5 — 3cdot1cdot7) =frac{1}{6}cdot( 56 + 36 + 25 — 60 — 40 — 21)=frac{1}{6}cdot(-4)=-frac{2}{3}approx-0.7

Мы должны взять модуль этого числа, так как объем это неотрицательная величина:

V=0.7 см3V=0.7text{ см}^3

Ответ

0.7 см3.0.7text{ см}^3.

Не знаете, где можно оформить заказ контрольных работ недорого? Наши эксперты помогут вам с решением работ по объемам фигур!

Тест по теме “Объем пирамиды”

Источник

В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.

Формула вычисления объема пирамиды
- 1. Общая формула
- 2. Объем правильной треугольной пирамиды
- 3. Объем правильной четырехугольной пирамиды
- 4. Объем правильной шестиугольной пирамиды
Примеры задач

Формула вычисления объема пирамиды

1. Общая формула

Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.

ABCD – основание;
E – вершина;
h – высота, перпендикулярная основанию.

2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:

3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a², где а – длина его стороны.

Следовательно, формулу объема можно представить в виде:

4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):

С учетом этого, объем фигуры считается так:

Примеры задач

Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:

Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.

Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см² (3 см ⋅ 3 см). Следовательно, объем равен:

Источник

Как рассчитать объем пирамиды

На данной странице калькулятор поможет рассчитать объем пирамиды онлайн. Для расчета задайте площадь, высоту, сторону или количество сторон. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.

Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.

Пирамида

Формула объема пирамиды через высоту и площадь основания:

S — площадь основания; h — высота пирамиды.

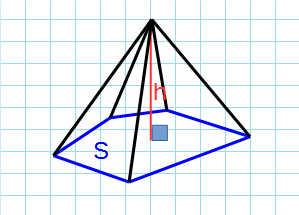
Правильная пирамида

Правильная пирамида — пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр основания.

Формула объема правильной пирамиды через сторону основания, высоту и количество сторон:

a — сторона основания; h — высота пирамиды; n — количество сторон многогранника в основании.

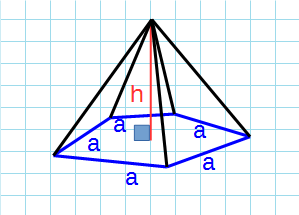
Правильная треугольная пирамида

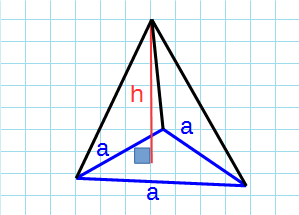
Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Формула объема правильной треугольной пирамиды через сторону основания и высоту:

a — сторона основания; h — высота пирамиды.

Правильная четырехугольная пирамида

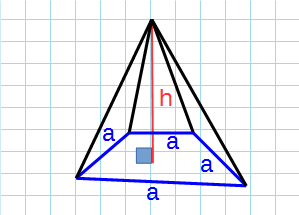
Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Формула объема правильной четырехугольной пирамиды через сторону основания и высоту:

a — сторона основания; h — высота пирамиды.

Тетраэдр

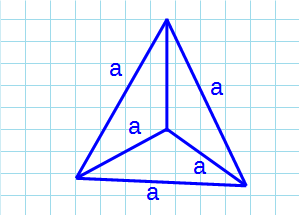
Тетраэдр — пирамида, у которой все грани равносторонние треугольники.

Формула объема тетраэдра:

a — ребро тетраэдра.

Источник

Download Article

To calculate the volume of a pyramid, use the formula $V={frac {1}{3}}lwh$ , where l and w are the length and width of the base, and h is the height. You can also use the equivalent formula $V={frac {1}{3}}A_{{b}}h$ , where $A_{{b}}$ is the area of the base and h is the height. The method varies slightly depending on whether the pyramid has a triangular or a rectangular base. If you want to know how to calculate the volume of a pyramid, just follow these steps.

Volume Help

1

Find the length and width of the base. In this example, the length of the base is 4 cm and the width is 3 cm. If you’re working with a square base, the method is the same, except the length and width of the square base will be equal. Write down these measurements.^[1]
2

Multiply the length and width to find the area of the base. To get the area of the base, simply multiply 3 cm by 4 cm.^[2]²^[3]

Advertisement
3

Multiply the area of the base by the height. The area of the base is 12 cm² and the height is 4 cm, so you can multiply 12 cm² by 4 cm.
4

Multiply your result so far by ${frac {1}{3}}$ . Or, in other words, divide by 3. Remember to state your answer in cubic units whenever you’re working with three-dimensional space.^[4]

1

Find the length and width of the base. The length and width of the base must be perpendicular to each other for this method to work. They can also be considered the base and height of the triangle. In this example, the width of the base is 2 cm and the length of the triangle is 4 cm.^[5]
2

Calculate the area of the base. To calculate the area of the base, just plug the base and height of the triangle into the following formula: $A_{{b}}={frac {1}{2}}bh$ .^[6]
3

Multiply the area of the base by the height of the pyramid. The area of the base is 4 cm² and the height is 5 cm.
4

Multiply your result so far by ${frac {1}{3}}$ . Or, in other words, divide by 3. Your result will show that the volume of a pyramid with a height of 5 cm and a triangular base with a width of 2 cm and a length of 4 cm is 6.67 cm.^[7]³

Add New Question

Question

How do I calculate the volume of a three square tier pyramid?

Determine the area of the base. If it is a rectangle, that’s length x width, if it is a triangle it’s 1/2 x the base (one side) x the height (a line perpendicular to the base to the opposite vertex). Determine the height of the pyramid. It is a line perpendicular (straight up) from the base of the pyramid to the opposite vertex. Muliply (1) x (2) and divide by 3. The formula is 1/3 x the area of the base x the height of the pyramid
Question

How do I find the height if given the volume and the base length for a square pyramid?

Triple the volume and divide that by the area of the base (which is the square of the length of an edge).
Question

How do I double the volume of a square pyramid?

Either double the height of the pyramid or double the area of the base. Accomplish the latter by multiplying the length of each side of the base by the square root of 2 (1.414).

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

This method can be further generalized to such objects as pentagonal pyramids, hexagonal pyramids, etc. The overall process is: A) calculate the area of the base shape; B) measure the height from the tip of the pyramid to the center of the base shape; C) multiply A with B; D) divide by 3.
In a square pyramid, the true height, slant height, and length of the edge of the base face are all related by the Pythagorean theorem: (edge ÷ 2)² + (true height)² = (slant height)²
In all regular pyramids, the slant height, edge height, and edge length are also related by the Pythagorean theorem: (edge ÷ 2)² + (slant height)² = (edge height)²

Thanks for submitting a tip for review!

Pyramids have three kinds of height — a slant height, down the center of the triangular sides; a true height or perpendicular height, that goes from the tip of the pyramid to the center of the base face; and an edge height, that goes down one edge of the triangular sides. For volume, you must use the true height.

References

About This Article

Article SummaryX

To calculate the volume of a pyramid, you need to know its height and the area of the base. Once you have that information, you can find the volume using the formula V (volume) = 1/3 x Ab (the area of the base) x h (height). If the pyramid has a square or rectangular base, simply multiply the width of the base by its length to find the area. Then, multiply the area of the base by the height of the pyramid, and multiply the result by 1/3—which is the same as dividing by 3. For instance, if your pyramid has a square base that is 3 inches long by 3 inches wide, and a height of 4 inches, the volume would be (3 x 3 x 4)/3, or 12. Since you’re describing the volume of a 3-dimensional object, remember to write your answer in cubic units. In this case, the pyramid has a volume of 12 cubic inches. For pyramids with a triangular base, the technique is a little different. If you know the triangle’s height and the width of its base, plug those numbers into the formula ½ x b (base) x h (height) to find the area of the triangle. From there, you can use the same formula that you used for the square-based pyramid. For example, say your pyramid has a base that’s a triangle with a base width of 2 cm and a height of 4 cm, and the pyramid has a height of 6 cm. First, find the area of the triangle using the formula ½ x 2 x 4, which will give you a base area of 4 square centimeters. Next, multiply the area by the height of the pyramid, then multiply the product by 1/3. In this case, 6 x 4 x 1/3 = 8, which means the pyramid has a volume of 8 cubic centimeters. To learn how to calculate the volume of a pyramid with a triangular base, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 720,364 times.

Did this article help you?

Источник