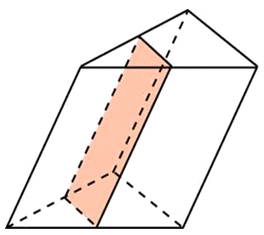
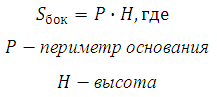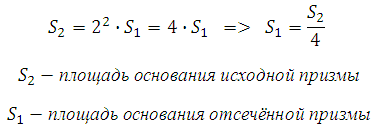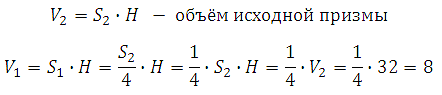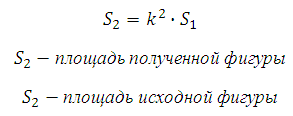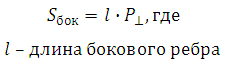Здравствуйте! Очередная порция задачек с призмами, рассматриваются треугольные призмы. Объединил несколько заданий схожих по одному «признаку» – у них через среднюю линию основания проходит сечение. Вопросы стоят о вычислении площади поверхности или объёма либо исходной призмы, либо отсечённой. Что важно здесь помнить?
Это свойство подобия фигур касающееся площади, в частности про треугольник уже речь была в одной из статей, посмотрите (п.2). Но даже, если вы вдруг забудете это, представленные задачи будут интуитивно понятны и решите вы их в одно действие.
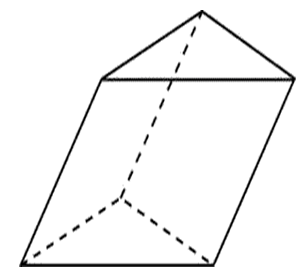
77111. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 6, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Сказано, что плоскость проходит через среднюю линию основания, то есть через точки, которые являются серединами соседних сторон треугольника. При чём она проходит параллельно боковому ребру – это означает, что указанная плоскость также проходит через середины соответствующих соседних сторон другого основания.
Без каких-либо вычислений понятно, что площадь боковой поверхности отсечённой призмы будет в два раза меньше, чем у исходной.
Посмотрите!
Высота у призм общая. Указанная плоскость разрезает две соседние боковые грани пополам.
Рассмотрим третью грань (параллельную плоскости сечения) – её площадь поверхности также в два раза меньше, так как средняя линия треугольника в два раза меньше параллельной ей стороны треугольника.
Учитывая, что высота остаётся неизменной (общая для обеих призм), можем сделать вывод, что площадь боковой поверхности (сумма площадей всех трёх граней) отсечённой призмы будет в два раза меньше.
Ответ: 3
76147. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 20. Найдите площадь боковой поверхности исходной призмы.
Задача обратная предыдущей. Формула для площади боковой поверхности призмы:
Значит для отсечённой призмы:
Высота у пирамид общая, поэтому площадь боковой поверхности исходной призмы зависит от периметра. Поскольку получившиеся треугольники в основании призмы подобны, и их соответствующие стороны относятся как 1:2, значит периметр основания исходной призмы вдвое больше периметра основания отсечённой.
А это означает, что и площадь боковой поверхности так же больше в 2 раза и равна 40.
Ответ: 40
27106. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Известно, что объём призмы равен произведению площади основания и высоты. Высота для указанных призм общая, значит изменение объёма зависит только от изменения площади поверхности.
Рассмотрим треугольники лежащие в основаниях призм – они подобны. Если рассматривать основание исходной призмы относительно основания отсечённой, то коэффициент подобия будет равен 2. Что это нам даёт?
Мы знаем, что пощади подобных фигур соотносятся как квадрат коэффициента подобия, значит:
Основание отсечённой призмы в 4 раза меньше.
Таким образом, и её объём будет в 4 раза меньше, то есть 8.
Формально можно расписать так:
Ответ: 8
74745. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 7. Найдите объем исходной призмы.
Задача обратная предыдущей. Объём призмы равен произведению площади основания на высоту:
Высота общая, значит объём меняется в зависимости от изменения площади основания.
Треугольник лежащий в основании исходной призмы, как уже сказано, подобен треугольнику лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию.
Площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть:
Таким образом, площадь основания исходной призмы больше площади основания отсечённой призмы в 4 раза.
Следовательно объем исходной призмы будет в 4 раза больше объема отсечённой призмы. Таким образом, искомый объём равен 28.
Ответ: 28
Ещё три задачи про площадь поверхности призмы
245356. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?
Увеличим все рёбра призмы в три раза. Что получается?
Получается, что каждая грань полученной призмы и соответствующая ей грань исходной призмы являются подобными фигурами. При чём коэффициент подобия равен 3. Мы, что площади подобных фигур пропорциональны квадрату коэффициента подобия, то есть:
Это означает, что площадь каждой отдельной грани нашей призмы увеличится в 9 раз. Так как площадь поверхности всей призмы это сумма площадей всех граней, то разумеется, что и вся площадь поверхности призмы также увеличится в 9 раз.
Ответ: 54
*На самом деле не важно о каком теле идёт речь (о призме, пирамиде, кубе, параллелепипеде), суть одна.
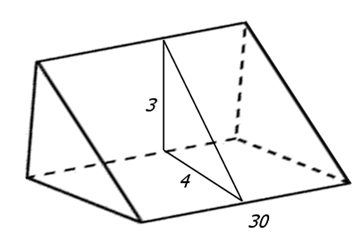
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 30 и отстоит от других боковых ребер на 3 и 4. Найдите площадь боковой поверхности этой призмы.
На момент написания статьи эта задача из открытого банка заданий ЕГЭ удалена, но мы её рассмотрим, так вернуться может туда в любой момент, а значит и быть на экзамене в будущие годы.
Для вычисления боковой поверхности призмы воспользуемся формулой:
В данном случае боковое ребро это общее ребро перпендикулярных друг другу граней, оно равно 30. Перпендикулярным сечением призмы является прямоугольный треугольник с катетами 3 и 4. По теореме Пифагора найдём его гипотенузу и сможем вычислить периметр:
Таким образом:
Второй путь решения!
Указанная выше формула для кого-то может быть не понятна. В чём её смысл и что она выражает?
Посмотрите на каждую отдельную грань (положив призму на бок) – это параллелограммы. При чём основания этих параллелограммов равны и равны они боковому ребру, то есть 30. Высоты у них будут разные.
Две нам известны 3 и 4, третья не известна. Но её мы можем найти. Разрежем призму перпендикулярно боковым рёбрам, сечением разреза будет прямоугольный треугольник с катетами 3 и 4, найдём гипотенузу:
Получается, что площадь боковой поверхности равна сумме площадей трёх параллелограммов:
Ответ: 360
72605. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота 2.
Призма правильная, значит гранями являются равные по площади прямоугольники. Так как призма шестиугольная, то имеем 6 таких прямоугольников. Площадь боковой поверхности равна сумме площадей всех боковых граней:
Ответ: 72
27068. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Посмотреть решение
27107. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Посмотреть решение
27153. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Посмотреть решение
27150. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Посмотреть решение
27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10.
Посмотреть решение
На этом всё, всего доброго!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
На чтение 4 мин Просмотров 65.8к. Опубликовано 13 февраля, 2019
Здесь вы найдёте: Объем правильной треугольной призмы понятие, Объем призмы треугольной формула нахождения, Площадь треугольной призмы
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Содержание
- Призма треугольная — определение
- Элементы треугольной призмы
- Виды треугольных призм
- Прямая треугольная призма
- Наклонная треугольная призма
- Основные формулы для расчета треугольной призмы
- Объем треугольной призмы
- Площадь боковой поверхности призмы
- Площадь полной поверхности призмы
- Правильная призма — прямая призма, основанием которой является правильный многоугольник.
- Пример призмы
- Задачи на расчет треугольной призмы
Призма треугольная — определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
Элементы треугольной призмы
Треугольники ABC и A1B1C1 являются основаниями призмы.
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы.
Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
Прямая треугольная призма
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
или
V=Sосн . h
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
или
Sбок=Pосн.h
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
так как Sбок=Pосн.h, то получим:
Sполн.пов.=Pосн.h+2Sосн
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы:
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см2, то высота должна быть выражена в сантиметрах, а объем — в см3 . Если площадь основания в мм2, то высота должна быть выражена в мм, а объем в мм3 и т. д.
Пример призмы
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k2 = S122 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 7.
Источники: os.fipi, Основная волна 2018.
Решение:
Разделим начальную треугольную призму средними линиями на равные части (такие же как отсечённая призма). Так как высоты равны, достаточно поделить только основание.
Получили 4 такие части.
Vисх. призмы = 4·7 = 28
Ответ: 28.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.3 / 5. Количество оценок: 9
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задания
Версия для печати и копирования в MS Word
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5.
Спрятать решение
Решение.
Площадь основания отсеченной части меньше площади основания всей призмы в 4 раза (так как и высота и основание треугольника уменьшились в 2 раза). Высоты обеих частей призмы одинаковы, поэтому объем отсеченной части в 4 раза меньше объема целой призмы. Тем самым, он равен 20.
Ответ: 20.
- Дисциплина: Математика профильная
- Номер вопроса в билете: 8
- Баллы: 1
- Сложность: Базовый
-
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсечённой треугольной призмы равен 5.
- Подробное решение
-
1) При́зма — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её основаниями.
2) Объём призмы равен произведению её высоты на площадь основания:
V=S*h3) Площадь основания отсеченной призмы в 4 раза меньше площади основания изначальной призмы. Высота отсеченной призмы не изменилась и равна высоте изначальной призмы. А так как объем призмы равен V=S(основания)*H, то объем отсеченной призмы будет в 4 раза меньше начальной призмы, а так как объем отсеченной призмы равен 5, то объем начальной призмы равен V=4*5=20
Ответ: 20
- Войти в свой аккаунт
-
Химия
-
Биология
-
Русский язык
-
Математика базовая
-
Математика профильная