Как найти объем призмы егэ - Исправление недочетов и поиск решений вместе с Examum.ru

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см³ воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см³.

В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.

Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота  — 10.

Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10.

Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

Пройти тестирование по этим заданиям

Источник

Задача 1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна а площадь поверхности равна

Решение: + показать

Задача 2. В правильной четырёхугольной призме известно, что Найдите угол между диагоналями и Ответ дайте в градусах.

Решение: + показать

Задача 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и боковое ребро равно Найдите объем призмы.

Решение: + показать

Задача 4. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и высота призмы равна Найдите площадь ее поверхности.

Решение: + показать

Задача 5. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и Площадь ее поверхности равна . Найдите высоту призмы.

Решение: + показать

Задача 6. Площадь поверхности правильной треугольной призмы равна Какой будет площадь поверхности призмы, если все ее ребра увеличить в два раза?

Решение: + показать

Задача 7. В правильной треугольной призме , все ребра которой равны найдите угол между прямыми и . Ответ дайте в градусах.

Решение: + показать

Задача 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными и и боковым ребром, равным

Решение: + показать

Задача 9. Гранью параллелепипеда является ромб со стороной и острым углом $60^{circ}.$ Одно из ребер параллелепипеда составляет с этой гранью угол в $60^{circ}$ и равно Найдите объем параллелепипеда.

Решение: + показать

Задача 10. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна а высота —

Решение: + показать

Задача 11. Найдите объем правильной шестиугольной призмы, стороны основания которой равны а боковые ребра равны

Решение: + показать

Задача 12. В правильной шестиугольной призме все ребра равны . Найдите расстояние между точками и .

Решение: + показать

Задача 13. В правильной шестиугольной призме все ребра равны Найдите угол . Ответ дайте в градусах.

Решение: + показать

Задача 14. В правильной шестиугольной призме , все ребра которой равны найдите угол между прямыми и . Ответ дайте в градусах.

Решение: + показать

Задача 15. В правильной шестиугольной призме все ребра равны Найдите тангенс угла

Решение: + показать

Задача 16. В сосуд, имеющий форму правильной треугольной призмы, налили см воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки см до отметки см. Найдите объем детали. Ответ выразите в см

Решение: + показать

Задача 17. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.

Решение: + показать

Задача 18. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 26, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

Решение: + показать

Задача 19. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен Найдите объем исходной призмы.

Решение: + показать

Задача 20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Задача 21. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами а боковые ребра равны и наклонены к плоскости основания под углом $30^{circ}.$

Решение: + показать

Задача 22. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно и отстоит от других боковых ребер на и Найдите площадь боковой поверхности этой призмы.

Решение: + показать

Задача 23. В правильной треугольной призме стороны оснований равны боковые рёбра равны Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер , и и точку

Решение: + показать

Задача 24. В правильной треугольной призме стороны оснований равны боковые рёбра равны Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер и

Решение: + показать

Задача 25. Объём куба равен Построено сечение проходящее через середины рёбер и и параллельное ребру Найдите объём треугольной призмы

Решение: + показать

Задача 26. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 27. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 28. Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 29. Найдите объём многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна а боковое ребро равно

Решение: + показать

Вы можете пройти тест «Призма»

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по теме «Прямая и правильная призмы»

(blacktriangleright) Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.
Тогда:

1) боковые грани представляют собой прямоугольники;

2) боковое ребро является высотой призмы.

(blacktriangleright) Призма называется правильной, если она прямая и ее основания – правильные многоугольники.
Тогда:

боковые грани представляют собой равные прямоугольники.

Задание
1

#2859

Уровень задания: Легче ЕГЭ

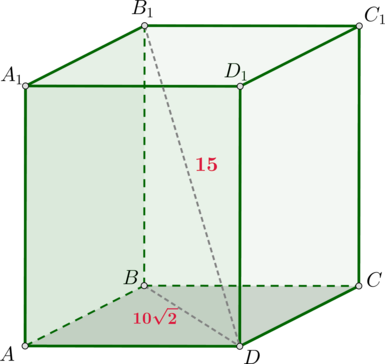
Дана правильная четырехугольная призма, диагональ которой равна (15), а диагональ основания равна (10sqrt2). Найдите площадь полной поверхности призмы.

Пусть (ABCDA_1B_1C_1D_1) – данная призма. Так как она правильная, то в основании лежит квадрат и она является прямой. Тогда (triangle
BB_1D) прямоугольный, следовательно, по теореме Пифагора [BB_1=sqrt{15^2-(10sqrt2)^2}=5.] Так как диагональ квадрата в (sqrt2) раз больше его стороны, то [AB=dfrac{BD}{sqrt2}=10.] Следовательно, [S_{text{пов-ти}}=2S_{ABCD}+4S_{AA_1D_1D}=2cdot 10^2+4cdot 10cdot 5=400.]

Ответ: 400

Задание
2

#2860

Уровень задания: Равен ЕГЭ

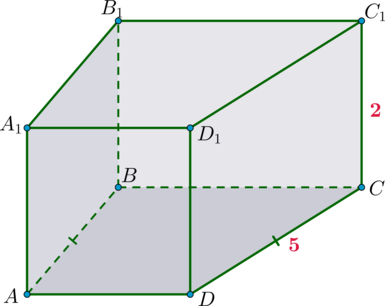
Дана прямая призма, в основании которой лежит равнобедренная описанная около окружности трапеция (ABCD) с боковой стороной, равной (5), и высотой, равной (3). Боковое ребро призмы равно (2). Найдите площадь полной поверхности призмы.

Пусть (AB=CD=5). Так как трапеция описанная, то суммы противоположных сторон равны, следовательно, (AD+BC=AB+CD=10). Следовательно, ее площадь равна [S_{ABCD}=dfrac{AD+BC}2cdot h=dfrac{10}2cdot 3=15.] Площадь боковой поверхности призмы равна [S’=(AB+BC+CD+AD)cdot AA_1=(10+10)cdot 2=40.] Следовательно, площадь полной поверхности равна [S_{text{пов-ти}}=40+15+15=70.]

Ответ: 70

Задание
3

#954

Уровень задания: Равен ЕГЭ

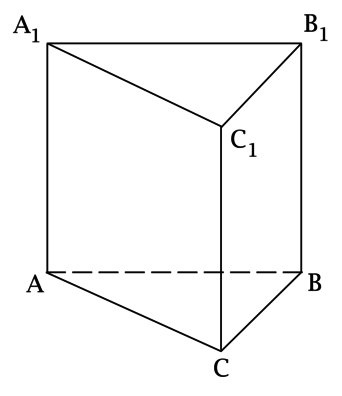
(ABCA_1B_1C_1) – правильная треугольная призма, (AB = sqrt[4]{3}), (AA_1 = sqrt[4]{27}). Найдите площадь полной поверхности призмы.

Площадь равностороннего треугольника со стороной (a) равна (dfrac{a^2sqrt{3}}{4}), тогда

[begin{aligned}
&S_{ABC} = S_{A_1B_1C_1} = dfrac{(sqrt[4]{3})^2sqrt{3}}{4} = dfrac{sqrt{3}cdotsqrt{3}}{4} = dfrac{3}{4},\
&S_{AA_1C_1C} = S_{CC_1B_1B} = S_{AA_1B_1B} = AA_1cdot AB = sqrt[4]{27}cdotsqrt[4]{3} = sqrt[4]{81} = 3.
end{aligned}]

Таким образом, площадь полной поверхности (ABCA_1B_1C_1) равна [2cdotdfrac{3}{4} + 3cdot 3 = 10,5.]

Ответ: 10,5

Задание
4

#1868

Уровень задания: Равен ЕГЭ

В прямоугольной треугольной призме все боковые грани являются квадратами со стороной (10sqrt3). Найдите объем призмы.

У квадрата все стороны равны (Rightarrow) в основаниях призмы лежат равносторонние треугольники со сторонами, равными (10sqrt3).

Тогда площадь основания:
(displaystyle S_{text{осн.}} = frac{1}{2}cdot10sqrt3cdot10sqrt3cdotsin 60^circ = frac{1}{2}cdot10sqrt3cdot10sqrt3cdotfrac{sqrt3}{2} = 75sqrt3). Высота призмы равна стороне квадрата, тогда объем призмы: [10sqrt3cdot75sqrt3 = 2250.]

Ответ: 2250

Задание
5

#1869

Уровень задания: Равен ЕГЭ

Дана правильная треугольная призма. Площадь основания равна площади одной из боковых граней и равна (4sqrt3). Найдите объем призмы.

Так как призма является правильной, то в основаниях призмы лежат равносторонние треугольники, поэтому все боковые грани равны друг другу и являются прямоугольниками. Обозначим высоту призмы за (h), а сторону правильного треугольника за (x). Тогда найдем площадь основания:
(displaystyle S_{text{осн.}} = frac{1}{2}cdot x^2cdotsin 60^circ = frac{1}{2}cdot x^2cdotfrac{sqrt3}{2} = frac{sqrt3}{4}cdot x^2 = 4sqrt3) (Rightarrow) (x^2 = 16) (Rightarrow) (x = 4). Высоту выразим из формулы для площади боковой грани: (S = 4sqrt3 = xcdot h = 4cdot h) (Rightarrow) (h = sqrt3). Наконец, найдем объем призмы: [V = hcdot S_{text{осн.}} = sqrt3cdot4sqrt3 = 12.]

Ответ: 12

Задание
6

#3116

Уровень задания: Равен ЕГЭ

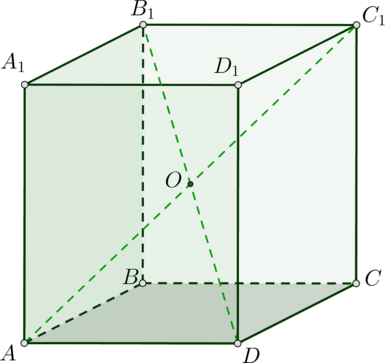
В правильной четырехугольной призме (ABCDA_1B_1C_1D_1) известно, что (DB_1=2CD). Найдите угол между диагоналями (AC_1) и (B_1D). Ответ дайте в градусах.

Так как призма четырехугольная и правильная, то в основании лежит квадрат и она прямая. Следовательно, (AD=CD) и (DB_1=2AD).
Диагонали призмы пересекаются и точкой пересечения (O) делятся пополам, следовательно, (OD=frac12DB_1=AD). Так как призма правильная, то диагонали равны, значит, (AO=OD=AD). Следовательно, (triangle AOD) правильный и (angle AOD=60^circ). Это и есть угол между (DB_1) и (AC_1).

Ответ: 60

Задание
7

#3115

Уровень задания: Равен ЕГЭ

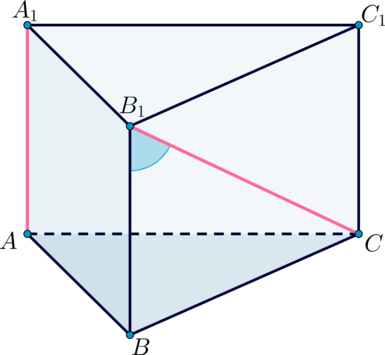
В правильной треугольной призме (ABCA_1B_1C_1), все ребра которой равны (1), найдите угол между прямыми (AA_1) и (CB_1). Ответ дайте в градусах.

Для того, чтобы найти угол между прямыми, не лежащими в одной плоскости, нужно одну из прямых параллельно перенести в плоскость, в которой лежит вторая прямая. Заметим, что (BB_1parallel AA_1). Следовательно, угол между (AA_1) и (CB_1) равен углу между прямыми (BB_1) и (CB_1).
Так как все ребра призмы равны, то грань (BCC_1B_1) представляет собой квадрат, где (CB_1) – диагональ. Следовательно, (angle
BB_1C=45^circ).

Ответ: 45

Школьникам, которые готовятся к сдаче ЕГЭ по математике, обязательно стоит научиться решать задачи на нахождение площади прямой и правильной призмы. Многолетняя практика подтверждает тот факт, что подобные задания по геометрии многие учащиеся считают достаточно сложными.

При этом уметь находить площадь и объем правильной и прямой призмы должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи ЕГЭ.

Основные моменты, которые стоит запомнить

Если боковые ребра призмы перпендикулярны основанию, она называется прямой. Все боковые грани этой фигуры являются прямоугольниками. Высота прямой призмы совпадает с ее ребром.
Правильной является призма, боковые ребра которой перпендикулярны основанию, в котором находится правильный многоугольник. Боковые грани этой фигуры — равные прямоугольники. Правильная призма всегда является прямой.

Подготовка к единому госэкзамену вместе со «Школково» — залог вашего успеха!

Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь представлен весь необходимый материал, который поможет подготовиться к прохождению аттестационного испытания.

Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы, теоремы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня.

Базовая информация систематизирована и понятно изложена в разделе «Теоретическая справка». Если вы уже успели повторить необходимый материал, рекомендуем вам попрактиковаться в решении задач на нахождение площади и объема прямой призмы. В разделе «Каталог» представлена большая подборка упражнений различной степени сложности.

Попробуйте рассчитать площадь прямой и правильной призмы или площадь боковой поверхности призмы прямо сейчас. Разберите любое задание. Если оно не вызвало сложностей, можете смело переходить к упражнениям экспертного уровня. А если определенные трудности все же возникли, рекомендуем вам регулярно готовиться к ЕГЭ в онлайн-режиме вместе с математическим порталом «Школково», и задачи по теме «Прямая и правильная призма» будут даваться вам легко.

УСТАЛ? Просто отдохни

Источник

Призма

Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.

Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.

Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

$С_1Н$ — высота

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

Формулы вычисления объема и площади поверхности призмы:

Чтобы были понятны формулы, введем обозначения:

$P_{осн}$ — периметр основания;

$S_{осн}$ — площадь основания;

$S_{бок}$ — площадь боковой поверхности;

$S_{п.п}$ — площадь полной поверхности;

$h$ — высота призмы.

$S_{бок}=P_{осн}·h$

$S_{п.п}=S_{бок}+2S_{осн}$

$V=S_{осн}·h$

В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

$S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
$S={a·b·sin⁡α}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
$S=p·r$, где $r$ — радиус вписанной окружности
$S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.

В основании лежит четырехугольник

1. Прямоугольник

$S=a·b$, где $а$ и $b$ — смежные стороны.

2. Ромб

$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба

$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

3. Трапеция

$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.

Прямая призма называется правильной, если ее основания – правильные многоугольники.

Рассмотрим площади правильных многоугольников:

1. Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны.

2. Квадрат

$S=a^2$, где $а$ — сторона квадрата.

3. Правильный шестиугольник

Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:

$S=6·S_{треугольника}={6·a^2√3}/{4}={3·a^2√3}/{2}$, где $а$ — сторона правильного шестиугольника.

Пример:

Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.

Решение:

Построим прямую призму, в основании которой лежит ромб.

Распишем формулу площади полной поверхности:

$S_{п.п}=S_{бок}+2S_{осн}=P_{осн}·h+2S_{ромба}$

В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$

Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.

Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.

$АВ=√{5^2+12^2}=√{25+144}=√{169}=13$

$Р=13·4=52$

Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.

$S_{основания}={d_1·d_2}/{2}={10·24}/{2}=120$

Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:

$S_{п.п}=P_{осн}·h+2S_{ромба}=52·20+2·120=1040+240=1280$

Ответ: $1280$

Цилиндр — это та же призма, в основании которой лежит круг.

$S_{бок}=P_{осн}·h=2πRh$

$S_{п.п}=S_{бок}+2S_{осн}=2πRh+2πR^2=2πR(h+R)$

$V=S_{осн}·h=πR^2 h$

Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.

Средняя линия треугольника параллельна основанию и равна его половине.

$MN$ — средняя линия, так как соединяет середины соседних сторон.

$MN {//} AC, MN = {AC}/{2}$

Подобие треугольников

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.

Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)

Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Прямоугольный треугольник и его свойства:

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$AC^2+BC^2=AB^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Теорема синусов

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.

Теорема косинусов

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

$a^2=b^2+c^2-2·b·c·cosα;$

$b^2=a^2+c^2-2·a·c·cos⁡β;$

$c^2=b^2+a^2-2·b·a·cosγ.$

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Куб		диагональ
Параллелепипед	$V=S_text{OCH}h, h -$ высота
Прямоугольный параллелепипед		$d=sqrt{a^2+b^2+c^2}$
Призма	$V=S_text{OCH}h$	$S = 2S_text{OCH}+$
Пирамида	$V=frac{1}{3}S_text{OCH}h$	$S = S_text{OCH}+$

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

$P_text{OCH}=8+6+6+2+2+4=28.$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник), $S_text{OCH}=36+8=44$

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Ответ: 424.

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

$P_text{OCH}=4+5+2+1+2+4=18.$

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), $S_text{OCH}=16+2=18$ (маленький прямоугольник).

Найдем площадь полной поверхности:

Ответ: 54

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда $angle{ABC}=120^{circ}$

Из по теореме косинусов найдем ребро АС:

$AC^2=AB^2+BC^2-2cdot ABcdot BC cdot cos120^{circ}$

$AC^2=25+9-2cdot5cdot3cdotleft(-frac{1}{2}right)=47, ~AC = 7$

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Поэтому или откуда h=5.

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

$AK=sqrt{AB^2-BK^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12.$

Из прямоугольного имеем:

$DK=sqrt{DA^2+AK^2}=sqrt{9^2+12^2}=sqrt{81+144}=sqrt{225}=15.$

(по двум катетам), тогда $S_{ADB}=S_{ADC},$ следовательно

$=2S_{ADB}+S_{BDC},$ $=2cdotfrac{1}{2}cdot13cdot9+frac{1}{2}cdot10cdot15=117+75=192.$

Ответ: 192

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

$h=sqrt{37^2-12^2}=sqrt{(37-12)(37+12)}=sqrt{25cdot49}=5cdot7=35$

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен $V=S_{OCH}cdot h$ , а так как призма прямая, то ее боковое ребро является и высотой, то есть h=6.

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

$S_{OCH}=frac{1}{2}cdot ab=frac{1}{2}cdot6cdot7=21.$

Ответ: 126

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.

Объем призмы равен $V = S_{OCH}cdot h$

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды h_2 должна быть в 81 раз меньше, чем h_1. Она равна (см).

Ответ: 4

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды ABDA_1.

Решение.
Опустим из вершины A_1 высоту A_1H Н на основание ABCD.

$=S_{ABCD}cdot A_1H$

$=frac{1}{3}S_{ABD}cdot A_1H$

Диагональ основания делит его на два равных треугольника, следовательно, $S_{ABD}=frac{1}{2}S_{ABCD}.$

Имеем:

$ABDA_1=frac{1}{3}S_{ABD}cdot A_1H=frac{1}{3}cdotfrac{1}{2}S_{ABCD}cdot A_1H=frac{1}{6}V_{ABCDA_1B_1C_1D_1}=frac{1}{6}cdot21=3,5.$

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна $S_{OCH}=frac{a^2sqrt{3}}{4}.$

$S_{OCH}=frac{8^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}.$

Объем пирамиды $V=frac{1}{3}cdot16sqrt{3}cdot6sqrt{3}=16cdot6=96.$

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть AD=x, тогда $S_{OCH}=x^2.$

Так как точки М и К – середины АD и DС соответственно, то $DM=DK=frac{x}{2}.$

$S_{MDK}=frac{1}{2}MDcdot DK=frac{1}{2}cdotfrac{x}{2}cdotfrac{x}{2}=frac{1}{8}x^2.$

Площадь треугольника MDK, лежащего в основании новой призмы, составляет $frac{1}{8}$ часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: $V=S_{OCH}cdot h$ , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен 32:8=4.

Ответ: 4

Докажем полезную теорему.

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

$S=P_{perp}cdot l.$

Больше задач на формулы объема и площади поверхности здесь.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник