Введите а — длину прямоугольника в мм (миллиметрах):
Введите b — ширину прямоугольника в мм (миллиметрах):
Введите h — толщину прямоугольника в мм (миллиметрах):
Как рассчитать объем прямоугольника?
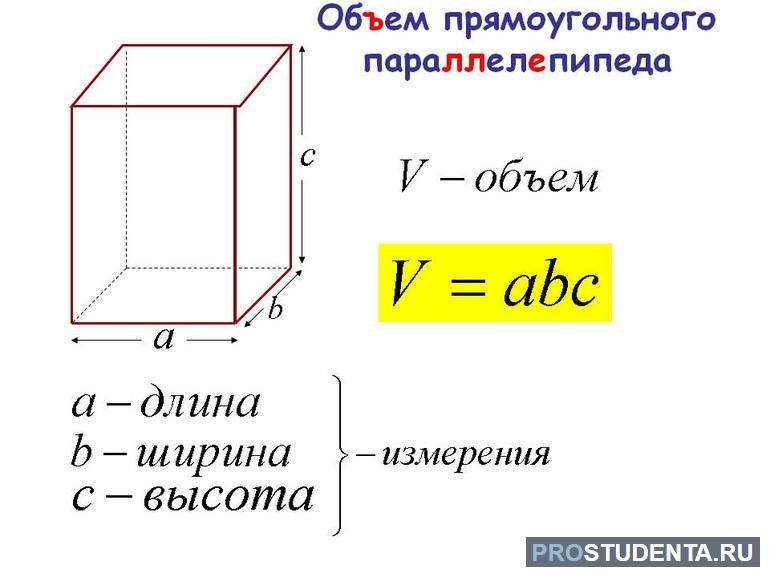
Если прямоугольник имеет толщину, то фактически это параллелепипед. Объем параллелепипед в общем случае рассчитывается по формуле:
V = a x b х h
V — объем параллелепипеда . Объем прямоугольника имеющего толщину (высоту).
a — длина прямоугольника основания параллелепипеда
b — ширина прямоугольника основания параллелепипеда
h — высота параллелепипеда. Толщина прямоугольника.
Объем в миллиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vмм3 = aмм х bмм х hмм
Vмм3 — объем в миллиметрах кубических (мм3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в сантиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vсм3 = aмм х bмм х hмм / 1 000
Vсм3 — объем в сантиметрах кубических (см3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в метрах кубических прямоугольника имеющего толщину (параллелепипед):
Vм3 = aмм х bмм х hмм / 1 000 000 000
Vм3 — объем в метрах кубических (м3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в литрах прямоугольника имеющего толщину (параллелепипед):
Vл = aмм х bмм х hмм / 1 000 000
Vл — объем в литрах (л).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Калькулятор для расчета объема параллелепипеда
C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер «a», «b», «c» и нажмите кнопку «Рассчитать». Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
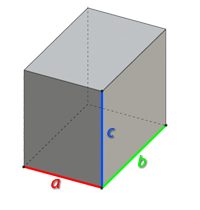
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку «Рассчитать»
Округлить результат до
знаков после запятой
Рассчитать
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.
Как найти объем, если известны длина, высота, ширина
Длина, ширина, высота — это параметры, которые характеризуют параллелепипед. Сам же параллелепипед представляет собой объемную фигуру, грани которой — параллелограммы. Достаточно знать эти параметры, чтобы вычислить объем фигуры.
Вам понадобится
- Калькулятор.
Инструкция
Предварительно нужно сделать оговорку. Длина, ширина и высота — это параметры, которые являются достаточными для вычисления объема лишь у прямоугольного параллелепипеда. Под прямоугольным параллелепипедом подразумевается фигура, у которой все грани образованы прямоугольниками, которые образуют между собой прямые углы. Это означает, что в прямоугольном параллелепипеде противоположные грани равны и параллельны.
Теперь, разобравшись с тем, в каком случае можно применять в качестве исходных данных параметры параллелепипеда, можно приступить к вычислению его объема. Объем — это мера, характеризующая количество занимаемого объектом пространства. Для вычисления объема параллелепипеда необходимо перемножить друг на друга все его параметры: длину, ширину и высоту. Формулой это можно выразить так:
V = a*b*c, где a, b и с — это параметры.
Для большей наглядности можно рассмотреть пример:
Имеется прямоугольный параллелепипед, площадь основания которого равна 42 см², а его высота составляет 15 см, требуется найти объем исходной фигуры.
Для решения задачи нужно заметить, что из всех параметров известной является только высота. Но дана площадь основания, которая находится умножением друг на друга длины и ширины прямоугольника. Из указанной выше формулы можно сделать вывод, что площадь основания — это a*b см², тогда объем прямоугольного параллелепипеда найдется так:
42*15 = 630 см³
Ответ: объем фигуры составит 630 см³
Обратите внимание
В широкой интерпретации, параллелепипед — это призма, у которой в основании находится параллелограмм. Существует несколько разновидностей данной фигуры, среди которых, помимо прямоугольного параллелепипеда, имеются:
— Прямой параллелепипед, у которого боковые грани являются прямоугольниками;
— Наклонный параллелепипед, в котором боковые грани не являются перпендикулярными основанию;
— Куб — это особая разновидность данного типа фигур, ведь все грани у него являются квадратами. При пересечении они образуют прямые углы, а противоположные грани параллельны друг другу, а это означает, что куб — частный случай прямоугольного параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
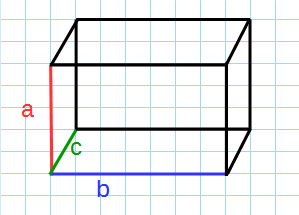
Формула объема параллелепипеда через его ребра:
a,b,c — ребра параллелепипеда.
Через стороны и высоту
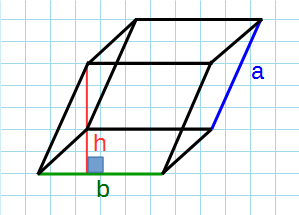
Формула объема параллелепипеда:
a,b — ребра параллелепипеда; h — высота параллелепипеда.
Форма объекта и его линейные размеры определяют один из важных с геометрической точки зрения параметров — объём. Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади.
Оглавление:
- Общие сведения
- Вычисление объёма
- Решение задач
- Использование калькулятора
Общие сведения
По своей сути объём является количественной характеристикой пространства, которое занимает тело или вещество. Простыми словами, этот параметр показывает вместимость. В качестве единицы измерения, согласно СИ, принят кубический метр. За обозначение же объёма взята латинская буква V.
У тел, имеющих простую форму, характеристики находятся путём перемножения площади на высоту. Например, для куба он равен a3, прямоугольной призмы — h * b * a, пирамиды — (S * b * h) / 3. В эллипсоидных фигурах при расчётах используется радиус. Так, для конуса объём равен (p * R2 * h) / 3, сферы — (4 * p * R3) / 3, тора — 2 * p2 * R1 * R22.
Объём плоских фигур, таких как треугольник, круг, квадрат, прямоугольник, равен нулю. Но если их стороны или окружности имеют связанные с ними попарно параллельные линии, то они уже являются объёмными фигурами. Например, прямоугольник в пространстве называют параллелепипедом. Таким образом, чтобы найти объём прямоугольника, необходимо, чтобы он представлял собой прямоугольный параллелепипед, иначе действие будет бессмысленным.
Определить объём — значит, знать две основные величины фигуры:
- площадь — двумерная характеристика, определяющая размер фигуры;
- высоту — это длина перпендикуляра, опущенного из вершины на основание в трёхмерном пространстве.
Так как площадь измеряется в метрах квадратных, а высота просто в метрах, то перемножение площади и высоты как раз и даст единицу измерения объёма — метр кубический.
Чтобы узнать площадь прямоугольника, используют его свойства. Изучают их обычно в седьмом классе средней школы. К основным из них относят правило равенства противоположных сторон и углов, деление диагонали пополам в точке пересечения и их равенство.
Именно одинаковые диагонали являются отличительным свойством прямоугольника от параллелограмма. Фактически же диагональ делит фигуру на два прямоугольных треугольника. Это свойство довольно часто используют при проведении расчётов площади или объёма.
Вычисление объёма
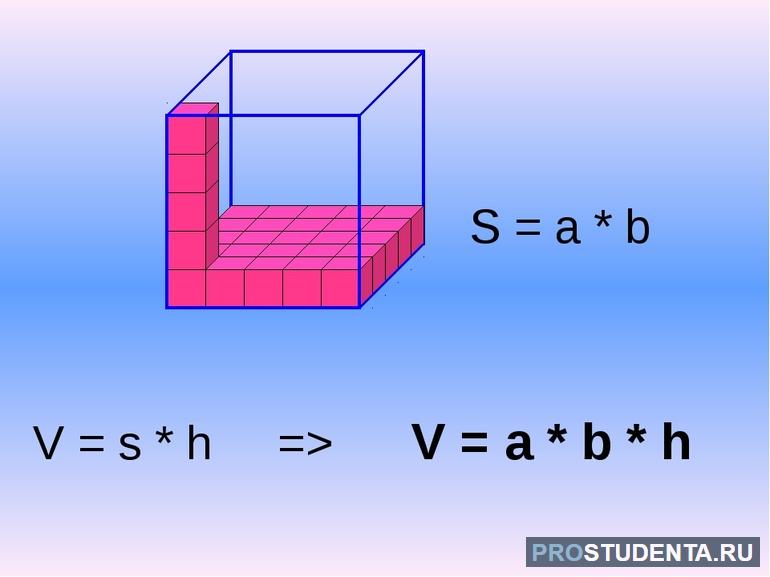
Существует теорема сообщающая, что объём параллелепипеда, то есть тела основанием которой является параллелограмм, можно рассчитать, умножив площадь основания на высоту фигуры. Записывается это формула как V = h * S, при этом S является произведением сторон прямоугольника.
Исходя из этого вычислить объём прямоугольника (параллелепипеда) можно по формуле: V = a * b * h, где: a, b — рёбра фигуры; h — высота тела.
Другими словами, параметр находится как произведение трёх измерений фигуры. Для доказательства нужно рассмотреть два возможных случая.
- Пусть имеется фигура, которая состоит из трёх измерений: a, b, c. Первые два являются основанием, к которому пристроена третье. Основание можно представить, как совокупность прямоугольников с площадью S = a * b, состоящую их квадратных единиц. На каждом из квадратов размещается кубическая единица. В итоге получается слой, состоящий из S единиц в кубе. Учитывая, что высота слоя это одна линейная единица, а высота всей фигуры состоит из энного количества таких единиц, то внутри тела можно поместить энное число слоёв. А значит, объём тела равен произведению этих кубических единиц, то есть V = a * b * c.
- Имеется прямоугольный параллелепипед. В его основании лежит прямоугольник с вершинами A, A1, B, B1. Соответственно плоскости ABCD и A1B1C1D1 будут боковыми гранями. В середине фигуры можно построить перпендикулярную плоскость MNPQ являющуюся сечением. Она будет равновеликим прямому параллелепипеду с основанием MNPQ и высотой (боковым ребром) BC. По признаку перпендикулярности, плоскости с двугранными углами являются прямыми. Отсюда можно утверждать, что MNPQ — прямоугольное тело, а значит и параллелепипед прямоугольный. Значит, его объём можно найти как произведение MN * MQ * BC. Исходя из того, что MQ перпендикулярно BC, площадь основания можно рассчитать как MQ * BC. А так как MN высота, то объём параллелепипеда можно вычислить, умножив площадь его основания на высоту.
Действительно, можно понять и без доказательств, что формула объёма верна. Если представить замкнутую фигуру с любым основанием, образованную в пространстве прямыми линиями, то в её середину можно будет поместить столько оснований, сколько позволит высота тела. Используя законы умножения, чтобы узнать, сколько же поместится в середине фигуры таких площадей, нужно основание умножить на высоту. То есть и получается доказываемая формула: V = S * h.
Решение задач
На самом деле вычисление объёма не только выполняют на уроках математики. Это знание востребовано в довольно многих специальностях и науках. Например, при строительстве, в архитектуре, инженерии, физике, химии. Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:
- Пусть есть параллелепипед с прямыми сторонами. Его рёбра у основания равняются 19 и 20 сантиметрам. Размер же боковой грани составляет 10 сантиметров. Вычислить объём фигуры. Эта задача на одну формулу, все данные для подстановки в неё известны. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
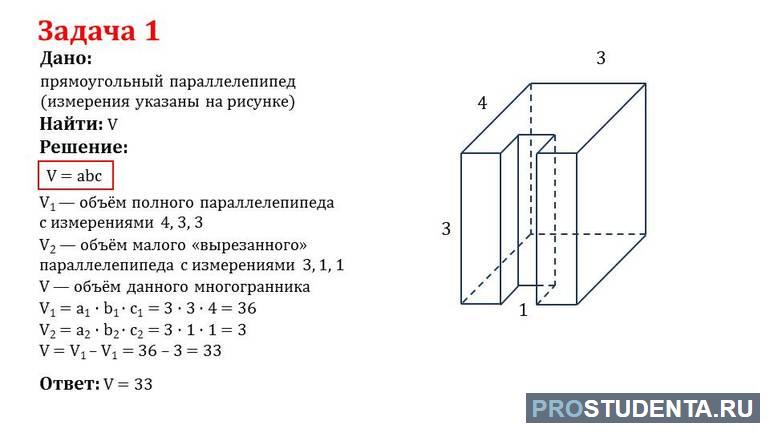
- Пусть имеется параллелепипед с основанием 1 см на 1,2 см и высотой 0,8 см. Из него был удалено другое прямоугольное тело с размерами 0,3 x 0,55 x 0,5. Найти объём получившейся фигуры. Так как искомый параметр новой фигуры равен разнице изначального и удалённого объёмов, то зная формулу найти ответ не составит труда: V = 0,8 * 1 * 1,2 — 0,3 * 0,5 * 0,55 = 0,877 см3.
- Дан прямоугольный параллелепипед с вершинами ABCD и A1B1C1D1. Сравнить объём образованного в середине пирамиды AA1BD тела со значением фигуры. Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.
- В гальванической ванне помещается три тысячи литров раствора. Высота наполнения ёмкости при этом достигает 75 сантиметров. В ванную поместили заготовку, после чего уровень поднялся на два сантиметра. Найти объём заготовки в метрах кубических. Итак, в одном кубическом метре содержится тысяча литров. Поэтому изначально в ёмкости было 3 м³ раствора. Значит, изначально в ванне раствор занимал: 3 = S * 75. Отсюда s = 3/75 = 1/25 см2. Объём детали составляет: V = S * 2 = (1/25) * 2 = 2 / 25 = 0,08 м³.
Использование калькулятора
Конечно же, на обычном калькуляторе объём прямоугольника не подсчитаешь. Разве что известны три его грани и формула нахождения параметра. Тогда нужно будет просто перемножить три числа. В других же случаях, когда нужно решить сложную задачу, связанную с громоздкими вычислениями, можно использовать математические сайты, имеющие название онлайн-калькуляторы.
Это интернет-сервисы, предлагающие своим пользователям бесплатно воспользоваться услугами по вычислению объёма геометрических фигур и выполнить другие математические операции. Для того чтобы воспользоваться сайтами-решателями, нужно иметь любой гаджет с возможностью подключения его к интернету и установленным на него веб-обозревателем.
После загрузки онлайн-калькулятора все действия пользователя сводятся к заполнению специальной формы в которую вносится условие задания. Конечно же, такое решение не может называться самостоятельным, но для проверки полученного результата или выявления ошибок в расчёте подходит идеально. Кроме, непосредственно автоматического вычисления объёма большинство сайтов содержат на своих страницах теоретический материал, а также примеры решений типовых заданий. Так что при обучении учащихся их использование на первых порах вполне оправданно.