Уже известны единицы измерения длины, например:
— и другие.
Для фигур на плоскости измеряют площадь в соответствующих квадратных единицах измерения:
мм2,см2,дм2,м2,км2…
Для геометрических тел измеряют объём, и для этого необходимы единицы измерения.
Единицей измерения объёма служит объём куба, у которого все грани равны (1) единице измерения длины:
мм3,см3,дм3,м3,км3…
Это кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр или даже кубический километр:
1км3=1000000000м3;1м3=1000дм3=1000000см3;1дм3=1000см3;1см3=1000мм3.
Часто для измерения объёма жидкости используют единицу измерения (1) литр:
1 л =1000см3=1дм3
.
Если измерять объём прямоугольного параллелепипеда, то можно представить, как маленькие кубики перекрывают прямоугольник в основании прямоугольного параллелепипеда.
Длины сторон прямоугольника определяют, сколько кубиков в ряду и сколько рядов с кубиками будет.
|
|
|
Если стороны равны, например, (3) см и (4) см, то прямоугольник перекрывается (3·4 = 12) кубиками.
Высота параллелепипеда определяет, сколько таких слоёв с кубиками можно поставить.
 |
|
Если высота прямоугольного параллелепипеда равна (3) см, то всего получится (3) слоя с кубиками. Итак, всего (3·3·4 = 36) кубиков, или объём равен (36) см³.
Значит, три измерения прямоугольного параллелепипеда позволяют посчитать, сколько всего кубиков поместилось в геометрическом теле, то есть вычислить объём прямоугольного параллелепипеда.
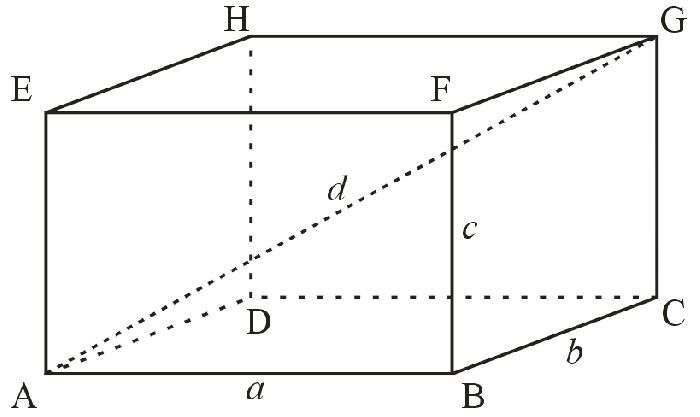
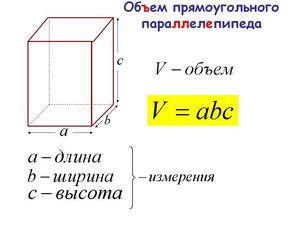
Пусть измерения прямоугольного параллелепипеда будут a, b и c единиц измерения.
Тогда объём (V = a·b·c) кубических единиц измерения.
Объем прямоугольника

4.6
Средняя оценка: 4.6
Всего получено оценок: 108.
4.6
Средняя оценка: 4.6
Всего получено оценок: 108.
В этой статье мы поговорим о разности определений объема и площади, а так же о прямоугольнике и параллелепипеде. Разделим все понятия, обсудим, как найти площадь и как определить объем.
Определения
Часто в жизни люди совершают математические ошибки. Причем зачастую не в силу какого-то грубого незнания, а просто из-за громоздкости названий. Это не совсем верно, поскольку ведет к увеличению числа ошибок.
Формулы объема прямоугольника не существует.
Фигура может быть:
- одномерной, то есть представлять собой точку или прямую
- двумерной, то есть быть составленной из точек или прямых в плоскости
- трехмерной, то есть воплощенной в пространстве. Трехмерные фигуры это то, что нас окружает. Арбуз идеальной формы – это пример шара, а пятирублевая монетка – круга; коробка здания представляет собой параллелепипед, колпаки волшебников из книг – конусы. Пространственная геометрия повсюду. Но если листовка с рекламой, это прямоугольник, то коробка – параллелепипед.
Разделение определений поможет избежать ошибок.
Двумерная фигура характеризуется периметром и площадью. Трехмерная имеет периметр, площадь поверхности и объем. Как понять, есть ли объем у фигуры? Достаточно представить себе, что засыпаешь в нее песок. Задержится ли он в фигуре?
В трехмерной: конусе, цилиндре, параллелепипеде – песок останется лежать, заполняя собой внутренне пространство (то есть объем). В двумерной песок просто насыплется сверху. Разделочную доску нельзя заполнить песком, так же как и нельзя найти объем прямоугольника.
Объем и площадь
Объем это пространственная характеристика. Она показывает, сколько место фигура занимает в пространстве или сколько нужно сыпучего материала или воды, чтобы заполнить фигуру изнутри.
Площадь это двумерная характеристика. Она показывает, к примеру, сколько места займет фигура на столе. Если нам нужно понять, сколько места занимает лист на столе, то считаем площадь, для того, что понять вместится ли учебник в ящик стола, нужно посчитать объем.
Из двумерных прямоугольников составляют трехмерную фигуру, которую называют прямоугольным параллелепипедом. Прямоугольный параллелепипед состоит из шести прямоугольников, которые называют гранями. Четыре боковых грани равны между собой, так же как равны между собой две оставшиеся грани-основания.
Чтобы найти площадь прямоугольника нужно перемножить между собой две стороны, выходящие из одной точки, то есть смежные. Для того, чтобы найти площадь поверхности прямоугольного параллелепипеда нужно сложить площади всех его граней.
Удивительно, но понятие объема появилось еще в Древней Греции. Им оперировал Евклид, Аристотель и Архимед. Но определение было размытым и неточным. Древние ученые увлекались двумерным пространством. Точное определение объема было дано лишь в 19 веке учеными Пеано и Жорданом.
Чтобы найти объем прямоугольного параллелепипеда, нужно так же перемножить между собой стороны, выходящие из одной точки. Но в пространстве их будет три: длина, ширина и высота.
Что мы узнали?
Мы разделили понятия фигур по пространственным характеристикам. Узнали как создается прямоугольный параллелепипед и разделили параллелепипед и прямоугольник, поговорили о расчете площади и объема. Привели примеры геометрических фигур из реальной жизни. Узнали, что объема прямоугольника не существует.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Ксения Кузнецова
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 108.
А какая ваша оценка?
Математика
5 класс
Урок №32
Объём прямоугольного параллелепипеда. Единицы объёма
Перечень рассматриваемых вопросов:
— куб;
— параллелепипед;
— элементы параллелепипеда;
— объём прямоугольного параллелепипеда, куба.
Тезаурус
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.
Высота, длина и ширина – это измерения прямоугольного параллелепипеда.
Единичный куб — куб, ребро которого равно линейной единице.
Обязательная литература
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Как вы думаете, что больше занимает места– 1 кг ваты или 1 кг гвоздей? Чтобы ответить на этот вопрос, нужно знать величину, которая называется объём. В данной задаче ответ очевиден, так как мы можем представить предметы визуально. Но не всегда ответ может быть таким простым. Чаще всего нужно произвести определённые вычисления.
Сегодня мы рассмотрим объём прямоугольного параллелепипеда и научимся его находить.
Объём можно измерить. Его измеряют в кубических миллиметрах, кубических сантиметрах, кубических метрах, литрах и т. д.
Найдём соотношение между единицами измерения объёма.
Так как 1 см = 10 дм, то 1 см3 = 1 000 мм3.
1 дм3 = 1000 см3 = 1 л
1 м3 = 1000 дм3
1 км3 = 1000000000 м3
В древности в разных частях планеты люди по-разному измеряли объём. Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.
На Руси основной мерой жидкостей считалось ведро, в котором 10 кружек или 12 литров. Также для подсчётов объём ведра делили пополам, то есть на два полуведра, которые, в свою очередь, тоже можно было поделить пополам. Для торговли с иностранцами использовали меру объёма, называемую бочка, которая равнялась 40 вёдрам.
Дадим определение единичного куба – это куб, ребро которого равно линейной единице. Его тоже принимают за единицу объёма.
Если прямоугольный параллелепипед можно разрезать на К единичных кубов, то говорят, что его объём V равен К кубическим единицам.
Например, на рисунке объём параллелепипеда равен 24 кубическим единицам.
V = 24 куб. единиц
Введём формулу объёма прямоугольного параллелепипеда.
Объём прямоугольного параллелепипеда равен произведению трёх его измерений, то есть произведению длины а, ширины bи высоты c, или произведению площади основания S на высоту c.
V = а · b · c = S · с
Так как куб является прямоугольным параллелепипедом, у которого все измерения равны, то его объём равен третьей степени длины его ребра а.
V = а3
Решим задачу.
Мальчик купил аквариум в форме прямоугольного параллелепипеда, который имеет площадь дна, равную 1400 см3, и высоту 6 дм. Какой объём воды он налил в аквариум, если уровень жидкости не доходил до края 5 см? Выразите ответ в кубических сантиметрах.
Чтобы решить эту задачу переведём единицы измерения длины в сантиметры.
6 дм = 60 см
Получается, что высота аквариума равна 60 см. Но по условию задачи требуется определить объём налитой жидкости, а её высота соответствует разности между высотой аквариума и уровнем жидкости, не доходящей до края:
с = 60 см – 5 см = 55 см
Получается, что высота жидкости в сосуде соответствует 55 см.
Теперь можно определить объём воды, которая налита в аквариум.
Для этого используем следующую формулу:
V = S · с = 1400 см2 · 55 см = 77000 см3
Ответ: мальчик налил в аквариум 77000 см3 воды.
Разбор решения заданий тренировочного модуля
№ 1. Чему равен объём куба, если длина его ребра равна 3 см?
Решение: для нахождения объёма куба нужно воспользоваться формулой.
V = а3 = (3 см)3 = 27 см3
Ответ: 27 см3.
№2. Как изменится объём прямоугольного параллелепипеда, если его длину увеличить в три раза. Подчеркните правильный ответ.
Решение: чтобы ответить на вопрос, нужно воспользоваться формулой для вычисления объёма прямоугольного параллелепипеда.
V = а · b · c, где а – длина прямоугольного параллелепипеда.
Если длина возрастет в три раза, то объём, соответственно, увеличится в три раза, так как, длина – это один из трёх множителей, входящих в формулу объёма прямоугольного параллелепипеда:
V = 3 · а · b · c
Ответ: объём увеличится в три раза.
Школа — это необъятная чаша знаний, которая включает в себя множество дисциплин, которые могут заинтересовать любого ребенка. Математика — царица точных наук. Строгая и дисциплинированная, она не терпит неточностей. Даже повзрослев, в обычной жизни мы можем столкнуться с разными математическими проблемами: вычисление квадратных метров для укладки плитки в ванной, кубических метров для определения объема бака и т. д., чего уж говорить о школьниках, которые только-только начинают свой математический путь.
Очень часто, начав изучать математику, точнее, геометрию, ученики путают плоские фигуры с объемными. Куб называют квадратом, шар — кругом, параллелепипед обычным прямоугольником. И здесь есть свои тонкости.
Сложно помочь ребенку в выполнении домашнего задания, не зная точно, объем или площадь какой фигуры — плоской или же объемной, нужно найти. Невозможно найти объем плоских фигур, таких как квадрат, круг, прямоугольник. В их случае можно найти лишь площадь. Прежде чем переходить к выполнению задачи, следует подготовить нужные атрибуты:
- Линейка, для того чтобы измерить необходимые нам данные.
- Калькулятор, для того чтобы в дальнейшем подсчитать расчеты.
Содержание:
- Вычисление объема прямоугольного параллелепипеда
- Пример первый
- Пример второй
- Пример третий
Вычисление объема прямоугольного параллелепипеда
Итак, вы знаете, что нужно рассчитать объем, но не забывайте, что обязательно нужно уточнить о какой именно фигуре идет речь: объем куба, или же объемного прямоугольника. Ведь расчет этих, казалось бы, одинаковых фигур, абсолютно разный.
Для начала рассмотрим само понятие объемного прямоугольника. Это параллелепипед. В его основании находится параллелограмм. Так как таковых у него шесть, следовательно все параллелограммы являются гранями параллелепипеда.
Что касается его граней, они могут отличаться, то есть, если прямые боковые грани представляют собой прямоугольники, тогда это прямой параллелепипед, ну, а если все шесть граней являются прямоугольниками, то перед нами прямоугольный параллелепипед.
- После прочтения задачи, нужно определить что именно следует найти; длину фигуры, объем или же площадь.
- Какая именно часть фигуры рассматривается в задаче — ребро, вершина, грань, сторона, а может быть, вся фигура целиком?
Определив все поставленные задачи, можно переходить непосредственно к вычислениям. Для этого нам понадобятся специальные формулы. Итак, для того чтобы найти объем прямоугольного параллелепипеда перемножается между собой длина, ширина и высота (то есть толщина фигуры). Формула вычисления объема прямоугольного параллелепипеда следующая:
V=a*b*h,
V является объемом параллелепипеда, где a — его длина b — ширина и h — высота соответственно.
Важно! Перед началом перевести все измерения в одну единицу исчисления. Ответ должен получится непременно в кубических единицах.
Пример первый
Определим объем бака для спирта, при следующих размерах:
- длина три метра;
- ширина два метра пятьдесят сантиметров;
- высота триста сантиметров.
Для начала обязательно согласовываем единицы измерения и перемножаем их:
3*2.5*3.
Перемножив данные, мы получим ответ в кубических метрах, то есть 3*2.5*3= 22.5 метра в кубе.
Пример второй
Шкаф имеет высоту четыре метра, ширину семьдесят сантиметров и глубину 80 сантиметров.
Зная формулу вычисления можно произвести умножение. Но не стоит торопиться, как и было сказано вначале, следует согласовать между собой единицы, то есть при желании вычислять в сантиметрах перевести все исчисления в сантиметры, ежели в метрах, то в метры. Сделаем оба варианта.
Итак, начнем с сантиметров. Переводим метры в сантиметры:
V = 400 * 70 * 80;
V = 2240000 сантиметров в кубе.
Теперь метры:
V = 4* 0.7 * 0.8;
V = 2.24 метра в кубе.
Исходя из вышеперечисленных манипуляции, очевидно, что работа с кубическими метрами более легка и понятна.
Пример третий
Дана комната, объем которой должен быть вычислен. Длина этой комнаты равна пяти метрам, ширина — трем, а высота потолка 2,5. Опять используем известную нам формулу:
V = a * b * h;
где, а длина комната и равна 5, b- ширина и равна 3 и h высота, которая равна 2.5
Так как все единицы даны в метрах, можно сразу приступать к вычислениям. Перемножая между собой a, b и h:
V = 5 * 3 * 2.5;
V = 37.5 метра в кубе.
Итак, в качестве заключения, можно сказать, что зная основные математические правила для вычисления объема или же площади фигур, а также правильно определив фигуры (плоские или же объемные), умея переводить сантиметры в метры и наоборот — можно облегчить изучение геометрии вашему ребенку, что не может не сделать этот процесс более интересным и привлекательным, ведь все накопленные знания в школе, могут быть успешно использованы в самой обычной бытовой жизни в будущем.
Представим себе такую историю…
– Паша, а ты когда-нибудь собирал кубик Рубика? – спросил Саша.
– Конечно! И не один раз, – ответил Паша. –
Кстати, кубик Рубика отличная игрушка-головоломка,
которая развивает логическое мышление.
– Да, мне тоже он очень нравится! – продолжил
Саша. – Я вот сегодня собрал кубик Рубика за 15 минут.
Пока собирал, задумался, а сколько всего маленьких кубиков в нём?
– И в правду, – задумался Паша, – и сколько
же их там?
– Не знаю! – ответил Саша. – Сколько ни
пытался их пересчитать, всё сбивался. В общем, так и не получилось у меня их
сосчитать.
– А давай спросим у Электроши!
– предложил Паша. – Он точно знает, как их посчитать.
– Ребята, прежде чем я вам расскажу о
прямоугольном параллелепипеде, давайте немного разомнёмся и выполним устные
задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас
должно было получиться!
– А теперь вернёмся к вашему вопросу, –
продолжил Электроша. – Только сначала ответьте мне на
вопрос: какую форму имеет кубик Рубика?
– Кубик Рубика
имеет форму прямоугольного параллелепипеда, а точнее – форму куба, – ответили
мальчишки.
– Молодцы! – похвалил ребят Электроша. – Важным свойством любого геометрического тела
является его вместимость, то есть объём фигуры. Величина объёма
даёт нам представление о том, какую часть пространства занимает интересующий
нас объект.
Кстати, с такой величиной, как объём, мы
очень часто встречаемся в нашей жизни. Может, вы сможете привести примеры,
когда мы интересуемся объёмом? – спросил у ребят Электроша.
– Например, объём коробки с соком, объём
бассейна, объём школьного кабинета, – начал Саша.
– Ещё нам нужно знать объём топливного бака
машины, показатели потребления газа или воды на счётчиках, – продолжил Паша.
– Хорошие примеры! – похвалил ребят Электроша. – А как вы думаете, что нужно знать для того,
чтобы измерить объём? – спросил у ребят Электроша.
– Наверное, нужно знать единицу измерения
объёмов, – предположили мальчишки.
– Правильно! – подтвердил Электроша.
– Напомню, что для измерения отрезков мы вводили единичный отрезок, для
измерения углов – единичный угол, а для измерения площадей фигур – единичный
квадрат.
Для измерения объёмов также вводятся единицы
измерения. За единицу измерения объёма выбирают куб, ребро которого равно
единичному отрезку. Такой куб называют единичным.
Например, объём куба с ребром 1 миллиметр
называют кубическим миллиметром. Пишут так: .
Объём куба с ребром 1 сантиметр называют кубическим
сантиметром. Пишут так: .
Объём куба с ребром 1 дециметр называют кубическим
дециметром. Пишут так: .
Всем хорошо известна и такая единица объёма,
как 1 литр. Пишут так дм3
л. Это другое название кубического
дециметра.
Объём куба с ребром 1 метр называют кубическим
метром. Пишут так: .
Объём куба с ребром 1 километр называют кубическим
километром. Пишут так: .
Легко заметить, что название единицы объёма
получается из названия единицы длины присоединением прилагательного
«кубический».
– Как вы думаете, что значит измерить объём
фигуры? – спросил у ребят Электроша.
– Измерить
объём фигуры – значит подсчитать, сколько единичных кубов в ней
помещается, –
сказали мальчишки.
– Молодцы! – похвалил ребят Электроша. – Проще всего измерить объём прямоугольного
параллелепипеда. Чем мы сейчас и займёмся.
– Посмотрите: на листке бумаги изображён
прямоугольный параллелепипед со следующими измерениями: длина 5 сантиметров,
ширина 2 сантиметра и высота 3 сантиметра. Давайте посчитаем, сколько единичных
кубов может в нём поместиться.
– Начнём укладывать кубики на дно
прямоугольного параллелепипеда, – предложили мальчишки. – Итак, сначала положим
на дно ряд единичных кубиков со стороной 1 сантиметр вдоль длинной стены.
Видим: поместилось 5 таких кубиков. Затем вдоль этих кубиков уложим ещё 1 ряд.
Тоже получим ещё пять кубиков.
– Хорошо! – сказал Электроша.
– Тогда сколько всего кубиков у вас поместилось на дне прямоугольного
параллелепипеда?
– На дне параллелепипеда помещается слой из единичных кубиков, то есть слой из 10 кубов.
– Молодцы! – похвалил ребят Электроша. – А чтобы заполнить
весь прямоугольный параллелепипед, сколько в него нужно вложить таких слоёв?
– Так как высота нашего параллелепипеда 3 сантиметра,
то в него вместится 3 слоя кубиков, в каждом из которых будет по 10 кубиков.
Тогда получается, что весь прямоугольный параллелепипед можно заполнить 30 кубиками.
– Всё правильно! – согласился Электроша. – Мы получили, что всего в нашем параллелепипеде
помещается единичных кубов. Поэтому объём нашего параллелепипеда равен
(см3).
– Электроша,
получается, что три измерения прямоугольного параллелепипеда позволяют
посчитать, сколько всего кубиков в нём поместится? – спросил Паша.
– Да, – ответил Электроша.
– Запомните! Объём прямоугольного параллелепипеда равен произведению
трёх его измерений.
Формулу для вычисления объёма прямоугольного
параллелепипеда в буквенном виде можно записать следующим образом: , где
– объём,
,
и
– измерения прямоугольного параллелепипеда.
При вычислениях обязательно нужно обращать внимание, чтобы все измерения
прямоугольного параллелепипеда были выражены в одинаковых единицах.
– А теперь давайте решим одну задачку, –
предложил Электроша. – Определите объём блока бумаги,
если длина одного листа 20 миллиметров, ширина – 15 миллиметров, а всего в
блоке помещается 500 таких листов (считать толщину листа равной 1 миллиметру).
– Сначала вычислим площадь одного листа, –
сказал Паша, – она будет равна (мм2).
– А потом площадь этого листа умножим на
количество листов, помещающихся в блоке, – продолжил Саша, – то есть (мм3).
– Молодцы! – похвалил ребят Электроша. – Обратите внимание: блок бумаги имеет форму
прямоугольного параллелепипеда. Значит, мы с вами сейчас нашли объём
параллелепипеда, но с помощью другой формулы. Запомните! Объём
прямоугольного параллелепипеда равен произведению площади основания на высоту.
В буквенном виде эту формулу записывают так: , где
– площадь основания прямоугольного
параллелепипеда, – его высота.
– А теперь давайте всё же вернёмся к вашему
первоначальному вопросу, – продолжил Электроша. – Вы
хотели выяснить, сколько кубиков содержится в кубике Рубика.
Мы с вами уже определили, что эта замечательная игрушка имеет форму прямоугольного
параллелепипеда, а если быть точнее, то форму куба. Может, вы уже сможете
посчитать количество маленьких кубиков, из которых состоит кубик Рубика?
– Так, – начал рассуждать Саша, – длина
нашего кубика Рубика состоит из 3 маленьких кубиков, точно
такие же ширина и высота. Значит, в нашем кубике Рубика
помещается маленьких кубиков.
– Всё правильно! – сказал Электроша.
– Изначально кубик Рубика состоял из 27 связных между
собой разноцветных кубиков, но затем его конструкция упростилась до набора из 26
маленьких кубиков, а вместо внутреннего кубика разместился хитроумный
скрепляющий механизм. Кстати, а вы знаете кем, как и когда была придумана эта
замечательная игрушка? – спросил Электроша.
– Не знаем, – ответили мальчишки.
– Скажу вам только, что знаменитый кубик Рубика придумал венгерский преподаватель архитектуры Эрно Рубик в 1974 году.
А вот уже историю его создания и
усовершенствования вы можете изучить на досуге.
– А теперь смотрите, мы с вами определили,
что наш кубик Рубика имеет форму куба. Поскольку у
куба все рёбра равны, то его объём вычисляют по формуле: , где
– длина ребра куба. Именно поэтому третью
степень числа называют кубом числа.
А теперь, ребята, давайте посмотрим, как вы
всё поняли, и выполним несколько заданий.
Задание первое: объём класса 96 кубических
метров. Найдите высоту стены, если площадь пола 32 квадратных метра.
Решение: класс имеет форму прямоугольного
параллелепипеда. Нам известна площадь пола, то есть площадь основания
прямоугольного параллелепипеда. Значит, можем воспользоваться формулой для
вычисления объёма прямоугольного параллелепипеда через площадь основания и
высоту: . Выразим из этой формулы высоту:
. И подставим в получившуюся формулу объём класса и площадь пола:
(м). Получаем, что высота стены равна 3 метрам.
Следующее задание: длина аквариума 80 сантиметров,
ширина 45 сантиметров, высота 65 сантиметров. Сколько литров воды нужно налить,
чтобы уровень воды был ниже верхнего края аквариума на 5 сантиметров?
Решение: высота нашего аквариума 65
сантиметров, а воду нужно налить так, чтобы её уровень был ниже верхнего края
аквариума на 5 сантиметров. Значит, от высоты аквариума отнимем 5 сантиметров: . Получим, что высота уровня воды равна 60 сантиметрам. Воспользуемся
формулой для вычисления объёма прямоугольного параллелепипеда:
. Получим, что в аквариум нужно налить
(см3). Переведём в литры. Мы знаем, что
л
дм3 , а значит, равен
см3 . Тогда получаем, что в
аквариум нужно налить см3
л.