Как найти объем прямоугольного параллелепипеда через диагональ

Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда

Определение.

Прямоугольный параллелепипед — это многогранная объемная фигура ограничена шестью прямоугольниками.

Куб является частным случаем прямоугольного параллелепипеда.

Рис.1

Основные свойства правильного прямоугольного параллелепипеда

Противоположные грани прямоугольного параллелепипеда параллельны и равны.

Ребра прямоугольного параллелепипеда, которые сходятся в одной вершине взаимно перпендикулярны.

Не параллельные грани прямоугольного параллелепипеда пересекаются под прямым углом.

У прямоугольного параллелепипеда четыре диагонали.

Диагонали прямоугольного параллелепипеда равны между собой и пересекаются в одной точке.

Объем прямоугольного параллелепипеда

Формула. Объем прямоугольного параллелепипеда равна произведению длин его сторон:

V = a · b · c

Площадь поверхности прямоугольного параллелепипеда

Определение. Поверхность прямоугольного параллелепипеда состоит из суммы площадей прямоугольников, ограничивающие его.

Формула. Площадь поверхности прямоугольного параллелепипеда через длины его сторон:

S = 2a·b + 2a·c + 2b·c

Диагональ прямоугольного параллелепипеда

Определение. Диагональ прямоугольного параллелепипеда — это отрезок, соединяющий две не соседние вершины, лежащие на разных гранях.

Формула. Длина диагонали прямоугольного параллелепипеда через длины его сторон:

d = √a² + b² + c²

На этом уроке мы поговорим о прямоугольном
параллелепипеде. Вспомним некоторые из его свойств. А затем подробно выведем
формулы для вычисления объёма прямоугольного параллелепипеда.

Ранее мы с вами уже познакомились с прямоугольным
параллелепипедом. Напомним, что параллелепипед называется прямоугольным,
если все его шесть граней прямоугольники.

Представление о форме прямоугольного
параллелепипеда дают спичечный коробок, коробка, холодильник и др.

Давайте представим себе, комнату, которая имеет
форму прямоугольного параллелепипеда.

Если говорить о её размерах, то обычно
употребляют слова «длина», «ширина» и «высота», имея в виду длины трех рёбер с
общей вершиной. В геометрии эти три величины объединяются общим названием: измерения
прямоугольного параллелепипеда.

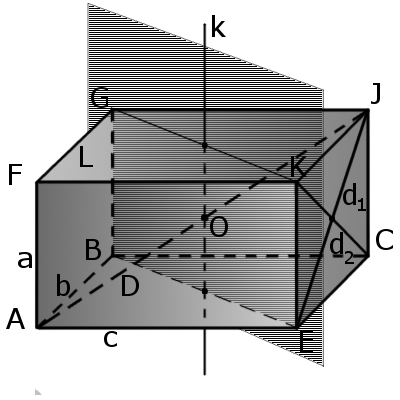
На экране изображён прямоугольный
параллелепипед .
В качестве его измерений можно взять, например, длины рёбер ,
 и
,
все эти рёбра имеют общую вершину .
Тогда ребро  –
это есть длина данного параллелепипеда,  –
ширина и  –
его высота.

Прямоугольный параллелепипед обладает
следующими свойствами:

1)               
квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов
трёх его измерений.

2)               
объём прямоугольного параллелепипеда равен произведению трёх его
измерений.

Итак, справедлива следующая теорема: объём
прямоугольного параллелепипеда равен произведению трёх его измерений.

Докажем эту теорему. Пусть дан
прямоугольный параллелепипед .
Обозначим его измерения буквами ,
 и
,
а его объём буквой .

Докажем, что объём прямоугольного
параллелепипеда равен .

Возможны два случая:

Рассмотрим первый случай. Измерения ,
 и
 представляют
собой конечные десятичные дроби, у которых число знаков после запятой не
превосходит  ().

В этом случае числа ,
 и
 являются
целыми.

Разделим каждое ребро параллелепипеда на
равные части длины .
Затем через точки разбиения проведём плоскости, перпендикулярные к этому ребру.

Тогда наш параллелепипед  разобьётся
на равные кубы с длиной каждого ребра .
Общее же количество таких кубов будет равно .

Так как объём каждого такого куба равен ,
то объём всего параллелепипеда  будет равен .

Этим мы доказали, что объём прямоугольного
параллелепипеда равен произведению трёх его измерений.

Что и требовалось доказать.

Перейдём ко второму случаю. Хотя бы одно из
измерений ,
 и
 представляет
собой бесконечную десятичную дробь.

Рассмотрим конечные десятичные дроби ,
,
,
которые получаются из чисел ,
,
,
если отбросить в каждом из них все цифры после запятой, начиная с -ой.

Заметим, что тогда справедливо неравенство ,
где .
Аналогичные неравенства будут выполняться и для чисел  и
:
,
,
где ,
.

Перемножим эти неравенства. Тогда видим, что .

Из неравенства понятно, что параллелепипед  содержит
в себе параллелепипед ,
а сам содержится в параллелепипеде .

А это говорит о том, что .

Теперь давайте будем неограниченно увеличивать
.
Тогда число  будет
становиться сколь угодно малым, и поэтому число  будет
сколь угодно мало отличаться от числа .

В итоге, они станут равны. Т.е. .
Что и требовалось доказать.

Из этой теоремы справедливы следующие следствия.

Первое следствие. Объём
прямоугольного параллелепипеда равен произведению площади основания на высоту.

Доказательство. Пусть грань с рёбрами
 и
 является основанием прямоугольного параллелепипеда. Тогда площадь
основания ,
а высота параллелепипеда .

Тогда можно заметить, что формулу для
вычисления объёма прямоугольного параллелепипеда  можно
записать в виде ,
где  –
площадь основания,  –
высота прямоугольного параллелепипеда.

Таким образом, мы доказали, что объём
прямоугольного параллелепипеда равен .
Что и требовалось доказать.

Второе следствие. Объём прямой
призмы, основанием которой является прямоугольный треугольник, равен
произведению площади основания на высоту.

Доказательство. Для
доказательства этого утверждения достроим прямую треугольную призму с
основанием  ()
до прямоугольного параллелепипеда так, как показано на экране.

Учитывая первое следствие, объём этого
параллелепипеда равен ,
где  –
площадь основания ,
 –
высота призмы.

Плоскость  разбивает
параллелепипед на две равные прямые призмы, одна из которых – данная. Эти
призмы равны, так как имеют равные основания и равные высоты.

Следовательно, объём  данной
призмы равен ,
т.е. равен .
Что и требовалось доказать.

Замечание. Рассмотрим квадрат со
стороной а.

Исходя из теоремы Пифагора его диагональ равна
.
Поэтому площадь построенного на ней квадрата вдвое больше площади данного
квадрата. Таким образом, не составляет труда построить сторону квадрата,
площадь которого вдвое больше площади данного квадрата.

Рассмотрим теперь куб со стороной а.

Возникает вопрос: можно ли с помощью циркуля и
линейки построить сторону куба, объём которого вдвое больше объёма данного
куба, т.е. построить отрезок, равный ? 

Эта задача была сформулирована ещё в глубокой
древности. Она получила название «задача об удвоении куба». Лишь в 1837 году
французский математик Пьер Лоран Ванцель доказал, что такое построение
невозможно. Одновременно им была доказана неразрешимость ещё одной задачи на
построение – задачи о трисекции угла (произвольный данный угол разделить на три
равных угла).

Напомним, что к числу классических
неразрешимых задач на построение относится также задача о квадратуре круга
(построить квадрат, площадь которого равна площади данного круга). Невозможность
такого построения была доказана в 1882 году немецким математиком Карлом Луизом
Фердинандом Линдеманом.

Задача: найдите объём прямоугольного
параллелепипеда с диагональю  см
и сторонами основания  см
и  см.

Решение: запишем формулу для
вычисления объёма прямоугольного параллелепипеда через его измерения.

Из условия задачи нам известны длина, ширина и
диагональ прямоугольного параллелепипеда, но неизвестна его высота. Напомним,
что .

Выразим из этой формулы высоту  прямоугольного
параллелепипеда. Получим, что высота равна  и
равна  (см).

Подставим измерения нашего прямоугольного
параллелепипеда в формулу объёма. Посчитаем. Получим, что объем параллелепипеда
равен  (см³).

Не забудем записать ответ.

Задача:  прямоугольный
параллелепипед, основание  –
квадрат. Объем прямоугольного параллелепипеда равен  см³.
Определите высоту прямоугольного параллелепипеда, если  см.

Решение: на этом уроке мы
доказали, что объём прямоугольного параллелепипеда равен .
Выразим из формулы высоту. Отсюда, высота равна .
Так как в основании нашего прямоугольного параллелепипеда лежит квадрат по
условию, то площадь основания равна  (см²).
По условию задачи, также известно, что объём прямоугольного параллелепипеда
равен .
Отсюда, высота равна  (см). Запишем ответ.

Итоги:

На этом уроке мы вспомнили понятие прямоугольного
параллелепипеда. Доказали, что объём прямоугольного параллелепипеда равен
произведению трёх его измерений. Доказали, что объём прямоугольного
параллелепипеда можно вычислить как произведение площади основания на высоту. А
также доказали, что объём прямой призмы, основанием которой является
прямоугольный треугольник, равен произведению площади основания на высоту.

Геометрический калькулятор для прямоугольного параллелепипеда можно запустить также, зная два из трех ребер тела и его диагональ. Поскольку диагональ параллелепипеда равна по теореме Пифагора квадратному корню из суммы квадратов всех трех его ребер, то из этого выражения алгебраически можно вывести формулу для третьего неизвестного ребра. (рис.22.4)
d_4=√(a^2+b^2+c^2 )
b=√(a^2+c^2-〖d_4〗^2 )

Имея возможность вычислить неизвестное ребро параллелепипеда, можно следом найти все остальные диагонали его боковых граней. (рис.22.1, 22.2, 22.3)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )=√(a^2+a^2+c^2-〖d_4〗^2 )=√(2a^2+c^2-〖d_4〗^2 )
d_3=√(b^2+c^2 )=√(a^2+c^2-〖d_4〗^2+c^2 )=√(a^2+2c^2-〖d_4〗^2 )

Чтобы найти угол α между диагональю прямоугольного параллелепипеда и диагональю его основания, необходимо воспользоваться отношением синуса — известного бокового ребра а к диагонали параллелепипеда. (рис.22.5)
sin⁡α=a/d_4

Периметр прямоугольного параллелепипеда равен учетверенной сумме ребер, составляющих параллелепипед. Для неизвестного ребра в формулу подставляется полученное из теоремы Пифагора выражение через диагональ параллелепипеда.
P=4(a+b+c)

Площадь полной поверхности прямоугольного параллелепипеда через диагональ также можно вычислить посредством замены неизвестной переменной на соответствующее выражение. Изначально площадь параллелепипеда равна удвоенной сумме попарных произведений его ребер.
S=2(ab+bc+ac)=2((a+c) √(a^2+c^2-〖d_4〗^2 )+ac)

Чтобы найти объем прямоугольного параллелепипеда, зная диагональ, нужно умножить два известных ребра параллелепипеда на квадратный корень из разности квадрата диагонали от суммы квадратов этих ребер.
V=abc=ac√(a^2+c^2-〖d_4〗^2 )

Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом.

Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником.

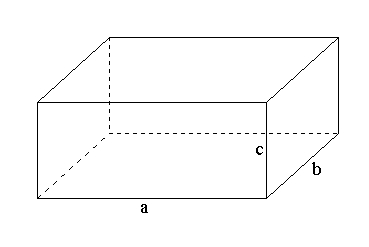
Любой параллелепипед характеризуется 3 сторонами a, b и c (см. рисунок) и диагональю. Именно эти характеристики используются в формулах параллелепипеда при вычислении объема и площади.

Диагональ параллелепипеда – это отрезок, соединяющий противоположные вершины параллелепипеда.

Формула диагонали параллелепипеда

Диагональ d прямоугольного параллелепипеда можно получить, зная его стороны:

d² = a² + b² + c²

Формула площади параллелепипеда

Площадь поверхности прямоугольного параллелепипеда можно получить, зная его стороны:

S = 2(ab + ac + bc)

Формула объема параллелепипеда

Объем прямоугольного параллелепипеда можно вычислить, зная его стороны:

V = abc

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

1. В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
2. Противоположные грани попарно равны и параллельны.
3. Все двугранные углы прямоугольного параллелепипеда – прямые.
4. Диагонали прямоугольного параллелепипеда равны.
5. Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

$B_1D^2=AD^2+DC^2+C_1C^2$

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$а$ — длина;

$b$ — ширина;

$с$ — высота(она же боковое ребро);

$P_{осн}$ — периметр основания;

$S_{осн}$ — площадь основания;

$S_{бок}$ — площадь боковой поверхности;

$S_{п.п}$ — площадь полной поверхности;

$V$ — объем.

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

$S_{п.п}=2(ab+bc+ac).$

Дополнительные сведения, которые пригодятся для решения задач:

Куб

$а$ — длина стороны.

$V=a^3;$

$S_{бок}=4а^2;$

$S_{п.п}=6а^2;$

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

$V={1}/{3}S_{осн}·h$

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

Площадь треугольника.

• $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
• $S={a·b·sin⁡α}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
• Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$.
• $S=p·r$, где $r$ — радиус вписанной окружности.
• $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности.
• Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
• Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны. 

В основании лежит четырехугольник.

1. Прямоугольник.
   $S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб.
   $S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба.
   $S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция.
   $S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
4. Квадрат.
   $S=a^2$, где $а$ — сторона квадрата.

Теорема Пифагора.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$