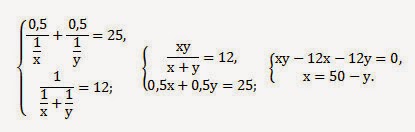Как найти объем работы математика - Исправление недочетов и поиск решений вместе с Examum.ru

2-й способ решения — без таблицы

Как обойтись без составления таблицы?

Сразу составить уравнение.

Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.

Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.

Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.

Напомню, что первый работал на ( displaystyle 2) часа дольше, поэтому к времени второго надо будет прибавить ( displaystyle 2):

( displaystyle frac{112}{x}=frac{112}{x+1}+2)

То же самое уравнение, что и в первом способе, только без таблицы и системы уравнений.

А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.

Во-первых, сравним формулы:

Движение	Работа
( displaystyle v=frac{S}{t})	( displaystyle P=frac{A}{t})
Скорость движения	Скорость выполнения работы, т.е. производительность
Пройденный путь	Выполненная работа
Потраченное на движение время	Потраченное на работу время

Теперь рассмотрим задачу:

Пример №1

Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.

Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?

Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).

Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:

( displaystyle frac{112}{x}=frac{112}{x+1}+2).

То же самое уравнение! Вот и получается, что работа и движение – одно и то же.

Как решать задачи на совместную работу

Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).

Пример №2

Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).

За какое время они заполнят бассейн, работая вместе?

Решение

Во-первых, давай придумаем аналогию с движением.

Придумал?

Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).

А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.

Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!

Тогда что нас просят найти? Время, через которое они встретятся.

Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.

Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).

С какой производительностью работают две трубы вместе (не забывай, это задачи на совместную работу)? Берем количество литров, которое налила в бассейн первая труба за один час, прибавляем количество литров, которое налила в бассейн вторая труба за один час, – именно столько наливают в бассейн обе трубы за один час. То есть производительности складываются:

( displaystyle P={{P}_{1}}+{{P}_{2}})

То же самое, что и относительная скорость: с какой скоростью второй автомобиль приближается к первому? Со скоростью, равной сумме скоростей: ( displaystyle v={{v}_{1}}+{{v}_{2}}).

Итак,

( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).

Тогда время, за которое с такой производительностью будет выполнена работа ( A):

( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)

Итак, правило:

При совместной работе производительности складываются

А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.

Пример 8

На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?

Решение:

Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).

Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).

Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).

( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.

То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).

Приравняв ( displaystyle {{t}_{1}}), получаем уравнение:

Источник

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Задачи на работу

В задачах на работу речь идёт о какой-то деятельности: трубы заполняют бассейн, комбайнёры убирают урожай, строители строят, копают и так далее.

В таких задачах всегда присутствуют одни и те же величины, их три:
— первая величина — это время, за которое выполняется та или иная работа. Обозначают время буквой t.
— вторая величина — объём работы: сколько сделано деталей, налито воды, вспахано полей и так далее. Обозначим объем буквой О.
— третья величина — производительность. По сути, это скорость работы. Обозначим производительность буквой П.

Скорость любой работы, т.е. производительность можно определить, как объём работы, сделанной за какое-то время.
Получим формулу для производительности: П = О : t.

Пример. Токарь делает 5 деталей в час. Сколько деталей он сделает за 7 часов?

5 деталей в час — производительность

7 часов — время работы

Найти объем.

5 · 7 = 35.

Ответ: 35 деталей.

Пример. Токарь делает 5 деталей в час. Ему нужно сделать 20 деталей. За какое время он выполнит эту работу?

Известны объем и производительность, найти время.

20 : 5 = 4.

Ответ: 4 часа

Пример. Красная Шапочка и Волк очень любят пирожки. Волк может съесть 24 пирожка за 4 часа, а Красная Шапочка — 35 пирожков за 7 часов. У Волка в корзинке 30 пирожков, а у Красной Шапочки — 20. Кто съест свои пирожки раньше, если они начали есть одновременно?

Определим производительности Волка и Красной Шапочки. Волк съест 24 пирожка (объём работы) за 4 часа (время). Значит, его производительность: П = О:t = 24:4 = 6 пирожков в час.
Производительность Красной Шапочки: П = О:t = 35:7 = 5 пирожков в час.
Посчитаем сколько времени затратит каждый на свои пирожки.
У Волка 30 пирожков. Значит, затратил времени: t = О:П= 30:6 = 5 часов.
Красная Шапочка потратила на свои 20 пирожков: t = О:П = 20:5 = 4 часа.
Красная Шапочка опередила Волка на один час.
Ответ: Красная Шапочка.

Как определить производительность в следующих задачах:
— труба заполняет бассейн за 3 часа… (объем работы — бассейн — 1 бассейн);
— бригада строителей строит дом за 150 дней…(объем работы — дом — 1 дом);

— трактор вспахивает поле за 12 часов… (объем работы — поле — 1 поле).
Следовательно, в задачах объем работы равен 1.

Задачи на совместную работу

Совместная работа возникает, когда несколько человек (бригад, насосов, тракторов и т.д.) выполняют одну и ту же работу вместе, причем они работают с разными скоростями.

Пример. Одна труба может наполнить бассейн за четыре часа. Вторая — за шесть часов. За какое время заполнится бассейн, если обе трубы включить одновременно?

Так как трубы работают вместе, складывают их производительности.
Для первой трубы, которая заполняет 1 бассейн за 4 часа: П = О:t = 1:4, т.е. за час первая труба заполнит 1/4 бассейна.
Для второй трубы: П = О:t = 1:6, т.е. вторая труба заполнит за час 1/6 бассейна.
Вместе, при совместной работе, трубы заполнят за час: 1/4 + 1/6 = 5/12 — две трубы за 1 час.
Объём работы 1 бассейн. Совместная производительность 5/12 бассейна в час.
t = О:П = 1 : 5/12 = 12/5 = 2,4 (ч.)
Ответ:2,4 часа.

УПРАЖНЕНИЯ

1. а) Одна труба заполняет бассейн за 3 ч, а вторая — за 5 ч. За какое время заполнится бассейн, если будут работать две трубы одновременно? Выберите правильное значение:

1) (3+5):2; 2) 1: (3+5); 3) 1: (1/3+1/5).

б) Один насос заполняет бак за 4 ч, а второй — за 2 ч. За какое время заполнится бак, если будут работать два насоса одновременно? Выберите правильное значение:

1) (4+2):2; 2) 1: (1/4+1/2); 3) 1: (4+2).

Решение:

а) Производительность первой трубы — 1/3, производительность второй трубы — 1/5. Общая производительность — 1/3+1/5. Для нахождения затраченного времени при совместной работе разделим объем работы -1 на производительность: 1:(1/3+1/5).

Ответ: 3.

2. а) Два строителя вместе сложили стену за 10 дней, один из них мог бы выполнить эту работу за 16 дней. За сколько дней может выполнить эту работу второй? Выберите правильное значение:

1)1: (1/10+1/16); 2) 1: (1/10-1/16); 3) 1: (16-10).

б) Одна наборщица может набрать рукопись за 12 ч, а две, работая вместе, — за 8 ч. За сколько часов выполнит эту работу вторая наборщица? Выберите правильное значение:

1)1: (1/8-1/12); 2) 1: (1/12+1/8); 3) 1: (12-8).

Решение:
а) Производительность первого строителя — 1/16, общая производительность — 1/10. Производительность второго строителя — 1/10-1/16. Для нахождения затраченного времени вторым строителем разделим объем работы -1 на производительность: 1:(1/10-1/16).
Ответ: 2.

3. а) Папа выполняет всю работу за 4 ч, а его сын— за 7 ч. Какую часть работы они сделают вместе за 1 ч?
б) Мама выполняет всю работу за 1 ч, а дочь эту же работу выполняет за 2 ч. Какую часть работы они сделают вместе за 1 ч?
Решение:
а) Производительность папы — 1/4, производительность сына — 1/7. Производительность общая: 1/4+ 1/7=11/28 всей работы за 1 час.
Ответ: 11/28 работы.

4. а) При одновременной работе 6 комбайнов уберут все поле за 14 ч. За сколько часов уберут поле 8 комбайнов?
б) При одновременной работе 7 комбайнов уберут поле за 14 ч. За сколько часов уберут поле 10 комбайнов?
Решение:
а) 1) 6*14=84 (ч) — понадобится одному комбайну, чтобы убрать все поле.
2) 84 : 8= 10,5 (ч) — понадобится 8 комбайнам, чтобы убрать все поле.
Ответ: 10,5 часов

5. а) 18 студентов, работая по 6 ч в день, прополют все поле все поле. Сколько понадобится студентов, чтобы прополоть это поле за то же время, если они будут работать по 9 ч в день?
б) 12 студентов, работая по 8 ч в день, соберут все яблоки в саду. Сколько понадобится студентов, чтобы убрать все яблоки в этом саду за то же время, если они будут работать по б ч в день?
Решение:
а) 1) 6*18=108 (ч) — понадобится одному студенту, чтобы прополоть все поле.
2) 108 : 9= 12(ст.) — понадобится, чтобы прополоть все поле, работая по 9 ч в день.
Ответ: 12 студентов.

6. а) Производительности дочери и мамы относятся как 2:3. Работая вместе, они прополют огород за 12 ч. За сколько часов прополет огород каждая, работая отдельно?
б) Производительности труда папы и сына относятся как 3 : 5. Работая вместе, они выполнят работу за 15 ч. За сколько часов каждый справится с данной работой, работая отдельно?

Решение:
а) Пусть х — коэффициент пропорциональности, тогда производительность дочери — 2х, а мамы — 3х. Производительность при совместной работе 2х+3х=5х. Объем работы равен 12*5х=60х.
1) 60х:2х=30 (ч) — затратит дочь.
2) 60х:3х=20 (ч) — затратит мама.
Ответ: 30 часов; 20 часов.

7. а) Заказ на печать учебников типография должна была выполнить по плану за 15 дней. Но уже за три дня до срока типография выполнила план, так как печатала ежедневно по 2 тыс. учебников сверх плана. Сколько учебников напечатала типография?
б) Заказ на выпуск станков завод должен был выполнить за 30 дней. Но за три дня до срока завод выполнил заказ, так как выпускал ежедневно по 3 станка сверх плана. Сколько станков выпустил завод?
Решение:
а) Пусть х учебников в день типография должна была печатать по плану, но печатала х+2000 учебников день.
1) 15-3=12 (дн.) — потратила типография на заказ.
15х — количество заказанных учебников, 12(х+2000) — количество напечатанных учебников. Эти количества равны. Составим и решим уравнение:
15х=12(х+2000),
15х=12х+24000,
3х=24000,
х=8000 (м.) — в день должна была печатать типография.
2) 8000*15=120000 (м.) — напечатала типография.
Ответ: 120000 учебников.

8. а) При совместной работе двух погрузчиков железнодорожный состав был загружен за 4 ч 12 мин. Сколько времени потребуется на загрузку такого же железнодорожного состава каждым погрузчиком, если одним из погрузчиков железнодорожный состав можно загрузить на 8 ч быстрее, чем другим?
б) При совместной работе двух кранов работа была выполнена за 2 ч 6 мин. Сколько времени потребуется для выполнения этой работы каждым краном, если один может выполнить ее на 4 ч быстрее другого?

Решение:
а) Пусть х — время загрузки состава первым погрузчиком, тогда х+8 — время загрузки состава вторым погрузчиком.
Производительность первого погрузчика — 1/х, второго погрузчика — 1/(х+8). Совместная производительность 1/х+1/(х+8)=(2х+8)/(х(х+8)).
Время совместной работы равно 1 : (2х+8) /(х(х+8))=х(х+8)/(2х+8).
По условию время равно 4 ч 12 мин = 4,2 ч. Составим и решим уравнение:
х(х+8)/(2х+8)=4,2,
х(х+8)=4,2(2х+8),

х²+8х-8,4х-33,6=0,
х²-0,4х-33,6=0,
D=(11,6)²

х1=6 (ч) — понадобится первому погрузчику, х2=(0,4-11,6):2=-5,6 — не подходит по условию задачи.
1) 6+8=14 (ч) — понадобится второму погрузчику.
Ответ: 6 часов, 14 часов.

9. а) Бассейн наполняется через две трубы за 6 ч. Через первую трубу бассейн наполняется на 5 ч быстрее, чем через вторую. За какое время может быть наполнен бассейн через каждую трубу в отдельности?
б) Бак наполняется через две трубы за 2 ч. Через первую трубу бак наполняется на 3 ч быстрее, чем через вторую. За какое время может быть наполнен бак через каждую трубу в отдельности? (№ 6.4.30 [7])

Решение:
а) Пусть х — время заполнения первой трубой, тогда х+5 — время заполнения второй трубой.
Производительность первой трубы 1/х, второй трубы 1/(х+5). Совместная производительность 1/х+1/(х+5)=(2х+5)/(х(х+5)).
Время совместной работы равно 1 : (2х+5) /(х(х+5))=х(х+5)/(2х+5).
По условию время равно 6 ч. Составим и решим уравнение:
х(х+5)/(2х+5)=6,
х(х+5)=6(2х+5),

х²+5х-12х-30=0,
х²-7х-30=0,
D=(13)²

х1=10 (ч) — понадобится первой трубе, х2=(7-13):2=-3 — не подходит по условию задачи.
1) 10+5=15 (ч) — понадобится второй трубе.
Ответ: 10 часов, 15 часов.

10. а) Двое плиточников облицевали стены за 12 ч. Если бы сначала первый облицевал половину стен, а затем второй — вторую половину, то облицовка была бы выполнена за 25 ч. За какое время мог бы облицевать стену каждый плиточник в отдельности?
б) Двое каменщиков сложили стену за 6 ч. Если бы сначала первый выложил половину стены, а затем второй — вторую половину стены, то вся стена была бы сложена за 12,5 ч. За какое время мог бы сложить эту стену каждый каменщик в отдельности?

Решение:
а) Пусть первый работал х часов, второй — у часов. Производительность первого 1/х, второго 1/у. При совместной работе их время равно 1: (1/х+1/у) =12.
Если первый и второй делают по половине работы, то их время равно 0,5:(1/х) +0,5:(1/у)=25. Решим систему из двух уравнений:

(50-у)у-12(80-у)-12у=0,

50у-у²-600+12у-12у=0,

у²-50у+600=0

D=(10)²

у1=20 (ч) — работал второй, х1=50-20=30 (ч) — работал первый.
у2=30 (ч) — работал второй, х1=50-30=20 (ч) — работал первый.
Ответ: 20 часов, 30 часов.

11. а) Рабочий копал траншею. Когда он проработал 7 ч, к нему присоединился второй рабочий. Вместе они проработали 2 ч. За сколько часов может выкопать траншею каждый рабочий, работая отдельно, если первому нужно на это на 4 ч больше, чем второму?
б) Один рабочий работал 9 ч, после чего к нему присоединился другой рабочий. После 7 ч совместной работы они выполнили всю работу. За сколько часов мог бы выполнить работу каждый рабочий, работая самостоятельно, если первому нужно для этого на 3 ч больше, чем второму?

Решение:
а) Пусть х — время работы первого, тогда х-4 — время работы второго.
Производительность первого — 1/х, второго — 1/(х-4).
Объем работы первого — 1/х*(7+2), объем работы второго — 1/(х-4)*2. Весь объем равен 1.
Составим и решим уравнение:
9/х + 2/(х-4)=1,
11х-36=х(х-4),

х²-15х+36=0,
D=(9)²

х1=3 (ч) — понадобится первому, 1) 3-4=-1(ч) — не подходит по условию задачи.
х2=12 (ч) — понадобится первому, 2) 12-4=8 (ч) — понадобится второму.
Ответ: 12 часов, 8 часов.

12. а) Двое рабочих выполняют некоторую работу. После 45 мин совместной работы первый был переведен на другую работу и второй рабочий закончил оставшуюся часть работы за 2 ч 15 мин. За какое время мог бы выполнить всю работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 ч больше, чем первому? (№6.5.34 [7])

б) Бассейн может наполняться водой из двух кранов. Если открыть первый кран на 10 мин, а второй — на 20 мин, то бассейн будет наполнен. Если первый кран открыть на 5 мин, а второй — на 15 мин, то заполнится — бассейна. За какое время из каждого крана в отдельности может заполниться весь бассейн?

Решение:
а) Пусть х — время первого, тогда х+1 — время второго. Производительность первого 1/х, производительность второго 1/(х+1). Вместе они работали 45 мин=0,75 ч и выполнили (1/х + 1/(х+1)) * 0,75 часть работы. Второй за 2ч 15 мин=2,25 ч выполнил 1/(х+1)*2,25 часть работы. Составим и решим уравнение:
(1/х + 1/(х+1)) * 0,75 + 1/(х+1)*2,25 =1,
4х²-11х-3=0,
D=(13)²

х1=3 (ч) — понадобится первому,
х2=(11-13):2= -1 не подходит по условию задачи.
1) 3+1=4 (ч) — понадобится второму.
Ответ: 3 часа, 4 часа.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Два экскаватора различной мощности роют котлован. Работая отдельно, первый может вырыть котлован за 5 дней, второй — за 7 дней. За сколько дней они выроют котлован, работая совместно? Выберите правильное значение:

1) (7+5):2; 2) 1: (7+5); 3) 1: (1/7+1/5).

2. Одна из труб может наполнить бассейн за 3 ч, вторая — за 5 ч. За сколько часов наполнится бассейн, если открыть сразу две трубы? Запишите выражение для решения задачи.

3. Два экскаватора роют траншею. Работая отдельно, первый может вырыть траншею за 10 дней, второй — за 16 дней. За сколько дней они выроют траншею, работая совместно?

4. Водоем заполняется первой трубой за 5 ч, а второй трубой за 4 ч. За сколько часов наполнится водоем, если будут одновременно работать две трубы?

5. Две наборщицы должны были набрать по 120 страниц каждая. Вторая наборщица набирала за 1 ч на 5 страниц меньше, чем первая, поэтому закончила работу на 2 ч позже. Сколько страниц в час набирала первая наборщица?

6. Две бригады рабочих должны по плану изготовить 240 деталей. Первая бригада работала 6 ч, а вторая — 5 ч. Сколько деталей в час изготавливала каждая бригада, если первая делала на 4 детали в час меньше, чем вторая?

7. По плану колхоз каждый день должен был засевать по 20 га. Начав сев, колхоз ежедневно засевал на 5 га больше, чем было предусмотрено планом, поэтому сев был закончен на 2 дня раньше срока. Определите засеянную площадь.

8. Два каменщика сложили стену за 20 дней. За сколько
дней выполнил бы эту работу каждый из них в отдельности, если известно, что
первому пришлось бы работать на 9 дней больше, чем второму?

9. Теплоход загружается подъемными кранами. Сначала в течение 4 ч работали три крана одинаковой мощности, затем к ним присоединились еще два крана большей мощности, и через 3 ч после этого загрузка была закончена. Если бы все краны начали работать одновременно, то погрузка была бы закончена за 6 ч. За какое время выполнят погрузку один кран меньшей мощности и один кран большей мощности, работая вместе?

10. Вода из трех кранов заполнила резервуар за 12 минут, причем первый кран был открыт 4 минуты, и за это время было заполнено 40 % резервуара. За сколько минут заполнил бы резервуар каждый кран, если известно, что второй кран за 5 минут наливает столько воды, сколько третий кран за 6 минут?

Источник

Суть задач на производительность следующая: некоторую работу выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью. Они могут выполнять эту работу либо по отдельности, либо совместно друг с другом. Алгоритм решения здесь такой же, как и алгоритм решения задач на движение:

Анализ данных.
Составление таблицы.
Составление уравнения.
Решение уравнения.

Основные особенности решения задач на производительность:

Задачи на производительность схожи с задачами на движение. Основная формула при решении: V = v·t. Сравните её с формулой для решения задач на движение S = v·t. Роль скорости v здесь играет производительность труда, а роль расстояния S — объем работы V.
Объем работы может быть не дан по условию и его не нужно находить при решении задачи (нам просто напросто не важно, какой объем работы выполняется). В таком случае его можно обозначить какой-нибудь буквой, например, V или A. В процессе решения эта переменная, которой мы обозначили объем, сократится и её значение не придется находить.
Также, если объем работы не дан по условию, удобно принять его просто за 1; тогда время t, требующееся для выполнения всей работы, иv – производительность труда, связаны формулой:

$ t=frac{1}{upsilon}. $

В отличие от задач на движение, в задачах на производительность скорости выполнения работы не могут вычитаться, а могут только складываться друг с другом. Если два человека или механизма по отдельности работают с производительностями v₁и v₂, то вместе они будут работать быстрее (никак не медленнее), с суммарной производительностью v₁+ v₂, а время совместной работы будет равно:

$ t=frac{1}{upsilon_{1}+upsilon_{2}} $

Пример:

Первый рабочий за час делает на 5 деталей больше, чем второй, и выполняет заказ, состоящий из 200 деталей, на 2 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?

Решение:

В задаче требуется найти производительность второго рабочего. Примем его скорость за x. Заполним таблицу.

	v, дет/ч	t, ч	V, дет
Первый рабочий	x + 5	$ frac{200}{x+5} $	200
Второй рабочий	x	$ frac{200}{x} $	200

В условии задачи сказано, что первый рабочий выполняет заказ на 2 часа быстрее, чем второй. На основании этого составим уравнение:

$ {frac{200}{x+5}+2=frac{200}{x} frac{200+2x+10}{x+5}=frac{200}{x}.} $

2x² + 210x = 200x + 1000;

x² + 5x – 500 = 0.

Получаем два корня, x₁= 20 и x₂= –25. Второй корень не подходит, так как производительность не может быть отрицательной.

Ответ: 20 дет/ч.

Виды задач на производительность:

1. Задачи на совместную работу:

Задачи на совместную работу — это тип задач, в которых объектами, выполняющими работу, являются люди или группы людей: рабочие, ученики, операторы, бригады рабочих и т п. Объекты могут выполнять работу по отдельности, а могут — вместе.

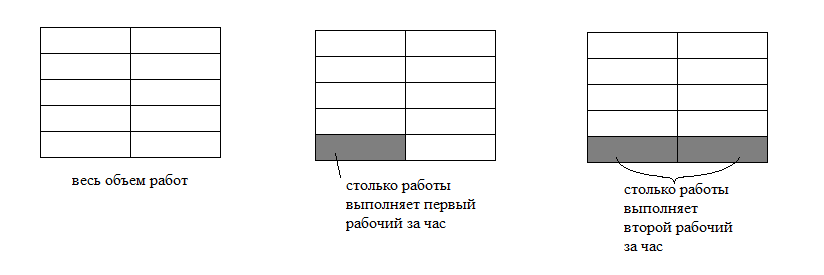
Разберем простой пример. Двум рабочим требуется выполнить работу. Допустим, первый рабочий выполняет всю работу за 10 часов, а второй — за 5. Давайте найдем, за сколько часов рабочие справятся с работой, выполняя её вместе.

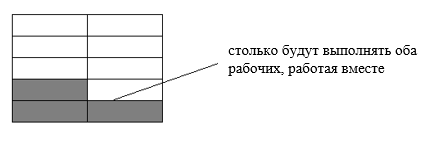
Получается, что если принять весь объем работ за 1, то первый рабочий выполняет $ frac{1}{10} $ всей работы за час, а второй $ frac{1}{10} $ то есть $ frac{1}{10} $ всей работы за час. На рисунке весь объем работ — это 10 «кирпичиков», первый выполняет 1 «кирпичик» за час, а второй — 2. Тогда вместе они будут выполнять $ frac{1}{10}+ frac{1}{5}= frac{3}{10} $ всей работы за час, или 3 «кирпичика»:

Чтобы найти совместную производительность рабочих, мы сложили друг с другом их собственные производительности. Теперь, чтобы найти время, за которое оба рабочих справятся с работой, выполняя её вместе, разделим полный объем работ на совместную производительность:

$ 1/frac{3}{10}=frac{10}{3}=3frac{1}{3} $

То есть вместе рабочие справятся с работой за 3 $ frac{1}{3} $ часа, или за 3 часа 20 минут.

2. Задачи на бассейны и трубы:

Отдельно можно выделить группу задач на производительность — задачи на заполнение бассейна несколькими трубами. В таких задачах рабочим будут соответствовать насосы (или трубы) разной производительности, а объему работы — объем бассейна или иного резервуара.

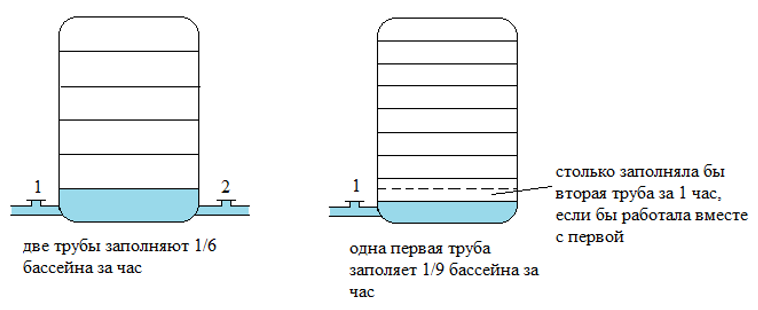
Рассмотрим пример. Две трубы наполняют бассейн за 6 часов, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?

Получается, что за 1 час две трубы наполняют $ frac{1}{6} $ часть бассейна, а одна первая труба наполняет $ frac{1}{9} $ часть бассейна: Так как вместе трубы наполняют бассейн водой со скоростью, равной сумме скоростей отдельно каждой из труб, то вторая труба наполняет бассейн со скоростью $ frac{1}{6}- frac{1}{9}= frac{1}{18} $.

Таким образом, вторая труба заполнит бассейн за $ 1/frac{1}{18}=18 $ часов.

Источник

Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.

Задачи на работу также решаются с помощью одной-единственной формулы: . Здесь — работа, — время, а величина , которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, продавец в супермаркете надувает воздушные шарики. Количество шариков, которые он надует за час — это и есть его производительность.

Правила решения задач на работу очень просты.

, то есть работа производительность время. Из этой формулы легко найти или .
Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один). Написана книга (одна). А вот если речь идет о количестве кирпичей, страниц или построенных домов — работа как раз и равна этому количеству.
Если трудятся двое рабочих (два экскаватора, два завода…) — их производительности складываются. Очень логичное правило.
В качестве переменной удобно взять именно производительность.

Покажем, как все это применяется на практике.

1. Заказ на 110 деталей первый рабочий выполняет на час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на деталь больше?

Так же, как и в задачах на движение, заполним таблицу.

В колонке «работа» и для первого, и для второго рабочего запишем: 110 . В задаче спрашивается, сколько деталей в час делает второй рабочий, то есть какова его производительность. Примем ее за . Тогда производительность первого рабочего равна x+1 (он делает на одну деталь в час больше). $t=genfrac{}{}{}{0}{displaystyle A}{displaystyle p}$ , время работы первого рабочего равно $t_1=genfrac{}{}{}{0}{displaystyle 110}{displaystyle x+1}$ , время работы второго равно $t_2=genfrac{}{}{}{0}{displaystyle 110}{displaystyle x}$ .


первый рабочий		$t_1=genfrac{}{}{}{0}{displaystyle 110}{displaystyle x+1}$
второй рабочий		$t_2=genfrac{}{}{}{0}{displaystyle 110}{displaystyle x}$

Первый рабочий выполнил заказ на час быстрее. Следовательно, t_1 на меньше, чем t_2 , то есть

$genfrac{}{}{}{0}{displaystyle 110}{displaystyle x+1}=genfrac{}{}{}{0}{displaystyle 110}{displaystyle x}-1$

Мы уже решали такие уравнения. Оно легко сводится к квадратному:

Дискриминант равен 441 . Корни уравнения: x_1=10 , x_2=-11 . Очевидно, производительность рабочего не может быть отрицательной — ведь он производит детали, а не уничтожает их Значит, отрицательный корень не подходит.

Ответ: .

2. Двое рабочих, работая вместе, могут выполнить работу за дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?

В этой задаче (в отличие от предыдущей) ничего не сказано о том, какая это работа, чему равен ее объем. Значит, работу можем принять за единицу.

А что же обозначить за переменные? Мы уже говорили, что за переменную удобно обозначить производительность. Пусть — производительность первого рабочего. Но тогда производительность второго нам тоже понадобится, и ее мы обозначим за .

По условию, первый рабочий за два дня делает такую же часть работы, какую второй — за три дня. Значит, 2x=3y . Отсюда $y=genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}x$ .

Работая вместе, эти двое сделали всю работу за дней. При совместной работе производительности складываются, значит,

$left( x+genfrac{}{}{}{0}{displaystyle 2}{displaystyle 3}x right) cdot 12 = 1$

$genfrac{}{}{}{0}{displaystyle 5}{displaystyle 3}x cdot 12 = 1$

20x=1

$x=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 20}$ .

Итак, первый рабочий за день выполняет $genfrac{}{}{}{0}{displaystyle 1}{displaystyle 20}$ всей работы. Значит, на всю работу ему понадобится дней.

Ответ: .

3. Первая труба пропускает на литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на минуты дольше, чем вторая труба заполняет резервуар объемом литров?

Всевозможные задачи про две трубы, которые наполняют какой-либо резервуар для воды — это тоже задачи на работу. В них также фигурируют известные вам величины — производительность, время и работа.

Примем производительность первой трубы за . Именно эту величину и требуется найти в задаче. Тогда производительность второй трубы равна x+1 , поскольку она пропускает на один литр в минуту больше, чем первая. Заполним таблицу


первая труба		$t_1=genfrac{}{}{}{0}{displaystyle 110}{displaystyle x}$
вторая труба		$t_2=genfrac{}{}{}{0}{displaystyle 99}{displaystyle x+1}$

Первая труба заполняет резервуар на две минуты дольше, чем вторая. Значит, . Составим уравнение:

$genfrac{}{}{}{0}{displaystyle 110}{displaystyle x}-genfrac{}{}{}{0}{displaystyle 99}{displaystyle x+1}=2$ и решим его.

Ответ: .

. Андрей и Паша красят забор за часов. Паша и Володя красят этот же забор за часов, а Володя и Андрей — за часов. За сколько часов мальчики покрасят забор, работая втроем?

Мы уже решали задачи на движение. Правила те же. Отличие лишь в том, что здесь работают трое, и переменных будет тоже три. Пусть — производительность Андрея, — производительность Паши, а — производительность Володи. Забор, то есть величину работы, примем за — ведь мы ничего не можем сказать о его размере.

	производительность	работа
Андрей
Паша
Володя
Вместе

Андрей и Паша покрасили забор за часов. Мы помним, что при совместной работе производительности складываются. Запишем уравнение:

Аналогично,

Тогда
$x+y=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 9}$
$y+z=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 12}$
$x+z=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 18}$ .
Можно искать , и по отдельности, но лучше просто сложить все три уравнения. Получим, что
$2left( x+y+z right)=genfrac{}{}{}{0}{displaystyle 1}{displaystyle 9}+genfrac{}{}{}{0}{displaystyle 1}{displaystyle 12}+genfrac{}{}{}{0}{displaystyle 1}{displaystyle 18}$
Значит, работая втроем, Андрей, Паша и Володя красят за час одну восьмую часть забора. Весь забор они покрасят за часов.
Ответ: .

Читаем дальше: Задачи на проценты

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи на работу на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Задачи на совместную работу

Рассмотрим задачи, в которых речь идёт о совместном выполнении некоторой работы. При этом всё равно, какую работу выполняют и чем эту работу измеряют — числом деталей, количеством вспаханных гектаров и т. п. Если, например, некоторая работа выполняется за 10 часов, то за 1 час, очевидно, выполняется всей работы, а вся работа составляет десять таких частей . Поэтому обычно в таких задачах всю работу принято считать равной единице, объём выполненной работы выражают как часть этой единицы.

Задача 1. Первая бригада может выполнить задание за 36 часов, а вторая бригада может выполнить то же задание за 18 часов. За сколько часов это задание выполнят две бригады при совместной работе?

Решение: Примем всю работу за единицу, тогда за 1 час первая бригада выполняет

а вторая

всей работы. При совместной работе за 1 час две бригады выполняют

всей работы, поэтому всю работу они выполнят за

Ответ: При совместной работе бригады выполнят задание за 12 часов.

Под совместной работой можно понимать и одновременную работу двух труб при наполнении бассейна, и прохождение некоторого пути при движении навстречу друг другу и т. п. Метод решения остаётся тем же.

Задача 2. Расстояние между двумя сёлами пешеход проходит за 60 минут, а велосипедист проезжает за 20 минут. Через сколько минут они встретятся, если отправятся одновременно навстречу друг другу из этих сёл?

Решение: Примем расстояние между сёлами за единицу.

— проходит пешеход за 1 минуту.

— проезжает велосипедист за 1 минуту.

— такую часть расстояния они проходят за 1 минуту при движении навстречу друг другу.

— время движения до встречи.

Ответ: Они встретятся через 15 минут.

Задача 3. Два печника сложили печь за 16 часов. Известно, что первый из них, работая один, сложил бы печь за 24 часа. За сколько часов второй печник, работая один, сложил бы ту же печь?

Решение: Примем объём всей работы за 1 (единицу).

— выполняют два печника за 1 час, работая вместе.

— выполняет первый печник за 1 час, работая один.

— выполняет второй печник за 1 час, работая один.

— за столько времени сложил бы печь второй печник.

Ответ: Второй печник, работая один, сложил бы печь за 48 часов.

Задача 4. Из пунктов A и B одновременно вышли два пешехода. Они встретились через 40 минут после своего выхода, а через 32 мин после встречи первый пришёл в пункт B. Через сколько минут после своего выхода из B второй пришёл в пункт A?

Решение: Примем расстояние между пунктами A и B за единицу.

— такую часть расстояния проходят два пешехода за 1 минуту при движении навстречу друг другу.

2) 40 + 32 = 72 (мин) — время первого пешехода за весь путь.

— проходит первый пешеход за 1 минуту.

— проходит второй пешеход за 1 минуту.

— время второго пешехода за весь путь.

Ответ: Через 90 минут после своего выхода из пункта B второй пешеход пришёл в пункт A.

Источник