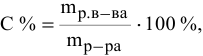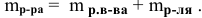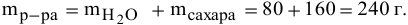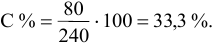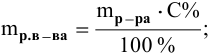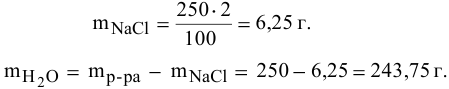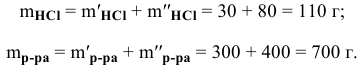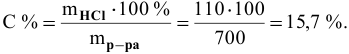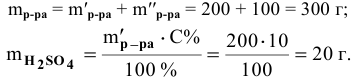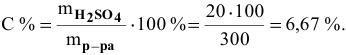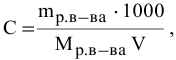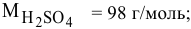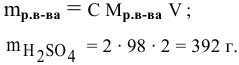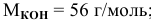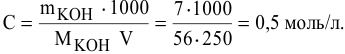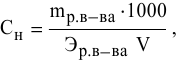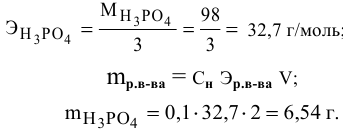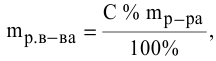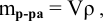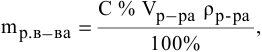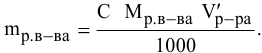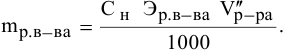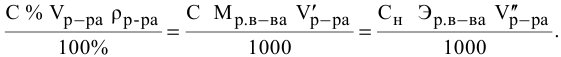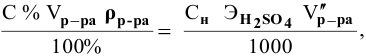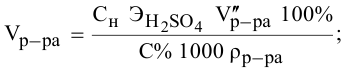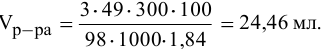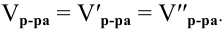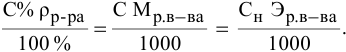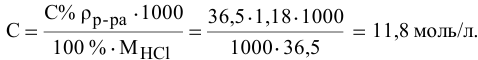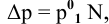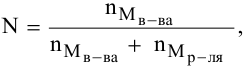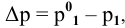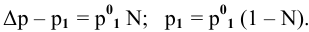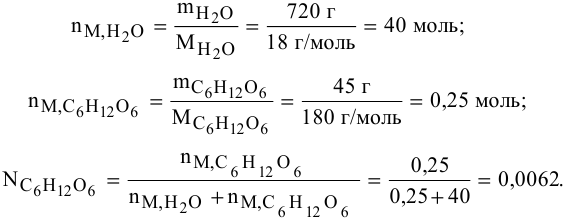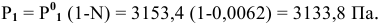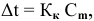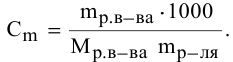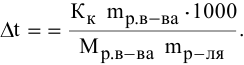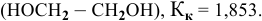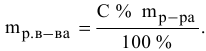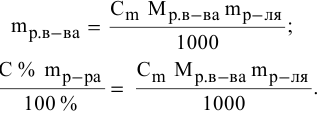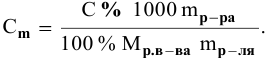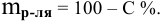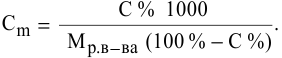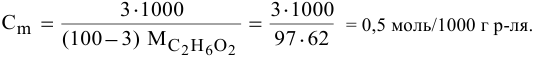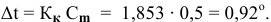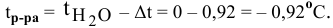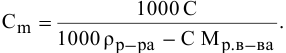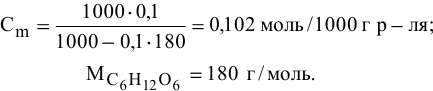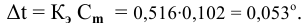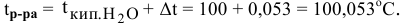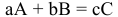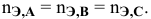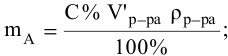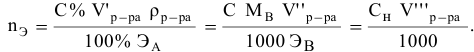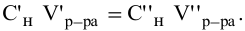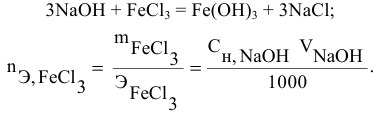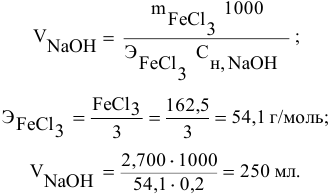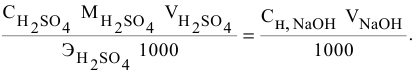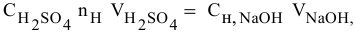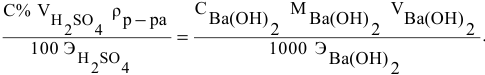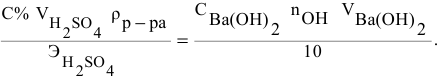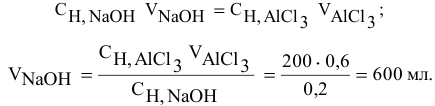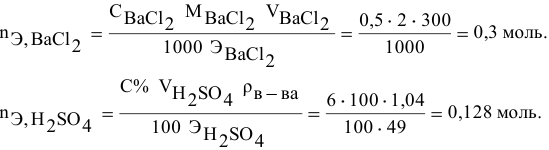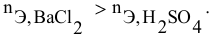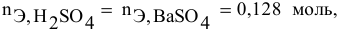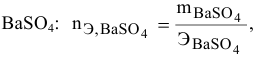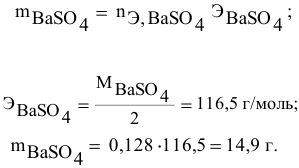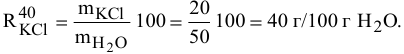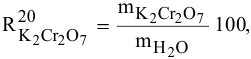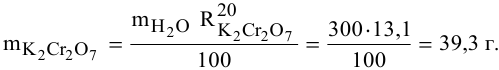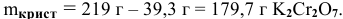Алгоритм расчета объема исходного раствора кислоты
1. Найти,
сколько моль эквивалентов кислоты
необходимо для приготовления заданного
раствора по формуле:
экв.
(кислоты)
= Vр-ра·СN
,
где:
Vр-ра
— объем раствора, в литрах, который надо
приготовить;
СN
— нормальная концентрация заданного
раствора.
2. Найти
массу данного количества эквивалентов
кислоты по формуле:
m
= экв.·МЭ
,
где:
МЭ
— молярная масса эквивалента кислоты.
МЭ(HCl)
= M/1
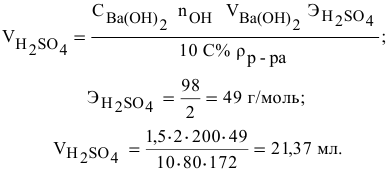
= 36.5 г/моль; МЭ(H2SO4)
= M/2
= 49 г/моль.
3. Найти, в какой
массе исходного раствора содержится
нужная Вам масса кислоты:
где:
— массовая доля кислоты в исходном
растворе.
4. Найти
объем исходного раствора по формуле:
,
где:
— плотность, определенная экспериментально
с помощью ареометра.
Определение точной концентрации кислоты методом титрования
Определение
концентрации раствора кислоты, основанное
на реакции нейтрализации, выполняется
следующим образом:
1. Чисто вымытую бюретку
установите вертикально в зажиме штатива
и ополосните ее несколькими миллилитрами
того раствора кислоты, который будет
затем наливаться в бюретку.
2. Налейте
в бюретку приготовленный раствор кислоты
и установите уровень жидкости на нулевом
делении, считая по нижнему мениску,
уберите воронку из бюретки. Следите,
чтобы кончик бюретки был заполнен
раствором и не содержал пузырьков
воздуха.
3. Ополосните
чистую пипетку раствором щелочи известной
концентрации, отмерьте ею 10 мл раствора
и вылейте его в коническую колбочку,
прибавив туда 1-2 капли индикатора
метилоранжа.
4. Поместите
колбочку с раствором щелочи под бюретку
и приливайте постепенно раствор кислоты
из бюретки в колбочку до нейтрализации
раствора щелочи, то есть до изменения
цвета раствора от желтого до слаборозового.
Прибавляйте раствор в колбу небольшими
порциями при непрерывном перемешивании.
Изменение окраски раствора должно
произойти от прибавления одной лишней
капли раствора кислоты. После этого
отмерьте уровень жидкости в бюретке,
считая по нижнему
мениску. Титрование повторите 3 раза.
Отклонение результатов отдельных
титрований не должно превышать 0.2 мл
(данные с большим отклонением в расчет
не принимать).
Результаты
занесите в таблицу:
|
№ опыта |
Объем |
Объем |
По
результатам титрования вычислите
нормальность кислоты. Для растворов
нормальной концентрации существует
соотношение, вытекающее из закона
эквивалентов:
,
где:
V1 —
объем раствора щелочи известной
концентрации:
— нормальность раствора щелочи;
V2 —
объем исследуемого раствора кислоты;
— нормальность исследуемого раствора
кислоты.
Из
приведенного равенства легко подсчитать
нормальную концентрацию исследуемого
раствора:
.
Лабораторная работа «Изучение зависимости скорости химических реакций от различных факторов. Химическое равновесие»
Опыт
№ 1 Зависимость скорости химической
реакции от концентрации реагирующих
веществ
Налейте
в четыре стаканчика следующие растворы:
1)
10 мл 0.1 М раствора тиосульфата
натрия + 30 мл воды;
2)
20 мл 0.1 М раствора тиосульфата
натрия + 20 мл воды;
3)
30 мл 0.1 М раствора тиосульфата
натрия + 10 мл воды;
4)
40 мл 0.1 М раствора тиосульфата
натрия.
Последовательно
в каждый стаканчик прилейте по 10 мл
0.05 М раствора кислоты. Отметьте с
помощью секундомера промежуток времени
от момента сливания растворов до
появления мути, вызванной началом
выпадения в осадок серы, в соответствии
с уравнением:
Na2S2O3
+ H2SO4
Na2SO4
+ SO2
+ S
+ H2O.
Вычислите
относительную скорость реакции по
формуле:
,
где
– время (по секундомеру), в секундах.
Результаты
занесите в таблицу:
|
№ опыта |
Объем |
Объем натрия (мл) |
Объем воды (мл) |
Общий |
Молярная |
Время
в |
Относительная
реакции |
Найденную
зависимость скорости от концентрации
изобразите графически, отложив по оси
абсцисс концентрацию тиосульфата, а по
оси ординат — относительную скорость.
Сделайте вывод.
Опыт
№ 2 Зависимость скорости реакции от
температуры.
Налейте
в стаканчик 10 мл 0.1 М раствора
тиосульфата натрия. Прилейте к нему при
комнатной температуре 10 мл 0.05 М
раствора серной кислоты. Определите с
помощью секундомера время прохождения
реакции (аналогично опыту 1). Второй
опыт проведите аналогично, но при
температуре, на 10С
выше комнатной. Для этого стаканчики с
растворами нагрейте на водяной бане,
контролируя температуру воды термометром
(следует выдержать растворы не менее 5
минут).
Сделайте
вывод о влиянии температуры на скорость
реакции.
Опыт
№ 3 Влияние катализатора на скорость
химической реакции.
В
две пробирки налейте по 5 мл 3%‑ного
раствора перекиси водорода. В одну из
них поместите несколько кристалликов
оксида марганца(IV). Качественно сравните
скорость реакции разложения перекиси
в этих пробирках:
2H2O2
= 2H2O
+ O2.
Какую
роль играет оксид марганца(IV)?
Опыт
№ 4 Влияние величины поверхности на
скорость гетерогенной химической
реакции.
Уравновесьте
на весах маленький кусочек мрамора и
порошкообразный мрамор. Приготовьте
две пробирки с равными объемами растворов
соляной кислоты (2-3 мл). Одновременно
стряхните с бумажек кусочек мрамора в
одну пробирку, порошок – в другую.
Отметьте с помощью секундомера время
окончания реакций в обеих пробирках.
Сделайте вывод о влиянии величины
поверхности на скорость реакции.
Опыт № 5
Смещение химического равновесия.
Налейте
в стакан 15 мл 0.1 N
раствора хлорида железа(III) и такой же
объем 0.1 N
раствора роданида калия. Обратите
внимание на появление красной окраски
при смешении растворов. Напишите
уравнение реакции.
Полученный
раствор разделите поровну в 4 пробирки.
В первую пробирку добавьте несколько
капель концентрированного раствора
хлорида железа(III), в другую – несколько
капель концентрированного раствор
роданида калия. В третью пробирку
добавьте щепотку кристаллического
хлорида калия. Четвертую пробирку
оставьте для сравнения.
Дайте
объяснение различной интенсивности
окраски растворов в пробирках. Напишите
выражения константы химического
равновесия данной реакции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти объем раствора
Существует несколько формул для нахождения объема раствора. В зависимости от того, что дано в условии задачи, можно выбрать одну из них. Порой данных в задаче недостаточно, и приходится применять дополнительные формулы для их нахождения.

Инструкция
Одна из наиболее часто используемых формул выглядит так: V = m/p, где V — объем, m — масса(г), p — плотность(г/мл). Соответственно, если даны эти величины, можно без труда найти объем. Иногда бывает так, что не дана масса вещества, но дано количество вещества (n) и указано, какое это вещество. В этом случае массу находим по формуле: m = n*M, где n — количество вещества (моль), а M — молярная масса(г/моль). Лучше всего рассмотреть это на примере задачи.
Количество вещества раствора сульфата натрия равно 0,2 моль, а плотность — 1,14 г/мл, найти его объем.Сначала пишем основную формулу для нахождения объема: V = m/p. Из этой формулы по условию задачи мы имеем только плотность (1,14 г/мл). Находим массу: m = n*M. Количество вещества дано, осталось определить молярную массу. Молярная масса равна относительной молекулярной массе, которая в свою очередь складывается из относительных атомных масс простых веществ, входящих в состав сложного. На самом деле все просто: в таблице Менделеева под каждым веществом указывается его относительная атомная масса. Формула нашего вещества Na2SO4, считаем. M (Na2SO4) = 23*2+32+16*4=142 г/моль. Подставляем в формулу, получаем: m = n*M = 0,2*142 = 28,4 г. Теперь полученное значение подставляем в общую формулу: V = m/p = 28,4/1,14 = 24,9 мл. Задача решена.
Бывают еще другие типы задач, где присутствует объем раствора – это задачи на концентрации раствора. Формула, необходимая для нахождения объема раствора, выглядит так: V = n/c, где V – объем раствора(л), n – количество растворенного вещества(моль), c – молярная концентрация вещества(моль/л). При необходимости найти количество растворенного вещества, это можно сделать по формуле: n = m/M, где n – количество растворенного вещества(моль), m – масса(г), M – молярная масса(г/моль).
Обратите внимание
Единицы измерения данных величин должны соответствовать друг другу. Например, если масса дана в кг, то соответствующий ей объем измеряется в литрах. А если масса в г, то объем в мл.
Полезный совет
Всегда внимательно читайте условие задачи. Порой из-за неправильно прочитанного условия можно не решить даже самую легкую задачу.
Источники:
- «Сборник задач по химии», Г.П. Хомченко, И.Г. Хомченко, 2002.
- определить объем раствора
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Светило науки — 2432 ответа — 10471 помощь
1) Находим молярную массу гидроарсената натрия:
М(Na₂HAsO₄) = 2*23 + 1 + 75 + 4*16 = 186 г/моль
2) Определяем молярную концентрацию исходного раствора: См₁:
См₁ = 10*ρ*С/М
где: ρ — плотность раствора, г/мл
С — концентрация раствора, %
М — молярная масса растворенного вещества, моль/л
См₁ = 10*1,06*10/186 = 0,57 моль/л
3) Так при разбавлении раствора масса растворенного вещества, а соответственно и число молей растворенного вещества не изменяется, то можем записать:
См₁*V₁ = См₂*V₂
где: См₁ и См₂ — концентрации исходного и полученного раствора,
моль/л;
V₁ и V₂ — объёмы исходного и полученного раствора, л
Отсюда:
V₁ = См₂*V₂/См₁ = 0,02*3/0,57 = 0,105 л = 105 мл
Смесь, состоящая из частиц растворителя, растворяемого вещества и продуктов их взаимодействия, называется раствором. Это гомогенные структуры однородной консистенции, состоящие из двух либо нескольких компонентов. Решение задач на растворы – определение их концентрации, степени растворимости веществ, условий протекания растворообразующих процессов.
Задачи на растворы по химии
Чистое вещество либо смесь нескольких компонентов, попадая в растворитель, могут проявлять свойства:
- хорошей растворимости;
- малой растворимости;
- быть нерастворимыми.
При растворении в воде образуются многочисленные атомно-молекулярные связи. Их количество зависит от коэффициента растворимости – химической величины, которая рассчитывается путем деления массы растворяемого вещества на массу растворителя.
Кроме этого, в задачах могут присутствовать массовая доля вещества, растворенного в соответствующем растворителе.
Как решать задачи с процентными растворами
Растворы с выраженной концентрацией активного (растворенного) вещества носят название процентных. В задачах по химии ставятся цели определить содержание массы растворенного вещества, массы образовавшегося либо первоначального раствора, процентного содержания вещества до или после растворения.
Растворы, о которых идет речь в задачах по химии, обладают общими свойствами:
- они однородны;
- смешивание компонентов происходит за малый отрезок времени, как и изменение их концентрации;
- в результате смешивания двух (или более) растворов с различной концентрацией, происходит не только увеличение общей массы и объема раствора, но и усреднение процентного содержания растворенного вещества.
Поэтому существуют общие принципы их решения. Так, увеличение концентрации происходит в результате упаривания (испарения растворителя), а уменьшение – разбавления. В результате смешения может наблюдаться как увеличение, так и уменьшение, в зависимости от конкретных условий задачи.
В любом случае характеристики начального и конечного продуктов будут различаться, поэтому важно, данные в условии сведения не перепутать. Для этого применяется их нумерация.
Чтобы грамотно составить алгоритм решения, часто бывает полезно использовать уравнение химической реакции относительно активного вещества либо кислоты.
Концентрация растворов и способы ее выражения
На бытовом уровне понятие концентрации раствора выражается в отношении массы растворенного вещества к массе раствора, выраженном в процентах. Однако правомерно более широкое определение, охватывающее различные способы выражения концентрации.
Концентрация раствора – количественный показатель состава активного вещества в растворе, выраженное в определенных единицах и заключенное в единице массы или объема. Выражается в долях, процентах, массовых долях, молярности, мольных долях, титрах. Из них чаще применяются молярность и мольная доля.
1. О массовой доле ((omega)) идет речь в задачах, когда можно составить соотношение масс растворенного компонента и всего раствора. Для ее выражения существует формула:
(omega=M_{в-ва}div M_{р-ра})
Выражается она в процентах либо долевых частях единицы.
2. Молярность (по-другому – молярная концентрация) или (С) показывает сколько молей растворяемого компонента содержится в литре раствора. Ее формула имеет вид:
(С=ndiv V)
где (n) – это растворенное вещество в молях. Исходя из его значения, раствор может быть одномолярным (содержит 1 моль в 1 литре), децимолярным (0,1 моля в 1 л), сантимолярным (0,01 моль) и т.д.
3. Концентрация моляльная (обозначается (С_х)) – моляльность – показатель количества (n) молей растворенного компонента в 1 кг растворителя ((M_{р-ля})).
(C_x=ndiv M_{р-ля})
4. Для определения содержания (в граммах) вещества в 1 л раствора применяется понятие «титр» ((Т)).
(T=M_{в-ва}div V_{р-ра})
5. Под растворимостью ((S)) понимают максимальную массу растворяемого вещества, способного раствориться в 100 г растворителя:
(S=(M_{в-ва}div M_{р-ля})times100 {})
6. Коэффициент растворимости ((K_s)) – показатель, который определяется отношением массы вещества к массе растворителя при условии получения насыщенного раствора при обозначенной температуре:
(K_s=M_{в-ва}div M_{р-ля})
Решение задач на упаривание растворов
Выпаривание раствора происходит в результате испарения воды, что ведет за собой уменьшение общего объема и массы. В то же время масса растворенного вещества остается без изменений. Существуют случаи, когда, кроме растворителя, испаряется растворенное вещество, если оно обладает повышенной летучестью.
Пример. Водный раствор аммиака
Рассмотрим пример решения задачи на упаривание.
Условие: В наличии 800 г раствора с 15%-ной концентрацией определенного вещества. Нужно увеличить его массовую долю на 5%. Сколько г воды должно испариться?
Этапы решения:
- Какова масса вещества в первичном растворе?
(M_в=omega_вtimes M_р=0,15×800=120)г, где (M_в) — масса вещества, (M_р) — масса раствора
Найденное значение останется постоянным, поскольку при выпаривании изменения массы растворенного вещества не происходит. Значит M’=120г
2. (M_р=M_вdivomega_в= 120÷0.2=600)г
3. Теперь можно найти массу испаренной воды:
(M{исп;в}=M_р-M’=800-600=200)г
Решение задач на разбавление растворов
В результате процесса разбавления масса того вещества, которое растворено, не меняется в отличие от массы всего раствора и растворителя.
Задача
Масса имеющегося раствора NaCl 200г, его концентрация – 15%. К раствору добавлено 40г воды. Определить массовую долю NaCl в конце реакции.
Решение
1. Определение массы раствора в конце процесса:
(M’=M_{р-ра}+M_{добH2O}=240)г
2. Определение массы NaCl в начале процесса:
(M_{NaCl}=(omega_{NaCl}times M_р)div100%=15%times200гdiv100%=30 {})г
В конечном растворе (M’_ {NaCl}=M_{NaCl})
3. Определение массовой доли NaCl в конце процесса:
(omega’_{NaCl}=M_{NaCl}div M’_рtimes100%=12,5%)
Решение задач на концентрирование растворов
Повышение концентрации происходит при добавлении вещества в раствор. При этом конечная масса растворенного вещества равна сумме первоначального содержимого и того, который добавлен.
Задача. Имеется 180 г раствора с 8%-ной концентрацией соли (формула NaCl). В этот раствор всыпали еще 20 г поваренной соли. Какая массовая доля NaCl получилась в конце реакции?
Решение
1. Определение окончательной массы раствора:
(M’_р=M_р+M_{доб}=200)г
2. Определение конечной массы NaCl:
M’=M+Mдоб
Следовательно, нужно найти (M) – массу в начале процесса.
(M=(omega_{NaCl}times M_р)÷100%=14,4)г
Тогда (M’=14,4г+20г=34,4)г
3. Определение массовой доли NaCl в конечном продукте:
(omega’=M’_{NaCl}div M’_рtimes100%=17,2%)
Решение задач на смешение растворов
Смешение растворов с различной концентрацией растворенного вещества происходит с соблюдением «конверта Пирсона». Это – диагональная модель, при которой нельзя складывать массовые доли, а можно – лишь массы растворенных компонентов и растворов.
Задача
Дано два раствора с массами (M) и (M_1). Массовые доли растворенного вещества обозначим соответственно (ω) и (ω_1). В конечном продукте аналогичная величина – (ω_3). Необходимо приготовить третий раствор с отличной от имеющихся концентраций.
Решение
1. Определение общей массы растворенного вещества:
(M_1omega_1+M_2omega_2=omega_3(M_1+M_2))
2. Математические действия:
(M_1(omega_1-omega_3)=M_2=(omega_3-omega_2))
(M_1div M_2=(omega_3-omega_2)div(omega_1-omega_3))
Следовательно, согласно этому математическому выражению, и нужно взять соотношение растворов.
Задачи на определение процентной концентрации раствора
Задача 1
Какая процентная концентрация раствора (KNO_3), если нормальная равна (0,2) моль/л. Плотность равна (1) г/мл.
Решение:
1. Определение массы раствора объемом (1000) мл:
(M=rhotimes V=1times1000=1000)г
2. Составление и решение следующей пропорции:
(20,0)г (KNO_3) — (1000) г раствора
(Х_г) — (100) г раствора
(Х=2,02) г или (ω=2,02%)
Задача 2
Нужно приготовить (300) г 25%-ного раствора соли, имея 60%-ный и 10%-ный. Сколько нужно взять таких компонентов (m1 и m2)?
Для решения применим правило Креста:
1. Определение веса одной из 50-ти частей образуемого раствора:
(300div5=6)
2. Определение массы каждой части (m_1) и (m_2):
(m_1=6times15=90)
(m_2=6times35=210)
Задача 3
Используя 250г 45%-ного раствора соли, нужно понизить его концентрацию до 10%. Сколько воды необходимо использовать?
Концентрация соли в воде, используемой в качестве добавки, равна 0.
По методу креста образуется 45 частей раствора:
Решение
1. Масса одной части первичного раствора равна: (250div10=25)г
2. Определение массы воды, что необходима: (25times35=875)г
С целью проверки можно выполнить следующие действия:
1. Определение массы конечного продукта-раствора:
(875+25=1125г)
2. Для исходного раствора действует пропорция:
В 250г 40%-ного р-ра содержится Хг соли
в 100 г – 45г
Отсюда Х=112,5 г соли
3. Определение конечной концентрации раствора:
1125 г раствора – 112,5 соли
100г – Х
Х=10г или 10%
Следовательно, нужно взять 875 г воды.
Решать задачи на растворы – интересное занятие! Знание основных закономерностей будет полезно с теоретической и практической точек зрения. Однако бывают случаи, когда нужно быстро сдать контрольную либо перепроверить собственные решения. Тогда можно обратиться на сайт ФениксХелп.
Концентрация растворов. Растворы неэлектролитов. Растворимость
Задача:
Расчеты по процентной концентрации растворов. Формула, выражающая процентную концентрацию раствора —
где 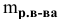
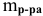
Задача:
Рассчитать процентную концентрацию раствора, полученного растворением 80 г сахара в 160 г воды.
Решение:
Задача:
Рассчитать массы поваренной соли и воды, необходимые для приготовления 250 г 2,5%-ного раствора.
Решение:
Задача:
Рассчитать концентрацию раствора, полученного смешением З00 г 10%-ного раствора хлороводорода и 400г 20%-ного раствора хлороводорода.
Решение:
Определяем массы растворенной 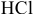
После смешивания
Определяем концентрацию полученного раствора:
Задача:
Какова концентрация серной кислоты в растворе, полученном смешиванием 200г 10%-ного раствора серной кислоты и 100г 5%-ного раствора сульфата натрия?
Решение:
Масса полученного раствора определяется как сумма масс смешанных растворов:
Далее определим концентрацию серной кислоты в полученном растворе:
Задача:
Расчеты по молярной концентрации (молярности) раствора.
Формула для расчета молярности раствора —
где С — молярность раствора, моль/л;
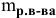
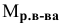
V — объем раствора, мл; если объем выражается в литрах, тогда в формуле исчезает коэффициент 1000.
Задача:
Какая масса серной кислоты необходима для приготовления 2 л 2-молярного раствора?
Решение:
Задача:
250 мл раствора содержат 7г КОН. Какова молярность этого раствора?
Решение:
Задача:
Расчеты по нормальной концентрации (нормальности) раствора.
Для расчета нормальности пользуемся следующей формулой:
где 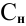
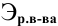
Задача:
Какая масса фосфорной кислоты необходима для приготовления 2 л 0,1 н раствора?
Решение:
Задача:
Расчеты по разбавлению растворов.
Выведем формулу для расчетов при разбавлении растворов, учитывая, что концентрация как исходного, так и приготовленного растворов может быть выражена любым способом 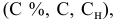
Для раствора, концентрация которого выражена в процентах,
а так как
то
где 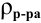
Для молярной концентрации
Для нормальной концентрации
Приравниваем правые части уравнений:
Задача:
Сколько миллилитров 98%-ного раствора серной кислоты
(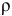
Решение:
Воспользуемся первым членом приведенного выше уравнения для концентрированного исходного раствора кислоты и третьим членом — для приготовления разбавленного раствора серной кислоты:
где С% = 98 %;
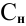
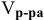
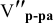
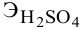
Отсюда
Задача:
Расчеты по переходу от одного способа выражения концентрации данного раствора к другому.
При переходе от одной концентрации данного раствора к другой остаются постоянными не только масса растворенного вещества, но и объем раствора, т.е.
Предыдущая формула принимает следующий вид:
Задача:
Определить молярность 36,5%-ного раствора соляной кислоты (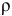
Решение:
Воспользуется первым и вторым членами последнего уравнения и выведем выражение для определения молярности:
Задача:
Расчеты по законам Рауля. Давление паров разбавленного раствора.
По закону Рауля, понижение давления пара 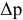
где 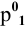
N — мольная доля растворенного вещества,
где 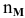
где 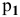
Отсюда
Задача:
Определить давление насыщенных паров раствора, содержащего 45 г глюкозы 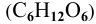
Решение:
Рассчитываем мольную долю растворенного вещества:
Определяем давление паров воды над раствором:
Задача:
Расчеты по понижению температуры замерзания растворов.
По закону Рауля понижение температуры замерзания прямо пропорционально моляльной концентрации раствора:
где 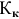
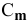
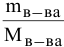
Отсюда
Задача:
Рассчитать температуру замерзания 3%-ного водного раствора этиленгликоля
Решение:
Выведем формулу для перехода от процентной концентрации к моляльности раствора.
Для процентной концентрации
Для моляльности
Отсюда
Если принять 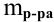
Находим моляльность рассматриваемого раствора:
Рассчитаем понижение температуры замерзания раствора:
Температура замерзания водного раствора
Задача:
Рассчитать температуру кипения 0,1 молярного водного раствора глюкозы (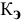
Решение:
Формула для перехода от молярной концентрации к моляльной —
Так как раствор разбавленный, то принимаем 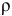
Определяем повышение температуры кипения раствора:
Температура кипения этого раствора
Задача:
Расчеты по уравнению химической реакции, протекающей в растворе.
Для химического уравнения общего вида
верно следующее соотношение числа эквивалентов:
Если участвующие в реакции вещества взяты в виде растворов и если их концентрации выражены:
а) для вещества А — С %;
б) для вещества В — С (молярность);
в) для вещества С — 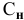
тогда массы и число эквивалентов каждого из веществ, находящихся в определенных объемах растворов этих веществ, определяются по формулам:
Так как числа эквивалентов, участвующих в реакции веществ, равны между собой, то можно записать:
Если концентрации участвующих в реакции веществ выражены в нормальности, то формула для расчетов приобретает вид:
Задача:
Какой объем 0,2 н раствора щелочи необходим для осаждения 2,708 г хлорида трехвалентного железа в виде гидроксида железа?
Решение:
Предложенный метод не требует обязательного написания уравнения реакции для осуществления таких расчетов.
Отсюда
Задача:
Для нейтрализации 20 мл 2-молярного раствора 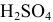
Решение:
Формула для расчета —
Так как 
откуда
Задача:
Какой объем 80 %-ного раствора 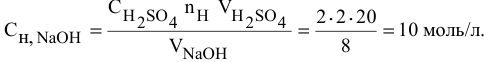
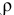
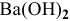
Решение:
Формула для расчета —
Так как 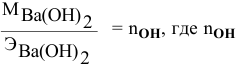
Отсюда
Задача:
Какой объем 0,2 н раствора щелочи необходим для реакции осаждения 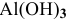
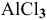
Решение:
Формула для расчета —
Задача:
Смешивается 300 мл 0,5 М раствора хлорида бария со 100 мл 6 %-ного раствора серной кислоты (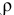
Решение:
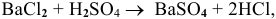
Так как указаны количества обоих реагирующих веществ, то необходимо определить вещество, взятое в избытке.
Таким образом, 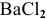
Дальнейший расчет производим по веществу, взятому в недостатке, т.е. по серной кислоте.
Так как
находим массу
откуда
Задача:
Для приготовления насыщенного раствора К.С1 при 40°С взято 50г воды и 20г КС1. Какова растворимость К.С1 в воде при данной температуре?
Решение:
Задача:
В 300г горячей воды растворено 219г 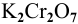
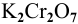
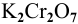
Решение:
Определяем, сколько может быть растворено 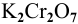
Откуда
Масса кристаллов — это разность массы растворенного вещества в горячем растворе и массы растворенного вещества в охлажденном растворе (рис.З):
Рис. 3 — Графическое изображение процесса выпадения кристаллов при охлаждении раствора:
1 — участок охлаждения ненасыщенного раствора от заданной температуры до температуры образования насыщенного раствора;
2 — участок охлаждения насыщенного раствора до заданной температуры с уменьшением растворимости вещества, что приводит к его кристаллизации (в данном случае мы предполагаем, что пересыщенный раствор не образуется).
Эти задачи взяты со страницы решения задач по неорганической химии:
Задачи с решением по неорганической химии
Возможно эти страницы вам будут полезны: