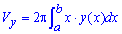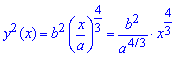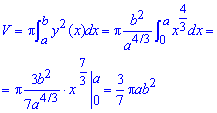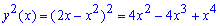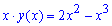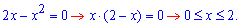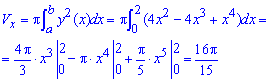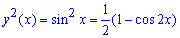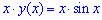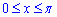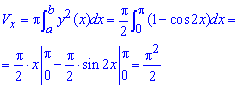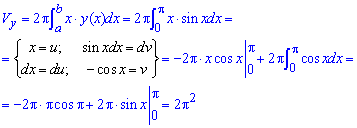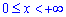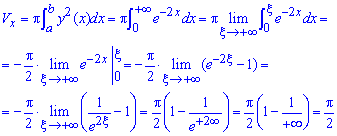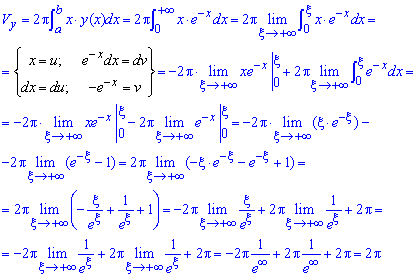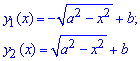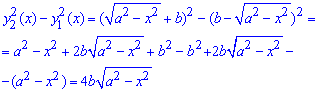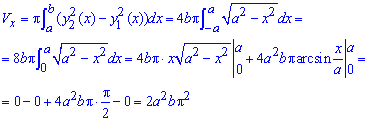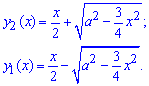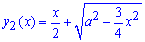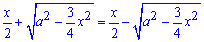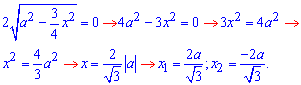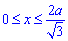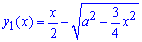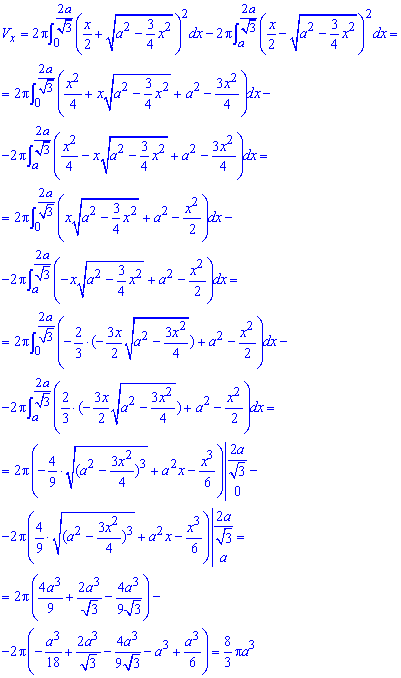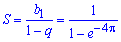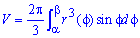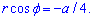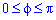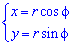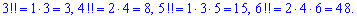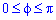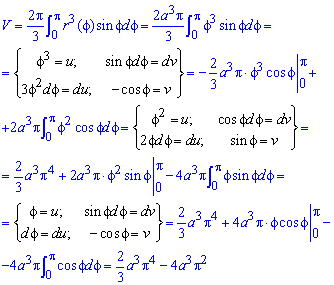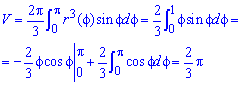Как найти объем синуса - Исправление недочетов и поиск решений вместе с Examum.ru

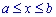
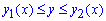
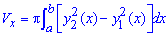
Объем тела V, образованного вращением вокруг оси Ox фигуры , , где y₁(x) и y₂(x) — непрерывные неотъемлемые функции, равняется определенному интегралу от разницы квадратов функций y_i(x) по переменной x

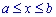
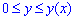
Объем тела V, образованного вращением вокруг оси Oy фигуры , , где y(x) — однозначная непрерывная функция, равняется определенному интегралу, рассчитанному по формуле

Примеры выбраны из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.

Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления объема тела вращения будут повторяться из примера в пример.

ІV. Найти объемы тел, ограниченными поверхностями, полученными при вращении отрезков следующих линий

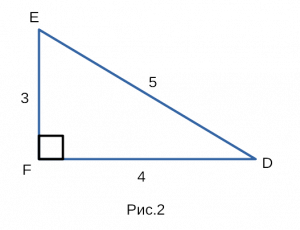
Пример 2.139 (2472) Найти объем тела, образованного вращением кривой 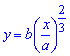(нейлоїд) xє[0;a] вокруг оси Ox.
Решение: Складываем подинтегральную функцию:

Пределы интегрирования известны за условием: [0;a].
Найдем объем тела интегрированием:

Всегда помните, что объем измеряется в кубических единицах.

Пример 2.140 (2473) Найти объем тела, образованного вращением кривой y=2x-x^2, y=0
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Запишем подинтегральные функции:
а)
б)
Из приведенных формул Вы можете видеть разницу, в каких случаях применять каждую из формул объема.
Найдем пределы интегрирования:

И заключительным шагом вычисляем объемы интегрированием.
а) Найдем объем тела вращения вокруг оси Ox:

б) Вычислим объем тела вращения вокруг оси Oy:

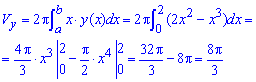
В этом примере интегралы легко берутся и нет потребности объяснять детали операций.

Пример 2.141 (2474) Вычислить объем тела, образованного вращением кривой y=sin(x)

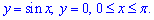
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Выпишем подинтегральные функции:
а)
б)
Пределы интегрирования берем из начального условия:

Осталось вычислить определенные интегралы:
а) Найдем объем тела вращения вокруг оси Ox:

б) Выполняем вычисление объема тела при вращении вокруг оси Oy:

Замена переменных помогает найти последний интеграл.

Пример 2.143 (2476) Найти объем тела, образованного вращением кривой y=e^{— x}, y=0,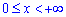
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Уравнение подинтегральных функций :
а) y²=e^-2x;
б) x*y (x) =xe^-x.
Запишем пределы интегрирования (известно за условием):

а) Находим объем тела вращения вокруг оси Ox:

б) Найдем объем тела вращения вокруг оси Oy:

Здесь, чтобы вычислить интегралы придется находить границу при переменной направляющейся к безграничности.
Во втором интеграле выполняем интегрирование частями.

Пример 2.144 (2477) Вычислить объем тела, образованного вращением кривой x²+(y-b)²=a², 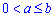, вокруг оси Ox.
Решение: Фигурой вращения является круг с центром в точке (0;b) и радиусом a.
При выражении самой функции получим две ветки корневых функций:

При поднесении к квадрату разница слагаемых сложит такое выражение подинтегральной функции:

Запишем пределы интегрирования: для круга они равны xє[-a;a] или два полукруга из на промежутке xє[0;a].
Через интеграл находим объем тела вращения вокруг оси Ox:

Внимательно разберите приведенный пример.

Пример 2.145 (2478) Найти объем тела, образованного вращением кривой x²-xy+y²=a², вокруг оси Ox.
Решение: Сведем кривую к каноническому виду (методами из аналитической геометрии) устанавливаем, что заданная линия является эллипсом
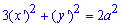
— уравнение в канонической системы координат.
В приведенной системе координат уравнения эллипса имеет вид:

Прямая y=x/2 является осью симметрии этой фигуры.
Запишем подинтегральную функцию:

Найдем пределы интегрирования из условия равности функций y₂(x)=y₁(x):

или двукратный объем на интервале

Но тогда еще нужно отнять объем тела в пределах

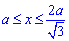
(которая не принадлежит эллипсу) и ограничена первой кривой

и результат умножить на 2 (симметрия).

Последним шагом вычисляем объем тела вращения вокруг оси Ox:

Формула интеграла вышла достаточно длинным, однако его удобно читать пользователям, которые заходят на сайт из мобильных устройств.

Пример 2.146 (2479) Найти объем тела, образованного вращением кривой 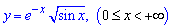вокруг оси Ox.
Решение: Запишем подинтегральную функцию:
y²(x)=e^-2x*sin (x).
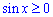
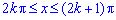
Установим пределы интегрирования: при , где k=0,1,2.
Таким образом имеем бесконечный ряд промежутков интегрирования.
При нахождении объема тела вращения вокруг оси Ox получим бесконечный ряд интегралов, который совпадает:

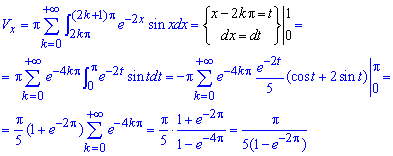
Здесь вычислили интеграл дважды выполнив замену переменных:

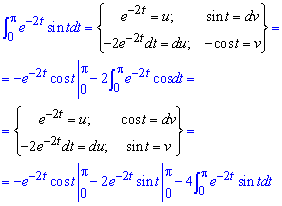
тому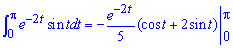
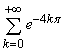
— это числовой ряд.
В данном случае бесконечно нисходящая геометрическая прогрессия, у которой b₁=1, b₂=e^-4Pi, поэтому q=e^{— 4Pi}, а сумма прогрессии равна

Объем тела, образованного вращением вокруг полярной оси плоской фигуры

Чтобы найти объем тела V, образованного в результате вращением вокруг полярной оси плоской фигуры r(phi)
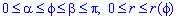
необходимо вычислить определенный интеграл по формуле

Пример 2483 Найти объем тела, образованного вращением кривой r=a (1+cos (phi)), 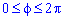, y=0
а) вокруг полярной оси;
б) вокруг прямой

Решение: Чтобы достать подинтегральную функцию подносим к кубу заданную функцию: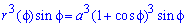

Пределы интегрирования записываем из начального условия:

а) Сначала найдем объем тела вращения вокруг полярной оси:

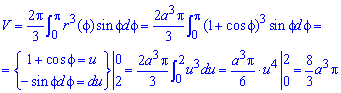
Для упрощения вычислений переходим к новой переменной под интегралом.
б) Перейдем к новым координатам с помощью формул: x₁=y, y₁=-x-a/4.
Определяем пределы интегрирования:
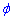
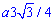
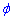
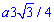
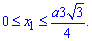
при росте угла от 0 к Pi/2 координата x₁ растет от 0 к , при росте от Pi/2 к Pi переменная x₁ спадает от к 0, поэтому пределы ограничены интервалом

Запишем подинтегральную функцию:
Уравнения перехода между системами координат имеют вид

Подстановкой в уравнение получим:
,
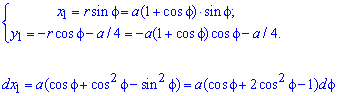
Найдем объем тела вращения вокруг прямой :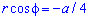

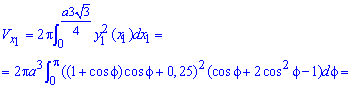
откроем скобки, возведем подобные слагаемые и, приняв во внимание, что интеграл равен нулю 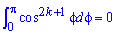получим

Здесь последние интегралы 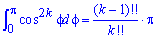выражаются через факториалы

(смотри пример 2.59, часть І).
Парные факториалы вычисляем по правилу

Пример 2484.1 Найти объем тела, образованного вращением кривой r=a*phi 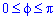(a>0)вокруг полярной оси.
Решение: Запишем подинтегральную функцию:

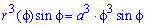
С пределами интегрирования проблем нет:

Чтобы найти объем тела вращения вокруг полярной оси выполняем ряд манипуляций с интегралами:

Внимательно проанализируйте, как находится этот «тригонометрический» интеграл.

Пример 2484.2 Найти объем тела, образованного вращением кривой phi=Pi*r³, phi=Pi, вокруг полярной оси.
Решение: Запишем подинтегральную функцию:

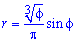
Пределы интегрирования:

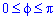
Вычисляем объем тела вращения вокруг полярной оси:

Здесь синус вносим под дифференциал и выполняем интегрирование частями.
На данное время это все примеры, которые мы смогли подготовить для Вас по данной теме.

Источник

Сообщения без ответов | Активные темы

Автор

Сообщение

annabelle

Заголовок сообщения: Найти объем фигуры вращения

Добавлено: 25 апр 2010, 12:59

Начинающий

Зарегистрирован:
25 апр 2010, 12:54
Сообщений: 2
Cпасибо сказано: 1
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

Добрый день!
Догадываюсь, что это задача несложная. ) Тем не менее никогда не сталкивалась с такими, разобраться до конца не получилось(в своем ответе не уверена). Случай единичный, но необходимо с ним справиться. Помогите, пожалуйста.

Дан график синуса. На интервала от нуля до «П» синусоида начинает «вращаться» вокруг оси ОХ, образуя фигуру по типу лимона(извиняюсь за нематематическую терминологию). Нужно найти объем половины этой фигуры(он нуля до П/2). Как?

Вернуться к началу

annabelle	Заголовок сообщения: Re: Найти объем фигуры вращения Добавлено: 25 апр 2010, 16:45
	Огромное спасибо вам!
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Объем тела вращения плоской фигуры вокруг оси OY в форуме Интегральное исчисление	Jobber	0	371	05 май 2015, 19:52
Объем тела вращения плоской фигуры вокруг оси OY в форуме Интегральное исчисление	Jobber	10	1131	05 май 2015, 19:50
Вычислить объем тела вращения фигуры, ограниченной указанным в форуме Интегральное исчисление	horvod	2	172	02 апр 2020, 21:50
Найти объем тел вращения в форуме Интегральное исчисление	MathSamurai	13	295	31 авг 2019, 17:15
Как найти ось вращения плоской фигуры под действием силы в форуме Механика	constantin01	1	172	07 дек 2020, 09:54
Найти объем тела вращения в форуме Интегральное исчисление	Ryslannn	10	405	24 окт 2017, 15:00
Найти объём тела вращения в форуме Интегральное исчисление	Sirom	7	344	09 июн 2018, 22:46
Найти объем тела вращения в форуме Интегральное исчисление	Ryslannn	8	289	17 окт 2017, 17:15
Найти объем тела вращения в форуме Интегральное исчисление	Kostia	15	809	12 июн 2014, 09:26
Найти объём тела вращения вокруг оси OY в форуме Интегральное исчисление	Proton2002	1	128	23 апр 2020, 19:08

Кто сейчас на конференции

Сейчас этот форум просматривают: mrlegendapredela и гости: 7

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group

Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru

Русская поддержка phpBB

Источник

Решение.

а) Вычислим

площадь поверхности,

полученной вращением отрезка прямой

y = x (0 ≤ x ≤ R)

вокруг оси

(рис.

1.15).

Найдем

производную:

Рис. 1.15

y′ = (x)′ = 1. Подставляя в формулу (1.6) получим:

S = 2π ∫x 1 + 12 dx = 2π

2 ∫xdx = 2

= 2π R2 .

2π

б) В параметрической форме формулу (1.6) можно записать в

следующем виде:

′

(x)]

dt .

(1.7)

S = 2π∫y(t) [x (t)]

+[y

Тогда площадь поверхности, образованной вращением одной арки циклоиды вокруг оси Ox, будет равна

2π

S = 2π ∫ a(1 − cost) (asin t)2 + a2 (1 − cost)2 dt =

0
2π	64
= 2 2π a2 ∫( 1 − cost)3/ 2 dt =	πa2 .
0	3

Объем тела вращения

Если площадь S(x) сечения тела плоскостью, перпендикулярной оси

Ox, является непрерывной функцией на отрезке [a; b], то объем тела вычисляется по формуле:

Выражение для функции S(x) получается достаточно просто в случае тел вращения. Если криволинейная трапеция, ограниченная кривой y = f (x), a ≤ x ≤ b , вращается вокруг оси Ox или оси Oy, то объемы тел

вращения вычисляются по формулам:

b	b
Vx =π ∫ f 2 (x)dx или	Vy =π ∫ϕ2 ( y)dy .	(1.9)
a	a

Если криволинейный сектор, ограниченный кривой ρ = ρ(ϕ) и лучами ϕ =α , ϕ = β , вращается вокруг полярной оси, то объем тела вращения равен:

Рис. 1.16 V = 2 π ∫ρ3 sinϕdϕ . (1.10)

3 α

Пример. Найти объем тела, образованного вращением фигуры,

ограниченной а)

линиями

y =

, x =0, y = 2

вокруг

оси Oy; б)

кардиоидой ρ = 2a(1 − cosϕ)

вокруг полярной оси.

Решение. а) Используя формулу (1.9), найдем объем данного тела (рис.

1.16):

Vy =π ∫ 2 ydy = 2π

8π (ед. )

б) Используя формулу (1.10), найдем объем

Рис. 1.17

данного тела (рис.1.17):

V = 2 π

∫(2a(1 − cosϕ))3 sinϕdϕ =

16a3 π ∫(1 − cosϕ)3 d (1 − cosϕ) =

= 16a3

π (1 − cosϕ)4

= 16a3 π

4 = 64

πa3

= 21

1πa3 .

1.3 Несобственные интегралы

Несобственными интегралами называются: 1) интегралы с бесконечными пределами (несобственные интегралы 1-го рода); 2)

интегралы от неограниченных функций (несобственные интегралы 2-го рода).

Несобственный интеграл от функции f (x) в пределах от a до +∞

определяется равенством

b
f (x)dx = blim→+∞∫ f (x)dx .	(1.11)
a

Если этот предел существует и конечен, то интеграл называется сходящимся, если же предел не существует или равен бесконечности, то интеграл называется расходящимся.

Аналогично определяются:

a		a		+∞		b
∫	f (x)dx = blim→−∞∫ f (x)dx и	∫ f (x)dx = blim→+∞∫ f (x)dx .	(1.12)
−∞		b		−∞		a→−∞a
Если функция имеет бесконечный разрыв в точке c отрезка [a;b] и
непрерывна при	a ≤ x < c и	при	c < x ≤ b ,	то несобственный интеграл 2-го
рода определяется следующим равенством:
	b		c−ε		b
	∫ f (x)dx =	εlim→0	∫ f (x)dx +	εlim→0	∫	f (x)dx .	(1.13)
	a		a		c+ε

Несобственный интеграл 2-го рода называется сходящимся, если оба предела в правой части существуют и конечны; если же хотя бы один из интегралов не существует или бесконечен, то несобственный интеграл называется расходящимся.

Пример. Вычислить несобственные интегралы (или установить их

		+∞	+∞	dx		1
расходимость): а)	∫ sin xdx ; б)	∫		;	в) ∫dx .
	2
		0	−∞ 1	+ x		0	x
	Решение. а) Согласно формуле (1.12)	получим
+∞	b						b	= lim (−cosb + 1)=1 − lim cosb ,
	sin xdx = lim	sin xdx = lim (−cos x)

∫	b→+∞ ∫	b→+∞					0		b→+∞	b→+∞

0	0

т.е. предел не существует и несобственный интеграл расходится.

б) Используя четность подынтегральной функции и формулу (1.12), получим:

+∞

0b = 2 lim arctgb = 2

∫

= 2 ∫

= 2 lim

∫

= 2 lim arctg x

=π .

1 + x

−∞

b→+∞

Следовательно, несобственный интеграл сходится и равен π .

в) Используя формулу (1.13), получим:

1			1
∫dx	= lim	∫dx	= lim ln x		ε1 = lim (−lnε) = +∞ .

0	x	ε→+0	ε	x	ε→+0	ε→+0

Следовательно, несобственный интеграл расходится.

1.4. Задания на контрольную работу Задание 1.. Найти неопределенные интегралы. Первый и второй проверить дифференцированием.

1. а)

∫2−2x+1 dx,

б) ∫ x3x dx,

в) ∫

2x2 −1

dx,

− 5x

+6x

г) ∫

, д) ∫

3 − 2sinx + cosx

1 + x

2. а)	∫	2xdx	,
2
		x		+ 2
г) ∫				dx	,
sin	2	xcos	4	x

3. а) ∫sin3 x cos xdx,

г) ∫		dx		,
3cos x + 2

4. а)	∫	ln2 x	dx,
x

г)	∫tg2 xsin2 xdx,
5.	а)	∫		arctgx	dx ,
1 + x2
г)	∫tg6 xdx,
6.	а)	∫ex3 x2dx,	б)
г)	∫	cos2 x	dx,
sin	6	x

б) ∫ x2 sin 3xdx,

в)

∫

x3 −2x2 +4

dx,

−

д) ∫

(x2

− a2 ) x2 − a2

б) ∫(x2 − 2x)e−xdx,

в)

∫

+ 2x

д) ∫

xdx

x +1

+ 3

x +1

б) ∫(5 − x)exdx,

в)

∫

x4 +1

dx,

−1

д) ∫

1 − x dx

1 + x

б) ∫(3x2 +5)ln xdx,

в)

∫

д) ∫ x2

4 − x2 dx,

∫(5x +1)e2xdx,

в)

∫

x4 +3x3 +3x2 −5

dx,

+3x +

д) ∫(x2 +16) 9 − x2 ,

7.а) ∫6xsin(x2 +3)dx,	б) ∫(2x −1)2x dx, в)	∫	x2	− x +4	dx,
(x +1)(x −2)(x	−3)

г) ∫sin4 xcos4 xdx,	д) ∫	x +1 +1	dx,

		x +1 −1

8. а)

∫

tgx

dx ,

б) ∫ x5x dx,

в) ∫

4x(x −2)

dx,

cos

−1) (x

x +

x + 3 x2

г)

∫

д)

∫

dx,

sin

x(1 +

x )

9.а)

∫

,б) ∫(x3 + 5x −1)lnxdx, в) ∫

dx,

(1+ x

)arctgx

(x +1)(x

+1)

г) ∫

cos3 x

dx,

д)

∫

dx,

sin

x −

3 x2

∫e

dx2 ,

10.

а)

б)

∫ x2 cos xdx,

в)

∫

2x2 −3x −3

dx,

(x −1)(x2 −2x +5)

г)

∫sin4 xdx,

д)

∫

+ 3 x2

Задание 2. Вычислить определенный интеграл.

π/2

б) ∫x cos3xdx

1. а)

∫

cos(lnx)dx

1/2

а) ∫

б) ∫x e

π/2

3. а)

∫

б) ∫x sinxdx

xlnx

exdx

4. а) ∫

б) ∫x 5

	e2	2 + lnxdx
	5. а) ∫	,
	x
	1

1x2dx

6.а) ∫0 4 + x3 ,

7. а) ∫x(2 + x2 )7 dx,

0dx

8.а) —∫1 1 + 3 x +1,

	1/2arctg2xdx	,
9. а)	∫	1 + 4x	2
	0
	2	exdx
10.а)	∫			,
1 + e	2x
	1

Задание 3. Вычислить несобственный расходимость.

		∞
1.	а) ∫x e— x2 dx ,
		0
		0
2.	а) ∫x2 ex3 dx ,
		—∞
		-3			xdx
3.	а)	∫		,
	2 3
		—∞(x	+1)
		∞	dx
4.	а)	—∫1
	,
x2 + x +1

	1/2
б)	∫arcsin2xdx
	0
	1/2
б)	∫arctg2xdx
	0
		π/4
	б)	∫x2 sinxdx
		0
	1
б)	∫ln(x + 2)dx
	0
	2
б)	∫x lnxdx
	0
		1
	б)	∫x arctgxdx .
		0
интеграл	или доказать его
		1			dx
	б) ∫0				,
	x2 − 4x + 3
		2			dx
	б)	∫				,
		(x — 1)2
		0 3
		2			xdx
	б)	∫0		,
	x2 − 4
		1			x2dx
	б)	∫				,
		x3 −	1
		0

		∞ arctgxdx				2				dx
5.	а) ∫					2					,		б) ∫						,
		x	+1						2
		0								0	(x — 2)
		∞				dx							4				dx
6.	а) ∫					,				б) ∫				,
x		2	x						3
		2	ln						3	(x — 3)
		∞ lnxdx							2				dx
7.	а)	∫							,					б)	∫					,
			x							x	2	− x	−	2
		1											1
		∞				xdx						1
8.	а)	∫					,			б)	∫lnxdx ,
(x	2	2
		0		+1)					0
		∞						dx						3				dx
9.	а) ∫								,	б) ∫						,
		2	− 4x +7					2
		—∞ x					1	(x − 2)
		∞													2				dx
10.	а)	∫e—		x dx ,					б)	∫			.
					3	x −1
		0													-1

Задание 4. Задачи на геометрические приложения определенного интеграла.

1.	Вычислить площадь фигуры, ограниченной параболами	y = x2 + 1 ,
y =	1	x2	и прямой y = 5 .
2
2.	Вычислить длину дуги параболы y2 = 4x от вершины	до	точки
М(1;2).
3.	Вычислить объем тела, полученного вращением вокруг оси 0у
криволинейной трапеции, ограниченной гиперболой xy = 4 , прямыми	y =1,

y= 2 и осью 0у.

4.Вычислить площадь фигуры, ограниченной линиями, заданными

x = 9cost

уравнениями , y = 2(y ≥ 2).

y = 4sint

5. Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах r = cos2ϕ .

6	Вычислить	длину	дуги	кривой,	заданной	параметрически
	x = 5(t − sint)	,	0 ≤ t ≤ π.
уравнениями
	y = 5(1 − cost)
7.	Вычислить длину дуги кривой, заданной уравнением в полярных
координатах r = 2(1 — cosϕ) , — π ≤ϕ ≤ −π/2.
8.	Вычислить объем тела, полученного вращением вокруг оси 0x
фигуры, ограниченной графиками функций y = −x2 + 5x −6, y =0.
9.	Вычислить объем тела, полученного вращением вокруг оси 0у
фигуры, ограниченной графиками функций y = x2 — 2x + 1,	y =0, x = 2.
10. Вычислить	площадь	фигуры,	ограниченной кардиоидой
r = 3(1 + cosϕ) .

2.Дифференциальные уравнения

2.1.Краткие сведения из теории

2.1.1.Дифференциальные уравнения первого порядка

Дифференциальное	уравнение первого	порядка	имеет	вид
	dy	, x – независимая переменная, y – искомая функция.
F x, y,		= 0

	dx
Дифференциальное	уравнение вида f1 (x)g1 ( y)dx + f2 (x)g2 ( y)dy = 0 ,	где
f1 (x),	g1 ( y),	f2 (x), g2 ( y)	–	непрерывные	функции,	называется

дифференциальным уравнением с разделяющимися переменными и его

решение находится в виде: ∫	f1	(x)	dx +∫	g1	( y)	dy = C .
f2		g2	( y)
		(x)
Дифференциальное	уравнение	вида	P(x, y)dx + Q(x, y)dy = 0	называется
однородным, если P(x, y) и Q(x, y) — однородные функции	от x и y
одинакового измерения. Оно решается подстановкой t =	y	.

							x
Дифференциальное		уравнение	вида y′+ P(x) y = Q(x)	называется

линейным неоднородным уравнением. Оно решается подстановкой y = u v ,

где u = u(x) , v = v(x) .

Дифференциальное уравнение вида y′+ P(x) y = Q(x) ya , где a —

действительное число называется уравнением Бернулли. Во всех случаях оно сводится к линейному с помощью подстановки z = y1−a . При a=0, a=1

уравнение становиться неоднородным линейным.

2.1.2. Дифференциальные уравнения, допускающие понижения порядка

Уравнение вида F(x, y, y‘, y»,K, y(n) ) = 0 называется дифференциальным

уравнением n-го порядка. Интегрирование дифференциальных уравнений

n-го порядка (в конечном виде) удается произвести только для некоторых частных случаев.

Решение уравнение y(n) = f (x) находится интегрированием данного уравнения n раз.

y = ∫∫∫K∫ f (x)dxn + C1 xn−1 + C2 xn−2 +K+ Cn−1 x + Cn .

n раз

Порядок уравнения вида F(x, y(k ) , y(k −1) ,K, y(n) ) = 0 можно понизить, взяв за новую неизвестную функцию z = y(k ) , и таким образом понижаем порядок на k единиц.

Уравнение вида F( y, y‘, y»,K, y(n) ) = 0 допускает понижение порядка на единицу, если положить y‘ = z , а за новый аргумент принять сам y.

2.1.3. Линейные уравнения с постоянными коэффициентами.

Дифференциальное уравнение y(n) + a1 y(n−1) + a2 y(n−2) +K+ an−1 y‘+an y = 0

называется линейным однородным уравнением n-го порядка с

постоянными коэффициентами.

Для нахождения общего решения дифференциального уравнения составляется характеристическое уравнение, которое получают заменой производных соответствующими степенями переменной k, а сама функция заменяется единицей. В зависимости от корней характеристического уравнения находится общее решение дифференциального уравнения. Если корни характеристического уравнения k1, k2 ,K действительные и не кратные,


то	решение	уравнения	имеет	вид:	y = C1ek1x +C2ek2 x +K.	Если корни
k1, k2 ,Kдействительные	и	имеют	кратность		l1, l2 ,K	,то
y = ek1x (C0 +C1x)l1 −1 + ek2 x (D0 + D1 x)l2 −1 +K.	Если	корни k1, k2 ,K	комплексные
k1	= a1 ±b1i, k2 = a2 ±b2i,K, то y = ea1x ( A1 cos b1x + B1 sin b1x) +ea2 x ( A2 cos b2 x + B2 sin b2 x) +K
	Дифференциальное	уравнение	y(n) + a1 y(n−1) + a2 y(n−2)	+K+ an−1 y‘+an y = f (x)
называется	линейным	неоднородным	уравнением	n-го порядка	с

постоянными коэффициентами. Общее решение данного уравнения может быть найдено с помощью метода вариации постоянных (метод Лагранжа). Если правая часть данного дифференциального уравнения имеет специальный вид, то общее решение определяется формулой y = yн + yо , где yо – общее решение соответствующего однородного уравнения, а yн , —

частное решение данного неоднородного уравнения, которое находится с помощью метода неопределенных коэффициентов.

Метод вариации постоянных. Если y = C1 y1 +C2 y2 +K+Cn yn общее решение однородного уравнения, то общее решение неоднородного

уравнения ищут в	виде			y = C1 (x) y1 +C2 (x) y2 +K+Cn (x) yn . Функции
C1 (x),C2 (x),K,Cn (x) находят из решения системы уравнений:
C′y +C′y	2	+K+C′y	n	= 0
	1 1	2		n
C1′y1′ +C2′y2′ +K+Cn′yn′ = 0
							.
KKKKKKKKKKKKKK
	(n−2)			(n−2)	(n−2)	= 0
C1′y1	+C2′y2	+K+Cn′yn
	′ (n−1)			′ (n−1)	′ (n−1)	= f (x)
C1 y1	+C2 y2	+K+Cn yn

Метод неопределенных коэффициентов.

Укажем возможные случаи и соответствующие им виды частных решений:

Вид правой части			Вид, соответствующего частного
дифференциального уравнения	решения yн
y(n) + a y(n−1)	+ a	y(n−2) +K+ a	n−1	y‘+a	n	y = f (x)
1	2

f (x) = Pm (x) – полином от x, степени m	yн = Qm (x) ,	если 0	не	является
, где m может быть равным 0.			корнем	характеристического
							уравнения,

							yн = xk Qm (x) ,	если	0	является
							корнем	характеристического
							уравнения с кратностью k.

f (x) = Pm (x)eax , где	m может быть	yн = Qm (x)eax , если a	не	является
равным 0.		корнем		характеристического
		уравнения,

		yн = xk Qm (x)eax ,	если	a	является
		корнем		характеристического
		уравнения с кратностью k.

f (x) = (Pm (x) cosbx + Pm (x)sin bx)eax .	yн = (Qm (x) cos bx + Rm (x) sin bx)eax , если
1	2
Пусть m – наивысшая из степеней	a+bi	не	является	корнем
данных полиномов.		характеристического уравнения,

		yн = xk (Qm (x) cos bx + Rm (x) sin bx)eax ,
		если	a+bi	является	корнем
		характеристического	уравнения с
		кратностью k.

Если правая часть дифференциального уравнения, является суммой из вышеперечисленных функций, то частное решение тоже будет суммой в соответствии с каждым слагаемым.

2.1.4. Система дифференциальных уравнений

Совокупность уравнений вида

F	(x, y	, y	,K, y	, y′, y′	,K, y′) = 0
1	1	2	n	1	2	n
				′	′	′
F2 (x, y1, y2 ,K, yn , y1	, y2	,K, yn ) = 0	,

KKKKKKKKKKKKK
	(x, y1, y2		′	′	′
Fn	,K, yn , y1	, y2	,K, yn ) = 0

называется системой дифференциальных уравнений первого порядка.

Если система принимает вид

y′ = P	(x) y	+ P	(x) y	+K+ P	(x) y	+ f	(x)
	1	11	1	12	2	1n	n	1
y2′	= P21 (x) y1 + P22 (x) y2 +K+ P2n (x) yn	+ f2 (x)	,
		KKKKKKKKKKKKK

								+ fn (x)
yn′ = Pn1 (x) y1 + Pn2 (x) y2 +K+ Pnn (x) yn

то она называется линейной. Если функции f1 (x), f2 (x),K, fn (x) тождественно равны нулю, то линейная система является однородной.

Одним из способов решения системы является метод исключения неизвестных. Из уравнений последовательно исключают неизвестные функции, и система сводится к одному дифференциальному уравнению n-го порядка относительно одной неизвестной функции. (Ниже рассмотрен пример.)

2.2. Решение типовых примеров и задач.

Задание 1. Найти общее решение дифференциального уравнения

5xy′+ x2 y = 0 .

Решение. Данное уравнение можно представить в виде

5x dydx + x2 y = 0 или . 5 dyy + xdx = 0

Решаем данное уравнение с разделяющимися переменными

5∫dyy + ∫xdx = 0

Интегрируем и получаем общее решение

5 ln y + x2 = C .

Задание 2. Найти общее решение дифференциального уравнения

2x2 y′ = y2 + xy .

Решение. Разделим на x 2 правую и левую части уравнения, получим

y	2	y	.
2 y′ =			+
	x
x

Делаем подстановку y = xt , тогда y′ = t + xt′ и уравнение принимает вид:

2(t + xt ) = t

+ t

или 2xt

= t

− t .

′

Разделим переменные

2dt

t(t −1)

Решаем

∫

2dt

= ∫

или 2∫

− 2∫

= ∫

t(t −1)

t −1

Интегрируем и получаем

2 (ln

)= ln

или

t −1

t − 1

− ln

+ ln C

= C

Делаем обратную замену

1 −

= C

Если есть возможность, то выражаем

y =

1−

Задание

Найти

решение

дифференциального уравнения,

y(1)=1.

удовлетворяющее начальным условиям : 8y′−

=18x ,

Решение. Разделим на 8 правую и левую части уравнения, получим

y′−

5 y

x .

Делаем замену

y = uv , тогда y

′

и уравнение принимает вид:

= u v

+ uv

′

5 uv

′

u v

+ uv

−

x или u v + u v

−

x . (*)

24 x

Выражение в скобках приравниваем к нулю.

v′ − 245 vx = 0 .

Решаем его, разделяя переменные

dvv = 245 dxx .

Решаем

24∫dvv = 5∫dxx .

Интегрируем и получаем

24 ln v = 5ln x или v = x 24 .

Подставляем полученное в уравнение (*)

′	5		9	или u	′		9	1−	5	.
24				24
u x	+ u 0 =		x	=		x
4		4

Решаем его, разделяя переменные

				19
			du =	9	x		dx .
			24

				4
Интегрируем и получаем
				43
		u =		54		x	+ С .
			24
		43

Делаем обратную замену
	5		54		43			54		2		5
									+ Cx 24 .
y = uv = x 24		x 24 + C		=		x

			43								43

Получили

y = 54 x2 + Cx 5 .

Подставим начальные условия для того чтобы найти неопределенный коэффициент C

	54	12	5		или C =1 −	54		11	.
1 =	+ C 1	24		= −
43	43	43

Следовательно, искомое уравнение имеет вид:
								5
			y =	54	x2	−	11	x		.
			24

			43		43

Задание 4. Найти общее решение дифференциального уравнения

xy′′ + y′ = 3 .
Решение.	Введем замену	y′ = z и y′′ = z′ , исходное уравнение
принимает вид:
xz′+ z =3	или		xdz = (3 − z)dx .
Разделим переменные
			dz	=	dx	.
		(3 − z)
				x
Решаем
	∫		dz		= ∫	dx	.
	(3	− z)
					x

Интегрируем и получаем

ln	3 − z	= −(ln	x		+ ln C1 ) или z = 3 −	1	.

		C x

								1
Делаем обратную замену
			y′ = 3 −	1	.
			C x
						1

Решаем полученное дифференциальное уравнение, получаем

		y = 3x −	ln	C2 x	.

			C
				1
	Задание	5. Найти решение	дифференциального уравнения
y′′ + 4y′ + 3y =9x2	+ 24x + 6 удовлетворяющего начальным условиям y(0) = 0 ,
′	= −2 .
y (0)

Решение. Составим характеристическое уравнение, соответствующие однородному дифференциальному уравнению y′′ + 4 y′ + 3y = 0 , оно имеет вид:

k 2 + 4k + 3 = 0 .

Оно имеет корни	k1 = −1, k2 = −3 , поэтому общее	уравнение
соответствующего однородного уравнения
	yo = C1e−x + C2 e−3x .
Частное решение, соответствующее правой части дифференциального
уравнения следует искать в виде
			= Ax2 + Bx + C .
		y
Дифференцируем это	уравнение дважды и подставим	полученные

производные в исходное уравнение

2 A + 8Ax + 4B + 3Ax2 + 3Bx + 3C = 9x2 + 24x + 6 .

Приравнивая коэффициенты, стоящие при одинаковых степенях x, получаем систему равенств

	2	:	3A = 9
x
x :	8A +3B = 24 .
	0	: 2A + 4B +3C = 6
x

Получаем

A = 3,

B = 0,

C = 0 .

Следовательно,

частное

решение

исходного уравнения имеет вид

= 3x2 .

Общее

уравнение

y = yo +

= C1e−x + C2 e−3x + 3x2 .

Теперь,

используя

начальные условия, найдем неопределенные коэффициенты. Имеем

y′ = −C1e−x −3C2 e−3x + 6x ,

таким образом, получаем

y(0) = C1e−0

+ C2 e−3 0 + 3 02 = C1 + C2 = 0 ,

′

−0

−3C2 e

−3 0

+ 6 0

= — C1 −3C2 = −2 ,

y (0) = −C1e

отсюда

= −1,

=1.

Решение

дифференциального

уравнения,

удовлетворяющего начальным условиям, имеет вид

y = −e−x + e−3x + 3x2 .

Задание 6. Решить систему дифференциальных уравнений

x′

= 5x + 4 y

2x − 2 y

y′

Решение. С помощью метода замены переменных:

Выразим из первого уравнения

y =

(x′−5x)

и продифференцируем его

y′ =

(x′′−5x′) ,

подставим полученные выражения во второе уравнение системы

(x′−5x) ,

(x′′−5x′) = 2x − 2

приводим подобные, помножив на 4

′′

′

−18x = 0 ,

x −3x

Таким образом, получили линейное однородное уравнение с постоянными коэффициентами, решаем его. Составим характеристическое

уравнение, соответствующие однородному дифференциальному уравнению x′′−3x′−18x = 0 , оно имеет вид:

k 2 −3k −18 = 0 .

Оно имеет корни

k1 = −3, k2

= 6 ,

поэтому общее уравнение

соответствующего однородного уравнения

x = C1e−3x +C2e6 x .

Подставим полученный x в y, выраженный из первого уравнения

−3x

6 x ′

−3x

6 x

)) ,

y =

((C1e

+C2e

) −5(C1e

+C2e

Делаем преобразования и получаем

y = −2C1e−3 x +

C2e6 x .

Общее решение системы принимает вид

x = C1e

−3x

+C2e

6 x

6 x .

y = −2C e

−3x

Решаем систему через характеристическое уравнение:

Ищем частное решение системы в виде

x = p 1 e kx , y = p 2 e kx

возьмем производные от функций и подставим в исходную систему

kp1e

= 5 p1e

4 p2 e

ekx

= 2 p ekx

− 2 p

ekx

сократим все на ekx

(5 − k) p1 + 4 p2

= 0

2 p1

− (2 + k) p2 = 0

Составляем характеристическое уравнение, соответствующее данной системе

5 − k	4	= 0 ,

2 − 2 − k

или k 2 − 3k −18 = 0 , его корни k1 = −3, k2 = 6 вещественны и различны.

При k1 = −3 система принимает вид

8 p	+ 4 p		= 0	.
1		2	= 0
2 p1 + p2

Пусть p1 = C1 , тогда p2 = −2C1 и искомое частное решение

x1 = C1e−3x , y1 = −2C1e−3x .

При k1 = 6 система принимает вид

— p	+ 4 p		= 0	.
1		2	= 0
2 p1 −8 p2

Пусть p1 = 4C2 , тогда p2 = C2 и искомое частное решение

x2 = 4C2 e6 x , y2 = C2 e6 x .

Общее решение системы принимает вид

x = C1e−3x + 4C2 e6 x
y = −2C e−3x + C	2	e6 x .
	1

Задача 7. Найти кривую, проходящую через точку (2;1), если угловой коэффициент касательной к ней в любой ее точке вдвое больше абциссы точки касания.

Решение. Угловой коэффициент касательной равен производной функции, задающую искомую кривую. Получаем уравнение

y′ = 2x .

Ищем решение этого дифференциального уравнения. y = x2 + C .

Найдем неопределенный коэффициент: y(2) =1 . Получаем

22 + C =1,

C = −3 .

Искомая кривая имеет вид y = x2 −3 .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Площадь треугольника через синус

Определение

Площадь треугольника через синус — это площадь треугольника,
выраженная через две любые стороны треугольника и синус угла между ними.

Синус угла — это число, которое используется для нахождения
разных величин в треугольниках, его можно найти в специальных таблицах.

Введение

Площадь треугольника кроме половины произведения высоты
на основания, можно также найти и другим способом.
Мало кто знает, но через синусы углов можно найти обычно
не только стороны, но и площадь любого треугольника!

Площадь треугольника выраженная без синуса численно равна
половине произведения двух сторон друг на друга
на синус угла между ними.

Площадь треугольника через синус ищется только в том случае,
если по другой формуле площадь треугольника найти нельзя.

Теорема

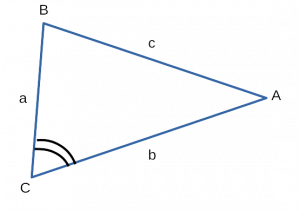
( S = frac<1>2 * BC * AC * sin angle BCA )

Площадь произвольного треугольника равна полусумме
произведения двух любых сторон треугольника друг на друга,
и на синус угла между этими сторонами.

Формула

[ S = frac<1>2 * a * b * sin α ]

Где a, b — две стороны треугольника, синус α — синус угла α.

Пример

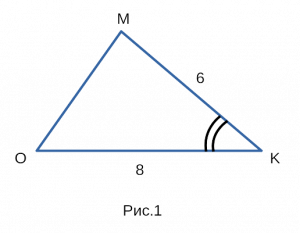
Для примера, возьмем треугольник omk, изображенный на рисунке 1, со сторонами om, mk, ok.
Известно, что mk равен 6, ok равен 8, синус угла okm равен 1/4.

Нужно найти площадь треугольника omk.

Дано: △omk, mk = 6, ok = 8, sin okm = 1/4.

Найти: S △omk — ?

Решение:

1) ( S = frac<1>2*a*b*sin α ) ( implies ) ( S = frac<1>2*mk*ok*sin okm )

2) S = 1/2 * 6 * 8 * 1/4 = 1/2 * 6 * 8 * 0.25 = 1/2 * 48 * 0.25 = 1/2 * 12 = 6

Ответ: Площадь треугольника omk равна 6.

Доказательство

Докажем, что площадь произвольного треугольника
равна полусумме произведения двух любых сторон
друг на друга, и на синус угла между этими сторонами.

Чтобы вам наглядно было видно, как мы доказываем,
используем один из известнейших треугольников — египетский треугольник.
Высота в египетском треугольнике равна длине одного из катетов.
Построим прямоугольный треугольник, изображенный на рисунке 2,
со сторонами 3,4,5 с одним из углов 90 градусов.

Первым делом найдем площадь обычной формулой,
затем с помощью синуса. Площадь равна половине
основания на высоту — ½3*4 = 6. Теперь найдем с
помощью синуса: ½3*4*sin90 = 6 * 1 = 6. Как видим,
полученные значения площадей сходятся, соответственно
через синус можно найти площадь треугольника ч.т.д.

Теперь, чтобы найти площадь треугольника нам не нужно
знать основание и высоту, можно знать только
две стороны и синус угла между ними.

Заключение

В заключение, можно сказать, что площадь
треугольника можно найти разными способами.
Например, в прямоугольном треугольнике площадь
рассчитать легче чем в любом другом треугольнике,
так как высота уже известна. Именно поэтому,
в школьном курсе, отчасти так подробно изучаются
прямоугольные треугольники. В Древнем Египте были
распространены прямоугольные треугольники со
сторонами 3,4,5; 6,8,10; 5,12,13. Длины этих прямоугольных
треугольников треугольников целые, что значительно,
упрощало разного рода вычисления.

Формулу площади треугольника делает универсальной то,
что она может применена к абсолютно любым треугольникам.
Главное, чтобы были известные две стороны,
и угол или синус угла между ними.

Формула площади треугольника через синус — универсальна,
поэтому может быть применена к любым видам треугольников.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

sin120° = sin(180° — 60°) = sin60° = 3/√2;
sin150° = sin(180° — 30°) = sin30° = 1/2;
sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

источники:

http://www-formula.ru/2011-10-09-11-08-41

http://skysmart.ru/articles/mathematic/teorema-sinusov

Источник