Как найти объем сложной фигуры 5 класс

План урока:

Вычисление объема тела с помощью интеграла

Вычисление объема тел вращения

Объем наклонной призмы

Объем пирамиды

Объем конуса

Объем шара

Шаровой сегмент

Площадь сферы

Вычисление объема тела с помощью интеграла

Пусть у нас есть произвольная фигура, расположенная между двумя параллельными плоскостями:

Как найти ее объем? Поступим следующим образом. Проведем прямую, перпендикулярную этим плоскостям. Эта прямая будет осью координат х. Пусть одна из плоскостей пересекает эту ось в точке а, а другая – в точке b. Таким образом, на координатной прямой появляется отрезок [a; b]. Далее разобьем этот отрезок на n равных отрезков, длина каждого из них будет равна величина ∆х. Обозначим концы этих отрезков как х₀, х₁, х₂…, х_n, причем точке х₀ будет совпадать с точкой а, а точка х_n – с точкой b. Ниже показано такое построение для n = 10:

Далее через полученные точки проведем сечения, параллельные двум плоскостям, ограничивающим фигуру. Площадь сечения, проходящую через точку с номером i, обозначим как S(x_i). Эти плоскости рассекут тело на n других тел. Обозначим объем тела, заключенного между сечениями с площадями S(x_i) и S(x_i+1) как V(x_i). Можно приближенно считать, что эти тела имеют форму прямых цилиндров (напомним, что в общем случае цилиндром необязательно считается фигура, основанием которой является круг, основание может иметь и любую другую форму). Высота всех этих цилиндров будет равна величине ∆х. Тогда объем V(x_i) может быть приближенно рассчитан так:

Общий же объем исследуемой фигуры будет суммой объемов этих прямых цилиндров:

Здесь знак ∑ означает сумму i слагаемых, каждое из которых равно величине S(x_i)•∆х. Ясно, что чем больше мы возьмем число n, тем точнее будет полученная нами формула. Поэтому будет увеличивать число n до бесконечности, тогда приближенная формула станет точной:

В правой части стоит предел суммы бесконечного числа слагаемых. Мы уже сталкивались с такими пределами, когда изучали определенный интеграл в курсе алгебры. Так как х₀ = a, а число х_n-1 при бесконечном увеличении n приближается к числу х_n, то есть к b, то можно записать следующее:

Здесь S(x) – это некоторая функция, которая устанавливает зависимость между площадью сечения объемной фигуры и координатой х, указывающей расположение этого сечения. Данная формула позволяет вычислять объем с помощью интеграла.

Итак, для вычисления объема тела необходимо:

1) выбрать в пространстве какую-то удобную ось координат Ох;

2) найти площадь произвольного сечения фигуры, проходящей перпендикулярно оси Ох через некоторую координату х;

3) найти значение чисел а и b – координат сечений, ограничивающих тело в пространстве;

4) выполнить интегрирование.

Понятно, что сразу понять, как используется эта формула, тяжело. Поэтому рассмотрим простой пример.

Задание. Фигура расположена в пространстве между двумя плоскостями, перпендикулярными оси Ох, причем координаты этих сечений равны 1 и 2. Каждое сечение фигуры с координатой х является квадратом, причем его сторона равна величине 1/х. Найдите объем тела.

Решение. В данной задаче ось Ох уже проведена. Известны и числа а и b – это 1 и 2, ведь именно плоскости, проходящие через точки х =1 и х = 2, ограничивают исследуемое тело. Теперь найдем площадь произвольного сечения с координатой х. Так как оно является квадратом со стороной 1/х, то его площадь будет квадратом этой стороны:

Вычисление объема тел вращения

Телом вращения называют тело, которое может быть получено вращением какой-то плоской фигуры относительно некоторой оси вращения. Например, цилиндр получают вращением прямоугольника вокруг одной из его сторон, а усеченный конус – вращением прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

В задачах на вычисление объемов таких тел ось координат Ох уже задана естественным образом – это ось вращения тела. Ясно, что каждое сечение тела, перпендикулярное оси вращения, будет являться кругом.

Рассмотрим случай, когда вокруг оси Ох поворачивают график некоторой функции у = f(x), ограниченный прямыми х = а и у = b. Тогда получится тело, сечениями которого являются круги, причем их радиусы будут равны величине f(x). Напомним, что площадь круга вычисляют по формуле:

Рассмотрим, как на практике используется эта формула.

Задание. Объемное тело получено вращением ветви параболы

вокруг оси Ох. Оно ограничено плоскостями х = 0 и х = 4. Каков объем такой фигуры?

Решение. Здесь пределами интегрирования, то есть числами а и b, будут 0 и 4. Используем формулу для тела вращения:

Объем наклонной призмы

Теперь, используя методы интегрирования, мы можем составить формулы для вычисления объема некоторых фигур. Начнем с треугольной наклонной призмы.

Пусть есть треугольная призма АВСА₂В₂С₂. Проведем ось Ох так, чтобы точка О располагалась в плоскости АВС. Пусть Ох пересечет плоскость А₂В₂С₂ в некоторой точке О₂. Тогда отрезок ОО₂ будет высотой призмы, ведь он окажется перпендикулярным к обоим основаниям.

Обозначим длину высоты ОО₂ буквой h. Далее докажем, что всякое сечение А₁В₁С₁ призмы, перпендикулярное оси Ох, будет равно ∆АВС. Действительно, если АВС⊥ОО₂ и А₁В₁С₁⊥ОО₂, то АВС||А₁В₁С₁. Прямые АВ и А₁В₁ принадлежат одной грани АВВ₂А₁, но не пересекаются, ведь они находятся в параллельных плоскостях. Аналогично АС||А₁С₁ и ВС||В₁С₁. Теперь посмотрим на четырехугольник АВВ₁А₁. АВ||A₁В₁ и АА₁||ВВ₁. Тогда АВВ₁А₁ по определению является параллелограммом. Это означает, что отрезки АВ и А₁В₁ одинаковы. Аналогично доказывается, что одинаковы отрезки АС и А₁С₁, а также ВС и В₁С₁. Но тогда одинаковы и ∆АВС и ∆А₁В₁С₁.

Итак, площади всех сечений одинаковы и равны площади основания призмы. Обозначим ее как S. Так как S не зависит от координаты, то интегрирование будет выглядеть так:

Итак, объем треугольной наклонной призмы – это произведение площади ее основания на высоту. Теперь рассмотрим произвольную призму, в чьем основании находится n-угольник. Такой n-угольник можно разбить на треугольные призмы с общей высотой h и площадями оснований S₁, S₂, S₃, …

Тогда площадь S основания всей призмы будет суммой этих чисел:

Задание. Основание призмы – это треугольник со сторонами 10, 10 и 12. Боковое ребро имеет длину 8 и образует с основанием угол в 60°. Вычислите объем призмы.

Решение. Пусть в основании призмы АВСА₁В₁С₁ лежит ∆АВС со сторонами АВ = 12 и АС = ВС = 10. Его площадь можно найти разными способами, но быстрее всего применить формулу Герона. Сначала найдем полупериметр ∆АВС:

Далее надо найти высоту призмы. Опустим из точки В₁ перпендикуляр В₁О на плоскость АВС. Тогда в прямоугольном ∆ОВВ₁ ∠В = 60° (по условию задачи и по определению угла между плоскостью и прямой). Зная длину бокового ребра ВВ₁, найдем высоту ОВ₁:

Объем пирамиды

Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.

Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.

Далее построим сечение А₁В₁С₁, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ₁. Тогда ОМ₁ – это координата х, характеризующая расположение сечения А₁В₁С₁.

Осталось составить выражение для площади ∆А₁В₁С₁. Так как АВ||A₁B₁, то ∠АВО и ∠А₁В₁О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А₁В₁О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что

Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ₁В₁. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому

Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:

Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S₁, S₂, S₃…, которые в сумме составляют площадь многоугольника S.

Объем треугольных пирамид рассчитывается по выведенной нами формуле:

Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.

Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:

Задание. В кубе АВСDA₁В₁С₁D₁ отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С₁EFC меньше объема куба?

Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:

Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?

Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.

Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.

Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А₁В₁С₁, параллельное основанию.

Обозначим площадь нижнего основания пирамиды как S₂, а площадь верхнего основания – как S₁. Далее высоту усеченной пирамиды (отрезок ММ₁) обозначим как h. Мы уже выяснили ранее, что основания АВС и А₁В₁С₁ – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ₁. Тогда можно записать:

Далее используем основное свойство пропорции:

Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:

Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.

Сначала вычислим площади оснований:

Объем конуса

Рассмотрим конус с высотой h и радиусом основания R. Совместим начало координат с вершиной конуса и направим ось Ох в сторону основания конуса. Тогда она пересечет основание в какой-то точке М c координатой h. Далее через точку М₁ на оси Ох, имеющей координату х, проведем сечение, перпендикулярное оси Ох. Это сечение будет окружностью.

Также построим образующую ОА, которая будет проходить через сечение в точке А₁. Теперь сравним ∆ОАМ и ∆ОА₁М₁. Они прямоугольные, и у них есть общий угол ∠АОМ. Это значит, что они подобны, и поэтому справедливо отношение:

Полученную формулу можно переписать в другом виде так, чтобы она содержала площадь основания, причем она будет похожа на аналогичную формулу для пирамиды:

Задание. Радиус конуса – 8 см, а его высота составляет 12 см. Определите его объем.

Решение. Здесь надо просто применить выведенную формулу:

Задание. В сосуде, имеющем форму перевернутого конуса, вода доходит до уровня, соответствующего 2/3 высоты сосуда. При этом ее объем составляет 192 мл. Каков объем всего сосуда?

Решение. В задаче фигурируют два конуса. Один из них – это сам сосуд, а второй – его часть, заполненная водой. При выведении формулы объема мы уже выяснили, что радиусы таких конусов пропорциональны их высотам:

Мы уже заметили, что формулы для объема пирамида и конуса идентичны. По сути, конус можно рассматривать как особый случай пирамиды, у которой в основании лежит не многоугольник, а окружность. Аналогично и усеченный конус можно считать особым случаем усеченной пирамиды, а поэтому для расчета его объема можно применять такую же формулу:

Задание. Вычислите объем усеченного конуса с высотой 9 и радиусами оснований 7 и 4.

Решение. Сначала находим площади оснований:

Объем шара

Пришло время разобраться и с таким телом, как шар. Здесь можно использовать тот же метод интегрирования, что и в случае с конусом и пирамидой. Но можно поступить и иначе – использовать выведенную нами для тел вращения формулу

Шар как раз является телом вращения. Он получается при вращении полуокружности вокруг диаметра, на который эта дуга опирается.

Напомним известное нам уравнение окружности, чей центр совпадает с началом координат:

Здесь надо уточнить, что если у получившейся функции впереди записан знак «+», то ее график соответствует полуокружности, находящейся над осью Ох. Если же используется знак «–», то получается уже нижняя полуокружность, расположенная под осью Ох:

В принципе мы можем поворачивать любую из этих полуокружностей вокруг Ох, но мы выберем верхнюю полуокружность. Заметим, что эта дуга начинается в точке х = – R и заканчивается в точке х = R, эти числа будут пределами интегрирования. Тогда объем шара равен:

Задание. Найдите объем шара с радиусом 6.

Решение. Подставляем радиус из условия в формулу:

Задание. В цилиндр вписан шар. Во сколько раз объем цилиндра больше объема такого шара?

Решение. Ясно, что так как шар вписан в цилиндр, то радиусы этих тел одинаковы. Обозначим этот радиус как R. Также ясно, что раз шар касается оснований цилиндра, то расстояние между ними (то есть высота цилиндра) равно двум радиусам шара:

Шаровой сегмент

Когда плоскость проходит через шар, она рассекает его на две фигуры, которые именуются шаровым сегментом. Если из центра шара О провести радиус ОА длиной R в направлении плоскости сечения, который перпендикулярен этой плоскости, то он пересечет ее какой-то точке В. Длину отрезка АВ называют высотой шарового сегмента и обозначают буквой h:

Ясно, что при этом отрезок ОВ – это расстояние от секущей плоскости (или от основания сегмента) до центра шара, причем этот отрезок имеет длину R –h.

Можно считать, что шаровой сегмент, как и шар, получается при вращении дуги окружности вокруг оси Ох. Однако если сам шар при этом ограничен плоскостями x = R и х = – R, то сегмент ограничен другими плоскостями: х = R и х = R – h. Это значит, что его объем можно вычислить с помощью интеграла также, как и объем шара, отличаться будет лишь нижний предел интегрирования:

Заметим, что шар можно рассматривать как шаровой сегмент, чья высота вдвое больше его радиуса. И действительно, если в выведенную формулу мы подставим значение h = 2R, то получим уже известную нам формулу объема шара.

Задание. Найдите объем шарового сегмента высотой 6, если он отсечен от шара радиусом 15.

Решение. Используем выведенную формулу:

Задание. Диаметр шара разделили на три равных отрезка. Через концы этих отрезков провели секущие плоскости, перпендикулярные диаметру. Чему равен объем тела, заключенного между этими двумя плоскостями (оно называется шаровым слоем), если радиус шара обозначен буквой R?

Решение. Ясно, что для вычисления объема шарового слоя достаточно вычесть из объема шара объемы двух шаровых сегментов, образующихся при проведении секущих плоскостей. Так как они разделили диаметр на три одинаковых отрезка, то высота этих сегментов будет в три раза меньше диаметра шара:

Площадь сферы

В предыдущих уроках мы уже узнали формулу для вычисления площади сферы, однако тогда мы ее не доказывали. Однако теперь мы можем ее доказать, используя формулу объема шара. Но сначала напомним саму формулу:

Впишем сферу в многогранник с n гранями. Ясно, что расстояние от граней этого многогранника до центра сферы равно радиусы сферы R. Далее построим пирамиды, чьи вершины находятся в центре сферы, а основания – это грани многогранника. Заметим, что такие пирамиды будут иметь одинаковые высоты длиной R.

Обозначим площади граней многогранника как S₁, S₂, S₃,…S_n. Тогда объемы пирамид, построенных на этих гранях, вычисляются так:

Заметим, что в сумме эти объемы дают объем всего многогранника, а сумма площадей S₁, S₂, S₃,…S_n – это площадь всей его поверхности. Тогда можно записать:

Теперь начнем неограниченно уменьшать размеры граней многогранника. Тогда число n будет расти, объем многогранника будет приближаться к объему шара, а площадь многогранника – к площади к сфере. Тогда и доказанное равенство можно будет записать так:

Задание. Необходимо изготовить закрытый сосуд с заранее заданным объемом V. Предлагается два варианта формы этого сосуда – шар и куб. Так как поверхность сосуда покрывается очень дорогой краской, то необходимо выбрать вариант с меньшей площадью поверхности. Какую форму для сосуда следует выбрать?

Решение. Обозначим радиус шара как R, а ребро куба как а. Тогда можно записать:

Теперь надо выяснить, какое из полученных значений больше. Для этого поделим площадь куба на площадь сферы. Если получится число, большее единицы, то площадь куба больше:

Получившееся число больше единицы, ведь 6 больше числа π, равного 3,1415926… Значит, и площадь куба больше, а потому необходимо выбрать сосуд, имеющий форму шара.

Ответ: шар.

Примечание. Более сложными математическими методами можно доказать, что если второй сосуд имеет не форму куба, а вообще любую форму, отличную от шара, то всё равно следует выбирать именно сосуд в форме шара. То есть из всех поверхностей, ограничивающих определенный объем, именно сфера имеет наименьшую площадь. Этот факт имеет и физическое следствие – капли дождя и мыльные пузыри стремятся принять форму шара, также как и любые жидкости, находящиеся в невесомости.

Итак, мы научились вычислять объемы таких тел, как конус, пирамида, шар, призма. Также помощью интегрирования можно находить объемы и ещё более сложных тел, если мы можем составить функцию, описывающую площадь их сечения.

В каждом конкретном случае используют разные методы. Все зависит от того, что нам известно (какие входные данные) и какая точность нам нужна.

Если возможно, то разбивают фигуру на более простые тела, объем которых можно посчитать: параллелепипед, цилиндр, эллипсоид и т.п. Объемы простых фигур складывают.

Если известна функция, которая описывает ограничивающую поверхность, то считают тройной интеграл.

Если аналитические методы не подходят или очень сложные, то можно изготовить такое тело, например, из гипса и бросить в воду. Объем вытесненной воды будет равен объему тела.

Есть и косвенные методы измерения.

Если известна масса тела и материал, из которого оно сделано, то можно вычислить объем по плотности материала.

Это не полный список методов. Наверняка, можно найти другие.

ОБЪЕМ ФИГУР В ПРОСТРАНСТВЕ

Объем – величина, аналогичная площади и сопоставляющая фигурам в пространстве неотрицательные действительные числа. За единицу объема принимается куб, ребро которого равно единице измерения длины.

Для объемов пространственных фигур справедливы свойства, аналогичные свойствам площадей плоских фигур, а именно:

1. Объем фигуры в пространстве является неотрицательным числом.

2. Равные фигуры имеют равные объемы.

3. Если фигура Ф составлена из двух неперекрывающихся фигур Ф 1 и Ф 2 , то объем фигуры Ф равен сумме объемов фигур Ф 1 и Ф 2 , т.е.

V ( Ф )= V ( Ф 1 )+ V ( Ф 2 ).

Две фигуры, имеющие равные объемы, называются равновеликими.

В режиме слайдов ответы и решения появляются после кликанья мышкой

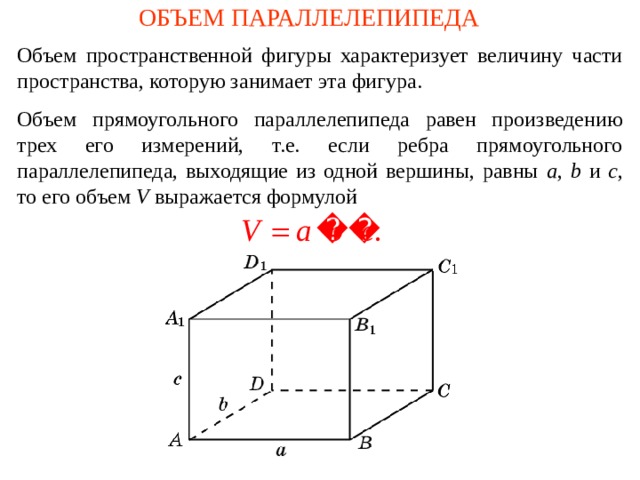
ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА

Объем пространственной фигуры характеризует величину части пространства, которую занимает эта фигура.

О бъем прямоугольного параллелепипеда равен произведению трех его измерений, т.е. если ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны a , b и c , то его объем V выражается формулой

В режиме слайдов формулировки появляются после кликанья мышкой

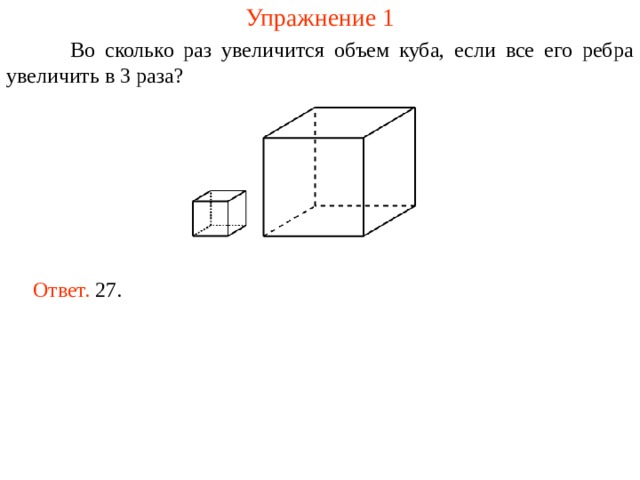
Упражнение 1

Во сколько раз увеличится объем куба, если все его ребра увеличить в 3 раза?

Ответ. 27.

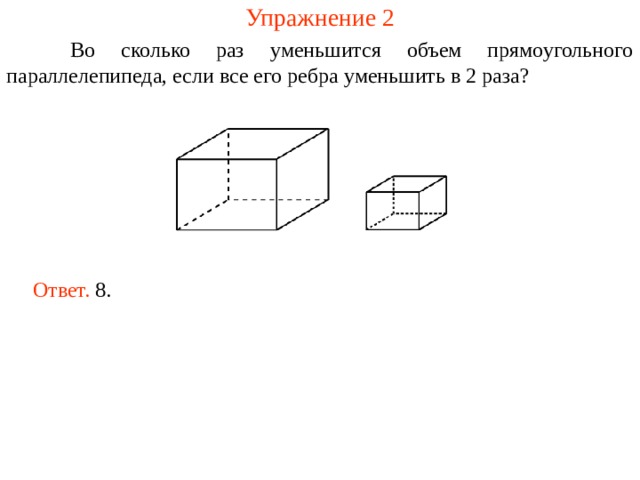
Упражнение 2

Во сколько раз уменьшится объем прямоугольного параллелепипеда, если все его ребра уменьшить в 2 раза?

Ответ. 8.

Упражнение 3

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 3. Каким должно быть третье ребро, выходящее из той же вершины, чтобы объем этого параллелепипеда равнялся 30?

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 5.

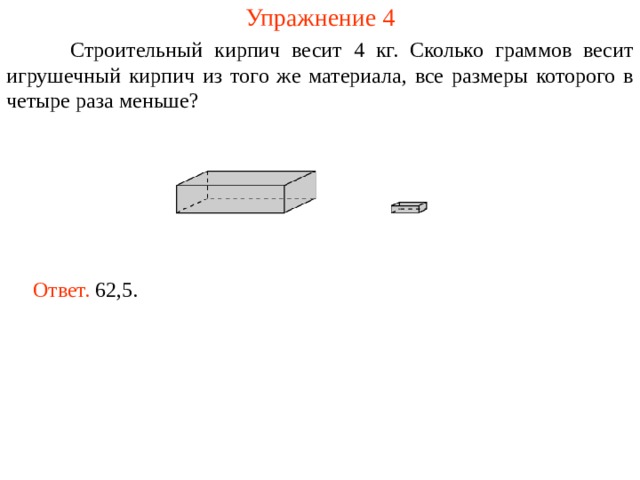
Упражнение 4

Строительный кирпич весит 4 кг. Сколько граммов весит игрушечный кирпич из того же материала, все размеры которого в четыре раза меньше?

Ответ. 62,5.

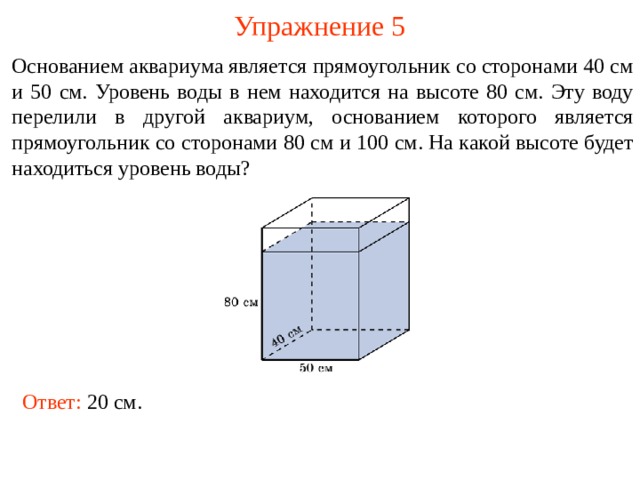
Упражнение 5

Основанием аквариума является прямоугольник со сторонами 40 см и 50 см. Уровень воды в нем находится на высоте 80 см. Эту воду перелили в другой аквариум, основанием которого является прямоугольник со сторонами 80 см и 100 см. На какой высоте будет находиться уровень воды?

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 20 см .

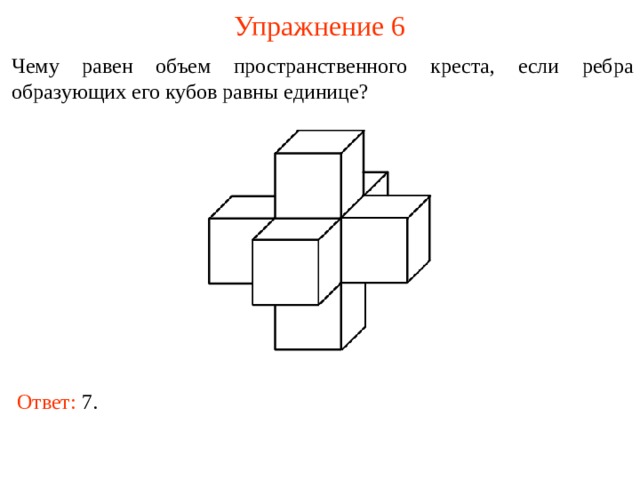
Упражнение 6

Чему равен объем пространственного креста, если ребра образующих его кубов равны единице?

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 7 .

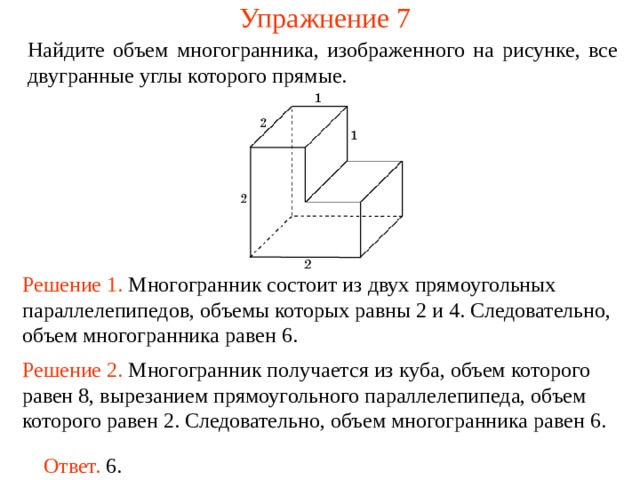
Упражнение 7

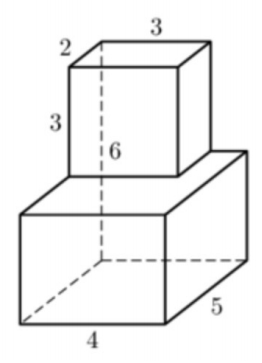
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .

Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .

Ответ. 6.

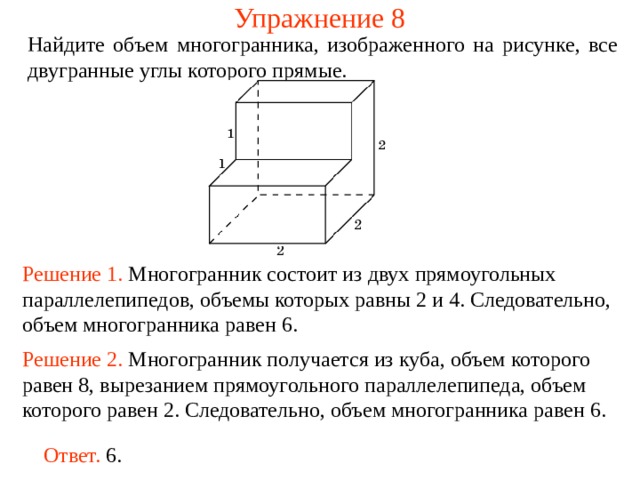
Упражнение 8

Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .

Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .

Ответ. 6.

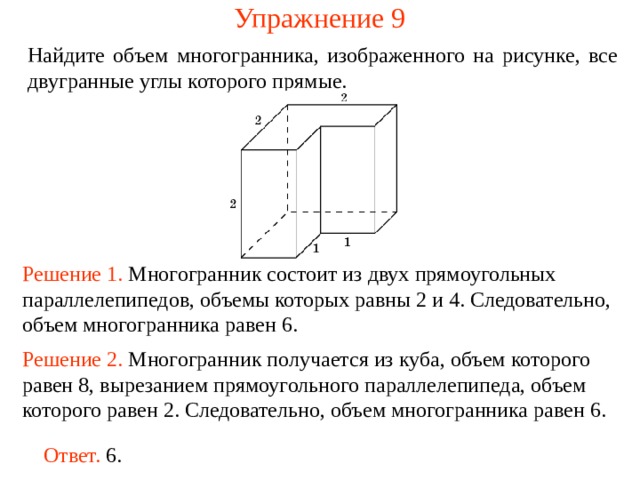
Упражнение 9

Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .

Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .

Ответ. 6.

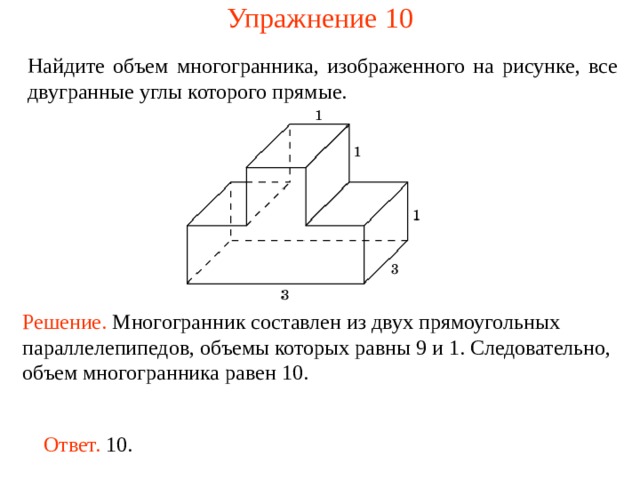
Упражнение 1 0

Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение. М ногогранник составлен из двух прямоугольных параллелепипедов, объемы которых равны 9 и 1. Следовательно, объем многогранника рав ен 10 .

Ответ. 10.

Упражнение 1 1

Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение. М ногогранник получается из куба, объем которого равен 8, вырезанием куба, объем которого равен 1. Следовательно, объем многогранника рав ен 7 .

Ответ. 7.

Упражнение 1 2

Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение. М ногогранник получается из прямоугольного параллелепипеда, объем которого равен 48, вырезанием прямоугольного параллелепипеда, объем которого равен 8. Следовательно, объем многогранника рав ен 40 .

Ответ. 48.

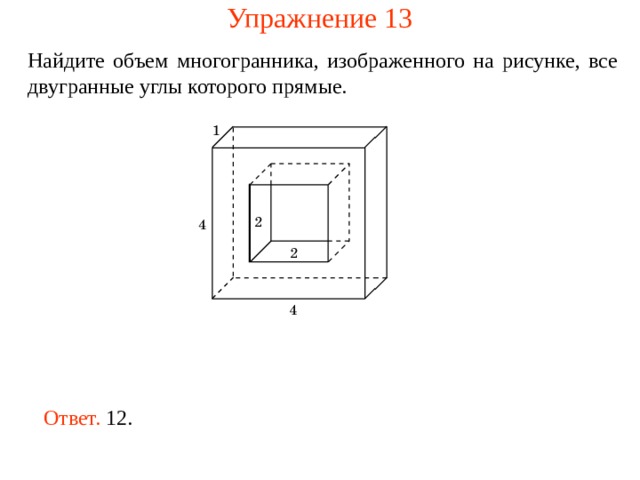
Упражнение 13

Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Ответ. 12.

Упражнение 14

Найдите объем детали, изображенной на рисунке (все углы – прямые).

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 1 0 см 3 .

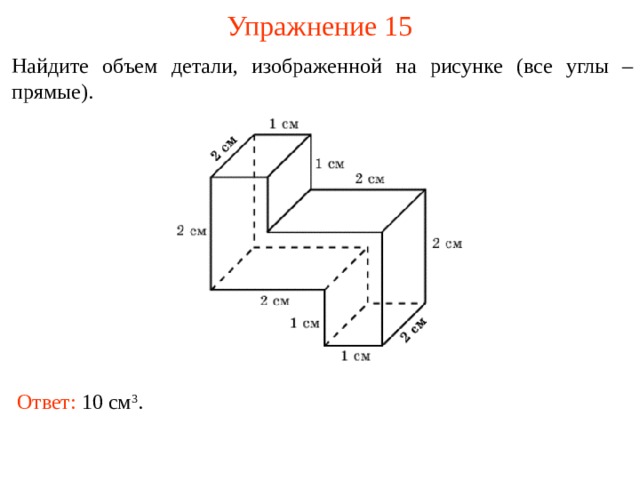
Упражнение 15

Найдите объем детали, изображенной на рисунке (все углы – прямые).

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 1 0 см 3 .

Упражнение 16

Найдите объем детали, изображенной на рисунке (все углы – прямые).

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 5 см 3 .

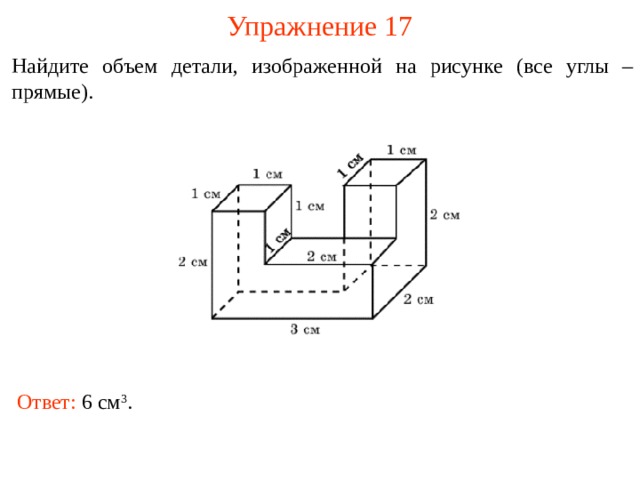
Упражнение 17

Найдите объем детали, изображенной на рисунке (все углы – прямые).

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 6 см 3 .

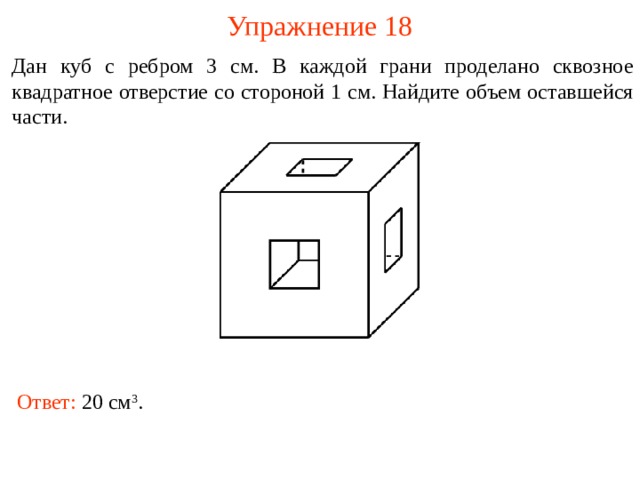
Упражнение 18

Дан куб с ребром 3 см. В каждой грани проделано сквозное квадратное отверстие со стороной 1 см. Найдите объем оставшейся части.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 20 см 3 .

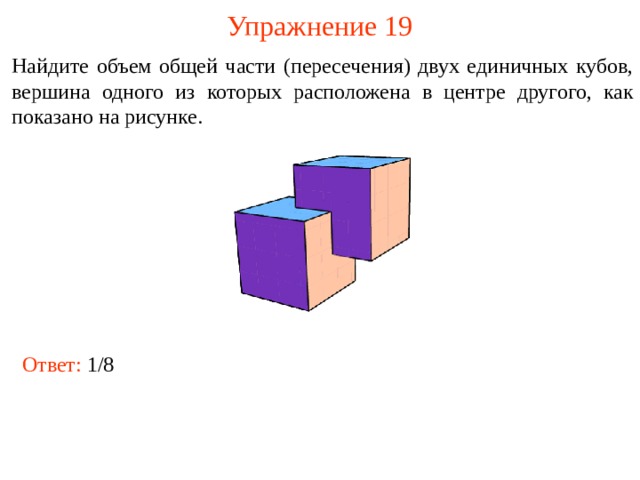
Упражнение 19

Найдите объем общей части (пересечения) двух единичных кубов, вершина одного из которых расположена в центре другого, как показано на рисунке.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 1/8

Упражнение 20

Найдите объем фигуры, составленной из двух единичных кубов, две вершины одного из которых расположены в центрах граней другого.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 1,75.

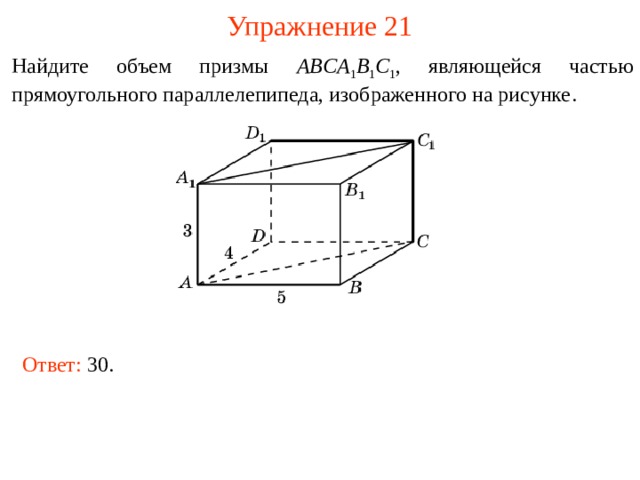
Упражнение 21

Найдите объем п ризмы ABCA 1 B 1 C 1 , являющейся частью прямоугольного параллелепипеда, изображенного на рисунке .

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 30 .

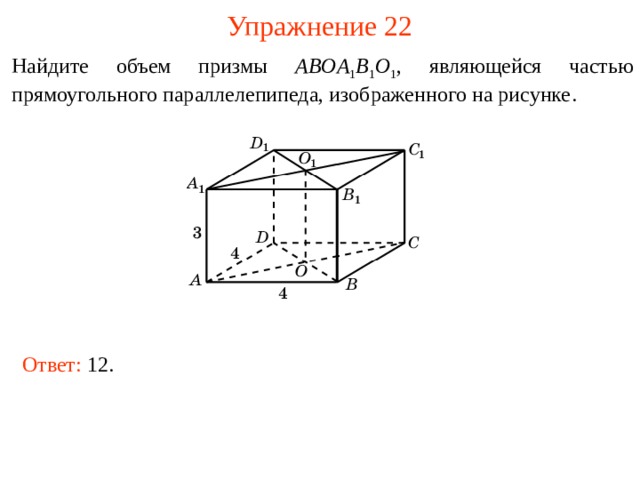
Упражнение 22

Найдите объем п ризмы ABOA 1 B 1 O 1 , являющейся частью прямоугольного параллелепипеда, изображенного на рисунке .

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 12.

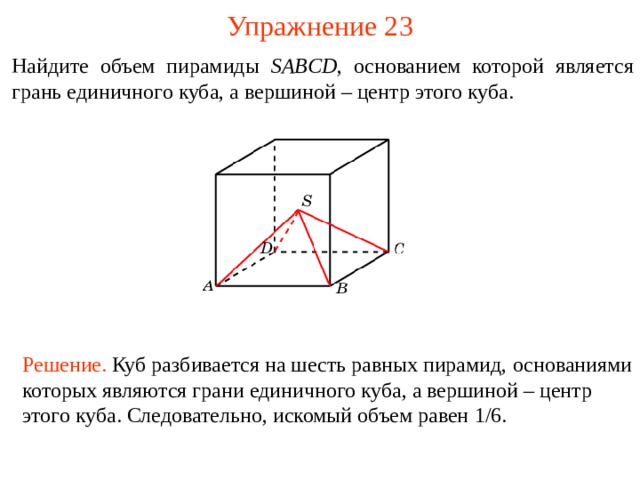
Упражнение 2 3

Найдите объем пирамиды SABCD , основанием которой является грань единичного куба, а вершиной – центр этого куба.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Решение. Куб разбивается на шесть равных пирамид, основани ями котор ых явля ю тся гран и единичного куба, а вершиной – центр этого куба . Следовательно, искомый объем равен 1/6.

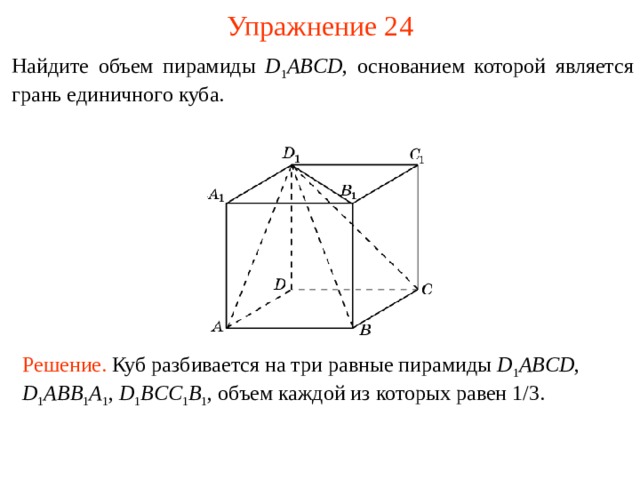
Упражнение 2 4

Найдите объем пирамиды D 1 ABCD , основанием которой является грань единичного куба.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Решение. Куб разбивается на три равные пирамиды D 1 ABCD , D 1 ABB 1 A 1 , D 1 BCC 1 B 1 , объем каждой из которых равен 1 /3.

26

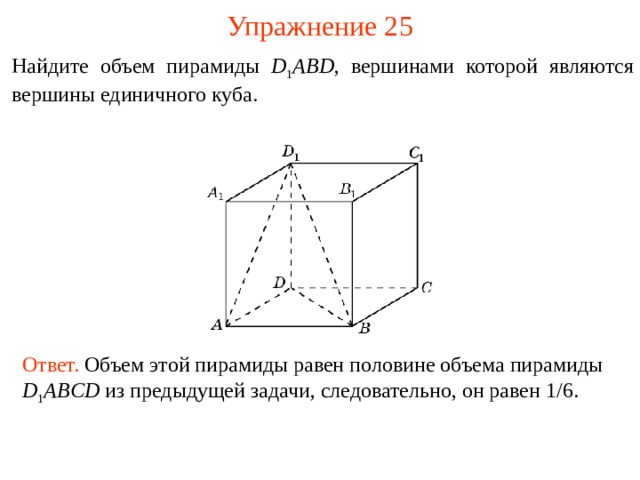
Упражнение 2 5

Найдите объем пирамиды D 1 ABD , вершинами которой явля ю тся вершины единичного куба.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ. Объем этой пирамиды равен половине объема пирамиды D 1 ABCD из предыдущей задачи, следовательно, он равен 1 / 6 .

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

01 апреля 2019

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

• V сохраняется при движениях.
• V удовлетворяет принципу Кавальери.
• Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
• Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

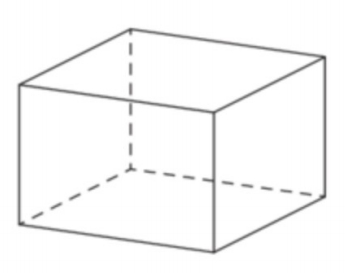
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

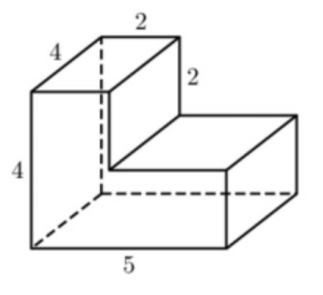
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Разберем, как можно вычислять объемы изучаемых в школе фигур.

Объем призмы

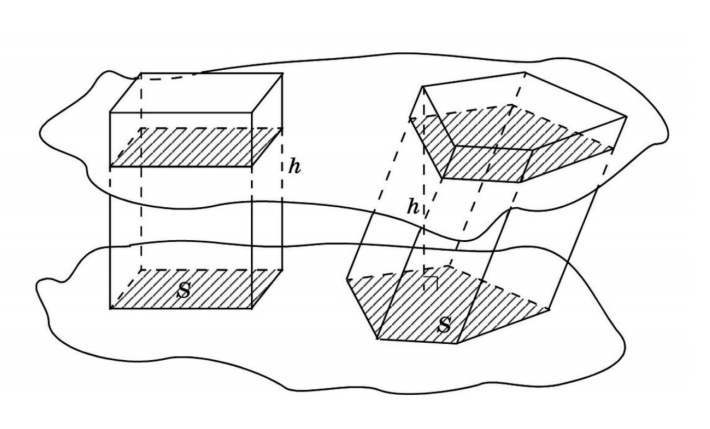
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

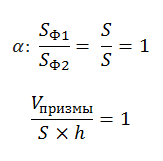
V S_осн h

Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

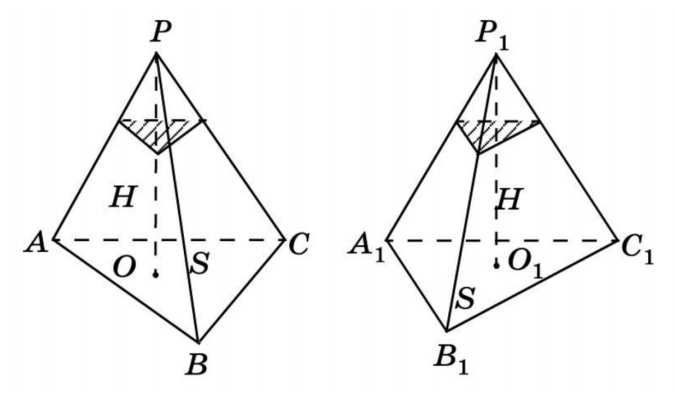
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V ₁/V₂ = 1 <=> V₁ = V₂

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

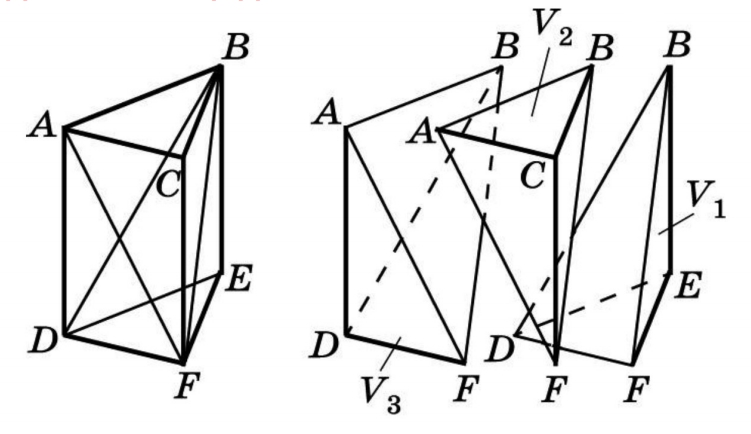
V₁ = V₂

V₂ = V₃

V_призмы S h = 3V

V = 1/3 Sh

Объем цилиндра

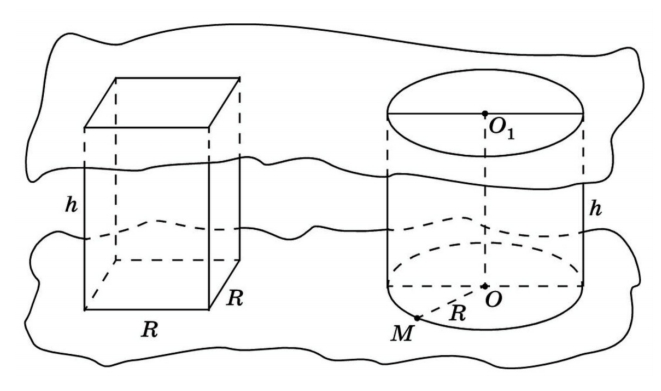
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

V_цил = πh × R²

Объем конуса

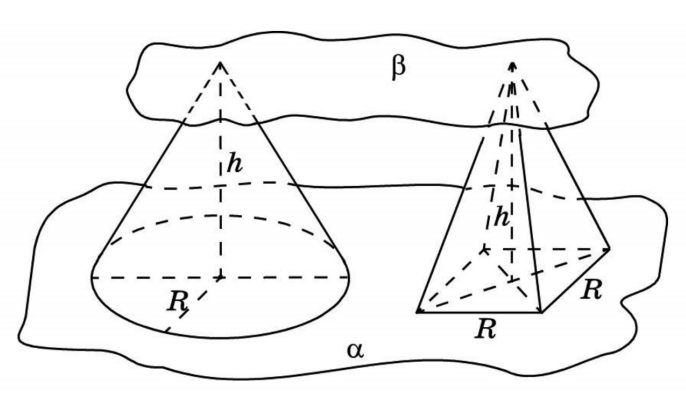
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

S_Ф1/S_Ф2 = π

V_конуса = 1/3 πR² h

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте
«Математические этюды», где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR². Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x². Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R² — x²).

Заметим, что: πR² + πR² — πR² = πR²

V_цил = πR² × R = πR³ = 1/3 R³ π + V_шара

V_шара = 4/3 πR³

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

#ADVERTISING_INSERT#

2 ответа:

Читайте также