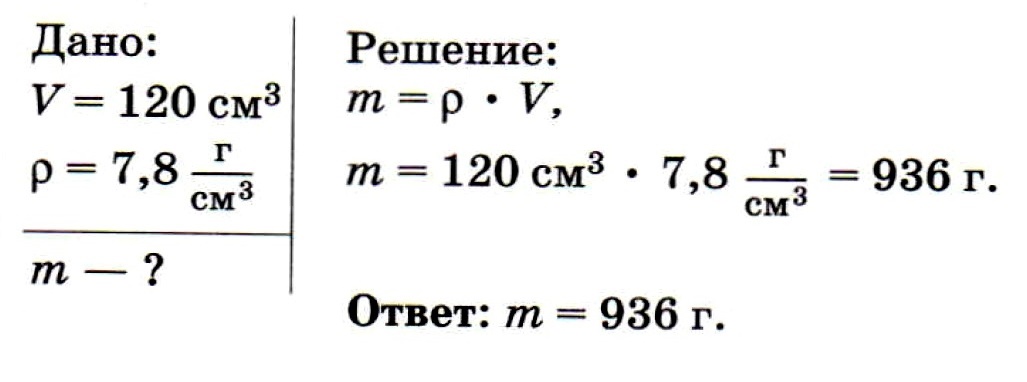Как найти объем тела бруска

Лабораторная работа «Измерение объема твердого тела»

Категория: Физика.

Лабораторная работа «Измерение объема твердого тела»

Цель – научиться определять объем твердого тела с помощью линейки и измерительного цилиндра (мензурки).

Приборы и материалы: измерительный цилиндр (мензурка), стакан с водой, брусок, линейка, фарфоровый ролик, нитки.

Ход работы:

I. Определение объема бруска при помощи линейки.

Измерьте при помощи линейки длину, ширину и высоту бруска, запишите результаты измерений:

длина а=… см,

высота в= …см;

ширина с= … см.

Рассчитайте объем бруска по формуле:

объем бруска V=а·в·с= ………………. см³.

II. Определение объема бруска при помощи мензурки.

Определите цену деления мензурки:

цена деления шкалы мензурки равна … мл = … см³.

Перелейте осторожно воду полностью из стакана в мензурку. Определите объем налитой воды:

начальный объем воды в мензурке V₁=… мл = … см³.

Погрузите брусок полностью в воду, удерживая его за нитку, и снова измерьте объем воды:

объем воды и бруска V₂=… мл = … см³.

Определите объем бруска по формуле:

объем бруска V= V₂– V₁= ………………. см³.

Определите при помощи мензурки таким же способом объем тела неправильной формы – фарфорового ролика.

начальный объем воды в мензурке V₁=… мл = … см³.

объем воды и ролика V₂=… мл = … см³.

объем ролика V= V₂– V₁= ………………. см³.

Сделайте вывод.

И. В. Литовко, МОАУ СОШ № 1, г. Свободный, Амурская область

Метки: Физика

Чтобы найти объем бруска необходимо измерить его длину, ширину и высоту. Например, у нас брусок длиной 1 м, шириной 5 см и высотой 5 см. Если смотреть на брусок с геометрической точки зрения, то брусок это параллелепипед. Вспомнив школу и формулы подсчета объемов, чтобы найти объем параллелепипеда необходимо перемножить между собой его длину, ширину и высоту. Для удобства необходимо все длины пперевести в едину систему измерения, допустим метры. То есть у нас брусок длиной 1 м, шириной 0,05 м (5 см/100=0,05м) и высотой 0,05 м (также 5см/100=0,05м). Теперь перемножаем, полученные размеры: 1*0,05*0,05=0,0025 м3. Это и есть объем бруска на 1 м. при необходимости просто умножить на ваши данные и всё.

Вот несколько наиболее эффективных способов расчета объема бревна. Пример алгоритма расчета кубатуры бруса.

Несколько способов вычисления кубатуры лесоматериалов

Древесина часто используется для строительства: избы, санузла, беседки и других построек. Но тогда, чтобы совершить покупку, изначально ориентируясь на реальное количество материалов, необходимо знать их объемы (кубатура). Как рассчитать объем бревна?

Традиционно ее измеряют в кубических метрах и все это называется кубатурой. Посмотрим, как правильно рассчитать. Существуют методы определения объемов круглого пиломатериала и других пиломатериалов, необходимых для покупки / продажи.

Формула массы через плотность и объем — одна из основных формул физики, изучаемая в контексте школьной программы седьмого класса. Она пригодится

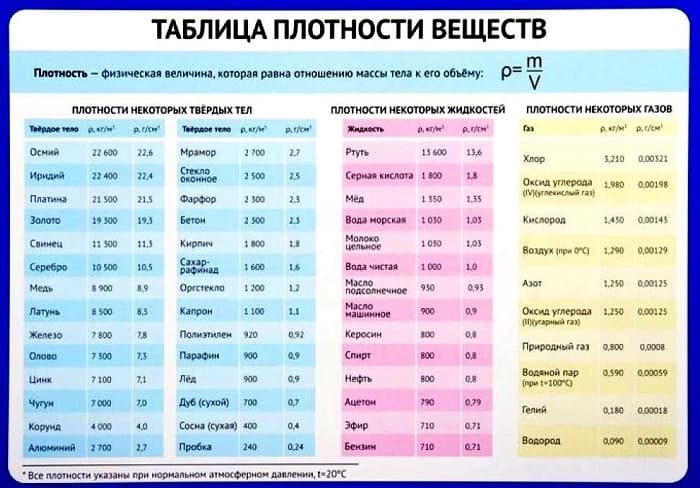
Таблица плотности некоторых веществ

Плотность многих веществ известна заранее и ее легко найти по соответствующей таблице.

При работе с ним важно обращать внимание на размер и не забывать, что все данные собираются в нормальных условиях: температура окружающей среды 20 градусов Цельсия, а также определенное давление, влажность и так далее.

Плотность других более редких веществ можно найти в Интернете.

Стоит запомнить хотя бы одно из значений плотности, так как оно часто встречается в задачах. Это плотность воды — 1000 кг / м3 или 1 г / см3.

Статьи

Расчет объема отдельных бревен

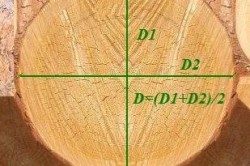
Рисунок 1. Измерение двух перпендикулярных диаметров в поперечном сечении стержня

Если кругляк имеет такую ​​же длину, что и бревна, и такой же диаметр, то можно выборочно рассчитать объем 3 балок, уменьшить их до расчетного среднего значения и умножить на количество материала бревна. В этом случае расчеты производятся следующим образом:

1. Выберите любые 3 луча.
2. Измерьте их диаметр и длину. Для удобства расчета производите измерения в метрах.
3. Вычислите кубическое пространство, занимаемое каждым из раундов, по формуле:

R — радиус, равный половине измеренного диаметра,

1. Полученные значения 3 кубометров круглого леса будут близки друг к другу. Их нужно сложить и сумму разделить на 3. Итак, мы получаем среднее значение объема бревна.
2. Далее умножаем полученное среднее значение на количество заготовок в машине или на складе.

Поскольку для строительства используются бревна одинакового диаметра и стандартной длины, этот метод широко используется для оценки объема строительных лесов.

Если форму бруска слегка придавить, его разрез будет не круглым, а слегка овальным. Как тогда определить значение диаметра? Для этого отмерьте размер 2-х перпендикулярных диаметров в сечении бруса — самого большого и самого маленького. Затем измеренные значения складываются и делятся на 2. Полученное значение будет средним диаметром, используемым в расчетах (рис. 1).

Как правильно найти объем параллелепипеда и не ошибиться? Формулы, наглядные примеры расчетов. Давайте просто поговорим о комплексе.

Задачи на самопроверку

Вы можете использовать онлайн-калькуляторы, когда вы уже обучены решать задачи и с закрытыми глазами можете рассчитать объем любого ящика. Давайте рассмотрим еще несколько примеров.

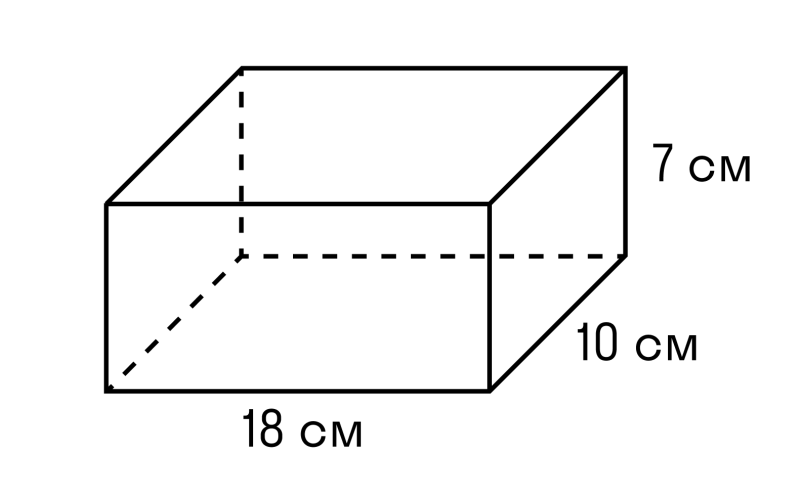
Задача 1. Найдите объем параллелепипеда со сторонами 18 см, 10 см, 7 см.

Формула для определения объема параллелепипеда:

Ответ: объем параллелепипеда 1260 см 3 .

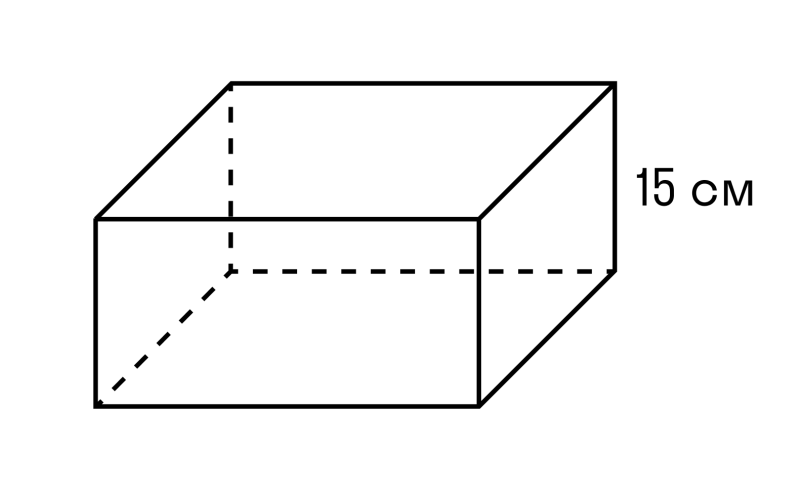
Задача 2. Найдите площадь основания параллелепипеда, если его объем составляет 120 см 3, а высота — 15 см.

Сб = 120 см 3:15 см = 8 см 2 .

Ответ: Площадь основания параллелепипеда 8 см 2 .

Задача 3. Найдите общую площадь прямоугольного параллелепипеда, если длина основания 30 сантиметров, ширина 12 сантиметров и высота 5 сантиметров.

SP п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см 2 .

Ответ: общая площадь параллелепипеда 1140 см 2 .

Имейте под рукой все необходимые формулы, когда они вам понадобятся. Сохраните шпаргалку на свой гаджет или распечатайте и храните в учебнике.

Сколько бревен в кубе: онлайн калькулятор Эта операция имеет очень простую математическую схему. Объем любого прямоугольного объекта рассчитывается путем умножения его ширины на

Чтобы рассчитать кубатуру на дом и определить точное количество стропил, нужно выполнить несложные расчеты. Для этого нужна некоторая информация: объем пиломатериалов и объем производимой детали. Это необходимо для деления одной величины на другую. В таблице ниже показаны размеры наиболее распространенных секций. При этом длина материала составляет 6 метров.

Формула для расчета количества деревяшек в кубе 150 * 150 * 6000:
0,15 (м) * 0,15 (м) * 6 (м) = 0,135 кубических метров
1 м³ / 0,135 м³ = 7 штук в одном кубе.

Как перевести погонные метры в кубические?

Подсчет количества пиломатериалов в кубе продаваемого материала также может рассчитать обычный студент. Например, чтобы рассчитать количество пиломатериалов 150 * 150 в деревянном кубе, необходимо выполнить следующие действия. Размер края балки, указываемый в миллиметрах, квадратный. Итак, 100000 нужно разделить на полученное значение. В итоге получается, что в одном кубе 44,4 погонных метра материала. Количество шестиметровых лучей в кубе составит 7,4 штук. Внутри будет 11 четырехметровых балок.

Производители и продавцы пиломатериалов не всегда честны с покупателями. Сечение пиломатериалов часто занижается по сравнению с заявленным. Часто бывает, что проданный брус размером 150 × 200 на самом деле имеет сечение 140 × 190. Перед покупкой бруса необходимо проверить реальные параметры материала. Также важно узнать у поставщика формирование цены за куб материала.

Урожайность панели при распиловке круглого бруса в одних и тех же условиях может существенно различаться. Поэтому я выбрала критерии, от которых все зависит

Как зависит процент получения пилопродукции от технологии пиления

Процент выхода доски зависит не только от диаметра, сорта, дефектов (кривизны) и длины, но и от технологии распиловки древесины и типа оборудования.

Различают два типа режущей техники:

• Одинарная срезка, процент полезной урожайности приближается к 75 %;
• Групповая обрезка, в зависимости от других параметров, полезная урожайность может достигать 70 %.

А оборудование для резки может быть следующим:

1. Ленточные пилорамы, на которых пиломатериалы производятся с минимальными коэффициентами расхода древесины;
2. Шиномонтажные пилорамы при распиловке бревен производят пиломатериалы с завышенным расходом, так как толщина цепи намного больше, чем у лент… Работать с тонкой древесиной на таком оборудовании недостаточно удобно. Поэтому в основном его пилит диаметром 20 — 22 см;
3. Кантовочные фрезерные линии. Этот тип оборудования имеет для человека преимущества и недостатки перед другими технологиями. Пила только разборную древесину;
4. Оборудование для дисковых пил пил по индивидуальным пропилам — это большое преимущество для получаемых материалов, как по качеству, так и по количеству.

Определение площади и объема в физике с примером

Содержание:

Определение площади и объема:

В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.

Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.

Рис. 6.1.

Рис. 6.2.

Рис. 6.3

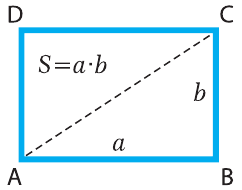
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.

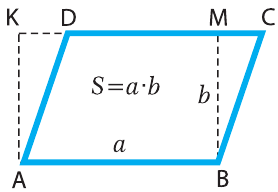
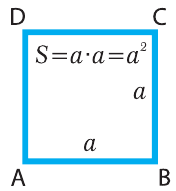
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a 2 , (6.2)

Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
, (6.3)

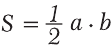
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R 2 , (6.4) .

Значение числа 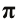можно получить, если разделить длину круга L на его диаметр. Причем не имеет значения, каков размер круга и в каких единицах измерены длина и диаметр (нужно только, чтобы это были одни и те же единицы).

Вычисление объема простых фигур

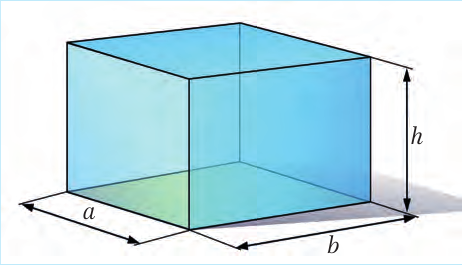
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):

Рис. 6.4.

Рис. 6.5.

Рис. 6.6.

V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:

V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a 3 (6.6)

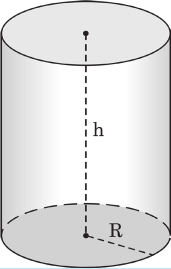
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR 2 · h (6.7)

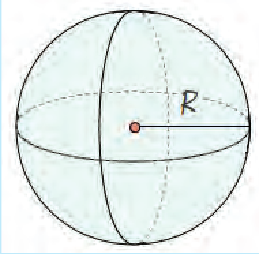
Объем шара (рис. 6.6)
(6.8)

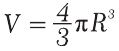
Единицы измерения объема

Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.

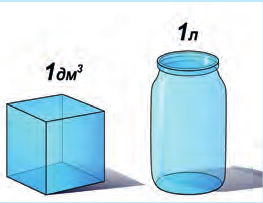
Куб с ребром 1 м имеет объем 1 м 3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм 3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см 3 . Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).

Рис. 6.7. Один литр – это 1дм 3

Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра

Таблица 6.1

1 м 3 = 1 000 л	1 м 3 = 1 000 000 см 3
1 л = 1 дм 3	1 л = 1000 см 3
1 дм 3 = 1 000 см 3	1 л = 1 000 мл
1 см3 = 1 мл	1 мл = 0,001 л

• Заказать решение задач по физике

Измерение объема тел неправильной формы

Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.

Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см 3 )

История:

Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!».

Итоги:

• Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
• Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
• Объем тел произвольной формы определяют с помощью мензурки
• Площадь круга определяют по формуле S = π · R 2 .
• Объем шара равен .

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Связь физики с другими науками
• Макромир, мегамир и микромир в физике
• Пространство и время
• Что изучает механика в физике
• Единая физическая картина мира
• Физика и научно-технический прогресс
• Физические величины и их единицы измерения
• Точность измерений и погрешности

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Как найти площадь бруска физика

Формулы, используемые в задачах по физике на плотность, массу и объем.

Название величины

Обозначение

Единицы измерения

Формула

Масса

m = p * V

Объем

V = m / p

Плотность

кг/м 3

p = m / V

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

Физика 7 класс: все формулы на трех страницах

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см 3 ?

Задача № 2. Определите объем кирпича, если его масса 5 кг?

Задача № 3. Определите массу стальной детали объёмом 120 см 3

Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м 3 ) меньше плотности стали (ρ₁ = 7800 кг/м 3 ). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

Задача № 5. Определите плотность мела, если масса его куска объемом 20 см 3 равна 48 г. Выразите эту плотность в кг/м 3 и в г/см 3 .

Ответ: Плотность мела 2,4 г/см 3 , или 2400 кг/м 3 .

Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м 2 ?

ОТВЕТ: 160 кг.

РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.

Вычисляем: m = 800 кг/м 3 • 0,04 м 2 • 5 м = 160 кг.

Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

РЕШЕНИЕ: Объем кубика V_K = а 3 = 216 см 3 . Объем стенок V_С можно вычислить, зная массу кубика m_К и плотность меди р: V_С = m_К / р = 91 см 3 . Следовательно, объем полости V_П = V_K — V_C = 125 см 3 . Поскольку 125 см 3 = (5 см) 3 , полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.

Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м 3

РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.

Задачи на плотность, массу и объем с решением. Таблица плотности веществ.

Справочный материал для «Задачи на плотность, массу и объем«

Как, зная только массу, рассчитать плотность?

1. Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
2. Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
3. Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
4. Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
5. Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
6. Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
7. Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

Конспект урока «Задачи на плотность, массу и объем с решением».

Расчёт количества и площади брусков, досок и бруса по объёму

Что может калькулятор ?

Просчитывает количество пиломатериалов(бруски, брус, доски) по заданному объёму.

Рассчитывает требуемое количество пиломатериалов для одного квадратного метра(например для половой доски или бруса для стен).

Отображает количество изделий в кубе.

Может рассчитывать неограниченное количество изделий.

Вся рассчитанная информация доступна для скачивания в формате pdf.

Инструкции

Площадь рассчитывается по ширине изделия.

Одновременно вы можете просчитать неограниченное количество изделий нажав на кнопку «Добавить изделие».

Ширина, толщина и длина указывается в миллиметрах, только целые числа.

К примеру если у вас отображается 22,2 шт и длина была указана 2000 мм то у вас получится 22 доски по 2000мм и одна доска (2000/10)*2 = 400мм.

Как считает калькулятор.

Пример: Дано 10м 3 досок шириной 150мм толщиной 50мм и длиной 6000мм.

Объём одной доски — 150мм * 0,001 * 50мм * 0,001 * 6000мм * 0,001 = 0,045м 3
Количество досок в 10м 3 — 10м 3 / 0,045м 3 = 222,2шт
Количество досок в кубе — 1м 3 / 0,045м 3 = 22,2шт
Площадь одной доски — 150мм * 0,001 * 6000мм * 0,001 = 0,9м 2
Количество досок в метре квадратном — 1м 2 / 0,9м 2 = 1,111111шт

Содержание:

Определение площади и объема:

В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски. 

Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.

Рис. 6.1.

Рис. 6.2.

Рис. 6.3

Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b,  (6.1)
где a – ширина прямоугольника, b – высота.

Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a² ,   (6.2)

Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле: 
  ,   (6.3)      

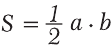
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение 
которого π  ≈ 3,14. 
Площадь круга равняется
S = π · R²,   (6.4)                                                                      .

Значение числа 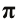  можно получить, если разделить длину круга L на его диаметр. Причем не имеет значения, каков размер круга и в каких единицах измерены длина и диаметр (нужно только, чтобы это были одни и те же единицы).

Вычисление объема простых фигур

Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):

Рис. 6.4.

Рис. 6.5.

Рис. 6.6.

V = a · b · h               (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так: 

V = S · h               (6.5)
У куба все ребра равны, потому его объем равняется: 
V = a · a · a = a³               (6.6)

Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR² · h               (6.7)

Объем шара (рис. 6.6)
               (6.8)

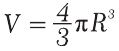
Единицы измерения объема

Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень. 

Куб с ребром 1 м имеет объем 1 м³ (один кубический метр). Один литр (1 л) по определению –  это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм³ (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см³. Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра  (1 мл = 0,001 л). 

Рис. 6.7. Один литр – это 1дм³

Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра

Таблица 6.1

1 м3 = 1 000 л	1 м3 = 1 000 000 см3
1 л = 1 дм3	1 л = 1000 см3
1 дм3 = 1 000 см3	1 л = 1 000 мл
1 см3 = 1 мл	1 мл = 0,001 л

• Заказать решение задач по физике

Измерение объема тел неправильной формы

Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела. 

Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см³)

История:

Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!».

Итоги:

• Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
• Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
• Объем тел произвольной формы определяют с помощью мензурки
• Площадь круга определяют по формуле S = π · R².
• Объем шара равен .