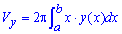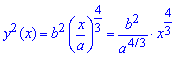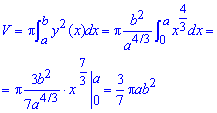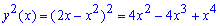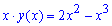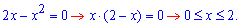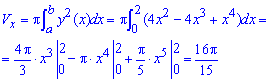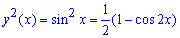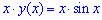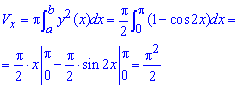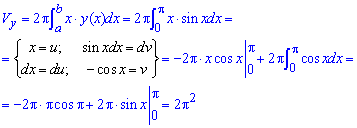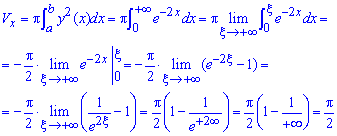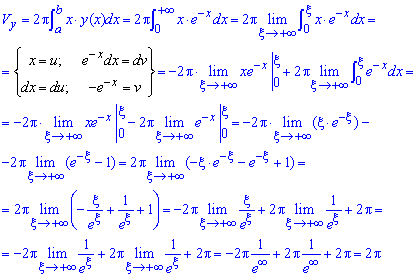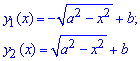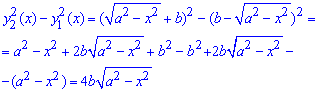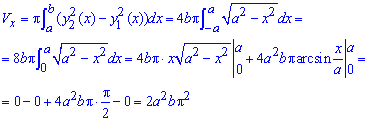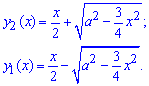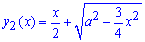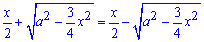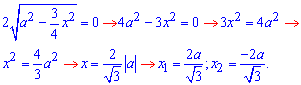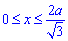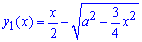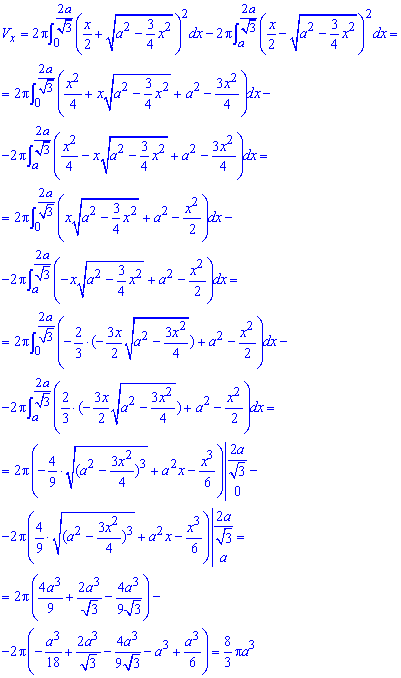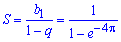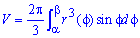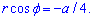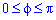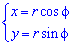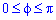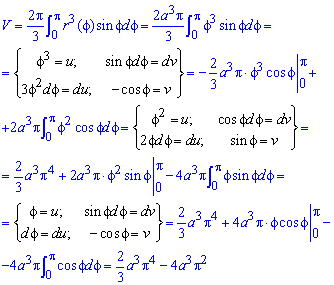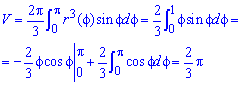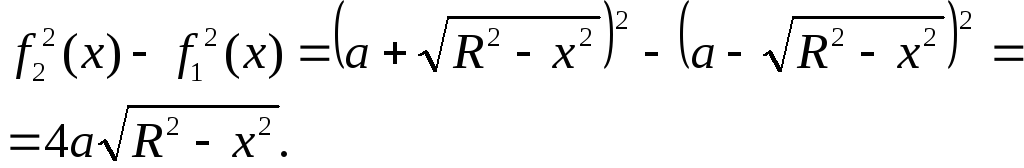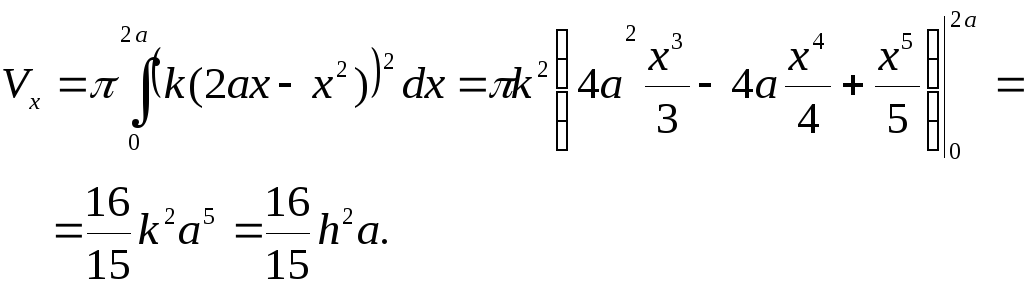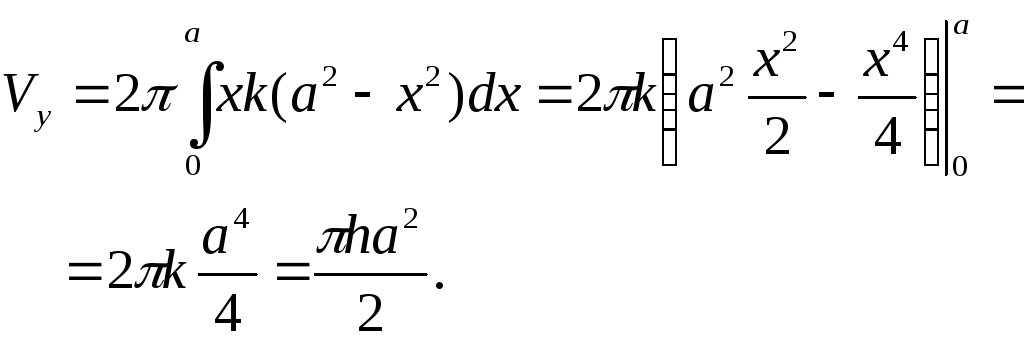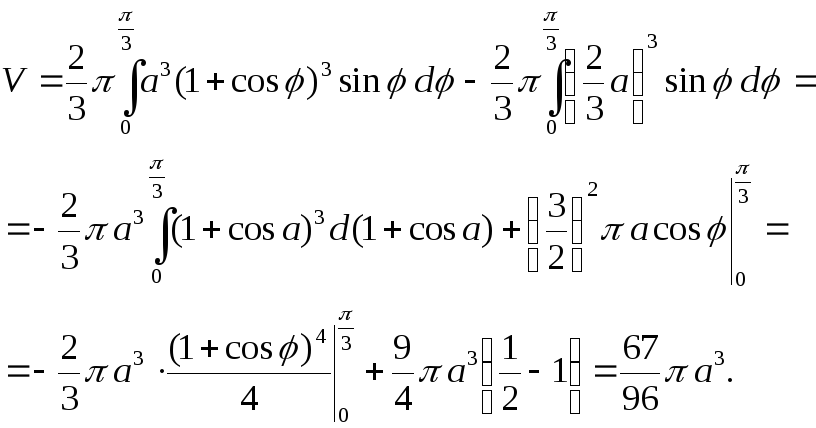Как найти объем тела образованного при вращении - Исправление недочетов и поиск решений вместе с Examum.ru

Дополнения

1.О применении определённого интеграла для нахождения объёмов тел вращения

1.1.Формула объёма тела вращения

В п.16.2 дано определение тела вращения.

Получим формулу для вычисления объёма тела вращения, применяя интеграл, о котором вам рассказали в курсе «Алгебры и начал математического анализа».

Пусть f(x) — непрерывная на отрезке [a; b] функция, не принимающая отрицательных значений; А, В — точки графика этой функции (рис. 225).

Рис. 225

Рассмотрим криволинейную трапецию aABb, ограниченную кривой графика функции y = f(x), отрезками aA, bB и отрезком [a; b] координатной оси Ох (см. рис. 225). При вращении этой трапеции вокруг оси Ох образуется тело вращения (рис. 226), которое обозначим Ф и поставим себе задачу: найти объём этого тела.

Рис. 226

Через произвольную точку х = с (a ⩽ с ⩽ b) отрезка [a; b] проведём плоскость, перпендикулярную оси Ox. Сечением тела Ф этой плоскостью является круг, радиус которого равен f(с), а площадь — πf2(с) (или точка (c; 0)).

Объём части тела Ф, заключённой между этой плоскостью и плоскостью х = a, изменяется при изменении x. Обозначим этот переменный объём V(х). Заметим, что V(x) = V(a) = 0 при х = a; при х = b имеем V(x) = V(b) = V — искомый объём тела вращения Ф.

Покажем, что функция V(x) имеет производную V′(х) и V′(х) = πf2(х).

Придадим абсциссе х приращение ∆х > 0, тогда объём V(х) получает приращение ∆V(х) = V(x + ∆x) – V(x). Пусть m и М — соответственно наименьшее и наибольшее значения функции f(х) на промежутке [х; х + ∆х]. Цилиндр, радиус основания которого равен m, содержится в теле вращения объёма ∆V(x), а цилиндр, радиус основания которого равен M, содержит тело объёма ∆V(х); образующие цилиндров параллельны оси Ох и имеют длину, равную ∆х. Объёмы этих цилиндров равны соответственно πm2•∆x и πM2•∆х. На основании свойства 2 объёмов (п. 10.1) получаем

πm2•∆x ⩽ ∆V(x) ⩽ πM2•∆x,

откуда

πm2 ⩽ ⩽ πM2.

Рассуждения для случая ∆х < 0 проводятся аналогично и дают тот же результат.

Пусть теперь ∆х 0. Имеем m = M = f(x), тогда

πm2 ⩽ ⩽ πM2

или

πf2(х) ⩽ ⩽ πf2(x).

Значит, = πf2(х). По определению производной функции = V′(x). Поэтому V ′(x) = πf2(х), следовательно, V(х) — первообразная для πf2(х).

Таким образом, переменный объём V(x) телa вращения представляет собой одну из первообразных для функции πf 2(х) на отрезке [a; b]. Эта первообразная обладает тем свойством, что при х = a она обращается в нуль (V(a) = 0), а при х = b значение функции V(x) равно объёму тела вращения Ф (V(b) = V).

Если F(х) — также некоторая первообразная для функции πf 2(x), то V(x) = F(x) + С, где С — произвольная постоянная. Так как V (a) = 0, то из равенства V(a) = F (a) + C = 0 находим С = –F(a). Значит, V(x) = F(x) – F(a). Toгдa V(b) = F(b) – F(a). Ho V(b) = V — искомый объём тела вращения Ф. Таким образом, V = F(b) – F(a), где F(b) и F(a) — значения первообразной для функции πf 2(х) соответственно при х = b и х = a. Это означает, что

V = f 2(x)dx = π(x)dx.

Вот почему объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = f(x), х = a, х = b, у = 0, вычисляется по формуле

Рис. 227

V = (x)dx.(*)

ЗАДАЧА. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = , х = 0, x = 2 и y = 0 (рис. 227).

Решение. Воспользуемся формулой V = π(x)dx, для чего из уравнения у = находим y2 = 2х. Тогда получаем

V = πdx = 2π• = = 4π.

Ответ: 4π.

1.2. Объёмы конуса, шара и его частей

Используя формулу V = (x)dx вычисления объёма тела вращения, получим формулы для вычисления объёма каждого изученного ранее тела вращения.

а) Объём конуса и усечённого конуса

Теорема 1 (об объёме полного конуса). Объём V конуса с высотой Н и радиусом основания R равен одной трети произведения площади основания на высоту:

V = R2Н.

Рис. 228

Доказательство. Конус с высотой Н и радиусом основания R можно рассматривать как тело, образованное вращением вокруг оси Ox прямоугольного треугольника с вершинами О(0; 0), А(Н; 0) и B(Н; R) (рис. 228). Треугольник АОВ является частным случаем криволинейной трапеции, которая ограничена графиком функции у = х (0 ⩽ х ⩽ H), осью Ох и отрезком прямой х = Н. Поэтому, используя формулу (*) п. 1.1 «Дополнений» для объёма V конуса, получаем:

V = dx = π • = πR2H,

где πR2 — площадь основания конуса. Теорема доказана. ▼

Теорема 2 (об объёме усечённого конуса). Объём усечённого конуса с высотой Н и радиусами оснований r и R равен сумме объёмов трёх конусов с высотой Н, радиусы оснований которых соответственно равны r, R и :

V = (r2 + R2 + rR)H.

Доказательство. Усечённый конус с высотой H и радиусами оснований r и R можно получить, вращая вокруг оси Oх прямоугольную трапецию OABC, где O(0; 0), A(0; r), В(Н; R), С(H; 0) (рис. 229).

Рис. 229

Прямая AВ проходит через точки (0; r) и (Н; R), поэтому её уравнение имеет вид у = х + r. Следовательно, трапеция ОАВС ограничена графиком функции y = х + r (0 ⩽ х ⩽ Н), осью Oх и отрезками прямых х = 0 и х = Н. Поэтому, используя формулу (*) из п. 1.1 для объёма V усечённого конуса, получаем:

V = dx.(1)

Для вычисления интеграла сделаем замену переменных

x + r = t.(2)

Тогда dx = dt, откуда dx = dt. Новые пределы интегрирования (по переменной t) найдём посредством подстановки формулы (2): х = 0 ⇒ t = r; х = Н ⇒ t = R. Таким образом, для объёма V усечённого конуса получаем:

что и требовалось доказать. ▼

б) Объём шарового слоя

В прямоугольной декартовой системе координат Оху рассмотрим криволинейную трапецию aABb, ограниченную дугой окружности х2 + у2 = R2, –R ⩽ a ⩽ х ⩽ b ⩽ R, отрезком [a; b] оси Ох и отрезками aА и bВ прямых соответственно x = a и х = b (рис. 230, а).

Рис. 230

При вращении криволинейной трапеции aАВb вокруг оси Ох образуется шаровой слой (рис. 230, б). Найдём его объём, применяя формулу (*) п. 1.1.

Из уравнения х2 + у2 = R2 имеем у2 = R2 – x2. Поэтому для вычисления объёма V шарового слоя получаем:

Таким образом, объём шарового слоя, отсекаемого от шара x2 + y2 + z2 ⩽ R2 радиуса R плоскостями x = a и x = b, вычисляется пo формуле

V = (**)

Пусть радиусы оснований шарового слоя равны r1 и r2 (r1 > r2), а высота — H (см. рис. 230, a).

Тогда Н = b – a, = R2 – a2, = R2 – b2.

Формулу (**) преобразуем к виду:

V = (3R2 – (b2 + ab + a2)) =

= ((R2 – b2) + (R2 – ab) + (R2 – a2)).

Из системы равенств (b – a)2 = H2, R2 – a2 = , R2 – b2 = после почленного сложения их левых и правых частей находим:

R2 – ab = .

Тогда:

V = ((R2 – b2) + (R2 – ab) + (R2 – a2)) =

= .

Таким образом, объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле

V = .(***)

в) Объём шара

Рис. 231

При вращении полукруга х2 + у2 = R2 (расположенного в плоскости Оху, рис. 231, а) вокруг оси Ох образуется шар радиуса R (рис. 231, б). Из уравнения окружности х2 + y2 = R2 данного полукруга имеем у2 = R2 – х2. Тогда, полагая a = –R, b = R в формуле (*) п. 1.1, находим объём V шара радиуса R:

Vш = =

= .

Таким образом, имеет место следующая теорема.

Теорема 3 (об объёме шара). Объём шара радиуса R вычисляется по формуле

Vш = .

г) Объём шарового сегмента

Если b = R (см. п. 1.2, б), то получаем криволинейную трапецию aAB (рис. 232, а), при вращении которой вокруг оси Ох образуется шаровой сегмент (рис. 232, б).

Рис. 232

Пусть высота шарового сегмента равна Н, тогда a = R – Н. Так как дуга AВ криволинейной трапеции aАВ является частью окружности x2 + y2 = R2 (в плоскости Оxу), то формулу объёма шарового сегмента получим по аналогии с выводом формулы для вычисления объёма шара, учитывая при этом, что пределы a и b интегрирования равны: a = R – H, b = R, т. е.

Vш. сегм = =

Таким образом, имеет место следующая теорема.

Теорема 4 (об объёме шарового сегмента). Объём шарового сегмента, отсекаемого от шара радиуса R и имеющего высоту Н, вычисляется по формуле

Vш. сегм =

Если в формуле (***) п. 1.2, б положить r2 = 0, r1 = r, то получим формулу для вычисления объёма шарового сегмента с радиусом основания r и высотой Н:

Vш. сегм = (3r2 + H2).

д) Объём шарового сектора

Рис. 233

Шаровой сектор состоит из конуса с вершиной в центре шара и шарового сегмента, имеющего с конусом общее основание (риc. 233). Пусть R = ОА — радиус шара; АС = r — радиус основания шарового сегмента, NC = H — его высота; N — точка сферы (рис. 233).

Найдём объёмы конуса и шарового сегмента, учитывая, что высота h конуса равна OC = ON – CN = R – Н.

Объём Vк конуса равен

π•АС2•ОС = πr2 (R – Н).

Выразим r2 через R и H.

B прямоугольном треугольнике AOC находим r2 = AC2 = ОА2 – OC2 = R2 – (R – H)2 = H(2R – H).

Значит,

Vк = πH(2R – H)(R – H) = (2R2 – 3RH + H2).

Для объёма шарового сегмента имеем:

Vш. сегм = (3AC2 + NC2) = (3H(2R – H) + H2) =

= (3RН – H2).

Тогда для объёма шарового сектора получаем

Vш. сект = Vк + Vш. сегм =

= (2R2 – 3RH + H2) + (3RH – H2) = πR2H.

Таким образом, доказана следующая теорема.

Теорема 5 (об объёме шарового сектора). Объём шарового сектора шара радиуса R вычисляется по формуле

Vш. сект = R2H,

где Н — длина высоты шарового сегмента, соответствующего данному шаровому сектору.

В курсе математического анализа, который вам предстоит изучать в высшей школе, будет дано строгое обоснование применения определённого интеграла не только для нахождения объёмов тел, но и для нахождения площадей поверхностей и длин дуг линий. Решите самостоятельно следующие задачи.

1)Найдите объём тела, которое получается при вращении вокруг оси Ох криволинейной трапеции, ограниченной гиперболой у = , прямыми х = 3, х = 12 и осью абсцисс. (Ответ: 4π.)

2)Найдите объём тела, образованного вращением вокруг оси Oх фигуры, ограниченной одной полуволной синусоиды у = sin x и отрезком 0 ⩽ х ⩽ π оси абсцисс. (Ответ: 0,5π2.)

3)Найдите объём тела, полученного при вращении кривой у = 0,25х2 вокруг оси Оу в пределах от у = 1 до у = 5. (Ответ: 48π.)

4)Найдите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми у = 2х2 и у = x3.

Источник

Объемы тел вращения

Краткая теория

Объемы тел, образованных вращением
криволинейной трапеции, ограниченной кривой

, осью

и двумя
вертикалями

, вокруг осей

, выражаются соответственно формулами:

Объем тела, образованного вращением
около оси

фигуры,
ограниченной кривой

, осью

и двумя
параллелями

, можно определять по формуле:

Если кривая задана в иной форме
(параметрически, в полярных координатах и т.д.), то в приведенных формулах
нужно сделать соответствующую замену переменной интегрирования.

В более общем случае объемы тел,
образованных вращением фигуры, ограниченной кривыми

(причем

) и прямыми

, вокруг координатных осей

, соответственно равны:

Объем тела, полученного при вращении
сектора, ограниченного дугой кривой

и двумя
полярными радиусами

, вокруг полярной оси, может быть вычислен по формуле:

Этой же формулой удобно пользоваться
при отыскании объема тела, полученного вращением вокруг полярной оси фигуры,
ограниченной некоторой замкнутой кривой, заданной в полярных координатах.

Если

– площадь
сечения тела плоскостью, перпендикулярной к некоторой прямой (которую принимаем
за ось

), в точке с абсциссой

, то объем этого тела равен:

где

– абсциссы
крайних сечений тела.

Примеры решения задач

Задача 1

С помощью
определенного интеграла вычислить объем тела, полученного вращением фигуры

вокруг указанной оси координат.

вокруг
оси

Решение

Сделаем
чертеж:

Объем
тела, образованного вращением вокруг оси

фигуры можно найти по формуле:

В нашем
случае получаем

Ответ:

Задача 2

Найдите
объем тела, полученного вращением вокруг оси абсцисс криволинейной трапеции,
ограниченной линиями:

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Сделаем
чертеж:

Объем
тела можно найти по формуле:

Ответ:

Задача 3

Определить
объем, образованный вращением кривой

вокруг
полярной оси.

Решение

Ответ:

Задача 4

Вычислить
объем тела, ограниченного однополосным гиперболоидом

и
плоскостями

Решение

Здесь
удобнее рассмотреть сечения данного тела плоскостями, перпендикулярными к оси

. Тогда объем выразится
формулой:

где

– площадь получаемого сечения, зависящая от
точки с аппликатой

, через которую проходит
секущая плоскость. При пересечении однополосного гиперболоида плоскостью

получается эллипс, который можно определить
уравнениями:

откуда
следует, что полуоси эллипса:

Учитывая, что площадь эллипса с
полуосями

равна

, воспользовавшись параметрическим заданием эллипса:

мы можем записать аналитическое
выражение функции

Тогда искомый объем:

Ответ:

Источник

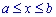
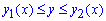
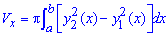
Объем тела V, образованного вращением вокруг оси Ox фигуры , , где y₁(x) и y₂(x) — непрерывные неотъемлемые функции, равняется определенному интегралу от разницы квадратов функций y_i(x) по переменной x

Объем тела V, образованного вращением вокруг оси Oy фигуры 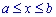, , где y(x) — однозначная непрерывная функция, равняется определенному интегралу, рассчитанному по формуле

Примеры выбраны из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.

Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления объема тела вращения будут повторяться из примера в пример.

ІV. Найти объемы тел, ограниченными поверхностями, полученными при вращении отрезков следующих линий

Пример 2.139 (2472) Найти объем тела, образованного вращением кривой 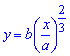(нейлоїд) xє[0;a] вокруг оси Ox.
Решение: Складываем подинтегральную функцию:

Пределы интегрирования известны за условием: [0;a].
Найдем объем тела интегрированием:

Всегда помните, что объем измеряется в кубических единицах.

Пример 2.140 (2473) Найти объем тела, образованного вращением кривой y=2x-x^2, y=0
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Запишем подинтегральные функции:
а)
б)
Из приведенных формул Вы можете видеть разницу, в каких случаях применять каждую из формул объема.
Найдем пределы интегрирования:

И заключительным шагом вычисляем объемы интегрированием.
а) Найдем объем тела вращения вокруг оси Ox:

б) Вычислим объем тела вращения вокруг оси Oy:

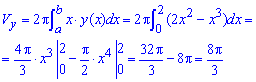
В этом примере интегралы легко берутся и нет потребности объяснять детали операций.

Пример 2.141 (2474) Вычислить объем тела, образованного вращением кривой y=sin(x)

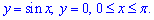
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Выпишем подинтегральные функции:
а)
б)
Пределы интегрирования берем из начального условия:

Осталось вычислить определенные интегралы:
а) Найдем объем тела вращения вокруг оси Ox:

б) Выполняем вычисление объема тела при вращении вокруг оси Oy:

Замена переменных помогает найти последний интеграл.

Пример 2.143 (2476) Найти объем тела, образованного вращением кривой y=e^{— x}, y=0,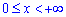
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Уравнение подинтегральных функций :
а) y²=e^-2x;
б) x*y (x) =xe^-x.
Запишем пределы интегрирования (известно за условием):

а) Находим объем тела вращения вокруг оси Ox:

б) Найдем объем тела вращения вокруг оси Oy:

Здесь, чтобы вычислить интегралы придется находить границу при переменной направляющейся к безграничности.
Во втором интеграле выполняем интегрирование частями.

Пример 2.144 (2477) Вычислить объем тела, образованного вращением кривой x²+(y-b)²=a², 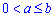, вокруг оси Ox.
Решение: Фигурой вращения является круг с центром в точке (0;b) и радиусом a.
При выражении самой функции получим две ветки корневых функций:

При поднесении к квадрату разница слагаемых сложит такое выражение подинтегральной функции:

Запишем пределы интегрирования: для круга они равны xє[-a;a] или два полукруга из на промежутке xє[0;a].
Через интеграл находим объем тела вращения вокруг оси Ox:

Внимательно разберите приведенный пример.

Пример 2.145 (2478) Найти объем тела, образованного вращением кривой x²-xy+y²=a², вокруг оси Ox.
Решение: Сведем кривую к каноническому виду (методами из аналитической геометрии) устанавливаем, что заданная линия является эллипсом
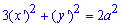
— уравнение в канонической системы координат.
В приведенной системе координат уравнения эллипса имеет вид:

Прямая y=x/2 является осью симметрии этой фигуры.
Запишем подинтегральную функцию:

Найдем пределы интегрирования из условия равности функций y₂(x)=y₁(x):

или двукратный объем на интервале

Но тогда еще нужно отнять объем тела в пределах

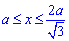
(которая не принадлежит эллипсу) и ограничена первой кривой

и результат умножить на 2 (симметрия).

Последним шагом вычисляем объем тела вращения вокруг оси Ox:

Формула интеграла вышла достаточно длинным, однако его удобно читать пользователям, которые заходят на сайт из мобильных устройств.

Пример 2.146 (2479) Найти объем тела, образованного вращением кривой 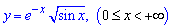вокруг оси Ox.
Решение: Запишем подинтегральную функцию:
y²(x)=e^-2x*sin (x).
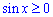
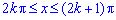
Установим пределы интегрирования: при , где k=0,1,2.
Таким образом имеем бесконечный ряд промежутков интегрирования.
При нахождении объема тела вращения вокруг оси Ox получим бесконечный ряд интегралов, который совпадает:

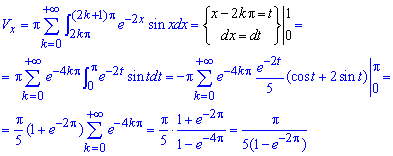
Здесь вычислили интеграл дважды выполнив замену переменных:

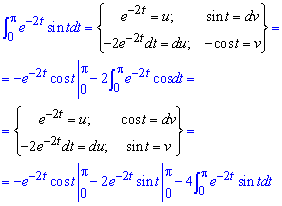
тому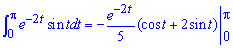
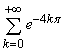
— это числовой ряд.
В данном случае бесконечно нисходящая геометрическая прогрессия, у которой b₁=1, b₂=e^-4Pi, поэтому q=e^{— 4Pi}, а сумма прогрессии равна

Объем тела, образованного вращением вокруг полярной оси плоской фигуры

Чтобы найти объем тела V, образованного в результате вращением вокруг полярной оси плоской фигуры r(phi)
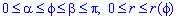
необходимо вычислить определенный интеграл по формуле

Пример 2483 Найти объем тела, образованного вращением кривой r=a (1+cos (phi)), 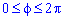, y=0
а) вокруг полярной оси;
б) вокруг прямой

Решение: Чтобы достать подинтегральную функцию подносим к кубу заданную функцию: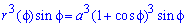

Пределы интегрирования записываем из начального условия:

а) Сначала найдем объем тела вращения вокруг полярной оси:

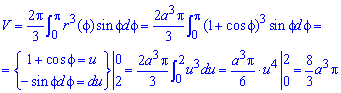
Для упрощения вычислений переходим к новой переменной под интегралом.
б) Перейдем к новым координатам с помощью формул: x₁=y, y₁=-x-a/4.
Определяем пределы интегрирования:
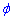
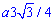
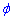
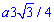
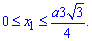
при росте угла от 0 к Pi/2 координата x₁ растет от 0 к , при росте от Pi/2 к Pi переменная x₁ спадает от к 0, поэтому пределы ограничены интервалом

Запишем подинтегральную функцию:
Уравнения перехода между системами координат имеют вид

Подстановкой в уравнение получим:
,
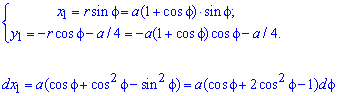
Найдем объем тела вращения вокруг прямой :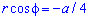

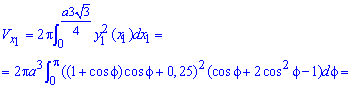
откроем скобки, возведем подобные слагаемые и, приняв во внимание, что интеграл равен нулю 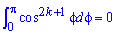получим

Здесь последние интегралы 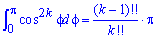выражаются через факториалы

(смотри пример 2.59, часть І).
Парные факториалы вычисляем по правилу

Пример 2484.1 Найти объем тела, образованного вращением кривой r=a*phi 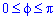(a>0)вокруг полярной оси.
Решение: Запишем подинтегральную функцию:

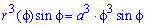
С пределами интегрирования проблем нет:

Чтобы найти объем тела вращения вокруг полярной оси выполняем ряд манипуляций с интегралами:

Внимательно проанализируйте, как находится этот «тригонометрический» интеграл.

Пример 2484.2 Найти объем тела, образованного вращением кривой phi=Pi*r³, phi=Pi, вокруг полярной оси.
Решение: Запишем подинтегральную функцию:

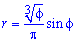
Пределы интегрирования:

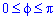
Вычисляем объем тела вращения вокруг полярной оси:

Здесь синус вносим под дифференциал и выполняем интегрирование частями.
На данное время это все примеры, которые мы смогли подготовить для Вас по данной теме.

Источник

Определение
3. Тело
вращения – это тело, полученное вращением
плоской фигуры вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.

Ось вращения может
и пересекать фигуру, если это ось
симметрии фигуры.

Теорема
2. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямыхивращается вокруг оси.
Тогда объём получающегося тела вращения
можно вычислить по формуле

(2)

Доказательство.
Для такого тела сечение с абсциссой
– это круг радиуса,
значити формула (1) даёт требуемый результат.

Если фигура
ограничена графиками двух непрерывных
функций
и,
и отрезками прямыхи,
причёми,
то при вращении вокруг оси абсцисс
получим тело, объём которого

Пример
3. Вычислить
объём тора, полученного вращением круга,
ограниченного окружностью вокруг оси абсцисс.

Решение.
Указанный круг снизу ограничен графиком
функции
,
а сверху –.
Разность квадратов этих функций:

Искомый объём

(графиком
подынтегральной функции является
верхняя полуокружность, поэтому
написанный выше интеграл – это площадь
полукруга).

Пример 4.
Параболический сегмент с основанием
,
и высотой,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).

Р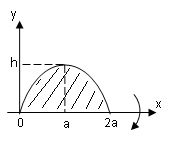ешение.
Параболу расположим как показано на
рисунке. Тогда её уравнение
,
причем.
Найдём значение параметра:.
Итак, искомый объём:

Теорема
3. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямыхи,
причём,
вращается вокруг оси.
Тогда объём получающегося тела вращения
может быть найден по формуле

(3)

Идея
доказательства.
Разбиваем отрезок
точками,
на части и проводим прямые.
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основаниеми высотой.

Получающийся при
вращении такого прямоугольника цилиндр
разрежем по образующей и развернём.
Получим «почти» параллелепипед с
размерами:
,и.
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство

Для получения
точного равенства надо перейти к пределу
при .
Написанная выше сумма есть интегральная
сумма для функции ,
следовательно, в пределе получим интеграл
из формулы (3). Теорема доказана.

Замечание
1. В теоремах
2 и 3 условие
можно опустить: формула (2) вообще
нечувствительна к знаку,
а в формуле (3) достаточнозаменить на.

Пример
5.
Параболический сегмент (основание
,
высота)
вращается вокруг высоты. Найти объём
получающегося тела.

Решение.
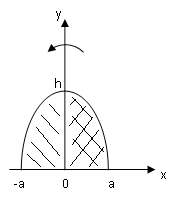
Расположим
параболу как показано на рисунке. И хотя
ось вращения пересекает фигуру, она –
ось – является осью симметрии. Поэтому
надо рассматривать лишь правую половину
сегмента. Уравнение параболы
,
причем,
значит.
Имеем для объёма:

Замечание
2. Если
криволинейная граница криволинейной
трапеции задана параметрическими
уравнениями
,,и,то можно использовать формулы (2) и (3) с
заменойнаинапри измененииt
от
до.

Пример
6. Фигура
ограничена первой аркой циклоиды
,,,
и осью абсцисс. Найти объём тела,
полученного вращением этой фигуры
вокруг: 1) оси;
2) оси.

Решение.
1) Общая формула
В нашем случае:

2) Общая формула
Для нашей фигуры:

Предлагаем
студентам самостоятельно провести все
вычисления.

Замечание
3. Пусть
криволинейный сектор, ограниченный
непре-рывной линией
и лучами,,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.

Пример
7. Часть
фигуры, ограниченной кардиоидой
,
лежащая вне окружности,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.

Решение.
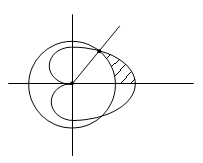
Обе линии, а значит и фигура, которую
они ограничивают, симметричны относительно
полярной оси. Поэтому необходимо
рассматривать лишь ту часть, для которой

.
Кривые пересекаются прии

при
.
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:

Задачи
для самостоятельного решения.

1. Круговой сегмент,
основание которого ,
высота
,
вращается вокруг основания. Найти объём
тела вращения.

2. Найти объём
параболоида вращения, основание которого
,
а высота равна.

3. Фигура, ограниченная
астроидой
,вращает-ся вокруг оси абсцисс. Найти
объём тела, которое получается при этом.

4. Фигура, ограниченная
линиями
ивращается вокруг оси абсцисс. Найти
объём тела вращения.

Соседние файлы в папке Лекции по мат.анализу

Источник

Объём тела вращения

Пусть — тело вращения, образованное вращением вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямыми x=a и x=b и графиком непрерывной функции y=f(x) .

Докажем, что это тело вращения кубируемо и его объем выражается формулой

$V=pi intlimits_{a}^{b} f^2(x),dx= pi intlimits_{a}^{b}y^2,dx,.$

Сначала докажем, что это тело вращения регулярно, если в качестве выберем плоскость Oyz , перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии от плоскости Oyz , является кругом радиуса f(x) и его площадь S(x) равна pi f^2(x) (рис. 46). Поэтому функция S(x) непрерывна в силу непрерывности f(x) . Далее, если S(x_1)leqslant S(x_2) , то это значит, что f(x_1)leqslant f(x_2) . Но проекциями сечений на плоскость Oyz являются круги радиусов f(x_1) и f(x_2) с центром , и из вытекает, что круг радиуса f(x_1) содержится в круге радиуса f(x_2) .

Чертёж тела вращения вокруг оси абсцисс

Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объем вычисляется по формуле

$V=pi intlimits_{a}^{b} S(x),dx= pi intlimits_{a}^{b}f^2(x),dx,.$

Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми y_1=f_1(x), y_2=f_2(x) , то

$V= pi intlimits_{a}^{b}y_2^2,dx- pi intlimits_{a}^{b}y_1^2,dx= piintlimits_{a}^{b}Bigl(f_2^2(x)-f_1^2(x)Bigr)dx,.$

Формулой (3) можно воспользоваться и для вычисления объема тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определенного интеграла.

В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида.

Например, найдем объем тела, получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдем объем, получаемый при вращении прямоугольника с высотой y#, в основании которого лежит отрезок $[x_k;x_{k+1}]$ . Этот объем равен разности объемов двух прямых круговых цилиндров

$Delta V_k= pi y_k x_{k+1}^2- pi y_k x_k^2= pi y_k bigl(x_{k+1}+x_kbigr) bigl(x_{k+1}-x_kbigr).$

Но теперь ясно, что искомый объем оценивается сверху и снизу следующим образом:

$2pi sum_{k=0}^{n-1} m_kx_kDelta x_k leqslant Vleqslant 2pi sum_{k=0}^{n-1} M_kx_kDelta x_k,.$

Отсюда легко следует формула объёма тела вращения вокруг оси ординат:

$V=2pi intlimits_{a}^{b} xy,dx,.$

(4)

Пример 4. Найдем объем шара радиуса .

Решение. Не теряя общности, будем рассматривать круг радиуса с центром в начале координат. Этот круг, вращаясь вокруг оси , образует шар. Уравнение окружности имеет вид x^2+y^2=R^2 , поэтому y^2=R^2-x^2 . Учитывая симметрию круга относительно оси ординат, найдем сначала половину искомого объема

$frac{1}{2}V= piintlimits_{0}^{R}y^2,dx= piintlimits_{0}^{R} (R^2-x^2),dx= left.{pi!left(R^2x- frac{x^3}{3}right)}right|_{0}^{R}= pi!left(R^3- frac{R^3}{3}right)= frac{2}{3}pi R^3.$

Следовательно, объем всего шара равен $frac{4}{3}pi R^3$ .

Конус, образованный вращением прямой вокруг оси абсцисс

Пример 5. Вычислить объем конуса, высота которого и радиус основания .

Решение. Выберем систему координат так, чтобы ось совпала с высотой h (рис. 47), а вершину конуса примем за начало координат. Тогда уравнение прямой запишется в виде $y=frac{r}{h},x$ .

Пользуясь формулой (3), получим:

$V=pi intlimits_{0}^{h} y^2,dx= pi intlimits_{0}^{h} frac{r^2}{h^2},x^2,dx= left.{frac{pi r^2}{h^2}cdot frac{x^3}{3}}right|_{0}^{h}= frac{pi}{3},r^2h,.$

Пример 6. Найдем объем тела, полученного при вращении вокруг оси абсцисс астроиды $begin{cases}x=acos^3t,,\ y=asin^3t,.end{cases}$ (рис. 48).

Объём тела, полученного при вращении вокруг оси абсцисс астроиды

Решение. Построим астроиду. Рассмотрим половину верхней части астроиды, расположенной симметрично относительно оси ординат. Используя формулу (3) и меняя переменную под знаком определенного интеграла, найдем для новой переменной пределы интегрирования.

Если x=acos^3t=0 , то $t=frac{pi}{2}$ , а если x=acos^3t=a , то t=0 . Учитывая, что y^2=a^2sin^6t и $dx=-3acos^2tsin{t},dt$ , получаем:

$V=pi intlimits_{a}^{b} y^2,dx= pi intlimits_{pi/2}^{0} a^2sin^6t bigl(-3acos^2tsin{t}bigr),dt= ldots= frac{16pi}{105},a^3.$

Объем всего тела, образованного вращением астроиды, будет $frac{32pi}{105},a^3$ .

Пример 7. Найдем объем тела, получаемого при вращении вокруг оси ординат криволинейной трапеции, ограниченной осью абсцисс и первой аркой циклоиды $begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}).end{cases}$ .

Решение. Воспользуемся формулой (4): $V=2pi intlimits_{a}^{b}xy,dx$ , и заменим переменную под знаком интеграла, учитывая, что первая арка циклоиды образуется при изменении переменной от до 2pi . Таким образом,

$begin{aligned}V&= 2pi intlimits_{0}^{2pi} a(t-sin{t})a(1-cos{t})a(1-cos{t}),dt= 2pi a^3 intlimits_{0}^{2pi} (t-sin{t})(1-cos{t})^2,dt=\ &= 2pi a^3 intlimits_{0}^{2pi}bigl(t-sin{t}- 2tcos{t}+ 2sin{t}cos{t}+ tcos^2t- sin{t}cos^2tbigr),dt=\ &= left.{2pi a^3!left( frac{t^2}{2}+ cos{t}- 2tsin{t}- 2cos{t}+ sin^2t+ frac{t^2}{4}+ frac{t}{4}sin2t+ frac{1}{8}cos2t+ frac{1}{3}cos^3tright)}right|_{0}^{2pi}=\ &= 2pi a^3!left( 2pi^2+1-2+pi^2+frac{1}{8}+ frac{1}{3}-1+2- frac{1}{8}- frac{1}{3}right)= 6pi^3a^3. end{aligned}$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник