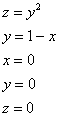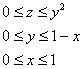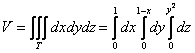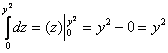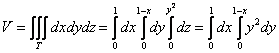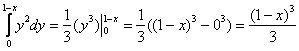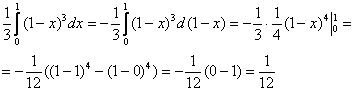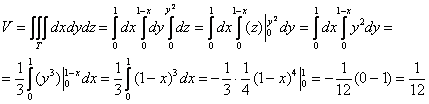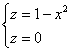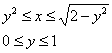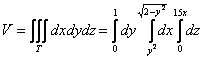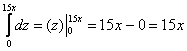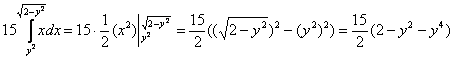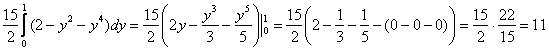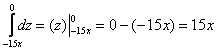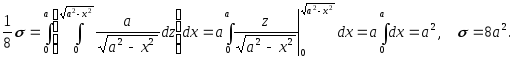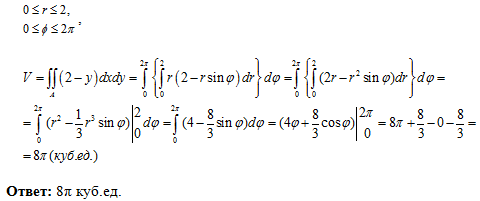Как найти объем тела ограниченной плоскостями

Вычисление объёмов

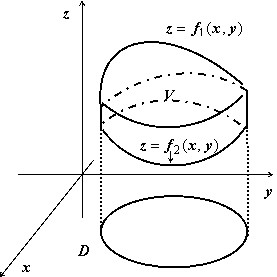
Объём тела, ограниченного сверху и снизу поверхностями $mathbf { textit { z } } =mathbf { textit { f } } _ { 1 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $mathbf { textit { z } } =mathbf { textit { f } } _ { 2 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $(x,y)in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $mathbf { textit { Oz } } $, равен $v=iintlimits_D { left[ { f_1 (x,y)-f_2 (x,y) }right]dxdy } $; эта формула очевидно следует из геометрического смысла двойного интеграла.

Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.

Пример 1

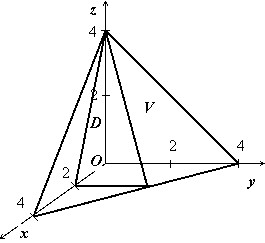
Найти объём тела $V:left[{ begin{array} { l } y=0,;z=0, \ x+y+z=4,; \ 2x+z=4. \ end{array} }right.$

Решение:

Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $mathbf { textit { Oxz } } $:

$V:left[{ begin{array} { l } (x,z)in D, \ 0leqslant yleqslant 4-x-z. \ end{array} }right.$

Область $mathbf { textit { D } } $ — треугольник, ограниченный прямыми $mathbf { textit { x } } $ = 0, $mathbf { textit { z } } $ = 0, 2$mathbf { textit { x } } +mathbf { textit { z } } $ = 4, поэтому

$V=iintlimits_D { (4-x-z)dxdz } =intlimits_0^2 { dxintlimits_0^ { 4-2x } { (4-x-z)dz } } = intlimits_0^2 { dxleft. { left( { 4z-xz-z^2/2 }right) }right|_0^ { 4-2x } } = intlimits_0^2 { left[ { 16-8x-4x+2x^2-(4-2x)^2/2 }right]dx } = \ = intlimits_0^2 { left( { 8-4x }right)dx } = left. { left( { 8x-2x^2 }right) }right|_0^2 =16-8=8$

Пример 2

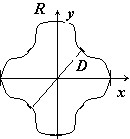
Найти объём области, ограниченной поверхностями $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { R } } ^ { 2 } $,

$(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$.

Решение:

Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $mathbf { textit { Oz } } $ { в уравнении нет $mathbf { textit { z } } $ в явной форме). Построить в плоскости $mathbf { textit { Oxy } } $ кривую шестого порядка, заданную уравнением $(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей { чётные степени } и точка $mathbf { textit { О } } (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(cos ^4varphi +sin ^4varphi );r^2=R^2((cos ^2varphi +sin ^2varphi )^2-2cos ^2varphi sin ^2varphi )=R^2(1-frac { sin ^22varphi } { 2 } )=$

$=R^2(1-frac { 1-cos 4varphi } { 4 } )=R^2frac { 3+cos 4varphi } { 4 } ;r=Rfrac { sqrt { 3+cos 4varphi } } { 2 } .$ Эту кривую построить уже можно. $r(varphi )$ максимально, когда $cos 4varphi =1;(varphi =0,frac { 2pi } { 4 } =frac { pi } { 2 } ,frac { 4pi } { 4 } =pi ,frac { 6pi } { 4 } =frac { 3pi } { 2 } )$, минимально, когда

$cos 4varphi =-1;(varphi =frac { pi } { 4 } ,frac { 3pi } { 4 } ,frac { 5pi } { 4 } ,frac { 7pi } { 4 } ),$ и гладко меняется между этими пределами { точка $mathbf { textit { О } } (0,0)$ не принадлежит этой кривой, где мы её потеряли? } .

Пользуясь симметрией, получаем $ V=16iintlimits_D { sqrt { R^2-x^2-y^2 } dxdy= } 16iintlimits_D { sqrt { R^2-r^2 } rdrdvarphi = } =16intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } rdr } = $ $ =-8intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } d(R^2-r^2) } =-8frac { 2 } { 3 } intlimits_0^ { frac { pi } { 4 } } { left. { (R^2-r^2)^ { frac { 3 } { 2 } } }right|_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } dvarphi } =-frac { 16 } { 3 } R^3intlimits_0^ { frac { pi } { 4 } } { left. { left[ { left( { frac { sin ^22varphi } { 2 } }right)^ { frac { 3 } { 2 } } -1 }right] }right|dvarphi } = $ и т.д.

Пример 3

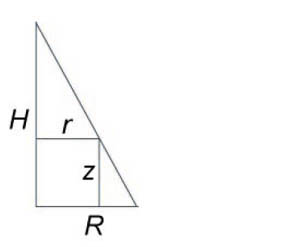
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)

Решение:

Данное тело показано на рисунке.

Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ { V = iintlimits_R { left[ { left( { 4 — x }right) — x }right]dxdy } } = { intlimits_0^2 { left[ { intlimits_0^2 { left( { 4 — 2x }right)dy } }right]dx } } = { intlimits_0^2 { left[ { left. { left( { 4y — 2xy }right) }right|_ { y = 0 } ^2 }right]dx } } = { intlimits_0^2 { left( { 8 — 4x }right)dx } } = { left. { left( { 8x — 2 { x^2 } }right) }right|_0^2 } = { 16 — 8 = 8. } $

Пример 4

Описать тело, объем которого определяется интегралом (V = intlimits_0^1 { dx } intlimits_0^ { 1 — x } { left( { { x^2 } + { y^2 } }right)dy } .)

Решение:

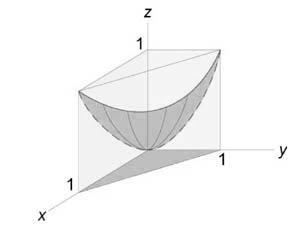
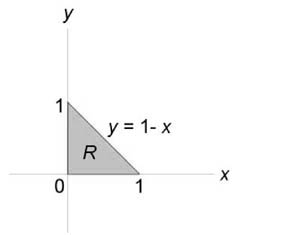
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = { x^2 } + { y^2 } .) Объем тела равен $ { V = intlimits_0^1 { dx } intlimits_0^ { 1 — x } { left( { { x^2 } + { y^2 } }right)dy } } = { intlimits_0^1 { left[ { left. { left( { { x^2 } y + frac { { { y^3 } } } { 3 } }right) }right|_ { y = 0 } ^ { 1 — x } }right]dx } } = { intlimits_0^1 { left[ { { x^2 } left( { 1 — x }right) + frac { { { { left( { 1 — x }right) } ^3 } } } { 3 } }right]dx } } = \ = { intlimits_0^1 { left( { { x^2 } — { x^3 } + frac { { 1 — 3x + 3 { x^2 } — { x^3 } } } { 3 } }right)dx } } = { intlimits_0^1 { left( { 2 { x^2 } — frac { { 4 { x^3 } } } { 3 } — x + frac { 1 } { 3 } }right)dx } } = { left. { left( { frac { { 2 { x^3 } } } { 3 } — frac { 4 } { 3 } cdot frac { { { x^4 } } } { 4 } — frac { { { x^2 } } } { 2 } + frac { x } { 3 } }right) }right|_0^1 } = { frac { 2 } { 3 } — frac { 1 } { 3 } — frac { 1 } { 2 } + frac { 1 } { 3 } = frac { 1 } { 6 } . } $

Пример 5

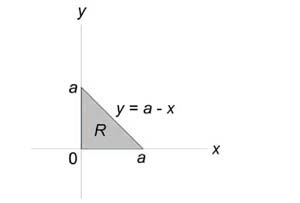
Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)

Решение:

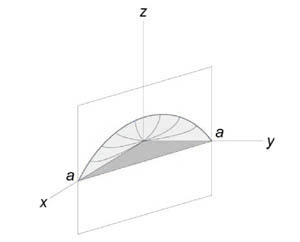
Данное тело лежит над треугольником (R) в плоскости (Oxy) ниже поверхности (z = xy.) Объем тела равен $ { V = iintlimits_R { xydxdy } } = { intlimits_0^a { left[ { intlimits_0^ { a — x } { xydy } }right]dx } } = { intlimits_0^a { left[ { left. { left( { frac { { x { y^2 } } } { 2 } }right) }right|_ { y = 0 } ^ { a — x } }right]dx } } = { frac { 1 } { 2 } intlimits_0^a { x { { left( { a — x }right) } ^2 } dx } } = { frac { 1 } { 2 } intlimits_0^a { xleft( { { a^2 } — 2ax + { x^2 } }right)dx } } = \ = { frac { 1 } { 2 } intlimits_0^a { left( { { a^2 } x — 2a { x^2 } + { x^3 } }right)dx } } = { frac { 1 } { 2 } left. { left( { { a^2 } cdot frac { { { x^2 } } } { 2 } — 2a cdot frac { { { x^3 } } } { 3 } + frac { { { x^4 } } } { 4 } }right) }right|_0^a } = { frac { 1 } { 2 } left( { frac { { { a^2 } } } { 2 } — frac { { 2 { a^4 } } } { 3 } + frac { { { a^4 } } } { 4 } }right) } = { frac { { { a^4 } } } { { 24 } } . } $

Пример 6

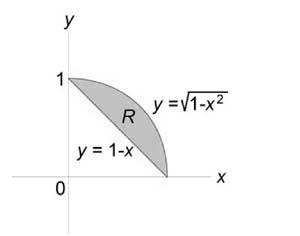
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( { x^2 } + { y^2 } = 1,) (z = 1 — x.)

Решение:

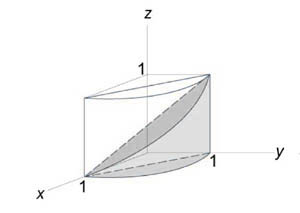
Как видно из рисунков, в области интегрирования (R) при (0 le x le 1) значения (y) изменяются от (1 — x) до (sqrt { 1 — { x^2 } } .)

Сверху тело ограничено плоскостью (z = 1 — x.) Следовательно, объем данного тела равен $ { V = iintlimits_R { left( { 1 — x }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_ { 1 — x } ^ { sqrt { 1 — { x^2 } } } { left( { 1 — x }right)dy } }right]dx } } = { intlimits_0^1 { left[ { left( { 1 — x }right)left. y right|_ { 1 — x } ^ { sqrt { 1 — { x^2 } } } }right]dx } } = { intlimits_0^1 { left( { 1 — x }right)left( { sqrt { 1 — { x^2 } } — 1 + x }right)dx } } = \ = { intlimits_0^1 { left( { sqrt { 1 — { x^2 } } — xsqrt { 1 — { x^2 } } — 1 + 2x — { x^2 } }right)dx } } = { intlimits_0^1 { sqrt { 1 — { x^2 } } dx } } — { intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } } — { intlimits_0^1 { left( { 1 + 2x — { x^2 } }right)dx } . } $

Вычислим полученные три интеграла отдельно. $ { I_1 } = intlimits_0^1 { sqrt { 1 — { x^2 } } dx } .$ Сделаем замену: (x = sin t.) Тогда (dx = cos tdt.) Видно, что (t = 0) при (x = 0) и (t = largefrac { pi } { 2 } normalsize) при (x = 1.) Следовательно, $ { { I_1 } = intlimits_0^1 { sqrt { 1 — { x^2 } } dx } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { sqrt { 1 — { { sin } ^2 } t } cos tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { cos } ^2 } tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { frac { { 1 + cos 2t } } { 2 } dt } } = { frac { 1 } { 2 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { left( { 1 + cos 2t }right)dt } } = { frac { 1 } { 2 } left. { left( { t + frac { { sin 2t } } { 2 } }right) }right|_0^ { largefrac { pi } { 2 } normalsize } } = { frac { 1 } { 2 } left( { frac { pi } { 2 } + frac { { sin pi } } { 2 } }right) = frac { pi } { 4 } . } $ { Сравните с площадью сектора единичного круга в первом квадранте).

Вычислим второй интеграл ( { I_2 } = intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } ,) используя замену переменной. Полагаем (1 — { x^2 } = w.) Тогда (-2xdx = dw) или (xdx = largefrac { { — dw } } { 2 } normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ { { I_2 } = intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } } = { intlimits_1^0 { sqrt w left( { — frac { { dw } } { 2 } }right) } } = { — frac { 1 } { 2 } intlimits_1^0 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { { w^ { largefrac { 1 } { 2 } normalsize } } dw } } = { frac { 1 } { 2 } left. { left( { frac { { 2 { w^ { largefrac { 3 } { 2 } normalsize } } } } { 3 } }right) }right|_0^1 = frac { 1 } { 3 } . } $ Наконец, вычислим третий интеграл. $require { cancel } { { I_3 } = intlimits_0^1 { left( { 1 — 2x + { x^2 } }right)dx } } = { left. { left( { x — { x^2 } + frac { { { x^3 } } } { 3 } }right) }right|_0^1 } = { cancel { 1 } — cancel { 1 } + frac { 1 } { 3 } = frac { 1 } { 3 } . } $ Таким образом, объем тела равен $ { V = { I_1 } — { I_2 } — { I_3 } } = { frac { pi } { 4 } — frac { 1 } { 3 } — frac { 1 } { 3 } = frac { pi } { 4 } — frac { 2 } { 3 } approx 0,12. } $

Пример 7

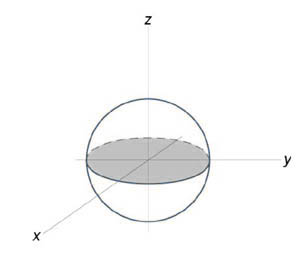
Вычислить объем единичного шара.

Решение:

Уравнение сферы радиусом (1) имеет вид ( { x^2 } + { y^2 } + { z^2 } = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = sqrt { 1 — left( { { x^2 } + { y^2 } }right) } .$ Преобразуя это уравнение в полярные координаты, получаем $zleft( { r,theta }right) = sqrt { 1 — { r^2 } } .$ В полярных координатах область интегрирования (R) описывается множеством (R = left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].) Следовательно, объем верхнего полушара выражается формулой $ { { V_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 — { r^2 } } rdrdtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } } = { 2pi intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } . } $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — { r^2 } = t.) Тогда (-2rdr = dt) или (rdr = — largefrac { { dt } } { 2 } normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ { { V_ { largefrac { 1 } { 2 } normalsize } } = 2pi intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } } = { 2pi intlimits_1^0 { sqrt t left( { — frac { { dt } } { 2 } }right) } } = { — pi intlimits_1^0 { sqrt t dt } } = { pi intlimits_0^1 { { t^ { largefrac { 1 } { 2 } normalsize } } dt } } = { pi left. { left( { frac { { { t^ { largefrac { 3 } { 2 } normalsize } } } } { { frac { 3 } { 2 } } } }right) }right|_0^1 } = { frac { { 2pi } } { 3 } . } $ Таким образом, объем единичного шара равен $V = 2 { V_ { largefrac { 1 } { 2 } normalsize } } = frac { { 4pi } } { 3 } .$

Пример 8

Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).

Решение:

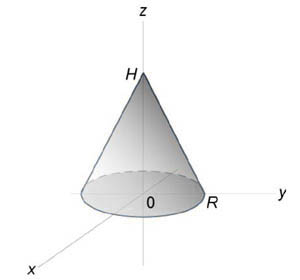
Сначала получим уравнение поверхности конуса. Используя подобные треугольники, можно записать $ { frac { r } { R } = frac { { H — z } } { H } , } ;; { text { где } ;;r = sqrt { { x^2 } + { y^2 } } . } $ Следовательно, $ { H — z = frac { { Hr } } { R } } ;; { text { или } ;;zleft( { x,y }right) } = { H — frac { { Hr } } { R } } = { frac { H } { R } left( { R — r }right) } = { frac { H } { R } left( { R — sqrt { { x^2 } + { y^2 } } }right). } $ Тогда объем конуса равен $ { V = iintlimits_R { zleft( { x,y }right)dxdy } } = { iintlimits_R { frac { H } { R } left( { R — sqrt { { x^2 } + { y^2 } } }right)dxdy } } = { frac { H } { R } iintlimits_R { left( { R — r }right)rdrdtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { left[ { intlimits_0^R { left( { R — r }right)drd } }right]dtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { dtheta } intlimits_0^R { left( { Rr — { r^2 } }right)dr } } = { frac { { 2pi H } } { R } intlimits_0^R { left( { Rr — { r^2 } }right)dr } } = \ = { frac { { 2pi H } } { R } left. { left( { frac { { R { r^2 } } } { 2 } — frac { { { r^3 } } } { 3 } }right) }right|_ { r = 0 } ^R } = { frac { { 2pi H } } { R } left( { frac { { { R^3 } } } { 2 } — frac { { { R^3 } } } { 3 } }right) } = { frac { { 2pi H } } { R } cdot frac { { { R^3 } } } { 6 } = frac { { pi { R^2 } H } } { 3 } . } $



2.2. Как вычислить объём тела с помощью тройного интеграла?

По формуле , где  – искомое тело.

Пример 32

С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями .

Пожалуйста, перепишите на бумагу следующий список:

и ответьте на вопросы: знаете ли Вы, какие поверхности задают эти уравнения? Понятен ли Вам неформальный смысл

этих уравнений? Представляете ли Вы, как данные поверхности расположены в пространстве?

Если Вы склоняетесь к общему ответу «скорее нет, чем да», то обязательно проработайте материалы по геометрии, которые я

рекомендовал на предыдущей странице. Без этого дальше никуда.

Решение: используем формулу .

Для того чтобы выяснить порядок обхода тела и перейти к повторным интегралам нужно (всё гениальное

просто) понять, что это за тело. И такому пониманию во многих случаях здОрово способствуют чертежи.

По условию, тело ограничено несколькими поверхностями. С чего начать построение? Предлагаю следующий порядок действий:

Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость . Это тень тела, когда солнышко светит на него прямо сверху :).

Коль скоро проецирование проводится вдоль оси , то в первую очередь целесообразно разобраться с поверхностями, которые

параллельны данной оси. Напоминаю, что уравнения таких поверхностей не содержат буквы «зет». В нашей задаче их

три:

– уравнение  задаёт координатную

плоскость , которая проходит через ось ;
– уравнение  задаёт координатную

плоскость , которая проходит через ось ;
– уравнение  задаёт

плоскость, проходящую через «одноимённую» «плоскую» прямую параллельно оси .

Исходя из вышесказанного, искомая проекция, скорее всего, представляет собой следующий треугольник:

Возможно, не все до конца поняли, о чём речь. Представьте, что из экрана монитора выходит ось  и утыкается прямо в вашу переносицу (т.е. получается, что

Вы смотрите на 3-мерный чертёж сверху). Исследуемое пространственное тело находится в бесконечном трёхгранном «коридоре»,

и его проекция на плоскость ,

вероятнее всего, представляет собой заштрихованный треугольник.

Обращаю особое внимание, что пока мы высказали лишь предположение о проекции и оговорки «скорее всего»,

«вероятнее всего» были не случайны. Дело в том, что проанализированы ещё не все поверхности и может статься так, что

какая-нибудь из них «оттяпает» часть треугольника. В качестве наглядного примера напрашивается сфера с центром в

начале координат радиусом мЕньшим единицы, например, сфера   – её проекция на плоскость  (круг ) не полностью «накроет» заштрихованную область, и итоговая проекция тела будет

вовсе не треугольником (круг «срежет» ему острые углы).

На втором этапе выясним, чем тело ограничено сверху, чем снизу и выполним пространственный чертёж. Возвращаемся к условию

задачи и смотрим, какие поверхности остались. Уравнение  задаёт саму координатную плоскость , а уравнение   – параболический цилиндр, который расположен над

плоскостью  и проходит через ось . Таким образом, проекция тела

действительно представляет собой треугольник.

Аккуратно изобразим фрагмент параболического цилиндра и искомое тело:

После выполнения чертежей с порядком обхода тела никаких проблем!

Сначала определим порядок обхода проекции (при этом ГОРАЗДО УДОБНЕЕ использовать двумерный чертеж – см. выше). Это

делается АБСОЛЮТНО ТАК ЖЕ, как и в двойных интегралах!

Вспоминаем лазерную указку и «сканирование» плоской области.

Выберем «традиционный» 1-й способ обхода:  

Далее берём в руки волшебный фонарик, смотрим на трёхмерный чертёж и строго снизу вверх просвечиваем

пациента. Лучи входят в тело через плоскость  и выходят из него через поверхность . Таким образом, порядок обхода тела:

Перейдём к повторным интегралам:

С интегралами вновь (ещё раз вновь) рекомендую разбираться по отдельности:

1) Начать следует с самого нутра – «зетового» интеграла:

Подставим результат в «игрековый» интеграл:

Что получилось? По существу решение свелось к двойному интегралу, и именно – к формуле  объёма цилиндрического

бруса! Дальнейшее хорошо знакомо:

2)

3) Последний интеграл удобно взять методом подведения под знак дифференциала – ещё раз заостряю внимание на этом

выгодном способе решения:

Ответ:

Вычисления всегда можно записать и «одной строкой»:

Но с этим способом будьте осторожнее – выигрыш в скорости чреват потерей качества, и чем труднее пример, тем больше шансов

допустить ошибку.

Ответим на важный технический вопрос:

Нужно ли делать чертежи, если условие задачи не требует их выполнения?

Можно пойти четырьмя путями:

1) Изобразить проекцию и само тело. Это самый выигрышный вариант – если есть возможность выполнить два приличных чертежа,

не ленитесь, делайте оба чертежа. Рекомендую в первую очередь.

2) Изобразить только тело. Годится, когда у тела несложная и очевидная проекция. Так, например, в разобранном примере

хватило бы и трёхмерного чертежа. Однако тут есть и минус – по 3D-картинке неудобно определять порядок обхода проекции, и этот

способ я бы советовал только людям с хорошим уровнем подготовки.

Следующее тело для  самостоятельного дела:

Пример 33

С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями

В данном случае область интегрирования задана преимущественно неравенствами, и это даже лучше – множество

неравенств  задаёт 1-й октант,

включая координатные плоскости, а неравенство  задаёт полупространство, содержащее начало координат

(проверьте) + саму плоскость .

«Вертикальная» плоскость  рассекает

параболоид по параболе и на чертеже желательно построить данное сечение. Для этого нужно найти дополнительную опорную

точку, лучше всего – вершину параболы (рассматриваем значения  и рассчитываем соответствующее «зет»).

…Тёмный лес? Вам сюда + сюда либо сюда – поднимаем геометрию!

Примерный образец оформления задачи в конце урока.

Продолжаем разминаться:

Пример 34

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Выполнить чертёж.

Решение: формулировка «выполнить чертёж» даёт нам некоторую свободу, но, скорее всего, подразумевает

выполнение пространственного чертежа. Однако и проекция тоже не помешает, тем более, она здесь не самая простая.

Придерживаемся отработанной ранее тактики, сначала разберёмся с поверхностями, параллельными оси аппликат.

Уравнения таких поверхностей не содержат в явном виде переменную «зет»:
– уравнение  задаёт координатную

плоскость , проходящую через ось  (ось абсцисс на плоскости  определяется «одноимённым» уравнением

);
– уравнение  задаёт плоскость,

проходящую через «одноимённую» «плоскую» прямую параллельно оси .

Но две прямые  не задают

ограниченную проекцию, и, очевидно, параболический цилиндр  своими линиями пересечения с координатной плоскостью  замыкает плоскую фигуру. Чтобы выяснить их уравнения нужно решить

простейшую систему:
Подставим  в первое уравнение:  – получены две прямые, лежащие в

плоскости  и параллельные оси .

Определим порядок обхода тела, при этом «иксовые» и «игрековые» пределы интегрирования удобнее выяснять по

двумерному чертежу:
 – луч лазера просвечивает тело

строго снизу вверх!
 – смотрим на проекцию тела.

Таким образом:
 

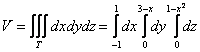
1)

2) Напоминаю, что при интегрировании по «игрек» – «икс» считается константой, поэтому константу  удобно сразу вынести за знак интеграла.

3) И заключительный, внимательный аккорд:

Ответ:

Да, чуть не забыл, в большинстве случаев полученный результат малополезно (и даже вредно) сверять с трёхмерным чертежом,

поскольку с большой вероятностью возникнет иллюзия объёма, о которой я рассказал в одной из статей сайта. Суть

иллюзии состоит в том, что люди склонны неверно оценивать объём «на глазок», мы его либо занижаем, либо завышаем.

Так, человек за среднестатистическую жизнь суммарно выпивает жидкости объёмом со стандартную комнату 18 кв. м., что кажется

очень малым объёмом. В нашей задаче наоборот – если вы посмотрите на пространственный чертёж, то вам покажется, что тело

содержит больше четырёх «кубиков».

И после познавательного отступления задание для самостоятельного решения:

Пример 35

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и

его проекции на плоскость .

Обратите внимание, что условие этой задачи безвариантно требует выполнения обоих чертежей.  Примерный образец оформления в

конце книги.

Не редкость, когда выполнение трёхмерного чертежа затруднено, и этой ситуации посвящены ближайшие примеры:

Пример 36

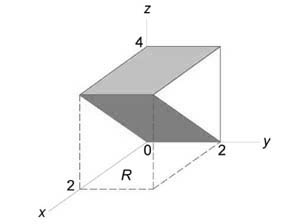
С помощью тройного интеграла найти объём тела, ограниченного поверхностями

Решение: проекция здесь несложная, но вот над порядком её обхода нужно подумать. Если

выбрать 1-й способ, то фигуру придётся разделить на 2 части, что

неиллюзорно грозит вычислением суммы двух тройных интегралов. В этой связи гораздо перспективнее выглядит 2-й путь. Выразим , изобразим проекцию на чертеже:

и выберем более выгодный порядок обхода фигуры:

Теперь дело за телом. Снизу оно ограничено плоскостью , сверху – плоскостью , которая проходит через ось . И всё бы было ничего, но последняя плоскость слишком крутА и построить

тело не так-то просто. Выбор тут незавиден: либо ювелирная работа в мелком масштабе (т.к. тело достаточно тонкое), либо чертёж

высотой порядка 20 сантиметров (да и то, если вместится на тетрадный лист). 

Но есть и третий, исконно русский метод решения проблемы – забить =). И вместо трёхмерного чертежа обойтись словесным

описанием: «Данное тело ограничено цилиндрами  и плоскостью  сбоку, плоскостью  – снизу и плоскостью  – сверху».

«Вертикальные» пределы интегрирования, очевидно, таковы:

Вычислим объём тела, не забывая, что проекцию мы обошли менее распространённым способом:

1)

2)

3)

Ответ:

Как вы заметили, предлагаемые в задачах телА часто ограничены плоскостью  снизу. Но это не есть какое-то правило, поэтому всегда нужно быть начеку –

может попасться задание, где тело расположено и под плоскостью . Так, например, если в рассмотренной задаче вместо  рассмотреть плоскость , то исследованное тело отобразится симметрично в нижнее

полупространство и будет ограничено плоскостью  снизу, а плоскостью  – уже сверху!

Легко убедиться, что получится тот же самый результат:

(помним, что тело нужно обходить строго снизу вверх!)

Кроме того, «любимая» плоскость может оказаться вообще не при делах, простейший пример: шар, расположенный выше

плоскости  – при вычислении его

объёма уравнение  не понадобится

вообще.

Все эти случаи мы рассмотрим, а пока аналогичное задание для самостоятельного решения:

Пример 37

С помощью тройного интеграла найти объём тела, ограниченного поверхностями:

Сверяемся с решением в конце книги и переходим к параграфу с не менее популярными материалами:

2.3. Тройной интеграл в цилиндрических координатах

2.1. Понятие тройного инетграла

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

а) Объём.

Как мы знаем, объем
V
тела, ограничен­ного поверхностью
,
где
—
неотрицательная функ­ция, плоскостьюи цилиндрической поверхностью,
направ­ляющей для которой служит
граница областиD,
а образующие параллельны оси Oz,
равен двойному интегралу от функции
по областиD
:

Пример 1. Вычислить
объем тела, ограниченного поверхностями
x=0,
у=0, х+у+z=1,
z=0
(рис. 17).

Рис.17
Рис.18

Решение.
D
— заштрихованная на рис. 17 треугольная
область в плоскости Оху,
ограниченная прямыми x=0,
у=0, x+y=1.
Расставляя пределы в двойном интеграле,
вычислим объем:

Итак,
куб. единиц.

Замечание 1.
Если тело, объем которого ищется,
ограни­чено сверху поверхностью
а снизу—поверхностью,
причем проекцией обеих поверхностей
на пло­скостьОху
является область D,
то объем V
этого тела равен разности объемов двух
«цилиндрических» тел; первое из этих
цилиндрических тел имеет нижним
основанием область D,
а верх­ним — поверхность
второе тело имеет нижним осно­ванием
также областьD,
а верхним — поверхность
(рис.18).

Поэтому объём V
равен разности двух двойных интегралов
:

или

(1)

Легко, далее,
доказать, что формула (1) верна не только
в том случае, когда
инеотрицательны, но и тогда, когдаи—
любые непрерывные функции, удовлетворяющие
соотношению

Замечание 2.
Если в области D
функция
меняет
знак, то разбиваем область на две части:
1) областьD₁
где
2) областьD₂
,где
.
Предположим, что областиD₁
и D₂
таковы, что двойные интегралы по этим
обла­стям существуют. Тогда интеграл
по области D₁
будет положи­телен и будет равен
объему тела, лежащего выше плоскости
Оху. Интеграл
по D₂
будет отрицателен и по абсолютной
величине равен объему тела, лежащего
ниже плоскости Оху,
Следовательно, интеграл по D
будет выражать раз­ность соответствующих
объемов.

б) Вычисление
площади плоской области.

Если мы со­ставим
интегральную сумму для функции
по областиD,
то эта сумма будет равна площа­ди S,

при любом способе
разбиения. Пере­ходя к пределу в правой
части равен­ства, получим

Если область D
правильная , то площадь выразится
двукратным интегралом

Производя
интегрирование в скобках, имеем,
очевидно,

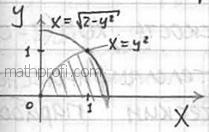
Пример 2. Вычислить
площадь области, ограниченной кривыми

Рис.19

Решение. Определим
точки пересечения данных кривых
(Рис.19). В точке пересечения ординаты
равны, т.е.
,
отсюдаМы
получили две точки пересечения

Следовательно,
искомая площадь

5. Вычисление площади поверхности.

Пусть требуется
вычислить площадь поверхности,
ограниченной линией Г (рис.20); поверхность
задана уравнением
где функциянепрерывна и имеет непрерывные частные
производные. Обозначим проекцию линии
Г на плоскостьOxy
через L.
Область на плоскости Oxy,
ограниченную линией L,
обозначим D.

Разобьём произвольным
образом область D
на n
элементарных площадок
В
каждой площадкевозьмём точкуТочкеP_i
будет соответствовать на поверхности
точка
Через точкуM_i
проведём касательную плоскость к
поверхности. Уравнение её примет вид

(1)

На этой плоскости
выделим такую пло­щадку
,
которая проектируется на плоскостьОху
в виде площадки
.
Рассмотрим сумму всех площадок

Предел
этой суммы, когда наибольший из диаметров
пло­щадок—
стремится к нулю, мы будем называтьплощадью
по­верхности,
т. е. по определению положим

(2)

Займемся теперь
вычислением площади поверхности.
Обозна­чим через

угол между
касательной плоскостью и плоскостью
Оху.

Рис.20
Рис.21

На основании
известной формулы аналитической
геометрии можно написать (рис.21)

или

(3)

Угол
есть в то же время угол между осьюOz
и перпендикуляром к плоскости (1). Поэтому
на основании уравнения (1) и формулы
аналитической геометрии имеем

Следовательно,

Подставляя это
выражение в формулу (2), получим

Так как предел
интегральной суммы, стоящей в правой
части последнего равенства, по определению
представляет собой двойной интеграл
то окончательно получаем

(4)

Это и есть формула,
по которой вычисляется площадь поверхности

Если уравнение
поверхности дано в виде
или в видето соответствующие формулы для вычисления
поверхности имеют вид

(3^’)

(3^’’)

где D^’
и D^’’
— области на плоскостях Oyz
и Oxz,
в которые проектируется данная
поверхность.

а) Примеры.

Пример 1. Вычислить
поверхность
сферы

Решение. Вычислим
поверхность верхней половины сферы
(рис.22). В этом случае

Следовательно,
подынтегральная функция примет вид

Область интегрирования
определяется условием
.
Таким образом, на основании формулы (4)
будем иметь

Для вычисления
полученного двойного интеграла перейдём
к полярным координатам. В полярных
координатах граница области интегрирования
определяется уравнением
Следовательно,

Пример2. Найти
площадь той части поверхности цилиндра
которая вырезается цилиндром

Рис.22
Рис.23

Решение. На рис.23
изображена
часть искомой поверхности. Уравнение
поверхности имеет вид;
поэтому

Область интегрирования
представляет собой четверть круга, т.е.
определяется условиями

Следовательно,

Список использованной
литературы.

1. А.Ф. Бермант ,И.Г.
   Араманович

Краткий курс
математического анализа для втузов:
Учебное пособие для втузов: — М.: Наука,
Главная редакция физико-математической
литературы , 1971 г.,736с.

1. Н.С. Пискунов

Дифференциальное
и интегральное исчисления для втузов,
Том 2:

Учебное пособие
для втузов.-13-е изд. -М. :Наука, Главная
редакция физико-математической
литературы, 1985.-560с.

1. В.С. Шипачёв

Высшая
математика: Учебное пособие для втузов:
— М: Наука,

Главная редакция
физико-математической литературы.

Соседние файлы в предмете Алгебра и геометрия

• #
• #
• #

(схема 41)

     Для функции трех переменных имеет место обобщение определенного интеграла — тройной интеграл (также кратный интеграл). Его теория аналогична теории двойного интеграла. 

      Пусть непрерывная функция u=f (x,y,z) задана в
некоторой ограниченной замкнутой пространственной области V (рис. 6.4). Разобьем эту область на пространственные
ячейки .

В каждой ячейке  выберем произвольную
точку   и умножим значение
функции  f в этой точке на объем ∆ν_i ячейки V_i. Сумма таких произведений по всем ячейкам называется
интегральной
суммой. Обозначим через d(V_i) диаметр ячейки V_i, то есть расстояние между наиболее удаленными точками
этой ячейки, и max d(V_i)
– наибольший из диаметров всех ячеек данного разбиения.

Тройным интегралом  от функции f(M) по области  V  называется предел интегральной суммы при условии max d(V_i)→0,
то есть при неограниченном увеличении числа ячеек, когда все ячейки стягиваются
в точку:

    .                                                                                                          

Если такой предел существует, то функция f(M)
называется интегрируемой в области V; всякая непрерывная в ограниченной замкнутой области V функция f(M)
интегрируема в ней. В дальнейшем мы будем рассматривать только непрерывные
функции.

В декартовых координатах элемент объема обычно
записывают в виде dν=dxdydz, а
тройной интеграл обозначают

 .                                                                                                                                                                (6.9)

Тройной интеграл (6.9) выражает массу неоднородного тела объема V, с плотностью в каждой точке γ=f (x,y,z) посредством формулы:

.                                                                                                                                                       (6.10)

Координаты
центра тяжести тела
вычисляются по формулам:

   .                                                                                        (6.11)

Если плотность γ=1,
то тройной интеграл (6.9) будет выражать собой объем области V, а формулы
(6.11) будут представлять координаты центра тяжести однородного тела.

1.
Вычисление тройного интеграла в декартовой системе координат

Пусть V проектируется в область D на плоскости x0y так, что всякая прямая, параллельная оси 0z и
проходящая внутри области D, пересекает границу области V ровно в
двух точках. В общем случае такая область ограничена сверху поверхностью z=ψ₂(x,y), снизу –
поверхностью z=ψ₁(x,y) и с боков – цилиндрической поверхностью с
образующими, параллельными оси 0z (рис. 52). Такая область V называется правильной. В частных случаях
боковая поверхность цилиндра может превратиться в линию. Функции ψ₁(x,y) и ψ₂(x,y) мы будем считать непрерывными. Тройной интеграл по
такой области вычисляется по формуле

.                                                                                                               (6.12)

Здесь
внутренний интеграл  берется по z при фиксированных, но
произвольных в D значениях x и y, от нижней границы области V до ее
верхней границы, то есть по отрезку KL (рис. 6.4). В
результате получается некоторая функция двух переменных x и y, которая
интегрируется затем по области D с помощью формул (6.5) или (6.6). Таким образом,
вычисление тройного интеграла сводится к трехкратному интегрированию.

Наиболее простой вид формула (6.12) принимает в
случае, когда V есть прямоугольный параллелепипед, ограниченный
плоскостями :

.                                                                                                       (6.13)

Если область V имеет более сложную форму, то ее разбивают на
конечное число областей , каждая из которых удовлетворяет условиям, изложенным выше.

Примечание. Аналогичные определения и формулы могут быть
получены и тогда, когда область V проектируется в область D, лежащую или в плоскости  x0z, или в плоскости 
y0z

             Пример 6.4. Вычислить тройной интеграл , где область V ограничена координатными плоскостями и плоскостью x+y+z=1 (рис. 6.5).

Решение. Область V – треугольная пирамида – ограничена снизу плоскостью z=0, сверху –
плоскостью z=1–x–y. Область V проектируется на плоскость x0y в виде
прямоугольного треугольника, который определяется неравенствами . Следовательно, используя (6.5) и (6.12), получим:

Пример 6.5. Найти объём тела ограниченного параболоидом z=x²+y²+2 и
плоскостями z=1, x=0, y=0, x+y=2 (рис. 6.6).

 
Решение. По условию область V задана
неравенствами:

.

Следовательно,

(единиц
объема)

Пример 6.6. Найти массу тела ограниченного координатными
плоскостями и плоскостью x+y+z=1, если плотность в каждой его точке равна
произведению координат этой точки, то есть γ = f(x,y,z) = x y z.

Решение. По условию область V совпадает с той областью, которая была рассмотрена в
примере 6.4 (см. рис. 6.5). Искомая масса M согласно
формуле (6.11) равна интегралу . Следовательно,

.

Чтобы
вычислить полученный интеграл, положим 1–x=t; тогда dx= – dt; при этом t=1 при x=0 и t=0 при x=1.

   (единиц массы)

Пример 6.7. Вычислить координаты центра тяжести куба , если плотность в каждой его точке равна произведению
координат этой точки.

Решение. По условию плотность γ=x y z. Вычислим массу M куба по (6.10): 

.

Из соображений симметрии следует x_c = y_c = z_c. Поэтому достаточно найти только одну координату x_c.
Вычислим числитель для x_c в формуле (6.11).

2.     Вычисление
тройного интеграла в цилиндрических координатах

Для упрощения вычисления тройного интеграла часто
бывает целесообразным перейти к цилиндрическим координатам. Точка M(x;y;z) в
пространстве 0xyz может быть определена заданием трех величин r; φ; z, где
r – длина
радиус-вектора проекции точки M  на плоскость x0y, φ – угол, образованный этим  радиус-вектором с осью 0x, z –
аппликата точки  M (рис. 6.7).   Эти
числа (r; φ; z) называются цилиндрическими координатами точки M. Эти
координаты связаны с ее декартовыми координатами соотношениями:

                                                                                                                                              (6.14)

.

В этом случае тройной
интеграл вычисляется по формуле

.                              (6.15)

После применения (6.15)
вычисление тройного интеграла сводится к 
трехкратному  по r, по φ и по z
согласно формуле (6.12).

Пример
6.8.  Вычислить , где V – область, ограниченная частью конуса  и плоскостью z=2.

Решение. Заданная область V – часть конуса, вершина которого расположена в начале
координат. Его уравнение в цилиндрических координатах (6.14) имеет вид

 или z=r. Граница области V – окружность x²+y² =4 запишется
как r=2. Новые переменные изменяются в следующих пределах:

,  (прямая, параллельная
оси 0z, пересекающая область D, входит в конус z=r и выходит
из него на высоте z=2).

С учетом формулы замены (6.15) можем вычислить
заданный тройной интеграл:

Обратим внимание на то, что, не переходя к
цилиндрическим координатам, мы получили бы достаточно сложное трехкратное
интегрирование согласно формуле (6.12)

Примечание. Переход
к цилиндрическим координатам рационален, когда область интегрирования
образована цилиндрической или конической поверхностью

3.    
Вычисление тройного интеграла в сферических
координатах

Если область интегрирования V представляет собой шар или
его часть (граница шара x²+y²+z²=R² в сферических координатах имеет очень простой вид ρ=R),  то удобно переходить к сферическим
координатам.

Сферическими координатами точки M(x;y;z) пространства 0xyz называется тройка чисел ρ; φ; θ (рис.
6.8), где ρ – длина радиус-вектора точки
M, φ – угол, образованный проекцией радиус-вектора на плоскость x0y и осью 0x, θ – угол отклонения радиус-вектора  от оси 0z. Эти координаты связаны с декартовыми координатами
точки M соотношениями:

.  (6.16)

В этом случае тройной
интеграл вычисляется по формуле

.                                                           (6.17)

Примечание. Переход к
сферическим координатам целесообразен также в том случае, когда подынтегральная
функция имеет вид f(x²+y²+z²)