Как найти объем тела полученного вращением кривой - Исправление недочетов и поиск решений вместе с Examum.ru

Объемы тел вращения

Краткая теория

Объемы тел, образованных вращением
криволинейной трапеции, ограниченной кривой

, осью

и двумя
вертикалями

, вокруг осей

, выражаются соответственно формулами:

Объем тела, образованного вращением
около оси

фигуры,
ограниченной кривой

, осью

и двумя
параллелями

, можно определять по формуле:

Если кривая задана в иной форме
(параметрически, в полярных координатах и т.д.), то в приведенных формулах
нужно сделать соответствующую замену переменной интегрирования.

В более общем случае объемы тел,
образованных вращением фигуры, ограниченной кривыми

(причем

) и прямыми

, вокруг координатных осей

, соответственно равны:

Объем тела, полученного при вращении
сектора, ограниченного дугой кривой

и двумя
полярными радиусами

, вокруг полярной оси, может быть вычислен по формуле:

Этой же формулой удобно пользоваться
при отыскании объема тела, полученного вращением вокруг полярной оси фигуры,
ограниченной некоторой замкнутой кривой, заданной в полярных координатах.

Если

– площадь
сечения тела плоскостью, перпендикулярной к некоторой прямой (которую принимаем
за ось

), в точке с абсциссой

, то объем этого тела равен:

где

– абсциссы
крайних сечений тела.

Примеры решения задач

Задача 1

С помощью
определенного интеграла вычислить объем тела, полученного вращением фигуры

вокруг указанной оси координат.

вокруг
оси

Решение

Сделаем
чертеж:

Объем
тела, образованного вращением вокруг оси

фигуры можно найти по формуле:

В нашем
случае получаем

Ответ:

Задача 2

Найдите
объем тела, полученного вращением вокруг оси абсцисс криволинейной трапеции,
ограниченной линиями:

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Сделаем
чертеж:

Объем
тела можно найти по формуле:

Ответ:

Задача 3

Определить
объем, образованный вращением кривой

вокруг
полярной оси.

Решение

Ответ:

Задача 4

Вычислить
объем тела, ограниченного однополосным гиперболоидом

и
плоскостями

Решение

Здесь
удобнее рассмотреть сечения данного тела плоскостями, перпендикулярными к оси

. Тогда объем выразится
формулой:

где

– площадь получаемого сечения, зависящая от
точки с аппликатой

, через которую проходит
секущая плоскость. При пересечении однополосного гиперболоида плоскостью

получается эллипс, который можно определить
уравнениями:

откуда
следует, что полуоси эллипса:

Учитывая, что площадь эллипса с
полуосями

равна

, воспользовавшись параметрическим заданием эллипса:

мы можем записать аналитическое
выражение функции

Тогда искомый объем:

Ответ:

Источник

Объём тела вращения

Пусть — тело вращения, образованное вращением вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямыми x=a и x=b и графиком непрерывной функции y=f(x) .

Докажем, что это тело вращения кубируемо и его объем выражается формулой

$V=pi intlimits_{a}^{b} f^2(x),dx= pi intlimits_{a}^{b}y^2,dx,.$

Сначала докажем, что это тело вращения регулярно, если в качестве выберем плоскость Oyz , перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии от плоскости Oyz , является кругом радиуса f(x) и его площадь S(x) равна pi f^2(x) (рис. 46). Поэтому функция S(x) непрерывна в силу непрерывности f(x) . Далее, если S(x_1)leqslant S(x_2) , то это значит, что f(x_1)leqslant f(x_2) . Но проекциями сечений на плоскость Oyz являются круги радиусов f(x_1) и f(x_2) с центром , и из вытекает, что круг радиуса f(x_1) содержится в круге радиуса f(x_2) .

Чертёж тела вращения вокруг оси абсцисс

Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объем вычисляется по формуле

$V=pi intlimits_{a}^{b} S(x),dx= pi intlimits_{a}^{b}f^2(x),dx,.$

Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми y_1=f_1(x), y_2=f_2(x) , то

$V= pi intlimits_{a}^{b}y_2^2,dx- pi intlimits_{a}^{b}y_1^2,dx= piintlimits_{a}^{b}Bigl(f_2^2(x)-f_1^2(x)Bigr)dx,.$

Формулой (3) можно воспользоваться и для вычисления объема тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определенного интеграла.

В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида.

Например, найдем объем тела, получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдем объем, получаемый при вращении прямоугольника с высотой y#, в основании которого лежит отрезок $[x_k;x_{k+1}]$ . Этот объем равен разности объемов двух прямых круговых цилиндров

$Delta V_k= pi y_k x_{k+1}^2- pi y_k x_k^2= pi y_k bigl(x_{k+1}+x_kbigr) bigl(x_{k+1}-x_kbigr).$

Но теперь ясно, что искомый объем оценивается сверху и снизу следующим образом:

$2pi sum_{k=0}^{n-1} m_kx_kDelta x_k leqslant Vleqslant 2pi sum_{k=0}^{n-1} M_kx_kDelta x_k,.$

Отсюда легко следует формула объёма тела вращения вокруг оси ординат:

$V=2pi intlimits_{a}^{b} xy,dx,.$

(4)

Пример 4. Найдем объем шара радиуса .

Решение. Не теряя общности, будем рассматривать круг радиуса с центром в начале координат. Этот круг, вращаясь вокруг оси , образует шар. Уравнение окружности имеет вид x^2+y^2=R^2 , поэтому y^2=R^2-x^2 . Учитывая симметрию круга относительно оси ординат, найдем сначала половину искомого объема

$frac{1}{2}V= piintlimits_{0}^{R}y^2,dx= piintlimits_{0}^{R} (R^2-x^2),dx= left.{pi!left(R^2x- frac{x^3}{3}right)}right|_{0}^{R}= pi!left(R^3- frac{R^3}{3}right)= frac{2}{3}pi R^3.$

Следовательно, объем всего шара равен $frac{4}{3}pi R^3$ .

Конус, образованный вращением прямой вокруг оси абсцисс

Пример 5. Вычислить объем конуса, высота которого и радиус основания .

Решение. Выберем систему координат так, чтобы ось совпала с высотой h (рис. 47), а вершину конуса примем за начало координат. Тогда уравнение прямой запишется в виде $y=frac{r}{h},x$ .

Пользуясь формулой (3), получим:

$V=pi intlimits_{0}^{h} y^2,dx= pi intlimits_{0}^{h} frac{r^2}{h^2},x^2,dx= left.{frac{pi r^2}{h^2}cdot frac{x^3}{3}}right|_{0}^{h}= frac{pi}{3},r^2h,.$

Пример 6. Найдем объем тела, полученного при вращении вокруг оси абсцисс астроиды $begin{cases}x=acos^3t,,\ y=asin^3t,.end{cases}$ (рис. 48).

Объём тела, полученного при вращении вокруг оси абсцисс астроиды

Решение. Построим астроиду. Рассмотрим половину верхней части астроиды, расположенной симметрично относительно оси ординат. Используя формулу (3) и меняя переменную под знаком определенного интеграла, найдем для новой переменной пределы интегрирования.

Если x=acos^3t=0 , то $t=frac{pi}{2}$ , а если x=acos^3t=a , то t=0 . Учитывая, что y^2=a^2sin^6t и $dx=-3acos^2tsin{t},dt$ , получаем:

$V=pi intlimits_{a}^{b} y^2,dx= pi intlimits_{pi/2}^{0} a^2sin^6t bigl(-3acos^2tsin{t}bigr),dt= ldots= frac{16pi}{105},a^3.$

Объем всего тела, образованного вращением астроиды, будет $frac{32pi}{105},a^3$ .

Пример 7. Найдем объем тела, получаемого при вращении вокруг оси ординат криволинейной трапеции, ограниченной осью абсцисс и первой аркой циклоиды $begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}).end{cases}$ .

Решение. Воспользуемся формулой (4): $V=2pi intlimits_{a}^{b}xy,dx$ , и заменим переменную под знаком интеграла, учитывая, что первая арка циклоиды образуется при изменении переменной от до 2pi . Таким образом,

$begin{aligned}V&= 2pi intlimits_{0}^{2pi} a(t-sin{t})a(1-cos{t})a(1-cos{t}),dt= 2pi a^3 intlimits_{0}^{2pi} (t-sin{t})(1-cos{t})^2,dt=\ &= 2pi a^3 intlimits_{0}^{2pi}bigl(t-sin{t}- 2tcos{t}+ 2sin{t}cos{t}+ tcos^2t- sin{t}cos^2tbigr),dt=\ &= left.{2pi a^3!left( frac{t^2}{2}+ cos{t}- 2tsin{t}- 2cos{t}+ sin^2t+ frac{t^2}{4}+ frac{t}{4}sin2t+ frac{1}{8}cos2t+ frac{1}{3}cos^3tright)}right|_{0}^{2pi}=\ &= 2pi a^3!left( 2pi^2+1-2+pi^2+frac{1}{8}+ frac{1}{3}-1+2- frac{1}{8}- frac{1}{3}right)= 6pi^3a^3. end{aligned}$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Дополнения

1.О применении определённого интеграла для нахождения объёмов тел вращения

1.1.Формула объёма тела вращения

В п.16.2 дано определение тела вращения.

Получим формулу для вычисления объёма тела вращения, применяя интеграл, о котором вам рассказали в курсе «Алгебры и начал математического анализа».

Пусть f(x) — непрерывная на отрезке [a; b] функция, не принимающая отрицательных значений; А, В — точки графика этой функции (рис. 225).

Рис. 225

Рассмотрим криволинейную трапецию aABb, ограниченную кривой графика функции y = f(x), отрезками aA, bB и отрезком [a; b] координатной оси Ох (см. рис. 225). При вращении этой трапеции вокруг оси Ох образуется тело вращения (рис. 226), которое обозначим Ф и поставим себе задачу: найти объём этого тела.

Рис. 226

Через произвольную точку х = с (a ⩽ с ⩽ b) отрезка [a; b] проведём плоскость, перпендикулярную оси Ox. Сечением тела Ф этой плоскостью является круг, радиус которого равен f(с), а площадь — πf2(с) (или точка (c; 0)).

Объём части тела Ф, заключённой между этой плоскостью и плоскостью х = a, изменяется при изменении x. Обозначим этот переменный объём V(х). Заметим, что V(x) = V(a) = 0 при х = a; при х = b имеем V(x) = V(b) = V — искомый объём тела вращения Ф.

Покажем, что функция V(x) имеет производную V′(х) и V′(х) = πf2(х).

Придадим абсциссе х приращение ∆х > 0, тогда объём V(х) получает приращение ∆V(х) = V(x + ∆x) – V(x). Пусть m и М — соответственно наименьшее и наибольшее значения функции f(х) на промежутке [х; х + ∆х]. Цилиндр, радиус основания которого равен m, содержится в теле вращения объёма ∆V(x), а цилиндр, радиус основания которого равен M, содержит тело объёма ∆V(х); образующие цилиндров параллельны оси Ох и имеют длину, равную ∆х. Объёмы этих цилиндров равны соответственно πm2•∆x и πM2•∆х. На основании свойства 2 объёмов (п. 10.1) получаем

πm2•∆x ⩽ ∆V(x) ⩽ πM2•∆x,

откуда

πm2 ⩽ ⩽ πM2.

Рассуждения для случая ∆х < 0 проводятся аналогично и дают тот же результат.

Пусть теперь ∆х 0. Имеем m = M = f(x), тогда

πm2 ⩽ ⩽ πM2

или

πf2(х) ⩽ ⩽ πf2(x).

Значит, = πf2(х). По определению производной функции = V′(x). Поэтому V ′(x) = πf2(х), следовательно, V(х) — первообразная для πf2(х).

Таким образом, переменный объём V(x) телa вращения представляет собой одну из первообразных для функции πf 2(х) на отрезке [a; b]. Эта первообразная обладает тем свойством, что при х = a она обращается в нуль (V(a) = 0), а при х = b значение функции V(x) равно объёму тела вращения Ф (V(b) = V).

Если F(х) — также некоторая первообразная для функции πf 2(x), то V(x) = F(x) + С, где С — произвольная постоянная. Так как V (a) = 0, то из равенства V(a) = F (a) + C = 0 находим С = –F(a). Значит, V(x) = F(x) – F(a). Toгдa V(b) = F(b) – F(a). Ho V(b) = V — искомый объём тела вращения Ф. Таким образом, V = F(b) – F(a), где F(b) и F(a) — значения первообразной для функции πf 2(х) соответственно при х = b и х = a. Это означает, что

V = f 2(x)dx = π(x)dx.

Вот почему объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = f(x), х = a, х = b, у = 0, вычисляется по формуле

Рис. 227

V = (x)dx.(*)

ЗАДАЧА. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = , х = 0, x = 2 и y = 0 (рис. 227).

Решение. Воспользуемся формулой V = π(x)dx, для чего из уравнения у = находим y2 = 2х. Тогда получаем

V = πdx = 2π• = = 4π.

Ответ: 4π.

1.2. Объёмы конуса, шара и его частей

Используя формулу V = (x)dx вычисления объёма тела вращения, получим формулы для вычисления объёма каждого изученного ранее тела вращения.

а) Объём конуса и усечённого конуса

Теорема 1 (об объёме полного конуса). Объём V конуса с высотой Н и радиусом основания R равен одной трети произведения площади основания на высоту:

V = R2Н.

Рис. 228

Доказательство. Конус с высотой Н и радиусом основания R можно рассматривать как тело, образованное вращением вокруг оси Ox прямоугольного треугольника с вершинами О(0; 0), А(Н; 0) и B(Н; R) (рис. 228). Треугольник АОВ является частным случаем криволинейной трапеции, которая ограничена графиком функции у = х (0 ⩽ х ⩽ H), осью Ох и отрезком прямой х = Н. Поэтому, используя формулу (*) п. 1.1 «Дополнений» для объёма V конуса, получаем:

V = dx = π • = πR2H,

где πR2 — площадь основания конуса. Теорема доказана. ▼

Теорема 2 (об объёме усечённого конуса). Объём усечённого конуса с высотой Н и радиусами оснований r и R равен сумме объёмов трёх конусов с высотой Н, радиусы оснований которых соответственно равны r, R и :

V = (r2 + R2 + rR)H.

Доказательство. Усечённый конус с высотой H и радиусами оснований r и R можно получить, вращая вокруг оси Oх прямоугольную трапецию OABC, где O(0; 0), A(0; r), В(Н; R), С(H; 0) (рис. 229).

Рис. 229

Прямая AВ проходит через точки (0; r) и (Н; R), поэтому её уравнение имеет вид у = х + r. Следовательно, трапеция ОАВС ограничена графиком функции y = х + r (0 ⩽ х ⩽ Н), осью Oх и отрезками прямых х = 0 и х = Н. Поэтому, используя формулу (*) из п. 1.1 для объёма V усечённого конуса, получаем:

V = dx.(1)

Для вычисления интеграла сделаем замену переменных

x + r = t.(2)

Тогда dx = dt, откуда dx = dt. Новые пределы интегрирования (по переменной t) найдём посредством подстановки формулы (2): х = 0 ⇒ t = r; х = Н ⇒ t = R. Таким образом, для объёма V усечённого конуса получаем:

что и требовалось доказать. ▼

б) Объём шарового слоя

В прямоугольной декартовой системе координат Оху рассмотрим криволинейную трапецию aABb, ограниченную дугой окружности х2 + у2 = R2, –R ⩽ a ⩽ х ⩽ b ⩽ R, отрезком [a; b] оси Ох и отрезками aА и bВ прямых соответственно x = a и х = b (рис. 230, а).

Рис. 230

При вращении криволинейной трапеции aАВb вокруг оси Ох образуется шаровой слой (рис. 230, б). Найдём его объём, применяя формулу (*) п. 1.1.

Из уравнения х2 + у2 = R2 имеем у2 = R2 – x2. Поэтому для вычисления объёма V шарового слоя получаем:

Таким образом, объём шарового слоя, отсекаемого от шара x2 + y2 + z2 ⩽ R2 радиуса R плоскостями x = a и x = b, вычисляется пo формуле

V = (**)

Пусть радиусы оснований шарового слоя равны r1 и r2 (r1 > r2), а высота — H (см. рис. 230, a).

Тогда Н = b – a, = R2 – a2, = R2 – b2.

Формулу (**) преобразуем к виду:

V = (3R2 – (b2 + ab + a2)) =

= ((R2 – b2) + (R2 – ab) + (R2 – a2)).

Из системы равенств (b – a)2 = H2, R2 – a2 = , R2 – b2 = после почленного сложения их левых и правых частей находим:

R2 – ab = .

Тогда:

V = ((R2 – b2) + (R2 – ab) + (R2 – a2)) =

= .

Таким образом, объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле

V = .(***)

в) Объём шара

Рис. 231

При вращении полукруга х2 + у2 = R2 (расположенного в плоскости Оху, рис. 231, а) вокруг оси Ох образуется шар радиуса R (рис. 231, б). Из уравнения окружности х2 + y2 = R2 данного полукруга имеем у2 = R2 – х2. Тогда, полагая a = –R, b = R в формуле (*) п. 1.1, находим объём V шара радиуса R:

Vш = =

= .

Таким образом, имеет место следующая теорема.

Теорема 3 (об объёме шара). Объём шара радиуса R вычисляется по формуле

Vш = .

г) Объём шарового сегмента

Если b = R (см. п. 1.2, б), то получаем криволинейную трапецию aAB (рис. 232, а), при вращении которой вокруг оси Ох образуется шаровой сегмент (рис. 232, б).

Рис. 232

Пусть высота шарового сегмента равна Н, тогда a = R – Н. Так как дуга AВ криволинейной трапеции aАВ является частью окружности x2 + y2 = R2 (в плоскости Оxу), то формулу объёма шарового сегмента получим по аналогии с выводом формулы для вычисления объёма шара, учитывая при этом, что пределы a и b интегрирования равны: a = R – H, b = R, т. е.

Vш. сегм = =

Таким образом, имеет место следующая теорема.

Теорема 4 (об объёме шарового сегмента). Объём шарового сегмента, отсекаемого от шара радиуса R и имеющего высоту Н, вычисляется по формуле

Vш. сегм =

Если в формуле (***) п. 1.2, б положить r2 = 0, r1 = r, то получим формулу для вычисления объёма шарового сегмента с радиусом основания r и высотой Н:

Vш. сегм = (3r2 + H2).

д) Объём шарового сектора

Рис. 233

Шаровой сектор состоит из конуса с вершиной в центре шара и шарового сегмента, имеющего с конусом общее основание (риc. 233). Пусть R = ОА — радиус шара; АС = r — радиус основания шарового сегмента, NC = H — его высота; N — точка сферы (рис. 233).

Найдём объёмы конуса и шарового сегмента, учитывая, что высота h конуса равна OC = ON – CN = R – Н.

Объём Vк конуса равен

π•АС2•ОС = πr2 (R – Н).

Выразим r2 через R и H.

B прямоугольном треугольнике AOC находим r2 = AC2 = ОА2 – OC2 = R2 – (R – H)2 = H(2R – H).

Значит,

Vк = πH(2R – H)(R – H) = (2R2 – 3RH + H2).

Для объёма шарового сегмента имеем:

Vш. сегм = (3AC2 + NC2) = (3H(2R – H) + H2) =

= (3RН – H2).

Тогда для объёма шарового сектора получаем

Vш. сект = Vк + Vш. сегм =

= (2R2 – 3RH + H2) + (3RH – H2) = πR2H.

Таким образом, доказана следующая теорема.

Теорема 5 (об объёме шарового сектора). Объём шарового сектора шара радиуса R вычисляется по формуле

Vш. сект = R2H,

где Н — длина высоты шарового сегмента, соответствующего данному шаровому сектору.

В курсе математического анализа, который вам предстоит изучать в высшей школе, будет дано строгое обоснование применения определённого интеграла не только для нахождения объёмов тел, но и для нахождения площадей поверхностей и длин дуг линий. Решите самостоятельно следующие задачи.

1)Найдите объём тела, которое получается при вращении вокруг оси Ох криволинейной трапеции, ограниченной гиперболой у = , прямыми х = 3, х = 12 и осью абсцисс. (Ответ: 4π.)

2)Найдите объём тела, образованного вращением вокруг оси Oх фигуры, ограниченной одной полуволной синусоиды у = sin x и отрезком 0 ⩽ х ⩽ π оси абсцисс. (Ответ: 0,5π2.)

3)Найдите объём тела, полученного при вращении кривой у = 0,25х2 вокруг оси Оу в пределах от у = 1 до у = 5. (Ответ: 48π.)

4)Найдите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми у = 2х2 и у = x3.

Источник

Для того, чтобы найти объем фигуры, образованной вращением вокруг оси Ox нужно вычислить определенный интеграл от квадрата функции, задающей график и умножить на число Пи.

$$ V = pi int_a^b y^2 dx $$

В формуле $ a $ и $ b $ значения отложены по оси Ox. Фукция $ y (x) $ задаёт график фигуры, объем вращения которой необходимо вычислить.

Строим график фигуры
Вычисляем определенный интеграл

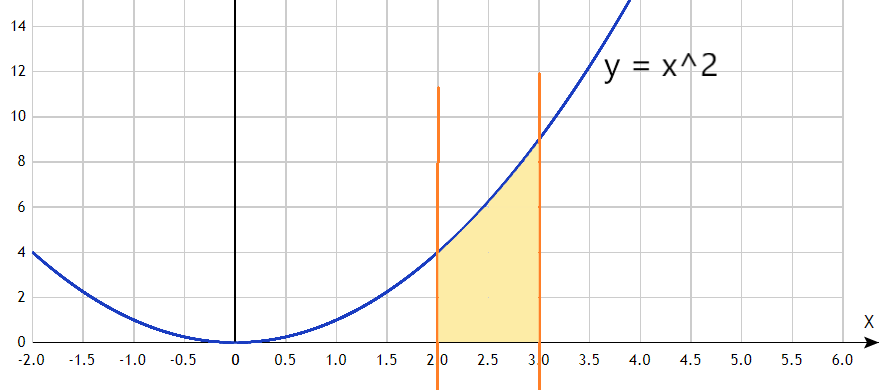
Пример 1

Вычислить объем тела вращения вокруг оси Ox: $ y = x^2 $ и $ a = 2, b = 3 $

Решение

Выполняем построение графика. Чертим на плоскости параболу $ y = x^2 $. Выставляем на чертеже оранжевые линии, соответствующие ограничениям $ a = 2, b = 3 $. Закрашиваемая область желтым цветом выделяет фигуру, объем вращения которой будем искать.

Подставляем в формулу функцию $ y = x^2 $ и пределы интегрирования. Вычисляем определенный интеграл $$ V = pi int_2^3 (x^2)^2 dx = pi int_2^3 x^4 dx = $$

Для взятия интеграла воспользуемся формулой $ int x^p dx = frac{x^{p+1}}{p+1} $

$$ = pi frac{x^5}{5} bigg |_2^3 = pi frac{243}{5} — pi frac{32}{5} = frac{211}{5} pi = 132.5 $$

Получили объем фигуры $ V = 132.5 $

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ V = 132.5 $$

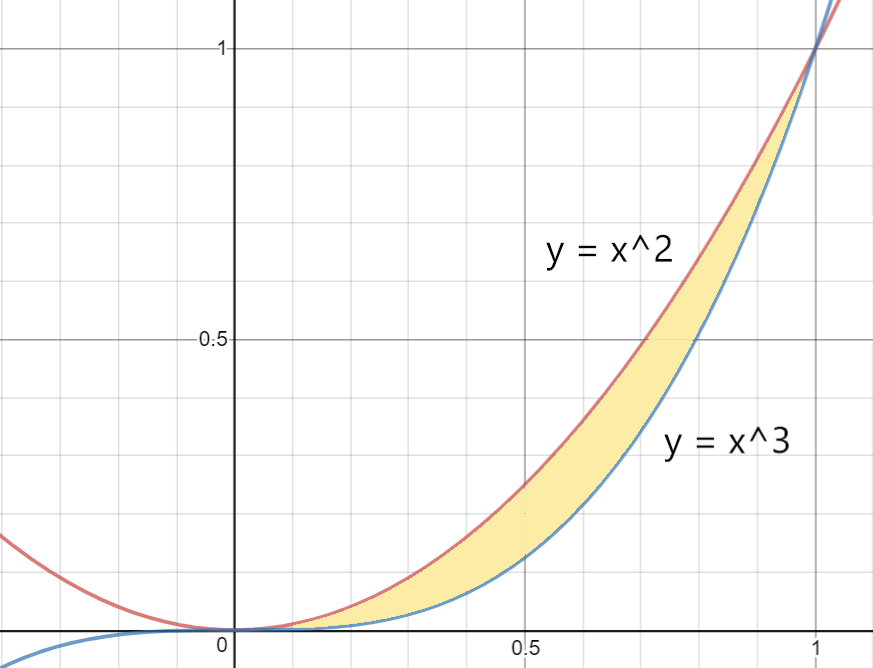
Пример 2

Найти объем тела вращения фигуры вокруг оси Ox, заданной двумя функциями $$ y = x^2, y = x^3 $$

Решение

В данном примере необходимо найти точки пересечения двух графиков функций. Приравниваем их друг к другу и решаем уравнение относительно одной переменной $ x $: $$ x^2 = x^3 $$ Переносим всё в одну строну $$ x^3 — x^2 = 0 $$ Выносим за скобку неизвестную $ x^2 $ и получаем корни уравнения: $$ x^2(x-1) = 0 $$ $$ x^2 = 0, x-1=0 $$ $$ x_1=0, x_2=1 $$

Выполняем построение графиков функций для наглядности. На рисунке закрашиваем область, ограниченную двумя функциями.

Для того, чтобы найти объем тела вращения, заданного с помощью двух функций, необходимо воспользоваться идеей разности объемов. А имеенно, находим сначала объем фигуры вращения, заданной функцией $ y = x^2 $, затем отдельно $ y = x^3 $.

$$ V_1 = pi int_0^1 (x^2)^2 dx = pi frac{x^5}{5} bigg |_0^1 = frac{pi}{5} $$

$$ V_2 = pi int_0^1 (x^3)^2 dx = pi frac{x^7}{7} bigg |_0^1 = frac{pi}{7} $$

Получаем искомый объем с помощью разности объемов $$ V = V_1 — V_2 = frac{pi}{5} — frac{pi}{7} = frac{2pi}{35} $$

Ответ

$$ V = frac{2pi}{35} $$

Источник

Рассмотрим ещё одно распространённое приложение определённого интеграла.

Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … интересно, кто что представил… Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать: вокруг оси или вокруг оси .
В рамках данного курса я остановлюсь на стандартном варианте:

Пример 17
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями , вокруг оси .

Решение: как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. Да, с точно такого же чертежа:

Искомая плоская фигура заштрихована серым цветом, именно она и вращается вокруг оси . В результате получается такое… загадочное яйцо.

Объем тела вращения можно вычислить по формуле:
, где – неотрицательная или неположительная функция, график которой ограничивает плоскую фигуру на отрезке . Заметьте, что здесь не нужно думать, над осью расположена криволинейная трапеция или под осью, т.к. возведение в квадрат стирает разницу между функциями и .

В нашей задаче:

Интеграл почти всегда получается простой, главное, быть ВНИМАТЕЛЬНЫМ.

Ответ: (кубических единиц — «кубиков» единичного объема)

Напоминаю, что , обычно принимают либо .

Пример 18
Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями , ,

Тренируемся и переходим к более содержательному случаю:

Пример 19
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями , , и .

Решение: изобразим на чертеже плоскую фигуру, ограниченную линиями , , , , не забывая, что уравнение задаёт ось :

Искомая фигура заштрихована синим цветом. При её вращении вокруг оси получается такой сюрреалистический бублик с четырьмя углами. Объем этого бублика вычислим как разность объёмов с помощью стандартной формулы .

1) Фигура, обведённая красным цветом ограничена сверху прямой , поэтому:

2) Фигура, обведенная зеленым цветом ограничена сверху прямой , поэтому:

3) Объем искомого тела вращения:

Ответ:

Решение можно оформить и короче, примерно в таком духе:
., но, как вы уже поняли, за скорость приходится расплачиваться повышенным риском допустить ошибку.

И ещё хочу вас предостеречь от оценки результата «на глазок». При вычислении объёмов этого делать НЕ НАДО. Дело в том, что человек склонен неверно оценивать объёмы. Посмотрите на плоскую фигуру в прорешанной задаче – она вроде бы невелика по площади, а объем тела вращения составил чуть более 50 «кубиков», что кажется слишком большим. Кстати, среднестатистический человек за всю свою жизнь выпивает жидкость объемом с комнату площадью 18 квадратных метров, что, наоборот, кажется слишком маленьким объемом.

И после лирического отступления уместно решить изящную и, конечно же, важную;) задачу:

Пример 20
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями , ,

Дополнительные примеры можно найти в соответствующей статье сайта, в том числе вращение вокруг оси , ну а сейчас есть более срочный материал:

1.10. Интеграл от чётной функции по симметричному относительно нуля отрезку

1.8. Как вычислить площадь фигуры с помощью определённого интеграла?

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник