Как найти объем тела полученного вращением прямоугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Объём тела вращения

Пусть — тело вращения, образованное вращением вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямыми x=a и x=b и графиком непрерывной функции y=f(x) .

Докажем, что это тело вращения кубируемо и его объем выражается формулой

$V=pi intlimits_{a}^{b} f^2(x),dx= pi intlimits_{a}^{b}y^2,dx,.$

Сначала докажем, что это тело вращения регулярно, если в качестве выберем плоскость Oyz , перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии от плоскости Oyz , является кругом радиуса f(x) и его площадь S(x) равна pi f^2(x) (рис. 46). Поэтому функция S(x) непрерывна в силу непрерывности f(x) . Далее, если S(x_1)leqslant S(x_2) , то это значит, что f(x_1)leqslant f(x_2) . Но проекциями сечений на плоскость Oyz являются круги радиусов f(x_1) и f(x_2) с центром , и из вытекает, что круг радиуса f(x_1) содержится в круге радиуса f(x_2) .

Чертёж тела вращения вокруг оси абсцисс

Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объем вычисляется по формуле

$V=pi intlimits_{a}^{b} S(x),dx= pi intlimits_{a}^{b}f^2(x),dx,.$

Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми y_1=f_1(x), y_2=f_2(x) , то

$V= pi intlimits_{a}^{b}y_2^2,dx- pi intlimits_{a}^{b}y_1^2,dx= piintlimits_{a}^{b}Bigl(f_2^2(x)-f_1^2(x)Bigr)dx,.$

Формулой (3) можно воспользоваться и для вычисления объема тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определенного интеграла.

В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида.

Например, найдем объем тела, получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдем объем, получаемый при вращении прямоугольника с высотой y#, в основании которого лежит отрезок $[x_k;x_{k+1}]$ . Этот объем равен разности объемов двух прямых круговых цилиндров

$Delta V_k= pi y_k x_{k+1}^2- pi y_k x_k^2= pi y_k bigl(x_{k+1}+x_kbigr) bigl(x_{k+1}-x_kbigr).$

Но теперь ясно, что искомый объем оценивается сверху и снизу следующим образом:

$2pi sum_{k=0}^{n-1} m_kx_kDelta x_k leqslant Vleqslant 2pi sum_{k=0}^{n-1} M_kx_kDelta x_k,.$

Отсюда легко следует формула объёма тела вращения вокруг оси ординат:

$V=2pi intlimits_{a}^{b} xy,dx,.$

(4)

Пример 4. Найдем объем шара радиуса .

Решение. Не теряя общности, будем рассматривать круг радиуса с центром в начале координат. Этот круг, вращаясь вокруг оси , образует шар. Уравнение окружности имеет вид x^2+y^2=R^2 , поэтому y^2=R^2-x^2 . Учитывая симметрию круга относительно оси ординат, найдем сначала половину искомого объема

$frac{1}{2}V= piintlimits_{0}^{R}y^2,dx= piintlimits_{0}^{R} (R^2-x^2),dx= left.{pi!left(R^2x- frac{x^3}{3}right)}right|_{0}^{R}= pi!left(R^3- frac{R^3}{3}right)= frac{2}{3}pi R^3.$

Следовательно, объем всего шара равен $frac{4}{3}pi R^3$ .

Конус, образованный вращением прямой вокруг оси абсцисс

Пример 5. Вычислить объем конуса, высота которого и радиус основания .

Решение. Выберем систему координат так, чтобы ось совпала с высотой h (рис. 47), а вершину конуса примем за начало координат. Тогда уравнение прямой запишется в виде $y=frac{r}{h},x$ .

Пользуясь формулой (3), получим:

$V=pi intlimits_{0}^{h} y^2,dx= pi intlimits_{0}^{h} frac{r^2}{h^2},x^2,dx= left.{frac{pi r^2}{h^2}cdot frac{x^3}{3}}right|_{0}^{h}= frac{pi}{3},r^2h,.$

Пример 6. Найдем объем тела, полученного при вращении вокруг оси абсцисс астроиды $begin{cases}x=acos^3t,,\ y=asin^3t,.end{cases}$ (рис. 48).

Объём тела, полученного при вращении вокруг оси абсцисс астроиды

Решение. Построим астроиду. Рассмотрим половину верхней части астроиды, расположенной симметрично относительно оси ординат. Используя формулу (3) и меняя переменную под знаком определенного интеграла, найдем для новой переменной пределы интегрирования.

Если x=acos^3t=0 , то $t=frac{pi}{2}$ , а если x=acos^3t=a , то t=0 . Учитывая, что y^2=a^2sin^6t и $dx=-3acos^2tsin{t},dt$ , получаем:

$V=pi intlimits_{a}^{b} y^2,dx= pi intlimits_{pi/2}^{0} a^2sin^6t bigl(-3acos^2tsin{t}bigr),dt= ldots= frac{16pi}{105},a^3.$

Объем всего тела, образованного вращением астроиды, будет $frac{32pi}{105},a^3$ .

Пример 7. Найдем объем тела, получаемого при вращении вокруг оси ординат криволинейной трапеции, ограниченной осью абсцисс и первой аркой циклоиды $begin{cases}x=a(t-sin{t}),\ y=a(1-cos{t}).end{cases}$ .

Решение. Воспользуемся формулой (4): $V=2pi intlimits_{a}^{b}xy,dx$ , и заменим переменную под знаком интеграла, учитывая, что первая арка циклоиды образуется при изменении переменной от до 2pi . Таким образом,

$begin{aligned}V&= 2pi intlimits_{0}^{2pi} a(t-sin{t})a(1-cos{t})a(1-cos{t}),dt= 2pi a^3 intlimits_{0}^{2pi} (t-sin{t})(1-cos{t})^2,dt=\ &= 2pi a^3 intlimits_{0}^{2pi}bigl(t-sin{t}- 2tcos{t}+ 2sin{t}cos{t}+ tcos^2t- sin{t}cos^2tbigr),dt=\ &= left.{2pi a^3!left( frac{t^2}{2}+ cos{t}- 2tsin{t}- 2cos{t}+ sin^2t+ frac{t^2}{4}+ frac{t}{4}sin2t+ frac{1}{8}cos2t+ frac{1}{3}cos^3tright)}right|_{0}^{2pi}=\ &= 2pi a^3!left( 2pi^2+1-2+pi^2+frac{1}{8}+ frac{1}{3}-1+2- frac{1}{8}- frac{1}{3}right)= 6pi^3a^3. end{aligned}$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Вычисление объемов тел вращения

Рассмотрим
тело, образованное вращением вокруг
оси
криволинейной трапеции(рис.
8.8.), ограниченной кривой,
осьюи прямымиВ этом случае любое сечение полученного
тела плоскостью, перпендикулярной оси,
есть круг радиуса,
площадь которого равна.

Составим
интегральную сумму. Разобьем отрезокпроизвольно начастей. Возьмем частичный отрезок,
выберем на нем произвольную точку.
В точкахивосставим перпендикуляры и построим
элементарный прямоугольник высотоюс основанием,
(рис. 8.9.). В результате вращения этого
прямоугольника вокруг осиполучится элементарное цилиндрическое
тело, радиус которого,
а высота.
Объем такого цилиндрического тела равен,
а сумма всехэлементарных
цилиндрических тел дает интегральную
сумму

Последовательность
интегральных суммдля непрерывной на отрезкефункции прииимеет предел. Его и называютобъемом
тела вращения
вокруг координатной оси
,
то есть

,
короче
(8.9)

Аналогично,
объем тела вращения вокруг оси
следует вычислить по формуле

или(8.10)

Если
вокруг оси
вращается фигура, ограниченная двумя
кривымии,
причем<на отрезке,
то

(8.11)

Аналогично
для фигуры, вращающейся вокруг оси

(8.12)

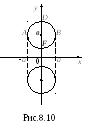
Пример
8.12. Найти
объем тора, образованного вращением
круга
вокруг оси.
Предполагается, что.

Решение.
Круг
радиусас центром в точке с координатамибудем рассматривать как фигуру,
ограниченную дугами двух полуокружностей:

верхней(дугаADB,
рис. 8.10)

и
нижней
(дугаAFB).

По формуле (8.11)
получим

Употреблена
подстановка
Новые пределы интегрирования такие:припри.

Приближенное вычисление определенных интегралов

Мы
уже знаем, что первообразные некоторых
функций не могут быть выражены в конечном
виде через элементарные функции.
Вычисление определенных интегралов
от таких функций возможно с помощью
приближенных методов, которые целесообразно
применять и в случаях интегрируемости
функции в конечном виде, когда отыскание
первообразной требует сложных выкладок.

Формулы приближенного
вычисления определенного интеграла
связаны с геометрическим решением
задачи о нахождении площади криволинейной
трапеции.

Пусть
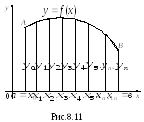
требуется найти приближенное значение
определенного интеграла.
Рассмотрим площадь криволинейной
трапеции(рис.
8.11) как геометрическое представление
заданного интеграла и будем искать
способы приближенного вычисления этой
площади.

Разделим
отрезок
и наравных частей точками.
Расстояние между каждой парой соседних
точек

Из
точек деления отрезка
восставим перпендикуляры к осидо пересечения с графиком функции.
Это будут ординаты соответствующих
точек деления:

Площадь
криволинейной трапеции
можно рассматривать как сумму площадейчастичных криволинейных трапеций, на
которые разделена фигура:.

Формулы прямоугольников

Заменим
площадь каждой частичной криволинейной
трапеции площадью прямоугольника с
основанием
и высотой, равной его левой ординате.
Тогда приближенное значение площади
фигурывыразится суммой

Иначе говоря,
получим следующую формулу приближенного
интегрирования

(8.11)

Если же в качестве
высот прямоугольников возьмем их
правые ординаты, то площадь фигуры
выразится суммой

что дает аналогичную
формулу

(8.12)

Формулы
(8.11) и (8.12) называются формулами
правых и левых прямоугольников.
Иногда используется
формула
средних прямоугольников:

Соседние файлы в папке математика

Источник

jungevanin902

Вопрос по геометрии:

Найти объем тела полученного при вращение прямоугольника со сторонами 6 см и 10 см вокруг большей стороны.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

qunentipl210

При вращении прямоугольника вокруг большей сторонв по лучается цилиндр с радиусом R, равной меньшей стороне, и высотой Н, равной большей стороне

R = 6см

H = 10см

Объём цилиндра

V = πR²·H = π·36·10 = 360π

Знаете ответ? Поделитесь им!

Гость

Гость ?

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете
правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и
пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее;
Использовать мат — это неуважительно по отношению к
пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Источник

Математика,

вопрос задал Pop1466,

5 лет назад

Ответы на вопрос

Ответил settom

Ответ:

768π

Пошаговое объяснение:

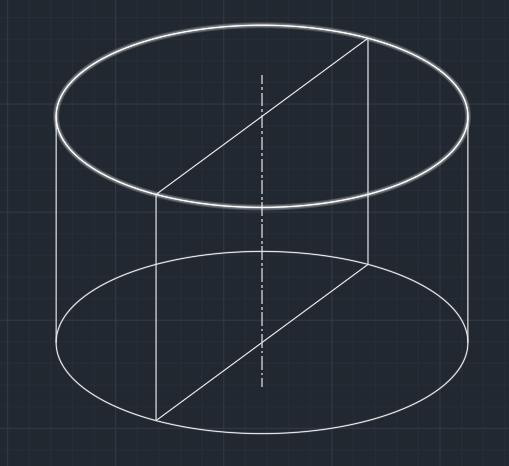
При таком вращении получится цилиндр диаметром D=16 и высотой h=12.

Объём тогда будет

$V=pi*frac{D^2}{4}*h=pi*frac{16^2}{4}*12= pi*256*3= 768pi$

Приложения:

Ответил Аноним

Решение на фото/////

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Другие предметы,
8 месяцев назад

қалаға айналған шумерлік елдімекендер плс ответьте …

Алгебра,
8 месяцев назад

Для функции y=x2 — 3x+ 4 найти наибольшее, наименьшее значения функции, промежутки возрастания, убывания, область определения, область значений (не выполняя построений).

Алгебра,
5 лет назад

ПРИВЕТ, ПОЖАЛУЙСТА РЕШИТЬ ДВЕ ЗАДАЧУ, ВНИЗ СКРИН…

Русский язык,
5 лет назад

1) Я взялся за перо и подумал: – «Что может быть интересного в жизни обычного мальчика и его соседей?» 2) – Отец рад твоему приезду, – ответила сестра и со вздохом прибавила: – Он очень по тебе…

Алгебра,
6 лет назад

Помогите решить 7 номер и 8…

Геометрия,
6 лет назад

лежат ли прямые а,б,с в одной плоскости если прямые а и б, а и с, б и с пересекаются и точки их пересечения не совпадают. Ответ объяснить…

Источник

Рассмотрим ещё одно распространённое приложение определённого интеграла.

Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … интересно, кто что представил… Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать: вокруг оси или вокруг оси .
В рамках данного курса я остановлюсь на стандартном варианте:

Пример 17
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями , вокруг оси .

Решение: как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. Да, с точно такого же чертежа:

Искомая плоская фигура заштрихована серым цветом, именно она и вращается вокруг оси . В результате получается такое… загадочное яйцо.

Объем тела вращения можно вычислить по формуле:
, где – неотрицательная или неположительная функция, график которой ограничивает плоскую фигуру на отрезке . Заметьте, что здесь не нужно думать, над осью расположена криволинейная трапеция или под осью, т.к. возведение в квадрат стирает разницу между функциями и .

В нашей задаче:

Интеграл почти всегда получается простой, главное, быть ВНИМАТЕЛЬНЫМ.

Ответ: (кубических единиц — «кубиков» единичного объема)

Напоминаю, что , обычно принимают либо .

Пример 18
Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями , ,

Тренируемся и переходим к более содержательному случаю:

Пример 19
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями , , и .

Решение: изобразим на чертеже плоскую фигуру, ограниченную линиями , , , , не забывая, что уравнение задаёт ось :

Искомая фигура заштрихована синим цветом. При её вращении вокруг оси получается такой сюрреалистический бублик с четырьмя углами. Объем этого бублика вычислим как разность объёмов с помощью стандартной формулы .

1) Фигура, обведённая красным цветом ограничена сверху прямой , поэтому:

2) Фигура, обведенная зеленым цветом ограничена сверху прямой , поэтому:

3) Объем искомого тела вращения:

Ответ:

Решение можно оформить и короче, примерно в таком духе:
., но, как вы уже поняли, за скорость приходится расплачиваться повышенным риском допустить ошибку.

И ещё хочу вас предостеречь от оценки результата «на глазок». При вычислении объёмов этого делать НЕ НАДО. Дело в том, что человек склонен неверно оценивать объёмы. Посмотрите на плоскую фигуру в прорешанной задаче – она вроде бы невелика по площади, а объем тела вращения составил чуть более 50 «кубиков», что кажется слишком большим. Кстати, среднестатистический человек за всю свою жизнь выпивает жидкость объемом с комнату площадью 18 квадратных метров, что, наоборот, кажется слишком маленьким объемом.

И после лирического отступления уместно решить изящную и, конечно же, важную;) задачу:

Пример 20
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями , ,

Дополнительные примеры можно найти в соответствующей статье сайта, в том числе вращение вокруг оси , ну а сейчас есть более срочный материал:

1.10. Интеграл от чётной функции по симметричному относительно нуля отрезку

1.8. Как вычислить площадь фигуры с помощью определённого интеграла?

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Объём тела вращения

Вычисление объемов тел вращения

Приближенное вычисление определенных интегралов

Формулы прямоугольников

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Есть сомнения?

Ответы на вопрос