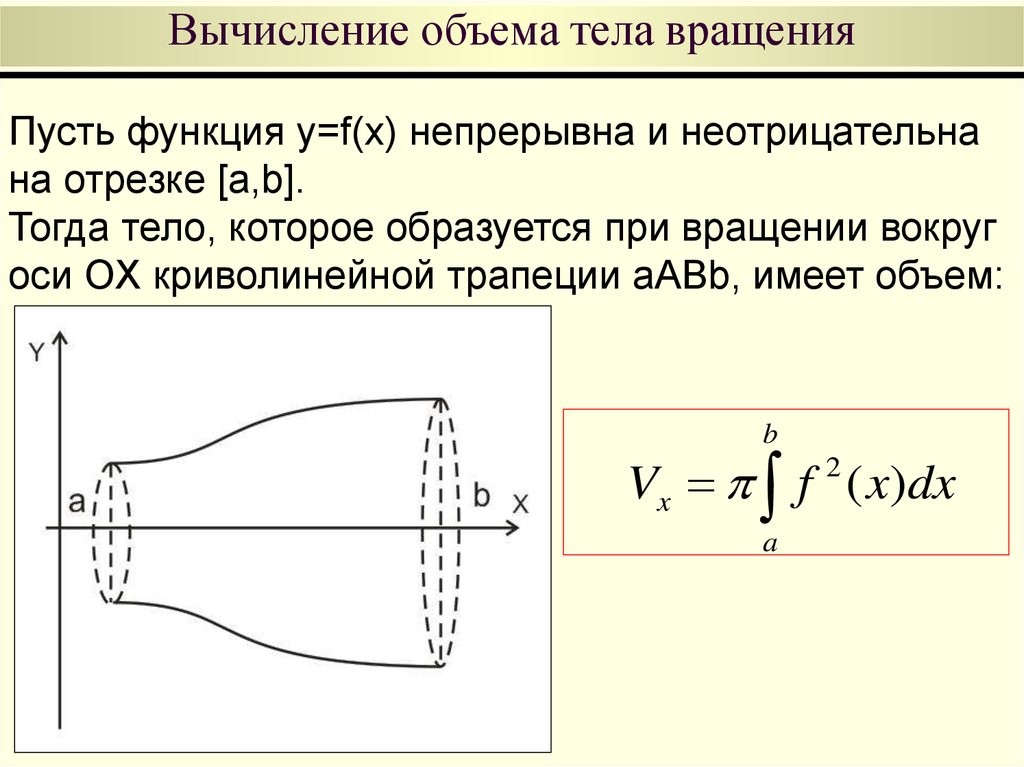
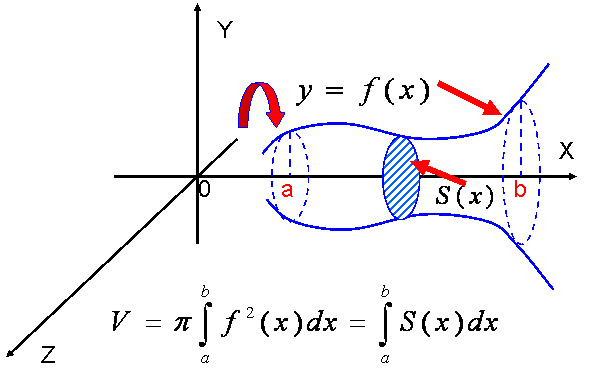
Для того, чтобы найти объем фигуры, образованной вращением вокруг оси Ox нужно вычислить определенный интеграл от квадрата функции, задающей график и умножить на число Пи.
$$ V = pi int_a^b y^2 dx $$
В формуле $ a $ и $ b $ значения отложены по оси Ox. Фукция $ y (x) $ задаёт график фигуры, объем вращения которой необходимо вычислить.
- Строим график фигуры
- Вычисляем определенный интеграл
| Пример 1 |
| Вычислить объем тела вращения вокруг оси Ox: $ y = x^2 $ и $ a = 2, b = 3 $ |
| Решение |
|
Выполняем построение графика. Чертим на плоскости параболу $ y = x^2 $. Выставляем на чертеже оранжевые линии, соответствующие ограничениям $ a = 2, b = 3 $. Закрашиваемая область желтым цветом выделяет фигуру, объем вращения которой будем искать. Подставляем в формулу функцию $ y = x^2 $ и пределы интегрирования. Вычисляем определенный интеграл $$ V = pi int_2^3 (x^2)^2 dx = pi int_2^3 x^4 dx = $$ Для взятия интеграла воспользуемся формулой $ int x^p dx = frac{x^{p+1}}{p+1} $ $$ = pi frac{x^5}{5} bigg |_2^3 = pi frac{243}{5} — pi frac{32}{5} = frac{211}{5} pi = 132.5 $$ Получили объем фигуры $ V = 132.5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ V = 132.5 $$ |
| Пример 2 |
| Найти объем тела вращения фигуры вокруг оси Ox, заданной двумя функциями $$ y = x^2, y = x^3 $$ |
| Решение |
|
В данном примере необходимо найти точки пересечения двух графиков функций. Приравниваем их друг к другу и решаем уравнение относительно одной переменной $ x $: $$ x^2 = x^3 $$ Переносим всё в одну строну $$ x^3 — x^2 = 0 $$ Выносим за скобку неизвестную $ x^2 $ и получаем корни уравнения: $$ x^2(x-1) = 0 $$ $$ x^2 = 0, x-1=0 $$ $$ x_1=0, x_2=1 $$ Выполняем построение графиков функций для наглядности. На рисунке закрашиваем область, ограниченную двумя функциями. Для того, чтобы найти объем тела вращения, заданного с помощью двух функций, необходимо воспользоваться идеей разности объемов. А имеенно, находим сначала объем фигуры вращения, заданной функцией $ y = x^2 $, затем отдельно $ y = x^3 $. $$ V_1 = pi int_0^1 (x^2)^2 dx = pi frac{x^5}{5} bigg |_0^1 = frac{pi}{5} $$ $$ V_2 = pi int_0^1 (x^3)^2 dx = pi frac{x^7}{7} bigg |_0^1 = frac{pi}{7} $$ Получаем искомый объем с помощью разности объемов $$ V = V_1 — V_2 = frac{pi}{5} — frac{pi}{7} = frac{2pi}{35} $$ |
| Ответ |
| $$ V = frac{2pi}{35} $$ |
Рассмотрим ещё одно распространённое приложение определённого интеграла.
Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … интересно, кто что представил… 
или вокруг оси
.
В рамках данного курса я остановлюсь на стандартном варианте:
Пример 17
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями ,
вокруг оси
.
Решение: как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. Да, с точно такого же чертежа:
Искомая плоская фигура заштрихована серым цветом, именно она и вращается вокруг оси . В результате получается такое… загадочное яйцо.
Объем тела вращения можно вычислить по формуле:

– неотрицательная или неположительная функция, график которой ограничивает плоскую фигуру на отрезке
. Заметьте, что здесь не нужно думать, над осью расположена криволинейная трапеция или под осью, т.к. возведение в квадрат стирает разницу между функциями
и
.
В нашей задаче:
Интеграл почти всегда получается простой, главное, быть ВНИМАТЕЛЬНЫМ.
Ответ: (кубических единиц — «кубиков» единичного объема)
Напоминаю, что , обычно принимают
либо
.
Пример 18
Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями
,
,
Тренируемся и переходим к более содержательному случаю:
Пример 19
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями ,
,
и
.
Решение: изобразим на чертеже плоскую фигуру, ограниченную линиями ,
,
,
, не забывая, что уравнение
задаёт ось
:
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси получается такой сюрреалистический бублик с четырьмя углами. Объем этого бублика вычислим как разность объёмов с помощью стандартной формулы

1) Фигура, обведённая красным цветом ограничена сверху прямой , поэтому:
2) Фигура, обведенная зеленым цветом ограничена сверху прямой , поэтому:
3) Объем искомого тела вращения:
Ответ:
Решение можно оформить и короче, примерно в таком духе:

И ещё хочу вас предостеречь от оценки результата «на глазок». При вычислении объёмов этого делать НЕ НАДО. Дело в том, что человек склонен неверно оценивать объёмы. Посмотрите на плоскую фигуру в прорешанной задаче – она вроде бы невелика по площади, а объем тела вращения составил чуть более 50 «кубиков», что кажется слишком большим. Кстати, среднестатистический человек за всю свою жизнь выпивает жидкость объемом с комнату площадью 18 квадратных метров, что, наоборот, кажется слишком маленьким объемом.
И после лирического отступления уместно решить изящную и, конечно же, важную;) задачу:
Пример 20
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями ,
,
Дополнительные примеры можно найти в соответствующей статье сайта, в том числе вращение вокруг оси , ну а сейчас есть более срочный материал:


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Показать Этапы
Номер Строки
Примеры
-
объем:y=(3x+1)^{frac{1}{4}},:x=0,:x=8,:y=0
-
объем:y=sqrt{49-x^{2}},:y=0
-
объем:y=x+1,:y=0,:x=0,:x=2
-
объем:y=11e-x^{2},:y=0,:x=0,:x=1
-
объем:около:x=-1,:y=sqrt[3]{x},:y=1
- Показать больше
Описание
Найдите объем тела вращения шаг за шагом
volume-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Practice, practice, practice
Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Объем тела V, образованного вращением вокруг оси Ox фигуры 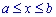
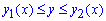
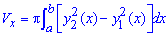
Объем тела V, образованного вращением вокруг оси Oy фигуры 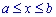
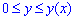
Примеры выбраны из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления объема тела вращения будут повторяться из примера в пример.
ІV. Найти объемы тел, ограниченными поверхностями, полученными при вращении отрезков следующих линий
Пример 2.139 (2472) Найти объем тела, образованного вращением кривой 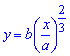
Решение: Складываем подинтегральную функцию:
Пределы интегрирования известны за условием: [0;a].
Найдем объем тела интегрированием:
Всегда помните, что объем измеряется в кубических единицах.
Пример 2.140 (2473) Найти объем тела, образованного вращением кривой y=2x-x^2, y=0
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Запишем подинтегральные функции:
а)
б)
Из приведенных формул Вы можете видеть разницу, в каких случаях применять каждую из формул объема.
Найдем пределы интегрирования:
И заключительным шагом вычисляем объемы интегрированием.
а) Найдем объем тела вращения вокруг оси Ox:
б) Вычислим объем тела вращения вокруг оси Oy:
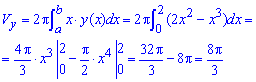
В этом примере интегралы легко берутся и нет потребности объяснять детали операций.
Пример 2.141 (2474) Вычислить объем тела, образованного вращением кривой y=sin(x)
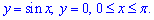
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Выпишем подинтегральные функции:
а)
б)
Пределы интегрирования берем из начального условия:
Осталось вычислить определенные интегралы:
а) Найдем объем тела вращения вокруг оси Ox:
б) Выполняем вычисление объема тела при вращении вокруг оси Oy:
Замена переменных помогает найти последний интеграл.
Пример 2.143 (2476) Найти объем тела, образованного вращением кривой y=e— x, y=0, 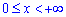
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Уравнение подинтегральных функций :
а) y2=e-2x;
б) x*y (x) =xe-x.
Запишем пределы интегрирования (известно за условием):
а) Находим объем тела вращения вокруг оси Ox:
б) Найдем объем тела вращения вокруг оси Oy:
Здесь, чтобы вычислить интегралы придется находить границу при переменной направляющейся к безграничности.
Во втором интеграле выполняем интегрирование частями.
Пример 2.144 (2477) Вычислить объем тела, образованного вращением кривой x2+(y-b)2=a2, 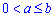
Решение: Фигурой вращения является круг с центром в точке (0;b) и радиусом a.
При выражении самой функции получим две ветки корневых функций:
При поднесении к квадрату разница слагаемых сложит такое выражение подинтегральной функции:
Запишем пределы интегрирования: для круга они равны xє[-a;a] или два полукруга из на промежутке xє[0;a].
Через интеграл находим объем тела вращения вокруг оси Ox:
Внимательно разберите приведенный пример.
Пример 2.145 (2478) Найти объем тела, образованного вращением кривой x2-xy+y2=a2, вокруг оси Ox.
Решение: Сведем кривую к каноническому виду (методами из аналитической геометрии) устанавливаем, что заданная линия является эллипсом
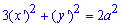
В приведенной системе координат уравнения эллипса имеет вид:
Прямая y=x/2 является осью симметрии этой фигуры.
Запишем подинтегральную функцию:
Найдем пределы интегрирования из условия равности функций y2(x)=y1(x):
или двукратный объем на интервале
Но тогда еще нужно отнять объем тела в пределах
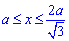
(которая не принадлежит эллипсу) и ограничена первой кривой
и результат умножить на 2 (симметрия).
Последним шагом вычисляем объем тела вращения вокруг оси Ox:
Формула интеграла вышла достаточно длинным, однако его удобно читать пользователям, которые заходят на сайт из мобильных устройств.
Пример 2.146 (2479) Найти объем тела, образованного вращением кривой 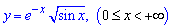
Решение: Запишем подинтегральную функцию:
y2(x)=e-2x*sin (x).
Установим пределы интегрирования: 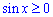
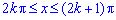
Таким образом имеем бесконечный ряд промежутков интегрирования.
При нахождении объема тела вращения вокруг оси Ox получим бесконечный ряд интегралов, который совпадает:
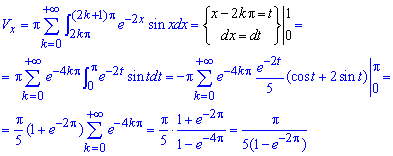
Здесь вычислили интеграл дважды выполнив замену переменных:
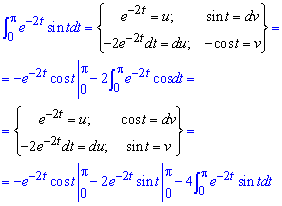
тому 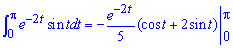
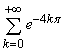
В данном случае бесконечно нисходящая геометрическая прогрессия, у которой b1=1, b2=e-4Pi, поэтому q=e— 4Pi, а сумма прогрессии равна
Объем тела, образованного вращением вокруг полярной оси плоской фигуры
Чтобы найти объем тела V, образованного в результате вращением вокруг полярной оси плоской фигуры r(phi)
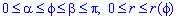
Пример 2483 Найти объем тела, образованного вращением кривой r=a (1+cos (phi)), 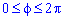
а) вокруг полярной оси;
б) вокруг прямой
Решение: Чтобы достать подинтегральную функцию подносим к кубу заданную функцию: 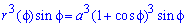
Пределы интегрирования записываем из начального условия:
а) Сначала найдем объем тела вращения вокруг полярной оси:
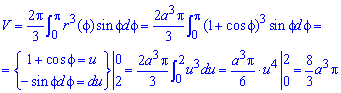
Для упрощения вычислений переходим к новой переменной под интегралом.
б) Перейдем к новым координатам с помощью формул: x1=y, y1=-x-a/4.
Определяем пределы интегрирования:
при росте угла 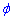
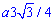
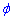
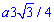
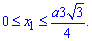
Запишем подинтегральную функцию:
Уравнения перехода между системами координат имеют вид
Подстановкой в уравнение получим:
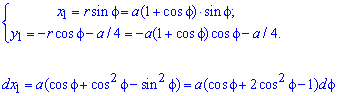
Найдем объем тела вращения вокруг прямой 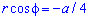
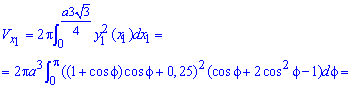
откроем скобки, возведем подобные слагаемые и, приняв во внимание, что интеграл равен нулю 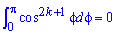

Здесь последние интегралы 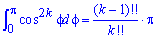
(смотри пример 2.59, часть І).
Парные факториалы вычисляем по правилу
Пример 2484.1 Найти объем тела, образованного вращением кривой r=a*phi 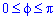
Решение: Запишем подинтегральную функцию:
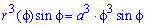
С пределами интегрирования проблем нет:
Чтобы найти объем тела вращения вокруг полярной оси выполняем ряд манипуляций с интегралами:
Внимательно проанализируйте, как находится этот «тригонометрический» интеграл.
Пример 2484.2 Найти объем тела, образованного вращением кривой phi=Pi*r3, phi=Pi, вокруг полярной оси.
Решение: Запишем подинтегральную функцию:
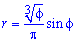
Пределы интегрирования:
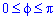
Вычисляем объем тела вращения вокруг полярной оси:
Здесь синус вносим под дифференциал и выполняем интегрирование частями.
На данное время это все примеры, которые мы смогли подготовить для Вас по данной теме.
Установите определенный интеграл, значение которого равно точному объему тела вращения, образованного вращением (R) вокруг линии (y = 2text{.}) 92текст{,}) и (х = 0текст{.})
-
Определите определенный интеграл, значением которого является площадь области, ограниченной двумя кривыми.
-
Найдите выражение, содержащее один или несколько определенных интегралов, значением которого является объем тела вращения, образованного вращением области (R) вокруг линии (y = -1text{.})
-
Определите выражение, включающее один или несколько определенных интегралов, значением которых является объем тела вращения, образованного вращением области (R) вокруг оси (y).
-
Найдите выражение, включающее один или несколько определенных интегралов, значением которых является периметр области (Rtext{.
})
6.2 Определение объемов с помощью срезов — Расчет, том 1
Цели обучения
- 6.2.1
Определить объем твердого тела путем интегрирования поперечного сечения (метод срезов). - 6.2.2
Найдите объем тела вращения методом круга. - 6.2.3
Найти объем тела вращения с полостью методом шайбы.
В предыдущем разделе мы использовали определенные интегралы, чтобы найти площадь между двумя кривыми. В этом разделе мы используем определенные интегралы для нахождения объемов трехмерных тел. Мы рассматриваем три подхода — срезы, диски и шайбы — для нахождения этих объемов в зависимости от характеристик твердого тела.
Объем и метод нарезки
Точно так же, как площадь является числовой мерой двумерной области, объем является числовой мерой трехмерного твердого тела. Большинство из нас вычисляли объемы твердых тел, используя основные геометрические формулы. Объем прямоугольного тела, например, можно вычислить, умножив длину, ширину и высоту: V=lwh.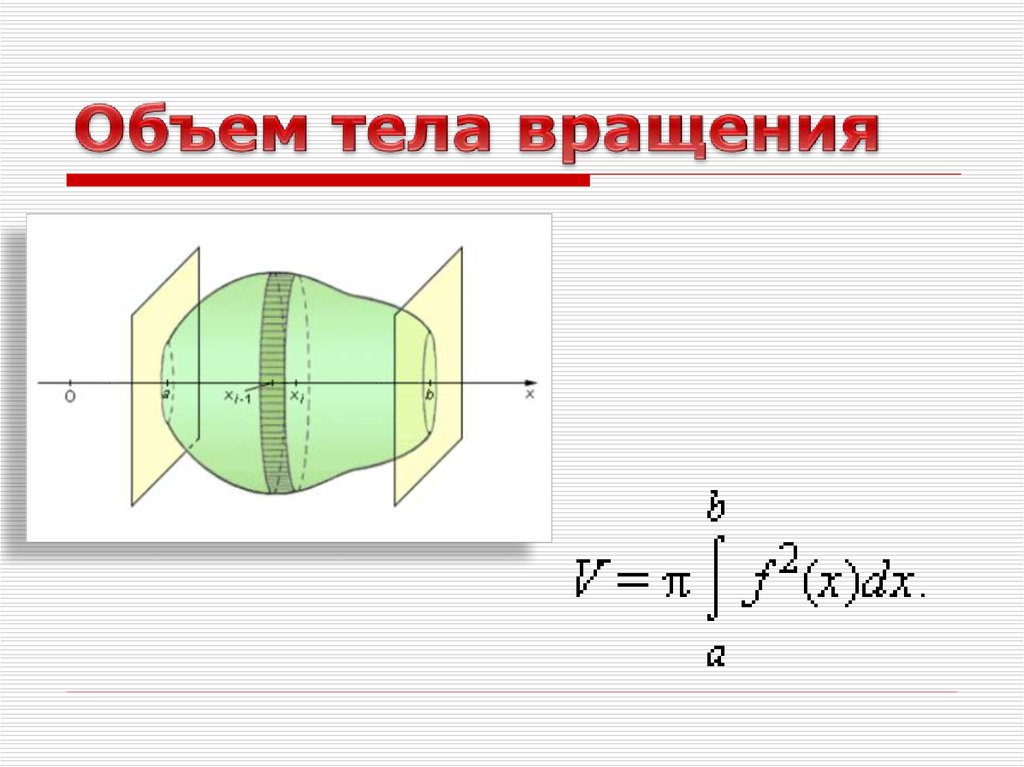
Мы также можем вычислить объем цилиндра. Хотя большинство из нас думает о цилиндре как о круглом основании, таком как банка для супа или металлический стержень, в математике слово цилиндр имеет более общее значение. Чтобы обсудить цилиндры в этом более общем контексте, нам сначала нужно определить некоторый словарь.
Мы определяем поперечное сечение твердого тела как пересечение плоскости с твердым телом. Цилиндр определяется как любое твердое тело, которое может быть создано путем перемещения плоской области вдоль линии, перпендикулярной области, называемой ось цилиндра. Таким образом, все сечения, перпендикулярные оси цилиндра, одинаковы.
Рисунок
6.11
Каждое сечение конкретного цилиндра идентично другим.
Если твердое тело не имеет постоянного поперечного сечения (и оно не является одним из других основных тел), у нас может не быть формулы для его объема. В этом случае мы можем использовать определенный интеграл для вычисления объема твердого тела. Мы делаем это, разрезая твердое тело на части, оценивая объем каждого среза, а затем складывая эти оценочные объемы вместе. Все срезы должны быть параллельны друг другу, и когда мы сложим все срезы вместе, мы должны получить цельное тело. Рассмотрим, например, твердую S , показанный на рис. 6.12, простирается вдоль оси х. ось х.
Рисунок
6.12
Твердое тело с переменным поперечным сечением.
Мы хотим разделить SS на срезы, перпендикулярные оси x.ось x. Как мы увидим позже в этой главе, могут быть случаи, когда мы хотим разрезать твердое тело в каком-то другом направлении, например, срезами, перпендикулярными оси y . Решение о том, каким образом разрезать твердое тело, очень важно. Если мы сделаем неправильный выбор, вычисления могут стать довольно запутанными. Далее в этой главе мы подробно рассмотрим некоторые из этих ситуаций и посмотрим, как решить, каким образом разрезать твердое тело. Однако для целей этого раздела мы используем срезы, перпендикулярные оси x.x-axis.
Поскольку площадь поперечного сечения непостоянна, пусть A(x)A(x) представляет собой площадь поперечного сечения в точке x.x. Пусть теперь P={x0,x1…,Xn}P={x0,x1…,Xn} — обычное разбиение [a,b],[a,b] и для i=1,2,…n i=1,2,…n, пусть SiSi представляет собой срез SS, простирающийся от xi−1toxi.
Рисунок
6.13
Сплошной SS был разделен на три среза, перпендикулярных оси абсцисс.
Наконец, для i=1,2,…n,i=1,2,…n пусть xi*xi* — произвольная точка в [xi−1,xi].[xi−1,xi]. Тогда объем среза SiSi можно оценить как V(Si)≈A(xi*)∆x.V(Si)≈A(xi*)∆x. Складывая эти приближения вместе, мы видим, что объем всего твердого СС может быть приблизительно равен
V(S)≈∑i=1nA(xi*)Δx.V(S)≈∑i=1nA(xi*)Δx.
К настоящему времени мы можем распознать это как сумму Римана, и наш следующий шаг — взять предел при n→∞.n→∞. Тогда у нас есть
V(S)=limn→∞∑i=1nA(xi*)Δx=∫abA(x)dx.V(S)=limn→∞∑i=1nA(xi*)Δx=∫abA(x)dx .
Метод, который мы только что описали, называется методом нарезки. Чтобы применить его, мы используем следующую стратегию.
Стратегия решения проблем
Стратегия решения проблем: поиск объемов методом нарезки
- Осмотрите твердое тело и определите форму поперечного сечения твердого тела.
Часто бывает полезно нарисовать рисунок, если его нет.
- Определите формулу площади поперечного сечения.
- Проинтегрируйте формулу площади по соответствующему интервалу, чтобы получить объем.
Напомним, что в этом разделе мы предполагаем, что срезы перпендикулярны оси x.ось x. Следовательно, формула площади выражается в виде x , а пределы интегрирования лежат на оси x.x-ось. Однако показанная здесь стратегия решения проблем действительна независимо от того, как мы решили разрезать твердое тело.
Пример
6,6
Вывод формулы объема пирамиды
Из геометрии мы знаем, что формула объема пирамиды V=13Ah.V=13Ah. Если у пирамиды квадратное основание, это становится V=13a2h, V=13a2h, где aa обозначает длину одной стороны основания. Мы собираемся использовать метод нарезки, чтобы вывести эту формулу.
Решение
Мы хотим применить метод разрезания к пирамиде с квадратным основанием.
Рисунок
6.14
(а) Пирамида с квадратным основанием ориентирована по оси х . (b) Двухмерный вид пирамиды сбоку.
Сначала мы хотим определить форму поперечного сечения пирамиды. Мы знаем, что основание квадратное, поэтому сечения тоже квадратные (шаг 1). Теперь мы хотим определить формулу площади одного из этих квадратов поперечного сечения. Глядя на рисунок 6.14(b) и используя пропорцию, поскольку это подобные треугольники, мы имеем
sa=xhors=axh.sa=xhors=axh.
Следовательно, площадь одного из квадратов поперечного сечения равна
A(x)=s2=(axh)2(шаг2).A(x)=s2=(axh)2(шаг2).
Затем находим объем пирамиды интегрированием от 0toh0toh (шаг 3):3):
V=∫0hA(x)dx=∫0h(axh)2dx=a2h3∫0hx2dx=[a2h3(13×3)] |0h=13a2h.V=∫0hA(x)dx=∫0h(axh)2dx=a2h3∫0hx2dx=[a2h3(13×3)]|0h=13a2h.
Это формула, которую мы искали.
Контрольно-пропускной пункт
6,6
Используйте метод срезов, чтобы вывести формулу V=13πr2hV=13πr2h для объема круглого конуса.
Тела революции
Если область на плоскости вращается вокруг линии на этой плоскости, полученное тело называется телом вращения, как показано на следующем рисунке.
Рисунок
6.15
(а) Это область, которая вращается вокруг оси x . (б) Когда область начинает вращаться вокруг оси, она выметает тело вращения. (c) Это твердое тело, которое получается после завершения вращения.
Тела вращения распространены в механических приложениях, таких как детали машин, изготовленные на токарном станке. Оставшуюся часть этого раздела мы посвятим рассмотрению твердых тел этого типа. В следующем примере используется метод срезов для вычисления объема тела вращения.
Пример
6.7
Использование метода срезов для нахождения объема тела вращения
Использование метода срезов для нахождения объема тела вращения, ограниченного графиками f(x)=x2−4x+5,x=1, иx=4,f(x)=x2−4x+5,x=1,andx=4, и вращается вокруг оси x.
Решение
Используя стратегию решения задач, мы сначала нарисуем график квадратичной функции на интервале [1,4][1,4], как показано на следующем рисунке.
Рисунок
6.16
Область, используемая для создания тела вращения.
Затем поверните область вокруг оси x , как показано на следующем рисунке.
Рисунок
6.17
Два вида (а) и (б) тела вращения, полученного вращением области на рис. 6.16 вокруг оси х.
Поскольку твердое тело было сформировано путем вращения области вокруг оси x, поперечные сечения представляют собой круги (шаг 1). Таким образом, площадь поперечного сечения — это площадь круга, а радиус круга равен f(x).f(x). Используйте формулу площади круга:
A(x)=πr2=π[f(x)]2=π(x2−4x+5)2(шаг 2).A(x)=πr2=π[f(x)]2=π( x2−4x+5)2(шаг 2).
Тогда объем равен (шаг 3)
V=∫abA(x)dx=∫14π(x2−4x+5)2dx=π∫14(x4−8×3+26×2−40x+25)dx= π(x55−2×4+26×33−20×2+25x)|14=785π.
Объем 78π/5,78π/5.
Контрольно-пропускной пункт
6.7
Используйте метод срезов, чтобы найти объем тела вращения, образованного вращением области между графиком функции f(x)=1/xf(x)=1/x и осью xx-ось над интервал [1,2][1,2] вокруг оси х.ось х. См. следующий рисунок.
Дисковый метод
Когда мы используем метод срезов с телами вращения, его часто называют дисковым методом, потому что для тел вращения срезы, используемые для аппроксимации объема тела, представляют собой диски. Чтобы увидеть это, рассмотрим тело вращения, образованное вращением области между графиком функции f(x)=(x−1)2+1f(x)=(x−1)2+1 и осью xx -ось в интервале [−1,3][−1,3] вокруг оси x.x-axis. График функции и репрезентативный диск показаны на рис. 6.18 (а) и (б). Область вращения и полученное твердое тело показаны на рис. 6.18 (в) и (г).
Рисунок
6.
(а) Тонкий прямоугольник для аппроксимации площади под кривой. (b) Репрезентативный диск, образованный вращением прямоугольника вокруг оси x.x. (c) Область под кривой вращается вокруг оси x, оси x, в результате чего (d) тело вращения.
Мы уже использовали формальную формулу суммы Римана для формулы объема, когда разрабатывали метод срезов. Мы знаем, что
V=∫abA(x)dx.V=∫abA(x)dx.
Единственная разница с дисковым методом заключается в том, что мы заранее знаем формулу площади поперечного сечения; это площадь круга. Это дает следующее правило.
Правило: Дисковый метод
Пусть f(x)f(x) непрерывна и неотрицательна. Определим RR как область, ограниченную сверху графиком f(x),f(x), снизу осью x, осью x, слева линией x=a,x=a и справа линией x=b.x=b. Тогда объем тела вращения, образованного вращением RR вокруг оси x x, равен
V=∫abπ[f(x)]2dx.V=∫abπ[f(x)]2dx.
(6.3)
Объем изучаемого нами твердого тела (рис.
V=∫abπ[f(x)]2dx=∫−13π[(x−1)2+1]2dx=π∫−13[(x−1)4+2(x−1)2+1] dx=π[15(x−1)5+23(x−1)3+x]|−13=π[(325+163+3)−(−325−163−1)]=412π15единиц3.V= ∫abπ[f(x)]2dx=∫−13π[(x−1)2+1]2dx=π∫−13[(x−1)4+2(x−1)2+1]dx=π [15(x−1)5+23(x−1)3+x]|−13=π[(325+163+3)−(−325−163−1)]=412π15единиц3.
Давайте рассмотрим несколько примеров.
Пример
6,8
Использование дискового метода для нахождения объема тела вращения 1
Использование дискового метода для нахождения объема тела вращения, образованного вращением области между графиком f(x)=xf(x)= х и ось х ось х в интервале [1,4][1,4] вокруг оси х.ось х.
Решение
Графики функции и тела вращения показаны на следующем рисунке.
Рисунок
6.19
(a) Функция f(x)=xf(x)=x на интервале [1,4].[1,4]. (b) Тело вращения, полученное вращением области под графиком f(x)f(x) вокруг оси х.
Имеем
V=∫abπ[f(x)]2dx=∫14π[x]2dx=π∫14xdx=π2×2|14=15π2.
Объем (15π)/2(15π)/2 единицы 3 .
Контрольно-пропускной пункт
6,8
Используйте метод диска, чтобы найти объем тела вращения, образованного вращением области между графиком f(x)=4−xf(x)=4−x и осью xx-ось на интервале [ 0,4][0,4] вокруг оси x.ось x.
До сих пор в наших примерах все соответствующие области вращались вокруг оси x, оси x, но мы можем создать тело вращения, вращая плоскую область вокруг любой горизонтальной или вертикальной линии. В следующем примере мы рассмотрим тело вращения, которое было создано путем вращения области вокруг оси y. Механика дискового метода почти такая же, как и в случае, когда ось x является осью вращения, но мы выражаем функцию через yy и интегрируем по и тоже. Это резюмируется в следующем правиле.
Правило: Дисковый метод для тел вращения вокруг оси
y
Пусть g(y)g(y) непрерывна и неотрицательна.
V=∫cdπ[g(y)]2dy.V=∫cdπ[g(y)]2dy.
(6.4)
Следующий пример показывает, как это правило работает на практике.
Пример
6,9
Использование метода диска для нахождения объема тела вращения 2
Пусть RR будет областью, ограниченной графиком g(y)=4−yg(y)=4−y и осью y в интервале оси Y [0,4].[0,4]. Используйте метод диска, чтобы найти объем тела вращения, образованного вращением RR вокруг оси y.ось y.
Решение
На рис. 6.20 показаны функция и репрезентативный диск, который можно использовать для оценки объема. Обратите внимание, что, поскольку мы вращаем функцию вокруг оси Y, диски расположены горизонтально, а не вертикально.
Рисунок
6.
(a) Показан тонкий прямоугольник между кривой функции g(y)=4−yg(y)=4−y и осью y.ось y. (b) Прямоугольник образует репрезентативный диск после вращения вокруг оси y.
Область вращения и полное тело вращения показаны на следующем рисунке.
Рисунок
6.21
(a) Область слева от функции g(y)=4−yg(y)=4−y на интервале оси y [0,4].[0,4]. (b) Тело вращения, образованное вращением области вокруг оси у.
Чтобы найти объем, проинтегрируем по y.y. Получаем
V=∫cdπ[g(y)]2dy=∫04π[4−y]2dy=π∫04(4−y)dy=π[4y−y22]|04=8π.V=∫cdπ [g(y)]2dy=∫04π[4−y]2dy=π∫04(4−y)dy=π[4y−y22]|04=8π.
Объем 8π8π единиц 3 .
Контрольно-пропускной пункт
6,9
Используйте метод диска, чтобы найти объем тела вращения, образованного вращением области между графиком g(y)=yg(y)=y и осью y на интервале [1,4] [1,4] вокруг оси y.ось y.
Метод мойки
Некоторые тела вращения имеют в середине полости; они не сплошные на всем пути до оси вращения.
Когда тело вращения имеет полость посередине, срезы, используемые для аппроксимации объема, представляют собой не диски, а шайбы (диски с отверстиями в центре). Например, рассмотрим область, ограниченную сверху графиком функции f(x)=xf(x)=x и снизу графиком функции g(x)=1g(x)=1 на интервале [1, 4].[1,4]. Когда эта область вращается вокруг оси х, получается твердое тело с полостью посередине, а срезы — шайбы. График функции и репрезентативная шайба показаны на рис. 6.22 (а) и (б). Область вращения и полученное твердое тело показаны на рис. 6.22 (в) и (г).
Рисунок
6.22
(а) Тонкий прямоугольник в области между двумя кривыми. (b) Репрезентативный диск, образованный вращением прямоугольника вокруг оси x.
Площадь поперечного сечения равна площади внешнего круга за вычетом площади внутреннего круга. В данном случае
A(x)=π(x)2−π(1)2=π(x−1).A(x)=π(x)2−π(1)2=π(x−1).
Тогда объем твердого тела равен
V=∫abA(x)dx=∫14π(x−1)dx=π[x22−x]|14=92πunits3.V=∫abA(x)dx=∫14π(x−1)dx=π[ x22−x]|14=92πединиц3.
Обобщение этого процесса дает метод шайбы.
Правило: метод шайбы
Предположим, что f(x)f(x) и g(x)g(x) — непрерывные неотрицательные функции такие, что f(x)≥g(x)f(x)≥g(x) над [a,b ].[а,б]. Обозначим через RR область, ограниченную сверху графиком f(x),f(x), снизу графиком g(x),g(x), слева линией x=a,x=a, а справа линией x=b.x=b. Тогда объем тела вращения, образованного вращением RR вокруг оси xx, равен
V=∫abπ[(f(x))2−(g(x))2]dx.V=∫abπ[(f(x))2−(g(x))2]dx.
(6,5)
Пример
6.10
Методом шайбы
Найти объем тела вращения, образованного вращением области, ограниченной сверху графиком f(x)=xf(x)=x и снизу графиком g(x)=1 /xg(x)=1/x в интервале [1,4][1,4] вокруг оси x.
Решение
Графики функций и тела вращения показаны на следующем рисунке.
Рисунок
6.23
(a) Область между графиками функций f(x)=xf(x)=x и g(x)=1/xg(x)=1/x на интервале [1,4].[1, 4]. (b) Вращение области вокруг оси xx порождает тело вращения с полостью посередине.
Имеем
V=∫abπ[(f(x))2−(g(x))2]dx=π∫14[x2−(1x)2]dx=π[x33+1x]|14 =81π4единиц3.V=∫abπ[(f(x))2−(g(x))2]dx=π∫14[x2−(1x)2]dx=π[x33+1x]|14=81π4единиц3.
Контрольно-пропускной пункт
6.10
Найти объем тела вращения, образованного вращением области, ограниченной графиками f(x)=xf(x)=x и g(x)=1/xg(x)=1/x на интервале [1,3][1,3] вокруг оси х.ось х.
Как и в случае с дисковым методом, мы также можем применить метод шайбы к телам вращения, которые образуются в результате вращения области вокруг оси y . В этом случае действует следующее правило.
Правило: метод шайбы для тел вращения вокруг оси
y
Предположим, что u(y)u(y) и v(y)v(y) — непрерывные неотрицательные функции такие, что v(y)≤u(y)v(y)≤u(y) при y∈[c ,d].
V=∫cdπ[(u(y))2−(v(y))2]dy.V=∫cdπ[(u(y))2−(v(y))2]dy.
Вместо того, чтобы рассматривать пример метода шайбы с осью Y в качестве оси вращения, мы теперь рассмотрим пример, в котором ось вращения является линией, отличной от одной из двух осей координат. Применяется тот же общий метод, но вам, возможно, придется визуализировать, как описать площадь поперечного сечения объема.
Пример
6.11
Метод шайбы с другой осью вращения
Найти объем тела вращения, образованного вращением области, ограниченной сверху f(x)=4−xf(x)=4−x и снизу осью xx-ось на интервале [0,4] [0,4] вокруг линии y=−2.y=−2.
Решение
График области и тела вращения показаны на следующем рисунке.
Рисунок
6.24
(a) Область между графиком функции f(x)=4−xf(x)=4−x и осью x на интервале [0,4].[0,4]. (b) Вращение области вокруг линии y=−2y=−2 порождает тело вращения с цилиндрическим отверстием в середине.
Мы не можем напрямую применить формулу объема к этой задаче, потому что ось вращения не является одной из осей координат. Однако мы все еще знаем, что площадь поперечного сечения равна площади внешнего круга за вычетом площади внутреннего круга. Глядя на график функции, мы видим, что радиус внешнего круга определяется как f(x)+2,f(x)+2, что упрощается до
f(x)+2=(4−x) +2=6−x.f(x)+2=(4−x)+2=6−x.
Радиус внутренней окружности равен g(x)=2.g(x)=2. Следовательно, у нас есть
V=∫04π[(6−x)2−(2)2]dx=π∫04(x2−12x+32)dx=π[x33−6×2+32x]|04=160π3единиц3.V=∫04π [(6−x)2−(2)2]dx=π∫04(x2−12x+32)dx=π[x33−6×2+32x]|04=160π3единиц3.
Контрольно-пропускной пункт
6.11
Найти объем тела вращения, образованного вращением области, ограниченной сверху графиком f(x)=x+2f(x)=x+2 и снизу осью xx-ось на интервале [0 ,3][0,3] вокруг линии y=−1.
Раздел 6.2 Упражнения
58.
Выведите формулу объема сферы, используя метод срезов.
59.
Используйте метод срезов, чтобы вывести формулу объема конуса.
60.
Используйте метод срезов, чтобы вывести формулу объема тетраэдра с длиной стороны a.a.a.
61.
Используйте метод дисков, чтобы вывести формулу объема трапециевидного цилиндра.
62.
Объясните, когда вы будете использовать дисковый метод, а когда шайбовый. Когда они взаимозаменяемы?
Для следующих упражнений нарисуйте типичный срез и найдите объем, используя метод среза для заданного объема.
63.
Пирамида высотой 6 единиц и квадратным основанием со стороной 2 единицы, как показано здесь.
64.
Пирамида высотой 4 единицы и прямоугольным основанием длиной 2 единицы и шириной 3 единицы, как показано здесь.
65.
Тетраэдр с основанием в 4 единицы, как показано здесь.
66.
Пирамида высотой 5 единиц и равнобедренным треугольным основанием длиной 6 единиц и 8 единиц, как показано здесь.
67.
Конус радиуса rr и высоты hh имеет меньший конус радиуса r/2r/2 и высоты h/2h/2, удаленный от вершины, как показано здесь. Полученное твердое тело называется усеченным .
Для следующих упражнений нарисуйте контур твердого тела и найдите объем, используя метод срезов.
68.
Основание представляет собой окружность радиусом а.а. Срезы, перпендикулярные основанию, представляют собой квадраты.
69.
Основание представляет собой треугольник с вершинами (0,0),(1,0),(0,0),(1,0) и (0,1).(0,1). Срезы, перпендикулярные оси x , представляют собой полукруги.
70.
Основание — это область под параболой y=1−x2y=1−x2 в первом квадранте. Срезы, перпендикулярные плоскости xy и параллельные оси y, являются квадратами.
71.
Основание — это область под параболой y=1−x2y=1−x2 и над осью x.ось x. Срезы, перпендикулярные оси Y, являются квадратами.
72.
Основание — это область, ограниченная y=x2y=x2 и y=9.y=9. Срезы, перпендикулярные оси x , представляют собой прямоугольные равнобедренные треугольники. Пересечение одного из этих отрезков и основания является катетом треугольника.
73.
Основание — это площадь между y=xy=x и y=x2.
Для следующих упражнений нарисуйте область, ограниченную кривыми. Затем используйте метод диска, чтобы найти объем, когда область вращается вокруг x — ось.
74.
х+у=8,х=0,и=0х+у=8,х=0,иу=0
75.
y=2×2,x=0,x=4,andy=0y=2×2,x=0,x=4,andy=0
76.
y=ex+1,x=0,x=1,andy=0y=ex+1,x=0,x=1,andy=0
77.
y=x4,x=0,andy=1дляx≥0y=x4,x=0,andy=1дляx≥0
78.
y=x,x=0,x=4,andy=0y=x,x=0,x=4,andy=0
79.
y=sinx,y=cosx,andx=0y=sinx,y=cosx,andx=0
80.
y=1x,x=2,andy=3y=1x,x=2,andy=3
81.
x2−y2=9иx+y=9,y=0иx=0x2−y2=9иx+y=9,y=0иx=0
Для следующих упражнений нарисуйте область, ограниченную кривыми. Затем найдите объем при вращении области вокруг оси y .
82.
y=4−12x,x=0,andy=0y=4−12x,x=0,andy=0
83.
y=2×3,x=0,x=1,andy=0y=2×3,x=0,x=1,andy=0
84.
y=3×2,x=0,andy=3y=3×2,x=0,andy=3
85.
y=4−x2,y=0 иx=0y=4−x2,y=0,andx=0
86.
y=1x+1,x=0 иx=3y=1x+1,x=0 иx=3
87.
x=sec(y)andy=π4,y=0andx=0x=sec(y)andy=π4,y=0andx=0
88.
y=1x+1,x=0 иx=2y=1x+1,x=0 иx=2
89.
y=4-x,y=x,andx=0y=4-x,y=x,andx=0
Для следующих упражнений нарисуйте область, ограниченную кривыми.
90.
y=x+2,y=x+6,x=0,andx=5y=x+2,y=x+6,x=0,andx=5
91.
y=x2andy=x+2y=x2andy=x+2
92.
x2=y3andx3=y2x2=y3andx3=y2
93.
y=4−x2andy=2−xy=4−x2andy=2−x
94.
[T] y=cosx,y=e−x,x=0,andx=1,2927y=cosx,y=e−x,x=0,andx=1,2927
95.
y=xandy=x2y=xandy=x2
96.
y=sinx,y=5sinx,x=0andx=πy=sinx,y=5sinx,x=0andx=π
97.
y=1+x2andy=4−x2y=1+x2andy=4−x2
Для следующих упражнений нарисуйте область, ограниченную кривыми. Затем используйте метод шайбы, чтобы найти объем, когда область вращается вокруг оси y .
98.
y=x,x=4,andy=0y=x,x=4,andy=0
99.
y=x+2,y=2x−1,andx=0y=x+2,y=2x−1,andx=0
100.
y=x3andy=x3y=x3andy=x3
101.
x=e2y,x=y2,y=0,andy=ln(2)x=e2y,x=y2,y=0,andy=ln(2)
102.
x=9−y2,x=e−y,y=0,andy=3x=9−y2,x=e−y,y=0,andy=3
103.
Контейнеры для йогурта могут иметь форму усеченного конуса. Поверните линию y=1mxy=1mx вокруг оси y , чтобы найти объем между y=aandy=b.y=aandy=b.
104.
Поверните эллипс (x2/a2)+(y2/b2)=1(x2/a2)+(y2/b2)=1 вокруг оси x , чтобы приблизительно получить объем футбольного мяча, как показано здесь.
105.
Повернуть эллипс (x2/a2)+(y2/b2)=1(x2/a2)+(y2/b2)=1 вокруг y — ось для приблизительного определения объема футбольного мяча.
106.
Лучшее приближение к объему футбольного мяча дает твердое тело, возникающее при вращении y=sinxy=sinx вокруг оси x от x=0x=0 до x=π.x=π. Каков объем этого футбольного приближения, как показано здесь?
107.
Каков объем пирога Бундта, который получается при вращении y=sinxy=sinx вокруг оси y от x=0x=0 до x=π?x=π?
Для следующих упражнений найдите объем описываемого твердого тела.
108.
Основание — это область между y=xy=x и y=x2.y=x2. Срезы, перпендикулярные оси x , представляют собой полукруги.
109.
Основание — это область, заключенная в общий эллипс (x2/a2)+(y2/b2)=1.(x2/a2)+(y2/b2)=1. Срезы, перпендикулярные оси x , представляют собой полукруги.
110.
Просверлите отверстие радиусом aa по оси прямого конуса и через основание радиусом b,b, как показано здесь.
111.
Найдите общий объем двух сфер радиусом rr с центрами, отстоящими друг от друга на 2h3h, как показано здесь.
112.
Найдите объем сферической шапки высотой hh и радиусом rr, где h
113.
Найдите объем сферы радиусом RR со снятой сверху крышкой высотой hh, как показано здесь.
Объемы тел вращения
Вы также можете использовать определенный интеграл, чтобы найти объем твердого тела, полученного путем вращения плоской области вокруг горизонтальной или вертикальной линии, не проходящей через плоскость. Этот тип твердого тела будет состоять из одного из трех типов элементов — дисков, шайб или цилиндрических оболочек, — каждый из которых требует своего подхода к составлению определенного интеграла для определения его объема.
Дисковый метод
Если ось вращения является границей плоской области, а поперечные сечения взяты перпендикулярно оси вращения, то для нахождения объема твердого тела используется дисковый метод . Поскольку поперечное сечение диска представляет собой круг с площадью π r 2 , объем каждого диска равен его площади, умноженной на его толщину. Если диск перпендикулярен оси x , то его радиус должен быть выражен как функция х . Если диск перпендикулярен оси y , то его радиус должен быть выражен как функция y .
Объем ( V ) твердого тела, образованного вращением области, ограниченной y = f(x ) и осью x на интервале [ a, b ] вокруг x -ось
Если область ограничена x = f(y ) и осью y на [ a, b ] вращается вокруг оси y , то его объем ( V ) равен
Обратите внимание, что f(x ) и f(y ) представляют радиусы дисков или расстояние от точки на кривой до оси вращения.
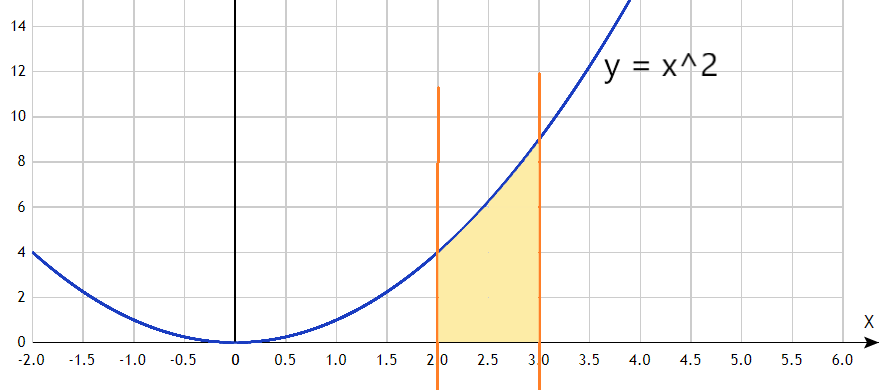
Пример 1: Найдите объем твердого тела, образованного вращением области, ограниченной y = x 2 и x -оси на [−2,3] вокруг x — ось.
Поскольку ось x является границей области, вы можете использовать дисковый метод (см. рис. 1).
Рисунок 1 Схема для примера 1.
Объем ( V ) твердого тела равен
Метод мойки
Если ось вращения не является границей плоской области и поперечные сечения взяты перпендикулярно оси вращения, используется метод шайбы , чтобы найти объем твердого тела. Думайте о шайбе как о «диске с отверстием в нем» или как о «диске с удаленным от центра диском». Если R – радиус внешнего диска, а r – радиус внутреннего диска, то площадь шайбы равна π R 2 – π r 2 , а ее объем будет быть его площадь, умноженная на его толщину.
где f(x ) ≥ г(x ), по оси x —
Если область ограничена x = f(y ) и x = г(y ) на [ a, b ], где f(y ) ≥ г(y ) вращается вокруг
7 6 y оси, то его объем ( V ) равен
Еще раз обратите внимание, что f(x ) и g(x ) и f(y ) и g(y ) представляют собой внешний и внутренний радиусы шайб или расстояние между точками на каждой кривой до ось вращения.
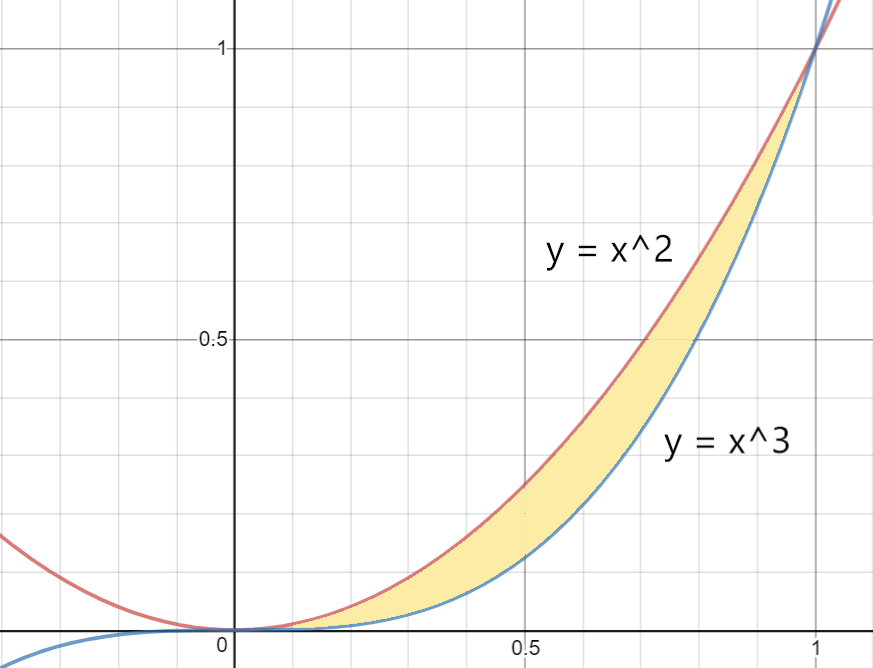
Пример 2: Найдите объем твердого тела, образованного вращением области, ограниченной y = x 2 + 2 и y = x + 4 вокруг оси x .
Поскольку y = x 2 + 2 и y = x + 4, вы находите, что
Графики будут пересекаться в точках (–1,3) и (2,6) с x + 4 ≥ x 2 + 2 на [–1,2] (рис. 2).
Рисунок 2 Схема для примера 2.
Поскольку ось x не является границей области, вы можете использовать метод шайбы, а объем ( V ) твердого тела равен
Метод цилиндрической оболочки
Если поперечные сечения твердого тела взяты параллельно оси вращения, то метод цилиндрической оболочки будет использоваться для нахождения объема твердого тела. Если цилиндрическая оболочка имеет радиус r и высота h, , то его объем будет в 2π rh умножить на толщину. Думайте о первой части этого произведения (2π rh ) как о площади прямоугольника, образованного путем разрезания оболочки перпендикулярно ее радиусу и плоской укладки.
Объем ( V ) твердого тела, образованного вращением области, ограниченной y = f(x ) и осью x на интервале [ a,b ], где f( x ) ≥ 0, относительно оси y ‐
Если область, ограниченная x = f(y ) и осью y на интервале [ a,b ], где f(y ) ≥ 0, вращается вокруг x ‐ось, то его объем ( V ) равен
Обратите внимание, что x и y в подынтегральных выражениях представляют радиусы цилиндрических оболочек или расстояние между цилиндрической оболочкой и осью вращения. Коэффициенты f(x ) и f(y ) представляют высоты цилиндрических оболочек.
Пример 3: Найдите объем твердого тела, образованного вращением области, ограниченной y = x 2 и ось x [1,3] относительно оси y .








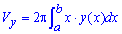
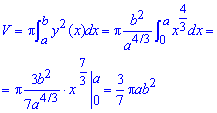
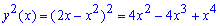
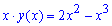
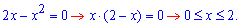
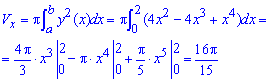
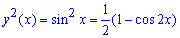
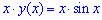
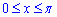
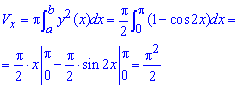
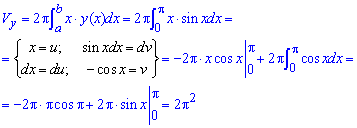
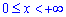
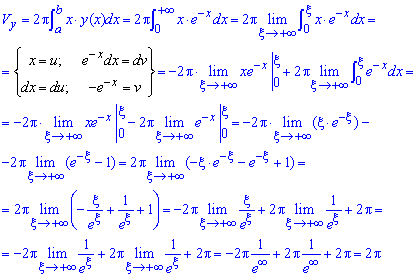
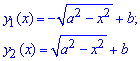
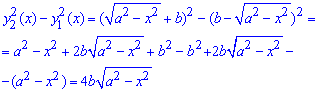
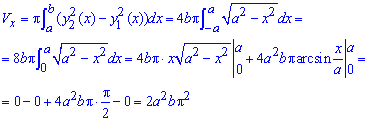
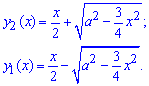
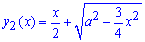
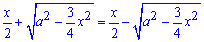
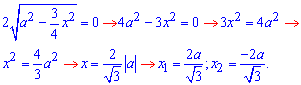
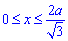
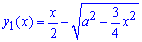
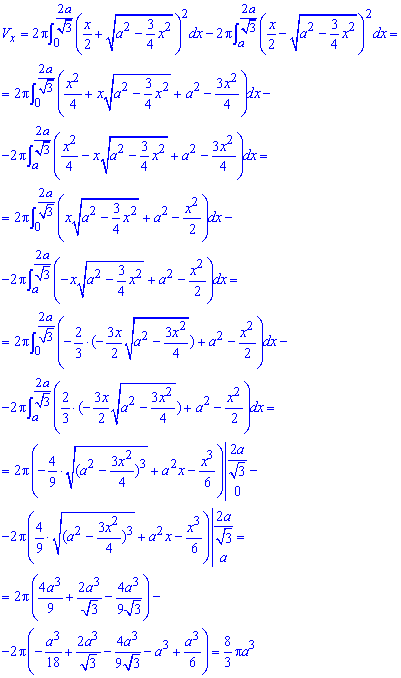
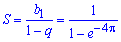
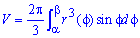
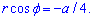
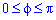
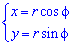
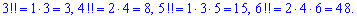
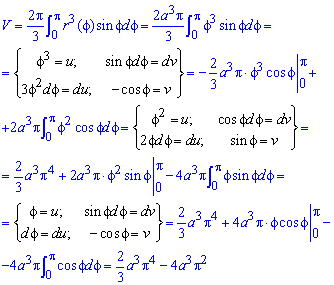
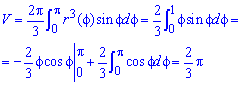
 })
})  Часто бывает полезно нарисовать рисунок, если его нет.
Часто бывает полезно нарисовать рисунок, если его нет.