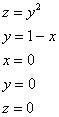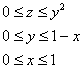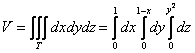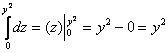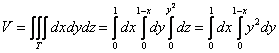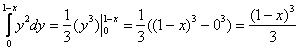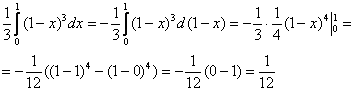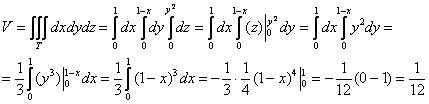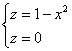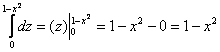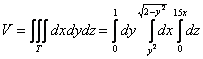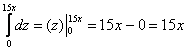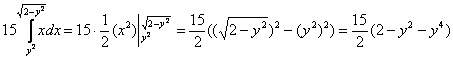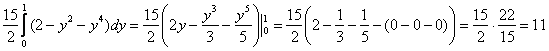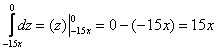Как найти объем тела заданного ограничивающими поверхностями

Вычисление объёмов

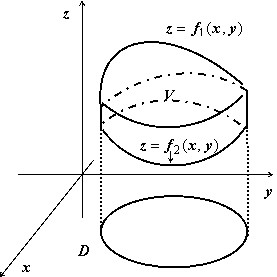
Объём тела, ограниченного сверху и снизу поверхностями $mathbf { textit { z } } =mathbf { textit { f } } _ { 1 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $mathbf { textit { z } } =mathbf { textit { f } } _ { 2 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $(x,y)in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $mathbf { textit { Oz } } $, равен $v=iintlimits_D { left[ { f_1 (x,y)-f_2 (x,y) }right]dxdy } $; эта формула очевидно следует из геометрического смысла двойного интеграла.

Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.

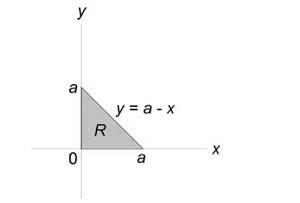
Пример 1

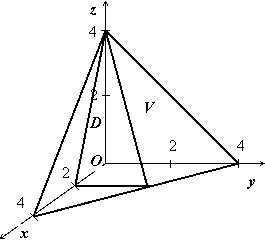
Найти объём тела $V:left[{ begin{array} { l } y=0,;z=0, \ x+y+z=4,; \ 2x+z=4. \ end{array} }right.$

Решение:

Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $mathbf { textit { Oxz } } $:

$V:left[{ begin{array} { l } (x,z)in D, \ 0leqslant yleqslant 4-x-z. \ end{array} }right.$

Область $mathbf { textit { D } } $ — треугольник, ограниченный прямыми $mathbf { textit { x } } $ = 0, $mathbf { textit { z } } $ = 0, 2$mathbf { textit { x } } +mathbf { textit { z } } $ = 4, поэтому

$V=iintlimits_D { (4-x-z)dxdz } =intlimits_0^2 { dxintlimits_0^ { 4-2x } { (4-x-z)dz } } = intlimits_0^2 { dxleft. { left( { 4z-xz-z^2/2 }right) }right|_0^ { 4-2x } } = intlimits_0^2 { left[ { 16-8x-4x+2x^2-(4-2x)^2/2 }right]dx } = \ = intlimits_0^2 { left( { 8-4x }right)dx } = left. { left( { 8x-2x^2 }right) }right|_0^2 =16-8=8$

Пример 2

Найти объём области, ограниченной поверхностями $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { R } } ^ { 2 } $,

$(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$.

Решение:

Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $mathbf { textit { Oz } } $ { в уравнении нет $mathbf { textit { z } } $ в явной форме). Построить в плоскости $mathbf { textit { Oxy } } $ кривую шестого порядка, заданную уравнением $(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей { чётные степени } и точка $mathbf { textit { О } } (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(cos ^4varphi +sin ^4varphi );r^2=R^2((cos ^2varphi +sin ^2varphi )^2-2cos ^2varphi sin ^2varphi )=R^2(1-frac { sin ^22varphi } { 2 } )=$

$=R^2(1-frac { 1-cos 4varphi } { 4 } )=R^2frac { 3+cos 4varphi } { 4 } ;r=Rfrac { sqrt { 3+cos 4varphi } } { 2 } .$ Эту кривую построить уже можно. $r(varphi )$ максимально, когда $cos 4varphi =1;(varphi =0,frac { 2pi } { 4 } =frac { pi } { 2 } ,frac { 4pi } { 4 } =pi ,frac { 6pi } { 4 } =frac { 3pi } { 2 } )$, минимально, когда

$cos 4varphi =-1;(varphi =frac { pi } { 4 } ,frac { 3pi } { 4 } ,frac { 5pi } { 4 } ,frac { 7pi } { 4 } ),$ и гладко меняется между этими пределами { точка $mathbf { textit { О } } (0,0)$ не принадлежит этой кривой, где мы её потеряли? } .

Пользуясь симметрией, получаем $ V=16iintlimits_D { sqrt { R^2-x^2-y^2 } dxdy= } 16iintlimits_D { sqrt { R^2-r^2 } rdrdvarphi = } =16intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } rdr } = $ $ =-8intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } d(R^2-r^2) } =-8frac { 2 } { 3 } intlimits_0^ { frac { pi } { 4 } } { left. { (R^2-r^2)^ { frac { 3 } { 2 } } }right|_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } dvarphi } =-frac { 16 } { 3 } R^3intlimits_0^ { frac { pi } { 4 } } { left. { left[ { left( { frac { sin ^22varphi } { 2 } }right)^ { frac { 3 } { 2 } } -1 }right] }right|dvarphi } = $ и т.д.

Пример 3

Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)

Решение:

Данное тело показано на рисунке.

Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ { V = iintlimits_R { left[ { left( { 4 — x }right) — x }right]dxdy } } = { intlimits_0^2 { left[ { intlimits_0^2 { left( { 4 — 2x }right)dy } }right]dx } } = { intlimits_0^2 { left[ { left. { left( { 4y — 2xy }right) }right|_ { y = 0 } ^2 }right]dx } } = { intlimits_0^2 { left( { 8 — 4x }right)dx } } = { left. { left( { 8x — 2 { x^2 } }right) }right|_0^2 } = { 16 — 8 = 8. } $

Пример 4

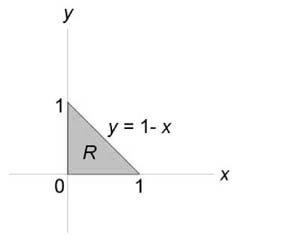
Описать тело, объем которого определяется интегралом (V = intlimits_0^1 { dx } intlimits_0^ { 1 — x } { left( { { x^2 } + { y^2 } }right)dy } .)

Решение:

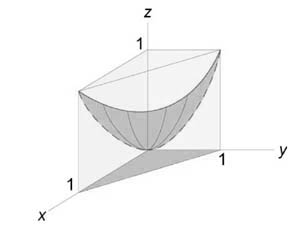
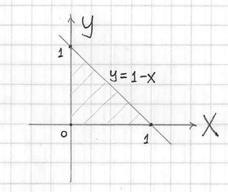
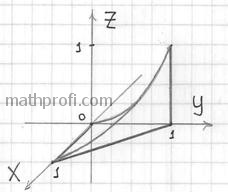
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = { x^2 } + { y^2 } .) Объем тела равен $ { V = intlimits_0^1 { dx } intlimits_0^ { 1 — x } { left( { { x^2 } + { y^2 } }right)dy } } = { intlimits_0^1 { left[ { left. { left( { { x^2 } y + frac { { { y^3 } } } { 3 } }right) }right|_ { y = 0 } ^ { 1 — x } }right]dx } } = { intlimits_0^1 { left[ { { x^2 } left( { 1 — x }right) + frac { { { { left( { 1 — x }right) } ^3 } } } { 3 } }right]dx } } = \ = { intlimits_0^1 { left( { { x^2 } — { x^3 } + frac { { 1 — 3x + 3 { x^2 } — { x^3 } } } { 3 } }right)dx } } = { intlimits_0^1 { left( { 2 { x^2 } — frac { { 4 { x^3 } } } { 3 } — x + frac { 1 } { 3 } }right)dx } } = { left. { left( { frac { { 2 { x^3 } } } { 3 } — frac { 4 } { 3 } cdot frac { { { x^4 } } } { 4 } — frac { { { x^2 } } } { 2 } + frac { x } { 3 } }right) }right|_0^1 } = { frac { 2 } { 3 } — frac { 1 } { 3 } — frac { 1 } { 2 } + frac { 1 } { 3 } = frac { 1 } { 6 } . } $

Пример 5

Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)

Решение:

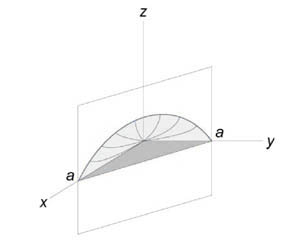
Данное тело лежит над треугольником (R) в плоскости (Oxy) ниже поверхности (z = xy.) Объем тела равен $ { V = iintlimits_R { xydxdy } } = { intlimits_0^a { left[ { intlimits_0^ { a — x } { xydy } }right]dx } } = { intlimits_0^a { left[ { left. { left( { frac { { x { y^2 } } } { 2 } }right) }right|_ { y = 0 } ^ { a — x } }right]dx } } = { frac { 1 } { 2 } intlimits_0^a { x { { left( { a — x }right) } ^2 } dx } } = { frac { 1 } { 2 } intlimits_0^a { xleft( { { a^2 } — 2ax + { x^2 } }right)dx } } = \ = { frac { 1 } { 2 } intlimits_0^a { left( { { a^2 } x — 2a { x^2 } + { x^3 } }right)dx } } = { frac { 1 } { 2 } left. { left( { { a^2 } cdot frac { { { x^2 } } } { 2 } — 2a cdot frac { { { x^3 } } } { 3 } + frac { { { x^4 } } } { 4 } }right) }right|_0^a } = { frac { 1 } { 2 } left( { frac { { { a^2 } } } { 2 } — frac { { 2 { a^4 } } } { 3 } + frac { { { a^4 } } } { 4 } }right) } = { frac { { { a^4 } } } { { 24 } } . } $

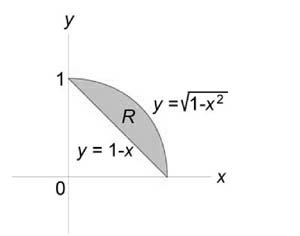
Пример 6

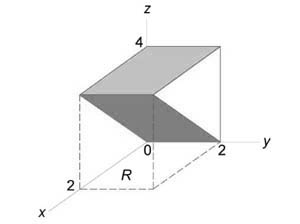
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( { x^2 } + { y^2 } = 1,) (z = 1 — x.)

Решение:

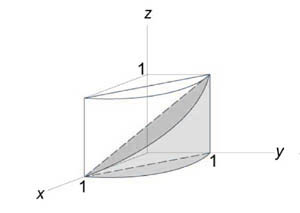
Как видно из рисунков, в области интегрирования (R) при (0 le x le 1) значения (y) изменяются от (1 — x) до (sqrt { 1 — { x^2 } } .)

Сверху тело ограничено плоскостью (z = 1 — x.) Следовательно, объем данного тела равен $ { V = iintlimits_R { left( { 1 — x }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_ { 1 — x } ^ { sqrt { 1 — { x^2 } } } { left( { 1 — x }right)dy } }right]dx } } = { intlimits_0^1 { left[ { left( { 1 — x }right)left. y right|_ { 1 — x } ^ { sqrt { 1 — { x^2 } } } }right]dx } } = { intlimits_0^1 { left( { 1 — x }right)left( { sqrt { 1 — { x^2 } } — 1 + x }right)dx } } = \ = { intlimits_0^1 { left( { sqrt { 1 — { x^2 } } — xsqrt { 1 — { x^2 } } — 1 + 2x — { x^2 } }right)dx } } = { intlimits_0^1 { sqrt { 1 — { x^2 } } dx } } — { intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } } — { intlimits_0^1 { left( { 1 + 2x — { x^2 } }right)dx } . } $

Вычислим полученные три интеграла отдельно. $ { I_1 } = intlimits_0^1 { sqrt { 1 — { x^2 } } dx } .$ Сделаем замену: (x = sin t.) Тогда (dx = cos tdt.) Видно, что (t = 0) при (x = 0) и (t = largefrac { pi } { 2 } normalsize) при (x = 1.) Следовательно, $ { { I_1 } = intlimits_0^1 { sqrt { 1 — { x^2 } } dx } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { sqrt { 1 — { { sin } ^2 } t } cos tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { cos } ^2 } tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { frac { { 1 + cos 2t } } { 2 } dt } } = { frac { 1 } { 2 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { left( { 1 + cos 2t }right)dt } } = { frac { 1 } { 2 } left. { left( { t + frac { { sin 2t } } { 2 } }right) }right|_0^ { largefrac { pi } { 2 } normalsize } } = { frac { 1 } { 2 } left( { frac { pi } { 2 } + frac { { sin pi } } { 2 } }right) = frac { pi } { 4 } . } $ { Сравните с площадью сектора единичного круга в первом квадранте).

Вычислим второй интеграл ( { I_2 } = intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } ,) используя замену переменной. Полагаем (1 — { x^2 } = w.) Тогда (-2xdx = dw) или (xdx = largefrac { { — dw } } { 2 } normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ { { I_2 } = intlimits_0^1 { xsqrt { 1 — { x^2 } } dx } } = { intlimits_1^0 { sqrt w left( { — frac { { dw } } { 2 } }right) } } = { — frac { 1 } { 2 } intlimits_1^0 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { { w^ { largefrac { 1 } { 2 } normalsize } } dw } } = { frac { 1 } { 2 } left. { left( { frac { { 2 { w^ { largefrac { 3 } { 2 } normalsize } } } } { 3 } }right) }right|_0^1 = frac { 1 } { 3 } . } $ Наконец, вычислим третий интеграл. $require { cancel } { { I_3 } = intlimits_0^1 { left( { 1 — 2x + { x^2 } }right)dx } } = { left. { left( { x — { x^2 } + frac { { { x^3 } } } { 3 } }right) }right|_0^1 } = { cancel { 1 } — cancel { 1 } + frac { 1 } { 3 } = frac { 1 } { 3 } . } $ Таким образом, объем тела равен $ { V = { I_1 } — { I_2 } — { I_3 } } = { frac { pi } { 4 } — frac { 1 } { 3 } — frac { 1 } { 3 } = frac { pi } { 4 } — frac { 2 } { 3 } approx 0,12. } $

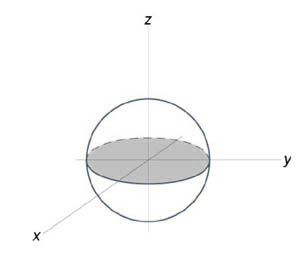
Пример 7

Вычислить объем единичного шара.

Решение:

Уравнение сферы радиусом (1) имеет вид ( { x^2 } + { y^2 } + { z^2 } = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = sqrt { 1 — left( { { x^2 } + { y^2 } }right) } .$ Преобразуя это уравнение в полярные координаты, получаем $zleft( { r,theta }right) = sqrt { 1 — { r^2 } } .$ В полярных координатах область интегрирования (R) описывается множеством (R = left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].) Следовательно, объем верхнего полушара выражается формулой $ { { V_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 — { r^2 } } rdrdtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } } = { 2pi intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } . } $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — { r^2 } = t.) Тогда (-2rdr = dt) или (rdr = — largefrac { { dt } } { 2 } normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ { { V_ { largefrac { 1 } { 2 } normalsize } } = 2pi intlimits_0^1 { sqrt { 1 — { r^2 } } rdr } } = { 2pi intlimits_1^0 { sqrt t left( { — frac { { dt } } { 2 } }right) } } = { — pi intlimits_1^0 { sqrt t dt } } = { pi intlimits_0^1 { { t^ { largefrac { 1 } { 2 } normalsize } } dt } } = { pi left. { left( { frac { { { t^ { largefrac { 3 } { 2 } normalsize } } } } { { frac { 3 } { 2 } } } }right) }right|_0^1 } = { frac { { 2pi } } { 3 } . } $ Таким образом, объем единичного шара равен $V = 2 { V_ { largefrac { 1 } { 2 } normalsize } } = frac { { 4pi } } { 3 } .$

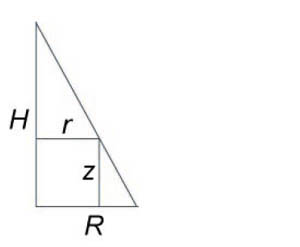
Пример 8

Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).

Решение:

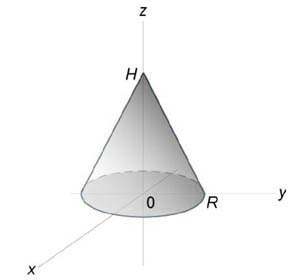
Сначала получим уравнение поверхности конуса. Используя подобные треугольники, можно записать $ { frac { r } { R } = frac { { H — z } } { H } , } ;; { text { где } ;;r = sqrt { { x^2 } + { y^2 } } . } $ Следовательно, $ { H — z = frac { { Hr } } { R } } ;; { text { или } ;;zleft( { x,y }right) } = { H — frac { { Hr } } { R } } = { frac { H } { R } left( { R — r }right) } = { frac { H } { R } left( { R — sqrt { { x^2 } + { y^2 } } }right). } $ Тогда объем конуса равен $ { V = iintlimits_R { zleft( { x,y }right)dxdy } } = { iintlimits_R { frac { H } { R } left( { R — sqrt { { x^2 } + { y^2 } } }right)dxdy } } = { frac { H } { R } iintlimits_R { left( { R — r }right)rdrdtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { left[ { intlimits_0^R { left( { R — r }right)drd } }right]dtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { dtheta } intlimits_0^R { left( { Rr — { r^2 } }right)dr } } = { frac { { 2pi H } } { R } intlimits_0^R { left( { Rr — { r^2 } }right)dr } } = \ = { frac { { 2pi H } } { R } left. { left( { frac { { R { r^2 } } } { 2 } — frac { { { r^3 } } } { 3 } }right) }right|_ { r = 0 } ^R } = { frac { { 2pi H } } { R } left( { frac { { { R^3 } } } { 2 } — frac { { { R^3 } } } { 3 } }right) } = { frac { { 2pi H } } { R } cdot frac { { { R^3 } } } { 6 } = frac { { pi { R^2 } H } } { 3 } . } $



2.2. Как вычислить объём тела с помощью тройного интеграла?

По формуле , где  – искомое тело.

Пример 32

С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями .

Пожалуйста, перепишите на бумагу следующий список:

и ответьте на вопросы: знаете ли Вы, какие поверхности задают эти уравнения? Понятен ли Вам неформальный смысл

этих уравнений? Представляете ли Вы, как данные поверхности расположены в пространстве?

Если Вы склоняетесь к общему ответу «скорее нет, чем да», то обязательно проработайте материалы по геометрии, которые я

рекомендовал на предыдущей странице. Без этого дальше никуда.

Решение: используем формулу .

Для того чтобы выяснить порядок обхода тела и перейти к повторным интегралам нужно (всё гениальное

просто) понять, что это за тело. И такому пониманию во многих случаях здОрово способствуют чертежи.

По условию, тело ограничено несколькими поверхностями. С чего начать построение? Предлагаю следующий порядок действий:

Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость . Это тень тела, когда солнышко светит на него прямо сверху :).

Коль скоро проецирование проводится вдоль оси , то в первую очередь целесообразно разобраться с поверхностями, которые

параллельны данной оси. Напоминаю, что уравнения таких поверхностей не содержат буквы «зет». В нашей задаче их

три:

– уравнение  задаёт координатную

плоскость , которая проходит через ось ;
– уравнение  задаёт координатную

плоскость , которая проходит через ось ;
– уравнение  задаёт

плоскость, проходящую через «одноимённую» «плоскую» прямую параллельно оси .

Исходя из вышесказанного, искомая проекция, скорее всего, представляет собой следующий треугольник:

Возможно, не все до конца поняли, о чём речь. Представьте, что из экрана монитора выходит ось  и утыкается прямо в вашу переносицу (т.е. получается, что

Вы смотрите на 3-мерный чертёж сверху). Исследуемое пространственное тело находится в бесконечном трёхгранном «коридоре»,

и его проекция на плоскость ,

вероятнее всего, представляет собой заштрихованный треугольник.

Обращаю особое внимание, что пока мы высказали лишь предположение о проекции и оговорки «скорее всего»,

«вероятнее всего» были не случайны. Дело в том, что проанализированы ещё не все поверхности и может статься так, что

какая-нибудь из них «оттяпает» часть треугольника. В качестве наглядного примера напрашивается сфера с центром в

начале координат радиусом мЕньшим единицы, например, сфера   – её проекция на плоскость  (круг ) не полностью «накроет» заштрихованную область, и итоговая проекция тела будет

вовсе не треугольником (круг «срежет» ему острые углы).

На втором этапе выясним, чем тело ограничено сверху, чем снизу и выполним пространственный чертёж. Возвращаемся к условию

задачи и смотрим, какие поверхности остались. Уравнение  задаёт саму координатную плоскость , а уравнение   – параболический цилиндр, который расположен над

плоскостью  и проходит через ось . Таким образом, проекция тела

действительно представляет собой треугольник.

Аккуратно изобразим фрагмент параболического цилиндра и искомое тело:

После выполнения чертежей с порядком обхода тела никаких проблем!

Сначала определим порядок обхода проекции (при этом ГОРАЗДО УДОБНЕЕ использовать двумерный чертеж – см. выше). Это

делается АБСОЛЮТНО ТАК ЖЕ, как и в двойных интегралах!

Вспоминаем лазерную указку и «сканирование» плоской области.

Выберем «традиционный» 1-й способ обхода:  

Далее берём в руки волшебный фонарик, смотрим на трёхмерный чертёж и строго снизу вверх просвечиваем

пациента. Лучи входят в тело через плоскость  и выходят из него через поверхность . Таким образом, порядок обхода тела:

Перейдём к повторным интегралам:

С интегралами вновь (ещё раз вновь) рекомендую разбираться по отдельности:

1) Начать следует с самого нутра – «зетового» интеграла:

Подставим результат в «игрековый» интеграл:

Что получилось? По существу решение свелось к двойному интегралу, и именно – к формуле  объёма цилиндрического

бруса! Дальнейшее хорошо знакомо:

2)

3) Последний интеграл удобно взять методом подведения под знак дифференциала – ещё раз заостряю внимание на этом

выгодном способе решения:

Ответ:

Вычисления всегда можно записать и «одной строкой»:

Но с этим способом будьте осторожнее – выигрыш в скорости чреват потерей качества, и чем труднее пример, тем больше шансов

допустить ошибку.

Ответим на важный технический вопрос:

Нужно ли делать чертежи, если условие задачи не требует их выполнения?

Можно пойти четырьмя путями:

1) Изобразить проекцию и само тело. Это самый выигрышный вариант – если есть возможность выполнить два приличных чертежа,

не ленитесь, делайте оба чертежа. Рекомендую в первую очередь.

2) Изобразить только тело. Годится, когда у тела несложная и очевидная проекция. Так, например, в разобранном примере

хватило бы и трёхмерного чертежа. Однако тут есть и минус – по 3D-картинке неудобно определять порядок обхода проекции, и этот

способ я бы советовал только людям с хорошим уровнем подготовки.

Следующее тело для  самостоятельного дела:

Пример 33

С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями

В данном случае область интегрирования задана преимущественно неравенствами, и это даже лучше – множество

неравенств  задаёт 1-й октант,

включая координатные плоскости, а неравенство  задаёт полупространство, содержащее начало координат

(проверьте) + саму плоскость .

«Вертикальная» плоскость  рассекает

параболоид по параболе и на чертеже желательно построить данное сечение. Для этого нужно найти дополнительную опорную

точку, лучше всего – вершину параболы (рассматриваем значения  и рассчитываем соответствующее «зет»).

…Тёмный лес? Вам сюда + сюда либо сюда – поднимаем геометрию!

Примерный образец оформления задачи в конце урока.

Продолжаем разминаться:

Пример 34

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Выполнить чертёж.

Решение: формулировка «выполнить чертёж» даёт нам некоторую свободу, но, скорее всего, подразумевает

выполнение пространственного чертежа. Однако и проекция тоже не помешает, тем более, она здесь не самая простая.

Придерживаемся отработанной ранее тактики, сначала разберёмся с поверхностями, параллельными оси аппликат.

Уравнения таких поверхностей не содержат в явном виде переменную «зет»:
– уравнение  задаёт координатную

плоскость , проходящую через ось  (ось абсцисс на плоскости  определяется «одноимённым» уравнением

);
– уравнение  задаёт плоскость,

проходящую через «одноимённую» «плоскую» прямую параллельно оси .

Но две прямые  не задают

ограниченную проекцию, и, очевидно, параболический цилиндр  своими линиями пересечения с координатной плоскостью  замыкает плоскую фигуру. Чтобы выяснить их уравнения нужно решить

простейшую систему:
Подставим  в первое уравнение:  – получены две прямые, лежащие в

плоскости  и параллельные оси .

Определим порядок обхода тела, при этом «иксовые» и «игрековые» пределы интегрирования удобнее выяснять по

двумерному чертежу:
 – луч лазера просвечивает тело

строго снизу вверх!
 – смотрим на проекцию тела.

Таким образом:
 

1)

2) Напоминаю, что при интегрировании по «игрек» – «икс» считается константой, поэтому константу  удобно сразу вынести за знак интеграла.

3) И заключительный, внимательный аккорд:

Ответ:

Да, чуть не забыл, в большинстве случаев полученный результат малополезно (и даже вредно) сверять с трёхмерным чертежом,

поскольку с большой вероятностью возникнет иллюзия объёма, о которой я рассказал в одной из статей сайта. Суть

иллюзии состоит в том, что люди склонны неверно оценивать объём «на глазок», мы его либо занижаем, либо завышаем.

Так, человек за среднестатистическую жизнь суммарно выпивает жидкости объёмом со стандартную комнату 18 кв. м., что кажется

очень малым объёмом. В нашей задаче наоборот – если вы посмотрите на пространственный чертёж, то вам покажется, что тело

содержит больше четырёх «кубиков».

И после познавательного отступления задание для самостоятельного решения:

Пример 35

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и

его проекции на плоскость .

Обратите внимание, что условие этой задачи безвариантно требует выполнения обоих чертежей.  Примерный образец оформления в

конце книги.

Не редкость, когда выполнение трёхмерного чертежа затруднено, и этой ситуации посвящены ближайшие примеры:

Пример 36

С помощью тройного интеграла найти объём тела, ограниченного поверхностями

Решение: проекция здесь несложная, но вот над порядком её обхода нужно подумать. Если

выбрать 1-й способ, то фигуру придётся разделить на 2 части, что

неиллюзорно грозит вычислением суммы двух тройных интегралов. В этой связи гораздо перспективнее выглядит 2-й путь. Выразим , изобразим проекцию на чертеже:

и выберем более выгодный порядок обхода фигуры:

Теперь дело за телом. Снизу оно ограничено плоскостью , сверху – плоскостью , которая проходит через ось . И всё бы было ничего, но последняя плоскость слишком крутА и построить

тело не так-то просто. Выбор тут незавиден: либо ювелирная работа в мелком масштабе (т.к. тело достаточно тонкое), либо чертёж

высотой порядка 20 сантиметров (да и то, если вместится на тетрадный лист). 

Но есть и третий, исконно русский метод решения проблемы – забить =). И вместо трёхмерного чертежа обойтись словесным

описанием: «Данное тело ограничено цилиндрами  и плоскостью  сбоку, плоскостью  – снизу и плоскостью  – сверху».

«Вертикальные» пределы интегрирования, очевидно, таковы:

Вычислим объём тела, не забывая, что проекцию мы обошли менее распространённым способом:

1)

2)

3)

Ответ:

Как вы заметили, предлагаемые в задачах телА часто ограничены плоскостью  снизу. Но это не есть какое-то правило, поэтому всегда нужно быть начеку –

может попасться задание, где тело расположено и под плоскостью . Так, например, если в рассмотренной задаче вместо  рассмотреть плоскость , то исследованное тело отобразится симметрично в нижнее

полупространство и будет ограничено плоскостью  снизу, а плоскостью  – уже сверху!

Легко убедиться, что получится тот же самый результат:

(помним, что тело нужно обходить строго снизу вверх!)

Кроме того, «любимая» плоскость может оказаться вообще не при делах, простейший пример: шар, расположенный выше

плоскости  – при вычислении его

объёма уравнение  не понадобится

вообще.

Все эти случаи мы рассмотрим, а пока аналогичное задание для самостоятельного решения:

Пример 37

С помощью тройного интеграла найти объём тела, ограниченного поверхностями:

Сверяемся с решением в конце книги и переходим к параграфу с не менее популярными материалами:

2.3. Тройной интеграл в цилиндрических координатах

2.1. Понятие тройного инетграла

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Примеры решений тройных интегралов

В этом разделе вы найдете подробные решения, связанные и вычислением и применением тройных интегралов: от непосредственного вычисления (в декартовых, цилиндрических, сферических координатах), до применения к нахождению объемов тел, массы, моментов и т.п. Примеры сгруппированы по темам:

Тройные интегралы: примеры решений

Задача 1. Вычислить тройной интеграл

$$iiint_V x^2yz dx dy dz, quad V: -1 le x le 2, 0le y le 3, 2 le z le 3. $$

Задача 2. Переходя к сферическим координатам, вычислить интеграл

$$iiint_V x^2 dxdydz, quad V: x^2+y^2+z^2=R^2,, zge 0, xgt 0.$$

Задача 3. Переходя к цилиндрическим координатам вычислить интеграл

$$iiint_V x^2 dxdydz, quad V: x^2+y^2=x,, z=x^2+y^2, z=0.$$

Задача 4. Решить тройной интеграл двумя способами (цилидрическая и сферическая замена координат)

$$iiint_G(x^2+y^2+z^2)^2 dxdydz,quad G={(x,y,z):x^2+y^2+z^2le a^2,x+zge0}$$

Трудности с задачами? МатБюро поможет с интегралами.

Объемы тел: примеры решений

Задача 5. Найти объем тела, заданного ограничивающими его поверхностями (внутри цилиндра).

$$z=sqrt{100-x^2-y^2},, z=6,, x^2+y^2=51$$

Задача 6. Найти объем тела, ограниченного поверхностями

$$x^2+y^2=9x, x^2+y^2=12x, z=sqrt{x^2+y^2}, z=0, y ge 0.$$

Задача 7. Вычислить тройным интегрированием объем тела, ограниченного данными поверхностями:

$$z=2-x, z=0, y=sqrt{x}, y=frac{1}{4}x^2.$$

Задача 8. Найти объем тела, ограниченного координатными плоскостями и поверхностью

$$
left(frac{x}{a}+ frac{y}{b} + frac{z}{c} right)^3 = sin left(pi frac{frac{x}{a}+ frac{y}{b}}{frac{x}{a}+ frac{y}{b} + frac{z}{c} } right)
$$

Задача 9. Найти объем тела, ограниченного поверхностью $x^2+y^2+z^2=2x+3y$.

Моменты, масса тела: примеры решений

Задача 10. Найти статический момент относительно $xOy$ однородного тела, ограниченного поверхностью
$$(x^2+y^2+z^2 )^3=frac{x^2+y^2}{z^2} $$
с плотностью $z=0$ $(z ge 0)$.

Задача 11. Используя тройной интеграл в цилиндрической системе координат, вычислить массу кругового цилиндра, нижнее основание которого лежит в плоскости $xOy$, а ось симметрии совпадает с осью $Oz$, если заданы радиус основания $R$, высота цилиндра $H$ и функция плотности $gamma(rho)$, где $rho$ – полярный радиус точки.

$$ R=2, H=0,5, gamma=2+rho^2+rho^3.$$

Задача 12. Найти массу тела, заданного системой неравенств, если плотность тела в каждой точке задана функцией $mu$.

$$ frac{1}{2}sqrt{x^2+y^2} le z le sqrt{4-x^2-y^2}, quad mu =frac{5}{8}z. $$

Задача 13. Найти момент инерции относительно оси Oz тела, ограниченного заданными поверхностями.

$$z=-x^2-y^2, z=x^2+y^2-8$$

Полезные ссылки

• Интегралы — примеры решений
• Применение интегралов — примеры решений
• Двойные интегралы — примеры решений
• Криволинейные интегралы — примеры решений
• Поверхностные интегралы — примеры решений
• Учебник с примерами онлайн по тройным интегралам