Как найти объем трапециевидной призмы


Download Article


Download Article

A prism is a solid, multi-sided geometric figure with two identical ends called bases. To find the volume of a prism, first calculate the area of one of the bases, then multiply it by the height of the prism. You can choose either the top or the bottom base since the bases are parallel and congruent polygons, or identical 2-dimensional shapes. Volume is measured in cubic units — don’t forget to add units or your teacher might dock you some points. Read on for step-by-step instructions for calculating the volume of 5 different types of prisms.

  1. Image titled Calculate the Volume of a Prism Step 1

    1

    Write down the formula for finding the volume of a triangular prism. The formula is simply V = 1/2 x length x width x height. However, we’ll be taking this formula apart further to use the formula V = area of base x height. You can find the area of the base by using the formula for finding the area of a triangle — multiplying 1/2 by the length and width of the base.[1]

  2. Image titled Calculate the Volume of a Prism Step 2

    2

    Find the area of the base face. To calculate the volume of a triangular prism, you need to first find the area of the triangular base. Find the area of the base of the prism by multiplying 1/2 times the base of the triangle times its height.[2]

    • Ex: If the height of the triangular base is 5 cm and the base of the triangular prism is 4 cm, then the area of the base is 1/2 x 5 cm x 4 cm, which is 10 cm2.

    Advertisement

  3. Image titled Calculate the Volume of a Prism Step 3

    3

    Find the height. Let’s say the height of this triangular prism is 7 cm.

  4. Image titled Calculate the Volume of a Prism Step 4

    4

    Multiply the area of the triangular base face times the height. Simply multiply the area of the base times the height. After you multiply the base and height, you’ll have the volume of the triangular prism.[3]

    • Ex:10 cm2 x 7 cm = 70 cm3

  5. Image titled Calculate the Volume of a Prism Step 5

    5

    State your answer in cubic units. You should always use cubic units when you’re calculating volume because you’re working with three dimensional objects. The final answer is 70 cm.3

    6. Advertisement

  1. Image titled Calculate the Volume of a Prism Step 6

    1

    Write down the formula for finding the volume of a cube. The formula is simply V = side3. A cube is a prism that happens to have three equal sides.[4]

  2. Image titled Calculate the Volume of a Prism Step 7

    2

    Find the length of one side of the cube. All of the sides are equal, so it doesn’t matter which side you choose.

    • Ex: Length = 3 cm.

  3. Image titled Calculate the Volume of a Prism Step 8

    3

    Cube it. To cube a number, just multiply it by itself twice. The cube of «a» is «a x a x a,» for example. Since all of the lengths of the sides of the cube are equal, you don’t have to find the area of the base and multiply it by the height and then multiply it by the length. Multiplying any two sides of the cube will give you the area of the base, and any third side could represent the height. You can still think of this as multiplying the length, width, and height when they all just happen to be the same.[5]

    • Ex: 3 cm3 = 3 cm. * 3 cm. * 3 cm. = 27 cm.3

  4. Image titled Calculate the Volume of a Prism Step 9

    4

    State your answer in cubic units. Don’t forget to put your final answer in cubic units. The final answer is 27 cm.3

    5. Advertisement

  1. Image titled Calculate the Volume of a Prism Step 10

    1

    Write down the formula for finding the volume of a rectangular prism. The formula is simply V = length * width * height. A rectangular prism is a prism with a rectangular base.[6]

  2. Image titled Calculate the Volume of a Prism Step 11

    2

    Find the length. The length is the longest side of the flat surface of the rectangle on the top or bottom of the rectangular prism.

    • Ex: Length = 10 cm.

  3. Image titled Calculate the Volume of a Prism Step 12

    3

    Find the width. The width of the rectangular prism is the shorter side of the flat surface of the rectangle on the top or bottom of the shape.

    • Ex: Width = in 8 cm.

  4. Image titled Calculate the Volume of a Prism Step 13

    4

    Find the height. The height is the part of the rectangular prism that rises up. You can imagine the height of the rectangular prism as the part that stretches up a flat rectangle and makes it three-dimensional.

    • Ex: Height = 5 cm.

  5. Image titled Calculate the Volume of a Prism Step 14

    5

    Multiply the length, the width, and the height. You can multiply them in any order to get the same result. Using this method, you have essentially found the area of the rectangular base ( 10 x 8) and then have multiplied it by its height, 5. But to find the volume of this prism, you can multiply the lengths of the sides in any order.[7]

    • Ex: 10 cm. * 8 cm. * 5 cm = 400 cm.3

  6. Image titled Calculate the Volume of a Prism Step 15

    6

    State your answer in cubic units.[8]
     The final answer is 400 cm.3

    7. Advertisement

  1. Image titled Calculate the Volume of a Prism Step 16

    1

    Write down the formula for calculating the volume of a trapezoidal prism. The formula is: V = [1/2 x (base1 + base2) x height] x height of the prism. You should use the first part of this formula to find the area of the trapezoidal base of the prism before you move forward.[9]

  2. Image titled Calculate the Volume of a Prism Step 17

    2

    Find the area of the trapezoidal base face. To do this, simply plug the two bases and the height of the trapezoidal base into the formula.

    • Let’s say base 1 = 8 cm, base 2 = 6 cm, and height = 10 cm.
    • Ex: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 70 cm2.

  3. Image titled Calculate the Volume of a Prism Step 18

    3

    Find the height of the trapezoidal prism. Let’s say the height of the trapezoidal prism is 12 cm.

  4. Image titled Calculate the Volume of a Prism Step 19

    4

    Multiply the area of the base face times the height. To calculate the volume of the trapezoidal prism, just multiply the area of the base times the height.[10]

    • 70 cm2 x 12 cm = 840 cm3.

  5. Image titled Calculate the Volume of a Prism Step 20

    5

    State your answer in cubic units. The final answer is 840 cm3

    6. Advertisement

  1. Image titled Calculate the Volume of a Prism Step 21

    1

    Write the formula for finding the volume of a regular pentagonal prism. The formula is V = [1/2 x 5 x side x apothem] x height of the prism. You can use the first part of the formula to find the area of the pentagonal base face. You can think of this as finding the area of the five triangles that make up a regular polygon. The side is simply the width of one triangle, and the apothem is the height of one of the triangles. You’ll be multiplying by 1/2 because that’s part of finding the area of a triangle and then multiplying this by 5 because 5 triangles make up the pentagon.[11]

    • For more information on finding the apothem if one is not provided for you, look here.[12]

  2. Image titled Calculate the Volume of a Prism Step 22

    2

    Find the area of the pentagonal base face. Let’s say the length of a side is 6 cm and the length of the apothem is 7 cm. Just plug these numbers into the formula:

    • A = 1/2 x 5 x side x apothem
    • A = 1/2 x 5 x 6 cm x 7 cm = 105 cm2

  3. Image titled Calculate the Volume of a Prism Step 23

    3

    Find the height. Let’s say the height of the shape is 10 cm.

  4. Image titled Calculate the Volume of a Prism Step 24

    4

    Multiply the area of the pentagonal base face times the height. Just multiply the area of the pentagonal base, 105 cm2, times the height, 10 cm, to find the volume of the regular pentagonal prism.[13]

    • 105 cm2 x 10 cm = 1050 cm3

  5. Image titled Calculate the Volume of a Prism Step 25

    5

    State your answer in cubic units. The final answer is 1050 cm3.

    6. Advertisement

Add New Question

  • Question

    How do I find the volume of rectangular prisms?

    Donagan

    Calculate the area of the base (length multiplied by width), then multiply by the height.

  • Question

    How do I calculate the volume of a rectangular prism if there are two different heights?

    Donagan

    A rectangular prism would not have two different heights. If you’re asking about a non-rectangular prism, the volume formula would involve finding the average height of some of the sides.

  • Question

    How do I find the volume of a circular prism?

    Donagan

    The volume of a cylinder is found by squaring the radius and then multiplying by the product of pi and the height of the cylinder. (V = πr²h.)

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

Video

  • Try not to confuse «base» with «base face». Base face refers to the 2-dimensional shape which forms the base of the entire prism (usually, its top and bottom). But that base face may have its own base — a 1-dimensional length along an edge which serves as the base measurement when finding the area of the 2-dimensional shape.

Thanks for submitting a tip for review!

Advertisement

References

About This Article

Article SummaryX

To find the volume of a triangular prism, use the equation V = ½ × length × width × height, or V = the area of the base × the height. Find the area of the base by multiplying ½ × the length and width of one of the triangular bases of the prism. Then, locate the height, and multiply the height by the area of the base. For example, a triangular prism with a length of 4 cm and a width of 5 cm would have an area of 10 cm^2. If the height was 7 cm, the volume of the prism would be 70 cm cubed. If you want to learn how to find the volume of a rectangular or pentagonal prism, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 670,445 times.

Did this article help you?

Источник


Ботулинотерапия в призме преломления зарубежного опыта. Алгоритм применения ботулотоксина Релатокс

Видео: Ботулинотерапия в призме преломления зарубежного опыта. Алгоритм применения ботулотоксина Релатокс

Содержание

  • Характеристики трапециевидной призмы
  • 1- Рисование трапециевидной призмы
  • 2- Свойства трапеции
  • 3- Площадь поверхности
  • 4- Объем
  • 5- Приложения
  • Ссылки

А трапециевидная призма представляет собой призму, в которой участвующие многоугольники являются трапециями. Определение призмы — это геометрическое тело, состоящее из двух равных и параллельных многоугольников, а остальные грани — параллелограммы.

Призма может иметь разные формы, которые зависят не только от количества сторон многоугольника, но и от самого многоугольника.

Если многоугольники, входящие в призму, являются квадратами, то это отличается от, например, призмы, содержащей ромбы, даже если оба многоугольника имеют одинаковое количество сторон. Поэтому все зависит от того, какой четырехугольник задействован.

Характеристики трапециевидной призмы

Чтобы увидеть характеристики трапециевидной призмы, нужно сначала узнать, как она нарисована, какие свойства выполняет основание, какова площадь поверхности и, наконец, как рассчитывается ее объем.

1- Рисование трапециевидной призмы

Чтобы ее нарисовать, необходимо сначала определить, что такое трапеция.

Трапеция — это неправильный с четырех сторон многоугольник (четырехугольник), у которого есть только две параллельные стороны, называемые основаниями, а расстояние между их основаниями называется высотой.

Чтобы нарисовать прямую трапециевидную призму, вы начнете с рисования трапеции. Затем из каждой вершины проецируется вертикальная линия длиной «h» и, наконец, рисуется другая трапеция, вершины которой совпадают с концами ранее нарисованных линий.

У вас также может быть наклонная трапецеидальная призма, конструкция которой аналогична предыдущей, вам просто нужно провести четыре линии, параллельные друг другу.

2- Свойства трапеции

Как указывалось ранее, форма призмы зависит от многоугольника. В частном случае трапеции мы можем найти три различных типа оснований:

-Прямоугольная трапеция: эта трапеция такая, что одна из ее сторон перпендикулярна параллельным сторонам, или что она просто имеет прямой угол.

-Трапеция равнобедренная: представляет собой трапецию, непараллельные стороны которой имеют одинаковую длину.

Скаленовая трапеция: это та трапеция, которая не является ни равнобедренной, ни прямоугольной; его четыре стороны имеют разную длину.

Как можно видеть, в зависимости от типа используемой трапеции получается разная призма.

3- Площадь поверхности

Чтобы рассчитать площадь поверхности трапециевидной призмы, нам нужно знать площадь трапеции и площадь каждого параллелограмма.

Как видно на предыдущем изображении, область включает две трапеции и четыре различных параллелограмма.

Площадь трапеции определяется как T = (b1 + b2) xa / 2, а площади параллелограммов равны P1 = hxb1, P2 = hxb2, P3 = hxd1 и P4 = hxd2, где «b1» и «b2» — основания трапеции, «d1» и «d2» — непараллельные стороны, «a» — высота трапеции, «h» — высота призмы.

Следовательно, площадь поверхности трапециевидной призмы равна A = 2T + P1 + P2 + P3 + P4.

4- Объем

Поскольку объем призмы определяется как V = (площадь многоугольника) x (высота), можно сделать вывод, что объем трапециевидной призмы равен V = Txh.

5- Приложения

Один из самых распространенных объектов, имеющих форму трапециевидной призмы, — это золотой слиток или рампы, используемые в гонках на мотоциклах.

Ссылки

  1. Клеменс, С. Р., О’Даффер, П. Г., и Куни, Т. Дж. (1998). Геометрия. Pearson Education.
  2. Гарсия, В. Ф. (s.f.). Спираль 9. От редакции Norma.
  3. Ицкович, Х. (2002). Изучение геометрических фигур и тел: занятия для первых классов школы. Книги Noveduc.
  4. Ландаверде, Ф. д. (1997). Геометрия (переиздание ред.). Редакция Прогресо.
  5. Ландаверде, Ф. д. (1997). Геометрия (Перепечатка ред.). Прогресс.
  6. Шмидт Р. (1993). Начертательная геометрия со стереоскопическими фигурами. Reverte.
  7. Урибе, Л., Гарсия, Г., Легуисамон, К., Сампер, К., и Серрано, К. (s.f.). Альфа 8. От редакции Norma.
Источник

В геометрии, трапецеидальный призмы представляет собой твердую форму, которая имеет трапецию (или трапецию в Великобритании) сечения в одном направлении и прямоугольного сечений в других направлениях. Для того, чтобы вычислить объем симметричной трапециевидной призмы, вы должны знать, четыре измерения: длина призмы L, высоту трапецеидального поперечного сечения H, ширина основания трапеции B, а также верхнюю ширину трапеции A ,

С другой стороны, если вы знаете трапеции боковые наклонная длин S, можно вычислить объем с L, S, B и A.

Обе формулы для объема трапециевидной пирамиды приведены ниже вместе с несколькими проблемами например. Смотрите также, Поверхность Формула зоны для трапециевидной Prism.

Формула для тома трапециевидной Prism

Если длина призмы L, трапецию ширина основания B, трапецию ширина верхней поверхности А, а высота трапецию Н, то объем призмы задается четырьмя переменной формулой:

V (L, В, А, Н) = ЛГ (А + В) / 2.

  • Другими словами, перемножить длину, высоту и среднее число А и В.

    Эта формула эквивалентна умножения длины призмы по площади трапециевидных сечений. Если вы не знаете, H, но вместо того, чтобы знать боковую наклонная длина S, формула немного сложнее. Это:

V (L, В, А, С) = Л (А + В) SQRT (4S2 + 2AB — В2 — А2) / 4.

Эта вторая формула получена из того факта, что:

H = SQRT [S2 — ((B — A) / 2) 2]

= SQRT (4S2 + 2AB — B2 — A2) / 2.

Вот несколько примеров проблем, которые помогут вам выработать призм объемы. В приведенных выше формулах и примерах, приведенных ниже, предполагается, что трапеций являются симметричными, то есть боковые наклонная длины равны с обеих сторон и в центре верхней длины выровнены по вертикали с центром базовой длины.

Пример 1

Трапецеидальной призмы имеет длину 8, ширину основания 7, ширина верхней части 4, и высоту 3.

Отзыв о Объем трапеции

Используя Н = 3, В = 7, А = 4 и L = 8, можно вычислить объем, используя первое уравнение. Затыкать переменные в этом уравнении дает нам:

V = ЛГ (А + В) / 2

= 8 * 3 * (4 + 7) / 2

= 24 * 11/2

= 132.

Пример 2

Трапециевидную пирамида имеет длину 6,03 см. Его ширина основания составляет 7,82 мм, ширина верхней 3,55 см, а наклонная сторона длина 4,71 см. Каков его объем в кубических сантиметрах?

Объем трапеции фото1

Эта проблема дает L = 6,03, В = 7,82, А = 3,55 и S = 4,71. Так как мы имеем S вместо H, мы используем второе уравнение объема. Подключение этих значений дает нам:

V = L (А + В) SQRT (4S ^ 2 + 2AB — B ^ 2 — Л ^ 2) / 4

= 6,03 (3,55 + 7,82) SQRT (4 * 4,71 ^ 2 + 2 * 3,55 * 7,82 — 7,82 ^ 2 — 3,55 ^ 2) / 4

= 143.92 см ^ 3.

Таким образом, объем 143.92 кубических сантиметров или, что эквивалентно 0,14392 литра.

Пример 3

Трапециевидной призмы имеет объем 1950 кубических дюймов. Высота составляет 6 дюймов, длина 25 дюймов, а верхняя ширина составляет 11 дюймов. Какова ширина трапеции основания?

Объем трапеции фото2

Здесь нам дают объем, но один из измерений отсутствует. Мы имеем V = 1950, Н = 6, L = 25, а = 11, но B неизвестна. Поэтому нам нужно подключить эти значения в первую формулу объема и решить для B. Это дает нам:

V = ЛГ (А + В) / 2

1950 = 25 * 6 * (11 + В) / 2

1950 / (25 * 6) = (11 + В) / 2

13 = (11 + В) / 2

2 * 13 = 11 + B

26 = 11 + B

26 — 11 = В

15 = B

Таким образом, ширина основания составляет 15 дюймов.

Исчисление Оптимизация Пример: Увеличить объем трапеции Prism с заданной длины и базы

Предположим, вы хотите, чтобы сделать коробку в форме трапециевидной призмы субъекта к этим трем условиям: длина коробки призмы должна быть 24 см, одна из параллельных сторон трапеции лица должны быть длиной 12 см, а по всему периметру трапециевидной лицо должно быть 34 см. Какую форму трапеции должно быть таким, чтобы объем коробки максимизируется?

Прежде всего, следует отметить, что это, по сути задача о максимизации площади трапециевидных сечений, так как длина постоянна и равна 24 см.

Для того, чтобы придумать уравнения, мы должны оптимизировать с исчислении, сначала пусть х равняться длине каждой стороны наклонной. Так как одна из параллельных сторон 12, другой должен быть 34 — 12 — х — х или 22 — 2x. Ниже приведены возможные формы трапеции, которые соответствуют ограничениям задачи; треугольник и плоская линия являются предельными случаями.

Объем трапеции фото3

Видео обзор

Все(5)

Источник

Рассчитать объем трапеции

Используя этот онлайн калькулятор для вычисления объема прямоугольного параллелепипеда , вы сможете очень просто и быстро найти объем прямоугольного параллелепипеда, зная значения его длины, ширины и высоты. Воспользовавшись онлайн калькулятором для вычисления объема прямоугольного параллелепипеда, вы получите детальное решение вашего примера, которое позволит понять алгоритм решения задач и закрепить пройденный материал. В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины , конвертером единиц площади и конвертером единиц объема.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.


По завершению появится ссылка для доступа к найденным материалам.

Содержание:

  • МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ. ПЛОЩАДЬ И ОБЪЕМ
  • Найти объем усеченной пирамиды
  • Как рассчитать объем усеченной пирамиды
  • Вычисления
  • Объем усеченной пирамиды
  • Объем геометрических фигур

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Площадь трапеции

МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ. ПЛОЩАДЬ И ОБЪЕМ

Трапеция — это четырехугольник, у которого две стороны параллельны основание , а две другие не параллельны боковые стороны.

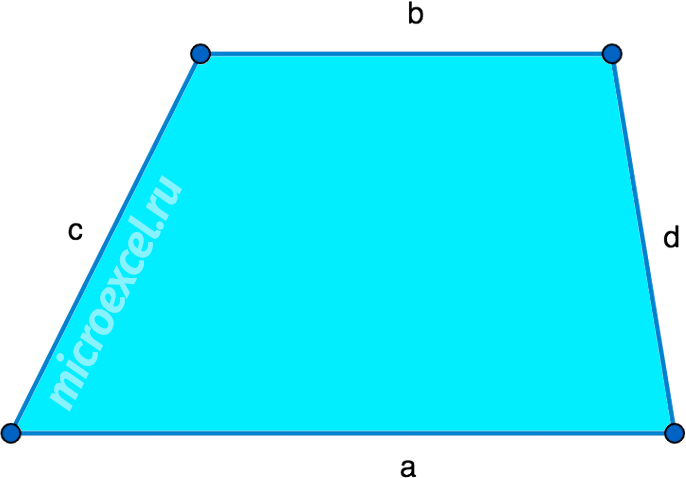
Формула площади трапеции: , где a, b — основания трапеции, h — высота. Формула площади трапеции: , где m — средняя линия, h — высота.

Формула площади трапеции: , где a, b — основания трапеции, c, d — боковые стороны. Трапецией — это четырехугольник, у которого две стороны параллельны основание , а две другие не параллельны боковые стороны. Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор.

Калькулятор справочный портал. Избранные сервисы. Кликните, чтобы добавить в избранные сервисы. Калькулятор площади трапеции покажет как находить площадь трапеции равнобедренной, прямоугольной, боковой и др. Способ расчета площади трапеции Через длины оснований и высоту Через среднюю линию и высоту По длинам сторон и оснований По диагоналям и углу между ними Для равнобедренной трапеции. Мы в соцсетях Присоединяйтесь!

Нашли ошибку? Есть предложения? Сообщите нам.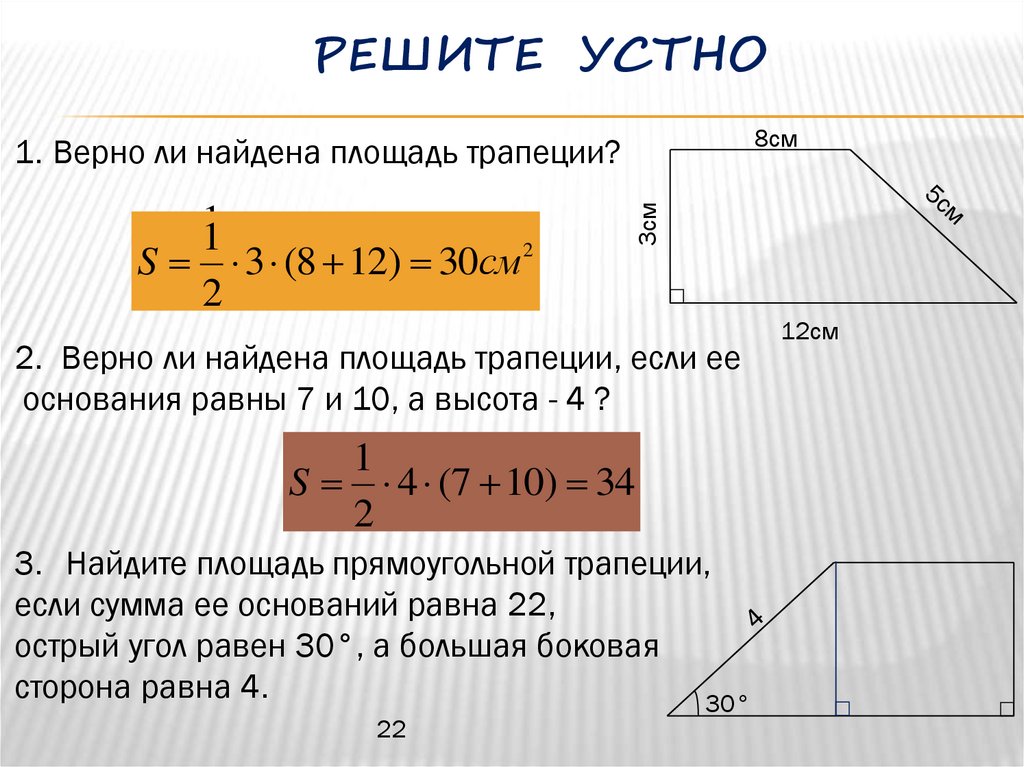 Этот калькулятор можно вставить на сайт, в блог. Создадим калькулятор для вас. Код для вставки без рекламы с прямой ссылкой на сайт Код для вставки с рекламой без прямой ссылки на сайт Код для вставки:. Cообщение: Что-то не нашли? Сообщите нам Что-то не нашли? Формула площади трапеции: , где a, b — основания трапеции, h — высота Трапеция — это четырехугольник, у которого две стороны параллельны основание , а две другие не параллельны боковые стороны.

Формула площади трапеции: , где m — средняя линия, h — высота Трапеция — это четырехугольник, у которого две стороны параллельны основание , а две другие не параллельны боковые стороны. Формула площади трапеции: , где a, b — основания трапеции, c, d — боковые стороны Трапеция — это четырехугольник, у которого две стороны параллельны основание , а две другие не параллельны боковые стороны.

Площади фигур. Расчет площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, круга площадь фигур. Калькуляторы по геометрии. Помощь в решении задач по геометрии, учебник онлайн все калькуляторы по геометрии.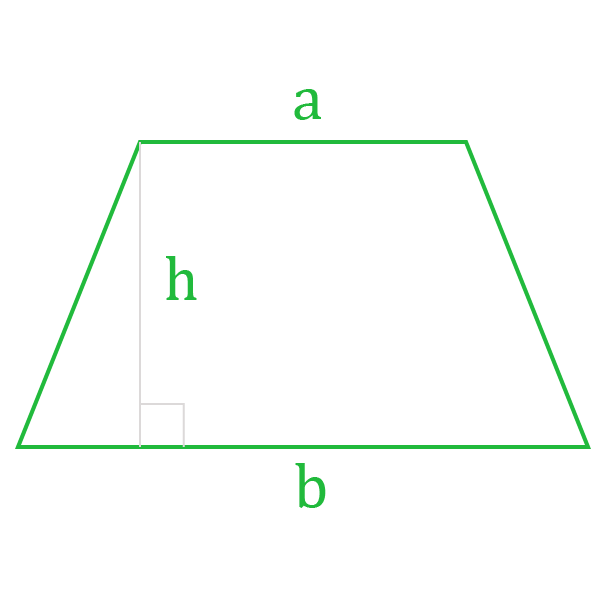 Площадь поверхности куба, онлайн расчет. Найти площадь поверхности куба по формуле через длину его ребра.

Площадь ромба. Определения и формулы расчета. Площади геометрических фигур. Площадь квадрата, круга, параллелограмма, ромба, трапеции, треугольника, эллипса.

Периметры фигур. Расчет периметра квадрата, прямоугольника, треугольника, круга периметры фигур. Этот калькулятор можно вставить на сайт, в блог Создадим калькулятор для вас. Код для вставки без рекламы с прямой ссылкой на сайт Код для вставки с рекламой без прямой ссылки на сайт. Код для вставки: Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор.

Если нужен ответ.

Найти объем усеченной пирамиды

Трапеция является нестандартной фигурой и геометрии, состоя из двух параллельных оснований и разнонаправленных боковых сторон. Тем не менее, в трапеции можно провести два прямоугольных треугольника через высоты , опущенные из вершин меньшего основания, благодаря чему, геометрический калькулятор трапеции может рассчитать все необходимые для нее параметры.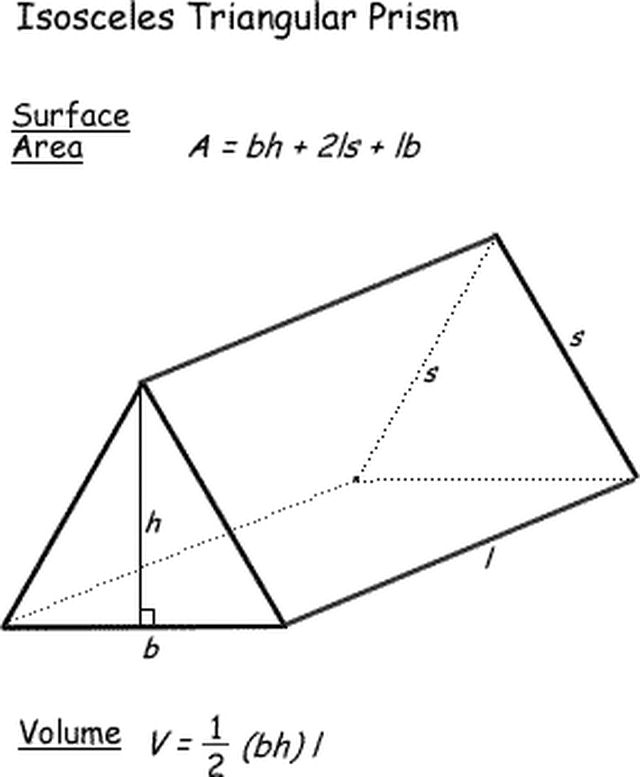 Среди них можно перечислить не только стороны трапеции, основания, диагонали и высоты, но и среднюю линию , периметр , площадь , биссектрисы , и другие возможные значения. Геометрический калькулятор трапеции вычисляет все вышеописанные длины на основе приведенных для каждой категории отдельно формул, преобразованных алгебраически таким образом, чтобы опираться именно на определенные вводные данные. Постройка Вес древесины Кубатура бревен Кубатура досок Утеплитель. Зная: Стороны трапеции.

Объем усеченной пирамиды рассчитывается через ее высоту и площадь оснований. Иногда можно рассчитать объем, зная только периметр одного.

Как рассчитать объем усеченной пирамиды

Объем тел. Пирамидой является геометрическое тело, боковыми гранями которого являются треугольники с общей вершиной, а в основании расположен многоугольник. Если параллельно основанию пирамиды провести сечение, которое разделит ее на 2 части. Расположенная между основанием и сечением часть пирамиды является усеченной пирамидой. Чтобы найти V усеченной пирамиды, нужно знать площади ее оснований нижнего и верхнего , а также высоту. Далее объем усеченной пирамиды рассчитывается по формуле:. В данной формуле: пл. Таким образом, V усеченной пирамиды равняется произведению трети ее высоты на сумму площадей оснований и корень квадратный из произведения площадей оснований.

Вычисления

В этой статье: Вычисление объема треугольной призмы Вычисление объема куба Вычисление объема прямоугольной призмы Вычисление объема трапецеидальной призмы Вычисление объема правильной пятиугольной призмы 5 Источники. Призма — объемная геометрическая фигура с двумя равными основаниями и плоскими гранями. Чтобы найти объем призмы, нужно просто вычислить площадь ее основания и умножить его на ее высоту; тем не менее вычисление площади основания может быть нетривиальной задачей. Вот как можно вычислить объем различных призм. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 17 человек а.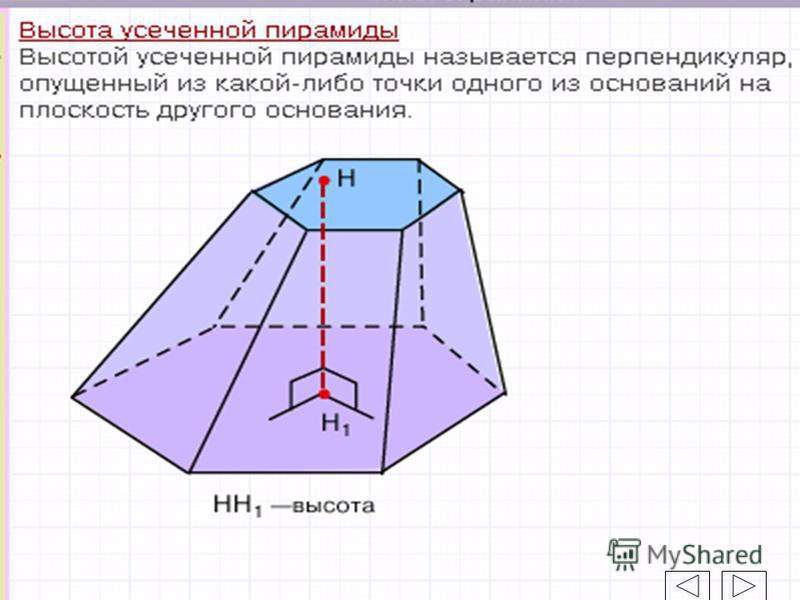

Описание Программа создана для подсчета кубатуры различных фигур, которые зачастую встречаются в строительстве.

Объем усеченной пирамиды

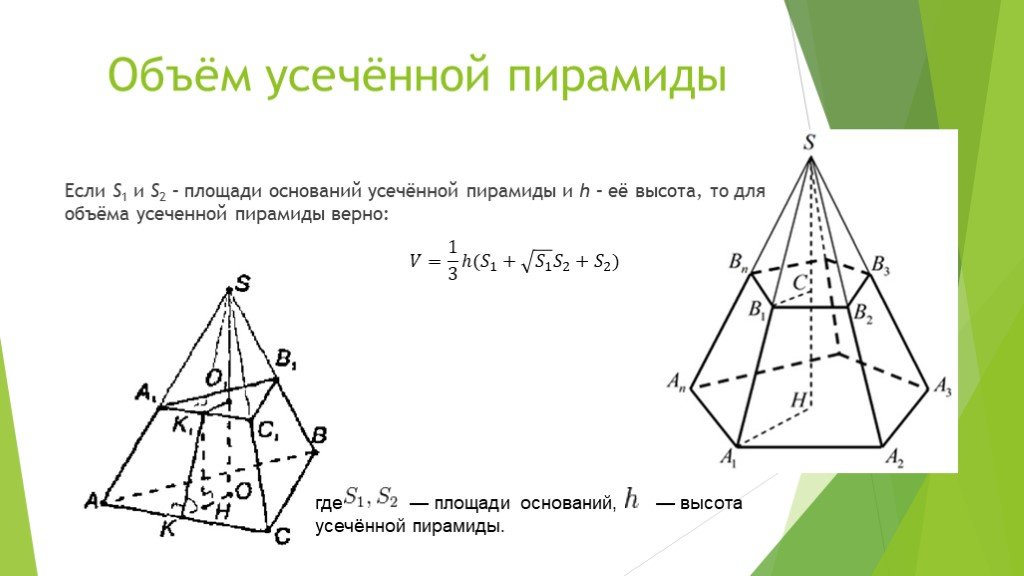
Как известно, площадь трапеции можно получить, взяв произведение полусуммы ее оснований на высоту, или же взяв произведение ее средней линии на высоту. Оба способа дают одно и то же, так как трапеция равновелика прямоугольнику, основанием которого служит средняя линия трапеции, а высота одинакова с высотой трапеции. В связи с этим возникает вопрос: нельзя ли вычислить объем усеченной пирамиды вместо обычного способа, основанного на формуле где высота усеченной пирамиды, и площади двух ее оснований, другим способом, основанным на замене усеченной пирамиды призмой, основанием которой служит среднее сечение усеченной пирамиды, а высота одинакова с высотой усеченной пирамиды? Средним сечением усеченной пирамиды называют такое ее сечение, которое производится параллельно ее основаниям через середину высоты. Заметим, что в технике при вычислении объема усеченной пирамиды например, при обмере песка, заготовленного для дорожных работ поступают обычно именно так: находят площадь среднего сечения, затем умножают ее на высоту усеченной пирамиды.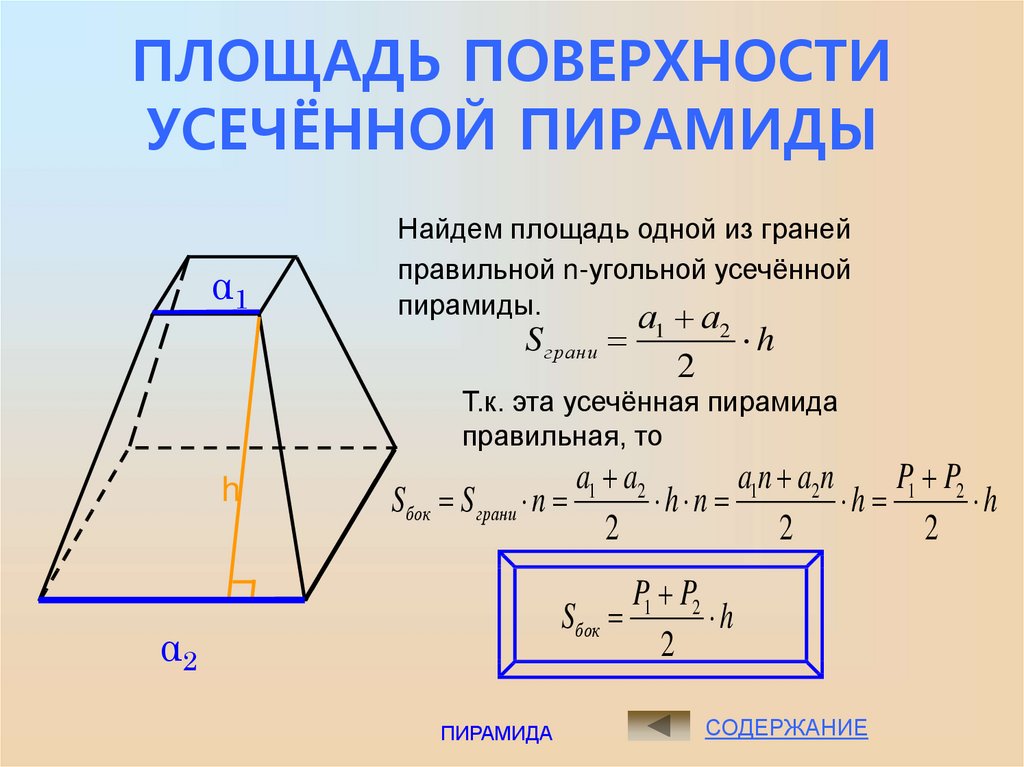

Объем геометрических фигур

Обсудить на форуме Записаться на курсы Обратиться к консультанту Пройти тест Полный список курсов обучения Бесплатные видеоуроки Нужна информация! Аксиомы планиметрии. Аксиома принадлежности точек и прямых. Аксиома расположения точек на прямой. Аксиома про длину отрезков. Аксиома расположения точек относительно прямой. Аксиома свойств измерения углов.

Чтобы вычислить площадь трапеции, надо измерить основания и Чтобы вычислить объем ведра так называемой цилиндрической формы (рис.

Данный калькулятор рассчитывает объем таких геометрических фигур как куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид и тороид. Please fill in this field. Expected number.

Земельные участки имеют разнообразные формы. Площадь любого участка можно вычислить, если знать, как вычисляются площади прямоугольника, квадрата, параллелограмма, трапеции, треугольника и круга. Чтобы вычислить площадь прямоугольника, надо измерить основание и высоту длину и ширину его в мерах длины одного и того же наименования и полученные числа перемножить.

Результат покажет площадь прямоугольника в квадратных мерах того же наименования.

При изготовлении самодельного корпусного сабвуфера для автомобиля всегда встает вопрос: как рассчитать корпус для сабвуфера? Для начала если неизвестен объем необходимо рассчитать объем короба для сабвуфера и затем, уже зная его сделать расчет короба для сабвуфера.

Пирамидой называют многогранник, у которого основание представлено произвольным многоугольником, а остальные грани — треугольниками с общей вершиной, которая соответствует вершине пирамиды. Если в пирамиде провести параллельное основанию сечение, то оно разделить фигуру на две части. Пространство межу нижним основанием и сечением, ограниченное гранями, называется усеченной пирамидой. Формула объема усеченной пирамиды представляет собой одну треть произведения высоты на сумму площадей верхнего и нижнего основания с их средним пропорциональным:. Таким образом, вычислив коэффициент подобия и рассчитав площадь оснований, мы нашли объем заданной усеченной пирамиды.

Задача: Дана треугольная усеченная пирамида. Найдите объем пирамиды.

Трапеция — это четырехугольник, у которого две стороны параллельны основание , а две другие не параллельны боковые стороны. Формула площади трапеции: , где a, b — основания трапеции, h — высота. Формула площади трапеции: , где m — средняя линия, h — высота. Формула площади трапеции: , где a, b — основания трапеции, c, d — боковые стороны.

Аквариумный калькулятор для расчёта объёма аквариумов разной формы.

Калькулятор поможет вычислить объём воды и количество грунта в аквариумах разной формы

  • Наши услуги

    • /

  • Аквариумный калькулятор
1. Расчет объема прямоугольного аквариума.

2. Расчет объема панорамного аквариума.

  Размер A (в см)
  Размер B (в см)  Размер C (в см)
  Размер D (в см)  Высота (в см)     
  Желаемый слой грунта (в см)
  Объем аквариума (в литрах)  Объем грунта (в литрах)  Кол-во грунта (в кг.)

3. Расчет объема панорамного аквариума с гнутым передним стеклом

ВАЖНО! Радиус кривизны переднего стекла у разных производителей может сильно различаться, следовательно, расчет приблизителен.

  Размер A (в см.)
  Размер B (в см.)  Размер C (в см.)
  Высота (в см.)  Желаемый слой грунта (в см. )
  Объем аквариума (в литрах)  Объем грунта (в литрах)  Кол-во грунта (в кг.)

4. Расчет объема углового аквариума.

  Размер A (в см.)  Высота (в см.)  Желаемый слой грунта (в см.)  Объем аквариума (в литрах)  Объем грунта (в литрах)  Кол-во грунта (в кг.)

5. Расчет объема углового панорамного аквариума

  Размер A (в см)
  Размер B (в см)  Размер C (в см)
  Высота (в см)   Желаемый слой грунта (в см)  Объем аквариума (в литрах)  Объем грунта (в литрах)  Кол-во грунта (в кг.)

6. Расчет объема углового аквариума с гнутым передним стеклом

ВАЖНО! Радиус кривизны переднего стекла у разных производителей может сильно различаться, следовательно, расчет приблизителен.
  Размер A (в см.)  Высота (в см.)   Желаемый слой грунта (в см.)  Объем аквариума (в литрах)  Объем грунта (в литрах)  Кол-во грунта (в кг.)

7. Расчет объема аквариума в виде равностороннего многогранника

  Размер A (в см)
  Высота (в см)  Число сторон
  Желаемый слой грунта (в см.)  Объем аквариума (в литрах)  Объем грунта (в литрах)  Кол-во грунта (в кг.)

8. Расчет объема аквариума в виде цилиндра

  Размер A (в см.)  Высота (в см.)  Желаемый слой грунта (в см. )  Объём аквариума (в литрах)  Объём грунта (в литрах)  Кол-во грунта (в кг.)

9. Расчет мощности нагревателя и терморегулятора.
10. Расчет содержания углекислого газа. расчет CO2 по pH и kH.

  Содержание углекислого газа, CO2 (мг/л)

  Кислотность, pH  Карбонатная жесткость, kH (градусы)

11. Определение магния (Mg) по жесткости (GH) и кальцию (Ca).

  Магний, Mg (мг/л)

  Жесткость, GH (нем.градусы)  Кальций, Ca (мг/л)

12. Расчет мощности ламп для аквариума.

Если у вас в аквариуме только рыбы, например, африканские цихлиды, и нет живых растений или кораллов, то тут все просто. Свет вам нужен только для того,
чтобы вам было удобно наблюдать за подводными обитателями.
Рыбам слишком яркое освещение ни к чему — оно только вызывает у них стресс и, как правило, болезни и остальные проблемы.
Обычно вам будет достаточно той лампы, которая входит в комплект аквариума. Можно поставить лампу с любым спектром.
Лампы, в спектре которых много синего света, выявляют окраску рыб за счет «свечения» чешуи рыбы (хотя является ли такая окраска естественной?) — например,
в аквариум с африканскими цихлидами — псевдотрофеусами, аулонокарами и т.д. можно поставить лампу с актиничным светом — синяя окраска рыб будет выглядеть очень красиво.
В общем, выбор спектра лампы определяется вашим вкусом, а выбор мощности этим калькулятором.

Объем аквариума   л
Нет живых растений
Есть растения нет подачи углекислого газаЕсть растения и подача углекислого газаРекомендуемая мощность   Вт

  • Наши услуги

    • /

  • Обслуживание и чистка аквариумов

Калькулятор объема трапециевидной призмы

Создано Wei Bin Loo

Отредактировано Анна Щепанек, доктор философии и Стивен Вудинг

Последнее обновление: 09 февраля 2023 г.

Содержание:

  • Что такое объем трехмерного объекта?
  • Как найти объем трапециевидной призмы?
  • Часто задаваемые вопросы

С помощью этого калькулятора объема трапециевидной призмы мы стремимся помочь вам рассчитать объем трапециевидной призмы . Вы можете проверить наш калькулятор трапеции и калькулятор площади трапеции, чтобы понять больше по этой теме.

Мы написали эту статью, чтобы помочь вам понять что такое объем трапециевидной призмы и как найти объем трапециевидной призмы . Мы также продемонстрируем несколько примеров, которые помогут вам понять формулу объема трапециевидной призмы.

Что такое объем трехмерного объекта?

Объем 3D-объекта – это объем пространства, занимаемый  3D-объектом. Чем больше объем, тем больше места занимает объект. Одним из способов измерения объема является измерение количества воды, которое вытесняет объект, когда его опускают в воду.

Пожалуйста, ознакомьтесь с нашим калькулятором объема, чтобы лучше понять эту тему.

Как найти объем трапециевидной призмы?

Трапециевидная призма

Чтобы понять формулу объема трапециевидной призмы, рассмотрим пример ниже:

  • Длина короткого основания (b): 5 м
  • Длина длинной базы (B): 5 м
  • Длина (ℓ): 5 м
  • Высота (в): 3 м

  1. Определите длину короткой базы (b).

    Первым шагом является определение длины короткого основания b трапециевидной призмы. Для нашего примера b равно 5 м .

  2. Определите длину длинной базы (B).

    Следующим шагом является определение длины длинного основания B трапециевидной призмы. Для нашего примера b равно 5 м .

  3. Рассчитать длину (ℓ).

    Теперь вам нужно вычислить длину ℓ трапециевидной призмы. л этой трапециевидной призмы составляет 5 м .

  4. Определить высоту (h).

    Кроме того, высота h трапециевидной призмы равна 3 м .

  5. Вычислите объем трапециевидной призмы.

    Последним шагом является расчет объема трапециевидной призмы по формуле:

    ((б + В) / 2) × ч × л

    Таким образом, объем трапециевидной призмы равен ((5 м + 5 м)/2) × 5 м × 3 м = 75 м³ .

Часто задаваемые вопросы

Может ли громкость быть отрицательной?

Нет , объем не может быть отрицательным. Это потому, что нулевого и отрицательного объема просто не существует. Объект не может иметь нулевой или отрицательный объем.

Каков объем трапециевидной призмы со всеми сторонами 1 м?

Объем этой трапециевидной призмы будет 1 м³ . Вы можете рассчитать его по следующей формуле:

объем = ((длина короткого основания + длина длинного основания) / 2) × высота × длина .

Как рассчитать объем трапециевидной призмы?

Объем трапециевидной призмы можно рассчитать за пять шагов:

  1. Определить длину короткой базы (б)

  2. Определить длину длинной базы (B)

  3. Рассчитать длину (ℓ)

  4. Определить высоту (h)

  5. Примените формулу объема трапециевидной призмы :

    ((б + В) / 2) × ч × л

Что такое боковая область для трехмерного объекта?

Боковая площадь трехмерного объекта представляет собой сумму площадей всех сторон трехмерного объекта, кроме основания и вершины .

Вэй Бин Лоо

Высота

Длина

Длинная база (B)

Короткая база (b)

Объем

Посмотреть 23 похожих калькулятора 3d геометрии

Объем трапециевидной призмы

Объем трапециевидной призмы — определение, формула и примеры

Содержание

Последнее изменение: 6 сентября 2022 г.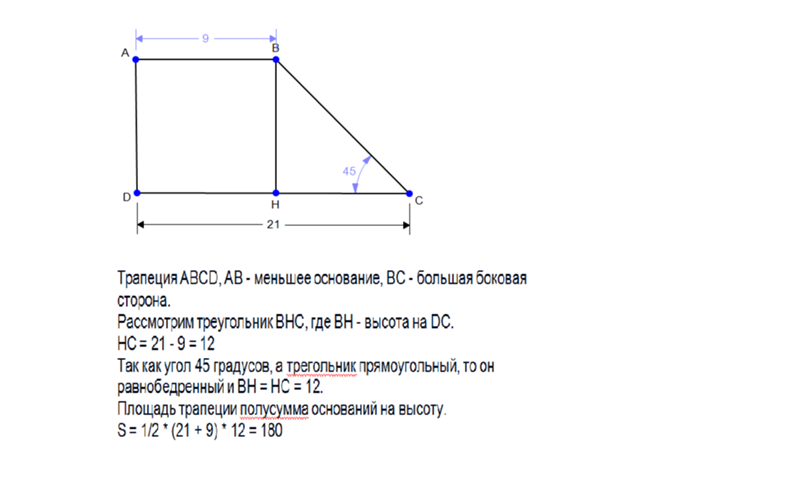


Оглавление

Объем трапециевидной призмы — это пространство, которое она занимает в трехмерной плоскости. Измеряется в кубических единицах, таких как м 3 , см 3 , мм 3 , фут 3 .

Формула

Формула приведена ниже:

Объем трапециевидной призмы

Давайте решим несколько примеров, чтобы лучше понять концепцию.

Решенные примеры

Найдите объем трапециевидной призмы, изображенной на рисунке.

Решение:

Как известно,
${Объемвлево(Vвправо) =dfrac{1}{2}влево(a+bвправо) times htimes l}$ , здесь a = 10 см, b = 8 см, h = 6 см, l = 13 см
${ следовательно V=dfrac{1}{2}times left( 10+8справа) умножить на 6умножить на 13}$
= 702 см 3

Нахождение объема трапециевидной призмы по известным ПЛОЩАДЬ ОСНОВАНИЯ и ДЛИНА 0003

Найдите объем трапециевидной призмы, изображенной на рисунке, площадь основания которой 361 м 2 , а длина 12,5 м.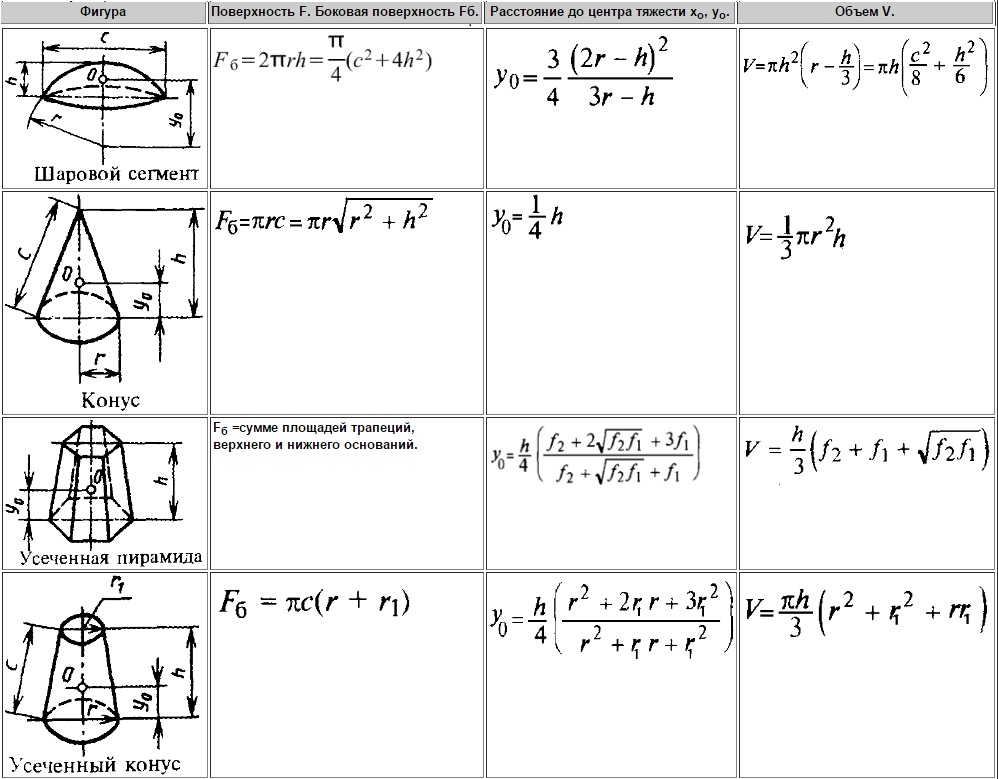

Решение:

Здесь мы будем использовать альтернативную формулу.
Volume ( V ) = Base Area × l , here base area = 361 m 2 , l = 12.5 m
∴ V = 361 × 12.5
= 4512.5 m 3

Нахождение объема наклонной трапециевидной призмы при 9

Найдите объем наклонной трапециевидной призмы, данной на рисунке.

Решение:

Как известно,
Объем прямой трапециевидной призмы длиной ‘l’ = Объем наклонной трапециевидной призмы длиной ‘l’
${Объемвлево( Vвправо) =dfrac{ 1}{2}left( a+bright) times htimes l}$, здесь a = 12 м, b = 9 м, h = 5 м, l = 11 м
$ { следовательно V = dfrac {1} {2} раз влево ( 12 + 9 вправо) раз 5 раз 11} $
= 577,5 м 3

  • Больше ресурсов:
    • объем призмы
    • Площадь поверхности призмы
    • Правая призма
    • Наклонная призма
    • Прямоугольная призма
    • Торговая ПРИЗМА
    • Площадь поверхности прямоугольной ПРИЗМ
    • Триан.
Источник
Определение призмы

Призма — многогранное тело, основаниями которого являются два равных многоугольника, лежащие в параллельных плоскостях. Остальными гранями являются параллелограммы.

Такие параллелограммы в призме называются боковыми.

obemprizmy.svg

Онлайн-калькулятор объема призмы

Призмы разделяют на некоторые типы:

  1. Треугольная призма — у нее основания — треугольники;
  2. Четырехугольная призма — у нее основания — четырехугольники;
  3. Пентапризма — пятиугольная призма.

Деление, в общем, продолжается до бесконечности.

Виды призм

Прямая — у такой призмы боковые грани образуют с основаниями прямой угол.
Правильная — ее основанием является какой-либо правильный многоугольник.
Усеченной называется призма, у которой основания не параллельны друг другу.

Формула объема призмы

Объем прямой призмы находится так же, как и объем других многогранников — путем умножения площади основания на высоту.

Объем призмы

V=Sосн⋅hV=S_{text{осн}}cdot h

SоснS_{text{осн}} — площадь основания призмы;
hh — высота призмы.

Разберем задачу на нахождение объема прямой призмы.

Задача

Найти объем призмы, если ее основанием является равнобедренный треугольник с равными сторонами по 5 см5text{ см} и основанием в 6 см6text{ см}. Высота призмы равна 10 см10text{ см}.

Решение

a=5a=5
b=6b=6
h=10h=10

Вычисляем площадь основания. Нужно провести высоту в данном равнобедренном треугольнике. Тогда, по теореме Пифагора, получаем:

a2=l2+(b2)2a^2=l^2+Big(frac{b}{2}Big)^2,

где ll — высота равнобедренного треугольника.

Отсюда:

l2=a2−(b2)2l^2=a^2-Big(frac{b}{2}Big)^2

l=a2−(b2)2l=sqrt{a^2-Big(frac{b}{2}Big)^2}

l=25−9l=sqrt{25-9}

l=4l=4

Площадь равнобедренного треугольника SS это половина от произведения его основания на высоту:

S=12⋅b⋅l=12⋅6⋅4=12S=frac{1}{2}cdot bcdot l=frac{1}{2}cdot 6cdot 4=12

В нашем случае этот треугольник является основанием призмы, поэтому:

S=SоснS=S_{text{осн}}

Тогда объем призмы найдется по формуле:

V=Sосн⋅h=12⋅10=120 см3V=S_{text{осн}}cdot h=12cdot 10=120text{ см}^3

Ответ

120 см3.120text{ см}^3.

На нашем сайте вы можете оформить решение задач на заказ по самым низким ценам!

Тест по теме «Объем призмы»

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти цифровой товар
  • Как найти красивое имя для мальчика
  • Как найти провода кан шины
  • Как найти клиентов для хостинга
  • Как найти что гудит в машине