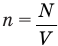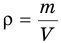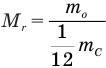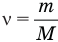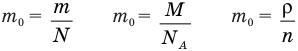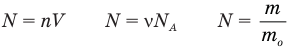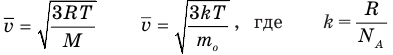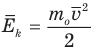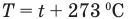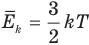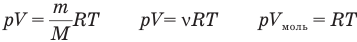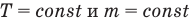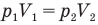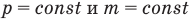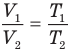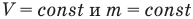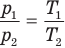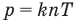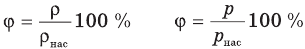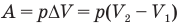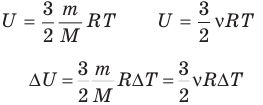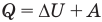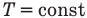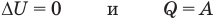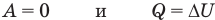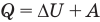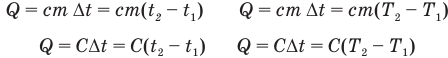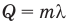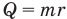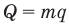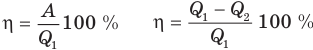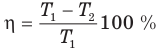Содержание:
- § 1 Расчет массы и объема вещества по его плотности
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Расчет массы и объема вещества по его плотности
В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества.
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p.
Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
§ 2 Решение задач
Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.
Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.
§ 3 Важно запомнить
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: V = m : p.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. — М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс — М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
Измерение объёма тела по формуле — возможные способы, единицы измерения
Содержание:
- Понятие объема тела
- Свойства объема тела
- Как вычислить объем тела: все формулы
- Примеры решения задач
- Задания для самостоятельной работы
Понятие объема тела
Объем является количественным параметром пространства, занятого телом или веществом.
Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:
- форма;
- линейные размеры.
Главным свойством объема принято считать аддитивность.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.
Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.
Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.
Свойства объема тела
В процессе решения разнообразных задач по физике, алгебре и геометрии целесообразно использовать свойства, которыми обладает объем тела. Перечислим основные из них:
- Объем тела не может быть отрицательной величиной.
- В том случае, когда некое геометрическое тело состоит из определенного количества геометрических тел, не обладающих едиными внутренними точками, объем такого тела складывается из объемов составляющих его тел.
- Объем фигуры в виде куба с ребром, значение которого равно единице измерения длины, равен единице.
- Аналогичные друг другу геометрические тела обладают одинаковыми объемами.
- В том случае, когда тело имеет объем V1 и расположено в другом теле с объемом V2, справедливо следующее соотношение: (V1<V2
).
Как вычислить объем тела: все формулы
Существует практический способ определения объема тела, включая тела, обладающие сложной формой и геометрией. Данная методика основана на законе Архимеда и предполагает погружение рассматриваемого тела в некую жидкость. По результатам следует измерить объем вытесненной телом жидкости. Данная величина равна объему измеряемого тела.
Формула расчета объема тела, исходя из известных величин массы и плотности:
(V={frac {m}{rho }})
Здесь m определяется, как масса, а rho является средней плотностью тела.
В том случае, когда тела обладают простыми геометрическими формами, в решении задач допустимо использовать специальные формулы. К примеру, для того чтобы найти объем куба, ребро которого равно а, следует применить такую формулу: (V=a^{3}).
Вычислить объем некого прямоугольного параллелепипеда можно путем умножения длины, ширины и высоты. Запишем другие распространенные формулы для расчета объемов геометрических фигур:
- куб, формула объема: (V=a^{3}):
- прямоугольный параллелепипед, формула объема: (V=abc) (произведение длин трех сторон):
- призма, формула объема: ( V=Bh) (произведение площади основания и высоты):
- пирамида, формула объема: (V={frac {1}{3}}Bh:)
- параллелепипед, формула объема: (V=abc{sqrt {K}}, {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}:
) -
- тетраэдр, формула объема: (V={{sqrt {2}} over 12}a^{3}:)
- шар, формула объема: (V={frac {4}{3}}pi r^{3}):
- эллипсоид, формула объема: (V={frac {4}{3}}pi abc):
- прямой круговой цилиндр, формула объема: (V=pi r^{2}h):
- конус, формула объема: (V={frac {1}{3}}pi r^{2}h):
- тело вращения, формула объема: (V=pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x):
В том случае, когда необходимо определить объем, которым обладает некое тело, имеющее сложную форму, нужно разбить мысленно данное тело на отдельные части. Такие части целого должны иметь простую форму. Далее следует сложить вычисленные объемы простых тел. Результат будет являться значением объема начального тела.
Примеры решения задач
Задача 1
Задача
Имеется пара шаров. Радиус первого шара в 5 раз превышает радиус второго шара.
Требуется определить, во сколько раз площадь поверхности второго шара меньше по сравнению с площадью поверхности первого шара
Решение
Рассчитать площадь поверхности можно по формуле:
(S=4pi R^2)
Тогда запишем отношения площадей пары шаров:
(dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2})
Сравним радиусы геометрических фигур:
(R_1=5R_2)
В результате:
(dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25)
Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.
Ответ: 25.
Задача 2
На рисунке изображены конусы. Назовем их (K_1) и (K_2).
Полная поверхность (K_1) по площади относится к площади полной поверхности (K_2) как 4:1.
Фигура (K_1) обладает радиусом, который в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2).
Требуется вычислить, как относится образующая (K_2) к образующей (K_1.)
Решение
Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:
(S=pi R (R+l))
Запишем отношения площадей полной поверхности заданных конусов:
(dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)})
Согласно условию задачи, имеем:
(R_1=4l_1, R_2=frac12R_1=2l_1)
В результате:
(dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)} quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5)
Ответ: 0,5.
Задача 3
Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.
Решение
Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b, с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:
V=abc
Применительно к нашей задаче, запишем:
(dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2})
Известно, что:
(a_1=7a_2, b_2=2b_1, c_1=3c_2)
В результате:
(dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}= dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot 2}{21}=10)
Ответ: 10.
Задача 4
Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.
Решение
Составим формулу для расчета площади боковой поверхности конуса:
(S=pi Rl)
Запишем отношения площадей боковых поверхностей для первого и второго конусов:
(dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2})
Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:
(frac{R_1}{R_2}=frac{15}7, то dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2)
Ответ: 0,2.
Задача 5
Имеется пара шаров. Объем первой фигуры составляет 54. Радиус второй фигуры в 3 раза меньше по сравнению с радиусом первой. Нужно определить объем второго шара.
Решение
Запишем формулу, согласно которой можно определить объем шара:
(V=dfrac43 pi R^3)
Составим отношение объемов двух фигур:
(dfrac{54}{V_2}=dfrac{V_1}{V_2}= dfrac{frac43 pi ,R_1^3}{frac43 pi ,R_2^3}=left(dfrac{R_1}{R_2}right)^3)
По условиям задачи:
(R_1=3R_2)
В результате:
(dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad V_2=dfrac{54}{27}=2)
Ответ: 2.
Задача 6
Имеется некая емкость конусообразной формы. Ее заполнили до половины с помощью 75 гр жидкости. Необходимо вычислить вес жидкости, которую нужно добавить в емкость, чтобы заполнить ее до верхнего края.
Решение
Вспомним формулу объема из курса физики:
(V=frac{m}{rho})
Предположим, что O является центром основания большего конуса. Пусть Q — центр основания меньшего конуса, а S обозначает общую вершину данных фигур. В одной плоскости построим радиусы OA и QB:
В таком случае:
(QBparallel OA)
(triangle SQBsim triangle SOA)
В результате:
(dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21)
Получим, что:
(m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho= dfrac13cdot picdot QScdot QB^2 cdot rho)
Можно сделать вывод, что:
(m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho= dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot 75=600 {small{text{грамм}}})
Таким образом, потребуется долить в емкость:
(600-75=525 {small{text{грамм}}})
Ответ: 525.
Задача 7
Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.
Решение
Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, B’C’, C’D’, D’A’, параллельным соответственно AB, BC, CD, DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой.
Исследуем плоскость ASO. Построим (A’Hparallel SO), где SO представляет собой высоту начальной фигуры. В таком случае:
(A’Hperp ABC)
В результате получилось расстояние, которое равно (frac13SO:)
(triangle AA’Hsim triangle ASO)
(dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad SA=3AA’ quadRightarrowquad SA’=dfrac23SA)
Таким образом:
(SQ=frac23SO)
(triangle ASBsim triangle A’SB’)
Получим, что:
(dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad A’B’=dfrac23AB)
Запишем отношения объемов пирамид:
(dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}= dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot AB^2}=dfrac{SQ}{SO}cdot left(dfrac{A’B’}{AB}right)^2=dfrac23cdot left(dfrac23right)^2=dfrac8{27})
В результате объем малой фигуры составит:
(V_{{small{text{м}}}}=dfrac8{27}cdot 54=16)
Ответ: 16.
Задания для самостоятельной работы
Задание 1
Имеется пара конусов. Вторая фигура обладает радиусом, который в три раза больше по сравнению с радиусом первой фигуры. Второй конус выше первого в шесть раз. Объем второй фигуры равен 18. Требуется вычислить, чему равен объем первого конуса.
Решение
Формула определения объема конуса:
(V=frac13pi R^2h)
Запишем отношения объемов двух фигур:
(dfrac{V_1}{18}=dfrac{V_1}{V_2}= dfrac{frac13pi ,R_1^2,h_1}{frac13 pi ,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot dfrac{h_1}{h_2})
Исходя из условий задачи:
(R_2=3R_1)
(h_1=6h_2)
В результате:
(dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}= dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot 18=12)
Ответ: 12
Задание 2
Дано два шара. Объем первого шара в 343 раза больше по сравнению с объемом второго шара. Нужно вычислить, во сколько раз радиус первой фигуры больше, чем радиус второй фигуры.
Решение
Запишем формулу для нахождения объема шара:
(V=dfrac43 pi R^3)
Составим отношения объемов данных шаров:
(dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}= left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad dfrac{R_1}{R_2}=sqrt[3]{343}=7)
Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.
Ответ: 7.
Задание 3
На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:
(S=2pi RH)
Составим отношение площадей боковых поверхностей двух фигур:
(dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}= dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2})
В результате:
(R_2=4R_1, H_1=5H_2)
Таким образом:
(dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}= dfrac14cdot 5=dfrac54)
Получим, что:
(S_2=dfrac{16cdot 4}5=12,8)
Ответ: 12,8.
Задание 4
Имеется некая емкость конусообразной формы. Объем этой емкости составляет 2700 мл. Требуется рассчитать количество жидкости, налитой в емкость, если ее уровень в 3 раза меньше по сравнению с высотой емкости.
Решение
Введем обозначения, как на рисунке:
В таком случае:
(QBparallel OA и triangle SQBsim triangle SOA)
Таким образом:
(dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13)
Соотношение объемов жидкости до определенной линии и емкости:
(dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}= dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27})
В результате:
(V_{small{text{ж}}}=dfrac1{27}V=100)
Ответ: 100.
Задача 5
На рисунке изображены фигуры в виде шаров. Первый шар имеет радиус 6. Второй шар имеет радиус 2. Нужно вычислить, во сколько раз объем первой фигуры превышает объем второй фигуры.
Решение
Запишем формулу для расчета объема шара, который не может изменяться:
(V=dfrac43 pi R^3)
Составим отношение объемов двух шаров:
(dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}= left(dfrac62right)^3=27)
В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.
Ответ: 27.
Формулы молекулярной физики
Формула концентрации молекул
Здесь n — концентрация 

Формула плотности
Здесь 


Формула относительной молекулярной массы
Здесь 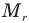

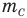
Формула количества вещества (количества молей)
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
Здесь 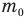
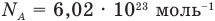



Формулы количества молекул
Здесь A — количество молекул (безразмерное), п — концентрация молекул 

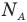
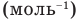

Формулы средней квадратичной скорости молекул
Здесь 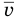
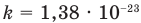

Основное уравнение кинетической теории идеального газа
Здесь р — давление газа (Па), 

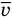

Формула средней кинетической энергии молекул
Здесь 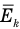
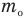
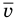
Связь шкал Цельсия и Кельвина
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
Здесь 
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
Здесь р — давление газа (Па), V — объем 
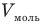
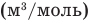
Объединенный газовый закон — уравнение Клапейрона
при
Здесь 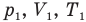

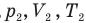

Закон Бойля — Мариотта (изотермический процесс)
при
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 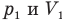

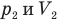

Закон Гей-Люссака (изобарный процесс)
при
Здесь р — давление газа (Па), m — масса газа (кг), 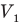
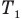

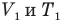

Закон Шарля
при
Здесь V — объем газа 
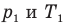
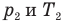
Связь давления идеального газа с концентрацией его молекул и температурой
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа 
Формулы относительной влажности
Здесь 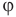
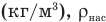
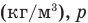
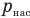
Работа при изобарном изменении объема газа
Здесь А — работа (Дж), р — давление газа (Па), 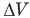
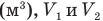

Внутренняя энергия идеального одноатомного газа
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 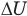
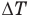
Первый закон термодинамики
Здесь Q — количество теплоты, переданное термодинамической системе (Дж), 
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при
к изохорному: при V = const
к изобарному: при р = const
к адиабатному: при Q = 0
Здесь Т — абсолютная температура (К), 
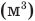
Формулы количества теплоты при нагревании или охлаждении тел
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 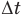
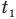
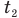
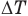
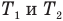
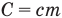
Формула количества теплоты при плавлении или кристаллизации
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 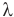
Формула количества теплоты при парообразовании или конденсации
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
Здесь 
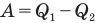
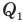
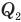
Коэффициент полезного действия идеального теплового двигателя
Здесь 
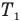
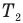
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
На прошлом уроке мы познакомились с определением плотности тела, узнали формулу, по которой можно ее рассчитать: $rho = frac{m}{V}$.
Сейчас нам предстоит взглянуть на эту формулу с других сторон. Мы научимся находить объем и массу по известной плотности материала тела, решать задачи, используя полученные знания.
Расчет массы тела по его плотности
Знание плотности веществ очень важно для многих практических целей. Для инженеров и строителей, например, знание плотности имеет колоссальное значение — так они могут рассчитать массу будущего механизма или строения.
Как вычисляется масса тела по его плотности и объему?
Плотность определяется по формуле $rho = frac{m}{V}$. Выразим отсюда массу:
$m = rho V$.
Чтобы рассчитать массу тела, если известны его объем и плотность, нужно плотность умножить на объем.
Задача на расчет массы
Рассмотрим пример задачи на расчет массы.
Рассчитайте массу детали, изготовленной из латуни, объемом $0.15 space м^3$.
Из таблицы 1 предыдущего урока берем значение плотности латуни. Она равна $8500 frac{кг}{м^3}$.
Дано:
$rho = 8500 frac{кг}{м^3}$
$V = 0.15 space м^3$
$m -?$
Показать решение и ответ
Скрыть
Решение:
$m = rho cdot V$,
$m = 8500 frac{кг}{м^3} cdot 0.15 space м^3 = 1275 space кг approx 1.3 space т$.
Ответ: $m = 1275 space кг approx 1.3 space т$.
Расчет объема тела по его плотности
По какой формуле можно определить объем тела?
Подобным образом выразим из формулы плотности объем:
$V = frac{m}{rho}$.
Чтобы рассчитать объем тела, если известны его масса и плотность, нужно массу разделить на плотность.
Данной формулой для определения объема часто пользуются в тех случаях, когда тела имеют сложную неправильную форму.
Задача на расчет объема
Рассмотрим пример задачи на расчет объема.
Молоко в бутылке имеет массу $1.03 space кг$. Рассчитайте объем бутылки.
В таблице 2 прошлого параграфа находим молоко: его плотность равна $1030 frac{кг}{м^3}$.
Дано:
$rho = 1030 frac{кг}{м^3}$
$m = 1.03 space кг$
$V -?$
Решение:
$V = frac{m}{rho}$,
$V = frac{1.03 space кг}{1030 frac{кг}{м^3}} = 0.001 space м^3 = 1 space л$.
Ответ: $V = 1 space л$.
Дополнительные задачи
Задача №1
На рисунке 1 изображен кусок хозяйственного мыла в упаковке. По данным производителя размеры размеры его полиэтиленовой упаковки составляют 6 см x 9 см x 5,5 см.
Масса одного куска 200 г. Масса брутто (масса товара вместе с упаковкой) указан 211 г. Найдите объем куска мыла без упаковки. Выразите ответ в СИ.
Обозначим стороны упаковки как $a, b space и space с$, массу куска была $m_м$, массу куска мыла в упаковке — $m$, а общую массу мыла в упаковке — $m_{уп}$.
Объем куска мыла будем обозначать как $V_м$, а вместе с упаковкой — $V$.
Дано:
$a = 6 space см$
$b = 9 space см$
$c = 5.5 space см$
$m_м = 200 space г$
$m = 211 space г$
$V_м -?$
Показать решение и ответ
Срыть
Решение:
Найдем массу упаковки:
$m_{уп} = m — m_м$,
$m_{уп} = 211 space г — 200 space г = 11 space г$.
Общий объем упаковки и мыла:
$V = a cdot b cdot c$,
$V = 6 space см cdot 9 space см cdot 5.5 space см = 297 space см^3$.
Указано, что упаковка изготовлена из полиэтилена (из таблицы 1 предыдущего параграфа его плотность $rho_п$ равна $0.92 frac{г}{см^3}$).
Найдем объем упаковки $V_{уп}$:
$V_{уп} = frac{m_{уп}}{rho_{уп}}$,
$V_{уп} = frac{11 space г}{0.92 frac{г}{см^3}} approx 12 space см^3$.
Общий объем куска мыла в упаковке складывается из объема самого куска и объема упаковки. Так мы можем найти объем куска мыла:
$V_м = V — V_{уп}$,
$V_м = 297 space см^3 — 12 space см^3 = 285 space см^3$.
Выразим в СИ:
$285 space см^3 = 285 cdot 1 space см cdot 1 space см cdot 1 space см = 285 cdot 0.01 space м cdot 0.01 space м cdot 0.01 space м = 285 cdot 0.000001 space м^3 = 0.000285 space м^3$.
Ответ: $V_м = 0.000285 space м^3$
Задача №2
Масса чугунного шара составляет 800 г. Его объем — $125 space см^3$. Будет ли этот шар сплошным (отлитым полностью из одного материала) или полым (иметь пространство внутри, заполненное, например, воздухом)?
Показать решение
Скрыть
Проверить это достаточно просто: рассчитаем плотность этого шара:
$rho = frac{m}{V}$,
$rho = frac{800 г}{125 space см^3} = 6.4 frac{г}{см^3}$.
Сравним полученное значение с табличной плотностью чугуна:
$rho = 7 frac{г}{см^3}$
Сколько бы тогда весил сплошной шар?
$m = rho V$,
$m = 7 frac{г}{см^3} cdot 125 space см^3 = 875 space г$.
Разница между массами реального и предполагаемого сплошного шара составляет 75 г.
Следовательно, реальный шар имеет внутри какую-то полость, он не полностью выполнен из чугуна.
Задача №3
В грузовой автомобиль загрузили 48 сосновых бревен. Масса каждого соснового бревна составляет $20 space дм^3$. На сколько увеличилась масса автомобиля после загрузки?
Из таблицы 1 предыдущего параграфа возьмем плотность сухой сосны ($400 frac{кг}{м^3}$). Переведем $20 space дм^3$ в $м^3$:
$20 space дм^3 = 20 cdot 0.1 space м cdot 0.1 space м cdot 0.1 space м = 20 cdot 0.001 space м^3 = 0.02 space м^3$.
Количество брусков — $n$.
Дано:
$V = 20 space дм^3$
$rho = 400 frac{кг}{м^3}$
$n = 48$
СИ:
$V = 0.02 space м^3$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем массу одного соснового бревна:
$m = rho cdot V$,
$m = 400 frac{кг}{м^3} cdot 0.02 space м^3 = 8 space кг$.
Масса всех сосновых бревен (M) будет равна:
$M = n cdot m$,
$M = 48 cdot 8 space кг = 384 space кг$
Ответ: масса автомобиля после загрузки увеличится на 384 кг.
Упражнения
Упражнение №1
Какова масса $0.5 space л$ спирта, молока, ртути?
Дано:
$V = 0.5 space л$
$rho_1 = 800 frac{кг}{м^3}$
$rho_2 = 1030 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-4} space м^3$
$m_1 — ?$
$m_2 — ?$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Зная объем и плотность тела, мы может рассчитать его массу по формуле: $m = rho V$.
Рассчитаем массу спирта:
$m_1 = rho_1 V$,
$m_1 = 800 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.4 space кг$.
Рассчитаем массу молока:
$m_2 = rho_2 V$,
$m_2 = 1030 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.515 space кг$.
Рассчитаем массу ртути:
$m_3 = rho_3 V$,
$m_3 = 13600 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 6.8 space кг$.
Ответ: $m_1 = 0.4 space кг$, $m_2 = 0.515 space кг$, $m_3 = 6.8 space кг$.
Упражнение №2
Определите объем льдинки, масса которой $108 space г$.
Дано:
$m = 108 space г$
$rho = 900 frac{кг}{м^3}$
СИ:
$m = 0.108 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность льда, рассчитаем его объем:
$V = frac{m}{rho}$,
$V = frac{0.108 space кг}{900 frac{кг}{м^3}} = 0.00012 space м^3 = 120 space см^3$.
Ответ: $V = 120 space см^3$.
Упражнение №3
Сколько килограммов керосина входит в пятилитровую бутыль?
Дано:
$V = 5 space л$
$rho = 800 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Зная плотность и объем, найдем массу керосина:
$m = rho V$,
$m = 800 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 4 space кг$.
Ответ: $m = 4 space кг$.
Упражнение №4
Грузоподъемность лифта составляет $3 space т$. Сколько листов железа можно погрузить в лифт, если длина каждого листа равна $3 space м$, ширина — $60 space см$ и толщина — $4 space мм$?
Дано:
$M = 3 space т$
$a = 60 space см$
$b = 4 space мм$
$c = 3 space м$
$rho = 7800 frac{кг}{м^3}$
СИ:
$M = 3000 space кг$
$a = 0.6 space м$
$b = 0.004 space м$
$n — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем массу одного железного листа. Для этого нам нужно знать его объем (плотность мы взяли из таблицы). Объем мы может вычислить, перемножив друг на друга ширину, высоту и длину: $V = a cdot b cdot c$.
Масса железного листа:
$m = rho V = rho cdot a cdot b cdot c$,
$m = 7800 frac{кг}{м^3} cdot 0.6 space м cdot 0.004 space м cdot 3 space м = 56.16 space кг$.
Теперь разделим грузоподъемность лифта на массу одного лифта. Полученное целое число и будет ответом на вопрос задачи:
$n = frac{M}{m}$,
$n = frac{3000 space кг}{56.16 space кг} approx 53$.
Ответ: $n = 53$.
Упражнение №5
Кружка доверху наполнена молоком. Определите объем кружки, если масса молока в кружке $515 space г$, плотность молока найдите в таблице.
Дано:
$m = 515 space г$
$rho = 1030 frac{кг}{м^3}$
СИ:
$m = 0.515 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность молока, найдем объем, который оно занимает в кружке:
$V = frac{m}{rho}$,
$V = frac{0.515 space кг}{1030 frac{кг}{м^3}} = 0.0005 space м^3 = 0.5 space л$.
Ответ: $V = 0.5 space л$.
Задание
Возьмите баночку из-под меда. Рассмотрите внимательно этикетку. Найдите на ней, какова масса меда и объем баночки. Затем рассчитайте плотность меда. Полученный результат проверьте по таблице.
Дано:
$m = 800 space г$
$V = 500 space мл$
СИ:
$m = 0.8 space кг$
$V = 0.0005 space м^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем плотность меда:
$rho = frac{m}{V}$,
$rho = frac{0.8 space кг}{0.0005 space м^3} = 1600 frac{кг}{м^3}$.
По таблице плотность меда составляет $1350 frac{кг}{м^3}$. Существует множество различных сортов меда, плотность которых отличается друг от друга. Наше значение плотности не сильно отличается от табличного, поэтому можно сказать, что результат получен правильный.
Ответ: $rho = 1600 frac{кг}{м^3}$.
Основные формулы молекулярной физики
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
В кодификаторе ЕГЭ нет тем, непосредственно относящихся к содержанию данного листка. Однако без этого вводного материала дальнейшее изучение молекулярной физики невозможно.
Введём основные величины молекулярной физики и соотношения между ними.
— масса вещества,
— объём вещества,
— плотность вещества (масса единицы объёма). Отсюда
— число частиц вещества (атомов или молекул).
— масса частицы вещества. Тогда
— концентрация вещества (число частиц в единице объёма),
. Отсюда
Что получится, если умножить на
? Произведение массы частицы на число частиц в единице объёма даст массу единицы объёма, т. е. плотность. Формально:
Итак,
Массы и размеры частиц невообразимо малы по нашим обычным меркам. Например, масса атома водорода порядка г, размер атома порядка
см. Из-за столь малых значений масс и размеров число частиц в макроскопическом теле огромно.
Оперировать столь грандиозными числами, как число частиц, неудобно. Поэтому для измерения количества вещества используют специальную единицу — моль.
Один моль — это количество вещества, в котором содержится столько же атомов или молекул, сколько атомов содержится в граммах углерода. А в
граммах углерода содержится примерно
атомов. Стало быть, в одном моле вещества содержится
частиц. Это число называется постоянной Авогадро:
моль
.
Количество вещества обозначается . Это число молей данного вещества.
Что получится, если умножить на
? Число молей, умноженное на число частиц в моле, даст общее число частиц:
Масса одного моля вещества называется молярной массой этого вещества и обозначается (
= кг/моль). Ясно, что
Как найти молярную массу химического элемента? Оказывается, для этого достаточно заглянуть в таблицу Менделеева! Нужно просто взять атомную массу (число нуклонов) данного элемента — это будет его молярная масса, выраженная в г/моль. Например, для алюминия
, поэтому молярная масса алюминия равна
г/моль или
кг/моль.
Почему так получается? Очень просто. Молярная масса углерода равна г/моль по определению. В то же время ядро атома углерода содержит
нуклонов. Выходит, что каждый нуклон вносит в молярную массу
г/моль. Поэтому молярная масса химического элемента с атомной массой
оказывается равной
г/моль.
Молярная масса вещества, молекула которого состоит из нескольких атомов, получается простым суммированием молярных масс. Так, молярная масса углекислого газа равна
г/моль
кг/моль.
Будьте внимательны с молярными массами некоторых газов! Так, молярная масса газообразного водорода равна г/моль, поскольку его молекула состоит из двух атомов
. То же касается часто встречающихся в задачах азота и кислорода
Вместе с тем, наиболее частый персонаж задач — гелий
— является одноатомным газом и имеет молярную массу
г/моль, предписанную таблицей Менделеева.
Ещё раз предостережение: при расчётах не забывайте переводить молярную массу в кг/моль! Если ваш ответ отличается от правильного на три порядка, то вы наверняка сделали именно эту, очень распространённую ошибку 
Что получится, если умножить на
? Масса частицы, умноженная на число частиц в моле, даст массу моля, т. е. молярную массу:
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Основные формулы молекулярной физики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023