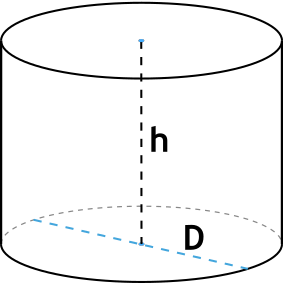
Как рассчитать объем цилиндра
На данной странице калькулятор поможет рассчитать объем цилиндра онлайн. Для расчета задайте высоту, радиус или площадь основания. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
По высоте и радиусу
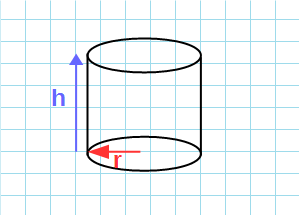
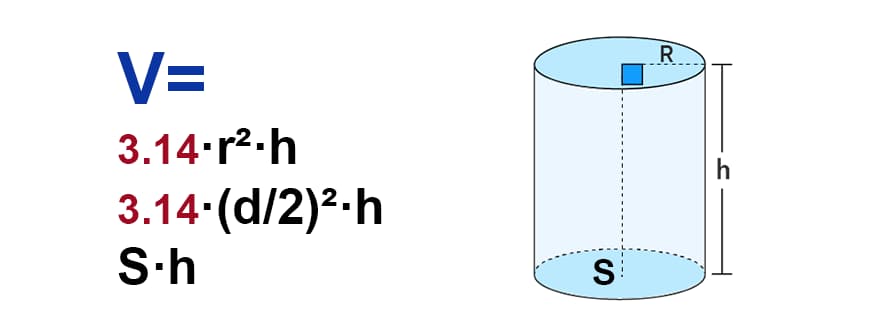
Формула объема цилиндра через высоту и радиус:
V=π·r²·h
π — константа равная (3.14); r — радиус основания; h — высота цилиндра.
Через площадь основания и высоту
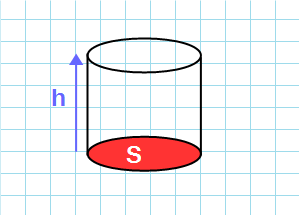
Формула объема цилиндра через высоту и площадь основания:
V=S·h
S — площадь основания цилиндра; h — высота цилиндра.
Калькулятор объема цилиндра
Рассчитайте онлайн объем любого цилиндрического объекта: трубы, бочки, банки.
Что известно
Размерность
Радиус основания
см
Диаметр основания
см
Площадь основания
см2
Высота
см
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🛢️ Когда требуется знать объем цилиндра?
Знание объема цилиндра может потребоваться в различных ситуациях, к примеру:
- Расчет объема бака или резервуара: если вы планируете хранить жидкость или газ в баке или резервуаре, то может быть важно знать его объем, чтобы знать, сколько материала вы можете в него поместить.
- Расчет объема емкости для транспортировки: если вы занимаетесь перевозкой жидкостей или газов, то может потребоваться знать объем емкости, чтобы убедиться, что вы можете перевезти нужное количество материала.
- Расчет объема цилиндрических труб: если вы занимаетесь установкой трубопроводов или работой с другими цилиндрическими объектами, то может быть полезно знать их объем, чтобы правильно рассчитать количество материала, необходимого для работы.
- Расчет объема бутылки или бочки: если вы хотите знать, сколько жидкости вы можете вместить в определенную бутылку или бочку, то калькулятор объема цилиндра может помочь рассчитать объем емкости.
- Определение объема цилиндрических объектов, используемых в декоративных целях, например, колонн, скульптур и других элементов архитектуры и дизайна.
Также умение рассчитывать объем цилиндра пригодится в строительстве, химии и фармацевтике, механике и технике, производстве, учебе и творчестве.
📏 Как рассчитывается объем цилиндра?
Объем цилиндра можно рассчитать по формуле:
V = πr²h
где V – объем цилиндра, r – радиус основания цилиндра, h – высота цилиндра, π (пи) – математическая константа, приблизительно равная 3,14.
Чтобы использовать эту формулу, необходимо знать значения радиуса основания и высоты цилиндра. Радиус основания – это расстояние от центра основания до края, высота цилиндра – это расстояние между основаниями цилиндра.
Например, если радиус основания цилиндра равен 5 см, а высота цилиндра составляет 10 см, то объем цилиндра можно рассчитать следующим образом:
V = 3,14 x 5² x 10 = 785 см3
Обратите внимание, что единицы измерения должны быть одинаковыми, чтобы получить правильный ответ. Если радиус основания и высота цилиндра измеряются в сантиметрах, то и объем цилиндра должен быть выражен в кубических сантиметрах.
🧮 Что такое калькулятор объема цилиндра?
Калькулятор объема цилиндра – это инструмент, который позволяет автоматически рассчитывать объем цилиндра по его размерам. Обычно калькулятор объема цилиндра предоставляет пользователю простую форму, где нужно ввести значение радиуса основания и высоты цилиндра, а затем нажать кнопку «Рассчитать». Калькулятор объема цилиндра может быть представлен в виде программы на компьютере или мобильном устройстве, а также в виде онлайн-сервиса на веб-сайте, как у нас.
Использование калькулятора объема цилиндра упрощает и ускоряет процесс расчета объема цилиндра, особенно если нужно рассчитать объем нескольких цилиндров или если значения радиуса и высоты цилиндра имеют сложные числовые значения. Калькулятор объема цилиндра может быть полезен в различных областях, включая науку, технику, строительство, производство, учебу и домашнее хозяйство.
📏 Как работает калькулятор объема цилиндра?
Калькулятор объема цилиндра работает на основе математической формулы для расчета объема цилиндра, рассмотренной выше.
Чтобы рассчитать объем цилиндра, пользователь должен ввести значения радиуса основания и высоты цилиндра в соответствующие поля калькулятора и нажать кнопку «Рассчитать». Калькулятор использует введенные значения, выполняет математическую операцию по формуле и выводит результат в соответствующем поле на экране.
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения (например, сантиметры или дюймы) и возможность рассчитать объем цилиндра, используя диаметр основания вместо радиуса.
🛢 Как использовать калькулятор объема цилиндра?
Для использования калькулятора объема цилиндра следуйте этим простым шагам:
- Откройте калькулятор объема цилиндра, который находится на компьютере, мобильном устройстве или на веб-сайте.
- Введите значение радиуса основания цилиндра в соответствующее поле калькулятора. Если вы используете калькулятор, который принимает во внимание диаметр, убедитесь, что вы выбрали правильную единицу измерения.
- Введите значение высоты цилиндра в соответствующее поле калькулятора. Убедитесь, что вы выбрали правильную единицу измерения.
- Нажмите кнопку «Рассчитать» или «Получить результат». Калькулятор выполнит расчеты и выведет объем цилиндра в соответствующем поле.
- Проверьте результаты и убедитесь, что все значения введены правильно и выбраны правильные единицы измерения.
- Если нужно рассчитать объем нескольких цилиндров, повторите шаги 2-5 для каждого цилиндра.
- Сохраните результаты или скопируйте их в буфер обмена, если нужно использовать их в другой программе или приложении.
В зависимости от функционала калькулятор может иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
В чем измеряется объем цилиндра?
Объем цилиндра измеряется в кубических единицах длины. Например, если размеры цилиндра измеряются в метрах, то его объем будет выражаться в кубических метрах (м³). Если размеры измеряются в сантиметрах, то объем будет выражаться в кубических сантиметрах (см³). Также можно использовать другие единицы измерения, такие как литры или галлоны, которые также выражают объем жидкости или газа, но они не являются кубическими единицами длины.
Несколько лайфхаков
Если вы хотите упростить расчет объема цилиндра, есть несколько лайфхаков, которые могут пригодиться:
- Используйте формулу площади основания цилиндра. Объем цилиндра можно вычислить, умножив площадь основания на высоту. Если вы знаете формулу площади основания цилиндра, то можете сначала вычислить ее, а затем умножить на высоту, чтобы найти объем.
- Используйте приближенное значение числа Пи. Число Пи является бесконечной десятичной дробью, но для большинства расчетов достаточно использовать его приближенное значение. Например, можно использовать значение 3,14 или 22/7 вместо точного значения числа Пи, которое равно примерно 3,14159265359.
- Используйте онлайн калькулятор. Наш онлайн калькулятор объема цилиндра поможет быстро выполнить расчеты за вас. Просто введите значения радиуса и высоты, и калькулятор автоматически вычислит объем.
- Используйте замены единиц измерения. Если вы хотите перевести объем из одной единицы измерения в другую, например, из кубических сантиметров в литры, можете также воспользоваться калькулятором на нашем сайте.
❓ Вопросы и ответы
Сейчас мы представим ответы на вопросы, которые часто возникают по данной теме.
Что такое цилиндр?
Цилиндр — это геометрическая фигура, которая имеет два плоских основания, обычно круглой формы, и боковую поверхность, которая состоит из параллельных прямых линий.
Как вычислить объем цилиндра?
Объем цилиндра можно вычислить, используя формулу:
V = πr²h
где V — объем цилиндра, π — число Пи (приблизительно равно 3.14), r — радиус основания цилиндра и h — высота цилиндра.
Можно ли использовать формулу объема цилиндра для вычисления объема других фигур?
Нет, формула объема цилиндра может использоваться только для вычисления объема цилиндра. Для других фигур существуют свои собственные формулы для расчета объема.
Как найти радиус или диаметр цилиндра, если они неизвестны?
Если известна площадь основания цилиндра, можно найти радиус, используя формулу:
r = √(A/π)
где A — площадь основания цилиндра.
Если известен объем цилиндра, можно найти радиус, используя формулу:
r = √(V/πh)
где V — объем цилиндра, h — высота цилиндра.
Диаметр можно найти, удваивая радиус.
Как найти объем трубы или канала?
Для трубы или канала формула для вычисления объема имеет немного другой вид:
V = πr²h
где V — объем, r — радиус, h — длина (высота) трубы или канала.
Например, если радиус трубы равен 10 см, а длина трубы составляет 2 м, то объем трубы будет:
V = 3.14 * 10² * 200 = 62,800 см³, что равно 62.8 литрам.
Как узнать, сколько литров вмещает бочка?
Чтобы узнать, сколько литров вмещает бочка, нужно знать ее объем. Если известны диаметр и высота бочки, то можно использовать формулу для объема цилиндра. Например, если диаметр бочки составляет 1 метр, а высота — 1,5 метра, то ее объем будет:
V = πr²h = 3.14 * (1/2)² * 1.5 = 1.18 кубических метров, что равно 1180 литрам. Таким образом, бочка вмещает 1180 литров жидкости.
Как узнать, сколько литров вмещает труба?
Для расчета объема трубы нужно знать ее длину и радиус. Если известны диаметр и длина трубы, то радиус можно найти, разделив диаметр на 2. Например, если диаметр трубы составляет 10 см, а длина трубы — 2 метра, то радиус будет 5 см. Тогда объем трубы можно найти, используя формулу:
V = πr²h = 3.14 * (5/100)² * 200 = 15.7 литров. Таким образом, труба вмещает 15.7 литров жидкости.
Какой тип калькулятора нужен для расчета объема цилиндра?
Для расчета объема цилиндра нужен специальный калькулятор, который может выполнить математические операции с использованием формулы для объема цилиндра.
Какие значения нужно ввести в калькулятор объема цилиндра?
Для расчета объема цилиндра необходимо ввести значение радиуса основания цилиндра и высоты цилиндра.
Какие единицы измерения могут использоваться при вводе значений в калькулятор объема цилиндра?
Единицы измерения, которые могут использоваться при вводе значений в калькулятор объема цилиндра, это сантиметры, метры, дюймы и т.д.
Какие дополнительные функции могут быть включены в калькулятор объема цилиндра?
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
Где можно найти калькулятор объема цилиндра?
Калькулятор объема цилиндра можно найти в Интернете на специализированных сайтах, в приложениях для мобильных устройств и на компьютерах, а также в других программных приложениях, связанных с инженерными и научными расчетами.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Расчет объёма цилиндра — онлайн калькулятор
Калькулятор поможет определить объем цилиндра, если известна его высота и радиус/диаметр/площадь основания. Результат вычисляется сразу в кубических миллиметрах, кубических сантиметрах, литрах (кубических дециметрах) и кубических метрах. Все результаты даны с точностью до 2 десятичных знаков с классическим округлением (0-4 округляются в меньшую сторону, 5-9 в большую).
Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема.
Формула расчета объема цилиндра
Объем цилиндра вычисляется как произведение площади основания на высоту цилиндра. Так как основанием цилиндра является круг, площадь основания можно рассчитать через радиус или диаметр.
В
процессе
наполнения
цилиндр наполняется воздухом,
обеспечивающим сгорание топлива в
очередном цикле. Чем больше поступит в
цилиндр воздуха, тем большее количество
топлива может сгореть и тем большую
мощность может развить двигатель при
прочих равных условиях
Процесс
наполнения в любом из двигателей
неразрывно связан с процессом выпуска:
он начинается либо сразу после выпуска
(в четырехтактных двигателях), либо с
ним совмещается (в двухтактных двигателях).
На рис. 6.1 графически представлены
процессы наполнения roaao
и выпуска b’rro
четырехтактного двигателя без наддува.
К концу процесса выпуска газов и началу
наполнения, когда поршень начнет
двигаться от ВМТ к НМТ (точка r),
камера сжатия будет заполнена остаточными
газами с температурой Тr
и давлением рr.
Это давление превышает давление
окружающей среды ро
па величину потерь давления Δрr,
обусловленных сопротивлениями выпускной
системы (клапанов, трубопроводов,
глушителей и т. д.). В начале нисходящего
движения поршня остаточные газы в
цилиндре расширяются по политропе rro
до давления окружающей среды ро
(точка rо),
а затем – до давления меньше атмосферного.
С момента, когда в цилиндре наступит
разрежение, в него начнет поступать
воздух, и в конце наполнения (точка а)
давление ра
будет
ниже ро
на величину потери давления Δра,
обусловленной сопротивлениями и затратой
энергии на создание скорости перемещения
заряда во впускной системе двигателя.
Основное
отличие в протекании процесса наполнения
для четырехтактного двигателя с наддувом
показано на рис. 6.2. Как известно, в этих
двигателях воздух поступает в цилиндр
после предварительного сжатия в
компрессоре с давлением ниже давления
наддува рs
на величину потери Δра
во впускном тракте от компрессора до
цилиндра двигателя. При этом линия
процесса наполнения raak
на диаграмме расположена выше линиb
выпуска b‘r
(для
двигателей с большим перекрытием
клапанов).
|
|
|
|
6.1. |
6.2. |
В
двухтактных двигателях ходы поршня,
отведенные на процессы наполнения и
выпуска, отсутствуют, поэтому процесс
наполнения совмещается с процессом
выпуска и совершаются эти процессы лишь
на части хода поршня ψVs
занятой продувочными и выпускными
окнами (рис. 6.3).
6.3. Схема наполнения и выпуска двухтактного двигателя
К
моменту открытия продувочных окон
(точка d)
давление газов должно быть ниже давления
воздуха рs,
поступающего от компрессора. Поэтому
воздух будет вытеснять оставшиеся
продукты сгорания, заполняя пространство
цилиндра. Этот процесс продолжается
при нисходящем движении поршня до точки
0,
а также при восходящем движении до
момента закрытия продувочных окон
(точка s).
Оценивая
параметры рабочей смеси в конце процесса
наполнения, количество воздуха, которое
могло бы поместиться в рабочем объеме
цилиндра Vs
при параметрах, характеризующих состояние
воздуха перед впускными органами рs
и Ts,
принимают за теоретическое. Действительное
количество воздуха, оставшееся в цилиндре
к началу процесса сжатия, оказывается
меньше теоретического. На это влияют
следующие факторы:
– аэродинамические
потери во впускном тракте;
– наличие
в цилиндре остаточных газон, количество
которых зависит от совершенства системы
газообмена;
– подогрев
поступающего воздуха остаточными
газами, имеющими температуру воздуха
Tr,
которая выше температуры воздуха Ts;
– подогрев
воздуха от соприкосновения со стенками
втулки цилиндра, донышком поршня,
клапанами или продувочными окнами.
В
качестве критериев количественной
оценки совершенства процесса наполнения
принимают коэффициент остаточных газов
γr
и коэффициент наполнения ηн.
Коэффициент
остаточных газов γr,
представляет собой отношение количества
остаточных газов Мr
к количеству воздуха L,
поступившего в цилиндр:
γr
= Мr/L
Коэффициент
наполнения ηн
представляет собой отношение
действительного количества поступившего
в цилиндр воздуха Vк
к тому количеству, которое могло бы
заполнить рабочий объем цилиндра Vs
при давлении рs
и температуре Ts
воздуха непосредственно перед впускными
органами двигателя:
ηн
= Vк/Vs
Для
четырехтактных двигателей коэффициент
наполнения ηн
для двухтактных
двигателей, отнесенный к полному ходу
поршня, равен
Основными
параметрами конца процесса наполнения
являются ра
и Tа.
Tа
определяется из уравнения
Подогрев
воздуха от стенок цилиндра у двухтактных
двигателей составляет ΔТ
= 5…10 К, у четырехтактных ΔТ
= 5…20 К. Температура остаточных газов
обычно составляет Tr
= 700…800 К.
В
процессе
сжатия
достигается температура, достаточная
для самовоспламенения впрыскиваемого
в конце сжатия топлива, а также
обеспечивается перепад температур в
цикле с целью увеличения его КПД. Процесс
сжатия происходит при движении поршня
от НМТ к ВМТ после закрытия органов
газообмена (клапанов – в четырехтактных
и окон – в двухтактных двигателях).
К
параметрам, характеризующим процесс
сжатия, относятся: показатель политропы
сжатия n1,
давление рс
и температура Тс
в конце сжатия, а также степень сжатия
ε.
При
отсутствии утечек поступившего воздуха
и теплообмена со стенками цилиндра
(линия aс’
на рис. 6.4), процесс сжатия подчинился
бы закону адиабатного сжатия и описывался
бы математическим уравнением
где
k1
– показатель адиабаты сжатия.
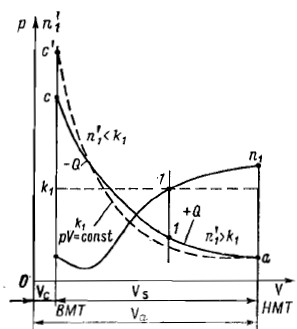
Рис. 6.4. Схема
процесса сжатия в теоретическом и
расчетном циклах
Сжатие
представляет собой сложный процесс,
зависящий от переменного теплообмена
между поступившим воздухом и стенками
цилиндра, изменяющегося по величине и
по знаку; уменьшения поверхности
охлаждения по мере приближения поршня
к ВМТ и других факторов.
В
начале хода сжатия температура
поступившего воздуха ниже средней
температуры стенок цилиндра, что вызывает
подогрев воздуха. На этом участке теплота
от нагретых деталей передается рабочему
телу, поэтому действительная кривая
процесса сжатия идет круче адиабаты,
что показано на рис. 6.4, а показатель
политропы сжатия n1
будет
выше показателя адиабаты k1.
По
мере сжатии поступившего воздуха и
повышения его температуры передача
теплоты от стенок к воздуху уменьшается
и наступает момент (точка 1),
когда температура воздуха становится
равной средней температуре стенок, т.
е, имеет место мгновенный адиабатный
процесс n1’
=
k1.
При
дальнейшем сжатии температура воздуха
становится выше средней температуры
стенок, вследствие чего начинается
отдача теплоты от воздуха к стенкам.
Кривая действительного процесса сжатия
становится более пологой, чем адиабата,
а показатель n1’
<
k1,
причем значение n1’
по мере приближения к ВМТ непрерывно
уменьшается. В результате давление
конца сжатия рс
(точка с)
действительного процесса оказывается
ниже давления конца адиабатного сжатия
(точка с’).
Около
ВМТ, несмотря на максимальную температуру
рабочего тела, показатель политропы
сжатия n1’,
оставаясь ниже показателя адиабаты
k1
все же несколько увеличивается. Это
можно объяснить тем, что в конце сжатия
уменьшается поверхность охлаждения,
рабочее тело в камере сгорания
соприкасается с более нагретыми деталями
и теплоотдача в стенки несколько
снижается, а также начинающимся
тепловыделением при сгорании. Утечка
воздуха через неплотности поршневых
колец на линии сжатия при нормальном
состоянии невелика и незначительно
снижает рс
и Тс
в конце сжатия, поэтому ее, как правило,
не учитывают.
Из
сказанного следует, что показатель
политропы сжатия действительного
процесса переменный на всем протяжении
хода поршня; у судовых двигателей по
опытным данным истинное значение
показателя n1’
изменяется
в пределах от 1,5 (у НМТ) до 1,1 (у ВМТ).
В
расчетах рабочего цикла для упрощения
полагают, что процесс сжатия происходит
по политропе с условным средним постоянным
показателем политропы n1,
который выбирают таким образом, чтобы
при определенных значениях начальных
параметров процесса сжатия получалась
та же работа, что и при истинном переменном
показателе. По опытным данным в МОД с
охлаждаемыми поршнями n1
=
1,34…1,38, в СОД и ВОД n1
= 1,38…1,42.
Средний
показатель политропы сжатия n1
может быть определен с помощью уравнения
политропы в начале и в конце процесса
сжатия по индикаторной диаграмме, снятой
с двигателя,
Основными
параметрами конца процесса наполнения
являются рс
и Tс:
Степень сжатия
различают геометрическую и действительную.
Геометрическая
степень сжатия εг
– это отношение полного объема рабочего
цилиндра Vа
в момент нахождения поршня в НМТ к объему
камеры сжатия Vс,
т, е. к объему цилиндра при положении
поршня в ВМТ
Действительная
степень сжатия ε представляет собой
отношение объема рабочего цилиндра в
момент закрытия органов газораспределения
к объему камеры сжатияVс:
где ψ
– доля хода поршня S
на ходе сжатия, занятая процессами
газообмена. Она соответствует объему
цилиндра при закрытии впускного клапана
в четырехтактных двигателях и закрытии
продувочных или выпускных окон в
двухтактных двигателях.
При
расчете рабочих процессов четырехтактных
двигателей пользуются геометрической
(номинальной) степенью сжатия, так как
за время запаздывания закрытия впускных
клапанов давление в цилиндре изменяется
незначительно. В двухтактных двигателях
обычно пользуются действительной
степенью сжатия, причем долю хода поршня
принимают для окон или клапанов,
закрывающихся в процессе сжатия
последними.
Степени
сжатия 11…15 – для МОД; 12…16 – для СОД и
15…18 –для ВОД.
Нижний
предел степени сжатия выбирают из
условия надежности самовоспламенения
топлива, которое впрыскивается в рабочий
цилиндр с конце процесса сжатия. Для
этого минимальное значение температуры
принимают
где
Тв
= 650 К – средняя температура воспламенения
жидкого топлива; ΔТ = 150…250 – дополнительная
разность температур, увеличивающая
надежность осуществления самовоспламенения.
Степень
сжатия выбирают достаточной для
обеспечения устойчивого самовоспламенении
топлива на пусковых режимах.
Тема
7. Процесс сгорания. Условия выделения
и использования тепла при сгорании
топлива. Количество воздуха необходимое
для сгорания топлива. Факторы, влияющие
на эти процессы. Процесс расширения.
Параметры рабочего тела в конце процесса.
Работа процесса. Процесс выпуска
отработавших газов.
Сгорание
топлива
– основной процесс расчетного цикла,
при котором происходит выделение
теплоты, преобразуемой в двигателе в
полезную механическую работу.
Самовоспламенение и сгорание топлива
представляют сложный процесс химического
соединения горючих элементов топлива
с кислородом воздуха, сопровождаемый
выделением теплоты. При расчете процесса
сгорания топлива промежуточные
физико-химические изменения не
рассматривают, а учитывают лишь конечные
результаты химических реакций.
Процесс
сгорания рассчитывают исходя из 1 кг
сжигаемого топлива. Для удобства расчета
количество воздуха и образующихся
газообразных продуктов сгорания измеряют
в киломолях, под которым подразумевается
количество газа, масса которого в
килограммах равна молекулярной массе
данного газа.
Для определения
конечных параметров процесса сгорания
– максимальных значений давления Рz
и температуры Тz
– необходимо прежде всего определить
количество воздуха L, которое вводится
в цилиндр для сгорания 1 кг топлива, и
количество образовавшихся продуктов
сгорания М.
Примем элементарный
массовый состав топлива
где массовые доли
условно обозначены химическими символами
соответствующих элементов.
Теоретически
необходимое количество воздуха при
сгорании 1 кг топлива Lo
определяется стехиометрическими
соотношениями, т. е. уравнениями окисления
составных частей топлива при полном
сгорании. Из этих условий определяют
количество кислорода, необходимое для
полного сгорания.
В качестве примера
рассмотрим уравнение реакции окисления
С в СО2:
Из последнего
равенства следует, что для полного
сгорания С кг углерода требуется С/12
кмоль кислорода и в результате сгорания
будет получено С/12 кмоль углекислого
газа. Аналогично можно определить
количество кислорода для сгорания
водорода и серы и количество продуктов
их сгорания. Общее количество кислорода,
необходимое для сгорания, определяют
в результате суммирования количеств
кислорода, необходимого для сгорания
каждого из горючих элементов.
Учитывая, что в 1
кг топлива содержится О/32 кмоль кислорода,
необходимое его мольное количество
следует уменьшить на величину О/32 кмоль.
Таким образом,
теоретически необходимое мольное
количество кислорода для сжигания 1 кг
топлива будет равно
Воздух по объему
состоит из 21 % О2
и 79 % N2.
Следовательно, теоретически необходимое
мольное количество воздуха для сжигания
1 кг топлива составит, кмоль/кг
То же значение в
килограммах на 1 кг топлива будет
где μв
= 28,97 – масса 1 кмоль воздуха.
Для дизельного
топлива среднего состава (С = 0,87, Н =
0,126, О = 0,004) получим Lo
= 0,495 кмоль/кг и L’o = 14,3 кг/кг.
Следует заметить,
что сгорание топлива при теоретически
необходимом количестве воздуха является
частным случаем, встречающимся только
в карбюраторных двигателях, в которых
пары легкого топлива и воздуха
перемешиваются более интенсивно.
Из-за ограниченного
времени на смесеобразование в дизелях
и недостаточно полного перемешивания
топлива с воздухом топливовоздушная
смесь в камере сгорания оказывается
неоднородной. Чтобы обеспечить
качественное сгорание топлива в дизелях,
приходится вводить в цилиндр воздух в
количестве, превышающем теоретически
необходимое, т.е. действительное
количество воздуха L > Lo.
Отношение действительного количества
воздуха L, участвующего в процессе
сгорания, к теоретически необходимому
Lo
называется коэффициентом
избытка воздуха:
Согласно
опытным данным α изменяется в следующих
пределах:
α =1,8…2,7 для МОД, α =1,6…2,2 для СОД и α =
1,5…2,0 для ВОД.
В
состав смеси газов, образующихся в
цилиндре в конце процесса
сгорания, кроме продуктов сгорания СО2,
Н2О
и SO2
входят
кислород О2
(вследствие его избытка) и азот N2
(в горении
не участвует).
Количество
продуктов сгорания, образующихся при
сгорании 1
кг топлива, определяется приведенными
ранее стехиометрическими
уравнениями сгорания, кмоль/кг
Количество
избыточного кислорода О2
в продуктах сгорания может быть определено
по количеству избыточного воздуха:
следовательно,
Оставшееся
количество молей в продуктах сгорания
приходится
на инертный азот N2,
входящий в состав воздуха:
Общее
количество М
продуктов
полного сгорания 1 кг топлива
при а
>
1 определяется суммированием всех
составляющих:
Если
обозначить через Мα
=
1 количество продуктов сгорания
1 кг топлива с теоретически необходимым
количеством воздуха
(α
=
1), то
Из
последнего выражения следует, что
продукты сгорания 1
кг топлива данного состава при а
>
1 представляют собой смесь
одного и того же количества чистых
продуктов сгорания (ЧПС)
Ма
=
[ с избыточным количеством воздуха (α –
1)L0.
Масса
продуктов сгорания равна сумме масс
количеств воздуха
и топлива до сгорания, тогда как объемные
количества рабочей
смеси до сгорания и после него не равны.
Приращение
объема продуктов сгорания (количества
молей) происходит
вследствие увеличения суммарного
количества молекул
газообразных продуктов сгорания и может
быть определено
разностью
или
Таким
образом, приращение объема при сгорании
не зависит
от L,
а
определяется содержанием в топливе Н
и О.
В
качестве критерия, оценивающего
приращение объема (числа
молей) продуктов сгорания, используется
введенный Е.
К. Мазингом теоретический
(химический) коэффициент молекулярного
изменения
βо,
который представляет отношение количества
молей газообразных продуктов сгорания
М
к
количеству
молей воздуха L
без
учета остаточных газов в цилиндре:
Например, для
дизельного топлива среднего состава
Кроме перечисленных
выше компонентов в составе продуктов
сгорания содержатся остаточные газы
Мr,
которые остаются в цилиндре от предыдущего
цикла и влияют па изменение объема
продуктов сгорания. Поэтому вводится
понятие расчетного (действительного)
коэффициента молекулярного изменения
β, который представляет собой отношение
числа молей газа после сгорания к числу
молей воздуха с учетом наличия остаточных
газов, т. е.
Значение расчетного
коэффициента молекулярного изменения
лежит в пределах β = 1,03…1,04.
Расчетный коэффициент
молекулярного изменения в промежуточный
момент процесса сгорания определяется
с учетом доли топлива х,
сгоревшего к моменту времени t
от начала воспламенения, по формуле
Из этой формулы
следует, что на линии сжатия и в начальный
момент воспламенения, т. е. при х
= 0, βх
= 1, а в конце процесса сгорания при х
= 1 достигает максимального значения,
равного β.
Для повышения
точности расчета процесса сгорания и
других процессов цикла следует учитывать
зависимость теплоемкости рабочего тела
от его температуры и химического состава.
В расчетах рабочего цикла (по методу
Гриневецкого – Мазннга) используются
понятия средней мольной изобарной
теплоемкости ср
и средней мольной изохорной теплоемкости
сv.
Средняя мольная
изохорная теплоемкость сухого воздуха
может быть определена по формуле
Средняя мольная
изохорная теплоемкость ЧПС для топлива
среднего элементарного состава
Погрешность в
расчете теплоемкостей по этим эмпирическим
формулам не превышает 1 %.
Температура
рабочего тела в конце видимого сгорания
определяется из решения уравнения
первого закона термодинамики, которое
применительно к процессу сгорания может
быть выражено в конечных разностях в
виде
Преобразуя уравнение
в итоге получим зависимость для
определения температуры конца сгорания
Преобразовав
уравнения и подставив все известные
значения получим
Это уравнение
удобнее всего решается методом
последовательных приближений, для чего
задаются в первом приближении произвольные
значения температуры в пределах Tz
= = 1700…2000 К.
Для судовых ДВС
значения температуры в конце видимого
сгорания Tz
лежат в пределах: 1700…1800 К для МОД,
1800…1900 К для СОД и 1900…2000 К для ВОД.
Повышение температуры
Tz
более 2000 К нежелательно из-за возможности
значительной диссоциации газов, которая
до 2000 К не превышает 2 %.
Значение максимального
давления сгорания pz
обычно принимается на основании опытных
данных по прототипам проектируемого
двигателя или определяется из выражения
pz
= λpc
после предварительного выбора степени
повышения давления λ.
Объем цилиндра Vz
в конце видимого сгорания определяется
в зависимости от степени предварительного
расширения
Степень
предварительного расширения может быть
определена в результате совместного
решения уравнения состояния газа в
точках z
и с:
У судовых ДВС
значение ρ находится в пределах 1,2…1,6.
Расширение
продуктов сгорания
в цилиндре происходит при движении
поршня от ВМТ к НМТ в течение такта,
называемого рабочим
ходом. На
участке yz
(рис. 7.1) расчетного цикла увеличение
объема рабочего тела сопровождается
подводом к нему теплоты. Давление в
цилиндре принимают постоянным.
Рис. 7.1. Схема
процесса расширения в теоретическом и
расчетном циклах
В расчетном цикле
считается, что процесс расширения
начинается в конце видимого сгорания
в точке z,
в результате чего происходит политропическое
понижение давления и температуры газов.
В действительном
цикле расширение заканчивается в момент
открытия выпускных окон или клапанов.
В расчетном цикле конец расширения
относят к точке b,
расположенной в НМТ у четырехтактных
двигателей и на уровне верхней кромки
выпускных окон – у двухтактных.
На процесс расширения
влияют теплообмен расширяющихся газов
со стенками цилиндра, догорание в первой
части процесса, иногда растягивающееся
на весь процесс, возможность утечки
части газов через неплотности поршневых
колец и восстановление (рекомбинация)
некоторого количества продуктов
диссоциации, возникающих в процессе
сгорания. Все эти факторы обусловливают
изменение показателя политропы
расширения.
В первой части
процесса вследствие подвода теплоты
от догорания и восстановления продуктов
диссоциации показатель политропы
расширения n2’
меньше показателя адиабаты k2
и достигает значений, меньших единицы.
Политропа расширения приобретает более
пологий характер, чем адиабата.
По мере перемещения
поршня к НМТ процесс догорания топлива
становится менее интенсивным, а отдача
теплоты стенкам из-за большой поверхности
охлаждения возрастает. При этом показатель
политропы расширения непрерывно
увеличивается. При некотором положении
поршня подвод теплоты за счет догорания
топлива и восстановления продуктов
диссоциации становится равным отдаче
теплоты стенкам цилиндра, а мгновенное
значение показателя политропы n2’
достигает значения показателя адиабаты
(точка 2),
т. е. n2’
= k2.
Это и есть
точка мгновенного теплового равновесного
состояния газов и стенок цилиндра. При
дальнейшем расширении преобладающее
значение имеет отвод в стенки цилиндра
и показатель n2’
становится выше показателя адиабаты и
по мере приближения поршни к НМТ
увеличивается до 1,4…1,5; на этом отрезке
политропа идет круче адиабаты. Таким
образом, процесс расширения в реальном
двигателе осуществляется по политропе
с переменным показателем от 1,1 до 1,5.
В связи с трудностью
учета всех факторов, сопровождающих
процесс расширения, для определения
параметров газов в процессе расширения
используют политропу с усредненным
показателем n2,
постоянным за процесс и дающим такую
же работу, как н при действительном
расширении с переменным показателем
политропы.
Среднее значение
показателя политропы расширения в
расчетах рабочих процессов определяют
из уравнения первого закона термодинамики,
которое применительно к процессу
расширения на участке zb.
В результате преобразований получим:
Температура и
давления конца процесса расширения
определяется из выражения соответственно:
В
процессе
выпуска
продукты сгорания удаляются из цилиндра,
за счет чего обеспечивается осуществление
последующих
рабочих циклов. Процесс выпуска у
четырехтактных и двухтактных
двигателей протекает по-разному.
В
четырехтактных двигателях
процесс выпуска делят на три фазы
(рис. 7.2):
фаза
I
– после открытия выпускного клапана
примерно до НМТ
газы вытекают из цилиндра за счет
перепада давлений в цилиндре
и выпускном коллекторе;
фаза
II
– при движении поршня от НМТ к ВМТ газы
выталкиваются из цилиндра перемещающимся
поршнем на протяжении
всего хода;
фаза
III
– при одновременном открытии выпускного
и впускного
клапанов в районе ВМТ (перекрытие
клапанов) осуществляются одновременно
очистка цилиндра за счет динамического
действия выпускных газов, движущихся
по выпускному
трубопроводу, и заполнение его некоторым
количеством свежего
воздуха – продувка камеры сгорания.
Рис. 7.2. Схема
процесса выпуска в четырехтактном
двигателе
В
двухтактных двигателях удаление
продуктов сгорания из цилиндра
и его наполнение свежим зарядом происходят
одновременно
за счет поступающего из ресивера
продувочного воздуха.
Особенности
процессов очистки и наполнения цилиндров
двухтактных
двигателей
сводятся к следующему (рис. 7.3):
– процессы
газообмена происходят лишь в конце
рабочего хода поршня и в начале
хода сжатия, занимая всего 140…150°
ПКВ;
– для газообмена
необходимо предварительное сжатие
воздуха в наддувочном агрегате до
давления, превышающего давление газов
в выпускном коллекторе в период
продувки цилиндра;
– функции
управления процессами газообмена
выполняет поршень, открывающий и
закрывающий выпускные и продувочные
окна. При прямоточно-клапанной системе
газообмена выпуском управляют выпускные
клапаны.
Рис. 7.3. Схема
процесса выпуска в двухтактном двигателе
Процесс выпуска
в двухтактных двигателях
можно разделить на три фазы:
фаза I
– свободный выпуск продуктов сгорания,
при котором газы из цилиндра удаляются
за счет перепада давлений между цилиндром
и выпускным трубопроводом. Свободный
выпуск газов начинается с момента
открытия поршнем выпускных окон (точка
b) и заканчивается в момент открытия
поршнем продувочных окон. Свободный
выпуск по продолжительности составляет
относительно небольшую долю по отношению
ко всему периоду выпуска. Но за этот,
относительно небольшой отрезок времени,
давление в цилиндре быстро падает от
значения в начале выпуска рb
до значения ps,
при котором начинается продувка.
фаза II
– поступление из продувочного ресивера
в цилиндр воздуха (процесс продувки
рабочего цилиндра) и истечение в выпускной
трубопровод вытесняемых продувочным
воздухом продуктов сгорания (принужденный
выпуск, который охватывает период от
начала поступления воздуха в цилиндр
до момента закрытия продувочных окон).
Эта фаза протекает при стабильно
сохраняющемся соотношении давлений ps
> рц
> рт.
фаза III
– потеря заряда, если выпускные органы
закрываются после продувочных (в
бесклапанных системах), или дозарядка,
если выпускные окна закрываются раньше
продувочных (в асимметричных системах
продувки). Эта фаза может отсутствовать,
если продувочные и выпускные окна
закрываются одновременно.
Процесс выпуска
аналогично процессу наполнения
сопровождается газодинамическими
потерями давления Δрг:
где Δр’ – потери
давления в выпускном клапане (или
клапанах) и газоотводном канале в крышке;
Δр» – потери давления в выпускном
коллекторе и выпускном тракте; Δр»‘
– потери давления в специальных
устройствах выпускного тракта –
глушителе, утилизационном парогенераторе.
По опытным данным
общая потеря давления в выпускной
системе у выполненных двигателей
составляет Δрг
= 0,005… 0,025 МПа. Увеличение противодавления
в выпускном тракте приводит к возрастанию
коэффициента остаточных газов и
уменьшению коэффициента наполнения.

{V= pi R^2 h}
Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон.
Другое определение: цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Рассчитать объем цилиндра можно по нескольким формулам. Для расчета необходимо знать высоту цилиндра и один из параметров — радиус основания, диаметр основания или площадь основания.
Содержание:
- калькулятор объема цилиндра
- формула объема цилиндра через высоту и радиус
- формула объема цилиндра через высоту и площадь основания
- формула объема цилиндра через высоту и диаметр
- примеры задач
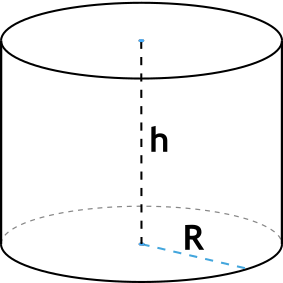
Формула объема цилиндра через высоту и радиус
{V= pi R^2 h}
R — радиус основания цилиндра
h — высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что {pi R^2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
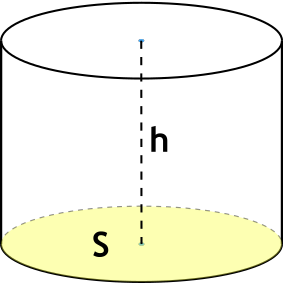
Формула объема цилиндра через высоту и площадь основания
{V= S h}
S — площадь основания цилиндра
h — высота цилиндра
Так как диаметр окружности равен двум радиусам, мы легко можем преобразовать формулу объема цилиндра через радиус и высоту в формулу через диаметр и высоту. Для этого выразим радиус через диаметр и получим необходимую формулу:
D = 2R to R = dfrac{D}{2}
V = pi R^2 h = pi {Big( dfrac{D}{2} Big) }^2 h = pi dfrac{D^2}{4} h
Формула объема цилиндра через высоту и диаметр
{V= pi {dfrac{D^2}{4}} h}
D — диаметр основания цилиндра
h — высота цилиндра
Примеры задач на нахождение объема цилиндра
Задача 1
Найти объём цилиндра с высотой 3см и диаметром основания 6см.
Решение
Так как в условии задачи нам дан диаметр основания цилиндра, мы будем использовать формулу объема через диаметр. Подставим в нее известные высоту и диаметр, чтобы получить объем цилиндра.
V = pi dfrac{D^2}{4} h = pi dfrac{6^2}{4} 3 = pi dfrac{36}{4} 3 = pi cdot 9 cdot 3 = 27 pi : см^3 approx 84.823 : см^3
Ответ: 27 pi : см^3 approx 84.823 : см^3
Ответ легко проверить с помощью калькулятора .
Задача 2
Найдите объем цилиндра с радиусом основания 5см и высотой 16см.
Решение
Для решения этой задачи воспользуемся формулой объема через радиус.
V = pi R^2 h = pi cdot 5^2 cdot 16 = pi cdot 25 cdot 16 = pi cdot 25 cdot 16 = 400 pi : см^3 approx 1 256.63706 : см^3
Ответ: 400 pi : см^3 approx 1 256.63706 : см^3
Проверить ответ поможет калькулятор .