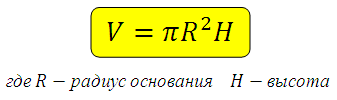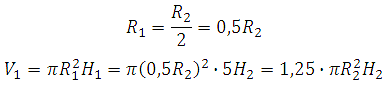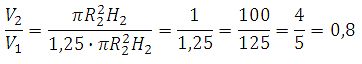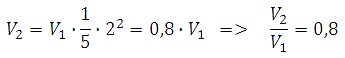Как найти объем второго цилиндра - Исправление недочетов и поиск решений вместе с Examum.ru

Каталог заданий.
Цилиндр

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

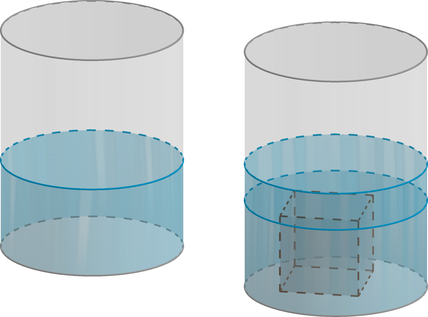
В цилиндрический сосуд налили 2000 см³ воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см³.

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ дайте в сантиметрах.

Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания  — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи .

В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.

Пройти тестирование по этим заданиям

Источник

10
Сен 2013

Категория: 02 Стереометрия

02. Цилиндр.

2013-09-10
2022-09-11

Задача 1. Радиус основания цилиндра равен высота равна Найдите площадь боковой поверхности цилиндра, деленную на .

Решение: + показать

Задача 2. Площадь боковой поверхности цилиндра равна а диаметр основания равен Найдите высоту цилиндра.

Решение: + показать

Задача 3. Длина окружности основания цилиндра равна высота равна Найдите площадь боковой поверхности цилиндра.

Решение: + показать

Задача 4. Площадь осевого сечения цилиндра равна Найдите площадь боковой поверхности цилиндра, деленную на .

Решение: + показать

Задача 5. Объём первого цилиндра равен 48 м У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м).

Решение: + показать

Задача 6. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.

Решение: + показать

Задача 7. В цилиндрический сосуд налили см воды. Уровень воды при этом достигает высоты см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на см. Чему равен объем детали? Ответ выразите в см

Решение: + показать

Задача 8. В цилиндрический сосуд налили см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в раза. Найдите объем детали.

Ответ выразите в см

Решение: + показать

Задача 9. В цилиндрическом сосуде уровень жидкости достигает см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в сантиметрах.

Решение: + показать

Задача 10. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 11. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 12. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Задача 13. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите $frac{V}{pi}$ .

Решение: + показать

Вы можете пройти тест “Цилиндр”

Автор: egeMax |

комментария 3

Печать страницы

Источник

Тема 2.

Геометрия в пространстве (стереометрия)

Отношение площадей поверхностей и отношение объемов тел

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия в пространстве (стереометрия)

Решаем задачи

Во сколько раз уменьшится объем конуса, если радиус его основания останется прежним, а высота уменьшится в 3
раза?

Показать ответ и решение

Пусть площадь основания конуса равна а его высота равна Тогда объём конуса равен

1
V1 = 3Sh

Если высота уменьшится в 3 раза, то объем конуса станет равен

( )
V2 = 1S⋅ h- = 1Sh = V1
3 3 9 3

Тогда объем конуса уменьшится в 3 раза.

Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?

Показать ответ и решение

Пусть — изначальный радиус шара. Площадь поверхности шара вычисляется по формуле

2
S = 4πR

После увеличения радиуса шара в 2 раза площадь поверхности равна

2 2
S1 = 4π(2R ) =16πR

Это в 4 раза больше, чем изначальная площадь поверхности.

В сосуд цилиндрической формы, объем которого 2400 см, налили жидкость, заполнив сосуд
на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего
уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических
сантиметрах.

Показать ответ и решение

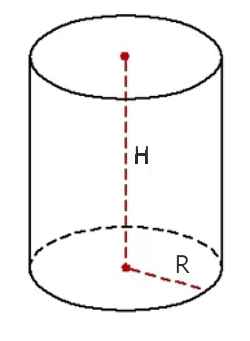
Объем цилиндра вычисляется по формуле , где – радиус основания, – высота. Таким
образом, во сколько раз увеличивается/уменьшается высота цилиндра, во столько же раз
увеличивается/уменьшается объем цилиндра.
Следовательно, если жидкость заполнила сосуд лишь на треть, то есть высота жидкости в 3 раза
меньше высоты сосуда, то и объем жидкости в 3 раза меньше объема сосуда, следовательно, объем
жидкости равен см.

Так как после погружения в жидкость предмета уровень повысился на четверть, то и занимаемый в
сосуде объем повысился на четверть.
Закон Архимеда гласит, что объем вытесненной жидкости равен объему погруженного в нее предмета.
Следовательно, объем предмета равен четверти объема жидкости, то есть см.

В цилиндрическом сосуде уровень жидкости достигает см. На какой
высоте будет находиться уровень жидкости, если её перелить во второй
цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого?
Ответ дайте в сантиметрах.

В цилиндрическом сосуде уровень воды достигает 384 см. На какой высоте будет находиться уровень воды, если её перелить во
второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ дайте в сантиметрах.

Показать ответ и решение

Пусть уровень воды в первом цилиндрическом сосуде равен см, а во втором — см.

Пусть диаметр первого сосуда равен см. Тогда площадь дна этого сосуда равна

π⋅D2
S1 = --4--см2

Значит, объем воды в сосуде равен

2
V = S1h1 = π-⋅D ⋅384 см3
4

По условию диаметр второго сосуда равен см. Тогда площадь его дна равна

π⋅(8D-)2 2
S2 = 4 см

Так как количество воды не изменилось, то

π⋅(8D)2
V = S2h2 = ---4---⋅h2 см3

Тогда искомый уровень воды равен

π-⋅D2- π⋅D2-
h = V- = --4--⋅384-= --4--⋅384= 384-= 6 см
2 S2 π⋅(8D)2 π-⋅D2 ⋅64 64
4 4

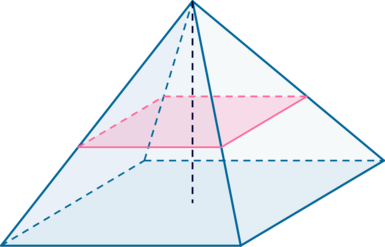
В правильной четырехугольной пирамиде с высотой через точку на боковом ребре, лежащую на расстоянии 1h
3 от плоскости
основания, проведена плоскость, параллельная плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите
объем полученной меньшей пирамиды, если объем исходной пирамиды равен 54.

Показать ответ и решение

Также отсюда следует, что 2
SQ = 3SO .

, следовательно,

′ ′ ′
2-= SA-- = A-B-- ⇒ A ′B ′ = 2AB
3 SA AB 3

Таким образом, объемы маленькой и большой пирамид относятся как

( ) ( )
Vм 1⋅ SQ ⋅ A ′B ′2 SQ A ′B′ 2 2 2 2 8
---= 31----------2--= ----⋅ ----- = --⋅ -- = ---
Vб 3 ⋅ SO ⋅ AB SO AB 3 3 27

Следовательно, объем маленькой пирамиды равен

Vм = 8--⋅ 54 = 16.
27

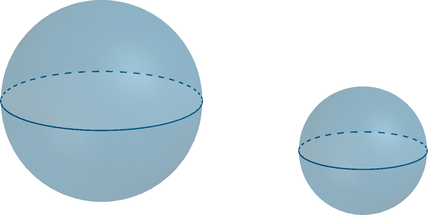
Радиус первого шара в 5 раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади
поверхности первого шара?

Показать ответ и решение

Площадь поверхности шара радиуса ищется по формуле Следовательно, площадь поверхности первого шара
относится к площади поверхности второго шара как

2 2
S1 = 4πR12= R12-
S2 4πR2 R2

Так как радиус первого шара больше радиуса второго шара в 5 раз, то Следовательно,

S (5R )2
S1= -R22--= 25
2 2

Тогда площадь поверхности второго шара в 25 раз меньше площади поверхности первого.

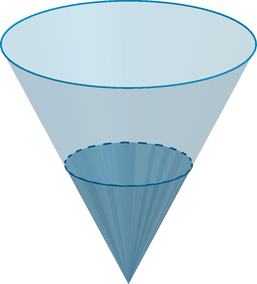
Сосуд имеет форму конуса и вмещает в себя 2700 мл жидкости. Определите, сколько мл жидкости
налито в сосуд, если высота жидкости в 3 раза меньше высоты сосуда.

Показать ответ и решение

QB--= QS--= 1-
OA OS 3

Тогда объем налитой жидкости к объему всего сосуда относится как

Следовательно объем жидкости равен

Vж = 1-V = 100
27

В сосуд, имеющий форму конуса, налили 75 грамм жидкости до половины высоты сосуда. Сколько
грамм этой же жидкости нужно долить в сосуд, чтобы заполнить его доверху?

Показать ответ и решение

OA-- OS-- 2-
QB = QS = 1

так
как по условию высота жидкости в два раза меньше высоты сосуда. Тогда для жидкости
имеем:

Следовательно, весь сосуд вмещает этой же жидкости

( )
1- 2 1- 2 1- 2
m = V ρ = 3 ⋅π⋅OS ⋅OA ⋅ρ = 3 ⋅π ⋅2QS ⋅(2QB ) ⋅ρ = 8 ⋅ 3 ⋅ π ⋅ QS ⋅ QB ⋅ ρ = 8⋅75 = 600 грам м

Значит, долить нужно

Заметим, что в данной задаче использование плотности – чистая формальность.

Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного
параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго,
ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины
второго.

Объем первого цилиндра равен 16, причем известно, что его радиус в 7 раз меньше радиуса второго цилиндра, а высота второго
цилиндра в 8 раз меньше высоты первого. Найдите объем второго цилиндра.

Показать ответ и решение

Объем цилиндра с высотой и радиусом основания ищется по формуле Тогда объем первого относится к объему
второго цилиндра как

2 ( )2
16 = πR-12H1-= R1- ⋅ H1
V2 πR 2H2 R2 H2

Из условия следует, что R1 = 1R2,
7 H2 = 1H1,
8 следовательно,

(1 )2
16 = 7R2- ⋅1H1-= -1 ⋅8 ⇒ V2 = 98
V2 R2 8H1 49

Площадь боковой поверхности первого цилиндра равна . Найдите площадь боковой поверхности
второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты
первого цилиндра.

Площадь боковой поверхности первого конуса относится к площади боковой
поверхности второго конуса как 3:7. Найдите отношение образующей первого
конуса к образующей второго конуса, если радиус первого конуса относится к
радиусу второго как 15 :7.

Показать ответ и решение

Площадь боковой поверхности конуса с образующей и радиусом основания ищется по формуле Тогда площадь бок.
поверхности первого конуса относится к площади бок. поверхности второго как

3 S πR l
7 = S1 = πR1l1
2 2 2

Так как радиус первого конуса относится к радиусу второго как 15 :7, то есть то

3 15 l1-
7 = 7 ⋅l2

Следовательно,

l1= 3 ⋅ 7-= 1= 0,2.
l2 7 15 5

Даны два конуса. Радиус второго конуса в 3 раза больше радиуса первого конуса, а высота второго конуса в 6 раз меньше высоты
первого конуса. Найдите объем первого конуса, если объем второго конуса равен 18.

Показать ответ и решение

Объем конуса с высотой и радиусом основания вычисляется по формуле V = 1πR2h.
3 Следовательно, объем первого конуса
относится к объему второго конуса как

1 2 ( )2
V1= V1= 31π-R12h1 = R1- ⋅ h1
18 V2 3π R2h2 R2 h2

Так как радиус второго в 3 раза больше радиуса первого, то Так как высота второго в 6 раз меньше высоты первого,
то Следовательно,

( )2
V1= R1-- ⋅ 6h2= 1 ⋅6= 2 ⇒ V1 = 2⋅18= 12
18 3R1 h2 9 3 3

Объем первого шара равен равен 54. Найдите объем второго шара, если его радиус в 3 раза меньше радиуса первого
шара.

Показать ответ и решение

Объем шара радиуса ищется по формуле 4 3
V = 3 πR . Следовательно, объем первого шара относится к объему второго
как

4 3 ( )3
54= V1 = 3π-R1= R1-
V2 V2 43π R32 R2

Так как радиус второго шара в 3 раза меньше радиуса первого шара, то следовательно,

( )3
54 = 3R2- = 27 ⇒ V2 = 54 = 2
V2 R2 27

Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в 343 раза больше объема второго
шара?

Показать ответ и решение

4 3 ( )3
343 = V1= -3πR1 = R1-
1 V2 43πR32 R2

Значит,

√---
R1= 3343= 7.
R2

Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.

Радиус первого шара равен 6, а радиус второго шара равен 2. Во сколько раз объем первого шара больше объема второго
шара?

Показать ответ и решение

4 3 ( )3
V1 = 3π-⋅6-= 6 = 27
V2 43π ⋅23 2

Следовательно, объем первого шара в 27 раз больше объема второго шара.

Показать ответ и решение

Пусть – объём шара, ограниченного первой сферой. Так как радиус в два раза больше, чем
радиус , то .

следовательно, .

Источник

Объём цилиндра. Здравствуйте, дорогие друзья! В этой статье мы с вами рассмотрим две задачи, в условии которых речь идёт об изменении параметров цилиндра, а именно радиуса основания и высоты. Поставленный вопрос касается изменения объёма. Необходимо знать формулу объёма цилиндра:

Также нужно понимать как «связать» объёмы двух данных тел учитывая условие задачи. Основная рекомендация будет такой:

1. Выражаем объёмы цилиндров, различно обозначив их радиусы и высоты (R₁и Н₁ также R₂и Н₂).

2. Затем связываем формально эти величины используя данные в условии.

3. Далее выражаем объёмы цилиндров через один и тот же радиус основания и высоту.

4. Затем определив взаимосвязь без труда можно ответить на поставленный вопрос, не важно требуется ли найти отношение объёмов, или конкретный объём одного из цилиндров.

На примерах ниже всё подробно посмотрим.

27053. Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.

Нужно найти как соотносятся объёмы цилиндров. Обозначим радиус основания 2-го цилиндра как R₂, а высоту как Н₂. Тогда её объем будет равен:

Объём первого цилиндра соответственно будет равен:

Сказано, что у второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, то есть можем записать:

Подставим значения высоты и радиуса в формулу (1) и получим объём второго цилиндра выраженный через высоту и радиус первого:

Получили, что объём второго цилиндра равен 0,75 объёма первого. Таким образом:

Ответ: 9

*Примечание! Есть ещё путь рассуждения для решения данной задачи. Посмотрите, высота второго цилиндра в три раза больше — это значит, что если мы так увеличим высоту, то объём второго цилиндра станет 36 м³. Затем при уменьшении радиуса основания этого цилиндра в два раза мы получим (0,5R)²=0,25R².

То есть произойдёт уменьшение в 4 раза и объём получится 36:4=9 м³. И решение задачи укладывается в одну строчку V₂=12∙3∙0,25=9.

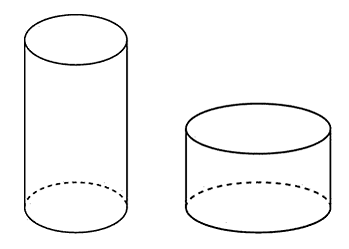
Первая цилиндрическая кружка в пять раз выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.

Нам необходимо найти отношение объёмов. Обозначим радиус основания 2-й кружки как R₂, а высоту как Н₂. Тогда её объем будет равен:

Объём первой кружки соответственно:

Сказано, что первая кружка в пять раз выше второй, а вторая в два раза шире, то есть можем записать:

Выразим R₁ и запишем формулу объёма для первой кружки:

Таким образом, отношение объема второй кружки к объему первой будет равно:

Ответ: 0,8

*Примечание! Решение можно записать кратко в таком виде:

Пояснение: взяли первый цилиндр, уменьшили его высоту в пять раз, а радиус увеличили в два раза (учитываем квадрат радиуса) и получили зависимость объёмов. Далее просто выразили отношение.

27118. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.

Посмотреть решение

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Объём цилиндра: V = S*h, где S — площадь основания, h высота, проведённая к этому основанию.
Основанием цилиндра является круг, следовательно его площадь будет равна S= π*r², где r-радиус.
Тогда формула объёма примет вид: V = π * r² * h

Объём первого цилиндра равен: V₁ = π * r₁² * h см³
Объём второго цилиндра равен: V₂ = π * (r₁/2)² * h = 1/4*V₁ = 1/4*20 = 5 см₃

Ответ: 5 см³

Источник