Статистическое распределение выборки. Полигон и гистограмма
Пусть из генеральной совокупности
извлечена выборка, причём


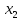


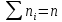
Наблюдаемые значения

а последовательность вариант, записанных
в возрастающем порядке, — вариационным
рядом. Числа наблюдений называютчастотами,
а их отношения к объёму выборки
Статистическим
распределением выборкиназывается перечень вариант и
соответствующих им частот или относительных
частот. Следует отметить, что в теории
вероятностей под распределением понимают
соответствие между возможными значениями
случайной величины и их вероятностями,
а в математической статистике –
соответствие между наблюдаемыми
вариантами и их частотами.
Пусть

значение признака, меньшее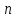
объём выборки. Относительная частота
события

Если
и относительная частота, т.е. относительная
частота

Так как эта функция находится опытным
путём, то её называют эмпирической.
Эмпирической функцией распределения
называется функция

определяющая для каждого значения

Итак

В отличие от эмпирической функции
распределения выборки функцию
распределения

теоретической функцией распределения.
Различие между эмпирической и теоретической
функциями состоит в том, что теоретическая
функция

а эмпирическая функция
же события.
Функция
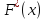
-
значения функции принадлежат отрезку
;
-
— неубывающая функция;
-
если
— наименьшая варианта, то
при
;
если—
наибольшая варианта, топри
.
Пример
1. Найти эмпирическую функцию по
данному распределению выборки:
1 4 6
10 15 25
Р е ш е н и е.

Наименьшая варианта равна 1, поэтому

Значение
а именно
наблюдалось 10 раз, значит,

Значение
а именно: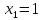

наблюдалось 10+15=25 раз; следовательно,

Так как


Для наглядности строят
различные графики статистического
распределения и, в частности, полигон
и гистограмму.
Полигоном
частот
называют ломаную линию, отрезки которой
соединяют
Полигоном
относительных частот называют ломаную,
отрезки которой соединяют точки


. . . ,
При непрерывном
распределении признака весь интервал,
в котором заключены все наблюдаемые
значения признака, разбивают на ряд
частичных интервалов длиной


интервал.
Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длины

а высоты равны отношению
Площадь частичного -го прямоугольника
равна
сумме частот вариант, попавших в
интервал. Площадь гистограммы частот
равна сумме всех частот, т.е. объёму
выборки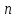
Гистограммой относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною
На рис. 3 изображена
гистограмма частот по данному распределению
выборки объёма

|
Частичный |
Сумма вариант |
Плотность частоты |
|
1 |
10 |
2,5 |
|
5 |
20 |
5 |
|
9 |
50 |
12,5 |
|
13 |
12 |
3 |
|
17 |
8 |
2 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Постройка полигона и гистограммы частот
Содержание:
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Определение
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),…, (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(W_i=frac{n_i}n)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Определение
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
(frac{n_ih}h=n_i)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Дисциплина – «Теория вероятностей»
Курс -3
Практическая
работа
Тема: «Графическое
представление статистического распределения»
Методические
указания
Цель:
1)
Формирование
умений представлять статистические данные графически
2)
Совершенствование
умений вычислять числовые характеристики величин на основе опытных данных
(частота, относительная частота),
3)
Формированию
умений составлять и графически представлять эмпирическую функцию распределения
4)
Продолжить
работу по формированию ОК 2,3,4
ОК 2. Организовывать
собственную деятельность, выбирать типовые методы и способы выполнения
профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и
нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование
информации, необходимой для эффективного выполнения профессиональных задач,
профессионального и личностного развития.
Теоретический материал и методические указания
1. Графическое представление
статистической совокупности.
2. Полигон
3. Гистограмма частот
4. Гистограмма относительных
частот
5. Эмпирическая функция
распределения
Статистическим
распределением выборки или статистическим рядом называют перечень
вариант и соответствующих им частот или относительных частот.
Пример 1. После группировки данных в выборке статистический
ряд задан таблицей 1 (где объём выборки n = 15).
Таблица 1
|
xi |
2 |
3 |
4 |
6 |
|
ni |
1 |
4 |
2 |
3 |
В таблице 1 значения xi называют
вариантами. Последовательность вариант, записанных в возрастающем порядке (вся
строка xi) называется вариационным рядом. Число
наблюдений ni называют частотами, i – номер
варианты.
Учитывая, что
n–
это объем выборки, можно найти относительную частоту wi
= ni/n, наблюдаемого значения xi –
варианты, k – количество вариант.
Тогда таблица будет иметь вид:
Таблица 2
|
xi |
2 |
3 |
4 |
6 |
|
wi = ni/n |
0,1 |
0,3 |
0,4 |
0,6 |
Табличные данные могут быть
представлены графически в виде полигона или гистограммы.
Если выборка задана в виде отдельных точек, а не интервалов, тогда строят
полигон частот. Полигоном относительных частот называется
ломанная, отрезки которой соединяют точки (x; wi). На
рис. 1 изображен полигон частот, приведённых в таблице 1.
Рис. 1.
Полигон
Пример 2. В этом примере наблюдаемые значения
случайной величины после группировки данных в выборке разбиты на
последовательные непересекающиеся частичные интервалы. В результате получается
статистический ряд, который задан таблицей 3.
Таблица 3
|
xi |
[0¸2) |
[2¸4) |
[4¸6) |
[6¸8] |
|
ni |
5 |
10 |
12 |
3 |
Данную таблицу можно представить через
относительную частоту wi =ni/n
(где объём выборки n = 30) в таблице 4.
Таблица 4
|
h=xi-xi-1 |
[0¸2) |
[2¸4) |
[4¸6) |
[6¸8] |
|
wi = ni/n |
0,17 |
0,33 |
0,4 |
0,1 |
При этом частоты wi удовлетворяют
условию
=1.
Если выборка задана в виде интервалов,
тогда строят гистограмму.
Гистограмма частот
Гистограммой
частот называется
ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат
частичные интервалы длиной h=xi-xi-1, а их высоты равны ni/h (для относительных частот — wi /h).
Если объем выборки из генеральной совокупности случайной непрерывной величины
велик, то прибегают к предварительной группировке данных: размах выборки
разбивают на k частичных интервалов Ji.
Количество интервалов подсчитывается по формуле:
или
, [x] – целая часть числа х.
Подсчитывается, сколько значений из n1, n2,…,nm попало
в каждый из к интервалов. Вариантами для выборки считают середины этих интервалов.
Пример
3. Измерения напряжения электросети (в вольтах) дали следующие
результаты: 210, 198, 215, 212 194 213 199 191, 205, 211, 189, 206, 204,
205, 201, 194, 190, 200, 202, 196, 200, 216, 214, 200, 196, 210, 206, 200, 215,
204.
Построить гистограмму относительных частот выборки и гистограмму частот
выборки.
Решение.
Объем выборки n=30. Составим вариационный ряд, расположив данные выборки в
возрастающем порядке: 189 190 191 194, 194, 196, 196, 198, 199, 200, 200,
200, 200, 201, 202, 204 204 105, 205, 206, 206, 210, 210, 211, 212, 213, 214,
215, 215, 216.
Размах выборки
равен 216-189=27.
Гистограмма относительных частот
Определим количество интервалов, на которые необходимо разбить
выборку: k=log230+1=5,8. Округлим это число до
ближайшего целого k=6. Так как размах выборки равен 27, то
длина каждого интервала h=27/6=4,5.
Подсчитаем, сколько измеренных значений попало в каждый из полученных
интервалов:
|
Частичный интервал |
Частота |
|
J1=[189;193.5) |
3 |
|
J2=[193.5;198) |
4 |
|
J3=[198;202.5) |
8 |
|
J4=[202.5;207) |
6 |
|
J5=[207;211.5) |
3 |
|
J6=[211.5;217] |
6 |
Сведем полученные данные в
таблицу:
|
Частичный интервал длиной h=4.5 |
Частота |
wi=ni/n |
Эмпирическая |
wi/h |
|
[189;193.5) |
3 |
0.1 |
0.66 |
0.02 |
|
[193.5;198) |
4 |
0.13 |
0.89 |
0.03 |
|
[198;202.5) |
8 |
0.27 |
1.78 |
0.06 |
|
[202.5;207) |
6 |
0.2 |
1.31 |
0.04 |
|
[207;211.5) |
3 |
0.1 |
0.66 |
0.02 |
|
[211.5;217] |
6 |
0.2 |
1.31 |
0.04 |
Гистограмма частот
 |
Гистограмма относительных частот

выборки (функцией распределения выборки) называется функция: , которую можно записать в следующем виде:
Данная
функция непрерывная, кусочно-постоянна и изменяется в каждой точке хi,
где хi — варианта рассматриваемого статистического
распределения.
Пример
4.
По заданной выборке построить эмпирическую функцию выборки.
|
хi |
2 |
4 |
5 |
6 |
7 |
|
ni |
5 |
3 |
4 |
5 |
3 |
|
|
0 |
=0 |
|
20 |
|
|
5 |
=0,25 |
|
20 |
|
|
5+3 |
=0,4 |
|
20 |
|
|
5+3+4 |
=0,6 |
|
20 |
|
|
5+3+4 +5 |
=0,85 |
|
20 |
|
|
5+3+4 +5 +3 |
=1 |
|
20 |
График
данной функции представлен ниже:
Дисциплина – «Теория вероятностей»
Курс -3
Практическая работа
Тема: «Графическое
представление статистического распределения»
Задание
1. Учебные достижения учащихся некоторого класса по
математике характеризуются данными, представленными в таблице:
|
Количество баллов |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Число учащихся |
1 |
1 |
2 |
3 |
4 |
4 |
6 |
5 |
3 |
3 |
2 |
1 |
Построить полигон частот.
Задание 2. Имеются
данные о количестве студентов в 30 группах физико-математического факультета:
|
26 |
25 |
25 |
26 |
25 |
23 |
|
23 |
24 |
19 |
23 |
20 |
19 |
|
22 |
24 |
24 |
23 |
20 |
23 |
|
24 |
19 |
21 |
18 |
21 |
18 |
|
20 |
18 |
18 |
21 |
15 |
15 |
Составить
статистическое распределение количества студентов в группах, найти объем и размах
выборки. Построить полигон частот.
Задание 3. Студентам предлагалось разгадать несколько числовых
закономерностей и вписать в пропуски недостающие числа. Оценка осуществлялась
по количеству правильно решенных задач и дала следующие результаты:
|
Количество баллов |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Количество студентов |
2 |
3 |
2 |
4 |
12 |
10 |
8 |
9 |
Составить статистическое распределение относительных
частот количества студентов по количеству набранных баллов и построить полигон
относительных частот.
Задание
4. По
заданной выборке построить эмпирическую функцию выборки.
|
хi |
3 |
7 |
9 |
11 |
12 |
|
ni |
5 |
3 |
4 |
5 |
3 |
Задание 5. В 2002 году количество служб, представляющих
гражданам жилищные субсидии, по сельским районам некоторой области распределено
следующим образом:
5, 1, 1, 1, 1, 1, 5, 1,
10, 1, 1, 1, 4, 4, 5, 1, 1.
Построить
эмпирическую функцию распределения и ее график.
Задание 6. Построить гистограмму частот и
относительных частот распределения (в первом столбце указан частичный интервал,
во в тором – сумма частот вариант частичного интервала – ).
2 — 5 9
5 — 8 10
8 — 11 25
11 — 14 6
Задание 7. При
изменении диаметра валика после шлифовки была получена следующая выборка:
Построить
гистограмму частот, предварительно построив ряд статистического распределения,
состоящий из семи интервалов.
- Середина урока
- Изучение новой темы.
- Задание: Было проведено измерение массы 25 детей от 13-14 лет. Полученные данные занесены в таблицу следующим образом:
- — установили, что среди результатов этих измерений минимальная масса – 39 кг, максимальная -57 кг.
- -вычислили размах: 57-39=18, разделили его на 3 и получили 6 интервалов:
— количество детей, масса которых попала в тот или иной интервал, записали в таблице:
| Интервалы | Масса детей (кг) | 39-42 | 42-45 | 45-48 | 48-51 | 51-54 | 54-57 |
| Число детей | 1 | 4 | 8 | 7 | 3 | 1 |
- Используя интервальную таблицу частот можно результаты наблюдения представить в виде гистограммы.
- Гистограмма представляет собой ступенчатую фигуру, состоящую из прямоугольников.
- Ширину прямоугольников берут одинаковую- соотвествующую интервалам, их высоту –соотвествующую частоте ( в примере – числу детей)
- Алгоритм построения гистограммы
- 1. Отложить значения интервалов на оси ОХ
- 2. Отложить частоты на оси ОУ
- 3. Построить прямоугольники, ширина которых соответствует длине интервалов, отложенных на оси ОХ, длина – пропорциональна частоте соответствующего интервала.
Пример 1: В таблице представлены проценты правильного выполнения тестовых заданий учащимися 8-го класса.

Пример 2.В таблице представлена информация о дистанциях, проезжая которые 40 автомобилей затрачивают полный бак бензина.

Для закрепления темы учащимся также предлагается выполнить задание, используя прием «Найди ошибку»
Задание: В лесопосадке растут 59 берез. Их высоты округлены до ближайшего целого значения в метрах и представлены в следующей таблице:
| Высота (м) | 5-9 | 10-12 | 13-15 | 16-18 | 19-28 |
| Кол-во берез | 14 | 18 | 15 | 4 | 8 |
По этим данным учащийся построил гистограмму. Найдите ошибки в построении гистограммы.

После того, как учащиеся выполнят задание, проводится обсуждение со всем классом, указываются ошибки в построении гистограммы.
1-ошибка: между столбцами не должно быть зазоров;
2-ошибка: не верно определены границы интервалов, верно вот так: [4,5; 9,5), [9,5;12,5), [12,5;15,5), [15,5;18,5), [18,5;28,5), так как высота берез – непрерывная величина. Если интервал 5-9 м взят с округлением, то на самом деле он равен [4,5;9,5).
3-ошибка: Так как эти интервалы различны по длине, то по оси ортинат должны рассматриваться не частоты, а плотности частот.
Контроль и самопроверка знаний. Предложите учащимся повторить пройденный материал с помощью метода «Думай – В паре – Делись».
- Цель: Структурированный способ развития идей и мыслей
- Как это работает:
- Предложите учащимся задания для решения.
- -Ученики думают и пишут ответы каждый индивидуально.
- -Ученики образуют пары и объединяют свои лучшие вопросы.
- -Ученики делятся своими новыми улучшенными ответами с классом.
Цель: проверить уровень усвоения темы. Задания разного уровня сложности. Каждый может выбрать задания своего уровня. За выполнение определенного задания вы получаете определенное количество баллов
Предложите учащимся провести самооценивание и взаимооценивание.
Предложите учащимся «Мешочек заданий». Составьте карточки с заданиями, сложите их в мешочек (контейнер). Учащиеся по очереди вынимают карточку из мешочка и выполняют задания. Остальные осуществляют проверку.
Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а так же с учетом скорости мышления и возрастных особенностей учащихся.
Уровень А.
Найдите накопленную частоту для каждого значения площади.
3) С какой торговой площадью наибольшее количество магазинов?
Уровень В
- Найдите накопленную частоту для каждого значения площади.
- 2) Сколько школьных площадок площадью, не превышающих ?
- 3) С какой площадью наибольшее число спортивных площадок?
- 4) Какую часть от всех школьных спортивных площадок составляют площадки с площадью ?
- Уровень С.
1.Составьте вариационный ряд для данных о потреблении электроэнергии (в киловаттах) в семье за 12 месяцев: 102; 108; 99;108; 109; 99; 102; 105; 108; 102; 108; 102.
- Разбейте полученный вариационный ряд на интервалы, составьте интервальную таблицу частот и постройте гистограмму.
- Учащиеся из одного уровня обмениваются решениями и проводят самооценивание и взаимооценивание.
- Презентация
- Стикеры
Источник: https://kopilkaurokov.ru/matematika/uroki/poligon_chastot_gistogramma_chastot
Студент МТУСИ
Описательная статистика используется для простого обобщения данных, полученных в рамках выборочного исследования. В свою очередь, статистические выводы необходимы для того, чтобы данные, полученные из выборки, можно было распространить на всю генеральную совокупность.
Эмпирической функцией выборки (функцией распределения выборки) называется функция
, которую можно записать в следующем виде:

- Данная функция непрерывная, кусочно-постоянна и изменяется в каждой точке хi, где хi — варианта рассматриваемого статистического распределения.
- Пример
- По заданной выборке построить эмпирическую функцию выборки.
| F20(X>7)= | 5+3+4 +5 +3 | =1 |
| 20 |

График данной функции представлен ниже:
Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), …, (xk; nk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат — соответствующие им частоты ni.
Точки ( xi;ni) соединяют отрезками прямых и получают полигон частот (Рис. 1).
Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x1; W1), (x2; W2), …, (xk; Wk).
Для построения полигона относительных частот на оси абсцисс откладывают варианты xi, а на оси ординат — соответствующие им относительные частоты Wi.
Точки ( xi; Wi) соединяют отрезками прямых и получают полигон относительных частот.
- В случае непрерывного признака целесообразно строить гистограмму.
- Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению ni / h (плотность частоты).
- Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni / h.
Площадь i — го частичного прямоугольника равна hni / h = ni — сумме частот вариант i — го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi / h (Рис. 2).
Площадь i — го частичного прямоугольника равна hWi / h = Wi — относительной частоте вариант попавших в i — й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
|
Рис. 1. Полигон частот |
Рис. 2. Гистограмма относительных частот |
Статистический ряд распределения — это упорядоченое распределение единиц совокупности на группы по определенному варьирующему признаку.
Следующим этапом обработки данных является вычисления числовых характеристик выборки. Главные из них:среднее значение, дисперсия, среднее квадратическое значение, моменты.
Так как функцию выборочных значений называют статистикой, то числовые характеристики, вычисленные по выборке, также называют статистиками.
Числовые характеристики, вычисленные по генеральной совокупности, называют параметрами генеральной совокупности.
Для конкретной выборки объема n ее выборочное среднее определяется соотношениемгде хi – значение элемента выборки.Обычно требуется описать статистические свойства произвольных случайных выборок одного объема, а не одной из них. Это значит, что рассматривается математическая модель, которая предполагает достаточно большое количество выборок объема n. В этом случае элементы выборки рассматриваются как независимые случайные величины Хi, принимающие значения хi с одной и тоже плотностью вероятностей f(x), являющейся плотностью вероятностей генеральной совокупности. Тогда выборочное среднее также является случайной величиной , равнойСреднее значение генеральной совокупности, из которой производится выборка, будем называть генеральным средним и обозначать mх. При значительном объеме выборки можно ожидать, что выборочное среднее не будет заметно отличаться от генерального среднего. Поскольку выборочное среднее является случайной величиной, то для нее можно найти математическое ожидание:Таким образом, математическое ожидание выборочного среднего равно генеральному среднему. В этом случае говорят, что выборочное среднее является несмещенной оценкой генерального среднего. В дальнейшем мы вернемся к этому термину. Так как выборочное среднее является случайной величиной, флуктуирующей вокруг генерального среднего, то желательно оценить эту флуктуацию с помощью дисперсии выборочного среднего. Рассмотрим выборку, объем которой n значительно меньше объема генеральной совокупности N (n
Источник: http://studentmtuci.blogspot.com/2016/01/blog-post_47.html
Полигон и гистограмма частот
Для наглядности в статистике часто пользуются геометрической интер-претацией статистического распределения выборки, строя, так называемые, полигон и гистограмму частот (или относительных частот).
Для построения полигона частот (или относительных частот) при дискретном распределении признака по оси абсцисс откладывают значения признака хi , а по оси ординат – частоты ni (или соответственно относительные частоты Wi ). Точки с координатами (xi , ni) (или (xi , Wi)) соединяют отрезками прямых. Полигон частот дает представление о том, насколько часто встречаются те или иные значения исследуемого признака.
Пример. Для распределения
полигон относительных частот имеет вид, показанный на рисунке.

Полигон относительных частот – это статистический аналог многоугольника распределения дискретной случайной величины в теории вероятностей.
Если исследуемый признак – непрерывная случайная величина, то целесообразно строить гистограмму частот.
Для этого интервал, в котором заключены все наблюдавшиеся значения признака, делят на ряд частичных интервалов одинаковой длины ∆.
Далее находят ni — сумму частот значений признака, попавших в i — ый частичный интервал, и строят ступенчатую фигуру из прямоугольников с основанием, равным ∆, и площадью, равной ni.
- Если значения признака совпадают с границей интервала, то их включают в сумму частот значений признака, принадлежащих соседним интервалам с частотами, равными половине частоты этого признака.
- Полученный график называется гистограммой частот.
- Площадь гистограммы частот равна сумме частот всех наблюдавшихся значений признака, то есть объему выборки.
Гистограмма относительных частот строится точно также, отличаясь от гистограммы частот лишь масштабом по оси ординат, а именно, по оси ординат откладывается плотность относительной частоты . Поэтому площадь i –го прямоугольника будет равна Wi – относительной частоте значений признака, попавших в i – ый интервал, а площадь гистограммы относительных частот будет равна сумме всех Wi , то есть единице.
Число интервалов r гистограммы определяют приближенно по формуле Старджесса для выборки объема n (округляя r до ближайшего целого значения):
Пример. Произведено 100 измерений диаметров валиков, результаты которых представлены в таблице 4.
Таблица 4
| 15,23 | 15,37 | 15,48 | 15,48 | 15,43 | 15,35 | 15,36 | 15,40 | 15,45 | 15,29 |
| 15,48 | 15,58 | 15,44 | 15,56 | 15,28 | 15,59 | 15,47 | 15,41 | 15,54 | 15,20 |
| 15,38 | 15,43 | 15,35 | 15,56 | 15,51 | 15,47 | 15,40 | 15,29 | 15,20 | 15,46 |
| 15,42 | 15,44 | 15,41 | 15,29 | 15,48 | 15,39 | 15,50 | 15,38 | 15,45 | 15,50 |
| 15,45 | 15,42 | 15,29 | 15,53 | 15,34 | 15,55 | 15,33 | 15,32 | 15,44 | 15,46 |
| 15,32 | 15,46 | 15,32 | 15,48 | 15,38 | 15,43 | 15,51 | 15,43 | 15,60 | 15,44 |
| 15,55 | 15,29 | 15,31 | 15,44 | 15,43 | 15,44 | 15,31 | 15,58 | 15,28 | 15,24 |
| 15,34 | 15,49 | 15,50 | 15,38 | 15,48 | 15,43 | 15,37 | 15,29 | 15,54 | 15,33 |
| 15,36 | 15,46 | 15,23 | 15,44 | 15,38 | 15,27 | 15,52 | 15,40 | 15,26 | 15,37 |
| 15,59 | 15,48 | 15,46 | 15,40 | 15,24 | 15,41 | 15,34 | 15,43 | 15,38 | 15,50 |
Построить гистограммы частот и относительных частот этого распределения.
Как видно из таблицы, наименьшее значение диаметра-15,20 мм, наи-большее-15,60 мм, длина этого промежутка — 0,4 мм. Число частичных интервалов принимаем по правилу Старджесса, равным восьми. Подсчитываем число значений признака, попадавших в каждый интервал. Для построения гистограмм частот (и относительных частот) составим таблицу 5.
Таблица 5
| Частичный интервал = 0,05 | Сумма частот значений признака в частичном интервале | Плотность частоты | Плотность относительной частоты | |
| 15,20-15,25 | 0,06 | 1,2 | ||
| 15,25-15,30 | 0,10 | 2,0 | ||
| 15,30-15,35 | 0,11 | 2,2 | ||
| 15,35-15,40 | 0,15 | 3,0 | ||
| 15,40-15,45 | 22,5 | 0,225 | 4,5 | |
| 15,45-15,50 | 18,5 | 0,185 | 3,7 | |
| 15,50-15,55 | 0,09 | 1,8 | ||
| 15,55-15,60 | 0,08 | 1,6 | ||
| N= 100 |
Соответствующие гистограммы изображены на рисунке.

- При увеличении объема выборочной совокупности гистограмма относительных частот приближается к дифференциальному закону распределения признака в генеральной совокупности, то есть гистограмма относительных частот является статистическим аналогом плотности вероятностей f(x) непрерывной случайной величины.
- СТАТИСТИЧЕСКИЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
- Точечные оценки
- Любое значение неизвестного параметра, от которого зависит закон распределения случайной величины, вычисленное по опытным данным, всегда является приближенным.
Оценкой параметра и называется в статистике его приближенное случайное значение, вычисленное на основе ограниченного числа опытов. Если оценка параметра характеризуется одним числом, то она называется точечной.
Пусть из генеральной совокупности произведена выборка объема n для изучения некоторого признака Х.
Обозначим неизвестный параметр теоретического распределения интересующего нас признака объектов генеральной совокупности через . Требуется по данным выборки найти “подходящую” оценку для параметра .
- Очевидно, для некоторой другой выборки оценка будет принимать иное значение, то есть — случайная величина, зависящая от данных опытов и их числа n.
- Чтобы оценка давала близкое приближение к оцениваемому параметру, она должна удовлетворять определенным требованиям.
- 1. При увеличении n оценка должна сходиться по вероятности к параметру , то есть должно выполняться равенство
- Оценка, обладающая таким свойством, называется состоятельной.
2. Необходимо, чтобы пользуясь вместо , мы не допускали систематической (неслучайной) ошибки в сторону занижения или завышения действительного значения оцениваемого параметра, то есть, чтобы .
- Оценка , математическое ожидание которой равна оцениваемому параметру, называется несмещенной.
- 3. Оценка должна обладать по сравнению с другими возможными оценками наименьшей дисперсией:
- Оценка, обладающая таким свойством, называется эффективной.
- Ниже рассмотрены повторные и бесповторные выборки и точечные оценки генеральной средней и генеральной дисперсии, удовлетворяющие указанным требованиям.
Источник: https://infopedia.su/10xc901.html
Статистическое распределение выборки
Статистическое распределение выборки
При систематизации данных выборочных обследований используются статистические дискретные и интервальные ряды распределения.
1. Статистическое дискретное распределение. Полигон. Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдалось n1 раз, х2 – n2 раз, хk – nk раз и ∑ni=n — объем выборки.
Наблюдаемые значения х1 называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.
Число наблюдений варианты называют частотой, а ее отношение к объему выборки — относительной частотой ni/n=wi
ОПРЕДЕЛЕНИЕ. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант хi и соответствующих им частот ni или относительных частот wi.
Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:
(сумма всех частот равна объему выборки ∑ni=n) или в виде таблицы распределения относительных частот:
(сумма всех относительных частот равна единице ∑wi=1)
Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72, 74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот.
Решение. 1) Статистический ряд распределения частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| ni | 2 | 4 | 8 | 2 | 4 |
2) Объем выборки: n=2+4+8+2+4=20. Найдем относительные частоты, для чего разделим частоты на объем выборки ni/n=wi: wi=2/20=0.1; w2=4/20=0.2; w3=0.4; w4=4/20=0.1; w5=2/20=0.2. Напишем распределение относительных частот:
| xi | 70 | 71 | 72 | 73 | 74 |
| wi | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
Контроль: 0,1+0,2+0,4+0,1+0,2=1.
Полигоном частот называют ломаную, отрезки, которой соединяют точки (х1,n1),(х2,n2),…,(хk,nk). Для построения полигона частот на оси абсцисс откладывают варианты х2, а на оси ординат – соответствующие им частоты ni. Точки (хi,ni) соединяют отрезками и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки (х1,w1),(х2,w2),…,(хk,wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты хi, а на оси ординат соответствующие им частоты wi. Точки (хi,wi) соединяют отрезками и получают полигон относительных частот.
Пример 2. Постройте полигон частот и относительных частот по данным примера 1. Решение: Используя дискретный статистический ряд распределения, составленный в примере 1 построим полигон частот и полигон относительных частот:

2. Статистический интервальный ряд распределения. Гистограмма.
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя.
Если же интересующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно ( или невозможно) учитывать, то варианты группируются в интервалы.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Замечание. Часто hi-hi-1=h при всех i, т.е. группировку осуществляют с равным шагом h. В этой ситуации можно руководствоваться следующими эмперическими рекомендациями по выборке а, k и hi:
1. Rразмах=Xmax-Xmin 2. h=R/k; k-число групп 3. k≥1+3.321lgn (формула Стерджеса)
- 4. a=xmin, b=xmax
- Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:
5. h=a+ih, i=0,1…k
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Частоты | n1 | n2 | … | nk-1 | nk |
Аналогическую таблицу можно образовать, заменяя частоты ni относительными частотами:
| Интервалы группировки | [h0;h1) | [h1;h2) | … | [hk-2;hk-1) | [hk-1;hk) |
| Отн. частоты | w1 | w2 | … | wk-1 | wk |
Пример 3.
Из очень большой партии деталей извлечена случайная выборка объема 50 интересующий нас признак Х-размеры деталей, измеренные с точностью до 1см, представлен следующим вариоционным рядом: 22, 47, 26, 26, 30, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти статистический интервальный ряд распределения.
Решение. Определим характеристики группировки с помощью замечания. k≥1+3.321lg50=1+3.32lg(5•10)=1+3.32(lg5+lg10)=6.6
Имеем, a=22, k=7, h=(50-22)/7=4, hi=22+4i, i=0,1,…,7.
| Интервалы группировки | 22-26 | 26-30 | 30-34 | 34-38 | 38-42 | 42-46 | 46-50 |
| Частоты ni | 1 | 4 | 10 | 18 | 9 | 5 | 3 |
| Отн.частоты wi | 0.02 | 0.08 | 0.2 | 0.36 | 0.18 | 0.1 | 0.06 |
Десятичные логарифмы от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| lnn≈ | 0.3 | 0.48 | 0.6 | 0.7 | 0.78 | 0.85 | 0.9 | 0.95 | 1 |
Наиболее информативной графической формой частот является специальный график, называемы гистограммой частот.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь i-го частичного прямоугольника равна h•ni/h=ni — сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению wi/h (плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии wi/h. Площадь i-го частичного прямоугольника равна h•wi/h=wi — относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.
Пример 4. Постройте гистограмму частот и относительных частот по данным примера 3.

Выборочная медиана – это середина вариационного ряда, значение, расположенное на одинаковом расстоянии от левой и правой границы выборки.
Выборочная мода – это наиболее вероятное, т.е. чаще всего встречающееся, значение в выборке.
Источник: http://testent.ru/publ/studenty/vysshaja_matematika/statisticheskoe_raspredelenie_vyborki/35-1-0-1145
Поурочное планирование урок по алгебре «Полигон частот, гистограмма частот»
Краткосрочный план
План урока
Раздел долгосрочного плана:
- Раздел Статистика и анализ данных
- Школа:
- Дата:
- ФИО учителя: Калшабеков Мухитжан
- Класс:
- Количество присутствующих: 7
- отсутствующих: 0
- Тема урока
- Полигон частот, гистограмма частот
- Тип урока
- Изучение новой темы
- Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
- Анализировать статистическую информацию, представленную в виде таблицы или полигона частот
- Цели урока
- Учащиеся отвечают на вопросы или задают вопросы, используя таблицу или полигон частот
- Критерии оценивания
- Учащийся достиг цель, если:
Навыки высокого порядка
- Анализирует данные, представленные в виде таблицы или полигона частот
- Языковые цели
- Языковые цели обучения:
- Учащиеся будут:
- обсуждать и комментировать способы определения абсолютных и относительных частот;
— презентовать всему классу собранные данные, представленные в виде таблиц частот, и делать комментарии о процессе сбора и обработки данных.
Предметная лексика и терминология:
- выборка;
- частота;
- абсолютная частота;
- относительная частота;
- таблица частот;
- таблица относительных частот;
- сбор данных;
- полигон частот.
- представление данных.
- Серияполезных фраз для диалога/письма:
- составить таблицу распределения данных;
- представить полученные данные в виде таблицы частот;
- представить полученные данные в виде таблицы относительных частот;
- для вычисления абсолютной частоты необходимо подсчитать…;
- для вычисления относительной частоты необходимо разделить … на количество
- Привитие ценностей
- Умение учиться, добывать самостоятельно информацию, анализировать ситуацию, адаптироваться к новым ситуациям, ставить проблемы и принимать решения, отвечать за качество своей работы и своей группы, умение организовывать свое время, воспитывать уважение к разнообразию культур и мнений на занятиях.
- Привитие ценностей осуществляется через все этапы деятельности на уроке.
- Межпредметные связи
- Математика, экономика, статистика.
- Предварительные знания
Умение находить размах, моду, медиану и среднее арифметическое числового ряда, абсолютную частоту, относительную частоту. Строить и читать диаграммы. Строить полигон частот.
- Ход урока
- Запланированные этапы урока
- Запланированная деятельность на уроке
- Ресурсы
- Начало урока
- 3 мин
- В начале урока учитель делает акценты на:
- — концентрацию внимания учащихся;
- — совместно с учащимися определяет цели урока;
- — определяет «зону ближайшего развития» учащихся, объединяя их по парам, группам (уровень А, В и С);
- — ожидания к концу урока.
- (Слайды №1-3).
- Середина урока
- 40 мин
В процессе выполнения различной деятельности на уроке учащиеся заполняют свой оценочный лист (приложение №1). В конце урока подводятся итоги и фиксируются в рабочем журнале учителя.
-
Проверка домашней работы – 10 мин (слайды № 4-6).
- Стараясь получить хороший результат учашийся разивает в себе такие ценности, как: упорство в достижении цели, трудолюбие, академическую честность).
- Учащиеся оценивают себя по образцу:
- Задание: Закинул старик в море невод. Пришел невод с таким уловом (в порядке вытаскивания):
П, О, Л, С, Я, П, К, О, З, К, П, К, Я, С, О, П, П, Л, О, О, Л, С, О, П, Л, П, К, Л, К, П, П, С, П, П, З, К, Я, П, З, С, О, О, Я, П, П, О, Л, С, Л, С, П, О, П, Л, К, С, О, Я, Л, П, С, О, Л, П, О, К, Л, П, О, О, П, О, Я, Л, П, С, П, О, Л, П, З. Буквами обозначены: З – Золотая рыбка; К — Карась; Л – Лещ; О – Окунь; П – Пескарь; С – Сом; Я – Язь.
а) Произведи ранжирование ряда данных в алфавитном порядке.
б) Составь таблицу частот:
Вид рыбы
- З
- К
- Л
- О
- П
- С
- Я
- Частота
- Относительная
- частота, %
- в) Какой процент пойманной рыбы составляют золотые рыбки?
- г) Используя полученную стариком выборку, оцените, какие виды рыб наиболее и наименее распространены в местах, где старик закинул невод.
- д) Построй полигон абсолютной частоты
- Ответ:
- а)
- З, З, З, З; К, К, К, К, К, К, К, К; Л, Л, Л, Л, Л, Л, Л, Л, Л, Л, Л, Л, Л; О, О, О, О, О, О, О, О, О, О, О, О, О, О, О, О, О; П, П, П, П, П, П, П, П, П, П, П, П, П, П, П, П, П, П, П, П, П, П; С, С, С, С, С, С, С, С, С, С;
- Я, Я, Я, Я, Я, Я.
- б)
Вид рыбы
- З
- К
- Л
- О
- П
- С
- Я
- Частота
- 4
- 8
- 13
- 17
- 22
- 10
- 6
- Относительная
- частота, %
- 5
- 10
- 16
- 21
- 28
- 12
- 8
- в) 5%;
- г) Более распространены в местах лова: лещи, окуни, пескари; менее – караси, язи, золотые рыбки.
- д)
Критерий оценивания: Заполняет таблицу, используя статистические данные. Строит полигон частот.
Дескрипторы:
-
Производит ранжирование ряда данных в алфавитном порядке.
-
Находит частоту для каждого вида рыб.
-
Находит относительную частоту для каждого вида рыб.
-
Определяет, какой процент пойманной рыбы составляют золотые рыбки, и какие виды рыб наиболее и наименее распространены в местах, где старик закинул невод.
-
Строит полигон абсолютной частоты.
-
Повторение ранее изученного материала — 7 мин(слайды №7-8).
На этом этапе у учащихся развивается ценность обучения на протяжении всей жизни. Кроме этого,работая в парах и выполняя задание на закрепление у учащихся развивается умение учиться, добывать самостоятельно информацию, анализировать ситуацию.
- Работа в парах
- Задание:
- Пример 1: Построите полигон частот по данному распределению:
xi
- 1
- 4
- 5
- 7
- ni
- 20
- 10
- 14
- 6
- Ответ:
- Пары обмениваются тетрадями и взаимооценивают друг друга.
- Критерий оценивания: Строит полигон частот.
- Дескрипторы:
-
Вводит обозначения на оси Оx
-
Вводит обозначения на оси Оy
-
Строит полигон частот
-
Работа над новым материалом – 20 мин (приложение №2)
На этом этапе у учащихся развиваются следующие ценности: ставить проблемы и принимать решения, отвечать за качество своей работы и своей группы, умение организовывать свое время, воспитывать уважение к разнообразию культур и мнений на занятиях.
Учитель предлагает выполнить задания в группах. Во время работы учащихся, учитель наблюдает за работой групп, задает рефлексирующие вопросы, побуждающие учащихся к осмыслению полученных результатов.
Уровень А
Задание:
-
В таблице приведены данные по температуре в городе N в июне 1980 г. и в июне 1990 г. В ней отражена информация об ежедневных наблюдениях.
- В каком году было больше дней, когда температура превышала 26o?
- Уровень В
- Задание:
Семиклассники отгадывали кроссворд (каждый самостоятельно). После этого они сравнили число неразгаданных слов. Данные представлены в таблице в %:
- Сколько % учащихся не разгадали более двух слов?
- Уровень С
- Задание:
- Найдите сколько времени в среднем, затратили учащиеся на дорогу от дома до школы.
После выполненного задания группы презентуют свои решения. Учитель дает учащимся обратную связь, обращая внимание учащихся на важные моменты, также дает рекомендации по данному виду деятельности.
-
Самостоятельная работа – 5 мин (приложение №3).
- У учащихся развиваются умения: учиться, добывать самостоятельно информацию, анализировать ситуацию, организовывать свое время.
- Задание:
- Распределение работников предприятия по возрасту
Категории работников
- Возраст работников, лет
- Всего работников
- До 30
- 30-40
- 40-50
- 50-60
- Свыше 60
- Рабочие
- 43
- 141
- 216
- 127
- 118
- 645
- Руководители
- 2
- 4
- 6
- 8
- 4
- 24
- Специалисты
- 3
- 18
- 30
- 34
- 22
- 107
- Всего работников
- 48
- 163
- 252
- 169
- 144
- 776
- Ответьте на вопросы, используя данные таблицы:
-
Найдите относительную частоту руководителей предприятия до 30 лет от общего количества людей в данном возрасте.
-
Сколько процентов составляют специалисты свыше 60 лет от общего количества работающих специалистов на данном предприятии. (Результат округли до сотых)
-
В каком возрасте и кто из категории работников составляют моду?
-
Придумай свой вопрос и ответь на него.
Критерий оценивания: Анализирует статистическую информацию, представленную в виде таблицы.
Дескрипторы:
-
Находит относительную частоту руководителей предприятия до 30 лет от общего количества людей в данном возрасте.
-
Определяет, сколько процентов составляют специалисты свыше 60 лет от общего количества работающих специалистов на данном предприятии.
-
Округляет результат.
-
Составляет вопрос к таблице.
-
Отвечает на поставленный вопрос.
Данную работу учитель оценивает сам и на следующий урок сообщает результаты самостоятельной работы, а также общий результат за урок. Также можно данные вопросы использовать во время повторения материала на последующем уроке.
-
Подведение итогов – 2 мин
Для обобщения и закрепления пройденной темы можно провести устный опрос по таблице, где учащиеся задают друг другу вопросы и отвечают на них (слайд №9).
-
Домашнее задание – 1 мин (приложение №4).
- (Слайд №10).
- Стараясь получить хороший результат учашийся разивает в себе такие ценности, как: упорство в достижении цели, трудолюбие, академическую честность).
- Задание:
- В таблице представлены результаты продаж женской обуви в некотором магазине за один день.
Размер обуви
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- Количество
- 3
- 5
- 5
- 7
- 10
- 11
- 5
- 4
- Найди: а) средний размер купленной обуви; б) медиану; в) моду.
- По данным таблицы построй полигон относительных частот.
- Рекомендуемые виды деятельности (учебный план 7 класса)
- Конец урока
- 2 мин
- (Приложение №5).
- «П» — «плюс»
- записывается, что понравилось на уроке, информация и формы работы, которые вызвали положительные эмоции, либо могут быть полезны для достижения каких-то целей
- «М» — «минус»
- записывается все, что не понравилось на уроке, показалось скучным, вызвало неприязнь, осталось непонятным, или информация, которая, оказалась не нужной, бесполезной с точки зрения решения жизненных ситуаций
- «И» — «интересно»
- записываются все любопытные факты, о которых узнали на уроке и что бы еще хотелось узнать по данной проблеме, вопросы к учителю.
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
- Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
- Здоровье и соблюдение техники безопасности
- Дифференциация на уроке присутствовала во время работы в группах.
После каждого этапа урока происходит оценивание работы (самооценивание, взаимооценивание или оценивание учителем). В конце урока учащиеся подсчитывают средний процент и озвучивают его учителю.
- Физминутка
- Рефлексия по уроку
- Были ли цели урока/цели обучения реалистичными?
- Все ли учащиеся достигли ЦО?
- Если нет, то почему?
- Правильно ли проведена дифференциация на уроке?
- Выдержаны ли были временные этапы урока?
- Какие отступления были от плана урока и почему?
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
- Общая оценка
- Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
- 1:.
- 2:
- Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?
- 1:
- 2:
- Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
Источник: https://infourok.ru/pourochnoe-planirovanie-urok-po-algebre-poligon-chastot-gistogramma-chastot-3691513.html
План-конспект занятия на тему: Построение полигонов частот и гистограмм | Социальная сеть работников образования
- Выселковский филиал государственного бюджетного профессионального
- образовательного учреждения «Кропоткинский медицинский колледж»
- министерства здравоохранения Краснодарского края
- (Выселковский филиал ГБПОУ «Кропоткинский медицинский колледж»)
- МЕТОДИЧЕСКАЯ РАЗРАБОТКА
- ПРАКТИЧЕСКОГО ЗАНЯТИЯ
- Дисциплина: «Математика»
- Тема: «Построение полигонов частот и гистограмм»
- Специальность: «Сестринское дело»
- Курс: 2
- Семестр: 3
- Составил преподаватель: Жмаченко Ольга Николаевна
- ст. Выселки
- 2018 год
- Выселковский филиал государственного бюджетного профессионального образовательного учреждения «Кропоткинский медицинский колледж»
- министерства здравоохранения Краснодарского края
- Технологическая карта практического занятия № 6
- Дисциплина (модуль) Математика
- Специальность Сестринское дело
- Курс 2 Семестр 3
- Тема: «Построение полигонов частот и гистограмм»
- Группы: 210 А-Ф, 211 А-Ф, 213 А-Ф
- Преподаватель Жмаченко Ольга Николаевна
- Продолжительность 90 минут Место проведения аудитория Выселковского филиала
- Цели учебного занятия:
- • личностных:
- — развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
- — овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;
- — готовность и способность к самостоятельной творческой и ответственной деятельности;
- • метапредметных:
- — умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;
- — умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
- — готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;
- — владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
- — владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения;
- предметных:
- — сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
- — владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач;
- — сформированность представлений об основных понятиях математического анализа и их свойствах,
- — использование полученных знаний для описания и анализа реальных зависимостей;
- уметь:
- рассчитать интенсивные показатели (коэффициент рождаемости, смертности, естественного прироста), экстенсивные показатели, структуру населения;
- дать оценку демографическим показателям; определить тип структуры на-селения;
- рассчитать показатели медицинской деятельности: нагрузка в день на приеме, посещаемость на дому в день, число обращений на 1 жителя в год и т.д.
знать:
- задачи медицинской статистики;
- основные формулы расчета экстенсивных и интенсивных показателей;
- примеры показателей медицинской деятельности и формулы их расчета.
- Образовательные технологии: технологии проблемного обучения
- Методы и приемы обучения: практическое, объяснительно-иллюстративное
- Средства обучения:
- Учебно-наглядные и натуральные пособия, раздаточный материал: м/у, карточки с заданиями
- Литература:
Основная литература: Математика М.И.Башмаков. М: АКАДЕМИЯ, 2016
Электронная библиотека медицинского колледжа www.medcollegelib.ru
- Межпредметные связи: медицина
- Внутрипредметные связи: статистика
- Хронологическая карта занятия
| № | Этапы учебного занятия | Время (минуты) |
| 1. | Организационный момент | 2 |
| 2. | Постановка целей, начальная мотивация | 3 |
| 3. | Инструкция по выполнению | 5 |
| 4. | Выполнение практической работы | 75 |
| 5. | Подведение итогов | 3 |
| 6. | Задания для самостоятельной работы студентов | 2 |
- 1. Организационный момент:
- Приветствую студентов, обращаю внимание на внешний вид студентов, санитарное состояние кабинета, проверяю готовность студентов к занятию, отмечаю отсутствующих.
- 2. Постановка целей, начальная мотивация
- Студент должен уметь:
- • рассчитать интенсивные показатели (коэффициент рождаемости, смертности, естественного прироста), экстенсивные показатели, структуру населения;
- • дать оценку демографическим показателям; определить тип структуры на-селения;
• рассчитать показатели медицинской деятельности: нагрузка в день на приеме, посещаемость на дому в день, число обращений на 1 жителя в год и т.д.
- Студент должен знать:
- • задачи медицинской статистики;
- • основные формулы расчета экстенсивных и интенсивных показателей;
- • примеры показателей медицинской деятельности и формулы их расчета.
- 3. Инструкция по выполнению
- 4. Выполнение практической работы
- Этапы самостоятельной работы:
| № п/п | ||
| 1 | Медицинская статистика, этапы статистического исследования, статистическая совокупность | задания 1-8 |
| 2 | Относительные величины и их графическое изображение. | задание 9-15 |
| 3 | Средние величины | задание 16-19 |
| 4 | Показатели работы поликлиники и стационара. | задание 20-21 |
| 5 | Медико-демографические показатели | задание 22 |
- 5. Подведение итогов:
- Подвожу итоги занятия, отмечаю наиболее активных студентов, определяю степень достижения целей и задач занятия, говорю об общем впечатлении от занятия.
- 6. Задания для самостоятельной работы студентов: Задачи прилагаются
Источник: https://nsportal.ru/npo-spo/estestvennye-nauki/library/2018/12/20/postroenie-poligonov-chastot-i-gistogramm



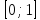 ;
; — неубывающая функция;
— неубывающая функция; — наименьшая варианта, то
— наименьшая варианта, то при
при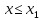 ;
; —
— при
при .
.