Размер генеральной совокупности
Размер общей популяции, также известной как население или генеральная совокупность, — это не что иное, как количество людей, о которых вы хотите сделать заявления на основе результатов опроса.
Если результаты опроса должны быть репрезентативными для сотрудников вашей компании, размер совокупности равен количеству всех сотрудников вашей компании. Если ваши результаты применимы ко всей Германии, то ее население составляет около 83 миллионов человек.
Чем меньше популяция, тем меньше вам потребуется выборка для репрезентативного обследования, но она будет расти в процентном выражении от популяции. Например, если для оценки мнения 10000 человек необходимо опросить 370 (3.7%), то для 100 человек – 80 (80%) при одинаковых параметрах погрешности и надежности 5% и 95% соответственно.
Во многих случаях размер популяции неизвестен. Это не большая проблема. В этом случае можно определить размер выборки для так называемой бесконечной совокупности. В конце концов, вам нужно опросить еще немного людей, но в то же время вы можете быть уверены, что результаты опроса будут репрезентативными.
Необходимый размер выборки
Необходимый размер выборки — это минимальное количество субъектов, с которыми вам нужно взять интервью, чтобы результаты вашего опроса можно было считать репрезентативными для населения.
Чем больше субъектов вы опрашиваете, тем более «репрезентативными» становятся результаты опроса. Так что не проблема, если вы опросите больше субъектов, чем указывает необходимый размер выборки.
Иначе обстоит дело, если вы опрашиваете меньшее количество испытуемых, чем требует необходимый размер выборки. В этом случае у вас нет оснований утверждать, что выводы, которые вы делаете на основании результатов вашего опроса, также применимы ко всему населению в случае социологического опроса. Ни предел погрешности, ни уровень достоверности не могут исправить это — если минимальный размер выборки не был достигнут, они бессмысленны.
Должен ли мой опрос быть репрезентативным?
Ответ на этот вопрос очень прост: все зависит от цели опроса!
Если вы хотите получить целостное представление о населении с помощью своего опроса, чтобы иметь возможность делать обобщенные утверждения или важные решения на его основе, вам обязательно следует стремиться к репрезентативности.
Так обстоит дело, например, с исследованиями рынка, которые собирают информацию о целевых рынках, чтобы, например, сегментировать рынки, чтобы иметь возможность оценить, как новый продукт воспринимается потенциальными клиентами или как потребители отреагируют на ваши рекламные сообщения. Если он не является репрезентативным, вы не можете использовать информацию, полученную в ходе опроса, следовательно, не знаете, отреагирует ли рынок на ваши меры так, как показывают результаты вашего опроса.
Аналогичным образом, в опросах сотрудников, например, в преддверии запланированной реструктуризации, и особенно в опросах общественного мнения и исследованиях выборов, следует добиваться репрезентативности.
Когда репрезентативность не так важна?
Если вы только собираете отзывы или ищете идеи и предложения от своих сотрудников или клиентов, репрезентативность не играет особо важной роли. Репрезентативность также не требуется в качественных исследованиях.
Как я могу самостоятельно рассчитать размер выборки?
Калькулятор выборки, представленный в этой статье, подходит для большинства исследовательских проектов и дает надежные оценки размера выборки для большинства практических случаев.
Калькулятор предполагает, что в преддверии опроса вы ничего не знаете о распределении интересующих вас переменных (например, доли недовольных потребителей) в популяции. Однако, если у вас есть такая информация, необходимый размер выборки может быть немного меньше.
Для этого можно использовать параметр «Доля признака в генеральной совокупности:» — если по предыдущим исследованиям известно, что для исследуемого признака больше 50%, то размер выборки уменьшается.
Автор: Dr. Пол Маркс
Этот текст защищен авторским правом. Все права защищены.
You can use this free sample size calculator to determine the sample size of a given survey per the sample proportion, margin of error, and required confidence level.
You can calculate the sample size in five simple steps:
- Choose the required confidence level from the dropdown menu
- Input the margin of error
- Input the proportion of the total population (%)
- If required, specify the population size
- Click on the «Calculate» button to generate the results.
What is Sample Size?
The sample size of a survey is the total number of complete responses that were received during the survey process. It is referred to as a sample because it does not include the full target population; it represents a selection of that population. For example, many studies involve random sampling by which a selection of a target population is randomly asked to complete a survey.
Some basic terms are of interest when calculating sample size. These are as follows:
Confidence level: The level of confidence of a sample is expressed as a percentage and describes the extent to which you can be sure it is representative of the target population; that is, how frequently the true percentage of the population who would select a response lies within the confidence interval. For example, if you have a confidence level of 90%, if you were to conduct the survey 100 times, the survey would yield the exact same results 90 times out of those 100 times.
Margin of Error: Margin of error is also measured in percentage terms. It indicates the extent to which the outputs of the sample population are reflective of the overall population. The lower the margin of error, the nearer the researcher is to having an accurate response at a given confidence level. To determine the margin of error, take a look at our margin of error calculator.
Percentage of population selecting a given choice: The accuracy of the research outputs also varies according to the percentage of the sample that chooses a given response. If 98% of the population select «Yes» and 2% select «No,» there is a low chance of error. However, if 35% of the population select «Yes» and 65% select «No», there is a higher chance an error will be made, regardless of the sample size. When selecting the sample size required for a given level of accuracy, researchers should use the worst-case percentage; i.e., 50%.
Population Size: The population size is the total number of people in the target population. For example, if you were performing research that was based on the people living in the UK, the full population would be approximately 66 million. Likewise, if you were conducting research on an organization, the total size of the population would be the number of employees who work for that organization.
Sample Size Formula
The Sample Size Calculator uses the following formulas:
1. n = z2 * p * (1 — p) / e2
2. n (with finite population correction) = [z2 * p * (1 — p) / e2] / [1 + (z2 * p * (1 — p) / (e2 * N))]
Where:
n is the sample size,
z is the z-score associated with a level of confidence,
p is the sample proportion, expressed as a decimal,
e is the margin of error, expressed as a decimal,
N is the population size.
Example of a Sample Size Calculation: Let’s say we want to calculate the proportion of patients who have been discharged from a given hospital who are happy with the level of care they received while hospitalized at a 90% confidence level of the proportion within 4%. What sample size would we require?
The sample size (n) can be calculated using the following formula:
n = z2 * p * (1 — p) / e2
where z = 1.645 for a confidence level (α) of 90%, p = proportion (expressed as a decimal), e = margin of error.
z = 1.645, p = 0.5, e = 0.04
n = 1.6452 * 0.5 * (1 — 0.5) / 0.042
n = 0.6765 / 0.0016 = 422.816
n ≈ 423 patients.
| Desired Confidence Level | Z-Score |
|---|---|
| 70% | 1.04 |
| 75% | 1.15 |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.645 |
| 91% | 1.70 |
| 92% | 1.75 |
| 93% | 1.81 |
| 94% | 1.88 |
| 95% | 1.96 |
| 96% | 2.05 |
| 97% | 2.17 |
| 98% | 2.33 |
| 99% | 2.576 |
| 99.5% | 2.807 |
| 99.9% | 3.29 |
| 99.99% | 3.89 |
Reference: Daniel WW (1999). Biostatistics: A Foundation for Analysis in the Health Sciences. 7th edition. New York: John Wiley & Sons.
You may also be interested in our Effect Size (Cohen’s d) Calculator or Relative Risk Calculator
Запуск рекламной кампании в маркетинге предполагает А/В-тестирование, однако не каждый проведенный тест будет показательным, а его результаты – значимыми для статистики. Одна из распространенных ошибок при проведении исследований – неправильное определение нормального размера выборки. Как следствие – запуск рекламы, которая не даст результатов, и зря потраченные деньги.
Что такое объем выборки
Объем выборки – это количество людей из общего числа целевой аудитории (ЦА) продукта или бренда, участвовавших в исследовании, или количество заполненных анкет, которые были учтены при подсчете результатов.
Термин «выборка» говорит о том, что из всей совокупности участников опроса проводится оценка лишь части ответов.
В зависимости от параметров проекта, которые были указаны изначально, выборка может быть разной. Например, при случайной выборке респонденты выбираются из целевой совокупности случайным образом.
Зачем необходимо рассчитывать
Объем выборки определяют перед запуском количественных исследований в маркетинге (например, контент-анализа), чтобы узнать, какое число представителей ЦА должно поучаствовать в тестировании, и получить достоверные результаты. Если данных о объеме выборки нет, это может стать причиной того, что исследователь получит некорректные результаты.
Для качественных исследований объем выборки не определяют. Также он неактуален, если речь идет о проведении пилотных, т. е. предварительных исследований.
Основные понятия определения
В определении размера выборки участвуют различные параметры:
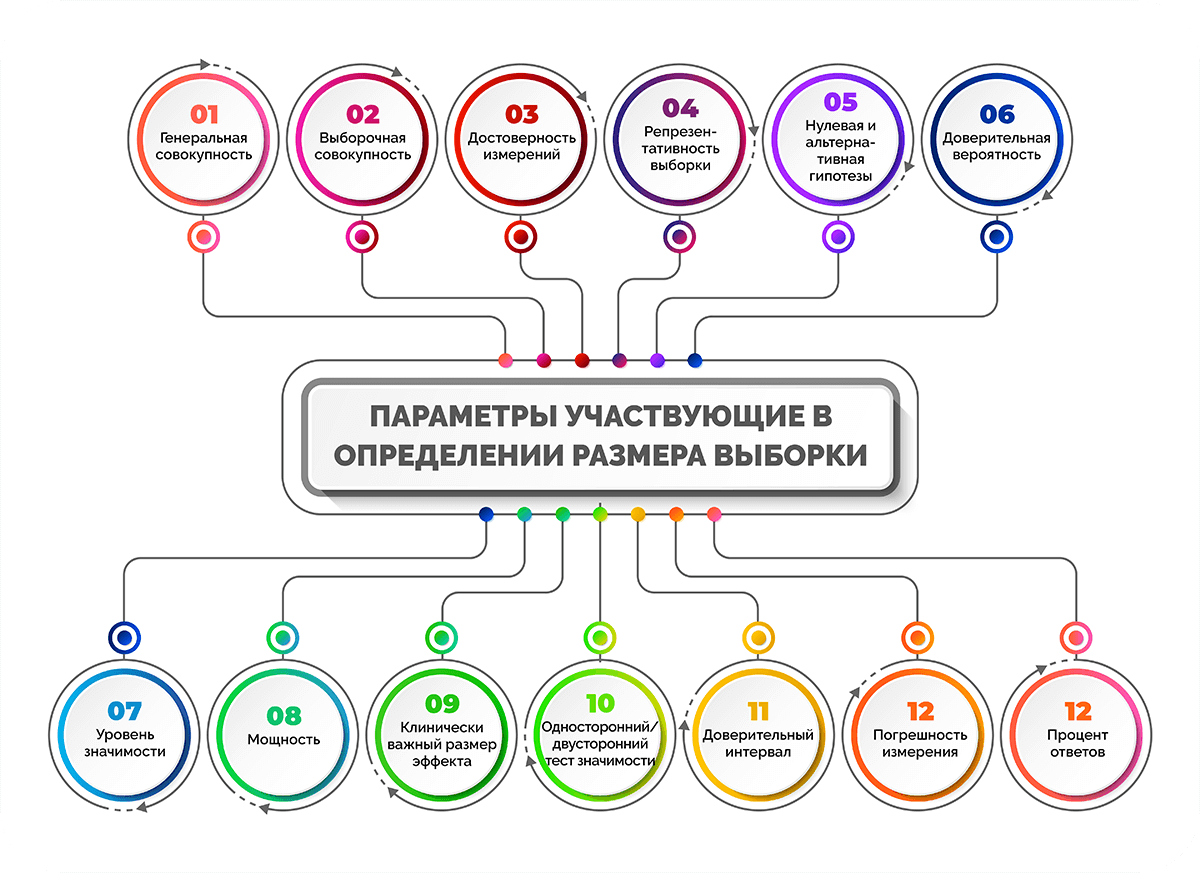
- генеральная совокупность;
- выборочная совокупность;
- достоверность измерений;
- репрезентативность выборки;
- нулевая и альтернативная гипотезы;
- доверительная вероятность;
- уровень значимости;
- мощность;
- клинически важный размер эффекта;
- односторонний / двусторонний тест значимости;
- доверительный интервал;
- погрешность измерения;
- процент ответов.
Разберем, что означают основные из них.
Генеральная совокупность
Генеральной совокупностью называется общее количество объектов наблюдения, которые обладают определенными общими признаками (возраст, пол, оборот, численность, доход и пр.) и о которых будут сделаны заявления после обработки результатов исследования.
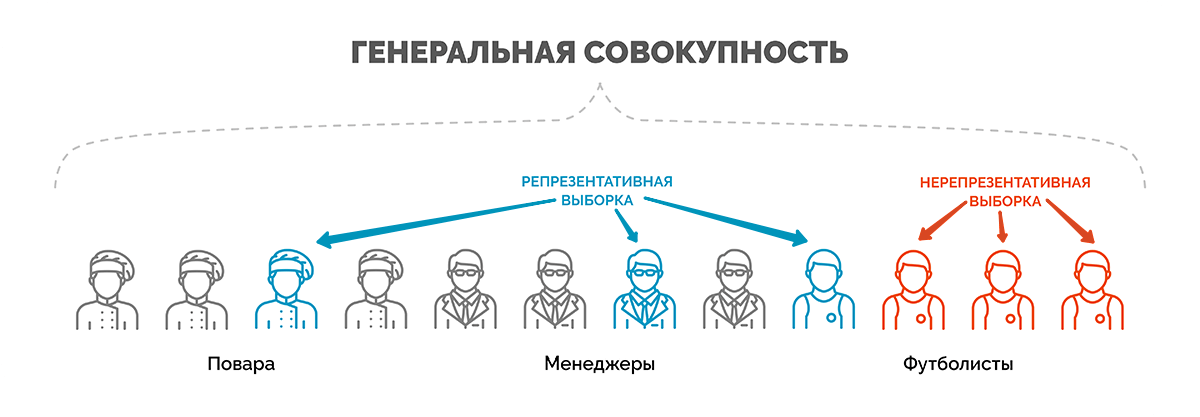
Объектами наблюдения могут быть люди, предприятия, домохозяйства, населенные пункты, отдельные малые социальные группы и т. д.
Если известно, что результаты опроса касаются всех жителей Москвы, то генеральная совокупность будет равна общей численности населения города, т. е. 13 млн человек (по данным 2021 года).
Оценивать свойства генеральный совокупностей, основываясь на выборочных методах, позволяет кривая нормального распределения.
Выборочная совокупность
Выборка или выборочная совокупность – это некоторая часть объектов из числа генеральной совокупности, отобранная для участия в исследовании с целью оценить распределение мнений и сделать итоговое заключение, которое будет распространяться на всю генеральную совокупность.
Характеристики выборочной совокупности должны корректно отражать параметры генеральной совокупности, т. е. обладать свойством репрезентативности. Только в данном случае заключение, сделанное исходя из результатов анализа выборки, будет с одинаковой вероятностью распространяться на представителей всей генеральной совокупности.
Выборка, состоящая из работников московских предприятий, не будет репрезентировать население города трудоспособного возраста и особенно все население столицы, т. к. не включает неработающих людей, женщин в декрете, удаленных сотрудников и т. д. Даже если мы будем увеличивать количество опрошенных работников столичных компаний, выборка все равно не сможет отразить характеристики генеральной совокупности, т. е. всего трудоспособного населения Москвы.
Погрешность измерений
Допустимая погрешность измерений – это процент возможной ошибки или отклонения результатов исследования, т. е. то значение, на которое истинный показатель может откланяться от значения, полученного в результате исследования.
Чем меньше погрешность, тем больше должна быть выборка.
Результаты опроса показали, что 60% опрощенных предпочитают делать покупки в сетевых магазинах. Предел погрешности 5% говорит о том, что в генеральной совокупности доля сторонников сетевых точек продаж может увеличиться или уменьшиться на 5% относительно уровня полученных 60%. Т. е. фактическое значение будет лежать в пределах значений от 55 до 65%.
Достоверность измерений
Уровень достоверности (надежности) измерений – это вероятность того, что полученные в результате исследования истинные результаты выбранного параметра генеральной совокупности находятся в пределах ее доверительного интервала (в примере выше это интервал 55-65%). Простыми словами, это степень уверенности в репрезентативности результатов.
Чем меньше доверительный интервал и выше заданный уровень достоверности, тем больше должна быть выборочная совокупность.
Если взять приведенный выше в статье пример с погрешностью в 5%, вы можете быть уверены в следующем: вероятность того факта, что от 55 до 65% людей предпочитают совершать покупки в сетевых магазинах, составляет не менее 95%.
Репрезентативность выборки
Под репрезентативностью понимают степень соответствия характеристик выборочной совокупности характеристикам генеральной совокупности, которые можно экстраполировать на всю популяцию.
- выборка, состоящая на 100% из автомобилистов Санкт-Петербурга, не репрезентирует всех жителей Санкт-Петербурга;
- выборка, состоящая только из российских фирм B2B с количеством сотрудников до 200 человек, не репрезентирует все компании страны, работающих в этом сегменте.
Исследование должно быть репрезентативным, если стоит задача по результатам количественного исследования сформировать представление о популяции в целом и правильно оценить ее. Если же исследование качественное или люди опрашиваются ради сбора мнений, предложений, идей, в этом случае репрезентативная выборка практически не играет роли.
Что влияет на результаты
Результаты тестирования могут изменяться под влиянием ряда факторов:
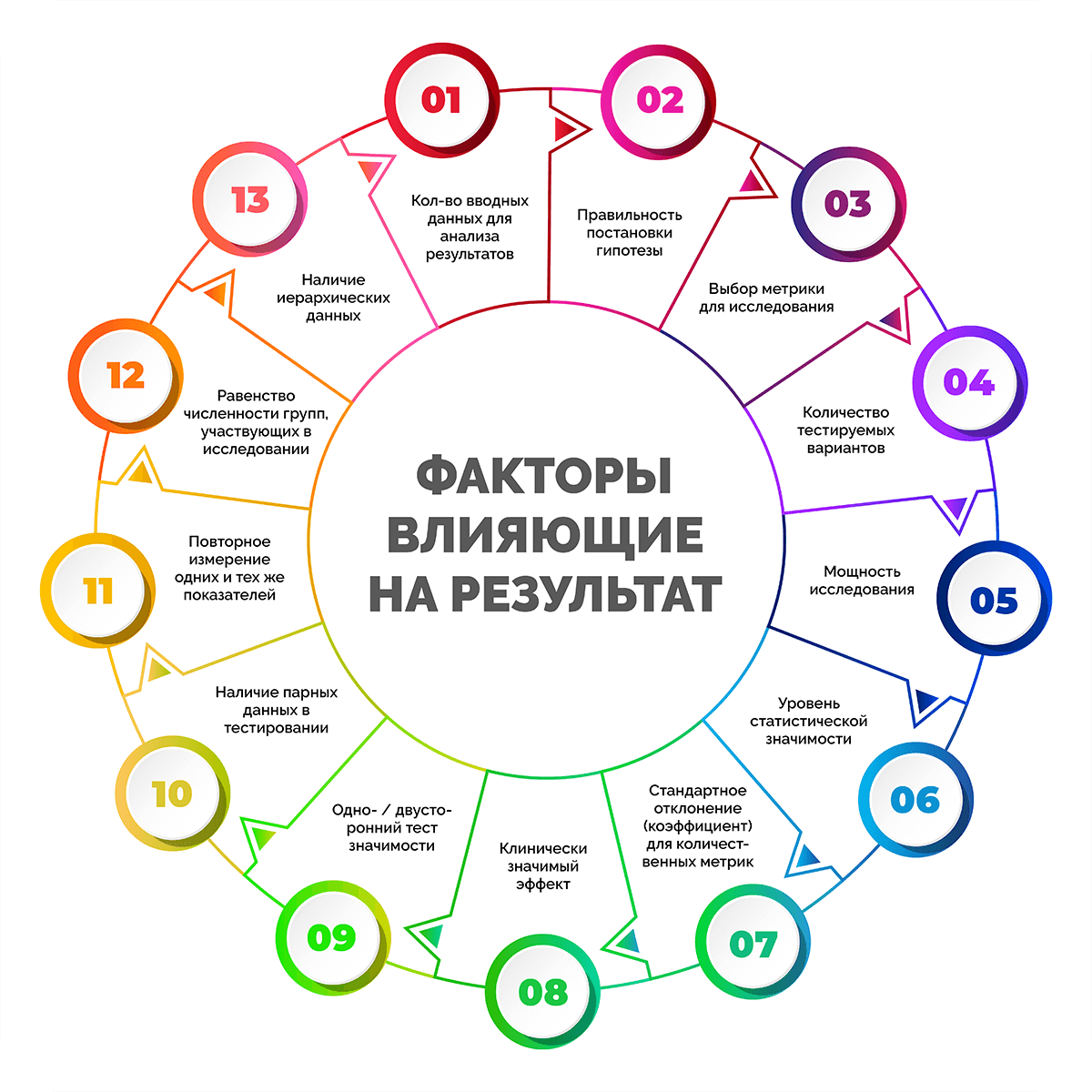
- количество вводных данных для анализа результатов;
- правильность постановки гипотезы;
- выбор той или иной метрики (показателя, переменных) для исследования;
- количество тестируемых вариантов;
- мощность исследования;
- уровень статистической значимости;
- стандартное отклонение (коэффициент) для количественных метрик;
- клинически значимый эффект;
- одно- / двусторонний тест значимости;
- наличие парных данных в тестировании;
- повторное измерение одних и тех же показателей;
- равенство численности групп, участвующих в исследовании;
- наличие иерархических данных.
Также расчет размера выборки может давать разные результаты, если анализ является:
- рандомизированным и контролируемым;
- рандомизированным и кластерным;
- нерандомизированным экспериментом вмешательства;
- исследованием эквивалентности;
- исследованием распространенности;
- обсервационным;
- изучением специфичности и чувствительности теста.
Нерандомизированные тестирования взаимосвязей или различий предполагают задействования в маркетинговых исследованиях выборки гораздо большего размера, чтобы при анализе было не сложно учесть влияние третьих факторов.
Типы выборок
Различают два типа выборок: вероятностные и невероятностные или детерминированные. Каждая группа включает в себя виды. Разберем, какие из них входят в каждый тип.
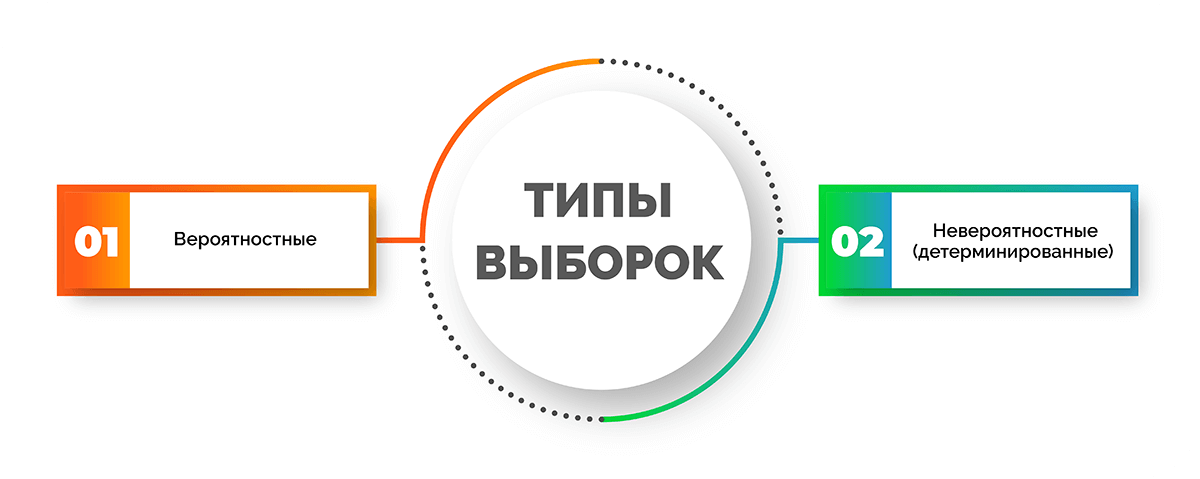
Вероятностные выборки:
- Случайная или простой случайный отбор – предполагает полный список элементов (отбираются при помощи таблицы случайных чисел), равную вероятность доступности всех из них и однородную генеральную совокупность;
- Механическая или систематическая – выступает в качестве разновидности случайной выборки, при этом упорядочивание происходит по тому или иному признаку, причем первый элемент отбирается случайно, затем с шагом n отбирается каждый последующий элемент;
- Стратифицированная или районированная – выборка используется при неоднородной генеральной совокупности, которая разделяется на страты (группы), в каждой из которых выполняется случайный отбор пропорционально их доле в генеральной совокупности;
- Серийная или кластерная, или гнездовая – единицами отбора выступают целые группы (гнезда или кластеры), которые могут попасть в выборку случайным образом, а все объекты внутри них подлежат сплошному исследованию.
Невероятностные (детерминированные) выборки:
- Квотная выборка – формируется несколько групп объектов, в каждой из которых зачастую пропорционально доле в генеральной совокупности задается определенное число объектов, которые нужно исследовать;
- Метод снежного кома – для формирования выборки каждый участник опроса предоставляет контакты своих знакомых; применяется для исследования труднодоступных групп респондентов;
- Стихийная выборка или выборка «первого встречного» – ее состав и размер заранее неизвестен и зависит от активности людей, опрос проводится среди самых доступных респондентов (интернет-опросы, опросы в журналах и газетах, анкеты на самозаполнение и т. д.);
- Выборка типичных случаев – для исследования отбираются отдельные представители генеральной совокупности, которым присуще среднее значение исследуемого признака.
Отбор в детерминированных выборках происходит не случайно, а по субъективным критериям: типичности, доступности, равного представительства каждой стороны и пр.
Расчет объема выборки
Расчет объема выборки – своего рода компромисс между требуемой мощностью исследования и возможностью реализовать его на практике с учетом имеющихся ресурсов и фокус-группы. При этом выбор метода расчета во многом определяется знаниями о параметрах и характеристиках изучаемых параметров.
Определить объем выборки можно двумя способами: по таблицам и с помощью формулы. Разберем эти методы.
По таблицам
Когда никаких данных о предстоящем исследовании нет, а сам эксперимент является инновационным, никто ранее ничего подобного не проводил и не предлагал решения, для определения объема выборки лучше выбрать табличный метод.
Ниже представлены различные методики. Выбор той или иной из них определяется имеющимися исходными данными или пожеланиями исследователя.
Таблица А. Определение объема выборки по методике К. А. Отдельновой
|
Уровень значимости |
Уровень точности |
||
|
Ориентировочное знакомство |
Исследование средней точности |
Исследование высокой точности |
|
|
0,01 |
100 |
225 |
900 |
|
0,05 |
44 |
100 |
400 |
Объем выборки указан в абсолютных значениях.
Таблица Б. Методика определения размера выборки В. И. Паниотто
|
Размер генеральной совокупности |
500 |
1000 |
2000 |
3000 |
4000 |
5000 |
10000 |
100000 |
∞ |
|
Объем выборки |
222 |
286 |
333 |
350 |
360 |
370 |
385 |
398 |
400 |
Данные указаны в единицах.
Таблица В. Методика N. Fox для определения объема выборки
|
Процент допускаемой ошибки |
Объем выборки в единицах |
|
10 |
88 |
|
5 |
350 |
|
3 |
971 |
|
2 |
2188 |
|
1 |
8750 |
Таблица Г. Определение размера согласно способу K. Mitra, S. Das, M. Mandal
|
Величина различий между основной и контрольной группами |
Уровень значимости |
Мощность |
Объем выборки |
|
0,2 |
0,5 |
80 |
586 |
|
0,2 |
0,1 |
80 |
773 |
|
0,2 |
0,5 |
90 |
746 |
|
0,4 |
0,5 |
80 |
146 |
|
0,4 |
0,1 |
80 |
193 |
|
0,4 |
0,5 |
90 |
186 |
|
0,6 |
0,5 |
80 |
65 |
|
0,6 |
0,1 |
80 |
86 |
|
0,6 |
0,5 |
90 |
83 |
По формулам
Объем выборки, достаточный для проведения новых исследований, определяется следующими параметрами:
- изменчивость признака;
- уровень доверия;
- размер эффекта.
Объем выборки всегда зависит от предполагаемой строгости эксперимента и изменчивости исследуемого признака.
Формула для оценки среднего значения размера выборки:
n = (z × σ / H)2, где:
n – размер выборки;
z – доверительный уровень (при р = 0,05 z = 1,96);
σ – стандартное отклонение;
Н – допустимая ошибка в натуральных величинах.
Формула для оценки доли выборки:
Где:
n – размер выборки;
z – доверительный уровень (при р = 0,05 z = 1,96);
p – доля признака (наибольшее значение достигается при р = 0,5);
H – допустимая ошибка в процентах.
Еще одна формула расчета объема выборки (чаще всего калькулятор размера выборки использует именно ее):
Где:
n – размер выборки;
z – нормированное отклонение;
p – вариация для выборки;
q = 1 – р;
е – допустимая ошибка.
Нормированное отклонение (z) определяется по таблице, зная основные значения доверительной вероятности (α).
|
α, % |
60 |
70 |
80 |
85 |
90 |
95 |
97 |
99 |
99,7 |
|
z |
0,84 |
1,03 |
1,29 |
1,44 |
1,65 |
1,96 |
2,18 |
2,58 |
3,0 |
Последняя формула расчета имеет особенности.
- Начинать считать размер выборки следует с проведения качественного анализа генеральной совокупности, чтобы выяснить степень схожести и близости исследуемых единиц совокупности относительно их географических, демографических, социальных и других характеристик.
- Рекомендуется предварительно выполнить пилотное исследование с целью определения приблизительного значения р.
- Если максимальная вариация р = 50%, то и значение q = 50%, что является наиболее худшим вариантом.
Пример расчета размера выборки
Маркетолог проводит исследование с целью определить, нужны ли компании визитки. Для этого промоутеру предстоит опросить потенциальных клиентов и задавать только один вопрос: «Вы пользуетесь визитками?». На что человек должен будет ответить «Да» или «Нет».
В таком случае размер выборки будет рассчитываться так. Принимаем, что уровень доверительности равен 95% (стандартное значение). При этом нормированное отклонение z составит 1,96. После предварительного анализа предположим, что 80% представителей генеральной совокупности дадут положительный ответ, а значит, р = 0,8. Соответственно, q = 1 – 0,8 = 0,2. Вероятность допустимой ошибки примем за 10%, т. е. e = 0,1. Теперь можно выполнить расчет.
Округлив значение, получаем размер выборки n = 62 человека. Соответственно, в опросе с заданными параметрами нужно задействовать 62 человека из числа целевой аудитории компании.
Подходы к определению размера выборки
Выделяют несколько подходов, которые позволяют установить объем выборки для проведения статистического исследования.
- Арбитражный подход. Объем выборки составляет определенный процент от генеральной совокупности. Например, 10% от общего количество потребителей.
- Традиционный подход. Выборка составляется на основе определенных норм, которые были выработаны в процессе проведенных ранее исследований. Подход игнорирует обстоятельства и условия, строгая логика отсутствует.
- Затратный подход. Объем выборки определяется в зависимости от стоимости сбора информации и возможных затрат на материалы для проведения исследования.
- Подход на основе использования доверительных интервалов. Размер выборки в этом случае рассчитывается по формуле, что обеспечивает высокую точность результата:
n = (p × q) / s2, где:
n – размер выборки;
p – вероятность того, что нужное событие наступит, %;
q = 100% – p;
s – стандартное отклонение, которое соответствует доверительному уровню.
Ошибки выборки
Объем выборки при массовом исследовании определяется двумя факторами:
- Точностью полученных данных или статистической погрешностью.
- Размером и количеством подгрупп, на которые будет разбита выборка при проведении анализа.
При любом исследовании, которое предполагает выборочный опрос респондентов из генеральной совокупности, может присутствовать погрешность данных или ошибка выборки. Выделяют два ее типа:
- случайная – обусловлена действием статистических законов, поэтому очень легко рассчитывается по формулам теории вероятности и математической статистики;
- систематическая – является следствием неточностей при проектировании выборки, определить ее степень смещения, направление и размер практически невозможно.
При расчете размера выборки важно так собрать данные, чтобы вероятность систематической ошибки в результате работы была минимальной.
Расчет случайной ошибки выборки зависит от объема последней, а также от степени однородности данных (дисперсии). Принцип такой: чем меньше дисперсия, тем меньше ошибка. Для расчета чаще всего используют онлайн калькуляторы.
Также выделяют:
- Ошибки первого рода – альфа-ошибка, при которой делается вывод о достоверности гипотезы, которая на самом деле неверна. Величина выбирается произвольно в диапазоне от 0 до 1, чаще всего это значение 0,05 или 0,01.
- Ошибки второго рода – бета-ошибка, при которой тот факт, что гипотеза неверна, остается не выявленным. Значение, как правило, устанавливается на уровне 0,2.
Расчет доверительного интервала
Для расчета доверительного интервала применяются достаточно простые формулы, выбор которых зависит от доли выборки в составе генеральной совокупности.
Если выборка значительно меньше генеральной совокупности:
Если выборка и генеральная совокупность сопоставимы:
В обеих формулах:
Δ – предельная ошибка выборки в процентах;
z – нормированное отклонение или z-фактор;
p – доля респондентов с наличием признака, который исследуется;
q – доля респондентов без исследуемого признака;
n – размер выборки;
N – объем генеральной совокупности (сколько всего респондентов).
Доверительный интервал удобно рассчитывать с помощью онлайн-калькулятора, который использует те же формулы, что мы привели выше. Просто введите необходимые переменные, и система рассчитает результат.
Расчет статистической значимости
Определить этот показатель проще всего с помощью онлайн-сервиса. Калькулятор позволяет проверить, существует ли статистически значимая разница между долями признака, которые были получены из независимых выборок.
Рассчитывать статистическую значимость можно только в том случае, если произведения (n × p) и (n × (1 – р)) превышают значение 5. При этом n – объем выборки, р – доля признака.
Часто задаваемые вопросы
Обычно размер выборки и ее статистическая значимость прямо пропорциональны, т. е. с ростом выборки получение случайных результатов сводится к минимуму. Важность статистической значимости зависит от определенной ситуации. Вот некоторые из них.
|
Ситуация |
Важность статистической значимости |
|
Опросы сотрудников |
Важна, т. к. повышает всесторонность выводов по итогам опроса. |
|
Опросы клиентов об уровне их удовлетворенности |
Не имеет значения, т. к. важен каждый ответ независимо от того, положительный он или отрицательный. |
|
Исследование рынка |
Имеет решающее значение, т. к. помогает сделать вывод о целевом рынке. |
|
Опросы об образовании |
Важна, если нужно использовать результаты исследования при внесении изменений в учебном заведении. |
|
Здравоохранение |
Помогает выявлять серьезные проблемы, делать выводы в исследованиях. Если же опрос проводится ради оценки удовлетворенности пациентов, то не имеет значения. |
|
Опросы для развлечения |
Не важна. |
Заданный размер выборки нужен для получения оценок с желаемым уровнем точности, если речь идет об исследовании распространенности в популяции конкретной характеристики.
- Мало просмотров.
- Узкая тематика.
- Низкий бюджет.
- Высокий бюджет.
Чтобы правильно рассчитать размер выборки и провести показательное исследование с учетом выдвинутых требований:
- наберитесь терпения и дождитесь, пока соберется требуемое количество респондентов;
- будьте последовательны и показывайте рекламу только ЦА в определенное время;
- устанавливайте высокий уровень достоверности при расчете выборки.
При определении объема выборки основную роль играет переменная исхода конкретного исследования. Если в расчет добавляются дополнительные важные переменные, то размер выборки должен позволять адекватно проанализировать их.
Это такое количество объектов исследования, которое позволит получить максимально точный и достоверный результат с предельно небольшой погрешностью. При этом его можно репрезентовать на более широкую аудиторию, в т. ч. по отношению к генеральной совокупности.
Заключение
Объем выборки – важный показатель, без которого невозможно провести адекватное исследование и сделать объективные выводы. Он отражает количество представителей целевой аудитории, которое будет принимать непосредственное участие в эксперименте, и требуется во всех случаях, когда стоит задача сделать определенные заключения по результатам опроса.
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Необходимый объем выборки
Необходимый объем выборки – объем (численность) выборочной совокупности, который с определенной вероятностью обеспечит заданную точность результатов наблюдения (при проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки).
Онлайн калькулятор необходимого объема выборки рассчитывает сколько респондентов надо опросить с приемлемой точностью, чтобы их мнение можно было экстраполировать на всю генеральную совокупность.
Поделиться страницей в социальных сетях:
Калькулятор размера выборки
сделано с ❤️
Оглавление
Как определяется размер выборки?
Количество ответов, которые вы получаете в ходе опроса, называется размером выборки. Поскольку только небольшой процент целевой аудитории интересуется вашим мнением и поведением, это называется «выборкой». Один из способов выборки — использовать «случайные выборки», когда респонденты выбираются случайным образом из всего населения.
Давайте взглянем на следующие темы с этим определением.
Понимание размеров выборки
Это ключевые термины, которые помогут вам рассчитать размер выборки.
Численность населения — это общее количество людей, проживающих в популяции, которую вы хотите изучить. Если вы возьмете случайную выборку из населения США, ваше население составит примерно 317 миллионов человек. Размер населения также определяется количеством сотрудников в вашей компании, если вы проводите опрос.
Предел погрешности: это процент, который показывает, насколько вероятно, что результаты вашего опроса будут точно отражать мнение всего населения. Чем ниже погрешность, тем ближе вы будете к получению точного ответа на определенном уровне достоверности.
Уровень достоверности выборки (или достоверность): это процент вашей уверенности в том, что население выберет ответ в заданном диапазоне. Например, уровень достоверности 95% означает, что вы можете быть уверены на 95%, что результаты находятся между числами xy.
Важно ли иметь статистически значимый размер выборки?
Эмпирическое правило заключается в том, что чем больше размер вашей выборки, с точки зрения статистики, тем выше значимость ваших результатов. Это означает, что вероятность совпадения меньше.
Вы можете задаться вопросом, важен ли статистически значимый размер выборки. Это индивидуальная ситуация. Даже если у вас нет достаточно большой выборки, чтобы представить все население, выборка опроса все равно может предоставить ценную информацию. Отзывы клиентов можно использовать независимо от того, имеете ли вы статистически значимый размер выборки. Вы можете получить ценную информацию от клиентов, прислушиваясь к их мнению.
Тем не менее, социологи должны быть осторожны, чтобы выбрать правильный размер выборки для представления населения.
Автор статьи
Parmis Kazemi
Пармис — создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.
Калькулятор Размера Выборки русский
Опубликовано: Tue May 31 2022
В категории Математические калькуляторы
Добавьте Калькулятор Размера Выборки на свой сайт










