Найти массу, плотность или объем онлайн
На данной странице калькулятор поможет найти плотность, массу или объем вещества онлайн. Для расчета введите значения в калькулятор.
Объем, масса и плотность
Найти
Масса:
Объем:
Плотность:
Ответы:
Формула для нахождения массы тела через плотность и объем:
m — масса; V — объем; p — плотность.
Формула для нахождения объема тела через плотность и массу:
m — масса; V — объем; p — плотность.
Формула для нахождения плотности тела через объем и массу:
m — масса; V — объем; p — плотность.
Калькулятор
Содержание:
- Введение
- 1 Расчет объема гидростатическим методом
- 1.1 Погрешность измерения
- 1.2 Геометрические особенности
- 1.3 Плотность продукта
- 2 Методы измерения плотности
- 3 Измерение объема с корректировкой по плотности
- Заключение
Введение
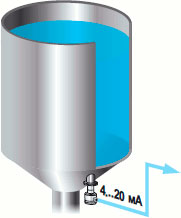
Практически на любых предприятиях, производящих жидкие пищевые продукты (молоко, пиво, соки, квас и другие), для хранения или обработки сырья, жидких компонентов или готового продукта используются различные емкости. В процессе автоматизации производства и мониторинга зачастую требуется непрерывный контроль уровня жидкого продукта в этих емкостях. Существует несколько различных методов измерения уровня, однако в пищевой промышленности наибольшее распространение получил гидростатический метод измерения. Для его реализации используются специализированные датчики давления в санитарном исполнении.
При этом, по измеренному уровню продукта можно производить вычисление его объема, основываясь на геометрической форме емкости и плотности самого продукта. Например, на молочном заводе контроль объема требуется для учета всего поступающего на предприятие молока (в приемных молочных емкостях) или для сличения с показаниями объемных расходомеров в процессе транспортировки продукта между технологическими цехами. Однако измерение объема может стать нетривиальной задачей, если емкость имеет сложную форму, либо если плотность продукта изменяется.
В данной статье будет рассмотрен метод измерения объема продукта для емкостей любой формы, с автоматической корректировкой по плотности.
1 Расчет объема гидростатическим методом
Для реализации гидростатического метода измерения применяются датчики давления, которые устанавливаются в нижнюю часть емкости (см. рисунок 1) и измеряют гидростатическое давление столба жидкости.
Далее, по измеренному давлению рассчитывается текущий уровень продукта:
h
=
p
ρ
⋅
g
(
1
)
h= {p} over { %rho cdot g } ~( 1 )
где:
p – измеренное датчиком гидростатическое давление, Па;
ρ — плотность жидкости, кг/м3;
g — ускорение свободного падения, 9,81 м/с2.
И в дальнейшем, уже по рассчитанному уровню можно вычислить объем продукта в емкости. Например, для вертикальной цилиндрической емкости:
V
=
S
⋅
h
(
2
)
V= S cdot h ~( 2 )
где:
S – площадь основания цилиндра, м2;
h – уровень продукта, м.
Объединив (1) и (2), окончательно получим:
V
=
S
⋅
p
ρ
⋅
g
(
3
)
V= { S cdot p } over { %rho cdot g } ~(3)
Исходя из полученной формулы (3), можно сделать вывод, что расчет объема зависит от трех параметров:
- от соответствия измеряемого давления фактическому уровню жидкости (иными словами — от погрешности измерения);
- от геометрических особенностей емкости (например, для цилиндрической емкости объем зависит только от площади дна);
- от плотности жидкости.
Рассмотрим каждый из параметров подробнее.
1.1 Погрешность измерения
Чем выше точность измерения датчика, тем больше рассчитываемый объем будет соответствовать реальному. Например, если используется датчик с классом точности 0,5 % и пределом измерения 0,4 бар, установленный в цилиндрической емкости с площадью дна 1 м2 и высотой 4 метра, полностью заполненной водой, абсолютная погрешность измерения объема составит:
Δ
V
=
1
⋅
40000
⋅
0,5
100
⋅
9,81
⋅
1000
=
0,02
м
3
=
20
л
(
4
)
%DELTA V= { 1 times 40000 times 0,5 } over { 100 times 9,81 times 1000 } =0,02м^3=20л~(4)
А в случае использования датчика с классом точности 0,1%, погрешность составит уже 4 литра, то есть в 5 раз меньше. Однако из-за особенностей производства жидких пищевых продуктов (молока, пива, вина и прочих) зачастую при измерении появляются дополнительные погрешности.
В пищевой промышленности, из-за непосредственного контакта со средой, применяются датчики давления с разделительной мембраной. Пространство под мембраной в датчике заполнено силиконовым пищевым маслом (утечка этого масла при повреждении мембраны не приводит к порче продукта). Сама мембрана имеет омываемую конструкцию, и таким образом продукт не имеет возможности застаиваться в датчике и со временем портиться. При этом емкости и технологическое оборудование, на которых установлены датчики, подвергаются высокотемпературной безразборной CIP-(Сleaning-in-place) или SIP-(Sterilization-in-place) мойке для устранения остатков продукта.
Из-за нагрева всего датчика, масло под разделительной мембраной расширяется и создает микродеформации конструкции мембраны и сенсора, оказывающих влияние на метрологические характеристики. После окончания мойки и остывания датчика, объем масла возвращается к первоначальной величине, однако метрологические характеристики измерительной системы полностью не восстанавливаются. В результате образуется так называемый «дрейф нуля» — показания датчика смещаются на определенную величину. Результирующая погрешность уровня и объема существенно возрастает, и для её компенсации требуется дополнительно производить «подстройку нуля» датчика после каждого цикла мойки. Эту особенность очень сложно устранить, однако можно свести её к минимуму, снизив объем заполняемого масла.
Эта идея реализована в датчиках, выпускаемых одним из ведущих в мире производителей датчиков давления с разделительной мембраной — компанией Klay Instruments (Нидерланды). В датчиках применена специальная технология Flush Diaphragm Technology (FDT), которая представлена на рисунке 2. Ее отличительные особенности:
- в датчике используется минимальное количество масла среди большинства датчиков, представленных на рынке — всего 1 капля. Это достигается за счет повторения волнистой формы мембраны подложкой, а также за счет малого диаметра (менее 0,5 мм) масляного канала и его малой длины, поскольку измерительный сенсор расположен максимально близко к процессу. Именно по этой причине в датчиках Klay Instruments эффект «дрейфа нуля» сведен к минимуму, как и итоговая погрешность измерения объема;
- мембрана датчика выполнена из химически стойкой нержавеющей стали AISI316L и приварена напрямую к корпусу без дополнительных уплотнений (см. рисунок 3). Таким образом обеспечивается санитарность присоединения к процессу без «мертвых зон», а также высокая химическая стойкость (при необходимости мембрана может покрываться дополнительным защитным слоем). Диаметр мембраны очень маленький, она обладает высокой жесткостью, что значительно повышает перегрузочную способность.
Помимо специализированной технологии изготовления мембраны, датчики обладают еще несколькими особенностями, очень важными для пищевой промышленности:
- в датчиках применяется активная температурная компенсация в диапазоне температур от -20 до 100 °С. При этом датчики выдерживают стерилизацию паром с температурой до 145 °С в течении 45 минут в процессе SIP мойки;
- датчики имеют прочный корпус из нержавеющей стали со степенью защиты IP66, при этом атмосферный канал защищен специальной дышащей мембраной Gore-Tex®, что препятствует проникновению влаги внутрь корпуса из-за повышенной влажности окружающего воздух или при мойке оборудования.
1.2 Геометрические особенности
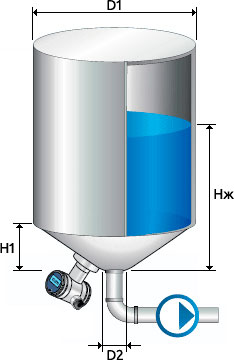
Разумеется, рассмотренный выше пример с идеальной цилиндрической емкостью редко можно встретить на практике. Чаще на пищевых предприятиях применяют вертикальные емкости со сферическим или конусным дном (так называемые цилиндро-конические танки, или ЦКТ), а также горизонтальные цилиндрические емкости. Если емкость достаточно близка по форме к идеальному геометрическому телу, то ее объем можно рассчитать при помощи геометрических формул. Например, для распространенных в пивоварении и виноделии ЦКТ (см. рисунок 4) расчет объема представлен ниже.
V
1
=
1
3
⋅
π
⋅
h
⋅
[
(
D
2
2
+
K
⋅
h
)
2
+
(
D
2
2
+
K
⋅
h
)
⋅
D
2
2
+
D
2
2
4
]
(
5
)
V_1= {1} over {3} cdot %pi cdot h cdot [{( {D_2} over {2} + K cdot h )}^2+{({D_2} over {2}+ K cdot h )} cdot {{D_2} over {2}}+ {D_2^2} over {4} ] ~(5)
(если текущая высота жидкости h < H1), где К — коэффициент конусности,
K
=
D
1
−
D
2
H
1
K= { D_1 — D_2 } over {H_1}
V
1
=
1
12
⋅
π
⋅
H
1
⋅
(
D
2
2
+
D
2
⋅
D
1
+
D
2
)
2
+
π
⋅
D
1
2
4
⋅
(
h
−
H
1
)
(
6
)
V_1= {1} over {12} cdot %pi cdot H_1 cdot {( {D^2_2} + D_2 cdot D_1+D_2 )}^2+ { %pi cdot D_1^2 } over {4} cdot (h-H_1 ) ~(6)
(если текущая высота жидкости h ≥ H1)
Рассмотренные выше расчеты можно производить программно на ПЛК, либо воспользоваться возможностями интеллектуальных датчиков давления. Например, в датчиках давления Klay Instruments серии 2000-SAN есть функция расчета объема по измеренному гидростатическому давлению для трех типов стандартных емкостей: вертикальных емкостей со сферическим дном, ЦКТ или горизонтальных емкостей круглой или овальной формы. После ввода требуемых геометрических размеров и текущей плотности жидкости датчик будет выдавать аналоговый сигнал 4…20 мА, пропорциональный объему в емкости (также возможна передача по HART-протоколу в цифровом виде).
Однако зачастую емкости имеют нестандартную форму или индивидуальные особенности. Например, если горизонтальная емкость имеет наклон (рисунок 5), либо в емкости есть перемешивающие устройства, технологические окна или люки (рисунок 6).
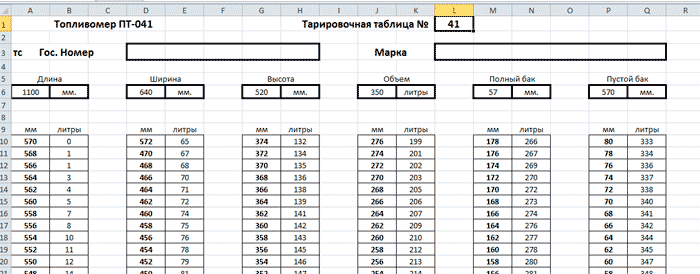
В этом случае необходима дополнительная процедура, называемая проливкой. Емкость последовательно заполняют фиксированными объемами воды (например, по 100 литров) известной плотности, и на каждом шаге наполнения фиксируют уровень по показаниям датчика давления. Тем самым, формируется функциональная зависимость между уровнем и пролитым объемом, индивидуальная для каждой емкости. Результаты проливки записываются в специальные проливочные или тарировочные таблицы — пример подобной таблицы представлен на рисунке 7.
Саму процедуру проливки можно реализовать на программируемом логическом контроллере (путем кусочно-линейной аппроксимации), либо использовать функциональные возможности интеллектуального датчика серии 4000-SAN. Эти датчики позволяют произвести проливку и создать проливочную таблицу в реальном времени, используя встроенное ПО, либо ввести данные из уже имеющейся проливочной таблицы, в удобных для пользователя величинах.
Более подробно процесс пересчета объема по измеренному уровню описан в статье «Современные способы измерения объема жидкости».
1.3 Плотность продукта
Рассмотренные выше примеры расчета объема в емкостях различной формы актуальны при условии, что плотность продукта, находящегося в емкости, известна и строго постоянна. Однако есть ряд технологических процессов, в которых выполнить данное условие невозможно. В таких процессах могут возникать задачи измерения уровня или объема продукта с автоматической корректировкой по плотности, либо задачи измерения непосредственно самой плотности продукта. К таким процессам относятся:
- производство сока из концентратов. На перерабатывающее предприятие поступают различные концентраты, хранение которых осуществляется в специальных емкостях. Для технологического учета сырья требуется контролировать объем в этих емкостях. При этом одни и те же емкости могут заполняться разными концентратами, имеющими различную плотность.
- производство вина. При производстве вина иногда применяются готовые виноматериалы, поступающие на завод в промежуточные емкости хранения. В этом случае необходимо знать уровень или объем в этих емкостях, вне зависимости от плотности поступающего виноматериала.
- приемка и переработка молока. Молоко, которое попадает в приемные или буферные емкости, имеет различную плотность, зависящую от его жирности. В случае, если требуется измерение объема, актуальной задачей становится корректировка по плотности в автоматическом режиме, для повышения точности измерения.
- производство сахара. На различных этапах производства требуется контролировать содержание сахара в сиропе. Это может производиться специализированными датчиками, называемыми бриксометрами (от названия меры измерения массового содержания сахарозы — brix), имеющими очень высокую стоимость. Также используются плотномеры, поскольку по плотности раствора можно косвенно судить о массовом содержании сахара.
- пивоварение. Одним из главных индикаторов готовности пива после брожения является его плотность, которая изменяется на протяжении всего технологического процесса. На небольших заводах плотность определяется путем отбора проб продукта и измерения плотности в лаборатории, однако на крупных заводах для этих целей могут использоваться плотномеры.
Рассмотрим подробнее упомянутые выше методы измерения плотности.
2 Методы измерения плотности
Плотность традиционно определяют одним из двух способов:
- ручной отбор проб продукта с последующим определением плотности при определенной температуре лабораторными исследованиями. В емкости контролируется температура продукта и вводится автоматическая корректировка плотности, поскольку она зависит от температуры. Однако этот метод не учитывает изменения химического состава самого продукта (например, в процессе брожения плотность изменяется — в результате необходимо снимать пробы повторно), а также снижается уровень автоматизации всего производства;
- применение специализированных плотномеров. Их несомненными преимуществами является высокая точность измерения, возможность автоматической корректировки плотности, а также возможность работы в потоке продукта в трубопроводе. Однако при установке в емкости, плотномер контролирует плотность только в одной точке (что является проблемой, если плотность продукта неравномерна по высоте). Также нельзя не отметить очень высокую стоимость подобных плотномеров.
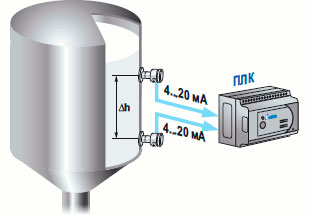
Альтернативой рассмотренным традиционным способам может являться измерение плотности по показаниям двух гидростатических датчиков давления, установленных на определенном расстоянии друг от друга. Принцип измерения показан на рисунке 8. Реализация производится или на ПЛК, или на вторичном приборе.
В случае использования ПЛК, аналоговые сигналы верхнего и нижнего датчиков давления подключаются к его входам, и программно производится вычисление плотности:
ρ
=
P
н
−
P
в
g
⋅
Δ
h
(
7
)
%rho = {{P_н} -{P_в}} over {g%DELTA h} ~(7)
где:
Pн – показания давления нижнего датчика;
Pв –показания давления верхнего датчика;
Δh – строго известное расстояние между датчиками.
Важным условием работоспособности данного метода является выбор величины Δh. С одной стороны, чем больше это расстояние, тем точнее измеряется плотность и тем её измеренное значение будет более усредненным. С другой стороны, верхний датчик должен располагаться ниже верхнего уровня продукта, в противном случае измерение плотности будет невозможно. По этой причине описываемый метод расчета плотности применим, если уровень заполнения емкостей продуктом всегда выше определенной высоты, на которой и устанавливается верхний датчик.
Для получения наилучшей возможной точности измерения, рекомендуется применение датчиков серий 2000-SAN (относительная погрешность 0,1 %) или 4000-SAN (относительная погрешность 0,075 %). Причем датчики обладают возможностью настройки верхнего предела измерения (ВПИ). Поэтому рекомендуется произвести их перенастройку, поскольку погрешность датчиков этих серий нормируется для текущего настроенного диапазона измерений.
Пример №1 расчета погрешности
Максимальный уровень продукта в емкости составляет 4 метра, и в рабочем режиме не опускается ниже 3,5 метров.
В этом случае можно использовать модель 2000-SAN-2-W-H-G0 (диапазон измерения 0…0,12-1,2 бар) в качестве верхнего и нижнего датчиков. Для нижнего датчика настраивается ВПИ 0,4 бар. Верхний датчик следует замонтировать на высоте 3 метра (разница в 0,5 метра выбрана условно — датчику нужен некоторый уровень продукта над местом его монтажа, чтобы производились значимые измерения). Перенастройка датчика не потребуется, поскольку на заводе он настроен на минимальный ВПИ 0,12 бар.
Рассчитаем итоговую абсолютную погрешность измерения плотности для данного примера. Подставим в формулу (5) вместо величин Pн и Pв соответствующие им абсолютные погрешности, предварительно переведя единицы измерения давления в паскали. Абсолютные погрешности определим как произведение относительной погрешности и настроенного ВПИ. Сами абсолютные погрешности будем суммировать, поскольку они могут иметь разный знак. Получим:
ρ
=
Δ
P
н
+
Δ
P
в
g
⋅
Δ
h
=
0,1
%
⋅
(
40000
+
12000
)
9,81
⋅
3
=
1,76
кг
м
3
(
8
)
%rho = {{%DELTA P_н}+{%DELTA P_в}} over {g times %DELTA h}=0,1% {( 40000 + 12000 )} over { 9,81 times 3 } = 1,76{кг} over {м^3} ~(8)
Примечание: для упрощения не учитывалась погрешность преобразования аналогового сигнала или дополнительная погрешность измерения, вызванная отклонением температуры от нормальных условий.
Пример реализации подобной системы измерения плотности на базе датчиков 2000-SAN представлен на рисунке 9 — это машина формовки сыра. Установленные датчики контролируют среднюю плотность сырной массы на разной высоте колонны.
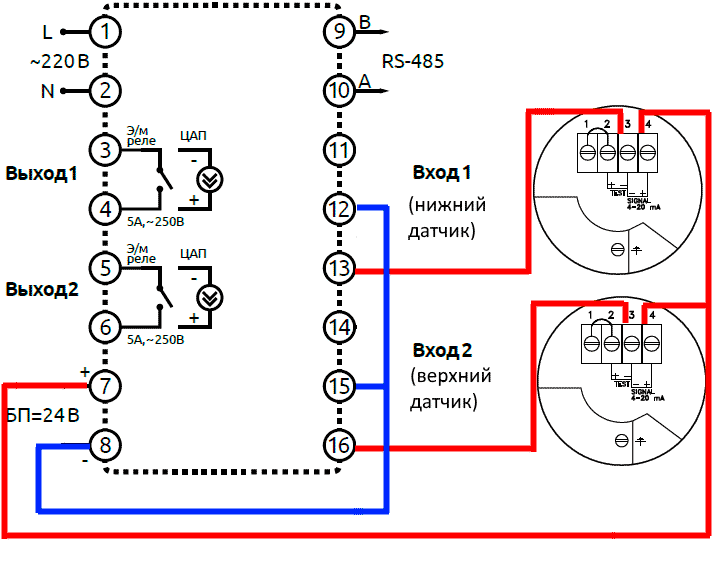
Однако не всегда есть возможность реализации программы на ПЛК. Поэтому расчет и индикацию плотности можно реализовать при помощи вторичного прибора ECV1-М производства ELHART (Россия). Это специализированный ПИД-регулятор, предназначенный для управления КЗР. Однако прибор обладает настолько широким функционалом, что может использоваться в качестве простого измерителя с возможностью дополнительных математических вычислений. А благодаря наличию интерфейса RS-485 (протокол ModBUS RTU), возможно как передавать вычисленные значения на верхний уровень АСУ ТП (в SCADA систему), так и производить конфигурацию прибора удаленно. Схема подключения обоих датчиков давления к прибору представлена на рисунке 10.
Параметры, которые необходимо настроить в приборе для вычисления и отображения, представлены в таблице 1.
| Номер параметра | Название параметра | Значение |
|---|---|---|
| 1-01 | Выбор типа подключаемого датчика (канал 1) | 34 |
| 1-05 | Верхнее значение пользовательского диапазона, (ед. изм.) (канал 1) | 400,0 (гПа) (нижний датчик) |
| 2-01 | Выбор типа подключаемого датчика (канал 2) | 34 |
| 2-05 | Верхнее значение пользовательского диапазона, (ед. изм.) (канал 2) | 120,0 (гПа) (верхний датчик) |
| 3-01 | Выбор входного сигнала ЛУ (канал 1) | 3 |
| 3-02 | Коэффициент k1 ЛУ (канал 1) |
100 9,81 h {100} over { 9,81 times %DELTA h } |
| 3-03 | Коэффициент k2 ЛУ (канал 1) |
− 100 9,81 h -{{100} over { 9,81 cdot %DELTA h }} |
| 4-01 | Выбор входного сигнала ЛУ (канал 2) | 1 (давление нижнего датчика) |
В результате настройки, на верхнем дисплее прибора будет отображаться вычисленное значение плотности (в кг/м3), а на нижнем дисплее — измеренное нижним датчиком значение давления (в гПа).
Необходимо учитывать, что погрешность может возрастать из-за вынужденного округления коэффициентов К1 и К2 (параметры 3-02 и 3-03 соответственно) при вводе пользователем в прибор. По этой причине, рекомендуется выбирать величину Δh при монтаже такой, чтобы вводимые коэффициенты были как можно ближе к целым числам. Например, выбирать расстояние монтажа Δh из ряда 0,51 м (К1=20, К2=-20), 1,02 м (К1=10, К2=-10), 2,04 м (К1=5, К2=-5) и так далее. Это удобно пользователю при вводе параметров, а также дальнейшие математические преобразования в приборе происходят с меньшей погрешностью. При этом надо учитывать, что величина коэффициентов К1 и К2 не может превышать числа 100 — поэтому Δh не может быть меньше 0,1 метра, что также не оправдано и с точки зрения точности расчета плотности.
Пример №2 расчета погрешности
Можно сравнить итоговую погрешность измерения плотности двумя описанными способами: при помощи ПЛК и прибора ECV1. Для подключения аналоговых сигналов к контроллерам зачастую требуются модули ввода — например, модуль Seneca Z-8AI, который имеет основную погрешность измерения 0,1 %. Для ECV1 основная погрешность собственных аналоговых входов составляет 0,25 % (для упрощения примем, что расстояние Δh выбрано таким, что погрешность из-за округления коэффициентов К1 и К2 отсутствует). Для примера возьмем расчет погрешности плотности, приведенный в формуле (8). Этот расчет не учитывал погрешность преобразования аналогового сигнала — соответственно теперь произведем расчет уже с учетом этой погрешности.
В этом случае относительные погрешности измерения давления и преобразования аналоговых сигналов будут просто суммироваться. Результирующая абсолютная погрешность измерения плотности для системы из ПЛК и модуля Z-8AI составит:
Δ
ρ
=
Δ
P
н
+
Δ
P
в
g
⋅
Δ
h
=
(
0,1
%
+
0,1
%
)
⋅
(
40000
+
12000
)
9,81
⋅
3
=
3,53
кг
м
3
(
9
)
%DELTA %rho = {%DELTA P_н + %DELTA P_в } over { g times %DELTA h } =( 0,1% + 0,1% ) {(40000 + 12000 )} over { 9,81 times 3 } =3,53 {кг} over {м^3} ~(9)
В свою очередь, абсолютная погрешность измерения плотности для прибора ECV1 составит:
Δ
ρ
=
Δ
P
н
+
Δ
P
в
g
⋅
Δ
h
=
(
0,1
%
+
0,25
%
)
⋅
(
40000
+
12000
)
9,81
⋅
3
=
6,18
кг
м
3
(
10
)
%DELTA %rho = {%DELTA P_н + %DELTA P_в } over { g times %DELTA h } =( 0,1% + 0,25% ) {(40000 + 12000 )} over { 9,81 times 3 } =6,18 {кг} over {м^3} ~(10)
3 Измерение объема с корректировкой по плотности
В случае, если задача сложнее, и требуется определять объем продукта в емкости с автоматической корректировкой по плотности, то в рассмотренной выше системе дополнительно используются показания нижнего датчика. Он установлен внизу емкости и измеряет давление всего столба жидкости. Поскольку функциональные возможности интеллектуальных датчиков 4000-SAN и 2000-SAN не поддерживают автоматическую корректировку по плотности, то реализация подобной системы возможна только на ПЛК. Значение измеренного давления пересчитывается в уровень по следующей формуле:
h
=
Δ
h
⋅
P
н
P
н
−
P
в
(
11
)
h=%DELTA h {P_н} over { P_н — P_в } ~(11)
И далее это значение уровня, откорректированное с учетом текущей плотности, может напрямую подставляться в геометрическую формулу расчета объема (если емкость имеет стандартную форму), либо использоваться в алгоритме, работающем с проливочной таблицей. Сам алгоритм расчета объема на ПЛК по методу проливки выглядит следующим образом:
- Шаг 1. Первоначальная проливка производится водой с известной плотностью (около 1000 кг/м3). Тем самым на каждом шаге проливки в контроллере измеренное датчиком значение давления перерасчитывается в уровень, исходя из стандратной формулы (1);
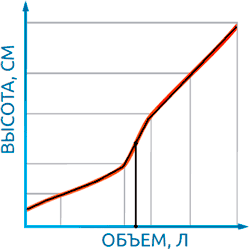
- Шаг 2. По окончании проливки получается функциональная зависимость между уровнем и объемом на основе кусочно-линейной аппроксимации (см. рисунок 11). Чем больше точек проливки, тем выше точность;
- Шаг 3. После окончания процесса проливки система переходит в рабочий режим. В емкость поступает основной продукт, и его уровень рассчитывается по формуле (11) с автоматической корректировкой по плотности (уровень продукта выше места монтажа верхнего датчика). Соответствующий этому скорректированному уровню объем определяется по результатам проливки, проведенной с помощью воды (шаги 1 и 2).
Однако рекомендуется добавить в алгоритм условие для случаев, когда продукт не достиг верхнего датчика (измеряемое им давление слишком мало для корректного измерения). Подобная ситуация происходит при наполнении или опустошении емкости. В обоих случаях расчет уровня производится по стандартной формуле (1). При опустошении, плотность принимается равной последнему рассчитанному значению до того момента, пока показания верхнего датчика не стали слишком малы для измерения. Зачастую, в процессе опустошения плотность не меняется и точность измерений наилучшая.
А при наполнении, значение плотности принимается равным типовому значению для данного продукта или какой-то средней величине (например, плотности воды). И в этом случае, пока уровень продукта не достиг верхнего датчика, измерение объема будет производиться с большей погрешностью, чем с учетом корректировки по плотности.
Пример №3 расчета погрешности
Для расчета погрешности измерения объема с корректировкой по плотности примем для упрощения, что объем однозначно соответствует уровню (согласно таблице проливки). В этом случае достаточно рассчитать только погрешность уровня. Запишем еще раз формулу (1):
h
=
p
ρ
⋅
g
(
12
)
h= p over { %rho g } ~(12)
Очевидно, что погрешность измерения уровня будет зависеть от погрешности измерения давления нижнего датчика и от погрешности расчета плотности на основе показаний верхнего и нижнего датчиков (величину g считаем константой). Исходные данные для расчета возьмем из 2-го примера расчета погрешности.
Результирующая относительная погрешность уровня по формуле (12) будет определяться как сумма относительных погрешностей давления и плотности. Относительная погрешность измерения давления для системы из нижнего датчика давления, ПЛК и модуля ввода Z-8AI уже известна и составляет 0,2 %. Соответственно, для расчета относительной погрешности плотности упрощенно примем, что максимально возможная плотность составит 1050 кг/м3. Подставляя известную абсолютную погрешность, получим:
δ
=
Δ
ρ
max
⋅
100
%
=
3,53
1050
⋅
100
%
=
0,34
%
(
13
)
%delta= {%DELTA} over { %rho _max} cdot 100% = {3,53} over {1050} cdot 100%=0,34% ~( 13) )
Результирующая относительная погрешность уровня составит 0,54 %. В свою очередь абсолютная погрешность при высоте жидкости 4 метра составит 2,16 см.
Чтобы оценить результирующую абсолютную погрешность измерения объема, примем, что емкость имеет цилиндрическую форму с диаметром дна 2 метра. Запишем формулу (2) для расчета объема цилиндра, преобразовав:
Δ
V
=
π
⋅
D
2
4
⋅
Δ
h
(
14
)
%DELTA V= { %pi D^2 } over {4} times %DELTA h ~( 14 )
Подставляя диаметр емкости D и рассчитанную абсолютную погрешность Δh (равную 2,16 см), получим абсолютную погрешность объема 67,8 литров с учетом автоматической корректировки по плотности.
И в свою очередь, рассмотрим алгоритм расчета абсолютной погрешности объема для емкости нестандартной формы. Для текущего рассчитанного уровня (400 ± 2,16) см определяются объемы, соответствующие уровням 397,84 см и 402,16 см, исходя из результатов кусочно-линейной аппроксимации, реализованной в программе контроллера. Абсолютная погрешность измерения в этом случае будет определяться как:
Δ
V
=
V
Δ
h
+
−
V
Δ
h
−
2
(
15
)
%DELTA V= {{{V rsub {%DELTA h+}} — {V rsub {%DELTA h-}}}}}} over {2} ~(15)
Заключение
В данной статье был рассмотрен метод измерения плотности жидких пищевых продуктов на основе показаний двух гидростатических датчиков давления в санитарном исполнении. Данный метод может успешно применяться в таких технологиях, как производство сока, вина, сахара, переработка молока, пивоварение, производство сыра. При этом, на основе этого метода может производиться измерение объема продукта в емкости с корректировкой показаний по усредненной плотности в автоматическом режиме.
Однако для корректного вычисления плотности, в данном методе необходимо осуществлять заполнение емкости продуктом в рабочем режиме до уровня выше места монтажа верхнего датчика. Также результирующая погрешность измерения данным методом будет хуже, чем в случае использования специализированных плотномеров, имеющих абсолютную погрешность измерения 0,2-0,5 кг/м3. Однако для многих технологических процессов столь малая погрешность не требуется, при этом стоимость системы из двух гидростатических датчиков давления существенно ниже, чем специализированных пищевых плотномеров.
Инженер ООО «КИП-Сервис»
Рывкин Е.Е.
Как найти объем жидкости
Жидкость – агрегатное состояние вещества, находясь в котором оно может менять свою форму, не изменяя при этом объем. Если перелить воду из стакана в банку, форма воды примет контур последнего сосуда, но больше или меньше ее не станет. Определить объем жидкости можно несколькими несложными способами.

Инструкция
Физический способ нахождения объема любого тела, находящегося в любом агрегатном состоянии, рассчитать, зная его массу и плотность. То есть, если известна плотность жидкости (для этого достаточно знать ее название и далее, найти по таблице плотностей в физическом справочнике) и ее масса, то просто разделите значение массы на значение плотности. При этом единицы измерения этих величин должны быть такими: если масса дана в килограммах, то плотность должна быть в кубических метрах, если масса измерена в граммах, то плотность — в кубических сантиметрах.Пример1: Пусть нужно найти объем 2 кг воды. Решение: Объем равен отношению массы (2кг) к плотности воды (она равна 1000 кг/(м) в кубе). Итого, объем равен 0,002 кубических метра.
Другой математический способ измерения объема жидкости: по ее форме. Ведь, как правило, она всегда налита в какой-либо сосуд. Тогда нужно знать, как найти объем геометрической формы, которую имеет посудина. Например, если вода налита в аквариум, и он – параллелепипед, то его объем, а значит и объем воды, можно рассчитайте как произведение высоты, длины и ширины аквариума. Так же можно поступить с любой формой. Основное правило нахождение объема: это произведение высоты на площадь основания. Пример 2: До краев аквариума налита вода, каков ее объем, если размеры аквариума: 20 см, 30 см, 40см. Решение. Для нахождения объема воды, надо определить объем посуды: объем равен произведению высоты, длины и ширины сосуда. V = 20см*30см*40см = 240000 кубических сантиметров. Ответ: объем воды равен 240000 кубических сантиметров.
Самый простой способ измерить объем жидкости измерительным сосудом, имеющим шкалу, цену деления, единицу измерения. Примером измерительного сосуда может быть мензурка, шприц, ведро, стакан и т.п. Главное в этом способе – не ошибиться с показаниями измерительного прибора. Пример 3. Стакан наполовину заполнен водой. Нужно найти ее объем. Решение: если в стакан максимально помещается 200 миллилитров воды, то в половине стакана — сто миллилитров.
Источники:
- как найти объем аквариума
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Объем через массу и плотность, формула
Объем тела выражается через массу и плотность следующей формулой:
Объем тела — есть отношение массы тела к плотности вещества из которого состоит тело.
[ V = frac{m}{ρ} ]
Здесь:
V — объем тела (м³),
m — масса тела, (килограмм),
ρ — плотность вещества, (кг/м³).
Вычислить, найти объем твердых тел или жидкостей через массу и плотность по формуле (1)
Выберите вещество ▼
| m (масса, килограмм) |
| ρ (плотность вещества, x103 кг/м³) |
Вычислить
нажмите кнопку для расчета
Вычислить, найти объем газа через массу и плотность по формуле (1)
Выберите вещество ▼
| m (масса газа, килограмм) |
| ρ (плотность газа, кг/м³) |
Вычислить
нажмите кнопку для расчета
Объем через массу и плотность |
стр. 444 |
|---|
Любые физические показатели можно измерить опытным путем и рассчитать производные от них. Например, измерив объем и массу, мы можем найти плотность — производную от них величину, или зная высоту поверхности и вес вещи можем рассчитать энергию.
Эксперименты по определению и изучению основных физических показателей помогут наглядно продемонстрировать и понять суть физических законов, которые действуют в нашем мире.
С помощью практических опытов ученики смогут легче запомнить формулы, разобраться с теоремами, уверенно объяснять физические явления, а также ответить на вопрос, какими экспериментами в физике можно это подтвердить. Например, изучить плавучесть, земное притяжение или доказать взаимосвязь массы и энергии.
Формула зависимости массы от объема и плотности
Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем.
Записывается это так:
И из нее можно вывести еще две формулы.
Формулу для объема тела:
А также формулу для расчета массы:
Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.
Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.
Несколько иначе обстоят дела с газами.
Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем.
Для этого пригодится понятие молярной массы, которую можно найти, сложив массу всех атомов в формуле вещества при помощи данных из периодической таблицы.
Вторая единица, которая нам понадобится – количество вещества в молях. Его можно вычислить по уравнению реакции. Подробнее об этом можно узнать в рамках курса химии.
Другой способ нахождения мольного количества – через объем газа, который нужно поделить на 22,4 литра. Последнее число – это объемная постоянная, которую стоит запомнить.
В итоге, зная две предыдущие величины, мы можем определить массу газа:
где M – это молярная масса, а n – количество вещества.
Результат получится в граммах, поэтому для решения физических задач важно не забыть перевести его в килограммы, поделив на 1000. Числа в этой формуле часто могут оказываться достаточно сложными, поэтому для вычислений может понадобиться калькулятор.
Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора
. Для этого существует формула средней плотности, построенная аналогично формулам других средних величин.
Для двух веществ посчитать ее можно так:
Также из этой формулы можно вывести несколько других в зависимости от того, какие из величин известны по условию задачи.
Проект: «Объём и вытеснение воды»
В ходе эксперимента установим, как объем вытесненной воды зависит от объема погруженной вещи.
Впервые соответствие объема воды, вытесненной объектом, и объема этого объекта установил Архимед, когда опустился в ванную и крикнул «Эврика!». В проекте мы наглядно покажем объем вымещения воды, а затем попробуем спрогнозировать результат.
Что нам понадобится:
- три стакана, два из которых полностью одинаковые;
- вода;
- карандаш;
- монеты;
- камни, по размеру крупнее монет;
- другие предметы для погружения в стакан;
- емкость для контроля объема вылитой воды.
Ход эксперимента:
- Возьмем одинаковые стаканы, которые не полностью, но одинаково наполним водой.
- Отметим уровень воды в обоих стаканах.
- Поочередно бросим сначала монету в один стакан, а потом камень во второй стакан. Что стало с уровнем воды?
- Бросим по 10 монет и камней в каждый стакан. Что произошло с уровнем воды?
- Бросаем монеты и камни до тех пор, пока вода не выливается через край стаканов. Сколько поместилось монет, а сколько камней, пока вода не стала вытекать?
- Возьмем третий стакан, также наполним его водой.
- Попробуем угадать, сколько монет или камней поместиться в стакан, прежде чем вода начнет вытекать? Проверяем на практике.
- Проделаем такой же опыт со стаканами других параметров, а также иными объектами.
- Предположим, сколько монет или камней нужно будет бросить в стакан, чтобы уровень воды стал таким же, как у стакана с другими объектами. Сравним их объем.
Вывод:
Погружая в воду различные объекты, по объему вытесненной жидкости мы смогли установить их объем, тем самым проверив закон Архимеда на практике.
Архимед установил, что объект, опущенный в воду, вытесняет такой объём жидкости, который равен объёму самого объекта. Соответственно, если объектов несколько (10 монет или камней), то объем вытекшей жидкости будет равен совокупному объему всех помещенных в воду объектов.
Таблица плотности некоторых веществ
Плотность многих веществ известна заранее и легко находится по соответствующей таблице.
В работе с ней важно обращать внимание на размерности и не забывать о том, что все данные собраны при нормальных условиях: комнатной температуре в 20 градусов Цельсия, а также определенном давлении, влажности воздуха и так далее.
Плотности других, более редких веществ можно найти онлайн.
Как минимум одно из значений плотности стоит запомнить, так как оно часто появляется в задачах. Это плотность воды – 1000 кг/м3 или 1 г/см3.
Как пользоваться калькулятором плотности:
Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!
Входы:
- Прежде всего, выберите во вкладке то, что вам нужно найти.
- Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
- Наконец, нажмите кнопку “Рассчитать”.
Выходы:
Как только вы заполните все поля, калькулятор покажет:
- Плотность объекта
- Масса объекта
- Объем объекта
- Корень кубический из объема
Заметка:
Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.
Расчет плотности тела и формулы расчета массы и объема тела по плотности
Окружающий мир состоит из множества различных веществ. Так, например, лавочка в парке или баня за городом сделаны из дерева, платформа утюга и сковорода сделаны из металла, покрышка на колесе и ластик на карандаше сделаны из резины. Различные предметы имеют различный вес — любой человек без труда донесёт с рынка сочный спелый арбуз, а вот гирю такого же размера вряд ли удастся оторвать от земли.
Всем известная знаменитая шутка: «Что тяжелее — килограмм ваты или килограмм гвоздей?» очень точно характеризует понятие плотности тела. Почему разные предметы, имея одинаковый объём, различаются по весу? Потому что они состоят из различных веществ и имеют разную плотность. В системе измерений данную величину принято измерять в кг/м³, но также возможно использование и других единиц: кг/л, г/см³.
Видео о плотности тела
Какие факторы влияют на плотность тела?
Плотность одних и тех же тел зависит от давления и температуры. Как правило, при высоком давлении молекулы утрамбованы плотнее, и, соответственно, вещество имеет бо́льшую плотность. Обычно при повышении температуры расстояние между молекулами увеличивается, что приводит к уменьшению плотности. Бывают случаи, когда такая зависимость имеет обратное значение. Так, например, плотность воды меньше плотности льда, несмотря на то что лёд имеет более низкую температуру. Причина такого явления — молекулярная структура льда. Часто вещество, переходя из жидкого в твёрдое состояние, изменяет свою молекулярную структуру таким образом, что расстояние между молекулами сокращается, и, соответственно, плотность становится больше. Когда образуется лёд, расстояние между молекулами и их объём становятся больше, а плотность — меньше. Поэтому в зимнее время, если забыть слить с труб воду, она замёрзнет, в результате чего труба разорвётся.
На плотность воды влияют и примеси, которые в ней находятся. Так, например, у морской воды плотность больше, чем у пресной. Если налить в сосуд солёную воду, а сверху — пресную, то последняя будет «плавать» на поверхности морской воды. Поскольку визуально данное явление увидеть сложно, то для эксперимента можно заполнить резиновый шар пресной водой и поместить его в солёную. Шар будет плавать на её поверхности. Можно сказать, что человеческое тело также представляет собой оболочку, наполненную пресной водой, поскольку, как известно, оно состоит из воды примерно на 50-75%. Поэтому держаться на поверхности солёной воды гораздо легче, чем пресной. И чем больше концентрация соли в воде, тем более она плотная.
Как рассчитать плотность тела?
Расчет плотности тела производится по следующей формуле:
К примеру, вода имеет плотность 1000 кг/м³, а лёд — 900 кг/м³. Поскольку лёд имеет меньшую массу по сравнению с водой, то зимой на водоёме он всегда находится на поверхности воды. В данном случае можно определить, что, если плотность льда равняется 900 кг/м³, значит, ледяной куб со стороной 1 м будет весить 900 кг.
Для того чтобы рассчитать плотность, необходимо знать его объём и массу. Это значит, что вещество можно взвесить, измерить, и на основании полученных данных вычислить плотность по формуле. Поскольку плотность измеряется в кг/л или в г/см³, то иногда приходится пересчитывать одни величины в другие. Делается это очень просто:
- 1 грамм = 0,001 кг, а 1 см³ = 0,000001 м³, и соответственно:
- 1 г/(см)^3 =1000кг/м^3
Иногда необходимо рассчитать плотность газообразного вещества. Для этого используется та же формула для расчета плотности тела, но несколько в другом виде:
где М — молярная масса газа, Vm— молярный объём (равен приблизительно 22,4 л/моль).
Масса всех тел всегда зависит не только от их размеров, но и от веществ, из которых они состоят. Так, тела, имеющие одинаковый объём, но состоящие из различных веществ, будут отличаться друг от друга своими массами. И наоборот, если у тел массы одинаковы, но состоят они из разных веществ, то их объёмы также будут отличаться. Например:
- Куб из железа с рёбрами по 10 см весит 7,8 кг.
- Куб из алюминия такого же размера весит 2,7 кг.
- Ледяной куб с аналогичными размерами весит 0,9 кг
Расчет массы тела и объёма по плотности
Часто возникает необходимость рассчитать массу или объём тела. При этом следует знать, что каждое тело имеет постоянную определённую плотность. К примеру, вода имеет плотность 1000 кг/м³, этиловый спирт — 800 кг/м³.
Поскольку величины постоянные, то для каждого вещества существуют специальные таблицы, которыми пользуются при расчетах.
Исходя из основной формулы определения плотности тела, можно легко рассчитать и его объём или массу:
Для примера можно решить простые задачи:
Необходимо определить массу детали, выполненной из стали, если известно, что её объём составляет 120 см³.
Для того чтобы вычислить массу, требуется знать объём и плотность вещества. По условию задачи объём известен, а плотность необходимо найти по таблице (плотность стали = 7,8 г/см³). Тогда расчет массы тела по его плотности и объёму будет иметь следующий вид:
Требуется рассчитать объём бутылки подсолнечного масла, если известно, что её масса составляет 930 г.
Для того чтобы определить объём, необходимо знать массу и плотность. Масса известна, а плотность нужно найти по таблице (плотность подсолнечного масла = 0.93 г/см³). Тогда:
Расчет массы и объёма тела по плотности выполняется при помощи следующих таблиц:
Плотность воды
- Если плотность вещества больше, чем плотность воды, то оно будет полностью погружаться в воду. И наоборот, предметы, сделанные из материала, плотность которого ниже плотности воды, будут плавать на её поверхности. Примером данного правила является лёд, плотность которого меньше плотности воды. Поэтому кусочек льда, брошенный в воду или другой напиток, сделанный из воды, всплывёт на поверхность.
- В практической жизни эти свойства веществ часто используются человеком. К примеру, конструируя корпуса судов, инженеры используют материалы, плотность которых выше, чем плотность воды. Поскольку таким материалам свойственно тонуть в воде, то в корпусах суден необходимо создавать полости с воздухом — ведь его плотность значительно ниже плотности воды.
- В другом примере, когда требуется, чтобы предмет погружался в воду, необходимо выбирать материалы с плотностью выше, чем плотность воды. К примеру, чтобы лёгкая наживка для рыб во время рыбалки погрузилась в воду на достаточную глубину, рыболов привязывает к леске грузило, сделанное из материала высокой плотности. Обычно в качестве грузила используется свинец.
- Плотность масла, жира, нефти меньше, чем плотность воды, поэтому, если их пролить в воду, они будут плавать на её поверхности. Это свойство очень помогает в ситуациях, когда в морях или океанах при транспортировке нефти она проливается в воду. Благодаря тому, что пролитая нефть не смешивается с водой и плавает на её поверхности, уже было предотвращено множество экологических катастроф, поскольку вода была быстро очищена от вредного для природы вещества.
- В кулинарии свойство жира всплывать на поверхность воды помогает эффективно удалять его излишки из ёмкости с блюдом. В супе, охлаждённом в холодильнике, жир застывает, что позволяет очень легко удалить его с поверхности. Это свойство жира помогает уменьшить количество калорий и холестерина в еде.
- Правило о плотности жидких веществ хорошо известно профессиональным барменам. При приготовлении многослойных коктейлей используются жидкости с разными плотностями. Для этого жидкость, обладающую меньшей плотностью, необходимо аккуратно налить на более плотную жидкость.
- Иногда низкая плотность жира может, наоборот, мешать. Так, например, в процессе приготовления холодных десертов или фруктовых коктейлей жирные продукты очень трудно смешивать с водой, на поверхности которой может образоваться отдельный слой из жира, ухудшив при этом внешний вид и вкус блюда.
Видео о расчете массы и объема тела по плотности
Метод вытеснения жидкости
Как уже известно, для определения плотности тела необходимо знать две величины — объём и массу. Если масса легко определяется с помощью обычных весов, то как посчитать плотность тела, если неизвестен его объём, может показаться довольно сложной задачей.
Но для определения объёма тела также существует очень простой метод, изобретённый Архимедом:
- Необходимо налить воду в мерный стакан и зафиксировать количество налитой воды.
- Затем следует полностью погрузить в эту воду предмет, объём которого требуется определить.
- Из количества воды, которая находилась в сосуде изначально, до погружения в неё тела, необходимо вычесть то количество воды, которое осталось после его погружения.
Конечно, такой метод нельзя использовать для вычисления объёма фотоаппарата или других предметов, которые испортятся от контакта с водой. Следует помнить, что данный метод не будет работать при погружении в воду тел, которые склонны её поглощать (например, плюшевый медвежонок).
В какой сфере жизни Вам пригодились знания о плотности тела? Расскажите об этом в комментариях.
Источник: www.rutvet.ru
Проект: «Масса или вес»
Масса и вес – это синонимы или есть различия? Выполнив настоящий проект, мы опытным путем узнаем отличие веса тела от массы.
Масса – это количество материи, содержащейся в объекте, тогда как вес – это сила притяжения, которая воздействует на объект.
Масса предмета или человека не изменяется при перемещении в пространстве. Что нельзя сказать о весе, который напрямую зависит от силы гравитации. Поэтому на Луне, где сила притяжения меньше чем на Земле, предметы всегда будут весить меньше.
В свою очередь сила гравитации зависит от массы. Чем выше масса предмета, тем выше показатель силы притяжения.
Научный проект способствует приобщению учеников к исследованиям, изучению массы, использованию контрольной точки, установлению зависимых и независимых переменных, сбору данных. Ученики составляют презентации, учатся принимать решения на основании полученных опытным путем данных. Дети смогут почувствовать себя настоящими учеными.
Что нам понадобится:
- канцелярские ножницы;
- степлер;
- маркер;
- весы;
- губка;
- водяной шарик;
- фрукт;
- камень;
- пачка попкорна.
Ход эксперимента:
- Подготовим все материалы, необходимые для проведения опыта. По желанию, для фотоотчета, можно взять фотоаппарат. Сделаем по две копии ниже представленных таблиц.
- Выбираем себе человека в пару, который, не зная ваши результаты, повторит все шаги, а потом оформим наблюдения таблицей.
- Определяем приблизительный вес каждого выбранного нами предмета по собственным ощущениям. Раскладываем все предметы по убыванию веса: от самого тяжелого до самого легкого.
- Пронумеруем расставленные предметы. Самый легкий – номер 1 и т.д.
- Теперь можно приступить к самому эксперименту – взвешиваем каждый предмет на весах по отдельности.
- Сверяем полученные результаты с записанными ранее. На сколько совпал вес? Как вы оценивали вес предмета без измерительного прибора? Возможно, вас смутил размер предмета?
- Все шаги, начиная с 4 пункта, заканчивая 7 пунктом, повторяет партнер.
- Сравниваем данные, записанные в вашей таблице, с результатами партнера. Все совпало? Вами допущены одинаковые ошибки? На каком этапе?
- Проанализируем полученные результаты. К какому выводу вы пришли? Опишите проект с использованием установленных данных, а также списка использованной литературы.
Таблица с упорядоченными по собственным ощущениям предметами: от более тяжелого объекта
| Моя последовательность |
| Последовательность моего партнёра |
Таблица с упорядоченными предметами на основании измерений весами
| Объекты | Настоящий вес |
| пачка попкорна | |
| фрукт | |
| камень | |
| ножницы | |
| фломастер | |
| губка | |
| шарик с водой | |
| степлер | |
| денежная купюра | |
| монета |
Вывод:
Как определяется масса воды в опыте? В ходе проекта мы установили, что массу тела можно измерить с помощью весов. Как вы думаете, на что влияет масса и вес предмета? Как с помощью массы рассчитать вес?
Зная массу можно рассчитать силу притяжения, то есть вес тела. Получается, что вес напрямую зависит от массы тела. Поскольку масса Луны меньше Земли, то вес объектов на этом небесном теле будет меньше. Луна гораздо слабее притягивает к себе предметы, чем Земля. Значение силы земного притяжения трудно переоценить, ведь она помогает нам сохранять равновесие и не падать при ходьбе.
Калькулятор массы
Для различных изделий сложной формы и профиля, с наличием прорезей и отверстий очень трудно рассчитать вес, а это очень важный момент – для транспортировки, для расчета монтажных параметров, для конструкторской документации и других целей. Процесс взвешивания также представляет собой сложности, особенно, когда изделия крупногабаритные – например, трубы, валы, турбины, металлические или деревянные конструкции, изделия из бетона и железобетона и т.д., или же вес небольшой детали, но сложной конфигурации.
Проект: «Работа и энергия»
Выполнив проект, мы узнаем, что такое энергия и работа, как их измерить, как наклонная поверхность, вес объекта влияют на расстояние, до которого скатиться предмет.
Чтобы понять, что такое энергия, в ходе эксперимента будем изменять угол наклона поверхности и вес объекта.
Для того чтобы рассчитать энергию воспользуемся формулой: E = HxW, где E – энергия, H – высота, а W – вес.
Единицы измерения энергии — граммы на сантиметры: в граммах измеряем вес выбранной вещи, сантиметрах — высоту.
В качестве предмета удобно взять банку, вес которой можно регулировать, наполняя водой. Что даст совершенно разные результаты, поскольку при плескании воды в банке часть энергии теряется.
Что нам понадобится:
- гладкая, ровная доска, шириной минимум 30 см, длиной около 120 см;
- две банки (одну большего размера, другую меньшего) цилиндрической формы с крышкой и широким горлышком. Например, банки из-под томатной пасты, майонеза, чипсов и т.д.;
- вода;
- карандаш;
- книги, учебники или другие вещи для подпорки доски;
- фотоаппарат;
- скотч.
Ход эксперимента:
- С использованием книг устанавливаем доску под наклоном так, чтобы расстояние от поднятой стороны до поверхности было 8 см. В этом месте начертим линию на доске.
- Приклеиваем скотч по длине доски, для того чтобы потом быть уверенными, что банка катиться по прямой.
- Десять раз скатываем большую банку по доске, начиная от размеченной линии. После каждого скатывания измеряем расстояние от нижнего края доски до места остановки банки. Подсчитываем средний результат.
- Увеличиваем угол наклона доски, подложив под нее еще одну книгу. Находим участок на доске, расстояние от которого до поверхности 8 см, чертим на этом месте линию. Далее повторяем действия из пункта 3. Изменились ли результаты? Что будет, если скатывать банку не с отмеченной линии, а выше или ниже?
- Теперь повторяем шаги 2-4 с маленькой банкой. Есть ли разница между полученными результатами, если рассчитывать энергию по вышеописанной формуле.
Для сравнения повторим шаги 2-4 для большой банки, наполненной водой. Как объяснить полученные результаты?
Вывод:
Результаты проекта показали, что неважно, на каком расстоянии над поверхностью земли мы начинаем скатывать предмет, независимо от угла наклона банка всегда останавливалась на одном расстоянии от конца доски. Как вы думаете, почему так происходит и, причем здесь энергия?
Такие результаты легко объяснимы, если рассчитать количество энергии, которое необходимо для скатывания банки. Расстояние, на которое прокатиться банка напрямую зависит от энергии, которой она будет обладать, когда докатиться до нижнего края доски.
Проделанный опыт подтверждает, что энергия у банки становится больше, если увеличиваются наклон доски или вес банки за счет наполнения ее водой.
За счет изменения энергии совершается работа всех внутренних и внешних сил, действующих на банку с разной мощностью.
Но, узнать точную массу таких изделий можно гораздо проще на нашем сайте
Мы предлагаем Вашему вниманию универсальный интерактивный калькулятор массы для самостоятельного расчета массы изделий самой разной формы из материалов цилиндрической или листовой формы. Его особенность в том, что он позволяет узнать вес детали или изделия не только из металлопроката и сплавов, но и любых других материалов: дерева и МДФ, пластиков и полимеров, бумаги, картона, резины, бетона, кирпича. Сделать это можно просто внеся габаритные показатели детали с вычетом размеров отверстий и прорезей, а также, величину коэффициента плотности материала, из которого деталь изготовлена. Точные данные можно найти в представленной рядом таблице.
| Диаметр | Длина | Плотность |
| мм | мм | кг/мм 3 |
| Масса общая | ||
| кг |
| Длина | Ширина | Толщина | Плотность |
| мм | мм | мм | кг/мм 3 |
| Масса общая | |||
| кг |
| Длина | Ширина | Количество |
| мм | мм | шт |
Масса цилиндрической детали рассчитывается следующим образом:
• В соответствующие поля калькулятора массы внести размерные показатели: диаметр, длину и справочную плотность материала – калькулятор рассчитает общую массу изделия. • Второй шаг – если на изделии есть выступы, ступени – надо добавить их габариты. • И третий шаг – вычесть размеры отверстий, выемок, прорезей. • Результат – точная расчетная масса цилиндрической детали.
Масса детали из листа рассчитывается следующим образом:
• В соответствующие поля калькулятора массы внести размерные показатели: ширину, длину, толщину и справочную плотность материала – калькулятор рассчитает общую массу изделия. • Второй шаг – если на изделии есть выступы – надо добавить их габариты. • И третий шаг – вычесть размеры прямоугольных или круглых отверстий. • Результат – точная расчетная масса детали из листа.
Наш калькулятор массы изделий будет полезен как конструктору, так и для заказчиков, ведь он позволяет очень быстро и почти со 100%-точностью получить необходимые данные относительно веса изделия без сложных математических расчетов и процедуры взвешивания.
Обратите внимание, что по умолчанию в калькуляторе стоит масса марки стали 40 ГОСТ 1050-88.
Источник: azmen.a-idea.ru