Содержание:
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
|
Рис. 6.1. |
Рис. 6.2. |
Рис. 6.3 |
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
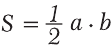
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R2, (6.4) .
Значение числа 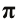
Вычисление объема простых фигур
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
|
Рис. 6.4. |
Рис. 6.5. |
|
V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a3 (6.6)
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR2 · h (6.7)
Объем шара (рис. 6.6)
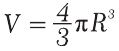
Единицы измерения объема
Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.
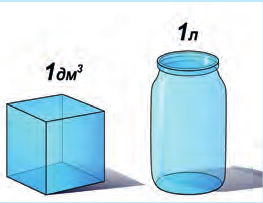
Куб с ребром 1 м имеет объем 1 м3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см3. Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).
Рис. 6.7. Один литр – это 1дм3
Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра
Таблица 6.1
| 1 м3 = 1 000 л | 1 м3 = 1 000 000 см3 |
| 1 л = 1 дм3 | 1 л = 1000 см3 |
| 1 дм3 = 1 000 см3 | 1 л = 1 000 мл |
| 1 см3 = 1 мл | 1 мл = 0,001 л |
- Заказать решение задач по физике
Измерение объема тел неправильной формы
Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.
Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см3)
История:
 |
Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!». |
Итоги:
- Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
- Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
- Объем тел произвольной формы определяют с помощью мензурки
- Площадь круга определяют по формуле S = π · R2.
- Объем шара равен
.
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Что изучает механика в физике
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
- Точность измерений и погрешности
Как найти объем в физике
Объем численно характеризует некоторую область пространства с заданными границами. В нескольких разделах математики его вычисляют по форме границ и размерам либо по площади сечения и координатам. Когда же говорят о физической формуле расчета объема, обычно имеют в виду расчеты по другим параметрам тела — плотности и массе.

Инструкция
Узнайте плотность (ρ) материала, составляющего физическое тело, объем которого нужно рассчитать. Плотность — одна из двух характеристик объекта, задействованных в формуле вычисления объема. Если речь идет о реальных объектах, в расчетах используется средняя плотность, так как абсолютно однородное физическое тело в реальных условиях представить трудно. В нем обязательно будут неравномерно распределенные хотя бы микроскопические пустоты или вкрапления посторонних материалов. Учитывайте при определении этого параметра и температуру — чем она выше, тем меньше плотность вещества, так как при нагревании увеличивается расстояние между его молекулами.
Второй параметр, который нужен для вычисления объема — масса (m) рассматриваемого тела. Эта величина определятся, как правило, по результатам взаимодействия объекта с другими объектами или создаваемыми ими гравитационными полями. Чаще всего приходится иметь дело с массой, выраженной через взаимодействие с силой притяжения Земли — весом тела. Способы определения этой величины для относительно небольших объектов просты — их нужно просто взвесить.
Для вычисления объема (V) тела разделите определенный на втором шаге параметр — массу — на параметр, полученный на первом шаге — плотность: V=m/ρ.
В практических расчетах для вычислений можно использовать, например, калькулятор объема. Он удобен тем, что не требует искать где-то еще плотность нужного материала и вводить его в вычислитель — в форме есть выпадающий список с перечнем наиболее часто используемых в расчетах материалов. Выбрав в нем нужную строку, введите в поле «Масса» вес, а в поле «Точность вычисления» задайте количество знаков после запятой, которые должны присутствовать в результате вычислений. Объем в литрах и кубометрах вы найдете в помещенной ниже таблице. Там же на всякий случай будут приведены радиус сферы и сторона куба, который должен соответствовать такой объем выбранного вещества.
Источники:
- Калькулятор объема
- объем формула физика
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример — объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a — длина, b — ширина, c — высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще — достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³. Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед — фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула. Galina7v7 7 лет назад Если ваш вопрос трактовать так: «как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах. Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона — 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3 Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно — длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических. moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать. vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы — это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3. EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |

{V= dfrac{4}{3} pi R^3}
На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.
Шар — это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.
Содержание:
- калькулятор объема шара
- формула объема шара через радиус
- формула объема шара через диаметр
- формула объема шара через длину окружности
- формула объема шара через площадь поверхности
- примеры задач
Формула объема шара через радиус
{V = dfrac{4}{3} pi R^3}
R — радиус шара
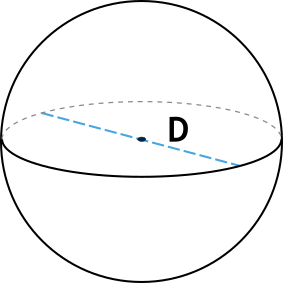
Формула объема шара через диаметр
{V = dfrac{1}{6} pi D^3}
D — диаметр шара
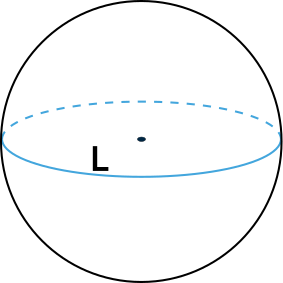
Формула объема шара через длину окружности
Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}
{V = dfrac{L^3}{6 pi^2}}
L — длина окружности
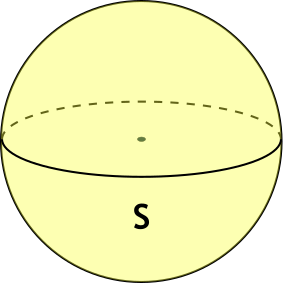
Формула объема шара через площадь поверхности
{V = sqrt{ dfrac{S^3}{36 pi}}}
S — площадь поверхности
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объем шара радиус которого равен 12см.
Решение
Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.
V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3
Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3
Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .
Задача 2
Найдите объем шара диаметр которого равен 12см.
Решение
В этой задаче воспользуемся формулой шара через диаметр.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3
Ответ: 288 pi : см^3 approx 904.77868 : см^3
И снова в проверке ответа нам поможет калькулятор .
Задача 3
Найдите объем шара диаметр которого равен 6см.
Решение
Эта задача аналогична задаче 2.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3
Ответ: 36 pi : см^3 approx 113.09734 : см^3
И снова в проверке ответа нам поможет калькулятор .
Долго жмите на любое свободное место на рабочем столе. Внизу экрана появится несколько иконок, среди которых будут «Виджеты». Нажмите туда, пролистайте варианты снизу, найдите виджеты «Google», ещё раз нажмите на них и выберите поисковую строку.
Как найти объем через массу и толщину?
Смотря что известно о теле, объем которого вы хотите вычислить.
- Зная массу и плотность V = m/ρ, где m — масса, а ρ — плотность
- Для геометрических фигур, например куб V = a^3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту
Как найти объем с помощью толщины?
Объем = Площадь х Толщина.
Как найти объем по площади и высоте?
Математически корректный ответ — взять интеграл по площади комнаты (от 0 до 2,5 метров) , наиболее популярный — умножить площадь комнаты на её высоту. Площадь умножить на высоту. 2,5 х 20 =50 куб. м.
Как найти массу зная плотность и толщину?
То есть воспользуйтесь формулой: m = V / ρ, где:V – объем, ρ – плотность, V – объем. Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения (СИ).
Как выразить массу через площадь?
Массу ( m ) делим на ( p ) плотность. Получаем ( v )объём, ( v ) объем делим на ( h ) высоту , получаем ( S ) площадь.
Как найти объем по длине ширине и высоте?
Как уже упоминалось, формула расчета объема выглядит следующим образом: V = Длина x Ширина x Высота; поэтому для получения объема необходимо просто перемножить все три стороны.
Как найти объем в физике Зная длину ширину и высоту?
Формулой это можно выразить так: V = a*b*c, где a, b и с — это параметры. Для большей наглядности можно рассмотреть пример: Имеется прямоугольный параллелепипед, площадь основания которого равна 42 см², а его высота составляет 15 см, требуется найти объем исходной фигуры.
Какая формула объема куба?
Куб – это геометрическая фигура, которая представляет собой правильный многогранник, где каждая его грань является квадратом. Объем куба можно вычислить, зная только значение длины его ребра. Так как все его ребра между собой равны. Говоря проще объем куба приравнивается кубу длины его ребра.
Как вычислить массу зная площадь и плотность?
Нужна плотность вещества. Плотность умноженная на объем (площадь умноженная на высоту) и даст массу.
Как найти массу тела в физике?
Чтобы найти массу тела нежно его плотность умножить на объем. Чтобы найти объем тела, нужно его массу разделить на плотность.

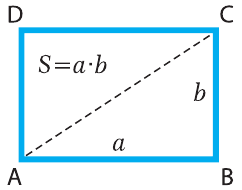
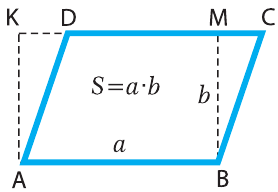
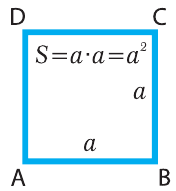
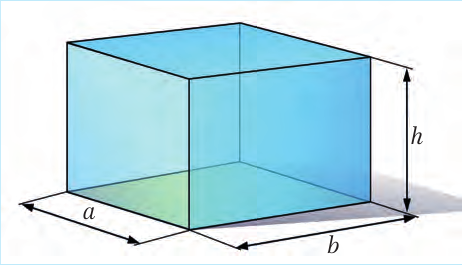
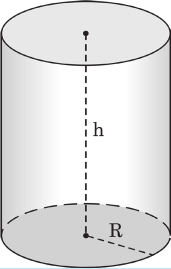
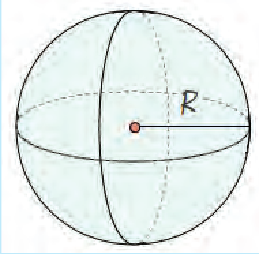 Рис. 6.6.
Рис. 6.6.