Смещенный объем
Смещенный объем – прибавленный или
удаленный в процессе деформации объем
в направлении одной из осей. Если
рассматривать деформацию по высоте,
смещенный объем – произведение начальной
площади поперечного сечения на абсолютное
обжатие.
Для более точных расчетов необходимо
интегрировать по всему
диапазону изменений высоты:
— истинный смещенный объем
Vdh
+ Vdb
+ VdL
= V
(ln
+ ln
+ ln
)
= 0, т.е. сумма истинных смещенных
объемов по трем главным осям равна нулю.
Если по некоторой оси происходит
уменьшение размеров тела, то истинный
смещенный объем меньше нуля, если
увеличение – больше нуля. Смещенный
объем может быть равен, больше или меньше
реального объема тела. Поскольку по
высоте происходит уменьшение размера,
т.е. h1<h0, то
будет
отрицательным. Смещенный объем по
величине равен истинному объему тела,
если
,
т.е.
,
или если
,
т.е.
.
Таким образом, истинный смещенный объем
будет больше объема тела, когда h<0.368
или
>2.718
(т.е.
>0.632
или
<1.718).
Общий случай деформации
В
общем случае деформация нелинейная, а
значит, кроме растяжения или сжатия в
металле имеется и угловая деформация,
т.е. кручение. А значит, в общем виде
деформированное состояние в точке
определяется не только линейными
деформациями, но и деформациями сдвига.
Рассмотрим деформацию элемента
прямоугольной формы, расположенного в
окрестностях произвольной точки (см.
рисунок). Растяжение элемента вдоль
трех осей определяется тремя линейными
деформациями
:
где u – проекция
перемещения точки на ось x,
v – на ось y, w – на ось z.
Изгиб элемента определяется шестью
деформациями сдвига
:
Относительная деформация сдвига
определяется углом между направлениями
ребер в исходном состоянии и после
деформации (при линейной деформации
углы и деформации сдвига равны нулю),
т.е.
.
Таким образом,
напряженное состояние в точке определяется
тензором деформаций:

В
каждой точке тела существуют оси
деформации, которые называют главными
осями деформации. Эти оси обладают
тем свойством, что волокна в теле, им
перпендикулярные, испытывают только
линейные деформации (укорачиваются или
удлиняются), но не поворачиваются, т.е.
сдвиги в главных осях деформации равны
нулю. Деформации вдоль главных осей
называются главными деформациями и
обозначаются
.
Тензор деформаций в главных осях имеет
вид:

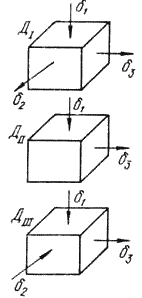
Существуют 3 схемы главных деформаций:
две объемные (растяжение-растяжение-сжатие
и растяжение-сжатие-сжатие) и одна
плоская (растяжение-сжатие, по третьей
оси деформации нет). Из закона постоянства
объема следует, что все главные деформации
не могу быть одного знака, т.е. растяжение
или сжатие не может быть по всем осям
осям одновременно.
Скорость деформации
Скорость деформации – изменение
степени деформации в единицу времени.
Совокупность всех скоростей деформации
описывается тензором скоростей
деформации:
,
где
Из формул
видно, что размерность скорости деформации
– c-1.
Скорость
деформирования – скорость хода
инструмента. Единица измерения – м/с.
Скорость деформации зависит от скорости
деформирования и размера тела в
направлении деформации.
,
где Vh
– скорость деформирования.
Даже если
скорость движения инструмента постоянна,
скорость деформации изменяется из-за
изменения размеров заготовки. Средняя
скорость деформации за время обработки:
.
Скорости
деформации, соответствующие главным
направлениям, называются главными
скоростями деформации.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Теоретическое объемное смещение с учетом площади поршня и длины хода Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Количество поршней: 5 —> Конверсия не требуется
Площадь поршня: 0.02 Квадратный метр —> 0.02 Квадратный метр Конверсия не требуется
Длина хода поршневого насоса: 0.2 метр —> 0.2 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.02 Кубический метр на оборот —> Конверсия не требуется
19 Поршневые насосы Калькуляторы
Теоретическое объемное смещение с учетом площади поршня и длины хода формула
Теоретическое объемное смещение = Количество поршней*Площадь поршня*Длина хода поршневого насоса
VD = n*Ap*SL
Каковы применения поршневых насосов?
Поршневые насосы используются в водяной и масляной гидравлике, промышленном технологическом оборудовании, очистке под высоким давлением и перекачивании жидкостей.
Просто щелкните объект решения правой кнопкой мыши и выберите «Вставить — Деформация — Всего». Это позволит рассчитать деформацию и смещение для всех тел в системе. Вы также можете рассчитать отклонения по определенным осям и для определенных тел или элементов.
Как найти узловое смещение в ANSYS Workbench?
Вы должны выбрать инструмент выбора узла и выбрать узлы из созданной структуры сетки.
- Выберите необходимые узлы для именованного выбора.
- Нажмите «Узловое смещение».
- Выберите необходимый именованный выбор для «Узлового смещения».
- Задайте величины узлового смещения.
Что такое поддержка смещения в ANSYS?
Опоры смещения используются для применения вынужденных перемещений и свободных перемещений в соответствующем направлении (X, Y и Z) в соответствии с условиями поддержки. Смещение такое же, как у фиксированной опоры, когда все поступательные движения равны нулю.
Что такое дистанционное смещение в ANSYS Workbench?
С помощью граничного условия Удаленное смещение можно указать управляемое смещение грани или объема с удаленной точкой.
Что такое поддержка только сжатия в Ansys Workbench?
Опора только на сжатие создает контакт без трения с жесткой поверхностью. Это как засунуть булавку в дырку. Нагрузка на подшипник создает силу в узлах, где максимальная сила находится под углом 0 градусов, а нулевая сила находится под углом 90 градусов с каждой стороны, а распределение силы является синусоидальным.
Что такое датчик деформации Ansys?
Ansys Mechanical Workbench поддерживает датчики деформации, которые на твердых телах могут измерять UX, UY, UZ и USUM геометрии или удаленных точек. Они не измеряют вращение. В этой статье показано, как использовать команды APDL для ссылки на существующую удаленную точку и измерения смещения и поворота в этой точке.
Как рассчитать узловое смещение?
Вкратце процедура в классе такова:
- Удалите строки и столбцы, соответствующие степеням свободы с заданным смещением/поворотом (bc задано смещение=0) из матрицы жесткости.
- Удалите строки, соответствующие заданному вектору нагрузки степеней свободы.
- Решите редуцированную систему уравнений, чтобы получить неизвестные перемещения.
Что такое узловое смещение?
Узлы будут иметь узловые (векторные) смещения или степени свободы, которые могут включать перемещения, повороты и, для специальных приложений, производные перемещений более высокого порядка. Когда узлы смещаются, они будут тянуть элементы определенным образом, продиктованным формулировкой элемента.
Грубый. Подобно настройке без трения, эта настройка моделирует совершенно грубый фрикционный контакт, в котором отсутствует скольжение. Он применяется только к областям граней (для 3D-тел) или ребер (для 2D-пластин). По умолчанию автоматическое закрытие гэпов не выполняется.
Как добавить фиксированную поддержку в Ansys?
Чтобы добавить фиксированную поддержку в ANSYS® Mechanical, щелкните грани, вершины или ребра, которым вы хотите назначить фиксированную поддержку, затем нажмите «Применить к разделу геометрии», как показано красной стрелкой выше. Назначается фиксированная поддержка.
Что такое поддержка без трения в Ansys?
Это тип поддержки, используемый для ограниченных степеней свободы в нормальных направлениях. Это опорное или граничное условие используется для предотвращения перемещения или деформации одной или нескольких плоских или изогнутых граней в нормальном направлении.
Как сделать удаленное смещение в Ansys?
Нажмите «Удаленное смещение». Чтобы определить удаленное смещение, щелкните правой кнопкой мыши анализ, как показано выше. Затем наведите курсор на «Вставить» и нажмите «Удаленное смещение», чтобы определить его в ANSYS® Mechanical. Выберите геометрические особенности для «Удаленного смещения».
В чем разница между смещением и удаленным смещением в Ansys?
Лучшие ответы. См. документацию по смещению и удаленному смещению — вкратце смещение применяется к узлам на этом ребре (выходит как команда D в файле ds.dat), при этом удаленное смещение не обязательно должно быть на ребре, оно может быть точкой вне модели.
Что дает дистанционное перемещение?
Дистанционное смещение позволяет передать в систему эффекты известного смещения любого удаленного элемента конструкции, связанного с конструкцией жесткой связью.
Плотность тока проводимости, смещения, насыщения: определение и формулы
В данной статье мы рассмотрим плотность тока и формулы для нахождения различных видов плотности тока: проводимости, смещения, насыщения.
Плотность тока – это векторная физическая величина, характеризующая насколько плотно друг к другу располагаются электрические заряды.
Плотность тока проводимости
Ток проводимости – это упорядоченное движение электрических зарядов, то есть обыкновенный электрический ток, который возникает в проводнике. В большинстве случаев, когда речь заходит о токе, имеют ввиду именно ток проводимости.
В данном случае плотность тока – это векторная характеристика тока равная отношению силы тока I в проводнике к площади S поперечного сечения проводника (перпендикулярному по отношению к направлению тока). Эта величина показывает насколько плотно заряды располагаются на всей площади поперечного сечения проводника. Она обозначается латинской буквой j. Модуль плотности электрического тока пропорционален электрическому заряду, который протекает за определенное время через определенную площадь сечения, расположенную перпендикулярно по отношению к его направлению.
Если рассмотреть идеализированной проводник, в котором электрический ток равномерно распределен по всему сечению проводника, то модуль плотности тока проводимости можно вычислить по следующей формуле:
j – Плотность тока [A/м 2 ]
S – Площадь поперечного сечения проводника [м 2 ]
Исходя из этого мы можем представить силу тока I как поток вектора плотности тока j, проходящий через поперечное сечение проводникаS. То есть для вычисления силы тока, текущей через определенное поперечное сечение нужно проинтегрировать (сложить) произведения плотности тока в каждой точке проводника jn на площадь поверхности этой точки dS:
jn — составляющая вектора плотности тока в направлении течения тока (по оси OX) [A/м 2 ]
dS — элемент поверхности площади [м 2 ]
Исходя из предположения, что все заряженные частицы двигаются с одинаковым вектором скорости v, имеют одинаковые по величине заряды e и их концентрация n в каждой точке одинаковая, получаем, что плотность тока проводимости j равна:
j – плотность тока [А/м 2 ]
n – концентрация зарядов [м -3 ]
e – величина заряда [Кл]
v – скорость, с которой движутся частицы [м/с]
Плотность тока смещения
В классической электродинамике существует понятие тока смещения, который пропорционально равен быстроте изменения индукции электрического поля. Он не связан с перемещением каких-либо частиц поэтому, по сути, не является электрическим током. Несмотря на то, что природа этих токов разная, единица измерения плотности у них одинаковая — A/м 2 .
Ток смещения – это поток вектора быстроты изменения электрического поля ∂E/∂t через S — некоторую поверхность. Формула тока смещения выглядит так:
ε0 – электрическая постоянная, равная 8,85·10 -12 Кл 2 /(H·м 2 )
∂E/∂t — скорость изменения электрического поля [Н/(Кл·с)]
ds – площадь поверхности [м 2 ]
Плотность тока смещения определяется по следующей формуле:
ε0 – электрическая постоянная, равная 8,85·10 -12 Кл 2 /(H·м 2 )
∂E/∂t — скорость изменения электрического поля [Н/(Кл·с)]
∂D/∂t — скорость изменения вектора эл. индукции [Кл/м 2 ·с)]
Плотность тока насыщения
В физической электронике используют понятие плотности тока насыщения. Эта величина характеризует эмиссионную способность металла, из которого сделан катод, и зависит от его вида и температуры.
Плотность тока насыщения выражается формулой, которая была выведена на основе квантовой статистики Ричардсоном и Дешманом:
j – плотность тока насыщения[А/м 2 ]
R — среднее значение коэффициента отражения электронов от потенциального барьера
A — термоэлектрическая постоянная со значением 120,4 А/(K 2 ·см 2 )
T— температура [К]
qφ — значение работы выхода из катода электронов [эВ], q – электронный заряд [Кл]
k — постоянная Больцмана, которая равна 1,38·10 -23 Дж/К
Понравилась статья, расскажите о ней друзьям:
Ток смещения
Вы будете перенаправлены на Автор24
Физическое содержание тока смещения
Мы знаем, что постоянный ток в цепи с конденсатором не течет, переменный — протекает. Сила квазистационарного тока во всех элементах цепи, если они соединяются последовательно, одинакова. В конденсаторе, обкладки которого разделяет диэлектрик, ток проводимости, вызванный перемещением электронов, идти не может. Значит, если ток переменный (присутствует переменное электрическое поле), происходит некоторый процесс, который замыкает ток проводимости без переноса заряда между обкладками конденсатора. Этот процесс называют током смещения.
Любое переменное магнитное поле порождает вихревое электрическое поле. Исследуя разные электромагнитные процессы, Максвелл сделал вывод о том, что существует обратное явление: изменение электрического поля вызывает появление вихревого магнитного поля. Это одно из основных утверждений в теории Максвелла.
Так как магнитное поле — обязательный признак любого тока, Максвелл назвал переменное электрическое поле током смещения. Ток смещения следует отличать от тока проводимости, который вызван движением заряженных частиц (электронов и ионов). Токи смещения появляются только в том случае, если электрическое смещение ($overrightarrow$) переменно. Объемная плотность тока смещения определяется как:
Именно вследствие этого физическое содержание предположения Максвелла о токах смещения сводится к утверждению о том, что переменные электрические поля — источники переменных магнитных полей.
Следует заметить, что плотность тока смещения определена производной вектора $overrightarrow$, а не самим вектором.
Готовые работы на аналогичную тему
Ток смещения в диэлектрике
По определению вектора электрической индукции ($overrightarrow$):
где $<varepsilon >_0$ — электрическая постоянная, $overrightarrow$ — вектор напряженность, $overrightarrow
$ — вектор поляризации. Следовательно, ток смещения можно записать как:
где величина $frac<partial overrightarrow
><partial t>$ — плотность тока поляризации. Токи поляризации — токи, которые вызваны движением связанных зарядов, которые принципиально не отличаются от свободных зарядов. Поэтому нет ни чего странного, что токи поляризации порождают магнитное поле. Принципиальная новизна содержится в утверждении, что вторая часть тока смещения ($<varepsilon >_0frac<partial overrightarrow><partial t>$), не связанная с движением зарядов, также порождает магнитное поле. Получается, что в вакууме, любое изменение электрического поля по времени вызывает магнитное поле.
Однако, надо заметить, что сам термин «ток смещения» для диэлектриков имеет какое-то обоснование, так как в них действительно происходит смещение зарядов в атомах и молекулах. Но этот термин применяется и к вакууму, где зарядов нет, значит, нет их смещения.
Полный ток
В том случае, если в проводнике течет переменный ток, то внутри него имеется переменное электрическое поле. Значит, в проводнике существует ток проводимости ($j$) и ток смещения. Магнитное поле проводника определено суммой вышеназванных токов, то есть полным током ($overrightarrow$):
В зависимости от электропроводности вещества, частоты переменного тока, слагаемые в выражении (4), играют разную роль. В веществах с хорошей проводимостью (например, металлах) и при низких частотах переменного тока плотность тока смещения невелика, тогда как ток проводимости существенен. В таком случае, током смещения пренебрегают, в сравнении с током проводимости. В веществах с высоким сопротивлением (изоляторах) и при больших частотах тока ведущую роль играет ток смещения.
Оба слагаемых в выражении (4) могут иметь одинаковые знаки и противоположные. Следовательно, полный ток может быть и больше и меньше тока проводимости, может даже быть равен нулю.
Значит, в общем случае переменных токов магнитное поле определяется полным током. Если контур разомкнут, то на концах проводника обрывается только ток проводимости. В диэлектрике между концами проводника присутствует ток смещения, который замыкает ток проводимости. Получается, что если под электрическим током понимать полный ток, то в природе все токи замкнуты.
Задание: Плоский конденсатор заряжен и отключен от источника заряда. Он медленно разряжается объемными токами проводимости, которые появляются между обкладками, так как присутствует небольшая электрическая проводимость. Чему равна напряжённость магнитного поля внутри конденсатора? Считать, что краевых эффектов в конденсаторе нет.
Решение:
Допустим, что поверхностная плотность заряда на обкладках равна $sigma и-sigma .$ В таком случае, модуль вектора электрического смещения ($D$) для плоского конденсатора равен:
Ток смещения можно найти как:
Подставив вместо $D$ правую часть выражения (1.1), имеем:
В соответствии с законом сохранения заряда, можно записать, что:
Полный ток равен:
Для нашего плоского конденсатора, учитывая полученные выражения (1.3), (1.4), имеем:
Ответ: Магнитное поле в конденсаторе равно нулю.
Задание: Допустим, что неограниченную однородную проводящую среду поместили в металлический шар, имеющий заряд $Q$. В этой среде возникнут электрические токи, которые потекут в радиальных направлениях. Покажите, что данная ситуация требует введения тока смещения при описании возникающих полей.
Решение:
Электрические токи, которые текут от (или к ) шару, возбуждают магнитное поле. Определим направление вектора магнитной индукции этого магнитного поля.
Вектор $overrightarrow$ не имеет радиальной составляющей. Система обдает сферической симметрией. Если бы радиальная составляющая вектора индукции имелась, то она была бы одинаковой для всех точек сферы $S$ (рис.1), концентрической с поверхностью шара, имела направление от центра шара или к его центру. В обоих случаях поток вектора индукции через сферу $S$ был бы не равен нулю, что противоречит уравнению из системы Максвелла:
Значит, вектор индукции магнитного поля должен быть перпендикулярен к радиусу, который проведен из центра шара к рассматриваемой точке. Это также невозможно, так как все направления, перпендикулярные к радиусу, равноправны. Единственная возможность, которая не противоречит симметрии шара, заключается в том, что векторы $overrightarrow и overrightarrow$ всюду равны нулю. Следовательно, равна нулю плотность тока проводимости $overrightarrow, $ что противоречит уравнению:
Для устранения полученного противоречия следует предположить, что магнитные поля порождаются не только токами проводимости. Добавим к току проводимости ток смещения ($I_$), который в нашем случае будет уничтожать возбуждаемое магнитное поле. Его величина определяется из условия:
Ток проводимости, который течет от заряженного шара можно выразить как:
Из выражения (2.3) следует, что:
В соответствии с законом Кулона заряженного проводящего шара, имеем:
[Q=4pi r^2D left(2.6right).]
Найдем производную по времени от заряда, получим:
Плотность тока смещения при этом будет равна:
Полученное выражение совпадает с определением плотности тока смещения.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 02 03 2022
9.2. Ток смещения
Дж.К. Максвелл (рис. 9.2) был первым, кто задался вопросом о модификации четвертого утверждения. Никаких экспериментальных фактов, к этому подводящих, в то время известно не было. Из четвертого утверждения следует, что токи, порождающие вихревое магнитное поле, должны быть замкнутыми, они нигде не могут прерываться. Действительно, на один и тот же контур L можно натянуть множество поверхностей S. Пусть, скажем, мы выберем две из них — S1 и S2. Так как левая часть (9.4) для них одинакова, то будут равны и правые части. Это значит, что весь ток, вошедший через S1, должен выйти через поверхность S2. Так с обычными токами и происходит. Но бывают нестационарные случаи, когда в каких-то точках меняется плотность электрического заряда. Линии тока будут кончаться в этих местах, что противоречит (9.4).
Рис. 9.2. Дж.К. Максвелл (1831–1879) — английский физик и математик
Чтобы проиллюстрировать подобные случаи, рассмотрим уже знакомый процесс разрядки конденсатора. Пусть имеются две пластины с зарядами +q и –q. Пока цепь разомкнута, равные и разноименные заряды создают в пространстве между пластинами постоянное электрическое поле. Ток по проводам не идет, и вокруг цепи нет магнитного поля (рис. 9.3-1).
Рис. 9.3. Токи смещения в конденсаторе: 1 — начальное состояние конденсатора, 2 — изменение поля в процессе разрядки. Производная напряженности электрического поля по времени направлена в ту же сторону, что и вектор плотности тока, и равна ему по величине
При разрядке конденсатора через проводник, соединяющий пластины, потечет ток от Р к N (рис. 9.3-2). Уменьшение заряда на пластине на величину dq означает, что это же количество электричества протечет по проводу, подсоединенному к пластине (закон сохранения заряда).
Рис. 9.4. Обкладки конденсатора отмечены синим. Поверхность S2 состоит из плоской поверхности, параллельной обкладкам конденсатора и боковой цилиндрической поверхности
которое мы хотели бы проверить на непротиворечивость.
Интегрируем его по поверхности S1 (рис. 9.4). Получаем
Из этого равенства обычно получают величину магнитного поля B для бесконечно длинного проводника. Напомним, что поверхность, по которой ведется интегрирование, может иметь любую форму, при условии, что она опирается на контур G. Воспользуемся этим и интегрируем это же уравнение (9.8) по поверхности S2. Получаем
Здесь краевыми эффектами пренебреженно, Интеграл по боковой (цилиндрической) поверхности равен нулю, если выбрать радиус цилиндра достаточно большим. Выражения (9.9) и (9.10) противоречат друг другу. Значит, уравнение (9.8) неверно и его надо изменить. Простейший путь — добавить в правую часть уравнения (9.8) неизвестный вектор, который мы обозначим как
Найдем неизвестный вектор 
— вместе с (9.8a) получили уравнение Максвелла
Максвелл назвал величину
плотностью тока смещения:
Так как численные значения плотности тока смещения jсм и плотности тока проводимости j равны, то, следовательно, линии плотности тока проводимости внутри проводника непрерывно переходят в линии плотности тока смещения между пластинами (обкладками конденсатора).
Если ввести понятие полного тока, который включает в себя сумму тока проводимости и тока смещения, то для его плотности имеем
На примере конденсатора мы обнаружили, что полный ток будет замкнут: его линии продолжаются, нигде не прерываясь (даже в пространстве между пластинами конденсатора). По этому своему свойству именно полный ток должен стоять в правой части уравнения (рис. 9.5). В этом и состояла идея Максвелла.
Рис. 9.5. Лампочка, подключенная к сети переменного тока через конденсатор,
постоянно горит, так как ток проводимости внутри проводника переходит в ток смещения между пластинами конденсатора
В результате мы можем сформулировать (рис. 9.6)
Утверждение 4.
Вихревое магнитное поле создается полным током, то есть током проводимости и током смещения, вызванным изменяющимся электрическим полем.
Рис. 9.6. Гипотеза Максвелла. Изменяющееся электрическое поле порождает вихревое магнитное поле
Математическим выражением этого утверждения является уравнение, получаемое из (9.11),
Таким образом, Максвелл предсказал новое явление, в известном смысле обратное электромагнитной индукции. Эксперимент подтвердил, что магнитное поле действительно может создаваться изменяющимся во времени электрическим полем (рис. 9.7).
Рис. 9.7. Переменное электрическое поле между пластинами конденсатора порождает вихревое магнитное поле, которое измеряется с помощью проволочной квадратной рамки и отображается на экране монитора
В ряду этих экспериментов первым и главным было экспериментальное доказательство существования электромагнитных волн, выполненное немецким физиком Генрихом Герцем в 1888 году (рис. 9.8). Интересно, что сам Герц не верил в их существование и своими экспериментами хотел опровергнуть теорию Максвелла, созданную им за 20 лет до этого в 1865 году.
Рис. 9.8. Генрих Герц (1857 — 1894) — немецкий физик.
Герц не только экспериментально доказал существование электромагнитных волн, но впервые начал изучать их свойства — поглощение и преломление в разных средах, отражение от металлических поверхностей и т. п. Ему удалось измерить на опыте длину волны и скорость распространения электромагнитных волн, которая оказалась равной скорости света (рис. 9.9).
Рис. 9.9. Гармоническая электромагнитная волна, бегущая вдоль оси z . Вектора напряженности электрического поля, индукции магнитного поля и скорости волны взаимно перпендикулярны
Опыты Герца сыграли решающую роль для доказательства и признания электромагнитной теории Максвелла. Через семь лет после этих опытов электромагнитные волны нашли применение в беспроводной связи, продемонстрированной А.С. Поповым в 1895 г. (рис. 9.10).
Рис. 9.10. А.С. Попов (1859–1905) — русский физик и электротехник
Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Простейшей системой, излучающей электромагнитные волны, является небольшой по размерам электрический диполь, дипольный момент p(t) которого быстро изменяется во времени. Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны λ (рис. 9.11).
Рис. 9.11. Элементарный электрический диполь, совершающий гармонические колебания
Рис. 9.12 дает представление о структуре электромагнитной волны, излучаемой таким диполем.
Рис. 9.12. Излучение элементарного электрического диполя. Дипольный момент направлен вдоль оси z, силовые линии электрического поля лежат в плоскости листа, а силовые линии магнитного поля перпендикулярны плоскости листа
Следует обратить внимание на то, что максимальный поток электромагнитной энергии излучается в плоскости, перпендикулярной оси диполя. Вдоль своей оси диполь не излучает энергии. Герц использовал элементарный диполь в качестве излучающей и приемной антенн при экспериментальном доказательстве существования электромагнитных волн.
http://spravochnick.ru/fizika/uravneniya_maksvella/tok_smescheniya/
http://online.mephi.ru/courses/physics/electricity/data/course/9/9.2.html
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.
Displacement[edit]
Figure 1. Motion of a continuum body.
The displacement of a body has two components: a rigid-body displacement and a deformation.
A change in the configuration of a continuum body can be described by a displacement field. A displacement field is a vector field of all displacement vectors for all particles in the body, which relates the deformed configuration with the undeformed configuration. The distance between any two particles changes if and only if deformation has occurred. If displacement occurs without deformation, then it is a rigid-body displacement.
Material coordinates (Lagrangian description)[edit]
The displacement of particles indexed by variable i may be expressed as follows. The vector joining the positions of a particle in the undeformed configuration 





where 
Expressed in terms of the material coordinates, i.e. 

where 
The partial derivative of the displacement vector with respect to the material coordinates yields the material displacement gradient tensor 
where 
Spatial coordinates (Eulerian description)[edit]
In the Eulerian description, the vector extending from a particle 
where 
Expressed in terms of spatial coordinates, i.e. 

The partial derivative of the displacement vector with respect to the spatial coordinates yields the spatial displacement gradient tensor 
Relationship between the material and spatial coordinate systems[edit]



The relationship between 

Knowing that
then
Combining the coordinate systems of deformed and undeformed configurations[edit]
It is common to superimpose the coordinate systems for the deformed and undeformed configurations, which results in 
Thus in material (undeformed) coordinates, the displacement may be expressed as:
And in spatial (deformed) coordinates, the displacement may be expressed as:
Deformation gradient tensor[edit]
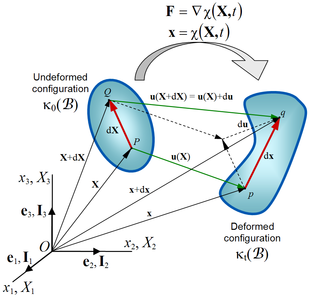
Figure 2. Deformation of a continuum body.
The deformation gradient tensor 


Due to the assumption of continuity of 





The material deformation gradient tensor 





Relative displacement vector[edit]
Consider a particle or material point 



Consider now a material point 










where 


Taylor approximation[edit]
For an infinitesimal element 


Thus, the previous equation 
Time-derivative of the deformation gradient[edit]
Calculations that involve the time-dependent deformation of a body often require a time derivative of the deformation gradient to be calculated. A geometrically consistent definition of such a derivative requires an excursion into differential geometry[2] but we avoid those issues in this article.
The time derivative of 
where 
where 


assuming 

Related quantities often used in continuum mechanics are the rate of deformation tensor and the spin tensor defined, respectively, as:
The rate of deformation tensor gives the rate of stretching of line elements while the spin tensor indicates the rate of rotation or vorticity of the motion.
The material time derivative of the inverse of the deformation gradient (keeping the reference configuration fixed) is often required in analyses that involve finite strains. This derivative is
The above relation can be verified by taking the material time derivative of 

Transformation of a surface and volume element[edit]
To transform quantities that are defined with respect to areas in a deformed configuration to those relative to areas in a reference configuration, and vice versa, we use Nanson’s relation, expressed as
where 





The corresponding formula for the transformation of the volume element is
Derivation of Nanson’s relation (see also [3])
To see how this formula is derived, we start with the oriented area elements in the reference and current configurations:
The reference and current volumes of an element are
where 
Therefore,
or,
so,
So we get
or,
Q.E.D.
Polar decomposition of the deformation gradient tensor[edit]
Figure 3. Representation of the polar decomposition of the deformation gradient
The deformation gradient 
where the tensor 












This decomposition implies that the deformation of a line element 










Due to the orthogonality of 
so that 



This polar decomposition, which is unique as 
Deformation tensors[edit]
Several rotation-independent deformation tensors are used in mechanics. In solid mechanics, the most popular of these are the right and left Cauchy–Green deformation tensors.
Since a pure rotation should not induce any strains in a deformable body, it is often convenient to use rotation-independent measures of deformation in continuum mechanics. As a rotation followed by its inverse rotation leads to no change (

The right Cauchy–Green deformation tensor[edit]
In 1839, George Green introduced a deformation tensor known as the right Cauchy–Green deformation tensor or Green’s deformation tensor, defined as:[4][5]
Physically, the Cauchy–Green tensor gives us the square of local change in distances due to deformation, i.e. 
Invariants of 
where 


The Finger deformation tensor[edit]
The IUPAC recommends[5] that the inverse of the right Cauchy–Green deformation tensor (called the Cauchy tensor in that document), i. e., 
The left Cauchy–Green or Finger deformation tensor[edit]
Reversing the order of multiplication in the formula for the right Green–Cauchy deformation tensor leads to the left Cauchy–Green deformation tensor which is defined as:
The left Cauchy–Green deformation tensor is often called the Finger deformation tensor, named after Josef Finger (1894).[5][6][7]
Invariants of 
where 
For compressible materials, a slightly different set of invariants is used:
The Cauchy deformation tensor[edit]
Earlier in 1828,[8] Augustin-Louis Cauchy introduced a deformation tensor defined as the inverse of the left Cauchy–Green deformation tensor, 
Spectral representation[edit]
If there are three distinct principal stretches 


Furthermore,
Observe that
Therefore, the uniqueness of the spectral decomposition also implies that 


The effect of 



In a similar vein,
Examples[edit]
- Uniaxial extension of an incompressible material
- This is the case where a specimen is stretched in 1-direction with a stretch ratio of
. If the volume remains constant, the contraction in the other two directions is such that
or
. Then:
- Simple shear
-
- Rigid body rotation
-
Derivatives of stretch[edit]
Derivatives of the stretch with respect to the right Cauchy–Green deformation tensor are used to derive the stress-strain relations of many solids, particularly hyperelastic materials. These derivatives are
and follow from the observations that
Physical interpretation of deformation tensors[edit]
Let 


![sin [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff1a54fbbee4a2677039524a5139e952fa86eb9)

The undeformed length of the curve is given by
After deformation, the length becomes
Note that the right Cauchy–Green deformation tensor is defined as
Hence,
which indicates that changes in length are characterized by 
Finite strain tensors[edit]
The concept of strain is used to evaluate how much a given displacement differs locally from a rigid body displacement.[1][10][11] One of such strains for large deformations is the Lagrangian finite strain tensor, also called the Green-Lagrangian strain tensor or Green – St-Venant strain tensor, defined as
or as a function of the displacement gradient tensor
or
The Green-Lagrangian strain tensor is a measure of how much 

The Eulerian-Almansi finite strain tensor, referenced to the deformed configuration, i.e. Eulerian description, is defined as
or as a function of the displacement gradients we have
Derivation of the Lagrangian and Eulerian finite strain tensors
A measure of deformation is the difference between the squares of the differential line element 

In the Lagrangian description, using the material coordinates as the frame of reference, the linear transformation between the differential lines is
Then we have,
where 

or
where 
In the Eulerian description, using the spatial coordinates as the frame of reference, the linear transformation between the differential lines is
where 

where the second order tensor 

or
where 
Both the Lagrangian and Eulerian finite strain tensors can be conveniently expressed in terms of the displacement gradient tensor. For the Lagrangian strain tensor, first we differentiate the displacement vector 


Replacing this equation into the expression for the Lagrangian finite strain tensor we have
or
Similarly, the Eulerian-Almansi finite strain tensor can be expressed as
Seth–Hill family of generalized strain tensors[edit]
B. R. Seth from the Indian Institute of Technology Kharagpur was the first to show that the Green and Almansi strain tensors are special cases of a more general strain measure.[12][13] The idea was further expanded upon by Rodney Hill in 1968.[14] The Seth–Hill family of strain measures (also called Doyle-Ericksen tensors)[15] can be expressed as
For different values of 
- Green-Lagrangian strain tensor
- Biot strain tensor
- Logarithmic strain, Natural strain, True strain, or Hencky strain
- Almansi strain
The second-order approximation of these tensors is
where 
Many other different definitions of tensors 
An example is the set of tensors
which do not belong to the Seth–Hill class, but have the same 2nd-order approximation as the Seth–Hill measures at 

Stretch ratio[edit]
The stretch ratio is a measure of the extensional or normal strain of a differential line element, which can be defined at either the undeformed configuration or the deformed configuration.
The stretch ratio for the differential element 


where 

Similarly, the stretch ratio for the differential element 


The normal strain 

This equation implies that the normal strain is zero, i.e. no deformation, when the stretch is equal to unity. Some materials, such as elastometers can sustain stretch ratios of 3 or 4 before they fail, whereas traditional engineering materials, such as concrete or steel, fail at much lower stretch ratios, perhaps of the order of 1.1 (reference?)
Physical interpretation of the finite strain tensor[edit]
The diagonal components 
where 

The off-diagonal components 
where 


Under certain circumstances, i.e. small displacements and small displacement rates, the components of the Lagrangian finite strain tensor may be approximated by the components of the infinitesimal strain tensor
Derivation of the physical interpretation of the Lagrangian and Eulerian finite strain tensors
The stretch ratio for the differential element 


where 

Similarly, the stretch ratio for the differential element 


The square of the stretch ratio is defined as
Knowing that
we have
where 

The normal strain or engineering strain 

Thus, the normal strain in the direction 

solving for 
The shear strain, or change in angle between two line elements 





where 



thus,
then
or
Deformation tensors in convected curvilinear coordinates[edit]
A representation of deformation tensors in curvilinear coordinates is useful for many problems in continuum mechanics such as nonlinear shell theories and large plastic deformations. Let 



The three tangent vectors at 
Let us define a second-order tensor field 
The Christoffel symbols of the first kind can be expressed as
To see how the Christoffel symbols are related to the Right Cauchy–Green deformation tensor let us similarly define two bases, the already mentioned one that is tangent to deformed grid lines and another that is tangent to the undeformed grid lines. Namely,
The deformation gradient in curvilinear coordinates[edit]
Using the definition of the gradient of a vector field in curvilinear coordinates, the deformation gradient can be written as
The right Cauchy–Green tensor in curvilinear coordinates[edit]
The right Cauchy–Green deformation tensor is given by
If we express 

Therefore,
and the corresponding Christoffel symbol of the first kind may be written in the following form.
Some relations between deformation measures and Christoffel symbols[edit]
Consider a one-to-one mapping from 



Then,
Noting that
and 
Define
Hence
Define
Then
Define the Christoffel symbols of the second kind as
Then
Therefore,
The invertibility of the mapping implies that
We can also formulate a similar result in terms of derivatives with respect to 
Compatibility conditions[edit]
The problem of compatibility in continuum mechanics involves the determination of allowable single-valued continuous fields on bodies. These allowable conditions leave the body without unphysical gaps or overlaps after a deformation. Most such conditions apply to simply-connected bodies. Additional conditions are required for the internal boundaries of multiply connected bodies.
Compatibility of the deformation gradient[edit]
The necessary and sufficient conditions for the existence of a compatible 
Compatibility of the right Cauchy–Green deformation tensor[edit]
The necessary and sufficient conditions for the existence of a compatible 
We can show these are the mixed components of the Riemann–Christoffel curvature tensor. Therefore, the necessary conditions for 
Compatibility of the left Cauchy–Green deformation tensor[edit]
No general sufficiency conditions are known for the left Cauchy–Green deformation tensor in three-dimensions. Compatibility conditions for two-dimensional 
See also[edit]
- Infinitesimal strain
- Compatibility (mechanics)
- Curvilinear coordinates
- Piola–Kirchhoff stress tensor, the stress tensor for finite deformations.
- Stress measures
- Strain partitioning
References[edit]
- ^ a b Lubliner, Jacob (2008). Plasticity Theory (PDF) (Revised ed.). Dover Publications. ISBN 978-0-486-46290-5. Archived from the original (PDF) on 2010-03-31.
- ^ A. Yavari, J.E. Marsden, and M. Ortiz, On spatial and material covariant balance laws in elasticity, Journal of Mathematical Physics, 47, 2006, 042903; pp. 1–53.
- ^ Eduardo de Souza Neto; Djordje Peric; Owens, David (2008). Computational methods for plasticity : theory and applications. Chichester, West Sussex, UK: Wiley. p. 65. ISBN 978-0-470-69452-7.
- ^ The IUPAC recommends that this tensor be called the Cauchy strain tensor.
- ^ a b c d A. Kaye, R. F. T. Stepto, W. J. Work, J. V. Aleman (Spain), A. Ya. Malkin (1998). «Definition of terms relating to the non-ultimate mechanical properties of polymers». Pure Appl. Chem. 70 (3): 701–754. doi:10.1351/pac199870030701.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Eduardo N. Dvorkin, Marcela B. Goldschmit, 2006 Nonlinear Continua, p. 25, Springer ISBN 3-540-24985-0.
- ^ The IUPAC recommends that this tensor be called the Green strain tensor.
- ^ Jirásek,Milan; Bažant, Z. P. (2002) Inelastic analysis of structures, Wiley, p. 463 ISBN 0-471-98716-6
- ^ J. N. Reddy, David K. Gartling (2000) The finite element method in heat transfer and fluid dynamics, p. 317, CRC Press ISBN 1-4200-8598-0.
- ^ Belytschko, Ted; Liu, Wing Kam; Moran, Brian (2000). Nonlinear Finite Elements for Continua and Structures (reprint with corrections, 2006 ed.). John Wiley & Sons Ltd. pp. 92–94. ISBN 978-0-471-98773-4.
- ^ Zeidi, Mahdi; Kim, Chun IL (2018). «Mechanics of an elastic solid reinforced with bidirectional fiber in finite plane elastostatics: complete analysis». Continuum Mechanics and Thermodynamics. 30 (3): 573–592. Bibcode:2018CMT….30..573Z. doi:10.1007/s00161-018-0623-0. ISSN 1432-0959. S2CID 253674037.
- ^ Seth, B. R. (1961), «Generalized strain measure with applications to physical problems», MRC Technical Summary Report #248, Mathematics Research Center, United States Army, University of Wisconsin: 1–18, archived from the original on August 22, 2013
- ^ Seth, B. R. (1962), «Generalized strain measure with applications to physical problems», IUTAM Symposium on Second Order Effects in Elasticity, Plasticity and Fluid Mechanics, Haifa, 1962.
- ^ Hill, R. (1968), «On constitutive inequalities for simple materials—I», Journal of the Mechanics and Physics of Solids, 16 (4): 229–242, Bibcode:1968JMPSo..16..229H, doi:10.1016/0022-5096(68)90031-8
- ^ T.C. Doyle and J.L. Eriksen (1956). «Non-linear elasticity.» Advances in Applied Mechanics 4, 53–115.
- ^ Z.P. Bažant and L. Cedolin (1991). Stability of Structures. Elastic, Inelastic, Fracture and Damage Theories. Oxford Univ. Press, New York (2nd ed. Dover Publ., New York 2003; 3rd ed., World Scientific 2010).
- ^ Z.P. Bažant (1998). «Easy-to-compute tensors with symmetric inverse approximating Hencky finite strain and its rate.» Journal of Materials of Technology ASME, 120 (April), 131–136.
- ^ Blume, J. A. (1989). «Compatibility conditions for a left Cauchy–Green strain field». Journal of Elasticity. 21 (3): 271–308. doi:10.1007/BF00045780. S2CID 54889553.
- ^ Acharya, A. (1999). «On Compatibility Conditions for the Left Cauchy–Green Deformation Field in Three Dimensions» (PDF). Journal of Elasticity. 56 (2): 95–105. doi:10.1023/A:1007653400249. S2CID 116767781.
Further reading[edit]
- Dill, Ellis Harold (2006). Continuum Mechanics: Elasticity, Plasticity, Viscoelasticity. Germany: CRC Press. ISBN 0-8493-9779-0.
- Dimitrienko, Yuriy (2011). Nonlinear Continuum Mechanics and Large Inelastic Deformations. Germany: Springer. ISBN 978-94-007-0033-8.
- Hutter, Kolumban; Klaus Jöhnk (2004). Continuum Methods of Physical Modeling. Germany: Springer. ISBN 3-540-20619-1.
- Lubarda, Vlado A. (2001). Elastoplasticity Theory. CRC Press. ISBN 0-8493-1138-1.
- Macosko, C. W. (1994). Rheology: principles, measurement and applications. VCH Publishers. ISBN 1-56081-579-5.
- Mase, George E. (1970). Continuum Mechanics. McGraw-Hill Professional. ISBN 0-07-040663-4.
- Mase, G. Thomas; George E. Mase (1999). Continuum Mechanics for Engineers (Second ed.). CRC Press. ISBN 0-8493-1855-6.
- Nemat-Nasser, Sia (2006). Plasticity: A Treatise on Finite Deformation of Heterogeneous Inelastic Materials. Cambridge: Cambridge University Press. ISBN 0-521-83979-3.
- Rees, David (2006). Basic Engineering Plasticity – An Introduction with Engineering and Manufacturing Applications. Butterworth-Heinemann. ISBN 0-7506-8025-3.
External links[edit]
- Prof. Amit Acharya’s notes on compatibility on iMechanica

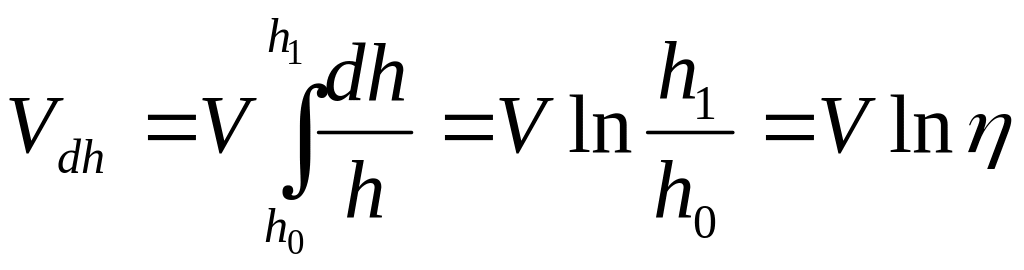
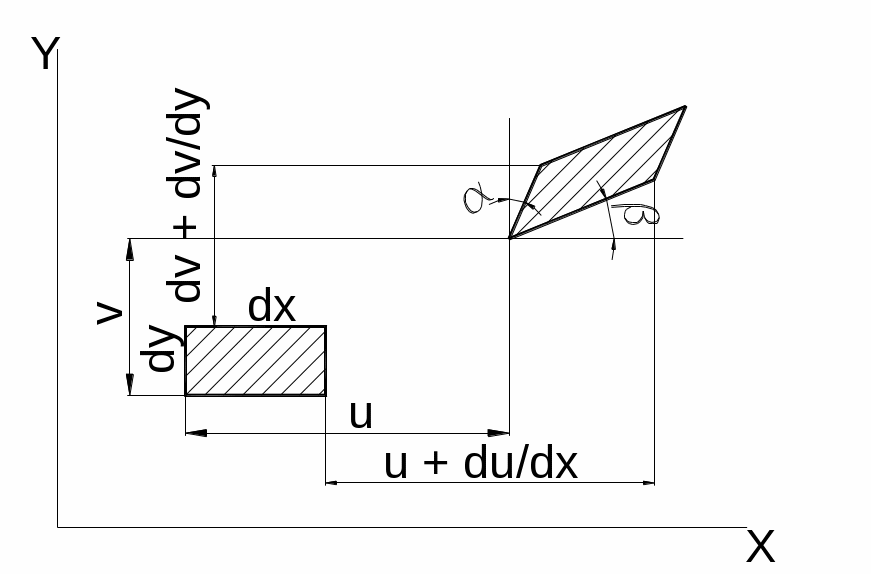
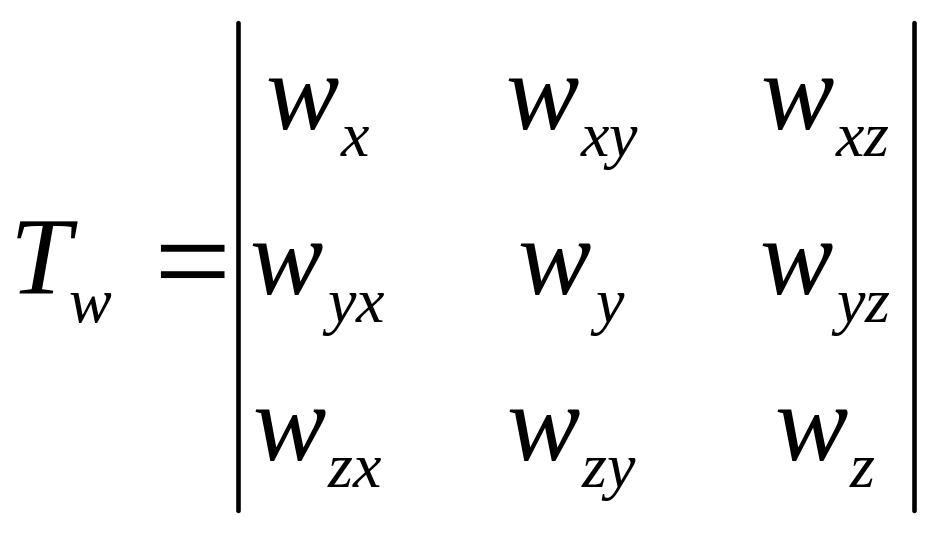









































![{displaystyle {dot {mathbf {F} }}={frac {partial mathbf {F} }{partial t}}={frac {partial }{partial t}}left[{frac {partial mathbf {x} (mathbf {X} ,t)}{partial mathbf {X} }}right]={frac {partial }{partial mathbf {X} }}left[{frac {partial mathbf {x} (mathbf {X} ,t)}{partial t}}right]={frac {partial }{partial mathbf {X} }}left[mathbf {V} (mathbf {X} ,t)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2666606a9db3c727de1e94fa372b590683f72c0)
![{displaystyle {dot {mathbf {F} }}={frac {partial }{partial mathbf {X} }}left[mathbf {V} (mathbf {X} ,t)right]={frac {partial }{partial mathbf {X} }}left[mathbf {v} (mathbf {x} (mathbf {X} ,t),t)right]=left.{frac {partial }{partial mathbf {x} }}left[mathbf {v} (mathbf {x} ,t)right]right|_{mathbf {x} =mathbf {x} (mathbf {X} ,t)}cdot {frac {partial mathbf {x} (mathbf {X} ,t)}{partial mathbf {X} }}={boldsymbol {l}}cdot mathbf {F} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/abbb3bd21a0c39cedc504214b5bb20503386c081)
















![{displaystyle {begin{aligned}I_{1}^{C}&:={text{tr}}(mathbf {C} )=C_{II}=lambda _{1}^{2}+lambda _{2}^{2}+lambda _{3}^{2}\I_{2}^{C}&:={tfrac {1}{2}}left[({text{tr}}~mathbf {C} )^{2}-{text{tr}}(mathbf {C} ^{2})right]={tfrac {1}{2}}left[(C_{JJ})^{2}-C_{IK}C_{KI}right]=lambda _{1}^{2}lambda _{2}^{2}+lambda _{2}^{2}lambda _{3}^{2}+lambda _{3}^{2}lambda _{1}^{2}\I_{3}^{C}&:=det(mathbf {C} )=J^{2}=lambda _{1}^{2}lambda _{2}^{2}lambda _{3}^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d05cca3762fe510c6252312cb22a66da138cfef)


![{displaystyle {begin{aligned}I_{1}&:={text{tr}}(mathbf {B} )=B_{ii}=lambda _{1}^{2}+lambda _{2}^{2}+lambda _{3}^{2}\I_{2}&:={tfrac {1}{2}}left[({text{tr}}~mathbf {B} )^{2}-{text{tr}}(mathbf {B} ^{2})right]={tfrac {1}{2}}left(B_{ii}^{2}-B_{jk}B_{kj}right)=lambda _{1}^{2}lambda _{2}^{2}+lambda _{2}^{2}lambda _{3}^{2}+lambda _{3}^{2}lambda _{1}^{2}\I_{3}&:=det mathbf {B} =J^{2}=lambda _{1}^{2}lambda _{2}^{2}lambda _{3}^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e88d7c726ee801990cc0dda3221b4a2edc04aa5)





















![{displaystyle {begin{aligned}l_{x}&=int _{0}^{1}left|{cfrac {dmathbf {x} }{ds}}right|~ds=int _{0}^{1}{sqrt {{cfrac {dmathbf {x} }{ds}}cdot {cfrac {dmathbf {x} }{ds}}}}~ds=int _{0}^{1}{sqrt {left({cfrac {dmathbf {x} }{dmathbf {X} }}cdot {cfrac {dmathbf {X} }{ds}}right)cdot left({cfrac {dmathbf {x} }{dmathbf {X} }}cdot {cfrac {dmathbf {X} }{ds}}right)}}~ds\&=int _{0}^{1}{sqrt {{cfrac {dmathbf {X} }{ds}}cdot left[left({cfrac {dmathbf {x} }{dmathbf {X} }}right)^{T}cdot {cfrac {dmathbf {x} }{dmathbf {X} }}right]cdot {cfrac {dmathbf {X} }{ds}}}}~dsend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1b639bab0e25d96cf46894973e1d2693800d94)



![{displaystyle mathbf {E} ={frac {1}{2}}left[(nabla _{mathbf {X} }mathbf {u} )^{T}+nabla _{mathbf {X} }mathbf {u} +(nabla _{mathbf {X} }mathbf {u} )^{T}cdot nabla _{mathbf {X} }mathbf {u} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/613f67ee25337f305e0fe930e90f5099becdc913)














![{displaystyle {begin{aligned}mathbf {E} &={frac {1}{2}}left(mathbf {F} ^{T}mathbf {F} -mathbf {I} right)\&={frac {1}{2}}left[left{(nabla _{mathbf {X} }mathbf {u} )^{T}+mathbf {I} right}left(nabla _{mathbf {X} }mathbf {u} +mathbf {I} right)-mathbf {I} right]\&={frac {1}{2}}left[(nabla _{mathbf {X} }mathbf {u} )^{T}+nabla _{mathbf {X} }mathbf {u} +(nabla _{mathbf {X} }mathbf {u} )^{T}cdot nabla _{mathbf {X} }mathbf {u} right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1bc4d02e18262b73b16470e4e4cfb36c933410b)
![{displaystyle {begin{aligned}E_{KL}&={frac {1}{2}}left({frac {partial x_{j}}{partial X_{K}}}{frac {partial x_{j}}{partial X_{L}}}-delta _{KL}right)\&={frac {1}{2}}left[delta _{jM}left({frac {partial U_{M}}{partial X_{K}}}+delta _{MK}right)delta _{jN}left({frac {partial U_{N}}{partial X_{L}}}+delta _{NL}right)-delta _{KL}right]\&={frac {1}{2}}left[delta _{MN}left({frac {partial U_{M}}{partial X_{K}}}+delta _{MK}right)left({frac {partial U_{N}}{partial X_{L}}}+delta _{NL}right)-delta _{KL}right]\&={frac {1}{2}}left[left({frac {partial U_{M}}{partial X_{K}}}+delta _{MK}right)left({frac {partial U_{M}}{partial X_{L}}}+delta _{ML}right)-delta _{KL}right]\&={frac {1}{2}}left({frac {partial U_{K}}{partial X_{L}}}+{frac {partial U_{L}}{partial X_{K}}}+{frac {partial U_{M}}{partial X_{K}}}{frac {partial U_{M}}{partial X_{L}}}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8613306031cc1580236c979b6aec6c795d3e4db9)
![{displaystyle mathbf {E} _{(m)}={frac {1}{2m}}(mathbf {U} ^{2m}-mathbf {I} )={frac {1}{2m}}left[mathbf {C} ^{m}-mathbf {I} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70e3f0b7ddba558d16a401580cf534133ef24d09)



![{displaystyle mathbf {E} _{(-1)}={frac {1}{2}}left[mathbf {I} -mathbf {U} ^{-2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0446d9edf116c655919b58ac4fc46fab8778af99)






















![{displaystyle Gamma _{ijk}={tfrac {1}{2}}[(mathbf {g} _{i}cdot mathbf {g} _{k})_{,j}+(mathbf {g} _{j}cdot mathbf {g} _{k})_{,i}-(mathbf {g} _{i}cdot mathbf {g} _{j})_{,k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c84f52a8b94bf81096fd54ad218ac8c8a794593)





![{displaystyle Gamma _{ijk}={tfrac {1}{2}}[C_{ik,j}+C_{jk,i}-C_{ij,k}]={tfrac {1}{2}}[(mathbf {G} _{i}cdot {boldsymbol {C}}cdot mathbf {G} _{k})_{,j}+(mathbf {G} _{j}cdot {boldsymbol {C}}cdot mathbf {G} _{k})_{,i}-(mathbf {G} _{i}cdot {boldsymbol {C}}cdot mathbf {G} _{j})_{,k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/626053366fba8dffc9ee988c8728f9b476cee63a)






![{displaystyle [G^{ij}]=[G_{ij}]^{-1}~;~~[g^{alpha beta }]=[g_{alpha beta }]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6168f5195b650daf063a1dd26b314242926f774)







![{displaystyle R_{alpha beta rho }^{gamma }:={frac {partial }{partial X^{rho }}}[,_{(X)}Gamma _{alpha beta }^{gamma }]-{frac {partial }{partial X^{beta }}}[,_{(X)}Gamma _{alpha rho }^{gamma }]+,_{(X)}Gamma _{mu rho }^{gamma },_{(X)}Gamma _{alpha beta }^{mu }-,_{(X)}Gamma _{mu beta }^{gamma },_{(X)}Gamma _{alpha rho }^{mu }=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29e1d54640569dc6ab58c0fca0c0ab634aef2180)