Как найти область истинности предиката онлайн

How to use the calculator

1. Enter in the field logic function (for example, x1 ∨ x2) or its vector (for example, 10110101)
2. Specify the actions to be performed using the switches
3. Specify whether the output of the solution is required by the «With solution (By the steps)» switch
4. Click the «Let’s go» button

Symbols used

As variables, the letters of the Latin alphabet are used, as well as numbers written after the letter (variable index).
Thus, the variable names will be: a,
x, a1, B, X, X1, Y1, A123
and so on.

To record logical operations you can use
both normal keyboard characters (*, +, !, ^,
->, =), and symbols established in literature (∧, ∨,
¬, ⊕, →, ≡). If your keyboard does not have the desired
operation symbol, then use the calculator keyboard (if it is not visible, press «Show Keyboard»),
where both all logical operations and a set of the most commonly used variables are available.

To change the order of operations round brackets are used ().

The designations of logical operations

• AND: & • ∧ *
• OR: ∨ +
• NOT: ¬ !
• Exclusive OR (XOR): ⊕ ^
• Implication: -> → =>
• Equivalence: = ~ ≡ <=>
• Schaeffer stroke: ↑ |
• Pierce Arrow: ↓

What the calculator can do

• Build a truth table of the function
• Build a truth table by a binary vector
• Construct a perfect conjunctive normal form (CNF)
• Construct a perfect disjunctive normal form (DNF)
• Construct the Zhegalkin polynomial (by Pascal, triangle, and undefined coefficients methods)
• Determine whether a function belongs to each of the five Post’s classes
• Build K-Map (Karnaugh Map)
• Minimize CNF and DNF
• Looking for fictitious variables

What is a Boolean function

Boolean function f(x1, x2, ... xn) — is any function of n variables x₁, x₂, … x_n,
in which its arguments take one of two values:
either 0 or 1, and the function itself takes values 0 or 1.
That is, it is a rule by which an arbitrary set of zeros and ones is assigned the value 0 or 1.
Read more about Boolean functions on Wikipedia.

What is a truth table?

Truth table — is a table describing a logical function,
namely reflecting all values of the function for all possible values of its arguments.
The table consists of n+1 columns and 2n rows, where n is the number of variables used.
The first n columns contain all possible values of arguments (variables) of the function,
and the n+1th column contains values of the function that it takes on a given set of arguments.

Quite often there is a variant of the table in which the number of columns is equal to n + the number of logical
operations. In such a table also the first n columns are filled with sets of arguments, and the remaining columns
are filled with values of subfunctions included into the record of the function, which allows to simplify the calculation of the final
value of the function at the expense of already intermediate calculations.

Logical operations

A logical operation is an operation on statements that allows you to make new statements by combining
simpler ones. Conjunction (∧ or &), disjunction (∨ or |) are commonly referred to as basic operations,
implication (→), negation (¬), equivalence (=), exclusive OR (⊕).

Truth table of logical operations

How to set a logic function

There are many ways to specify a Boolean function:

• truth table
• characteristic sets
• value vector
• Gray’s matrix
• formulas

Let’s look at some of them:

To define a function by a vector of values, you must write a vector of 2ⁿ zeros and ones,
where n is the number of arguments on which the function depends.
For example, a function of two arguments can be defined as follows: 0001 (AND operation), 0111 (OR operation).

To define a function as a formula, you need to write a mathematical expression consisting of function arguments and logical operations.
For example, we can specify the following function: a∧b ∨ b∧c ∨ a∧c

Ways to represent a Boolean function

You can use formulas to get a huge variety of functions, and with different formulas
you can get the same function. Sometimes it can be very useful to know how to construct a particular function,
using only a small set of given operations, or using as few arbitrary operations as possible.
Let’s look at the basic ways of defining Boolean functions:

• Perfect disjunctive normal form (DNF)
• Perfect conjunctive normal form (CNF)
• Algebraic Normal Form (ANF, Zhegalkin polynomial)

Disjunctive normal form (DNF)

A simple conjunction is a conjunction of some finite set of variables,
or their negations, with each variable occurring no more than once.
A disjunctive normal form (DNF) is a disjunction of simple conjunctions.
A perfect disjunctive normal form (DNF) is a DNF with respect to some given finite set of variables,
each conjunction of which includes all variables of this set.
For example, DNF is the function ¬abc ∨ ¬a¬bc
∨ ac, but it is not a disjunctive normal form because the last conjunction lacks the variable b.

Conjunctive normal form (CNF)

A simple disjunction is a disjunction of one or more variables, or their negations,
with each variable included no more than once.
Conjunctive normal form (CNF) is a conjunction of simple disjunctions.
A perfect conjunctive normal form (CNF) is a CNF with respect to some given finite set of variables,
each disjunction of which includes all variables of this set.
For example, the CNF is the function (a ∨ b) ∧ (a ∨ b ∨ c),
but it is not an SNF because the first disjunction lacks the variable c.

Algebraic Normal Form (ANF, Zhegalkin polynomial)

Algebraic normal form, Zhegalkin polynomial is a form of representation of logical function in the form of polynomial with coefficients of 0 and 1, where conjunction operation is used as product and exclusive OR is used as addition.
Examples of Zhegalkin polynomials: 1, a, a⊕b, ab⊕a⊕b⊕1

Algorithm for constructing an DNF for a Boolean function

1. Construct a truth table for the function
2. Find all sets of arguments on which the function takes value 1
3. Write simple conjunctions for each of the sets according to the following rule: if in a set the variable
   takes value 0, it enters the conjunction with negation, otherwise without negation
4. Combine all simple conjunctions with a disjunction

Algorithm of CNF construction for a Boolean function

1. Build a truth table for the function
2. Find all sets of arguments on which the function takes the value 0
3. Write simple disjunctions for each of the sets according to the following rule: if in a set the variable
   takes value 1, it enters the disjunction with negation, otherwise without negation
4. Combine all simple disjunctions with a conjunction

Algorithm for constructing the Zhegalkin polynomial of a Boolean function

There are several methods of constructing the Zhegalkin polynomial, in this article we will consider the most convenient and simple
of all.

1. Construct a truth table for the function
2. Add a new column to the truth table and write in 1, 3, 5… cells of the values from the same rows
   of the previous column of the truth table, and to the values in lines 2, 4, 6… add modulo two
   values from correspondingly 1, 3, 5… lines.
3. Add a new column to the truth table and overwrite the values of 1, 2, 5, 6, 9, 10…
   lines, and to 3, 4, 7, 8, 11, 12… lines add the overwritten values similarly to the previous point.
4. Repeat each time doubling the number of transferred and added elements until the length equals the number of rows in the table.
5. Write out Boolean sets where the value of the last column is one
6. Write the names of variables corresponding to the set instead of the ones in the sets (for the zero set write
   one) and join them using the exclusive OR operation.

Examples of constructing different representations of logical functions

Let us construct perfect disjunctive and disjunctive normal forms and the Zhegalkin polynomial
for the function of three variables F = ¬ab∨¬bc∨ca

1. Let’s build a truth table for the function

---

Construction of a perfect disjunctive normal form:

Let’s find the sets on which the function takes a true value: { 0, 0, 1 } { 0, 1, 0 }
{ 0, 1, 1 } { 1, 0, 1 } { 1, 1, 1 }

Let us match the found sets with elementary conjunctions for all variables, and if a variable
in the set takes value 0, it will be written with negation:

K₁: { 0, 0, 1 } — ¬a¬bc
K₂: { 0, 1, 0 } — ¬ab¬c
K₃: { 0, 1, 1 } — ¬abc
K₄: { 1, 0, 1 } — a¬bc
K₅: { 1, 1, 1 } — abc

Combine conjunctions using disjunction and get a perfect disjunctive normal form:

K₁ ∨ K₂ ∨ K₃ ∨ K₄ ∨ K₅ = ¬a¬bc ∨ ¬ab¬c ∨ ¬abc ∨ a¬bc ∨ abc

---

Construction of a perfect conjunctive normal form:

Find the sets on which the function takes a false value: { 0, 0, 0 } { 1, 0, 0 }
{ 1, 1, 0 }

Let us match the found sets with elementary disjunctions for all variables, and if a variable
in the set takes value 1, it will be written with negation:

D₁: { 0, 0, 0 } — a∨b∨c
D₂: { 1, 0, 0 } — ¬a∨b∨c
D₃: { 1, 1, 0 } — ¬a∨¬b∨c

Combine disjunctions with conjunctions and obtain a perfect conjunctive normal form:

D₁ ∧ D₂ ∧ D₃ = (a∨b∨c) ∧ (¬a∨b∨c)
∧ (¬a∨¬b∨c)

---

Construction of the Zhegalkin polynomial:

Add a new column to the truth table and write in lines 1, 3, 5, and 7 the values from the same lines
in the previous column of the truth table, and add the values in lines 2, 4, 6 and 8 modulo 2 with the values
from lines 1, 3, 5, and 7 correspondingly:

Add a new column to the truth table and write in lines 1 and 2, 5 and 6 the values from the same lines
of the previous column in the truth table, and add the values in lines 3 and 4, 7 and 8 modulo 2 with the values
from lines 1 and 2, 5 and 6 correspondingly:

Add a new column to the truth table and write in rows 1, 2, 3, and 4 the values from the same rows of the previous
column of the truth table, and add the values in lines 5, 6, 7 and 8 modulo 2 with the values from
correspondingly in lines 1, 2, 3, and 4:

The final result is the following table:

Write out the sets, on which the resulting vector takes a unit value, and instead of the units in the sets write
the names of variables corresponding to the set (for the zero set write one):

{ 0, 0, 1 } — c, { 0, 1, 0 } — b, { 0, 1, 1 } —
bc, { 1, 1, 0 } — ab, { 1, 1, 1 } — abc

Combining these conjunctions using the exclusive or operation, we obtain the Zhegalkin polynomial:
c⊕b⊕bc⊕ab⊕abc

Предикаты. Операции над предикатами

При изучении высказываний мы отмечали, что утверждение с переменными не является высказыванием. Можно, например, рассмотреть предложение %%P(x) : x^2 + 1 > 2%% с переменной %%x in mathbb R%%. Это предлождение не является высказыванием, так как нельзя сказать истинно оно или ложно. Однако, если заменить переменную %%x%% на какое-либо значение, например, %%x = 1%%, получаем высказывание %%2 > 2%%, которое является ложным. Заменив переменную %%x%% на значение %%x = 2%%, получим истинное высказывание %%5 > 2%%. Итак есть выражение %%P(x)%% не являющиееся высказыванием, но превращающееся в него при замене переменной %%x%% на ее произвольное значение из соответствующего множества.

Определение

Одноместным предикатом, определенным на множестве %%D%%, называется предложение с переменной, которое превращается в высказывание при замене этой переменной на ее значение из множества %%D%%. Одноместный предикат будем называть унарным или предикатом от одной переменной.

Примеры

Следующие предложения являются одноместными предикатами:

1. %%P(x): x^ 2 + 1 > 2%%, где %%D%% — множество действительных чисел.
2. %%Q(x):%% Длина отрезка равна %%1%%, где %%D%% — множество всех отрезков прямой.

Следующие предложения не являются одноместными предикатами:

1. %%1 > 2%%.
2. Прямая %%x%% параллельна прямой %%y%%.

%%n%%-местный предикат

%%n%%-местым предикатом с областью определения %%D = D_1 times D_2 times ldots times D_n%% называется предикат %%P(x_1, x_2, ldots, x_n)%% от %%n%% переменных, который превращается в высказывание при замене переменных %%x_1, x_2, ldots, x_n%% на их значения из множеств %%D_1, D_2, ldots, D_n%% соответственно.

Тогда предложение прямая %%x%% параллельна прямой %%y%% является двуместным предикатом %%P(x, y)%%, где %%X, Y%% — множество всех прямых.

Область определения предиката

Рассмотрим %%n%%-местный предикат %%P(x_1, x_2, ldots, x_n)%%. В этом случае переменные берутся из множеств %%D_1, D_2, ldots, D_n%% соответственно. Можно рассмотреть множество %%D = D_1 times D_2 times ldots times D_n%% — декартово произведение множеств %%D_1, D_2, ldots, D_n%%, элементами которого являются всевозможные упорядоченные %%n%%-ки %%(d_1, d_2, ldots, d_n)%% элементов исходных множеств.

Множество %%D%% называется областью определения предиката.

Область истинности

Областью истинности предиката %%P(x_1, x_2, ldots, x_n)%% называется множество всех %%n%%-ок %%(d_1, d_2, ldots, d_n) in D%% таких, что при замене %%x_1%% на %%d_1%%, %%x_2%% на %%d_2%%, …, %%x_n%% на %%d_n%% получается истинное высказывание.

Пример

На множестве %%D = { 1, 2, 3, 4, 5, 6, 7, 8, 9}%% рассмотрим одноместный предикат %%P(x): x%% — простое число. Найти область истинности предиката %%P(x)%%.

Обозначим область истинности буквой %%A%%. Тогда %%A%% состоит из таких элементов, при которых выполняется предикат %%P(x)%%. Поэтому %%A = {2, 3, 5, 7}%%.

Операции над предикатами

Аналогично операциям для высказываний вводятся операции для предикатов.

Пусть %%P(x)%% и %%Q(x)%% — одноместные предикаты, определенные на множестве %%D%%.

Отрицанием предиката %%P(x)%% называется новый предикат, обозначаемый %%overline{P(x)}%% и являющийся ложным для тех и только тех %%x%%, для которых предикат %%P(x)%% истинный.

Конъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) land Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% истинны.

Дизъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) lor Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% ложны.

Импликацией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) rightarrow Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% истинный, а %%Q(x)%% ложный.

Эквиваленцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) leftrightarrow Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% имеют одинаковые значения.

Применяя операции над предикатами, мы получаем составные предикаты, которые будем называть формулами алгебры предикатов.

Предикаты %%P(x)%% и %%Q(x)%% эквивалентные , если для любого значения переменной %%x%% их значения истинности совпадают. Обозначают $$P(x) equiv Q(x).$$

Законы алгебры предикатов

Для предикатов справедливы все законы, аналогичные законам алгебры логики высказываний¹.

В случае тождественно истинных и тождественно ложных предикатов имеем следующие определения.

Предикат %%P(x_1, x_2, ldots, x_n)%% называется тождественно истинным если при любой замене переменных %%x_1, x_2, ldots, x_n%% на их значения предикат превращается в истинное высказывание.

Предикат %%P(x_1, x_2, ldots, x_n)%% называется тождественно ложным если при любой замене переменных %%x_1, x_2, ldots, x_n%% на их значения предикат превращается в ложное высказывание.

---

Высказывание является частным случаем предиката, когда в предикате нет переменных. То есть высказывание является предикатом %%0%% порядка (от %%0%% переменных).

---

1. Законы алгебры логики высказываний.

Определение. Предикатом называется повествовательное предложение, содержащее предметные переменные, определённые на соответствующих мно- жествах; при замене переменных конкретными значениями (элементами) этих множеств предложение обращается в высказывание, т. е. принимает значение «истинно» или «ложно».

Определение. Предикатом называется функция P : M ⁿ → B , где B = { 0,1 } , M — любое множество, 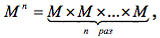т. е. функция P , сопоставляющая вектору (x₁ , x₂ ,…, x_n ) значения 0 или 1.

Множество M называется предметной областью предиката P ,

x₁ , x₂ ,…, x_n — предметные переменные,

P — предикатный символ,

n — местность предиката,

декартово произведение M × M × … × M область определения предиката P .

Обозначение: P (x₁ , x₂ ,…, x_n— n — местный предикат, заданный на множестве M .

Определение. Областью истинности предиката P называется подмножество I_p ⊆ Mⁿ его предметной области, на элементах которого значения предиката равны 1.

Область истинности предиката, выраженного предикатной формулой, определяется областями истинности составляющих и применяемыми в формуле операциями: I_PvQ = I_P ∪ I_Q, I_{P ∧ Q} = I_P ∩ I_Q , I_P→Q = I_P ∪ I_Q, I _P = I_P .

Задача 3.1. Найти область истинности предиката

P ( X, Y ) = (( X + Y ) — нечётно ) ∨ (( X — Y ) делятся на 3) , где X = {1;3;6;7}, Y = {2;4;5}.

Решение.

Составим таблицы истинности для предикатов P₁ ( X, Y ) = (( X + Y) — нечётно), P₂( X, Y ) = (( X — Y ) — делятся на 3) , P = P₁ ∨ P₂.

I_P = I _P1∨P2 = I_P1 ∪ I_P2 = {(1,2), (1,4), (3,2), (3,4), (6,5), (7,2), (7,4)} ∪ {(1,4), (7,4)} = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.
Ответ: I_P = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.

Задача 3.2. Найти область истинности предиката

P ( X ) = (( число 3 не делитель x ) → ( x ≤ 6 ))

на множестве однозначных натуральных чисел.

Решение.

Определим области истинности предикатов P₁ = {число 3 не не делитель x},

P₂ = {x ≤ 6}, P = P₁→ P₂ .

I_P1 = {1,2,4,5,7,8}, I_P2 = {1,2,3,4,5,6}, I_P = I_P1→P2 = I_P1 = {1,2,3,4,5,6,9}.

Ответ: I _P = {1,2,3,4,5,6,9}.

Задачи для самостоятельного решения

Найти область истинности предиката

1. P ( X, Y ) = ((( X — Y ) — нечетно ) ∧ ( min ( X, Y)  — четно )), где X = {2;5;6;8};
2. P ( X ,Y ) = (( X + Y )) — делится на 3) → (( X + Y ) > 5), где X = {2;5;6;8}, Y = {3;6;9};
3. P ( X, Y ) = ((( X — Y ) — нечётно ) ∧ ( |Y-X| ≤ 1 )), где X = {5;8;9}, Y = {4;7;8;10};
4. P ( X, Y ) = (( X — Y ) — чётно ) ∨ (( X + Y ) — делится на 3), где X = {5;8;9}, Y = {4;7;8;10};
5. P ( X ) = (( число 3 делитель x ) ∨ ( x ≤ 6 )), заданного на множестве однозначных натуральных чисел;
6. P ( X ) = ((( число 3 делитель x ) ∧ ( x > 6 )), заданного на множестве однозначных натуральных чисел;
7. P ( X ) = (( x ≥ 3 ) ∧ ( x ≤ 10 )), заданного на множестве всех действительных чисел;
8. P ( X ) = (( x² ≤ 4 ) ∧ ( x -1 ≥ 1 )), заданного на множестве всех действительных чисел;
9. P ( X ) = (( x ≤ 0 ) ∧ ( x² — 2x ≤ 0 )), заданного на множестве всех действительных чисел;
10. P ( X ) = (( x³ — 6x² +11x — 6 = 0 ) ∧ ( x² — 4x + 3 = 0 )),заданного на множестве всех действительных чисел.

Гусева
А.И. Дискретная
математика: Математическая логика

Лекции 14-15

Исчисление
предикатов

Основные понятия

Одноместным предикатом P(x)
называется всякая функция одного
переменного, аргумент который х
определен на некотором множестве М,
а значение функции определены на
множестве {0,1}[1].

Множество М, на котором задан
предикат, называется областью
определения предиката.

Множество I_p,
на котором предикат принимает только
истинные значения, называется областью
истинности предиката P(x).

Предикат P(x)
называется тождественно истинным
(тождественно ложным) на множестве
М, если I_p=М
(I_p=0).

N-местным
предикатом Q(x₁,
x₂,…,x_n)
называется всякая функция n
переменных, определенная на множестве
и принимающая значение на множестве
{0,1}.

Предикат P(x)
является следствием Q(x)
()
, если

Предикаты P(x)
и Q(x)
равносильны (),
если
,
т.е. они являются следствием друг друга.

Логические операции над предикатами

Так как предикаты принимают значения
0 и 1, к ним можно применять все операции
алгебры высказываний. Пусть на некотором
множестве М заданы два предиката P(x)
и Q(x).

Конъюнкцией двух предикатов
P(x)
и Q(x)
называется новый предикат
,
который равен 1 при тех и только при тех
значениях
,
при которых каждый из предикатов
принимает значение «истина», и принимает
значение «ложь» во всех остальных
случаях.

Очевидно, что областью истинностью
предиката

является
.

Дизъюнкцией двух предикатов
P(x)
и Q(x)
называется новый предикат
,
который равен 0 при тех и только при тех
значениях
,
при которых каждый из предикатов
принимает значение «ложь», и принимает
значение «истина» во всех остальных
случаях.

Очевидно, что областью истинностью
предиката

является
.

Отрицанием предиката P(x)
называется новый предикат
,
который равен 0 при всех значениях
,
при которых P(x)
равен значению «истина», и равен 1 при
всех значениях
,
при которых P(x)
равен значению «ложь».

Очевидно, что областью истинностью
предиката

является
.

Импликацией предикатов P(x)
и Q(x)
называется новый предикат
,
который равен 0 при тех и только при тех
значениях
,
при которых P(x)
принимает значение «истина», а Q(x)
— значение «ложь», и принимает значение
«истина» во всех остальных случаях.

Очевидно, что областью истинностью
предиката

является
.

Задача 1

Заданы предикаты
,
и

на множестве натуральных чисел N:
:
«число Х делится на 5»

:
«число Х четное».

Найти область истинности предикатов

,

,

.

Решение

Так как I_p
= {5, 10, 15, 20, …. 5n,
..} и I_Q
= {2, 4, 6, 8, 10, … 2n,
..}, то

={10,
20, …,20n,..},

={2,
4, 5, 6, 8, 10, … 2n,5n,
..},

={5,
10, 15,… ,5n,
..}
{1, 3, 5, … 2n-1,
..}= {1, 3, 5, 7, 9, 10, … 2n-1,5n,
..}.

Задача 2

Задан
предикат
:>0
на
множестве рациональных чисел R.
Найти
область истинности предиката
.

Решение

Найдем область, на которой данный
предикат может быть определен. Поскольку
знаменатель дроби не может быть равен
0, то
.
Для того, чтобы наша дробь была
положительной, необходимо, чтобы знаки
числителя и знаменателя совпадали:

Отсюда

Кванторные
операции над предикатами

Задан предикат,
определенный на множестве М.
Если а — некий элемент из
множества М, то его подстановка
вместо х в предикат,
превращает этот предикат в высказывание

.

В логике предикатов существуют две
кванторные операции, которые превращают
одноместный предикат в высказывание и
связывают переменные.

Пусть задан предикат,
определенный на множестве М.

Тогда под выражением
понимаем
высказывание, истинное тогда и только
тогда, когда

истинен для каждого элемента х
из М, и ложное в противном
случае. Это высказывание не зависит от
х, его словесное выражение
выглядит так «Для любого х

истинно». Символ

называется квантором всеобщности.

Переменная х в предикате

свободна, в высказывании

переменная х связана квантором
всеобщности.

Под выражением
понимаем
высказывание, истинное тогда и только
тогда, когда существует элемент х
из М, для которого

истинен, и ложное в противном
случае. Это высказывание не зависит от
х, его словесное выражение
выглядит так «Существует х, для
которого

истинно». Символ

называется квантором существования.

Переменная х в предикате

свободна, в высказывании

переменная х связана квантором
существования.

Кванторные
операции применяются и к многоместным
предикатам.

Например, применение кванторной операции

к двухместному предикату, превращает
его в одноместный, зависящий только от
переменной y.

Рассмотрим предикат
,
определенный на множестве M={a₁,
a₂,…,a_n}.
Если

тождественно истинен, то истинными
будут высказывания
….
При этом истинными будут выказывание


и конъюнкция
.
Если найдется хотя бы один элемент
a_j
из М, на котором
,
то ложными будут высказывания

и конъюнкция
.
Следовательно, существует равносильность

Рассмотрим предикат
,
определенный на множестве M={a₁,
a₂,…,a_n}.
Если

тождественно ложен, то ложными будут
высказывания
….
При этом ложными будут выказывание


и дизъюнкция
.
Если найдется хотя бы один элемент
a_j
из М, на котором
,
то истинными будут высказывания

и дизъюнкция
.
Следовательно, существует равносильность

Таким
образом, кванторные операции можно
трактовать, как обобщение дизъюнкции
и конъюнкции на случай бесконечных
множеств.

Исчисление предикатов

Исчисление предикатов – это формальная
теория, в которой определены следующие
компоненты [2].

Алфавит:

связки основные

вспомогательные

служебные символы ( , )

кванторы всеобщности

существования

предметные константы a,
b,…a₁,
b₁,

переменные x,y,….x₁,y₁

предметные предикаты P,
Q, R,
….

функторы f,
g, h,….

Формулы: (определены в нотации
Бэкуса-Наура)

<формула> ::=
<атом> ││<формула>
<формула>
│

<переменная>
<формула> │
<переменная><формула>

<атом> ::=
<предикат>( <список термов> )

<список
термов> ::= <терм> │<терм> , <список
термов>

<терм> ::=
<константа> │<переменная> │<функтор>
(<список термов> )

Аксиомы:

Кроме того, выполняется любая система
аксиом исчисления высказываний.

Правила вывода:

,
,

Исчисление предикатов, в котором кванторы
могут связывать только предметные
переменные, но не предикаты или функторы,
называется исчислением первого
порядка.

Исчисления, в которых кванторы связывают
не только предметные переменные, но и
предикаты, функторы и т.д., называются
исчислениями высших порядков.

Равносильные формулы

Рассмотрим основные равносильности
исчисления предикатов. Их можно разбить
на четыре группы [1,3].

1. Равносильности для двойственности

2. Равносильности для конъюнкции и
квантора всеобщности

3. Равносильности для дизъюнкции и
квантора существования

4. Вынесение константы

Задача 3

Доказать равносильность.

Решение

Если предикаты P(x)
и Q(x)
тождественно истинны, то тождественно
истинен предикат
,
а поэтому, будут истинны высказывания

т.е. обе части равносильности принимают
значение истина.

В случае, если один из предикатов,
например,
,
( а как следствие
)
будет не тождественно истинен, то ложными
будут

Предваренная нормальная
форма

Говорят, что формула исчисления предикатов
имеет нормальную форму, если она содержит
только операции конъюнкция, дизъюнкция
и кванторные операции, а оперция отрицания
отнесена к элементарным формулам.

Например, приведение формулы к нормальной
форме выглядит следующим образом.

Среди нормальных форм выделяют
предваренные нормальные формы (ПНФ), в
которых кванторные операции либо
полностью отсутствуют, либо они
используются после всех операций алгебры
логики.

Например, приведем рассматриваемую
формулу к ПНФ

=

=

А для формулы необходимы следующие
преобразования.

Теорема

Всякая
формула исчисления предикатов может
быть приведена к предваренной нормальной
форме

Общезначимость и
выполнимость

Формула А выполнима в области
М, если существуют значения
переменных, входящих в эту формулу и
отнесенных к области М, при
которых формула принимает истинные
значения.

Формула А выполнима, если
существует область, на которой она
выполнима.

Формула А тождественно истинна в
области М, если она принимает
истинные значения для всех значений
переменных, входящих в эту формулу и
отнесенных к этой области.

Формула А тождественно ложна в
области М, если она принимает ложные
значения для всех значений переменных,
входящих в эту формулу и отнесенных к
этой области.

Формула А общезначима, если она
тождественно истинна во всякой области.

Разрешимость

Проблема разрешимости для исчисления
предикатов ставится стандартно:
существует ли алгоритм, позволяющий
для любой формулы установить, является
ли она общезначимой, выполнимой или
тождественно ложной?

Ответ на этот вопрос для бесконечных
областей дает теорема Черча.

Теорема Черча

Проблема
разрешимости исчисления предикатов в
общем виде неразрешима

Очевидно, что проблема разрешимости
для конечных областей разрешима.

Литература

1. Лихтарникова
   Л.М., Сукачева Т.Г. Математическая
   логика/Курс лекций. — СПб.: Издательство
   «Лань», 1998.-288с

2. .Новиков Ф.А.
   Дискретная математика для программистов.
   — СПб.: Питер, 2001. – 304с

3. Горбатов В.А.
   Фундаментальные основы дискретной
   математики. — М.: Наука. Физматлит,
   1999.-544с

Соседние файлы в папке ДМ_К1

• #

  10.05.2014205.31 Кб291.doc

• #

  10.05.2014198.66 Кб3710.doc

• #
• #
• #

  10.05.2014158.21 Кб942.doc

• #

  10.05.2014144.9 Кб473.doc

• #

  10.05.2014123.39 Кб244.doc

• #

  10.05.2014127.49 Кб235.doc

• #

  10.05.2014119.81 Кб246.doc

Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.

Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.

Как пользоваться калькулятором

1. Введите в поле логическую функцию (например, x1 ∨ x2) или её вектор (например, 10110101)
2. Укажите действия, которые необходимо выполнить с помощью переключателей
3. Укажите, требуется ли вывод решения переключателем «С решением»
4. Нажмите на кнопку «Построить»

Видеоинструкция к калькулятору

Используемые символы

В качестве переменных используются буквы латинского и русского алфавитов (большие и маленькие), а также цифры, написанные после буквы (индекс переменной). Таким образом, именами переменных будут: a, x, a1, B, X, X1, Y1, A123 и так далее.

Для записи логических операций можно использовать
как обычные символы клавиатуры (*, +, !, ^, ->, =), так и символы, устоявшиеся в литературе (∧, ∨, ¬, ⊕, →, ≡). Если на вашей клавиатуре отсутствует нужный символ операции, то используйте клавиатуру калькулятора (если она не видна, нажмите «Показать клавиатуру»), в которой доступны как все логические операции, так и набор наиболее часто используемых переменных.

Для смены порядка выполнения операций используются круглые скобки ().

Обозначения логических операций

• И (AND): & • ∧ *
• ИЛИ (OR): ∨ +
• НЕ (NOT): ¬ !
• Исключающее ИЛИ (XOR): ⊕ ^
• Импликация: -> → =>
• Эквивалентность: = ~ ≡ <=>
• Штрих Шеффера: ↑ |
• Стрелка Пирса: ↓

Что умеет калькулятор

• Строить таблицу истинности по функции
• Строить таблицу истинности по двоичному вектору
• Строить совершенную конъюнктивную нормальную форму (СКНФ)
• Строить совершенную дизъюнктивную нормальную форму (СДНФ)
• Строить полином Жегалкина (методами Паскаля, треугольника, неопределённых коэффициентов)
• Определять принадлежность функции к каждому из пяти классов Поста
• Строить карту Карно
• Минимизировать ДНФ и КНФ
• Искать фиктивные переменные

Что такое булева функция

Булева функция f(x1, x2, ... xn) — это любая функция от n переменных x₁, x₂, … x_n, в которой её аргументы принимают одно из двух значений: либо 0, либо 1, и сама функция принимает значения 0 или 1. То есть это правило, по которому произвольному набору нулей и единиц ставится в соответствие значение 0 или 1. Подробнее про булевы функции можно посмотреть на Википедии.

Что такое таблица истинности?

Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица состоит из n+1 столбцов и 2n строк, где n — число используемых переменных. В первых n столбцах записываются всевозможные значения аргументов (переменных) функции, а в n+1-ом столбце записываются значения функции, которые она принимает на данном наборе аргументов.

Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.

Логические операции

Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).

Таблица истинности логических операций

Как задать логическую функцию

Есть множество способов задать булеву функцию:

• таблица истинности
• характеристические множества
• вектор значений
• матрица Грея
• формулы

Рассмотрим некоторые из них:

Чтобы задать функцию через вектор значений необходимо записать вектор из 2ⁿ нулей и единиц, где n — число аргументов, от которых зависит функция. Например, функцию двух аргументов можно задать так: 0001 (операция И), 0111 (операция ИЛИ).

Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c

Способы представления булевой функции

С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:

• Совершенная дизъюнктивная нормальная форма (СДНФ)
• Совершенная конъюнктивная нормальная форма (СКНФ)
• Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Совершенная дизъюнктивная нормальная форма (ДНФ)

Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.

Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.

Совершенная конъюнктивная нормальная форма (КНФ)

Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.

Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.

Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.

Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1

Алгоритм построения СДНФ для булевой функции

1. Построить таблицу истинности для функции
2. Найти все наборы аргументов, на которых функция принимает значение 1
3. Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
4. Объединить все простые конъюнкции с помощью дизъюнкции

Алгоритм построения СКНФ для булевой функции

1. Построить таблицу истинности для функции
2. Найти все наборы аргументов, на которых функция принимает значение 0
3. Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
4. Объединить все простые дизъюнкции с помощью конъюнкции

Алгоритм построения полинома Жегалкина булевой функции

Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.

1. Построить таблицу истинности для функции
2. Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
3. Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
4. Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
5. Выписать булевы наборы, на которых значение последнего столбца равно единице
6. Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.

Примеры построения различных представлений логических функций

Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬ab∨¬bc∨ca

1. Построим таблицу истинности для функции

---

Построение совершенной дизъюнктивной нормальной формы:

Найдём наборы, на которых функция принимает истинное значение: { 0, 0, 1 } { 0, 1, 0 } { 0, 1, 1 } { 1, 0, 1 } { 1, 1, 1 }

В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:

K₁: { 0, 0, 1 } — ¬a¬bc
K₂: { 0, 1, 0 } — ¬ab¬c
K₃: { 0, 1, 1 } — ¬abc
K₄: { 1, 0, 1 } — a¬bc
K₅: { 1, 1, 1 } — abc

Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:

K₁ ∨ K₂ ∨ K₃ ∨ K₄ ∨ K₅ = ¬a¬bc ∨ ¬ab¬c ∨ ¬abc ∨ a¬bc ∨ abc

---

Построение совершенной конъюнктивной нормальной формы:

Найдём наборы, на которых функция принимает ложное значение: { 0, 0, 0 } { 1, 0, 0 } { 1, 1, 0 }

В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:

D₁: { 0, 0, 0 } — a∨b∨c
D₂: { 1, 0, 0 } — ¬a∨b∨c
D₃: { 1, 1, 0 } — ¬a∨¬b∨c

Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:

D₁ ∧ D₂ ∧ D₃ = (a∨b∨c) ∧ (¬a∨b∨c) ∧ (¬a∨¬b∨c)

---

Построение полинома Жегалкина:

Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:

Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:

Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:

Окончательно получим такую таблицу:

Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):

{ 0, 0, 1 } — c, { 0, 1, 0 } — b, { 0, 1, 1 } — bc, { 1, 1, 0 } — ab, { 1, 1, 1 } — abc

Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc