Предикаты. Операции над предикатами
При изучении высказываний мы отмечали, что утверждение с переменными не является высказыванием. Можно, например, рассмотреть предложение %%P(x) : x^2 + 1 > 2%% с переменной %%x in mathbb R%%. Это предлождение не является высказыванием, так как нельзя сказать истинно оно или ложно. Однако, если заменить переменную %%x%% на какое-либо значение, например, %%x = 1%%, получаем высказывание %%2 > 2%%, которое является ложным. Заменив переменную %%x%% на значение %%x = 2%%, получим истинное высказывание %%5 > 2%%. Итак есть выражение %%P(x)%% не являющиееся высказыванием, но превращающееся в него при замене переменной %%x%% на ее произвольное значение из соответствующего множества.
Определение
Одноместным предикатом, определенным на множестве %%D%%, называется предложение с переменной, которое превращается в высказывание при замене этой переменной на ее значение из множества %%D%%. Одноместный предикат будем называть унарным или предикатом от одной переменной.
Примеры
Следующие предложения являются одноместными предикатами:
- %%P(x): x^ 2 + 1 > 2%%, где %%D%% — множество действительных чисел.
- %%Q(x):%% Длина отрезка равна %%1%%, где %%D%% — множество всех отрезков прямой.
Следующие предложения не являются одноместными предикатами:
- %%1 > 2%%.
- Прямая %%x%% параллельна прямой %%y%%.
%%n%%-местный предикат
%%n%%-местым предикатом с областью определения %%D = D_1 times D_2 times ldots times D_n%% называется предикат %%P(x_1, x_2, ldots, x_n)%% от %%n%% переменных, который превращается в высказывание при замене переменных %%x_1, x_2, ldots, x_n%% на их значения из множеств %%D_1, D_2, ldots, D_n%% соответственно.
Тогда предложение прямая %%x%% параллельна прямой %%y%% является двуместным предикатом %%P(x, y)%%, где %%X, Y%% — множество всех прямых.
Область определения предиката
Рассмотрим %%n%%-местный предикат %%P(x_1, x_2, ldots, x_n)%%. В этом случае переменные берутся из множеств %%D_1, D_2, ldots, D_n%% соответственно. Можно рассмотреть множество %%D = D_1 times D_2 times ldots times D_n%% — декартово произведение множеств %%D_1, D_2, ldots, D_n%%, элементами которого являются всевозможные упорядоченные %%n%%-ки %%(d_1, d_2, ldots, d_n)%% элементов исходных множеств.
Множество %%D%% называется областью определения предиката.
Область истинности
Областью истинности предиката %%P(x_1, x_2, ldots, x_n)%% называется множество всех %%n%%-ок %%(d_1, d_2, ldots, d_n) in D%% таких, что при замене %%x_1%% на %%d_1%%, %%x_2%% на %%d_2%%, …, %%x_n%% на %%d_n%% получается истинное высказывание.
Пример
На множестве %%D = { 1, 2, 3, 4, 5, 6, 7, 8, 9}%% рассмотрим одноместный предикат %%P(x): x%% — простое число. Найти область истинности предиката %%P(x)%%.
Обозначим область истинности буквой %%A%%. Тогда %%A%% состоит из таких элементов, при которых выполняется предикат %%P(x)%%. Поэтому %%A = {2, 3, 5, 7}%%.
Операции над предикатами
Аналогично операциям для высказываний вводятся операции для предикатов.
Пусть %%P(x)%% и %%Q(x)%% — одноместные предикаты, определенные на множестве %%D%%.
Отрицанием предиката %%P(x)%% называется новый предикат, обозначаемый %%overline{P(x)}%% и являющийся ложным для тех и только тех %%x%%, для которых предикат %%P(x)%% истинный.
Конъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) land Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% истинны.
Дизъюнкцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) lor Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% ложны.
Импликацией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) rightarrow Q(x)%% и являющийся ложным для тех и только тех %%x%%, для которых предикаты %%P(x)%% истинный, а %%Q(x)%% ложный.
Эквиваленцией предикатов %%P(x)%% и %%Q(x)%% называется новый предикат, обозначаемый %%P(x) leftrightarrow Q(x)%% и являющийся истинным для тех и только тех %%x%%, для которых предикаты %%P(x)%% и %%Q(x)%% имеют одинаковые значения.
Применяя операции над предикатами, мы получаем составные предикаты, которые будем называть формулами алгебры предикатов.
Предикаты %%P(x)%% и %%Q(x)%% эквивалентные , если для любого значения переменной %%x%% их значения истинности совпадают. Обозначают $$P(x) equiv Q(x).$$
Законы алгебры предикатов
Для предикатов справедливы все законы, аналогичные законам алгебры логики высказываний1.
В случае тождественно истинных и тождественно ложных предикатов имеем следующие определения.
Предикат %%P(x_1, x_2, ldots, x_n)%% называется тождественно истинным если при любой замене переменных %%x_1, x_2, ldots, x_n%% на их значения предикат превращается в истинное высказывание.
Предикат %%P(x_1, x_2, ldots, x_n)%% называется тождественно ложным если при любой замене переменных %%x_1, x_2, ldots, x_n%% на их значения предикат превращается в ложное высказывание.
Высказывание является частным случаем предиката, когда в предикате нет переменных. То есть высказывание является предикатом %%0%% порядка (от %%0%% переменных).
1. Законы алгебры логики высказываний.
Определение. Предикатом называется повествовательное предложение, содержащее предметные переменные, определённые на соответствующих мно- жествах; при замене переменных конкретными значениями (элементами) этих множеств предложение обращается в высказывание, т. е. принимает значение «истинно» или «ложно».
Определение. Предикатом называется функция P : M n → B , где B = { 0,1 } , M — любое множество, 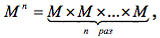
Множество M называется предметной областью предиката P ,
x1 , x2 ,…, xn — предметные переменные,
P — предикатный символ,
n — местность предиката,
декартово произведение M × M × … × M область определения предиката P .
Обозначение: P (x1 , x2 ,…, xn— n — местный предикат, заданный на множестве M .
Определение. Областью истинности предиката P называется подмножество Ip ⊆ Mn его предметной области, на элементах которого значения предиката равны 1.
Область истинности предиката, выраженного предикатной формулой, определяется областями истинности составляющих и применяемыми в формуле операциями: IPvQ = IP ∪ IQ, IP ∧ Q = IP ∩ IQ , IP→Q = IP ∪ IQ, I P = IP .
Задача 3.1. Найти область истинности предиката
P ( X, Y ) = (( X + Y ) — нечётно ) ∨ (( X — Y ) делятся на 3) , где X = {1;3;6;7}, Y = {2;4;5}.
Решение.
Составим таблицы истинности для предикатов P1 ( X, Y ) = (( X + Y) — нечётно), P2( X, Y ) = (( X — Y ) — делятся на 3) , P = P1 ∨ P2.
IP = I P1∨P2 = IP1 ∪ IP2 = {(1,2), (1,4), (3,2), (3,4), (6,5), (7,2), (7,4)} ∪ {(1,4), (7,4)} = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.
Ответ: IP = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.
Задача 3.2. Найти область истинности предиката
P ( X ) = (( число 3 не делитель x ) → ( x ≤ 6 ))
на множестве однозначных натуральных чисел.
Решение.
Определим области истинности предикатов P1 = {число 3 не не делитель x},
P2 = {x ≤ 6}, P = P1→ P2 .
IP1 = {1,2,4,5,7,8}, IP2 = {1,2,3,4,5,6}, IP = IP1→P2 = IP1 = {1,2,3,4,5,6,9}.
Ответ: I P = {1,2,3,4,5,6,9}.
Задачи для самостоятельного решения
Найти область истинности предиката
- P ( X, Y ) = ((( X — Y ) — нечетно ) ∧ ( min ( X, Y) — четно )), где X = {2;5;6;8};
- P ( X ,Y ) = (( X + Y )) — делится на 3) → (( X + Y ) > 5), где X = {2;5;6;8}, Y = {3;6;9};
- P ( X, Y ) = ((( X — Y ) — нечётно ) ∧ ( |Y-X| ≤ 1 )), где X = {5;8;9}, Y = {4;7;8;10};
- P ( X, Y ) = (( X — Y ) — чётно ) ∨ (( X + Y ) — делится на 3), где X = {5;8;9}, Y = {4;7;8;10};
- P ( X ) = (( число 3 делитель x ) ∨ ( x ≤ 6 )), заданного на множестве однозначных натуральных чисел;
- P ( X ) = ((( число 3 делитель x ) ∧ ( x > 6 )), заданного на множестве однозначных натуральных чисел;
- P ( X ) = (( x ≥ 3 ) ∧ ( x ≤ 10 )), заданного на множестве всех действительных чисел;
- P ( X ) = (( x2 ≤ 4 ) ∧ ( x -1 ≥ 1 )), заданного на множестве всех действительных чисел;
- P ( X ) = (( x ≤ 0 ) ∧ ( x2 — 2x ≤ 0 )), заданного на множестве всех действительных чисел;
- P ( X ) = (( x3 — 6x2 +11x — 6 = 0 ) ∧ ( x2 — 4x + 3 = 0 )),заданного на множестве всех действительных чисел.
Гусева
А.И. Дискретная
математика: Математическая логика
Лекции 14-15
Исчисление
предикатов
Основные понятия
Одноместным предикатом P(x)
называется всякая функция одного
переменного, аргумент который х
определен на некотором множестве М,
а значение функции определены на
множестве {0,1}[1].
Множество М, на котором задан
предикат, называется областью
определения предиката.
Множество Ip,
на котором предикат принимает только
истинные значения, называется областью
истинности предиката P(x).
Предикат P(x)
называется тождественно истинным
(тождественно ложным) на множестве
М, если Ip=М
(Ip=0).
N-местным
предикатом Q(x1,
x2,…,xn)
называется всякая функция n
переменных, определенная на множестве
и принимающая значение на множестве
{0,1}.
Предикат P(x)
является следствием Q(x)
()
, если
Предикаты P(x)
и Q(x)
равносильны (),
если
,
т.е. они являются следствием друг друга.
Логические операции над предикатами
Так как предикаты принимают значения
0 и 1, к ним можно применять все операции
алгебры высказываний. Пусть на некотором
множестве М заданы два предиката P(x)
и Q(x).
Конъюнкцией двух предикатов
P(x)
и Q(x)
называется новый предикат
,
который равен 1 при тех и только при тех
значениях
,
при которых каждый из предикатов
принимает значение «истина», и принимает
значение «ложь» во всех остальных
случаях.
Очевидно, что областью истинностью
предиката
является
.
Дизъюнкцией двух предикатов
P(x)
и Q(x)
называется новый предикат
,
который равен 0 при тех и только при тех
значениях
,
при которых каждый из предикатов
принимает значение «ложь», и принимает
значение «истина» во всех остальных
случаях.
Очевидно, что областью истинностью
предиката
является
.
Отрицанием предиката P(x)
называется новый предикат
,
который равен 0 при всех значениях
,
при которых P(x)
равен значению «истина», и равен 1 при
всех значениях
,
при которых P(x)
равен значению «ложь».
Очевидно, что областью истинностью
предиката
является
.
Импликацией предикатов P(x)
и Q(x)
называется новый предикат
,
который равен 0 при тех и только при тех
значениях
,
при которых P(x)
принимает значение «истина», а Q(x)
— значение «ложь», и принимает значение
«истина» во всех остальных случаях.
Очевидно, что областью истинностью
предиката
является
.
Задача 1
Заданы предикаты
,
и
на множестве натуральных чисел N:
:
«число Х делится на 5»
:
«число Х четное».
Найти область истинности предикатов
,
,
.
Решение
Так как Ip
= {5, 10, 15, 20, …. 5n,
..} и IQ
= {2, 4, 6, 8, 10, … 2n,
..}, то
={10,
20, …,20n,..},
={2,
4, 5, 6, 8, 10, … 2n,5n,
..},
={5,
10, 15,… ,5n,
..}
{1, 3, 5, … 2n-1,
..}= {1, 3, 5, 7, 9, 10, … 2n-1,5n,
..}.
Задача 2
Задан
предикат
:
>0
на
множестве рациональных чисел R.
Найти
область истинности предиката
.
Решение
Найдем область, на которой данный
предикат может быть определен. Поскольку
знаменатель дроби не может быть равен
0, то
.
Для того, чтобы наша дробь была
положительной, необходимо, чтобы знаки
числителя и знаменателя совпадали:
Отсюда
Кванторные
операции над предикатами
Задан предикат,
определенный на множестве М.
Если а — некий элемент из
множества М, то его подстановка
вместо х в предикат,
превращает этот предикат в высказывание
.
В логике предикатов существуют две
кванторные операции, которые превращают
одноместный предикат в высказывание и
связывают переменные.
Пусть задан предикат,
определенный на множестве М.
Тогда под выражением
понимаем
высказывание, истинное тогда и только
тогда, когда
истинен для каждого элемента х
из М, и ложное в противном
случае. Это высказывание не зависит от
х, его словесное выражение
выглядит так «Для любого х
истинно». Символ
называется квантором всеобщности.
Переменная х в предикате
свободна, в высказывании
переменная х связана квантором
всеобщности.
Под выражением
понимаем
высказывание, истинное тогда и только
тогда, когда существует элемент х
из М, для которого
истинен, и ложное в противном
случае. Это высказывание не зависит от
х, его словесное выражение
выглядит так «Существует х, для
которого
истинно». Символ
называется квантором существования.
Переменная х в предикате
свободна, в высказывании
переменная х связана квантором
существования.
Кванторные
операции применяются и к многоместным
предикатам.
Например, применение кванторной операции
к двухместному предикату, превращает
его в одноместный, зависящий только от
переменной y.
Рассмотрим предикат
,
определенный на множестве M={a1,
a2,…,an}.
Если
тождественно истинен, то истинными
будут высказывания
…
.
При этом истинными будут выказывание
и конъюнкция
.
Если найдется хотя бы один элемент
aj
из М, на котором
,
то ложными будут высказывания
и конъюнкция
.
Следовательно, существует равносильность
Рассмотрим предикат
,
определенный на множестве M={a1,
a2,…,an}.
Если
тождественно ложен, то ложными будут
высказывания
…
.
При этом ложными будут выказывание
и дизъюнкция
.
Если найдется хотя бы один элемент
aj
из М, на котором
,
то истинными будут высказывания
и дизъюнкция
.
Следовательно, существует равносильность
Таким
образом, кванторные операции можно
трактовать, как обобщение дизъюнкции
и конъюнкции на случай бесконечных
множеств.
Исчисление предикатов
Исчисление предикатов – это формальная
теория, в которой определены следующие
компоненты [2].
Алфавит:
связки основные
вспомогательные
служебные символы ( , )
кванторы всеобщности
существования
предметные константы a,
b,…a1,
b1,
переменные x,y,….x1,y1
предметные предикаты P,
Q, R,
….
функторы f,
g, h,….
Формулы: (определены в нотации
Бэкуса-Наура)
<формула> ::=
<атом> ││<формула>
<формула>
│
<переменная>
<формула> │
<переменная><формула>
<атом> ::=
<предикат>( <список термов> )
<список
термов> ::= <терм> │<терм> , <список
термов>
<терм> ::=
<константа> │<переменная> │<функтор>
(<список термов> )
Аксиомы:
Кроме того, выполняется любая система
аксиом исчисления высказываний.
Правила вывода:
,
,
Исчисление предикатов, в котором кванторы
могут связывать только предметные
переменные, но не предикаты или функторы,
называется исчислением первого
порядка.
Исчисления, в которых кванторы связывают
не только предметные переменные, но и
предикаты, функторы и т.д., называются
исчислениями высших порядков.
Равносильные формулы
Рассмотрим основные равносильности
исчисления предикатов. Их можно разбить
на четыре группы [1,3].
1. Равносильности для двойственности
2. Равносильности для конъюнкции и
квантора всеобщности
3. Равносильности для дизъюнкции и
квантора существования
4. Вынесение константы
Задача 3
Доказать равносильность.
Решение
Если предикаты P(x)
и Q(x)
тождественно истинны, то тождественно
истинен предикат
,
а поэтому, будут истинны высказывания
т.е. обе части равносильности принимают
значение истина.
В случае, если один из предикатов,
например,
,
( а как следствие
)
будет не тождественно истинен, то ложными
будут
Предваренная нормальная
форма
Говорят, что формула исчисления предикатов
имеет нормальную форму, если она содержит
только операции конъюнкция, дизъюнкция
и кванторные операции, а оперция отрицания
отнесена к элементарным формулам.
Например, приведение формулы к нормальной
форме выглядит следующим образом.
Среди нормальных форм выделяют
предваренные нормальные формы (ПНФ), в
которых кванторные операции либо
полностью отсутствуют, либо они
используются после всех операций алгебры
логики.
Например, приведем рассматриваемую
формулу к ПНФ
=
=
А для формулы необходимы следующие
преобразования.
Теорема
В
формула исчисления предикатов может
быть приведена к предваренной нормальной
форме
Общезначимость и
выполнимость
Формула А выполнима в области
М, если существуют значения
переменных, входящих в эту формулу и
отнесенных к области М, при
которых формула принимает истинные
значения.
Формула А выполнима, если
существует область, на которой она
выполнима.
Формула А тождественно истинна в
области М, если она принимает
истинные значения для всех значений
переменных, входящих в эту формулу и
отнесенных к этой области.
Формула А тождественно ложна в
области М, если она принимает ложные
значения для всех значений переменных,
входящих в эту формулу и отнесенных к
этой области.
Формула А общезначима, если она
тождественно истинна во всякой области.
Разрешимость
Проблема разрешимости для исчисления
предикатов ставится стандартно:
существует ли алгоритм, позволяющий
для любой формулы установить, является
ли она общезначимой, выполнимой или
тождественно ложной?
Ответ на этот вопрос для бесконечных
областей дает теорема Черча.
Теорема Черча
П
разрешимости исчисления предикатов в
общем виде неразрешима
Очевидно, что проблема разрешимости
для конечных областей разрешима.
Литература
-
Лихтарникова
Л.М., Сукачева Т.Г. Математическая
логика/Курс лекций. — СПб.: Издательство
«Лань», 1998.-288с -
.Новиков Ф.А.
Дискретная математика для программистов.
— СПб.: Питер, 2001. – 304с -
Горбатов В.А.
Фундаментальные основы дискретной
математики. — М.: Наука. Физматлит,
1999.-544с
Соседние файлы в папке ДМ_К1
- #
10.05.2014205.31 Кб291.doc
- #
10.05.2014198.66 Кб3710.doc
- #
- #
- #
10.05.2014158.21 Кб942.doc
- #
10.05.2014144.9 Кб473.doc
- #
10.05.2014123.39 Кб244.doc
- #
10.05.2014127.49 Кб235.doc
- #
10.05.2014119.81 Кб246.doc
Описание презентации по отдельным слайдам:
-
1 слайд
Понятие предиката. Область определения и область истинности предиката
-
2 слайд
1. Понятие предиката
Предложение «7 — простое число»
это истинное высказывание.Предложение «х — простое число»
это не высказывание.При одних значениях х это предложение дает истинное высказывание, а при других ложное.
-
3 слайд
1. Понятие предиката
Опр. Предложения с переменными, которые становятся высказываниями в результате замены переменных их допустимыми значениями, называются предикатами.Опр. Предикат с одной переменной называется одноместным, с двумя и более переменными — двуместным, трехместным и т.д.
Обозначение: P, Q, S, P(x), P(x;y).
-
4 слайд
1. Понятие предиката
Примеры:
1) P(x) — «х делится на 5»
2) Q(х) — «3х – 4 = 0»
3) P(x;y) — «х > у»
4) P(x;y;z) — «х + y = z» -
5 слайд
1. Понятие предиката
Если в предикате одну переменную заменить ее конкретным значением, то местность предиката уменьшается на 1.Т.к. одноместный предикат после подстановки вместо переменной конкретного значения превращается в высказывание, то высказывание – нульместный предикат
-
6 слайд
2. Область определения и
область истинности предиката
Область определения предиката (U) — это множество тех значений переменных, при которых предикат превращается в высказывание (т.е. можно определить истинно оно или ложно).
Область истинности предиката (I) — это те значения переменных, при которых предикат превращается в истинное высказывание.I является подмножеством U
-
7 слайд
2. Область определения и
область истинности предиката
Примеры:
1) Р(х) – «х –четное число»
UP = N
IP= {x| x = 2k, где k – натуральное число}
2) Q(x) – «2х – 3 = 0»
UQ = R,
IQ = {1,5}
3) P(x, y) – «х кратно у»
UP = N2
IP = {(x; y) | x делится на y} -
8 слайд
2. Область определения и
область истинности предиката
тождественно истинный
предикат
I = U
тождественно ложный
предикат
I = Ø
выполнимый предикат
I ⊂ U -
9 слайд
2. Область определения и
область истинности предиката
Напр.:
1) «(х – у)(х + у) = х2 – у2»
– тождественно истинный двуместный предикат
2) «х2 – 2х = 0»
– выполнимый одноместный предикат
3) «х + 1 = х»
– тождественно ложный одноместный предикат -
10 слайд
2. Область определения и
область истинности предиката
Опр. Два предиката называются эквивалентными (равносильными), если они определены на одном и том же множестве и их множества истинности совпадают. -
11 слайд
Определение области истинности предиката
На множестве М = {1, 2, 3…20} заданы предикаты. Сформулируйте следующие предикаты и найдите для каждого множества определения и истинности.
Вариант 1.
Р(Х) – «число Х кратно 5», Q(x) – «число Х четное»Вариант 2.
Р(Х) – «число Х кратно 5», R(x) – «число Х кратно 3», S(x) – «число Х составное»
Вариант 3.
Q(x) – «число Х четное», Р(Х) – «число Х кратно 5»
Вариант 4.
S(x) – «число Х составное», R(x) – «число Х кратно 3»
Занятие 19. Тема «Предикаты и операции над ними. Кванторы»
План лекции:
-
Понятие предиката
-
Основные множества для предикатов
-
Операции над предикатами
-
Кванторы. Операции навешивания квантора
Понятие предиката
В дискретной математике, как и в математической теории, основными неопределяемыми понятиями являются понятия суждение, истина, ложь. Суждение не может быть одновременно истинным и ложным. Например, все предложения, которые произносит человек, являются суждениями. Суждение, зависящее от переменной величины, которое при подстановке значений переменного становится высказыванием, называют предикатом. Для описания внутренней логической структуры простых высказываний используется понятие предиката. Сегодня мы изучим основные понятия предикатов, рассмотрим операции, совершаемые с предикатами.
Определение. Предложения, содержащие переменные, истинность или ложность которого зависит от значения переменного, входящего в него, называется предикатом. Другими словами, это функция, заданная на определенном множестве. Обозначение Р(х), Р(х,у), …, Р(х1,х2, …,хn).
Пример. Высказывание А=«Волк – это хищник»
Предикат Р(х)=«х – это хищник». Истинность Р(х) будет зависеть от того, что поставить вместо х, т.е. если поставим х=Лиса, то получим истину, а если поставим х=Коза, то получим ложь.
Основные множества для предикатов
-
Считается, что с каждым предикатом задано множество, из которого выбирают значение переменных. Такое множество называют областью определения предиката. Обозначение D(P).
Пример. Р(х)=«х+3 . Какое бы число не поставить вместо х, будем получать либо ложное либо истинное высказывание.

-
Подмножеством области определения предиката, на котором он принимает значение истинность, называется множеством истинности данного предиката. Обозначение М(Р). М(Р)
D(P).
Пример для Р(х)=«х+3
Значит, М(Р)=(-∞;3)
Операции над предикатами
Все операции будем рассматривать на примере Р(х)=«х-число, делящееся на 9», K(х)=«х-цифра». Для выполнения операций, нужно найти область определения предиката и множество истинности предиката и расписать эти множества как множество с перечислением элементов (с этого нужно начинать практическую), то есть
Для предиката Р(х)=«х-число, делящееся на 9»
D(P) ={1,2,3,4,5…95,96,97,98,…} М(Р) ={9,18,27,36,…,81,90,99,108,…}
K(х)=«х-цифра» D(К) ={1,2,3,4,5,6,7,8,9} М(К)={0,1,2,3,4,5,6,7,8,9}
-
Отрицанием предиката Р(х) называется новый предикат
, определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых предикат Р(х) ложен.
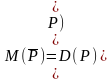
Пример. 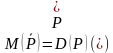
-
Конъюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)⋀Q(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых истины одновременно оба предиката P(x) и Q(x).
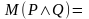
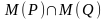
Пример. 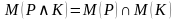
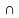
-
Дизъюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)VQ(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых истинен хотя бы один из предикатов P(x) и Q(x).
Пример.
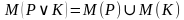
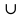
{0,1,2,3,4,5,6,7,8,9,18,27,36,…,81,90,99,108,…}
-
Импликацией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)
Q(x), определённый на множестве D(Р) и ложный при тех значениях переменных х, при которых предикат P(x) истинен, а предикат Q(x) ложен.
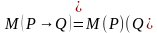
Пример. 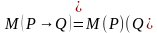
-
Эквиваленцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х) ↔ Q(x), определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых либо оба предиката истины, либо оба предиката ложны.
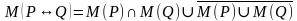
Пример.
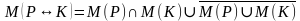
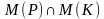

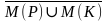
Кванторы. Операции навешивания квантора
Для количественных характеристик обычно используют понятия «все», «некоторые», «существуют» и др. В математике эти слова называются кванторами. От латинского слова quantum – сколько.
-
Операция, сопоставляющая предикату Р(х) высказывание «Для любого х имеет место Р(х)» — истинное, если М(Р) совпадает с D(Р), называется операцией навешивания квантора общности. Обозначается
— любой или
— для каждого, для любого, для всякого
Пример: если Р(х): «х+3=8» не известно истина оно или ложь, не подставляя значения, то (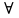
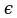
-
Операция, сопоставляющая предикату Р(х) высказывание «Существует х для Р(х)» — истинное, если М(Р)≠ǿ, называется операцией навешивания квантора существования. Обозначается
— существует или
— найдется х, существует х, для некоторого х.
Пример: если Р(х): «х+3=8» не известно истина оно или ложь, не подставляя значения, то ( х
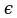
Предикатная формула – это формула, содержащая знаки булевых операций и кванторов, то есть в формуле участвуют: символы предметных переменных, символы предикатов, логические символы и символы кванторов.
Задания для самостоятельной работы
-
Объяснить, почему следующие выражения имеют значение истина или ложь, описать выражения словами
-
Для следующих предложений выделить предикаты и для каждого из них указать область истинности:
-
х+5=1;
-
х+2
-
однозначное число х кратно 3;
-
-
Пусть х определен на множестве людей М, а Р(х) – предикат «х – смертен». Дать словесную формулировку предикатной формулы
-
Пусть Р(х) – предикат «х – четное число», определенный на множестве М. Дать словесную формулировку высказыванию
, определить его истинность.
-
На множестве M = {3, 6, 9, 12, 42} определены предикаты: P(x) — «число Х делится на 6» и Q(x) — «число Х
30″. Найдите область истинности предикатов
,
,
,
,
-
Запишите приведенные ниже утверждения в символической форме, введя предикаты. В случае необходимости укажите предметную область.
а) Некоторые машины умнее людей.
б) Любой играет в теннис лучше Фрэда.
в) Для каждого действует существует равное и противоположно направленное противодействие.
г) Каждый игрок в гольф, в конце концов, будет обыгран более сильным игроком
Пользуясь этим и теоретическим материалом учебника М.С. Спирина «Дискретная математика» глава 5 п.5.3 стр.224, выполнить все задания.
Выполненное задание отправить на адрес https://vk.com/id52519522 в виде фото, сделанное из тетради.














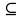 D(P).
D(P).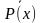 , определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых предикат Р(х) ложен.
, определённый на множестве D(Р) и истинный при тех значениях переменных х, при которых предикат Р(х) ложен. Q(x), определённый на множестве D(Р) и ложный при тех значениях переменных х, при которых предикат P(x) истинен, а предикат Q(x) ложен.
Q(x), определённый на множестве D(Р) и ложный при тех значениях переменных х, при которых предикат P(x) истинен, а предикат Q(x) ложен.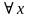 — для каждого, для любого, для всякого
— для каждого, для любого, для всякого