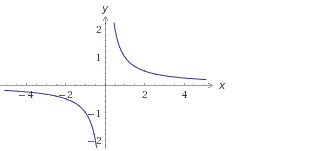
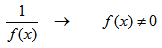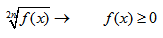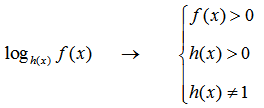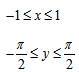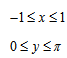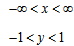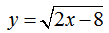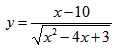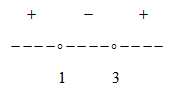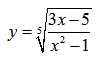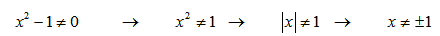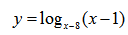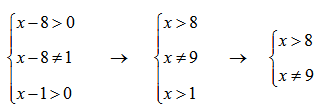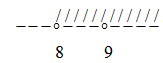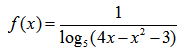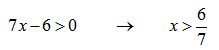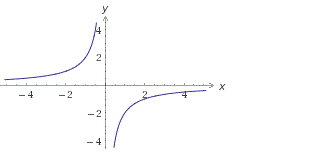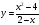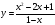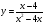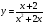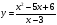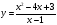Анализ дробно-рациональной функции. Асимптоты, экстремум
Функция $y=frac{k}{x}$ . Гипербола. Свойства.
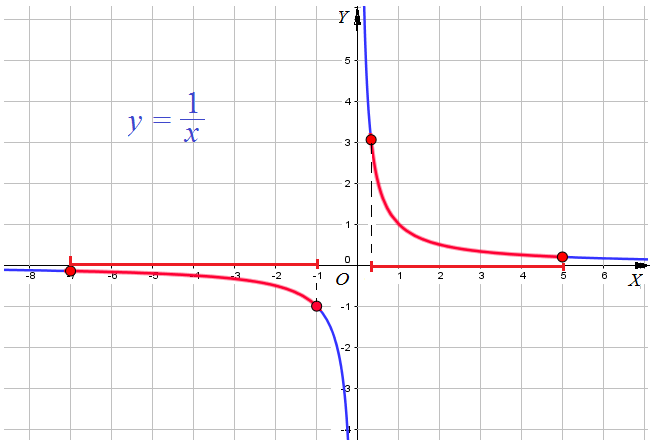
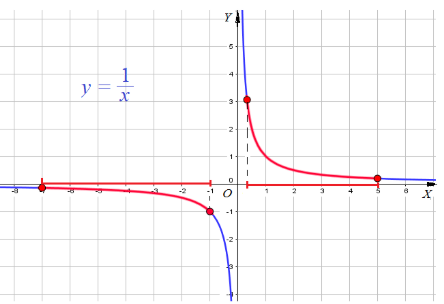
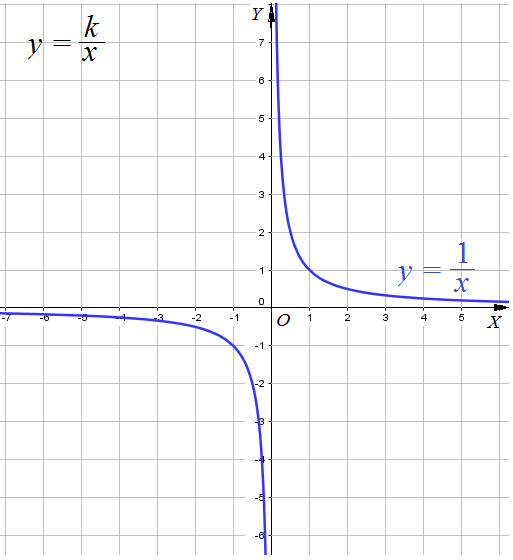
Пример 1: Построить график для функции $y=frac{1}{x}$, $fleft(xright)=frac{1}{x}$
- Вычислим значения функции в разнознаковых точках и нанесем точки с вычисленными координатами в системе $XOY$.
- $fleft(1right)=1$ $fleft(frac{1}{2}right)=2$ $fleft(-1right)=-1$ $x=-frac{1}{2}$ $fleft(-frac{1}{2}right)=-2$ $fleft(2right)=frac{1}{2}$ $fleft(frac{1}{4}right)=4$ $fleft(-frac{1}{4}right)=-4$ $fleft(4right)=frac{1}{4}$ $fleft(1right)=8$ $fleft(-4right)=-frac{1}{4}$ $fleft(-frac{1}{8}right)=-8$ .
- Точки Графика $(1;1)$, $(2;1/2)$, $(4;1/4)$, $(1/2;2)$, $(1/4;4)$, $(1/8;8)$, $(-1;-1)$, $(-2;-1/2)$, Еще точки: $(-4;-1/4)$, $(-1/2;-2)$, $(-1/4;-4)$, $(-1/8;-8)$ . По всем точкам построим кривые — график функции $y=frac{1}{x}$
- График имеет разрыв по вертикальной линии $x=0$. Ветви графика прижимаются к горизонтальной линии $y=0$.
Графиком функции $y=frac{k}{x}$ $kne0$ является гипербола , ветви прижимаются к асимптотическим линиям.
- если коэффициент $k > 0$ , в I и III координатных четвертях. Точка $(0;0)$ — центр симметрии.
- если $k < 0$ , то во II и IV координатных четвертях. Точка $(0;0)$ — центр симметрии.
- Асимптоты: Вертикальная асимптота, линия $x=0$, Горизонтальная асимптота, линия $y=0$
Cвойства функции $y=frac{k}{x}$ при $k > 0$ ( ветви гиперболы расположены в первом и третьем координатных углах) .
Свойство 1: Область Определения Функции — вся числовая прямая , кроме $x=0$. Свойство 2: $y > 0$ при $x > 0$; $y < 0$ при $x < 0$. Свойство 3: Функция убывает на промежутках $( — ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 4: Функция не ограничена ни снизу, ни сверху. Свойство 5: Ни наименьшего, ни наибольшего значений $у$ у функций нет. Свойство 6: Функция непрерывна на $( — ∞ ; 0 )$ и $( 0 ; + ∞)$. Свойство 7: Область значений функции — $( — ∞ ; 0 )$ U $( 0 ; + ∞)$. имеет разрыв в точке $x=0$.
Cвойства функции $y=frac{k}{x}$ при $k < 0$ (ветви гиперболы расположены во втором и четвертом координатных углах).
Свойство 1: Область Определения Функции — вся числовая прямая , кроме $x=0$. Свойство 2: $y > 0$ при $x < 0$ ; $y < 0$ при $x > 0$. Свойство 3: Функция возрастает на промежутках $( — ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 4: Функция не ограничена ни снизу, ни сверху. Свойство 5: Ни наименьшего, ни наибольшего значений $у$ у функций нет. Свойство 6: Функция непрерывна на $( — ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 7: Область значений функции — объединение $( — ∞ ; 0 )$ U $( 0 ; + ∞)$ . имеет разрыв в точке $x=0$.
Метод Замены для построения Графика Функции.
Мысль: Умеем строить график функции попроще … используем его для построения функции при «сдвинутых» аргументах и значениях.
Как построить график функции $y=kcdot fleft(xright)$, если известен график функции $y=fleft(xright)$.
- График $y=5cdot fleft(xright)$: Расстянуть вертикально вверх по оси $OY$ 5 раз все, что над $OX$ графика $y=fleft(xright)$ , $k$ раза.
- График $y=5cdot fleft(xright)$: Расстянуть вертикально вниз по оси $OY$ 5 раз все, что под $OX$ графика $y=fleft(xright)$ , $k$ раза.
- График $y=frac{1}{3}cdot fleft(xright)$: Сжать по вертикали, оси $OY$ график $y=fleft(xright)$ 3 раза.
- Еще способ: Перемасштабирование. Для $y=5cdot fleft(xright)$ … построить $y=fleft(xright)$, изменить масштаб: «1» станет «5», «-2» станет «-10», и т.д.
Как построить график функции $y=-fleft(xright)$, если известен график функции $y=fleft(xright)$.
- Эти функции принимают ровно противоположные значения. Значит: график $y=fleft(xright)$ надо отразить по оси $OX$, «перевернуть».
Как построить график функции $y=fleft(x+lright)$, если известен график функции $y=fleft(xright)$.
- Построить график $y=fleft(x+lright)$, где $l > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба влево.
- Построить график $y=fleft(x-lright)$, где $l < 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OX$ на $l$ единиц масштаба вправо.
Как построить график функции $y=fleft(xright)+m$, если известен график функции $y=fleft(xright)$.
- Построить график $y=fleft(xright)+m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вверх;
- Построить график $y=fleft(xright)-m$, где $m > 0$? Сдвинуть график $y=fleft(xright)$ вдоль оси $OY$ на $m$ единиц масштаба вниз.
Как построить график функции $y=fleft(x+lright)+m$, если известен график функции $y=fleft(xright)$.
- График функции $y=fleft(x+lright)+m$ можно получить из графика $y=fleft(xright)$ параллельными сдвигами по осям $OX$ и $OY$.
График Дробной Функции.
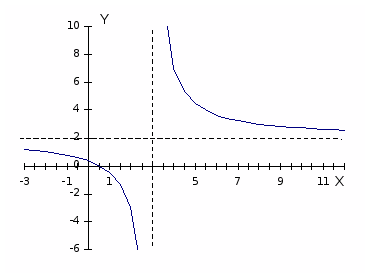
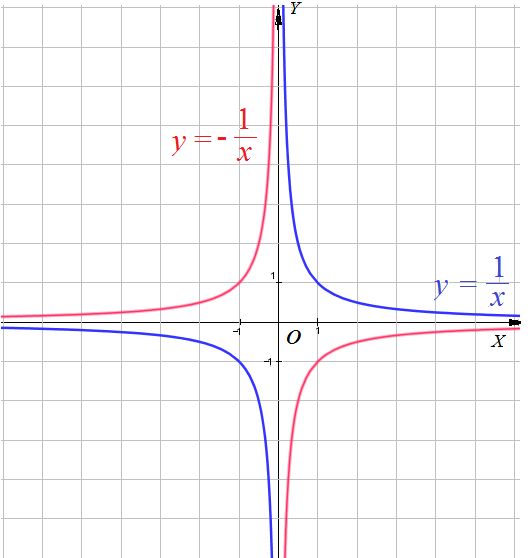
Пример 2: Построить график функции $y=-frac{5}{x+3}$ .
- сначала построим график функции $y=-frac{5}{x}$ … от графика $y=frac{1}{x}$ … отразим от $OX$ и растянем по вертикали 5 раз.
- сдвинем получившуюся гиперболу вдоль оси $OX$ на $3$ единицы влево, получится требуемый график.
- это гипербола с асимптотами $x=-3$; $y=0$. «почему так?» — как мы строим графики?
- берем несколько $x$ — точек и находим для каждого свои $y$ — значения в соответствии «с формулой функции».
- По точкам проводим график. Очевидно, если, скажем, $x=0,52$ функция $y=-frac{5}{x+3}$ дает какое-то значение,
- … то, конечно для $x=3,52$ другая функция, $y=-frac{5}{x}$ дает ровно такое же значение.
- значит, точки графиков будут различаться на $3$ единицы по $x$ — координате и совпадать по $y$ — координате.
- Ровно так и для всех точек. «Сравни две функции и вообрази их графики: каковы различия и что общего? «
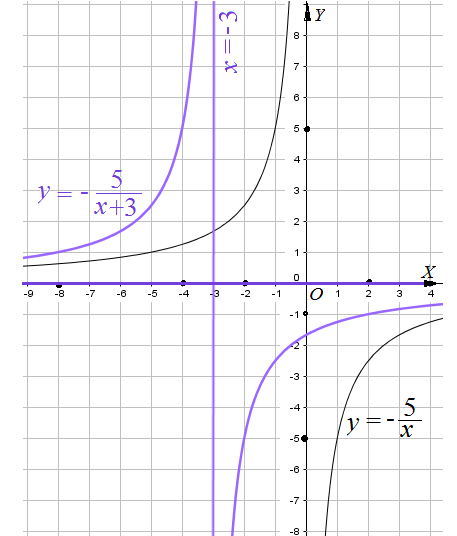
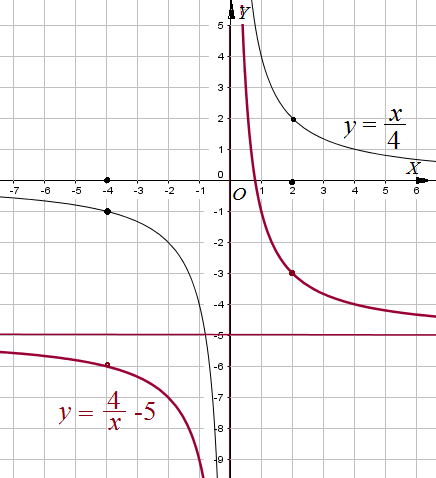
Пример 3: Построить график функции $y=frac{4}{x}-5$ .
- Сначала надо построить график функции $y=frac{4}{x}$ . Гиперболу $y=frac{1}{x}$ «растянем» четыре раза.
- Сдвинуть получившуюся гиперболу вдоль оси $OY$ на $5$ клеточек вниз. Т.к. каждое значение должно отличаться на 5 единиц.
- получится требуемый график. Это гипербола с асимптотами $x=0$; $y=-5$.
- Важно знать где пересекается с нулем. Решение, корень $frac{4}{x}-5=0$ дает абсциссу $x=0.8$. Точка графика $left(0,8;0right)$.
- Исследование: Найдем производное: $left(frac{4}{x}-5right)’=-frac{4}{x^2}$. Нигде не = 0, Экстремума нет!
- Производная для всех $x$ (кроме $0$) отрицательна — значит всюду убывает.
- Область Определения: $D_f=left(-infty;0right)+left(0;+inftyright)$ Область значений $E_f=left(-infty; -5right)+left(-5;+inftyright)$
- Знакопостоянство: $+Z_f=left(-infty;0,8right)$ — функция отрицательна, $-Z_f=left(0,8;+inftyright)$ — функция положительна.
- Монотонность: $+M_f=left(-infty;-3right)+left(-3;0right)$ — возрастает $-M_f=left(0;3right)+left(3;+inftyright)$ — функция убывает
Вертикальная асимптота ( $x=0$,) проходит в полюсе, точке разрыва функции. Точка обнуления знаменателя. Параллельно $OY$.
Горизонтальная асисмптота ( $y=-5$ ), линия, на которую «ложится» график при значениях $х$ около $+-infty$. Параллельно $OX$.
Гипербола — график простой дроби, две асимптоты делят на 4 четверти, ветви гиперболы «зажаты — прижаты» к асимптотическим линиям .
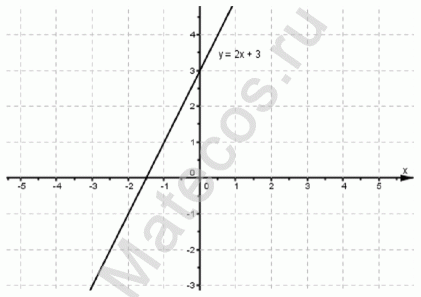
Наклонная асимптота — линия типа $y=2x+3$, к которой «прижимаются» ветви графика «на» или «около» + — бесконечнoсти.
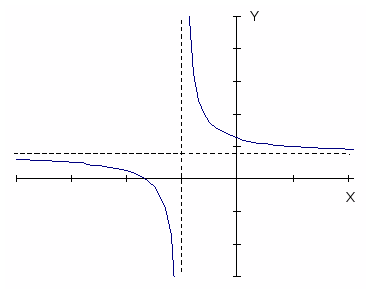
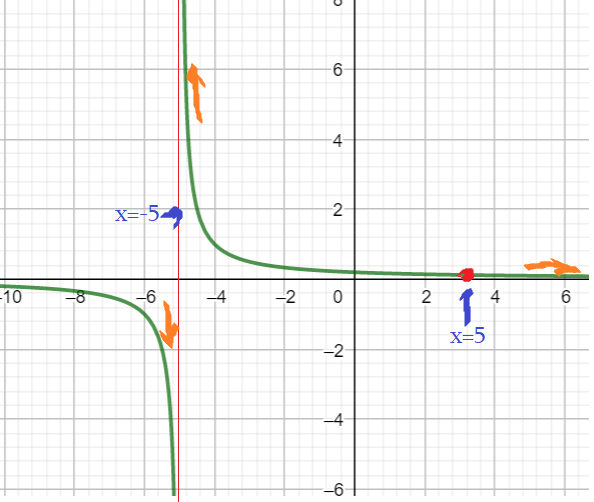
Пример 4: Построить график функции $y=frac{x-5}{x^2-25}$
- Если выражение функции упрощается, то следует это сделать. Ибо получится функция проще, легче вычисляемая и рисуемая.
- Тождественное преобразование, сокращение $frac{x-5}{x^2-25}=frac{x-5}{(x+5)(x-5)}=frac{1}{x+5}$. Так, что график $y=frac{1}{x+5}$ ?
- Не спеши! Мы сократили на $x-5$ , которое незаконно для $x=5$. Нарушается О.Д.З — в исходной функции нет места $x=5$.
- Значит: можем строить гиперболу $y=frac{1}{x+5}$ взамен нашей $y=frac{x-5}{x^2-25}$, но «без точки $x=5$».
- Точка $x=5$ разрывает «гладкий» график гиперболы. Она называется «выколотая точка с координатами $left(5;0,1right)$».
Важно уметь исследовать функцию — график около точек разрыва. + / — поблизости. Куда тянется?
- Исследуем около $x=-5$. Возьмем «близкие» точки $-5,01$ и $-4,99$. Вычислим приближенные значения.
- Чуть левее … $fleft(-5,01right)=frac{-5,01-5}{(-5,01)^2-5^2}approx -100$. Чуть правее … $fleft(-4,99right)=frac{-4,99-5}{(-4,99)^2-5^2}approx 100$.
- Прямая $x=-5$ — вертикальная асимптота. Ветвь слева прижимается «вниз», к $-infty$ . А справа поднимается вверх к $+infty$.
- Около $x=5$. Чуть левее $fleft(4,99right)=frac{4,99-5}{4,99^2-5^2}approx0,101$. $fleft(5,01right)=frac{5,01-5}{5,01^2-5^2}approx0,099$.
- Значит, $x=5$ точка разрыва, на графике выколотая точка $left(5;0,1right)$. Т.к. в ней $y=frac{1}{5+5}=0,1$.
- «О нулях»: при $x=0$ $y=0,2$ . Но функция нигде не обнуляется, $yne0$. Прямая $y=0$ — горизонтальная асимптота.
- Анализ: Найдем производное: $left(frac{x-5}{x^2-25}right)’=left(frac{1}{x+5}right)’=-frac{1}{left(x+5right)^2}$
- Производная не равна нулю нигде и всюду отрицательна. Экстремума нет, Всюду убывающая функция.
- Область Определения функции: $D_f=left(-infty;-5right)+left(-5;5right)+left(5;+inftyright)$ .
- Знакопостоянство: $+Z_f=left(-5;5right)+left(5;+inftyright)$ — функция положительна. $-Z_f=left(-infty;-5right)$ — функция отрицательна
- Монотонность: $+M_f=varnothing $ — нет роста. $-M_f=left(-infty;-5right)+left(-5;5right)+left(5;+inftyright)$ — функция убывает
- Область значений $E_f=left(-infty;0right)+left(0;0,8right)+left(0,8;inftyright)$
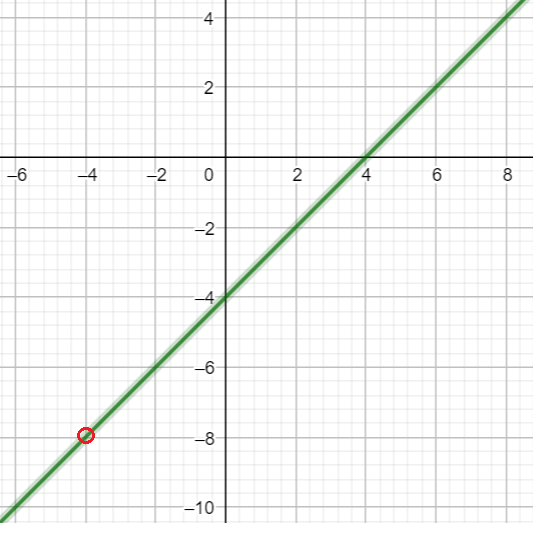
Пример 5: Построить график функции $y=frac{x^2-16}{x+4}$
- О.Д.З функции $xne-4$. Оговорив это, со спокойной совестью сократим $y=frac{x^2-16}{x+4}=x-4$.
- График нашей функции — прямая линия $y=x-4$ с выколотой точкой $left(-4;-8right)$ при $x=-4$.
- «Близко чуть левее»: $x=-4,01$ значение $fleft(-4,01right)=frac{(-4,01)^2-16}{-4,01+4}=-8,01$. Ближе? … Предел $approx-8$.
- «О нулях». при $x=0$ $y=-4$ . Обнуление функции $y=0$ при $x=4$ — пересечение с $x$ — осью.
- Анализ: Найдем производное: $left(frac{x^2-16}{x+4}right)’=left(x-4right)’=1$
- Производное всюду равно 1. Постоянный рост. Кроме разрыва, конечно. Нет точки Экстремума.
- Область Определения: $D_f=left(-infty;-4right)+left(4;+inftyright)$ Область значений $E_f=left(-infty;-8right)+left(-8;inftyright)$
- Знакопостоянство: $+Z_f=left(4;+inftyright)$ — функция положительна. $-Z_f=left(-infty;4right)$ — функция отрицательна
- Монотонность: $+M_f=left(-infty;-4right)+left(-4;inftyright)$ — возрастает
График Дробно — Рациональной Функции.
Определение: дробно-рациональной порядка $left(n;mright)$ называется функция вида $y=frac{acdot x^n+5x^3-x+c}{bcdot x^m-4x^2-7x+d}$
Числитель — многочлен степени $n$ , знаменатель — многочлен степени $m$ . Общий вид: $y=frac{Pleft(xright)}{Qleft(xright)}$
Нули функции — корни числителя $Pleft(xright)=0$ , Асимптоты (полюсы) — корни знаменателя $Qleft(xright)=0$.
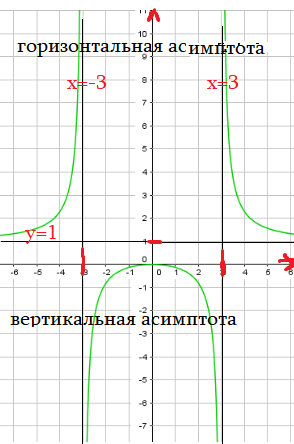
Пример 6: Построить график функции $y=frac{x^2}{x^2-9}$.
- Функция $fleft(xright)=frac{x^2}{x^2-9}$ — четная: $fleft(xright)=fleft(xright)$ $fleft(8right)=fleft(-8right)$ — Слева и справа от $OY$ симметрично.
- Вычисления: $fleft(-4right)=frac{left(-4right)^2}{left(-4right)^2-9}=frac{16}{7}approx2,3$ $fleft(-10right)=frac{100}{91}approx 1,1$ $fleft(-5right)=frac{25}{16}approx 1,6$ $fleft(-3,5right)=frac{12.25}{3,25}approx 3,8$
- $fleft(-2right)=fleft(2right)=frac{4}{-5}approx -0,8$ $fleft(-1right)=fleft(1right)approx -0,1$ $fleft(3,5right)approx 3,8$ $fleft(4right)approx 2,3$ $fleft(5right)approx 1,6$ $fleft(10right)approx 1,1$
- Наша функция имеет нули в точке $x=0$ , а вертикальные асимтоты — линии $x=-3$ , $x=3$
- Асимптота — прямая линия, к которой «прижимается» график функции, «подходя» к ней бесконечно близко.
- Чему равно $frac{x^2}{x^2-9}$ при очень больших $x$ ? $xapproxpm1000$ ? Конечно, $yapprox1$ горизонтальная асимптота $y=1$ .
- Анализ графика: 1) Обнуляется при $x=0$ . 2) Значение в нуле : $y=frac{x^2}{x^2-9}$ в $x=0$ равно $y=0$.
- 3) Поведение в разрывах: «чуть левее» полюса $xapprox-3-0,01$ значение $y > 0$ — «большое положительное».
- «чуть правее» разрыва $xapprox-3+0,01$ значение функции «большое отрицательное».
- Поведение около другого разрыва: когда $x$ «чуть левее» , например $xapprox3-0,01$ , то $y < 0$ ;
- когда $x$ «чуть правее» , например $xapprox3+0,01$ , то $y > 0$.
- 4) Поведение на бесконечности: при $xapproxpminfty$ значение «ложится» около $yapprox1$.
- 5) Область определения функции — все точки оси $x$ , кроме $x=pm3$
- 6) Функция положительна $y > 0$ на интервалах $x < -3$ , $x > 3$.
- 7) Функция отрицательна $y < 0$ на интервалах $-3 < x < 0$ , $0 < x < 3$.
Исследование Функции:
- Найдем производное: $left(frac{x^2}{x^2-9}right)’=frac{2xleft(x^2-9right)-x^2cdot2x}{left(x^2-9right)^2}=frac{-18x}{left(x^2-9right)^2}$
- Производное равно нулю дает точку Экстремума: $x=0$. Точка Максимума.
- Производная отрицательна — значит убывает $x > 0$. Производная положительна, значит возрастает: $x < 0$
- Область Определения: $D_f=left(-infty;-3right)+left(-3;3right)+left(3;+infty8right)$ — область определения функции.
- Знакопостоянство: $+Z_f=left(-infty;-3right)+left(3;+inftyright)$ — функция положительна. $-Z_f=left(-3;3right)$ — функция отрицательна
- Монотонность: $+M_f=left(-infty;-3right)+left(-3;0right)$ — возрастает $-M_f=left(0;3right)+left(3;+inftyright)$ — функция убывает
- Область значений $E_f=left(-infty;0right)+left(1;inftyright)$
пробaп 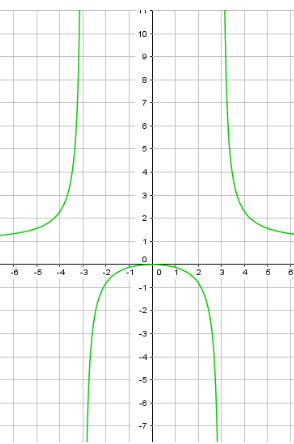
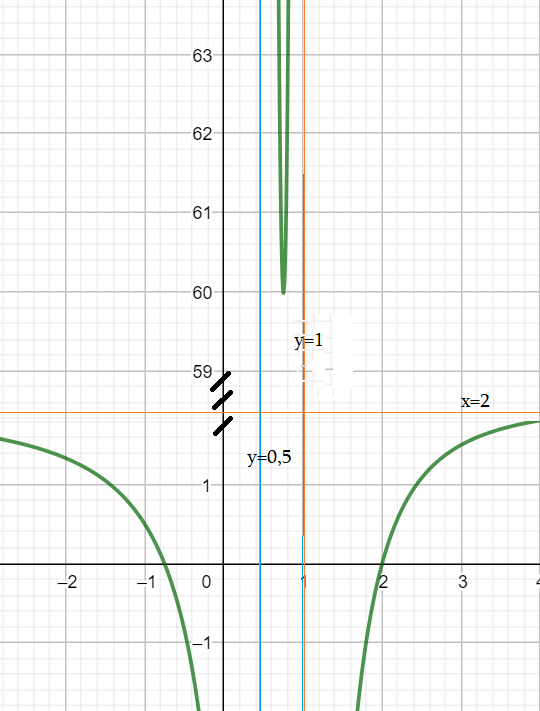
Пример 7: Анализ графика функции $y=frac{4x^2-5x-6}{2x^2-3x+1}$
- нули — точки обнуления числителя $4x^2-5x-6=0$ $x=2$ $x=-frac{3}{4}$
- Представление: $frac{4x^2-5x-6}{2x^2-3x+1}=frac{2cdot left(2x^2-3x+1right)+x-8}{2x^2-3x+1}=2+frac{x-8}{2x^2-3x+1}=2+frac{x-8}{left(2x-1right)left(x-1right)}=2+frac{15}{2x-1}-frac{7}{x-1}$
- разрыв (полюс): $2x^2-3x+1=0$ вертикальные асимптоты — $x=1$ и $x=0,5$.
- при $xapproxpm infty$ значение «ложится» около $yapprox2$. $-frac{30}{left(2x-1right)^2}+frac{7}{left(x-1right)^2}$ $x=0,75$ $x=15,24$
- Производное: $left(2+frac{15}{2x-1}-frac{7}{x-1}right)’=-frac{30}{left(2x-1right)^2}+frac{7}{left(x-1right)^2}=frac{-2x^2+32x-23}{left(2x-1right)^2cdotleft(x-1right)^2}$
- Или так: $left(frac{4x^2-5x-6}{2x^2-3x+1}right)’=frac{left(4x^2-5x-6right)’cdotleft(2x^2-3x+1right)-left(4x^2-5x-6right)cdotleft(2x^2-3x+1right)’}{left(2x^2-3x+1right)^2}=frac{left(8x-5right)cdotleft(2x^2-3x+1right)-left(4x^2-5x-6right)cdotleft(4x-3right)}{left(2x^2-3x+1right)^2}=frac{-2x^2+32x-23}{left(2x^2-3x+1right)^2}$
- Уравнение Экстремумов: $frac{-2x^2+32x-23}{left(2x^2-3x+1right)^2}=0$. $-2x^2+32x-23=0$. $x=8pm0,5sqrt{210}$
- Производная отрицательна на интервалах $-M_f=left(-infty;0,5right)+left(0,5;8-0,5sqrt{210}right)+left(8+0,5sqrt{210};inftyright)$. Убывает.
- Производная положительна на интервалах $+M_f=left(8-0,5sqrt{210};1right)+left(1;8+0,5sqrt{210}right)$. Возрастает.
- Точка Минимума: $x=8-0,5sqrt{210}$ $xapprox0,75$ . Точка Максимума: $x=8+0,5sqrt{210}$ $xapprox15,25$
- Область Определения: $D_f=left(-infty;0,5right)+left(0,5;1right)+left(1;+inftyright)$ .
- Знакопостоянство: $+Z_f=left(-infty;-0,75right)+left(0,5;1right)+left(2;+inftyright)$ — положительна. $-Z_f=left(-0,75;0right)+left(1;2right)$ — отрицательна.
- Область значений (приближенно!) $E_fapproxleft(-infty;2,001right)+left(60;inftyright)$
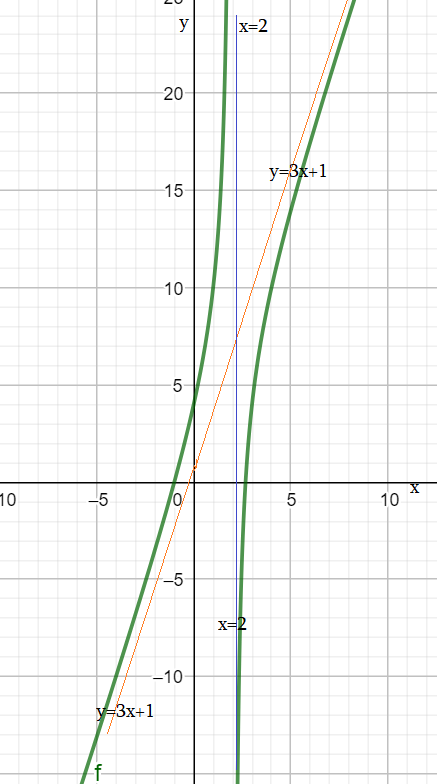
Пример 8: Анализ графика функции $y=frac{3x^2-5x-8}{x-2}$
- нули — точки обнуления числителя $3x^2-5x+8=0$ $x=-1$ $x=frac{8}{3}approx2,7$
- разрыв (полюс): $x-2=0$ вертикальные асимптоты — $x=2$ .
- «чуть левее»: $fleft(2-10^{-7}right)=frac{3cdotleft(2-10^{-7}right)^2-5left(2-10^{-7}right)-8}{2-10^{-7}-2}=frac{3cdot4-5cdot2-8-12cdot10^{-7}+5cdot10^{-7}+3cdotleft(10^{-7}right)^2}{-10^{-7}}approx6cdot10^7$ Значит, уходит к $+infty$
- Чуть правее: $fleft(2+10^{-7}right)=frac{3cdotleft(2+10^{-7}right)^2-5left(2+10^{-7}right)-8}{2+10^{-7}-2}=frac{3cdot4-5cdot2-8+12cdot10^{-7}-5cdot10^{-7}+3cdotleft(10^{-7}right)^2}{10^{-7}}approx-6cdot10^7$ …. бежит к $-infty$
- Представим нашу функцию по-другому : $frac{3x^2-5x-8}{x-2}=frac{3x^2-6x+x-2-6}{x-2}=3x+1-frac{6}{x-2}$
- Видно, что при больших $x=2$ она «почти совпадает» с линейной функцией $3x+1$. «прижимается к ней».
- $y=3x+1$ — наклонная асимптота нашей функции.
- Найдем производное: $left(frac{3x^2-5x-8}{x-2}right)’=frac{left(6x-5right)left(x-2right)-1cdotleft(3x^2-5x-8right)}{(x-2)^2}=frac{3x^2-12x+18}{(x-2)^2}=frac{3left(x^2-4x+6right)}{(x-2)^2}$
- Производное нигде не равно нулю, нет Экстремума: Производное всюду положительно, значит, возрастает.
- Область Определения: $D_f=left(-infty;2right)+left(2;+inftyright)$ . Полюс в $x=2$ .
- Знакопостоянство: $+Z_f=left(-1;2right)+left(frac{8}{3};+inftyright)$ — функция положительна. $-Z_f=left(-infty;-1right)+left(-1;frac{8}{3}right)$ — функция отрицательна
- Монотонность: $+M_f=left(-infty;2right)+left(2;inftyright)$ — всюду возрастает
- Область значений $E_f=left(-infty;+inftyright)$
Графический способ решения уравнений
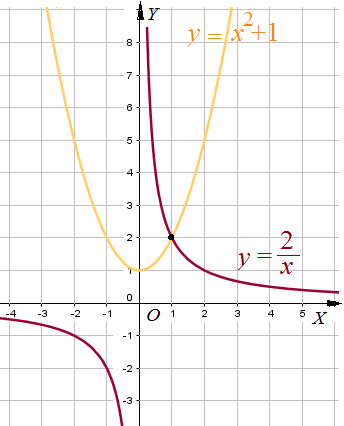
Пример 9: Решить уравнение $frac{2}{x}=x^2+1$ графическим способом.
- Построим гиперболу $y=frac{2}{x}$ и параболу $y=x^2+1$ . Равенство означает пересечение.
- Левая функция и правая функция приобретают одинаковые значения … графики этих функций пересекаются.
- По чертежу видно, что графики пересекаются в точке с координатами $left(1;2right)$. ответ: $x=1$.
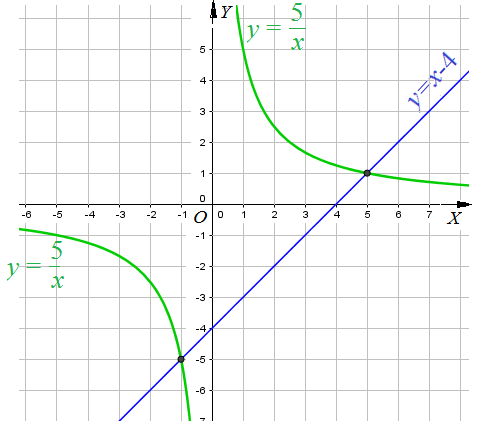
Пример 10: Решить уравнение $frac{5}{x}=x-4$.
- Построим их графики: гиперболу $y=frac{5}{x}$ и прямую $y=x-4$. пересекаются ?
- Гипербола и прямая пересекаются в точках $(-1;-5)$ и $(5;1)$. ответ: $x_1=-1$; $x_2=5$.
Пример 11: Найти наименьшее и наибольшее значения функции $y=frac{1}{x}$ на отрезках а) $left[frac{1}{3};5right]$ и б) $left[-7;-1right]$.
- Построим график функции $y=frac{1}{x}$ .
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[frac{1}{3};5right]$.
- Для выделенной части графика находим: наименьшее значение $y=frac{1}{5}$ при $x=5$ , наибольшее $y=3$ при $x=frac{1}{3}$.
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $left[-7;-1right]$.
- Для выделенной части графика находим: наименьшее значение $y=-frac{1}{7}$ при $x=-7$ наибольшее $y=-1$ при $x=-1$.
Упражнения
Дробно-рациональная функция определяется отношением двух многочленов и имеет вид:

Областью определения такой функции будут все значения кроме тех, в которых знаменатель функции обращается в нуль. Значения
, в которых
называются Точками разрыва функции.
Дробно-рациональной функцией является и функция 
Функция 
, имеет вид

, имеет вид

|
Свойства функции |
Свойства функции |
|
1. ( |
1. ( |
|
2. |
2. |
|
3. Функция не имеет нулей. График функции не пересекает ось |
3. Функция не имеет нулей. График функции не пересекает ось |
|
4. |
4. |
|
5. Функция монотонно убывает в каждом из интервалов
|
5. Функция монотонно возраста-ет в каждом из интервалов
|
|
6. Функция не имеет экстремумов. |
6. Функция не имеет экстремумов. |
|
7. Функция нечетная ( |
7. Функция нечетная ( |
|
8. График функции не пересекает оси координат. Оси |
8. График функции не пересекает оси координат. Оси |
Графиком функции есть Гипербола. Ординаты ее графика в
раз по модулю больше ординат графика функции


Отношение двух линейных функций представляет собой дробно-линейную функцию .
Дробно-линейную функцию , где
, можно записать в виде:
, где





Полученная формула позволяет построить график функции 

единиц вдоль оси
и на
единиц вдоль оси
(рис. 5.28).
Уравнение вертикальной асимптоты имеет вид: ,
а уравнение горизонтальной асимптоты имеет вид: .
Пример 2. Построить график функции .
Решение. В дробно-линейной функции коэффициенты
,
,
и
.
Вычислим значения ,
и
. Запишем преобразованную формулу функции:
.
Эту же формулу можно получить преобразованием заданной функции:
.
Построим график функций (рис. 5.29) и
(рис. 5.30).
Ответ. График функции получен сдвигом графика функции
на 1 единицу вдоль оси
влево и на 3 единицы вдоль оси
вверх.
| < Предыдущая | Следующая > |
|---|
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
Как найти область определения функции?
Синонимы: область допустимых значений или сокращенно ОДЗ. Первое, с чем Вы сталкиваетесь при изучении различных функций или же при построении графиков — это область определения функции.
Определение:
Областью определения называется множество значений, которые может принимать x. Обозначение D(f).
Как же это правило применить к заданной Вам функции?
В математике имеется достаточно небольшое количество элементарных функций, область определения которых ограничена. Все остальные «сложные» функции — это всего лишь их сочетания и комбинации.
1. Дробная функция — ограничение на знаменатель.
2. Корень четной степени — ограничение на подкоренное выражение.
3. Логарифмы — ограничение на основание логарифма и подлогарифмическое выражение.
3. Тригонометрические tg(x) и ctg(x) — ограничение на аргумент.
Для тангенса:
Для котангенса:
4. Обратные тригонометрические функции.
Пример нахождения области определения функции №1
Нахождение области определения любой линейной функции, т.е. функции первой степени:
y = 2x + 3 — уравнение задает прямую на плоскости.
Посмотрим внимательно на функцию и подумаем, какие же числовые значения мы сможем подставить в уравнение вместо переменной х?
Попробуем подставить значение х=0
Так как y = 2·0 + 3 = 3 — получили числовое значение, следовательно функция существует при взятом значении переменной х=0.
Попробуем подставить значение х=10
так как y = 2·10 + 3 = 23 — функция существует при взятом значении переменной х=10 .
Попробуем подставить значение х=-10
так как y = 2·(-10) + 3 = -17 — функция существует при взятом значении переменной х=-10 .
Уравнение задает прямую линию на плоcкости, а прямая не имеет ни начала ни конца, следовательно она существует для любых значений х.
Заметим, что какие бы числовые значения мы не подставляли в заданную функцию вместо х, всегда получим числовое значение переменной y.
Следовательно, функция существует для любого значения x ∈ R или запишем так: D(f) = R
Формы записи ответа: D(f)=R или D(f)=(-∞:+∞)или x∈R или x∈(-∞:+∞)
Для любой функции вида y = ax + b областью определения является множество действительных чисел.
Пример нахождения области определения функции №2
Задана функция вида:
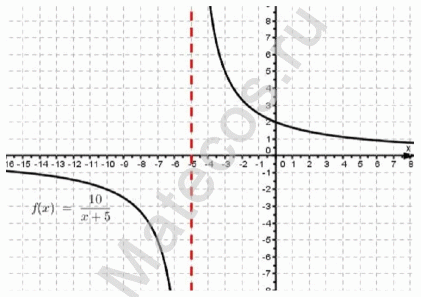
y = 10/(x + 5) — уравнение гиперболы
Имея дело с дробной функцией, вспомним, что на ноль делить нельзя. Следовательно функция будет существовать для всех значений х, которые не
обращают знаменатель в ноль. Попробуем подставить какие-либо произвольные значения х.
При х = 0 имеем y = 10/(0 + 5) = 2 — функция существует.
При х = 10 имеем y = 10/(10 + 5) = 10/15 = 2/ 3 — функция существует.
При х = -5 имеем y = 10/(-5 + 5) = 10/0 — функция в этой точке не существует.
Т.е. если заданная функция дробная, то необходимо знаменатель приравнять нулю и найти такую точку, в которой функция не существует.
x + 5 = 0 → x = -5 — в этой точке заданная функция не существует.
Для наглядности изобразим графически:
На графике также видим, что гипербола максимально близко приближается к прямой х = -5 , но самого значения -5 не достигает.
Видим, что заданная функция существует во всех точках действительной оси, кроме точки x = -5
Формы записи ответа: D(f)=R <-5>или D(f)=(-∞;-5) ∪ (-5;+∞) или x ∈ R <-5>или x ∈ (-∞;-5) ∪ (-5;+∞)
Если заданная функция дробная, то наличие знаменателя накладывает условие неравенства нулю знаменателя.
Пример нахождения области определения функции №3
Рассмотрим пример нахождения области определения функции с корнем четной степени:
Так как квадратный корень мы можем извлечь только из неотрицательного числа, следовательно, функция под корнем — неотрицательна.
Решим простое неравенство:
2х — 8 ≥ 0 → 2х ≥ 8 → х ≥ 4
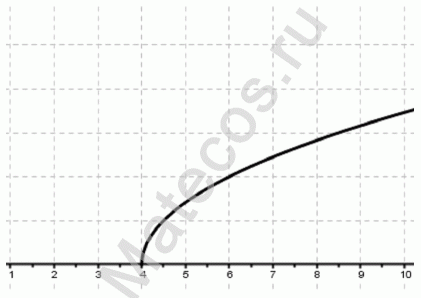
Заданная функция существует только при найденных значениях х ≥ 4 или D(f)=[4 ;+∞) или x ∈ [4 ;+∞) .
На графике видим, что функция существует для найденных значений х : х ≥ 4 или D(f)=[4 ;+∞) или x ∈ [4 ;+∞) .
При попытке подставить вместо х значения, отличные от найденных, под корнем получим отрицательное число, те в этих точках функция не существует.
Если заданная функция содержит квадратный корень (или корень любой четной степени), то обязательно накладывается условие неотрицательности (≥0) на подкоренное выражение. Если квадратный корень находится в знаменателе функции, у которой мы находим область определения, то на подкоренное выражение накладывается условие положительности (>0), так как знаменатель всегда должен быть отличен от нуля.
Пример нахождения области определения функции №4
Рассмотрим пример нахождения области определения функции с корнем четной степени в знаменателе:
В числителе имеем линейную функцию, область определения которой множество всех действительных чисел. (см. пример 1)
В знаменателе — квадратный корень, накладывает условие на подкоренное выражение, не забывая о том, что знаменатель всегда отличен от нуля.
x 2 — 4x + 3 > 0 → (x — 1)(x — 3) > 0
Решим строгое неравенство методом интервалов:
Видим, что функция положительна на следующих интервалах: x∈(-∞;1)∪(3;+∞)
Нашли такие значения переменной х, при которых функция существует — нашли ОДЗ функции.
Пример нахождения области определения функции №5
Рассмотрим пример нахождения области определения функции с корнем нечетной степени:
Имеем дело с корнем нечетной степени. Так как корень нечетной степени существует при любых значениях подкоренного выражения, то заданная дробная функция под корнем может принимать любые значения.
В числителе дробной функции — уравнение первой сnепени, которое существует при любых значениях переменной. Знаменатель любой дроби отличен от нуля. Следовательно, при нахождении ОДЗ заданного выражения имеем дело лишь с одним ограничением — ограничение на знаменатель дроби.
Пример нахождения области определения функции №6
Рассмотрим пример нахождения области определения логарифма:
Простенький пример на область определения логарифмической функции.
Помним, что основание логарифма положительно и отлично от нуля. Подлогарифмическое выражение положительно:
Покажем на числовой прямой:
Получили ОДЗ: x∈(8;9)∪(9;+∞)
Пример нахождения области определения функции №7
Задана функция вида:
1 ограничение основывается на наложении ограничения на знаменатель дроби (отличен от нуля):
Второе ограничение — подлогарифмическое выражение положительно:
Т.е. для определения области определения заданной функции необходимо решить систему:
Необходимо решить каждое из ограничений системы по отдельности и пересечь получившиеся результаты.
Допускаю, что читатель самостоятельно может это проделать и перехожу к разбору следующего примера.
Пример нахождения области определения функции №8
Рассмотрим следующий пример:
Имеем дело с корнем четной степени, следовательно первое ограничение на подкоренное выражение:
Имеем дело с логарифмом, следовательно ограничение на подлогарифмическую функцию:
Таким образом для определения области определения исходной функции необходимо решить систему неравенств:
Каждое из неравенств решим по отдельности.
Первое неравенство будем решать методом интервалов: найдем корни каждого из выражений неравенства, вынесем их на координатную плоскость и расставим знаки неравенства в каждом из полученных интервалов.
Выносим на координатную прямую:
Объясню как расставлены знаки в каждом из интервалов:
Значения левее 6/7 нет смысла рассматривать, так как логарифм для этих значений не существует.
1-ый интервал: (6/7;1]
Основание логарифма больше единицы, следовательно функция возрастающая. В корне x=1 логарифм меняет свое значение с » — » на » + «.
Как найти область определения функции
Что такое область определения функции?
Начнём с краткого определения. Область определения функции y=f(x) — это множество значений X, для которых существуют значения Y.
Войдём в тему более основательно. Каждой точке графика функции соответствуют:
- определённое значение «икса» — аргумента функции;
- определённое значение «игрека» — самой функции.
Верны следующие факты.
- От аргумента — «икса» — вычисляется «игрек» — значения функции.
- Область определения функции — это множества всех значений «икса», для которых существует, то есть может быть вычислен «игрек» — значение функции. Иначе говоря, множество значений аргумента, на котором «функция работает».
Можно понимать область определения функции и как проекцию графика функции на ось Ox.
Что требуется, чтобы уверенно находить область определения функции? Во-первых, нужно различать виды функций (корень, дробь, синус и др.). Во-вторых, решать уравнения и неравенства с учетом вида функции (например, на что нельзя делить, какое выражение не может быть под знаком корня и тому подобное). Согласитесь, не так уж много и не так сложно. При изучении темы области определения функции поможет материал Свойства и графики элементарных функций. А поскольку областью определения функции служат различные множества, а также их объединения и пересечения, то пригодится и материал Множества и операции над множествами.
Итак, чтобы находить области определения распространённых функций, порешаем уравнения и неравенства с одной переменной.
После этого экскурса в важную составную матанализа многие согласятся, что найти область определения функции не очень сложно.
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы. Приступаем к практике.
Общий принцип на самых простых примерах
Пример 1. На рисунке изображён график функции . Знаменатель дроби не может быть равен нулю, так как на нуль делить нельзя. Поэтому, приравнивая знаменатель нулю
и решая это уравнение:
получаем значение, не входящее в область определения функции: 1. То есть, область определения заданной функции — это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо видно на графике. Приведённый здесь пример функции относится к виду дробей. На уроке разберём решения всех распространённых видов функций.
Пример 2. Как найти область определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять) ()? Так как подкоренное выражение должно быть неотрицательным, нужно решить неравенство
Если перенести какое-либо слагаемое в другую часть неравенства с противоположным знаком, то мы получим равносильное неравенство с тем же знаком неравенства. Переносим минус 5 и получаем неравенство
Получаем решение: область определения функции — все значения икса больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).
На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.
Область определения корня n-й степени
В случае, функции корня n-й степени, то есть когда функция задана формулой и n — натуральное число:
если n — чётное число, то областью определения функции является множество всех неотрицательных действительных чисел, то есть [0; + ∞[ ;
если n — нечётное число, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ .
Пример 3. Найти область определения функции .
Решение. Как следует из определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно. Поэтому решаем неравенство
.
Это квадратное неравенство
,
По формуле находим дискриминант:
.
По формуле находим корни квадратного трёхчлена:
.
Найденные точки разбивают числовую прямую на три промежутка:
и .
При этом знак квадратного трёхчлена (больше или меньше нуля) совпадает со знаком коэффициента a во всех точках промежутков
и
и противоположен знаку коэффициента a во всех точках промежутка .
В нашем случае имеем отрицательный коэффициент a=-1 , поэтому квадратный трёхчлен неотрицателен во всех точках промежутка .
Следовательно, область определения данной функции — [- 1; 1] .
Заштрихованная область числовой прямой на чертеже сверху — это область определения данной функции.
Область определения степенной функции
Область определения степенной функции находится в зависимости от вида степени в выражении.
Область определения степенной функции с дробным показателем степени
В случае, когда функция задана формулой :
если — положительное, то областью определения функции является множество [0; + ∞[ , то есть нуль входит в область определения;
если — отрицательное, то областью определения функции является множество (0; + ∞[ , то есть нуль не входит в область определения.
Пример 4. Найти область определения функции .
Решение. Выражение функции можно представить так:
Квадратный трёхчлен в скобках в знаменателе должен быть строго больше нуля (ещё и потому, что дробный показатель степени данной степенной функции — отрицательный). Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля:
.
.
Дикриминант получился отрицательный. Следовательно сопряжённое неравенству квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях «икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или, что то же самое — множество R действительных чисел, или, что то же самое — ]- ∞; + ∞[ .
Пример 5. Найти область определения функции .
Решение. Оба слагаемых в выражении функции — степенные функции с положительными дробными показателями степеней. Следовательно, область определения данной функции — множество [0; + ∞[ .
На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше, причём штриховка продолжается вместе с самой прямой до плюс бесконечности.
Область определения степенной функции с целым показателем степени
В случае, когда функция задана формулой :
если a — положительное, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ ;
если a — отрицательное, то областью определения функции является множество ]- ∞; 0[ ∪ ]0 ;+ ∞[ , то есть вся числовая прямая за исключением нуля.
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка, соответствующая нулю, выколота (она не входит в область определения функции).
Пример 6. Найти область определения функции .
Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором слагаемом можно представить в виде единицы — так же целого числа. Следовательно, область определения данной функции — вся числовая прямая, то есть ]- ∞; + ∞[ .
Область определения показательной и логарифмической функции
Область определения показательной функции
В случае, когда функция задана формулой , областью определения функции является вся числовая прямая, то есть ]- ∞; + ∞[ . Подробнее о графике такой функции.
Область определения логарифмической функции
Логарифмическая функция определена при условии, если её аргумент положителен, то есть, областью её определения является множество ]0; + ∞[ . Подробнее о графике такой функции.
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 7. Найти область определения функции .
Пример 8. Найти область определения функции .
Область определения тригонометрических функций
Область определения функции y = cos(x) — так же множество R действительных чисел.
Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .
Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел .
Пример 9. Найти область определения функции .
Решение. Внешняя функция — десятичный логарифм и на область её определения распространяются условия области определения логарифмической функции вообще. То есть, её аргумент должен быть положительным. Аргумент здесь — синус «икса». Пользуясь тригонометической таблицей (или поворачивая воображаемый циркуль по окружности), видим, что условие sin x > 0 нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи» и любого чётного ( 2kπ ) или нечётного целого числа ( (2k+1)π ).
Таким образом, область определения данной функции задаётся выражением
,
где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) — множество [-1; 1] .
Область определения функции y = arccos(x) — так же множество [-1; 1] .
Область определения функции y = arctg(x) — множество R действительных чисел.
Область определения функции y = arcctg(x) — так же множество R действительных чисел.
Пример 10. Найти область определения функции .
Решение. Решим неравенство:
Решение получили, основываясь на свойстве неравенств: если все части верного неравенства умножить на одно и то же положительное число, то получится также верное неравество. В данном случае умножали на 4.
Таким образом, получаем область определения данной функции — отрезок [- 4; 4] .
Пример 11. Найти область определения функции .
Решение. Решим два неравенства:
Решение первого неравенства:
Решение получили, основываясь на свойстве неравенств: если обе части верного неравенства умножить на одно и то же отрицательное число изменить знак неравенства на противоположный, то получится верное неравенство. В данном случае умножали на минус 2.
Аналогично и решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок [0; 1] .
Область определения дроби
Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x , при которых знаменатель дроби обращается в нуль.
Пример 12. Найти область определения функции .
Решение. Решая равенство нулю знаменателя дроби:
находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[ , то есть все числа, кроме минус 2.
Пример 13. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[ , то есть все числа, кроме минус единицы и единицы.
Пример 14. Найти область определения функции .
Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — ]- ∞; — 2[ ∪ ]- 2 ; 2[ ∪ ]2 ;+ ∞[ , то есть все числа, кроме -2 и 2.
Пример 15. Найти область определения функции .
Решение. Решим уравнение:
Уравнение не имеет действительных корней. Но функция определена только на действительных числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что то же самое — множество R действительных чисел или, что то же самое — ]- ∞; + ∞[ .
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.
Пример 16. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[ .
Пример 17. Найти область определения функции .
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках 1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена на отрезке [1; 2] .
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 18. Найти область определения функции .
Пример 19. Найти область определения функции .
Область определения постоянной
Постоянная (константа) определена при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел. Это можно записать и так: областью определения данной функции является вся числовая прямая ]- ∞; + ∞[ .
Пример 20. Найти область определения функции y = 2 .
Решение. Область определения функции не указана, значит, в силу выше приведённого определения имеется в виду естественная область определения. Выражение f(x) = 2 определено при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел.
Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус бесконечности до плюс бесконечности.
Область определения линейной функции
Если функция задана формулой вида y = kx + b , то область определения функции — множество R действительных чисел.
http://matecos.ru/mat/matematika/kak-opredelit-oblast-opredeleniya-grafika-funktsii-5.html
http://function-x.ru/function_definition_area.html
Скачать материал

Скачать материал


- Сейчас обучается 83 человека из 35 регионов




- Сейчас обучается 105 человек из 36 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Нахождение
области значений
дробно-рациональных функций -
2 слайд
Областью (множеством) значений E(у) функции y = f(x) называется множество таких чисел y0, для каждого из которых найдётся такое число x0, что: f(x0) = y0.
-
3 слайд
Свойства функций, используемые при нахождении области значений функции:
непрерывность;
монотонность;
дифференцируемость;
чётность, нечётность;
обратимость.
-
4 слайд
Способы нахождения областей значений функций:
а) последовательное нахождение значений сложных аргументов функции;
б) метод оценок;
в) использование свойств непрерывности и монотонности функции;
г) использование производной;
д) использование наибольшего и наименьшего значений функции;
е) графический метод;
ж) метод введения параметра;
з) метод обратной функции. -
5 слайд
Определение. Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Определение. Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x.
-
6 слайд
Определение. Точка В называется инвертной точке А относительно данной прямой (оси) l, если:
эти точки лежат по одну сторону относительно оси l;
отрезок, их соединяющий, перпендикулярен оси l;
произведение расстояний от этих точек до оси lравно 1.
Определение. Преобразование плоскости, при котором каждая точка переходит в инвертную ей относительно данной прямой, называется инверсией. Для точек этой прямой преобразование не определяется.
Свойства инверсии:График функции получается из графика функции инверсией относительно оси Ох.
График функции получается из графика функции преобразованием инверсии относительно оси Оу.
Чем дальше от оси инверсии точка, тем ближе к ней инвертная ей точка.
-
7 слайд
Некоторые неравенства, используемые в работе
-
8 слайд
Пример 1.
Асимптоты:
Ответ:
.
(1. Строим график, используя инверсию)
Решение. -
9 слайд
Пример 1.
Ответ:
.
( 2. Метод введения параметра)
Решение. -
10 слайд
Пример 1.
Ответ:
.
( 3. Метод обратной функции)
Решение. -
11 слайд
Пример 1.
Ответ:
.
( 4. Метод применения производной)
Решение.
Вертикальная асимптота , график не пересекает ось абсцисс.Критическиx точек первого рода нет.
-
12 слайд
Применить алгебраические неравенства к Примеру 1 невозможно
-
13 слайд
Пример 2.
Асимптоты:
Ответ:
.
(1. Строим график, используя инверсию)
Решение. -
14 слайд
Пример 2.
Ответ:
.
(2. Введение параметра)
Решение. -
15 слайд
Пример 2.
Ответ:
.
(3. Метод обратной функции)
Решение. -
16 слайд
Пример 2.
Ответ:
.
(4. Метод применения производной)
Решение.
График имеет вертикальную асимптоту,
не пересекает ось абсцисс.
Горизонтальная асимптота: -
17 слайд
Применить алгебраические неравенства к Примеру 2 невозможно
-
18 слайд
Пример 6.
Ответ:
.
(1.
Решение.
Функция нечетная: -
19 слайд
Пример 6.
Ответ:
.
(2. Метод введения параметра)
Решение. -
20 слайд
Пример 6.
Ответ:
.
(3. Метод обратной функции)
Решение. -
21 слайд
Пример 6.
Ответ:
.
(4. Метод применения производной)
Решение.
Вертикальная асимптота:
График не пересекает ось абсцисс.
Наклонная асимптота: -
22 слайд
Применить инверсию к функции Примера 6 невозможно
-
23 слайд
ВЫВОД
Нахождение области значений функции имеет практическое применение.
2. Универсальный способ нахождения области значений функции — графический с применением производной, таких свойств как четность, асимптоты, нули функции.
3. Удобно использовать инверсию для построения график функций, но не все функции инвертируются.
4. Если есть выбор способов, то к рациональным способам можно отнести и введение параметра и метод обратной функции.
5. Знание различных способов решения одной и той же задачи позволяет осуществить проверку полученных результатов.
Краткое описание документа:
Презентация «Нахождение области значений дробно-рациональных функций» содержит информацию о параметре, инверсии, о способах нахождения области значений дробно-рациональных функций (на конкретных примерах некоторые способы применены).
Способы нахождения областей значений функций:
а) последовательное нахождение значений сложных аргументов функции;
б) метод оценок;
в) использование свойств непрерывности и монотонности функции;
г) использование производной;
д) использование наибольшего и наименьшего значений функции;
е) графический метод;
ж) метод введения параметра;
з) метод обратной функции.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 743 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра и начала математического анализа. Углубленный уровень», Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И.
Тема
Глава 3. Функции и последовательности
Больше материалов по этой теме
Другие материалы

Элективный курс по алгебре 10 класс
- Учебник: «Алгебра и начала математического анализа. Углубленный уровень», Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И.
- 27.05.2020
- 159
- 1


«Функцияның ең үлкен және еі кіші мәндері»
- Учебник: «Алгебра и начала математического анализа. Углубленный уровень», Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И.
- Тема: 4. Исследование функций на возрастание и убывание. Достаточное условие экстремума
- 03.05.2020
- 797
- 5



Практическое занятие по математике
- Учебник: «Алгебра и начала математического анализа. Углубленный уровень», Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И.
- Тема: Глава 1. Числа и координаты
- 03.03.2020
- 193
- 0


Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация маркетинга в туризме»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
-
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
Дробно-рациональная функция — это функция вида , где f(x) и g(x) — некоторые функции.
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты
Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x — нечетная
Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная
Пример1 . Построим график функции , т.е. представим ее в виде
: выделим целую часть дроби, разделив числитель на знаменатель, мы получим:
.
Итак, . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы
вверх на 2 единицы.
При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.
Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3. Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):
|
x |
-7 |
-2 |
-1 |
0 |
1 |
2 |
2,5 |
|
y |
1,5 |
1 |
0,75 |
0,33 |
-0,5 |
-3 |
-8 |
|
x |
3,5 |
4 |
5 |
6 |
7 |
8 |
13 |
|
y |
12 |
7 |
4,5 |
3,33 |
3,25 |
3 |
2,52 |
Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы. Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции изображен на рисунке 3.
Любую дробь можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.
Пример 2.
Построим график функции .
Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.
Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.
Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби относительно малы. Поэтому
.
Стало быть, горизонтальная асимптота – прямая у=3/2.
Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.
Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).
Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.
Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.
-
Найти область определения функции.
-
Разложить на множители квадратный трехчлен.
-
Сократить дробь.
-
Построить график (параболу, гиперболу, кубическую параболу).
-
Исключить из графика точки, не входящие в область определения («выколотые» точки).
-
Найти значение функции в «выколотых» точках.
-
Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.
ЗАДАНИЕ
Построить график функции (D(y), на графике – выколотые точки):