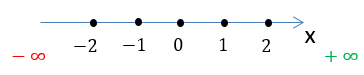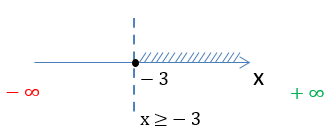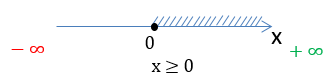Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Математическая гипербола.
Функция заданная формулой (y=frac{k}{x}), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac{k}{x}) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.


2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$yneqcolor{red} {frac{1}{x}}+0$$
(frac{1}{x}) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
$$y=color{red} {frac{1}{x+2}}-1$$
Дробь (color{red} {frac{1}{x+2}}) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Пример №3:
$$begin{align*}
&y=frac{2+x}{1+x} \\
&y=frac{color{red} {1+1}+x}{1+x} \\
&y=frac{1}{1+x}+frac{1+x}{1+x}\\
&y=frac{1}{1+x}+1\\
&y=frac{1}{color{red} {1+x}}+1
end{align*}$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
$$y=color{red}{frac{1}{1+x}}+1$$
(color{red}{frac{1}{1+x}}) Дробь убираем.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
$$y=frac{1}{x}$$
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
$$y=frac{1}{x}$$
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.
5. Гипербола нечетная функция.
$$f(-x)=frac{1}{-x}=-frac{1}{x}=-f(x)$$
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
$$y=frac{-1}{x-1}-1$$
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
$$y=color{red} {frac{-1}{x-1}}-1$$
Дробь (color{red} {frac{-1}{x-1}}) удаляем.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.
8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама
Свойства гиперболы
1) Область определения и область значений
По аналитическому заданию функции видно, что х ≠-a, поскольку знаменатель дроби не может ровняться нулю. Таким образом получим:
D(f)=(-∞;-а) U (-a;+∞)
Область значений
Е(f)=(-∞;+∞)
2) Нули функции
Если b=0, то график функции не пересекает ось ОХ;
Если b≠0, то гипербола имеет одну точку пересечения с ОХ:*
x=-(k+ab)/b
3) Промежутки знакопостоянства
Рассмотрим только 2 простых случая, остальные случаи вы можете рассмотреть аналитически самостоятельно по алгоритму из раздела Свойства функций -> Знакопостоянство
Случай 1: a=0, b=0, k>0
f(x)>0, при x ∈ (0; +∞)
f(x)<0, при x ∈ (-∞;0)
Случай 1: a=0, b=0, k<0
f(x)<0, при x ∈ (0; +∞)
f(x)>0, при x ∈ (-∞;0)
4) Промежутки монотонности
Аналогично с промежутками знакопостоянства рассмотрим только 2 случая
Случай 1: a=0, b=0, k>0
Функция убывает при
x ∈ (-∞;0) U (0; +∞)
Функция возрастает при
x ∈ (-∞;0) U (0; +∞)
5) Четность и нечетность
Функция является нечетной при a=0, b=0, то есть если имеет вид y=k/x
Гипербола
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой (y=frac), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=frac<1>-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
Дробь (color <frac<1>>) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment
Урок алгебры в 8-м классе по теме «Графический способ решения уравнений»
Разделы: Математика
Всякое учение и всякое обучение основано на некотором уже ранее имеющемся знании.
Цели:
- обобщить и систематизировать свойства графиков некоторых функций, алгоритмы их построения;
- научить решать уравнения графическим способом, в частности используя возможности компьютерных программ;
- учить анализировать, выделять главное, сравнивать.
Формирование компетенций: компетенции самосовершенствования – саморегулирование и саморазвитие, речевое развитие (через устную и самостоятельную работу, формулировка выводов); компетенции социального взаимодействия – сотрудничество; компетенции в общении – устном, письменном; компетенции познавательной деятельности – постановка и решение познавательных задач, проблемные ситуации (их создание и разрешение), прогнозирование деятельности; компетенции информационных технологий – приём, переработка и выдача информации, компьютерная грамотность.
Тип урока: урок изучения нового материала.
Средства обучения: компьютер, медиапроектор, презентация (Приложение 1).
Формы организации учебной деятельности: индивидуальная, коллективная, диалог, работа с текстом слайда, работа в тетради, парная.
Методы: наглядный, словесный, графический (практический).
Методы мотивации: поощрение, порицание; создание проблемной ситуации, побуждение к поиску решения; предъявление учебных требований, прогнозирование будущей деятельности, самооценка деятельности; создание ситуации взаимопомощи, заинтересованность в результатах коллективной работы.
1. Оргмомент (1 мин.)
2. Актуализация знаний (12 мин.)
А). По карточкам (на доске):
№1. Решите уравнение 4х + 8 = –17 + 9х.
№2. Решите уравнение х 2 + х – 2 = 0.
№3. Решите уравнение х 2 = 
№4. Заполните таблицу:
| х | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| у = х 2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| х | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
| у = | -1 | -2 | -3 | -6 | 6 | 3 | 2 | 1 |
(На этом этапе можно организовать взаимопроверку и взаимопомощь, если возникнет такая необходимость).
Б). Устная фронтальная работа. (Здесь и далее: подчёркивание – моменты управления презентацией)
Что называется функцией?
С какими функциями уже знакомы? (На партах – памятка, по которой учащиеся вспоминают связь между графиком и формулой, задающих функцию: Приложение 2).
Я предлагаю вашему вниманию формулы, задающие некоторые функции. Из этих функций нужно выбрать линейные. Но перед этим давайте вспомним определение линейной функции. (Работаем со слайдом 2).
Давайте вспомним, что является графиком (гиперссылка) линейной функции.
Среди выбранных нами линейных функций есть особенные. Что это за функции? Чем отличаются графики? (Разбейте линейные функции на две группы). (Работаем со слайдом 3).
Остались функции, о которых мы ничего ещё не сказали. Давайте дадим им название, и название их графикам. (Работаем со слайдом 4).
Что называется уравнением? Корнем уравнения? Что значит решить уравнение? Какие уравнения мы уже можем решать?
В) Проверяется работа по карточкам №1; №2; №3.
1) 4х + 8 = –17 + 9х,
4х – 9х = – 17 – 8,
– 5х = – 25,
х = 5.
Ответ: 5.
2) х 3 + х – 2 = 0,
D = в 3 – 4ас = 12 – 4 . 1 . (– 2) = 9 > 0, уравнение имеет два корня.
х1 = 1;
х2 = – 2.
Ответ: 1; – 2. (Могут решать по свойству корней: а + в + с = 0).
3) х 2 = 
х 3 = 6,
х 3 – 6 = 0. – Мы не располагаем никакими формулами для решения уравнений третьей степени. Как быть?
Значит, нужен другой способ решения таких уравнений. Как вы думаете, что это может быть за способ (исходя из устной работы). Одним из способов является графический способ. Записывается тема урока, (слайд 5).
Г). Давайте поставим цель урока. (Научиться решать уравнения с помощью графиков, слайд 6).
3. Изучение новой темы и первичное закрепление (15 мин.)
Мы получили уравнение х 3 – 6 = 0. Но строить график функции у = х 3 – 6 мы ещё не умеем. Т.е., что получается: это уравнение и графическим способом мы не можем решить? А может быть, нужно вернуться к первоначальному уравнению: х 2 = 

– Построить их графики.
– В одной координатной плоскости.
– Дальше найдём координаты точки пересечения.
– Нет, только значение х.
Итак, давайте ещё раз выработаем алгоритм решения уравнений графическим способом (каждый этап подтверждается показом в «Живой геометрии», Приложение 3). Используются результаты индивидуальной работы по заполнению таблицы (карточка №4). Учащиеся работают в тетрадях. Некоторые этапы в тетради записываются подробно, (слайд 7).
- Из уравнения выделяем знакомые нам функции.
- Строим графики функций в одной координатной плоскости.
- Находим координаты точек пересечения графиков.
- Из найденных координат выбираем значение абсциссы, т.е. х.
- Записываем ответ.
4. Физминутка (1 мин.)
5. Закрепление (5 мин.)
6. Домакшнее задание (слайд 10): (1 мин)
- п.26;
- № 623 (а), № 624(а);
- №4.10 на стр.117 (сборник Л.В.Кузнецовой): Наташа, Настя, Кирилл, Сергей.
7. Применение в образовательной области (1 мин)
Умения строить графики, читать графики, находить точки пересечения графиков нужны не только при изучении алгебры, но и при изучении физики, когда вы изучаете, н-р, зависимость плавления тела от температуры, зависимость скорости от времени движения двух тел. На уроках информатики, работая в электронных таблицах Excel, вы будете учиться строить графики, решать уравнения. На уроках химии скорость химических реакций также можно описать графически. Умение строить графики, диаграммы нужны и в повседневной жизни: для описания результатов голосования, удоя молока; в инженерных специальностях это умение очень важно.
8. Проверочная работа в виде теста (6 мин)
В – 1:
1. Какая из функций, приведённых ниже, является линейной:
а) у =
– 2; б) у = х – 2; в) у = х 2 – 2.
2. График функции у = 
а) прямой; б) гиперболой; в) параболой.
3. Установите соответствие между функциями и их графиками:
1) у =
; 2) у = 2х 2 ; 3) у = х – 2; 4) у = 2х.
А. Б. В. Г.
4. На рисунке 3 изображены графики функций у = х 3 и у = –2 х – 3. Используя графики, решите уравнение: х 3 = – 2х – 3.
В – 2:
1. Какая из функций, приведённых ниже, является линейной:
а) у =
+ 1; б) у =
+ 1; в) у = х 5 + 1.
2. График функции у = 3х 2 называется:
а) прямой; б) гиперболой; в) параболой.
3. Установите соответствие между функциями и их графиками:
1) у = –
; 2) у = х 2 – 1; 3) у = – х; 4) у = 1 – х.
А. Б. В. Г.
4. На рисунке 5 изображены графики функций у = – х 2 + 2 и у = 

Ответы:
В – 1: 1. б 2. б 3. 1 – Б; 2 – А; 3 – В; 4 – Г 4. б
В – 2: 1. а 2. в 3. 1 – В; 2 – Г; 3 – А; 4 – Б 4. а
9. Рефлексивно-оценочный этап (отвечают письменно в тетради после выполнения теста) (2 мин.) (Слайд 11)
а) за теоретический опрос;
б) за фронтальную работу;
в) за самостоятельную работу.
Что такое гипербола
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие гиперболы
Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы в алгебре выглядит так:
, где a и b — положительные действительные числа.
Кстати, канонический значит принятый за образец.
В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.
Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.
Вспомним особенности математической гиперболы:
- Две симметричные ветви.
- Две асимптоты. Асимптота — это прямая, которая обладает таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Их значение помогает найти специальное уравнение асимптот гиперболы.
Если гипербола задана каноническим уравнением, то асимптоты можно найти так:
Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) — 4(y^2) = 20.
Приведем данное уравнение к каноническому виду (x^2)/(a^2) — (y^2)/(b^2) = 1.
Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:
Можно было сделать проще и дроби левой части 5(x^2)/20 — 4(y^2)/20 = 1 сразу сократить и получить (x^2)/4 — (y^2)/5 = 1. Нам повезло с примером, потому что число 20 делится и на 4 и на 5. Рассмотрим пример посложнее.
Пример 2. Построить гиперболу, которая задана уравнением 3(x^2)/20 — 8(y^2)/20 = 1.
- Произведем сокращение при помощи трехэтажной дроби:
- Воспользуемся каноническим уравнением
- Найдем асимптоты гиперболы. Вот так:
Важно! Без этого шага ветви гиперболы «вылезут» за асимптоты. - Найдем две вершины гиперболы, которые расположены на оси абсцисс в точках A1(a; 0), A2(-a; 0).
- Найдем асимптоты гиперболы. Вот так:
Если y = 0, то каноническое уравнение (x^2)/(a^2) — (y^2)/(b^2) = 1 превращается в (x^2)/(a^2) = 1, из чего следует, что x^2 = a^2 -> x = a, x = -a.
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).
Найдем дополнительные точки — хватит двух-трех.
В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.
Способ такой же, как при построении эллипса. Из полученного канонического уравнения
на черновике выражаем:
Уравнение распадается на две функции:
— определяет верхние дуги гиперболы (то, что ищем);
— определяет нижние дуги гиперболы.
Далее найдем точки с абсциссами x = 3, x = 4:
Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.
Действительная ось гиперболы — отрезок А1А2.
Расстояние между вершинами — длина |A1A2| = 2a.
Действительная полуось гиперболы — число a = |OA1| = |OA2|.
Мнимая полуось гиперболы — число b.
В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.
Форма гиперболы
Повторим основные термины и узнаем, какие у гиперболы бывают формы.
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.
Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.
Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.
Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.
Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.
Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.
Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Фокальное свойство гиперболы
Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).
Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение e = a/c, где c = √(a^2 + b^2), называется эксцентриситетом гиперболы. Из определения (2a 1 .
Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:
Рассмотрим, как это выглядит на прямоугольной системе координат:
- пусть центр O гиперболы будет началом системы координат;
- прямую, которая проходит через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F1 к точке F2);
- прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).
Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:
Запишем это уравнение в координатной форме:
Избавимся от иррациональности и придем к каноническому уравнению гиперболы:
, т.е. выбранная система координат является канонической.
Если рассуждать в обратном порядке, можно убедиться, что все точки, координаты которых удовлетворяют уравнению (x^2)/(a^2) — (y^2)/(b^2) = 1, и только они, принадлежат геометрическому месту точек, называемому гиперболой. Именно поэтому аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисы гиперболы — это две прямые, которые проходят параллельно оси.
ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.
Директориальное свойство гиперболы звучит так:
Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.
Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
На самом деле для фокуса F2 и директрисы d2 условие
можно записать в координатной форме так:
Избавляясь от иррациональности и заменяя e = a/c, c^2 — a^2 = b^2, мы придем к каноническому уравнению гиперболы. Аналогичные рассуждения можно провести для фокуса F1 и директрисы d1:
Построение гиперболы
Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.
Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:
Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:
Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.
По определению эксцентриситет гиперболы равен
Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.
Так как b^2 = c^2 — a^2, то величина b изменится.
При этом ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы выражается в пределе в отрезок A1A2, а сама гипербола выражается в два луча на оси абсцисс: (-∞; -a] и [a; ∞).
При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.
При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.
Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.
Из определения следует, что в равносторонняя гиперболе a = b, поэтому ее каноническое уравнение выглядит так: x^2 — y^2 = a^2
Действительно, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 — a^2 = a^2. И так как а и b положительные числа, получаем a = b.
http://urok.1sept.ru/articles/570256
http://skysmart.ru/articles/mathematic/chto-takoe-giperbola
Обратная пропорциональность — коротко о главном
Определение:
Функция, описывающая обратную пропорциональность, – это функция вида ( displaystyle y=frac{k}{x-a}+b ), где ( kne 0), ( xne 0) и ( xne а)
По-другому эту функцию называют обратной зависимостью.
Область определения и область значений функции:
( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или, что то же самое, ( Dleft( y right)=mathbb{R}backslash left{ 0 right})
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).
График обратной пропорциональности (зависимости) – гипербола.
Коэффициент ( displaystyle k)
( displaystyle k) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента ( displaystyle k) влияет на то, в каких четвертях расположен график:
если ( displaystyle k>0), то ветви гиперболы расположены в ( displaystyle I) и ( displaystyle III) четвертях;
если ( displaystyle k<0), то во ( displaystyle II) и ( displaystyle IV).
Коэффициент ( displaystyle a)
Если внимательно посмотреть на знаменатель, видим, что ( displaystyle a) – это такое число, которому не может равняться ( displaystyle x).
То есть ( x=a) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции
Коэффициент ( b)
Число ( b) отвечает за смещение графика функции вверх на величину ( b), если ( b>0), и смещение вниз, если ( b<0).
Следовательно, ( y=b) – это горизонтальная асимптота.
Алгоритм построения графика функции ( displaystyle y=frac{k}{x-a}+b)
- Определяем коэффициенты ( displaystyle k), ( displaystyle a) и ( displaystyle b).
- Строим график функции ( displaystyle y=frac{k}{x}) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
- График должен быть сдвинут вправо на ( displaystyle a). Но проще двигать не график, а оси, так что ось ( displaystyle Oy) сдвигаем влево на ( displaystyle a).
- График должен быть сдвинут вверх на ( displaystyle b). Но проще двигать не график, а оси, так что ось ( displaystyle Ox) сдвигаем вниз на ( displaystyle b).
- Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.
Что такое функция
Ты помнишь, что функция – это определенного рода зависимость?
Если ты еще не читал тему «Функции», настоятельно рекомендую бросить все и прочитать, ведь нельзя изучать какую-либо конкретную функцию, не понимая, что это такое – функция.
Также очень полезно перед началом этой темы освоить две более простые функции: линейную и квадратичную.
Там ты закрепишь понятие функции и научишься работать с коэффициентами и графиками.
Ну и на всякий случай немного повторим…
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция ( y=fleft( x right)), это значит что каждому допустимому значению переменной ( x) (которую называют «аргументом») соответствует одно значение переменной ( y) (называемой «функцией»).
Что значит «допустимому значению»?
Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!
Все дело в понятии «область определения»: для некоторых функций не все аргументы можно подставить в зависимость. Например, для функции ( y=sqrt{x}) отрицательные значения аргумента ( x) – недопустимы.
Функция, описывающая обратную зависимость
Это функция вида ( displaystyle y=frac{k}{x}), где ( kne 0).
По-другому ее называют обратной пропорциональностью: увеличение аргумента вызывает пропорциональное уменьшение функции.
Давай определим область определения. Чему может быть равен ( x)? Или, по-другому, чему он не может быть равен?
Единственное число, на которое нельзя делить – это ( 0), поэтому ( xne 0):
( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right))
или, что то же самое,
( Dleft( y right)=mathbb{R}backslash left{ 0 right})
Такая запись означает, что ( x) может быть любым числом, кроме ( 0).
- Знак «( mathbb{R})» обозначает множество действительных чисел, то есть всех возможных чисел.
- Знаком «( backslash )» обозначается исключение чего-нибудь из этого множества (аналог знака «минус»).
- Число ( 0) в фигурных скобках означает просто число ( 0).
Получается, что из всех возможных чисел мы исключаем ( 0)).
Множество значений функции, оказывается, точно такое же: ведь если ( kne 0), то на что бы мы его не делили, ( 0) не получится:
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).
Также возможны некоторые вариации формулы ( y=frac{k}{x}). Например, ( y=frac{k}{x+a}) – это тоже функция, описывающая обратную зависимость.
Определи самостоятельно область определения и область значений этой функции. Должно получиться:
- ( Dleft( y right)=left( -infty ;-a right)cup left( -a;+infty right))
- ( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)).
Давай посмотрим на такую функцию: ( displaystyle y=frac{x-5}{{{x}^{2}}-25}).
Является ли она обратной зависимостью?
На первый взгляд сложно сказать: ведь при увеличении ( x) увеличивается и знаменатель дроби, и числитель, так что непонятно, будет ли функция уменьшаться, и если да, то будет ли она уменьшаться пропорционально?
Чтобы понять это, нам необходимо преобразовать выражение таким образом, чтобы в числителе не было переменной:
( displaystyle y=frac{x-5}{{{x}^{2}}-25}=frac{x-5}{left( x-5 right)left( x+5 right)}=frac{1}{x+5},text{ }xne 5).
Действительно, мы получили обратную зависимость, но с оговоркой: ( xne 5).
Почему так? А потому, что выражение ( left( x-5 right)) было в исходном выражении в знаменателе, поэтому если мы возьмём значение ( x=5) и подставим его в исходную функцию (а ведь именно её нам нужно исследовать), то что мы получим?
Ноль, делённый на ноль. Но ведь на ноль нельзя делить ничего, даже другой ноль. Поэтому ( x) никак не может быть равен ( 5).
Но почему тогда мы также не пишем ( xne -5)? Оно ведь тоже в знаменателе!
А всё потому, что оно как было в знаменателе, так там и осталось, следовательно мы и так видим, что такое значение икса невозможно.
А поэтому — зачем лишний раз писать? Да-да, математики — народ ленивый, без надобности напрягаться не станут:)
Решения
Пример 1
( displaystyle y=1-frac{3}{x+2})
Пример 2
Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).
Напомню, что для этого надо найти корни соответствующего квадратного уравнения: ( displaystyle {{x}^{2}}+4{x}-5=0).
Я найду их устно с помощью теоремы Виета: ( displaystyle {{x}_{1}}=-5), ( displaystyle {{x}_{2}}=1). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения».
Итак, получаем: ( displaystyle {{x}^{2}}+4{x}-5=left( x+5 right)left( x-1 right)), следовательно:
( displaystyle y=frac{x+5}{left( x+5 right)left( x-1 right)}=frac{1}{x-1},text{ }xne -5)
Пример 3
Ты уже попробовал решить сам? В чем загвоздка?
Наверняка в том, что в числителе у нас ( displaystyle 2x), а в знаменателе – просто ( displaystyle x).
Это не беда. Нам нужно будет сократить на ( displaystyle left( x+2 right)), поэтому в числителе следует вынести ( displaystyle 2) за скобки (чтобы в скобках ( displaystyle x) получился уже без коэффициента):
( displaystyle y=frac{2{x}-3}{x+1}=frac{2left( x-frac{3}{2} right)}{x+1}=2cdot frac{x-1,5}{x+1}=2cdot frac{x+1-1-1,5}{x+1}=…) дальше сам.
Ответ: ( displaystyle y=2-frac{5}{x+1}).
График обратной пропорциональности
Как всегда, начнем с самого простого случая: ( displaystyle y=frac{1}{x}).
Составим таблицу.
Таблица обратной пропорциональности (зависимости)
| ( displaystyle mathbf{x}) | ( displaystyle -3) | ( displaystyle -2) | ( displaystyle -1) | ( displaystyle -0,5) | ( displaystyle 0,5) | ( displaystyle 1) | ( displaystyle 2) | ( displaystyle 3) | ( displaystyle 4) |
| ( displaystyle mathbf{y}) | ( displaystyle -frac{1}{3}) | ( displaystyle -frac{1}{2}) | ( displaystyle -1) | ( displaystyle -2) | ( displaystyle 2) | ( displaystyle ;1) | ( displaystyle frac{1}{2}) | ( displaystyle frac{1}{3}) | ( displaystyle frac{1}{4}) |
Нарисуем точки на координатной плоскости:
Теперь их надо плавно соединить, но как?
Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.
Это график гиперболы и выглядит он так:
Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.
Каждая из них стремится своими концами приблизиться к осям ( displaystyle Ox) и ( displaystyle Oy), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:
Оно и понятно: так как ( displaystyle xne 0), график не может пересекать ось ( displaystyle Oy). Но и ( displaystyle yne 0), так что график никогда не коснется и оси ( displaystyle Ox).
Ну что же, теперь посмотрим на что влияют коэффициенты.
На что влияют коэффициенты
Рассмотрим такие функции:
( displaystyle y=frac{1}{x};text{ }y=frac{2}{x};text{ }y=frac{4}{x};text{ }y=-frac{1}{x};text{ }y=-frac{3}{x}):
Ух ты, какая красота!
Все графики построены разными цветами, чтобы легче было их друг от друга отличать.
Итак, на что обратим внимание в первую очередь?
Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси ( displaystyle Ox).
Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.
А что, если функция выглядит сложнее, например, ( displaystyle y=frac{1}{x-1}+2)?
В этом случае гипербола будет точно такой же, как обычная ( displaystyle y=frac{1}{x}), только она немного сместится. Давай думать, куда?
Чему теперь не может быть равен ( x)? Правильно, ( xne 1). Значит, график никогда не достигнет прямой ( x=1).
А чему не может быть равен ( y)? Теперь ( yne 2). Значит, теперь график будет стремиться к прямой ( y=2), но никогда ее не пересечет.
Итак, теперь прямые ( x=1) и ( y=2) выполняют ту же роль, которую выполняют координатные оси для функции ( displaystyle y=frac{1}{x}).
Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):
Более подробно о том, как строятся такие графики, мы выучим чуть позже.
А теперь попробуй решить несколько примеров для закрепления.
Обратная пропорциональность в жизни
Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный – это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние.
И правда, вспомним формулу скорости: ( displaystyle v=frac{S}{t}), где ( v) – скорость, ( t) – время в пути, ( S) – расстояние (путь).
Отсюда можно выразить время: ( displaystyle t=frac{S}{v})
Пример:
Человек едет на работу со средней скоростью ( 40) км/ч, и доезжает за ( 1) час. Сколько минут он потратит на эту же дорогу, если будет ехать со скоростью ( 60) км/ч?
Решение:
Вообще, такие задачи ты уже решал в 5 и 6 классе. Ты составлял пропорцию:
( displaystyle 60) км/ч – ( 60) мин.
( displaystyle 60) км/ч – ( x) мин.
Далее ты определял, что это обратная пропорциональность, так как чем больше скорость, тем меньше время. Значит, чтобы решить эту пропорцию, нужно поделить числа «крест-накрест»:
( displaystyle frac{40}{x}=frac{60}{60}text{ }Rightarrow text{ }x=40)(мин).
То есть понятие обратной пропорциональности тебе уже точно знакомо. Вот и вспомнили. А теперь то же самое, только по-взрослому: через функцию.
Функция (то есть зависимость) времени в минутах от скорости:
( displaystyle tleft( v right)=frac{S}{v}).
Известно, что ( tleft( 40 right)=60), тогда:
( frac{S}{40}=60text{ }Rightarrow text{ }S=40cdot 60=2400).
Нужно найти ( tleft( 60 right)):
( displaystyle tleft( 60 right)=frac{2400}{60}=40) (мин).
Теперь придумай сам несколько примеров из жизни, в которых присутствует обратная пропорциональность.
Придумал? Молодец, если да. Удачи!
Принципы построения графика обратной пропорциональности (гиперболы)
Теперь давай научимся строить простейшую гиперболу – ( displaystyle y=frac{k}{x}).
Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.
Например, построим гиперболу ( displaystyle y=frac{3}{x}).
Составим таблицу из ( 4) точек, которые принадлежат одной ветке (например, правой):
| ( x) | ( frac{1}{2}) | ( displaystyle 1) | ( displaystyle 3) | ( displaystyle 6) |
| ( y) | ( displaystyle 6) | ( displaystyle 3) | ( displaystyle 1) | ( frac{1}{2}) |
Отмечаем точки на рисунке:
Проводим через них плавную линию, которая краями приближается к осям:
Это одна ветвь гиперболы
Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:
Отлично, осталось вспомнить, что собой представляет вторая ветвь?
Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.
Вот:
Еще один полезный факт.
Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны ( sqrt{k}) для правой ветви гиперболы, и ( -sqrt{k}) для левой.
Для функций, у которых ( k) – точный квадрат (например, ( 1), ( 4) или ( displaystyle frac{1}{4})), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.
В этом случае достаточно даже трех точек, чтобы построить график.
Например, построим график функции ( displaystyle y=frac{4}{x})
Как и в прошлый раз, начнем с правой ветви.
Точка симметрии: ( displaystyle x=y=2). Выберем еще одну точку, например, ( displaystyle x=1), ( displaystyle y=4). У третьей точки координаты будут наоборот: ( displaystyle x=4), ( displaystyle y=1).
Рисуем:
И теперь симметрично отображаем эту ветвь в третью координатную четверть:
Теперь выясним, что будет, если ( displaystyle k<0)?
Очень просто: если есть график функции с таким же по величине, но положительным ( displaystyle k), то нужно просто отразить его относительно оси ( displaystyle Ox)
То есть правая ветвь теперь будет ниже оси ( displaystyle Ox) (в ( displaystyle IV) четверти), а левая – выше (в ( displaystyle III) четверти).
Принцип построения же останется прежним:
Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
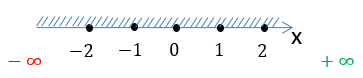
Запишем результат по правилам записи неравенств.
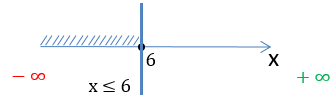
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
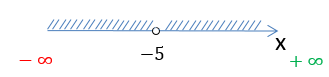
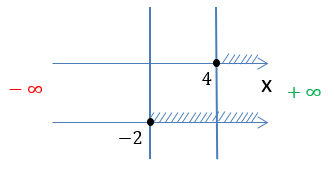
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
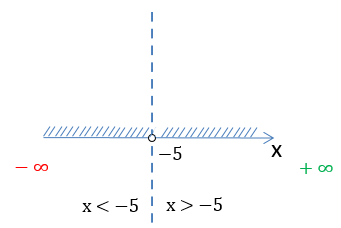
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
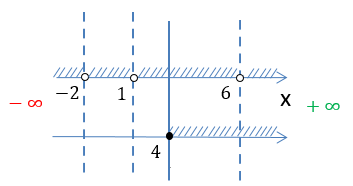
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
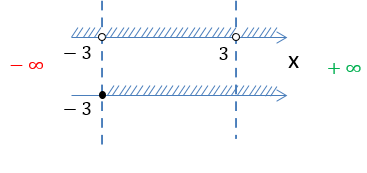
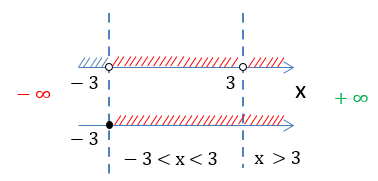
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить










 – 2; б) у = х – 2; в) у = х 2 – 2.
– 2; б) у = х – 2; в) у = х 2 – 2. ; 2) у = 2х 2 ; 3) у = х – 2; 4) у = 2х.
; 2) у = 2х 2 ; 3) у = х – 2; 4) у = 2х.

 + 1; б) у =
+ 1; б) у =  + 1; в) у = х 5 + 1.
+ 1; в) у = х 5 + 1.