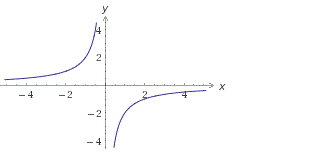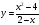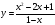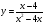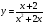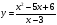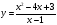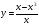Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
Запишем результат по правилам записи неравенств.
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
Область определения дроби
Когда дробь существует?
Дробь существует тогда, когда знаменатель не равен нулю.
Чтобы найти область определения дроби, нужно:
- весь знаменатель приравнять к нулю.
- найти значения, при которых знаменатель обращается в нуль.
Областью определения дроби будут все числа, кроме найденных значений, обращающих знаменатель в нуль.
Пример 1
Найти область определения дроби:
Приравняем знаменатель дроби к нулю:
Решим уравнение. Произведение равно нулю, если один из множителей равен нулю:
Решим каждое из линейных уравнений:
Итак, при x = -4 или x = 3 дробь будет равна нулю, следовательно, область определения этой дроби: все числа, кроме – 4 и 3.
Пример 2
Найти область определения дроби:
Приравняет знаменатель к нулю:
Произведение равно нулю, если один из множителей равен нулю:
Решим полученные линейные уравнения:
Итак, при x = 4 или x = -4 дробь будет равна нулю, следовательно, область определения этой дроби: все числа, кроме – 4 и 4.
Как найти область определения функции
Что такое область определения функции?
Начнём с краткого определения. Область определения функции y=f(x) — это множество значений X, для которых существуют значения Y.
Войдём в тему более основательно. Каждой точке графика функции соответствуют:
- определённое значение «икса» — аргумента функции;
- определённое значение «игрека» — самой функции.
Верны следующие факты.
- От аргумента — «икса» — вычисляется «игрек» — значения функции.
- Область определения функции — это множества всех значений «икса», для которых существует, то есть может быть вычислен «игрек» — значение функции. Иначе говоря, множество значений аргумента, на котором «функция работает».
Можно понимать область определения функции и как проекцию графика функции на ось Ox.
Что требуется, чтобы уверенно находить область определения функции? Во-первых, нужно различать виды функций (корень, дробь, синус и др.). Во-вторых, решать уравнения и неравенства с учетом вида функции (например, на что нельзя делить, какое выражение не может быть под знаком корня и тому подобное). Согласитесь, не так уж много и не так сложно. При изучении темы области определения функции поможет материал Свойства и графики элементарных функций. А поскольку областью определения функции служат различные множества, а также их объединения и пересечения, то пригодится и материал Множества и операции над множествами.
Итак, чтобы находить области определения распространённых функций, порешаем уравнения и неравенства с одной переменной.
После этого экскурса в важную составную матанализа многие согласятся, что найти область определения функции не очень сложно.
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы. Приступаем к практике.
Общий принцип на самых простых примерах
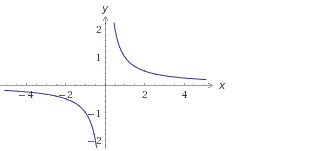
Пример 1. На рисунке изображён график функции . Знаменатель дроби не может быть равен нулю, так как на нуль делить нельзя. Поэтому, приравнивая знаменатель нулю
и решая это уравнение:
получаем значение, не входящее в область определения функции: 1. То есть, область определения заданной функции — это все значения «икса» от минус бесконечности до единицы и от единицы до плюс бесконечности. Это хорошо видно на графике. Приведённый здесь пример функции относится к виду дробей. На уроке разберём решения всех распространённых видов функций.
Пример 2. Как найти область определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять) ()? Так как подкоренное выражение должно быть неотрицательным, нужно решить неравенство
Если перенести какое-либо слагаемое в другую часть неравенства с противоположным знаком, то мы получим равносильное неравенство с тем же знаком неравенства. Переносим минус 5 и получаем неравенство
Получаем решение: область определения функции — все значения икса больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).
На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.
Область определения корня n-й степени
В случае, функции корня n-й степени, то есть когда функция задана формулой и n — натуральное число:
если n — чётное число, то областью определения функции является множество всех неотрицательных действительных чисел, то есть [0; + ∞[ ;
если n — нечётное число, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ .
Пример 3. Найти область определения функции .
Решение. Как следует из определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно. Поэтому решаем неравенство
.
Это квадратное неравенство
,
По формуле находим дискриминант:
.
По формуле находим корни квадратного трёхчлена:
.
Найденные точки разбивают числовую прямую на три промежутка:
и .
При этом знак квадратного трёхчлена (больше или меньше нуля) совпадает со знаком коэффициента a во всех точках промежутков
и
и противоположен знаку коэффициента a во всех точках промежутка .
В нашем случае имеем отрицательный коэффициент a=-1 , поэтому квадратный трёхчлен неотрицателен во всех точках промежутка .
Следовательно, область определения данной функции — [- 1; 1] .
Заштрихованная область числовой прямой на чертеже сверху — это область определения данной функции.
Область определения степенной функции
Область определения степенной функции находится в зависимости от вида степени в выражении.
Область определения степенной функции с дробным показателем степени
В случае, когда функция задана формулой :
если — положительное, то областью определения функции является множество [0; + ∞[ , то есть нуль входит в область определения;
если — отрицательное, то областью определения функции является множество (0; + ∞[ , то есть нуль не входит в область определения.
Пример 4. Найти область определения функции .
Решение. Выражение функции можно представить так:
Квадратный трёхчлен в скобках в знаменателе должен быть строго больше нуля (ещё и потому, что дробный показатель степени данной степенной функции — отрицательный). Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля:
.
.
Дикриминант получился отрицательный. Следовательно сопряжённое неравенству квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях «икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или, что то же самое — множество R действительных чисел, или, что то же самое — ]- ∞; + ∞[ .
Пример 5. Найти область определения функции .
Решение. Оба слагаемых в выражении функции — степенные функции с положительными дробными показателями степеней. Следовательно, область определения данной функции — множество [0; + ∞[ .
На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше, причём штриховка продолжается вместе с самой прямой до плюс бесконечности.
Область определения степенной функции с целым показателем степени
В случае, когда функция задана формулой :
если a — положительное, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[ ;
если a — отрицательное, то областью определения функции является множество ]- ∞; 0[ ∪ ]0 ;+ ∞[ , то есть вся числовая прямая за исключением нуля.
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка, соответствующая нулю, выколота (она не входит в область определения функции).
Пример 6. Найти область определения функции .
Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором слагаемом можно представить в виде единицы — так же целого числа. Следовательно, область определения данной функции — вся числовая прямая, то есть ]- ∞; + ∞[ .
Область определения показательной и логарифмической функции
Область определения показательной функции
В случае, когда функция задана формулой , областью определения функции является вся числовая прямая, то есть ]- ∞; + ∞[ . Подробнее о графике такой функции.
Область определения логарифмической функции
Логарифмическая функция определена при условии, если её аргумент положителен, то есть, областью её определения является множество ]0; + ∞[ . Подробнее о графике такой функции.
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 7. Найти область определения функции .
Пример 8. Найти область определения функции .
Область определения тригонометрических функций
Область определения функции y = cos(x) — так же множество R действительных чисел.
Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .
Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел .
Пример 9. Найти область определения функции .
Решение. Внешняя функция — десятичный логарифм и на область её определения распространяются условия области определения логарифмической функции вообще. То есть, её аргумент должен быть положительным. Аргумент здесь — синус «икса». Пользуясь тригонометической таблицей (или поворачивая воображаемый циркуль по окружности), видим, что условие sin x > 0 нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи» и любого чётного ( 2kπ ) или нечётного целого числа ( (2k+1)π ).
Таким образом, область определения данной функции задаётся выражением
,
где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) — множество [-1; 1] .
Область определения функции y = arccos(x) — так же множество [-1; 1] .
Область определения функции y = arctg(x) — множество R действительных чисел.
Область определения функции y = arcctg(x) — так же множество R действительных чисел.
Пример 10. Найти область определения функции .
Решение. Решим неравенство:
Решение получили, основываясь на свойстве неравенств: если все части верного неравенства умножить на одно и то же положительное число, то получится также верное неравество. В данном случае умножали на 4.
Таким образом, получаем область определения данной функции — отрезок [- 4; 4] .
Пример 11. Найти область определения функции .
Решение. Решим два неравенства:
Решение первого неравенства:
Решение получили, основываясь на свойстве неравенств: если обе части верного неравенства умножить на одно и то же отрицательное число изменить знак неравенства на противоположный, то получится верное неравенство. В данном случае умножали на минус 2.
Аналогично и решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок [0; 1] .
Область определения дроби
Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x , при которых знаменатель дроби обращается в нуль.
Пример 12. Найти область определения функции .
Решение. Решая равенство нулю знаменателя дроби:
находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[ , то есть все числа, кроме минус 2.
Пример 13. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[ , то есть все числа, кроме минус единицы и единицы.
Пример 14. Найти область определения функции .
Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — ]- ∞; — 2[ ∪ ]- 2 ; 2[ ∪ ]2 ;+ ∞[ , то есть все числа, кроме -2 и 2.
Пример 15. Найти область определения функции .
Решение. Решим уравнение:
Уравнение не имеет действительных корней. Но функция определена только на действительных числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что то же самое — множество R действительных чисел или, что то же самое — ]- ∞; + ∞[ .
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.
Пример 16. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[ .
Пример 17. Найти область определения функции .
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках 1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена на отрезке [1; 2] .
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 18. Найти область определения функции .
Пример 19. Найти область определения функции .
Область определения постоянной
Постоянная (константа) определена при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел. Это можно записать и так: областью определения данной функции является вся числовая прямая ]- ∞; + ∞[ .
Пример 20. Найти область определения функции y = 2 .
Решение. Область определения функции не указана, значит, в силу выше приведённого определения имеется в виду естественная область определения. Выражение f(x) = 2 определено при любых действительных значениях x , следовательно, данная функция определена на всём множестве R действительных чисел.
Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус бесконечности до плюс бесконечности.
Область определения линейной функции
Если функция задана формулой вида y = kx + b , то область определения функции — множество R действительных чисел.
График функции с переменной в знаменателе
График функции с переменной в знаменателе — следующая группа заданий из номера 23 ОГЭ по математике.
Исследование любой функции начинается с нахождения её области определения.
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, те значения переменной, при которых знаменатель обращается в нуль, не входят в область определения функции.
В этом случае возможно появление на графике выколотых точек.
Рассмотрим примеры построения графиков функций, содержащих переменную в знаменателе дроби.
1) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
ВАЖНО: прежде чем сократить дробь, следует найти область определения функции!
Дробь имеет смысл, если знаменатель отличен от нуля:
Область определения функции D(y): x∈(-∞;0)∪(0;8/5)∪(8/5;∞)
(или D(y): x∈R, кроме x=0 и x=8/5).
Теперь сократим дробь на 5x-8:
y=1/x — функция обратной пропорциональности. Её график — гипербола. Не забываем про выколотую точку: x≠8/5 (0 не входит в область определения функции y=1/x).
Для построения гиперболы возьмём несколько точек (в том числе, выколотую):
Отмечаем эти точки на координатной плоскости.
Строим гиперболу с выколотой точкой (8/5; 5/8):
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку:
Чтобы найти k, подставляем координаты выколотой точки
в формулу y=kx и находим k:
2) Постройте график функции
и определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
В знаменателе вынесем за скобки общий множитель
(Не забываем: сначала следует найти область определения функции, и лишь после этого упрощать выражение!)
Ищем область определения функции.
Сокращаем дробь на x+5:
— функция обратной пропорциональности. График — гипербола, полученная из гиперболы
Сначала найдём несколько точек для построения графика y=-1/x:
Отметим эти точки на координатной плоскости. Затем каждую из них перенесем на 3 единицы вверх вдоль оси ординат.
Прямая y=0 (ось абсцисс) для гиперболы y=-1/x является асимптотой (то есть прямой, к которой график стремится, но никогда её не достигнет). Асимптоты принято изображать пунктирными линиями. Так как y=0 совпадает с осью Ox, то она изображена сплошной линией. При параллельном переносе на 3 единицы вверх прямая y=0 переходит в прямую y=3. Прямая y=3 — асимптота, поэтому изображаем её пунктиром.
Через полученные точки проведём гиперболу y=3-1/x:
Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку либо совпадает с асимптотой y=3, то есть при m=3,2 и m=3:
3) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Найдём область определения функции.
и сократим её на (x+1):
y=-x²-4 — квадратичная функция. График — парабола ветвями вниз (так как a=-1
имеет одно решение.
Приравниваем правые части равенств:
Это квадратное уравнение имеет один корень в двух случаях: либо дискриминант равен нулю, либо дискриминант положителен, но один из корней равен -1.
k²-16=0 при k=4 или k=-4.
Если x=-1, подставив это значение в уравнение, найдём k:
4) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Формула функции содержит три квадратных трёхчлена. Чтобы разложить каждый из них на множители, решим три квадратных уравнения и воспользуемся теоремой о разложении квадратного трёхчлена на множители.
Ищем область определения функции.
Сокращаем дробь на (x+1)(x+3):
-квадратичная функция. График — парабола ветвями вверх (так как a=1>0).
Координаты вершины параболы
От вершины — точки (1,5; -0,25) — строим параболу y=x². Поскольку координаты вершины — не целые числа, для построения графика удобно найти дополнительные точки с целыми координатами.
При y=0 (x — 1)(x — 2)=0,
Находим координаты выколотых точек
Прямая y=m имеет с графиком ровно одну общую точку, если она проходит через одну из выколотых точек либо через вершину, то есть при m=2, m=6 и m=-0,25.
http://function-x.ru/function_definition_area.html
Найти область определения функции с примерами решения
Содержание:
- Примеры с решением
Областью определения функции (если она не указана особо) является множество , для каждого элемента которого выражение имеет смысл.
Область определения функции обозначается или .
Областью определения функции где — многочлен, является всё множество действительных чисел . В частности, для функций:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Высшая математика: лекции, формулы, теоремы, примеры задач с решением
Примеры с решением
Пример 1.
Для функции, так как её можно преобразовать:
Областью определения функции является множество всех действительных чисел .
Областью определения функций и вообще (где степень корня — нечётное число) является всё множество действительных чисел .
Пример 2.
Для функции
Областью определения функций и вообще (где степень корня — чётное число) является множество всех действительных неотрицательных чисел: .
Область определения функции задаётся неравенством .
Возможно вам будут полезны данные страницы:
|
Определитель матрицы примеры решения |
|
Как найти область определения функции: решение |
|
Формула Байеса |
|
Как найти производную: примеры решения |
Пример 3.
Область определения функции находится из условия . Отсюда .
Областью определения функцииявляется множество всех действительных чисел, кроме нуля: .
Чтобы найти область определения функции , надо из области определения функции исключить те значения , при которых знаменатель дроби обращается в ноль: .
Пример 4.
Для функции
Область определения функции задается неравенством
Область определения функции, составленной из нескольких функций, задаётся системой неравенств для нахождения области определения каждой из этих функций.
Пример 5.
Область определения функции находится из системы Отсюда
Область определения функции может быть задана графически. Область определения функции. Областью определения функции называется совокупность значений независимой переменной, при которых эта функция определена, т. е. область изменения независимой переменной (п. 1.5).
Обычно эта переменная является непрерывной, и тогда, как было указано в п. 1.5, эта область определения состоит из одного или нескольких интервалов.
В некоторых случаях область определения функции выясняется из физического или геометрического смысла этой функции. Например, если рассматривать зависимость площади круга от длины его радиуса, то областью определения этой функции будет интервал, так как по геометрическому смыслу может принимать именно такие значения. Если рассматривается зависимость плотности атмосферы надданной точкой земной поверхности от высоты над уровнем моря, то областью определения этой функции будет интервал , где — высота земной поверхности, а — условная высота, принимаемая за границу атмосферы, и т.
д.
Если функция задана просто формулой, то областью определения служит совокупность значений аргумента, при которых формула дает определенное вещественное (действительное) значение функции. (Мы пока будем рассматривать только вещественные функции от вещественного аргумента, т. е. функции, у которых зависимая и независимая переменные принимают лишь вещественные значения.)
Например, если , то может принимать любые значения, т. е. областью определения служит вся числовая ось . Если , то при вычислении встретится препятствие в извлечении корня, если окажется, что ; значит, должно быть ,т. е. , а это справедливо при или , т. е. область определения в данном случае состоит из двух интервалов: и (на рис. 1.10 эта область заштрихована). При нахождении области определения в аналогичных случаях надо выяснить, что может препятствовать получению значения функции, после чего выписывать неравенства (как в последнем примере ), гарантирующие возможность этого получения. Тогда задача сведется к решению этих неравенств.
Если независимая переменная дискретна, то область определения функции состоит из дискретных (отдельных)точек. Например, если
, то может принимать только значения 1,2, 3,… Если, как в этом примере, дискретный аргумент принимает лишь целые значения, то обычно его обозначают не , а буквами и т. п., а вместо пишут и говорят, что дана последовательность; например, последовательностью служит геометрическая прогрессия
и т. п. График функции от дискретного аргумента не является линией, а состоит из дискретных точек (рис. 1.11).
Область изменения самой функции называется иначе множеством значений этой функции. Например, для функции областью определения служит интервал , а множеством значений — интервал , так как в данном случае у принимает только такие значения.
Выяснение области определения функции важно для построения ее графика, так как эта область — это та часть оси абсцисс, над или под которой пройдет график; точнее говоря, это — проекция графика на ось абсцисс.

На рис. 1.12 показаны три простых графика; области определения этих функций заштрихованы. Ясно, что если область определения состоит из нескольких частей, то и график состоит из нескольких кусков.
Задача 1.
Найти область определения функции Идея. Получить ограничения на из условия неотрицательности подкоренного выражения. Указание. Решить неравенство Решение:
Областью определения функции являются те значения , при которых
Ответ.
Задача 2.
Найти область определения функции Идея. Получить ограничения на из условия неотрицательности подкоренных выражений. Указание. Решить систему неравенств Решение:
Радикалы определены при
Следовательно, областью определения являются три точки и . Ответ. ±2; 0.
Пример 6.
Найти область определения функции, т. е. те значения , которым соответствуют действительные значения.

Решение:
Очевидно, подкоренное выражение для этих не должно быть отрицательным: или .
Итак, функция определена для всех значений , меньших или равных единице:
Область определения функции изображена на рис. 7.
График функции будет располагаться слева от прямой, перпендикулярной к оси и проходящей через точку .
Пример 7.
Найти область определения функции .
Решение:
Так как при положительном основании отрицацательные числа
Рис. 8. не имеют действительных логарифмов, необходимо, чтобы выражение, стоящее под знаком логарифма, было положительным:
, или .
Это неравенство будет выполнено, если или .
Область определения исследуемой функции состоит из двух частей: и (рис. 8), а график имеет две ветви, которые располагаются слева от прямой и справа от прямой .
Область определения функции, в которой есть дробь
⇐ ПредыдущаяСтр 2 из 2
Итак, нам надо найти все допустимые значения икса для какой-то конкретной функции.
На первом этапе ищем в функции операции, которые могут оказаться недопустимыми при каких-то значениях икса. Т.е. ищем потенциально опасные операции.
На втором этапе определяем иксы, которые не приводят к запретному действию в этих самых операциях. Это и будет область определения функции.
Если эти этапы не очень понятны, читаем дальше, на примерах всё куда яснее будет.
Что такое потенциально опасные операции? Это операции, в которых существуют принципиальные ограничения. Не пугайтесь, таких операций всего ничего и вы их прекрасно знаете). Перечисляю:
До 9-го класса включительно:
1. Деление. Нельзя делить на ноль.
2. Извлечение корня. Нельзя извлекать корни чётной степени из отрицательных чисел.
В выпускных классах и ВУЗах:
3. Логарифмы. Ограничения в логарифмах: если logab = c, то а>0, a≠1, b>0.
4. Тригонометрия. Ограничения в тригонометрии: значения углов, для которых тангенс и котангенс не существуют, ограничения на выражения под знаком арксинуса, арккосинуса.
Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.
Не буду останавливаться на самых простых функциях вроде и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:
Пример 1
Найти область определения функции
Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:
Полученное уравнение имеет два корня: .
Ответ: область определения:
Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений ». Напоминаю, что значок обратного слеша в математике обозначает логическое вычитание, а фигурные скобки –
множество. Ответ можно равносильно записать в виде объединения трёх интервалов:
.
Пример 3
Найти область определения функции
Решение: попытаемся найти точки, в которых знаменатель обращается в ноль. Для этого решим квадратное уравнение:
Дискриминант получился отрицательным, а значит, действительных корней нет, и наша функция определена на всей числовой оси.
Ответ: область определения:
Определение.
Областью значений функции y = f(x) называется множество всех значений функции, которые она принимает при переборе всех x из области определения .
Пример.
Определите множество значений функции на интервале (-2; 2).
Решение.
Найдем точки экстремума функции, попадающие на промежуток
(-2; 2):
Точка x = 0 является точкой максимума, так как производная меняет знак с плюса на минус при переходе через нее, а график функции от возрастания переходит к убыванию.
есть соответствующий максимум функции.
Выясним поведение функции при x стремящемся к -2 справа и при xстремящемся к 2 слева, то есть, найдем односторонние пределы:
Что мы получили: при изменении аргумента от -2 к нулю значения функции возрастают от минус бесконечности до минус одной четвертой (максимума функции при x = 0), при изменении аргумента от нуля к 2 значения функции убывают к минус бесконечности.
P.S. Если вы ещё не прошли производную, воспользуйтесь первым способом.
⇐ Предыдущая12
Поиск по сайту:
Область определения функции, как обозначается
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи
из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Что называется областью определения функции
2. Как обозначается область определения
Что называется областью определения функции
Математической функции свойственно сопоставление значений множества $X$ значениям множества $Y$.
Определение 1
Областью определения функции (ООФ) принято называть
совокупность значений, принимаемых ее независимой переменной.
Пример 1
Найти область определения функции $у = frac{6х}{(5 + х)}$.
Поскольку в уравнении присутствует дробь, следует исключить ситуации деления на ноль, т.е. выяснить, при каких значениях $x$ может появиться ноль в знаменателе:
$5 + х neq 0 \ х neq -5$
Ответ:
ООФ этой функции есть объединение множеств $(-∞; -5) cup (-5; ∞)$, т.е. всё множество действительных чисел, кроме 5.
Сообщество экспертов Автор24
Автор этой статьи
Дата последнего обновления статьи: 04.03.2022
Выполнение любых типов работ по
математике
Решение задач по комбинаторике на заказ
Решение задачи Коши онлайн
Математика для заочников
Контрольная работа на тему числовые неравенства и их свойства
Контрольная работа на тему умножение и деление рациональных чисел
Контрольная работа на тему действия с рациональными числами
Дипломная работа на тему числа
Курсовая работа на тему дифференциальные уравнения
Контрольная работа на тему приближенные вычисления
Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы
Курсовые работы
Выпускные квалификационные работы
Рефераты
Сочинения
Доклады
Эссе
Отчеты по практике
Решения задач
Контрольные работы
Область определения показательной и логарифмической функции — Студопедия.

Область определения показательной функции
В случае, когда функция задана формулой , областью определения функции является вся числовая прямая, то есть ]- ∞; + ∞[.
Область определения логарифмической функции
Логарифмическая функция определена при условии, если её аргумент положителен, то есть, областью её определения является множество ]0; + ∞[.
Найти область определения функции самостоятельно, а затем посмотреть решение
Пример 6. Найти область определения функции .
Посмотреть правильное решение и ответ.
Пример 7. Найти область определения функции .
Посмотреть правильное решение и ответ.
Область определения тригонометрических функций
Область определения функции y = sin(x) — множество R действительных чисел.
Область определения функции y = cos(x) — так же множество R действительных чисел.
Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .
Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел .
Пример 8. Найти область определения функции .
Решение. Внешняя функция — десятичный логарифм и на область её определения распространяются условия области определения логарифмической функции вообще. То есть, её аргумент должен быть положительным. Аргумент здесь — синус «икса». Поворачивая воображаемый циркуль по окружности, видим, что условие sin x > 0 нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи» и любого чётного или нечётного целого числа.
Таким образом, область определения данной функции задаётся выражением
,
где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) — множество [-1; 1].
Область определения функции y = arccos(x) — так же множество [-1; 1].
Область определения функции y = arctg(x) — множество R действительных чисел.
Область определения функции y = arcctg(x) — так же множество R действительных чисел.
Пример 9. Найти область определения функции .
Решение. Решим неравенство:
Таким образом, получаем область определения данной функции — отрезок [- 4; 4].
Пример 10. Найти область определения функции .
Решение. Решим два неравенства:
Решение первого неравенства:
Решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок [0; 1].
Область определения дроби
Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x, при которых знаменатель дроби обращается в нуль.
Пример 11. Найти область определения функции .
Решение. Решая равенство нулю знаменателя дроби, находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[.
Пример 12. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[.
Пример 13. Найти область определения функции .
Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — все x, кроме -2 и 2.
Пример 14. Найти область определения функции .
Решение. Решим уравнение:
Уравнение не имеет действительных корней. Но функция определена только на действительных числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что то же самое — множество R действительных чисел или, что то же самое — ]- ∞; + ∞[.
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.
Пример 15. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[.
Пример 16. Найти область определения функции .
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках 1 и 2.
Понятие экстремума функции
График функции с переменной в знаменателе
График функции с переменной в знаменателе — следующая группа заданий из номера 23 ОГЭ по математике.
Исследование любой функции начинается с нахождения её области определения.
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, те значения переменной, при которых знаменатель обращается в нуль, не входят в область определения функции.
В этом случае возможно появление на графике выколотых точек.
Рассмотрим примеры построения графиков функций, содержащих переменную в знаменателе дроби.
1) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.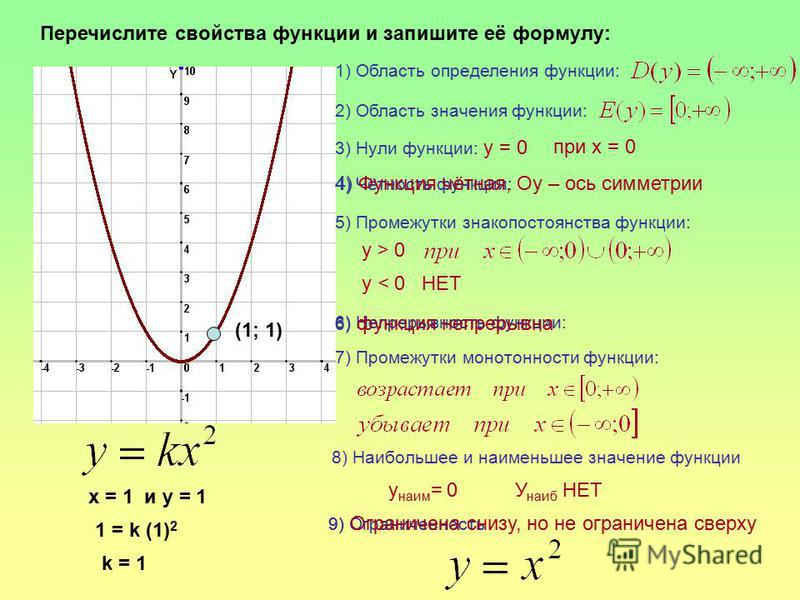
Решение:
В знаменателе вынесем за скобки общий множитель x:
ВАЖНО: прежде чем сократить дробь, следует найти область определения функции!
Дробь имеет смысл, если знаменатель отличен от нуля:
x(5x-8)≠0,
x≠0, x≠8/5.
Область определения функции D(y): x∈(-∞;0)∪(0;8/5)∪(8/5;∞)
(или D(y): x∈R, кроме x=0 и x=8/5).
Теперь сократим дробь на 5x-8:
y=1/x — функция обратной пропорциональности. Её график — гипербола. Не забываем про выколотую точку: x≠8/5 (0 не входит в область определения функции y=1/x).
Для построения гиперболы возьмём несколько точек (в том числе, выколотую):
Отмечаем эти точки на координатной плоскости.
Строим гиперболу с выколотой точкой (8/5; 5/8):
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку:
Чтобы найти k, подставляем координаты выколотой точки
(8/5; 5/8)
в формулу y=kx и находим k:
Ответ : 25/64.
2) Постройте график функции
и определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Решение:
В знаменателе вынесем за скобки общий множитель
(Не забываем: сначала следует найти область определения функции, и лишь после этого упрощать выражение!)
Ищем область определения функции.
x(x+5)≠0
x≠0; x≠-5;
D(y): x∈(-∞;-5)∪(-5;0)∪(0;∞).
Сокращаем дробь на x+5:
— функция обратной пропорциональности. График — гипербола, полученная из гиперболы
параллельным переносом на 3 единицы вверх вдоль оси Oy.
Сначала найдём несколько точек для построения графика y=-1/x:
Отметим эти точки на координатной плоскости. Затем каждую из них перенесем на 3 единицы вверх вдоль оси ординат.
Прямая y=0 (ось абсцисс) для гиперболы y=-1/x является асимптотой (то есть прямой, к которой график стремится, но никогда её не достигнет).
Через полученные точки проведём гиперболу y=3-1/x:
Прямая y=m не имеет с графиком ни одной общей точки, если она проходит через выколотую точку либо совпадает с асимптотой y=3, то есть при m=3,2 и m=3:
Ответ: 3; 3,2.
3) Постройте график функции
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Решение:
Найдём область определения функции.
-1-x≠0
x≠-1.
D(y):x∈(-∞;-1)∪(-1;∞).
Преобразуем дробь:
и сократим её на (x+1):
y=-x²-4 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).
График может быть получен из графика функции y=-x² параллельным переносом на 4 единицы вниз вдоль оси Oy (не забываем про выколотую точку! x≠-1):
Прямая y=kx имеет с графиком ровно одну общую точку, если она проходит через выколотую точку либо если она является касательной к параболе:
Значения k в данном случае удобнее искать аналитически, а не с помощью графика.
Прямая y=kx имеет с графиком функции y=-x²-4, где x≠-1 ровно одну общую точку, если система
имеет одно решение.
Приравниваем правые части равенств:
-x²-4=kx
x²+kx+4=0.
Это квадратное уравнение имеет один корень в двух случаях: либо дискриминант равен нулю, либо дискриминант положителен, но один из корней равен -1.
D=b²-4ac=k²-4·1·4=k²-16.
k²-16=0 при k=4 или k=-4.
Если x=-1, подставив это значение в уравнение, найдём k:
(-1)²+k·(-1)+4=0
k=5.
Ответ: -4; 4; 5.
4) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
Решение:
Формула функции содержит три квадратных трёхчлена. Чтобы разложить каждый из них на множители, решим три квадратных уравнения и воспользуемся теоремой о разложении квадратного трёхчлена на множители.
1)x²-4x+3=0
x1=1; x2=3
x²-4x+3=(x-1)(x-3).
2)x²-x-2=0
x1=-1; x2=2
x²-x-2=(x+1)(x-2).
3)x²-2x-3=0
x1=-1; x2=3
x²-2x-3=(x+1)(x-3).
Ищем область определения функции.
(x+1)(x-3)≠0
x≠-1, x≠3.
D(y): x∈(-∞;-1)∪(-1;3)∪(3;∞).
Сокращаем дробь на (x+1)(x+3):
-квадратичная функция. График — парабола ветвями вверх (так как a=1>0).
Координаты вершины параболы
От вершины — точки (1,5; -0,25) — строим параболу y=x². Поскольку координаты вершины — не целые числа, для построения графика удобно найти дополнительные точки с целыми координатами.
При y=0 (x — 1)(x — 2)=0,
x=1; x=2.
При x=0 y=0²-3·0+2=2.
Находим координаты выколотых точек
При x=-1 y=(-1)²-3·(-1)+2=6,
при x=3 y=3²-3·3+2=2.
Прямая y=m имеет с графиком ровно одну общую точку, если она проходит через одну из выколотых точек либо через вершину, то есть при m=2, m=6 и m=-0,25.
Ответ: -0,25; 2; 6.
Рубрика: ОГЭ задание 22
| Комментарии
Область определения функции
|
Как видно из описанного выше, первая функция имеет область определения — все множество действительных чисел, вторая не определяется при значении 5, а в область определения третьей функции не входит значение -3. 2080.1947 Функции | |
Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!
Рациональная функция — график, область, диапазон, асимптоты
Рациональная функция — это отношение многочленов, где многочлен в знаменателе не должен быть равен нулю. Разве это не похоже на определение рационального числа (которое имеет вид p/q, где q ≠ 0)? Знаете ли вы, что функции Rational находят применение в различных областях нашей повседневной жизни? Они не только описывают взаимосвязь между скоростью, расстоянием и временем, но также широко используются в медицинской и инженерной промышленности.
Давайте узнаем больше о рациональных функциях, а также о том, как их изображать, их область определения, диапазон, асимптоты и т. д., а также решаемые примеры.
| 1. | Что такое рациональная функция? |
| 2. | Как определить рациональную функцию? |
| 3. | Домен и диапазон рациональной функции |
| 4. | Асимптоты рациональной функции |
| 5. | Графики рациональных функций |
| 6. | Обратная рациональная функция |
| 7. | Часто задаваемые вопросы по Rational Functions |
Что такое рациональная функция?
Рациональная функция — это функция, представляющая собой отношение полиномов. Любая функция одной переменной x называется рациональной функцией, если ее можно представить в виде f(x) = p(x)/q(x), , где p(x) и q(x) — такие многочлены, что q(x) ≠ 0.
Мы знаем, что каждая константа является многочленом и, следовательно, числители рациональная функция также может быть константой. Например, f(x) = 1/(3x+1) может быть рациональной функцией. Но обратите внимание, что знаменатели рациональных функций не могут быть константами. Например, f(x) = (2x + 3)/4 НЕ является рациональной функцией, а скорее линейной функцией.
Как определить рациональную функцию?
По определению рациональной функции (из предыдущего раздела), если либо числитель, либо знаменатель не являются полиномами, то образованная дробь НЕ представляет собой рациональную функцию. Например, f(x) = (4 + √x)/(2-x), g(x) = (3 + (1/x))/(2 — x) и т. д. НЕ являются рациональными функциями как числители в эти примеры НЕ являются полиномами.
Домен и диапазон рациональной функции
Любая дробь не определена, если ее знаменатель равен 0.
Область определения рациональной функции
Область определения рациональной функции — это набор всех значений x, которые может принимать функция. Чтобы найти область определения рациональной функции y = f(x):
- Установите знаменатель ≠ 0 и решите его для x.
- Множество всех вещественных чисел, отличных от значений x, упомянутых на последнем шаге, является доменом.
Пример: Найдите область значений f(x) = (2x + 1) / (3x — 2).
Решение:
Примем знаменатель не равным нулю.
3x — 2 ≠ 0
x ≠ 2/3
Таким образом, область определения = {x ∈ R | x ≠ 2/3}
Диапазон рациональной функции
Диапазон рациональной функции — это набор всех выходных значений (значений y), которые она производит. Чтобы найти диапазон рациональной функции y = f(x):
- Если в уравнении есть f(x), замените его на y.
- Решите уравнение для x.
- Установите знаменатель полученного уравнения ≠ 0 и решите его относительно y.
- Набор всех действительных чисел, отличных от значений y, упомянутых в последнем шаге, является диапазоном.
Пример: Найдите диапазон f(x) = (2x + 1) / (3x — 2).
Решение:
Заменим f(x) на y. Тогда у = (2х + 1) / (3х — 2). Теперь мы решим это для х.
(3x — 2) у = (2x + 1)
3xy — 2y = 2x + 1
3xy — 2x = 2y + 1
х (3у — 2) = (2у + 1)
x = (2y + 1) / (3y — 2)
Теперь (3y — 2) ≠ 0
y ≠ 2/3
Таким образом, диапазон = {y ∈ R | у ≠ 2/3}
Асимптоты рациональной функции
Рациональная функция может иметь три типа асимптот: горизонтальные, вертикальные и наклонные асимптоты. Помимо этого, он может иметь и отверстия. Давайте посмотрим, как найти каждый из них.
Отверстия рациональной функции
Дырки рациональной функции — это точки, которые кажутся присутствующими на графике рациональной функции, но на самом деле их нет.
Пример: Найти дыры функции f(x) = (x 2 + 5x + 6) / (x 2 + x — 2).
Решение:
Разложим на множители числитель и знаменатель и посмотрим, есть ли общие множители.
f(x) = [ (x + 2)(x + 3) ] / [ (x + 2) (x — 1) ]
= [ ̶(̶x̶ ̶+̶ ̶2̶)̶(x + 3)] / [ ̶(̶x̶ ̶+̶ ̶2̶)̶ (x — 1)]
= (x + 3) / (x — 1)
Поскольку (x + 2) было вычеркнуто, в точке x = -2 есть дыра. Его координата y равна f(-2) = (-2 + 3) / (-2 — 1) = -1/3.
Таким образом, в точках (-2, -1/3) есть дыра.
Вертикальная асимптота рациональной функции
Вертикальная асимптота (ВА) функции представляет собой воображаемую вертикальную линию, к которой ее график кажется очень близким, но никогда не касающимся.
- Сначала упростите функцию, чтобы отменить все общие факторы (если они есть).
- Установите знаменатель = 0 и найдите (x) (или, что то же самое, просто получите исключенные значения из домена, избегая пробелов).
Пример: Найдите вертикальные асимптоты функции f(x) = (x 2 + 5x + 6) / (x 2 + x — 2).
Решение:
Мы уже видели, что эта функция упрощается до f(x) = (x + 3) / (x — 1).
Приравняв знаменатель к 0, получим
х — 1 = 0
x = 1
Таким образом, существует ВА данной рациональной функции, x = 1.
Горизонтальная асимптота рациональной функции
Горизонтальная асимптота (ГА) функции – это воображаемая горизонтальная линия, относительно которой находится ее график кажется, очень близко, но никогда не касаться. Оно имеет форму y = некоторое число. Здесь «некоторое число» тесно связано с исключенными значениями из диапазона. Рациональная функция может иметь не более одной горизонтальной асимптоты. Простой способ найти горизонтальную асимптоту рациональной функции — использовать степени числителя (N) и знаменателя (D).
- Если N < D, то существует HA при y = 0.
- Если N > D, то высокой доступности нет.
- Если N = D, то HA равен y = отношению старших коэффициентов.
Пример: Найдите горизонтальную асимптоту (если есть) функции f(x) = (x 2 + 5x + 6) / (x 2 + x — 2).
Решение:
Здесь степень числителя N = 2, а степень знаменателя D = 2,
Поскольку N = D, HA равен y = (старший коэффициент числителя) / (старший коэффициент знаменателя) = 1/1 = 1.
Таким образом, HA равен y = 1.
Наклонная (наклонная) асимптота рациональной функции
Наклонная асимптота — это также воображаемая наклонная линия, которой кажется касающейся часть графика. Рациональная функция имеет наклонную асимптоту только тогда, когда степень числителя (N) ровно на единицу больше степени знаменателя (D). Его уравнение y = частное, которое получается путем деления числителя на знаменатель с использованием длинного деления.
Пример: Найдите наклонную асимптоту функции f(x) = x 2 /(x+1).
Решение:
Здесь степень числителя равна 2, а степень знаменателя = 1. Таким образом, она имеет наклонную асимптоту.
Разделим x 2 на (x + 1) делением в длину (или можно использовать и синтетическое деление).
Таким образом, наклонная асимптота равна y = x — 1.
Графики рациональных функций
Вот шаги для построения графика рациональной функции:
- Определите и нарисуйте вертикальную асимптоту, используя пунктирную линию.
- Определите и нарисуйте горизонтальную асимптоту, используя пунктирную линию.
- Нанесите отверстия (если есть)
- Найдите точку пересечения по оси x (используя y = 0) и точку пересечения y (по x = 0) и нанесите их на график.
- Нарисуйте таблицу из двух столбцов x и y и поместите в нее точки пересечения x и вертикальные асимптоты. Затем возьмите несколько случайных чисел в столбце x по обе стороны от каждой из точек пересечения x и вертикальных асимптот.
- Вычислите соответствующие значения y, подставив каждое из них в функцию.
- Нанесите все точки из таблицы и соедините их кривыми, не касаясь асимптот.
Пример: Постройте график рациональной функции f(x) = (x 2 + 5x + 6) / (x 2 + x — 2).
Решение:
Мы уже определили, что его VA равна x = 1, его HA равна y = 1, а отверстие находится в точке (-2, -1/3). Мы используем пунктирные линии для асимптот, чтобы мы могли позаботиться о том, чтобы график не касался этих линий.
- Для точки пересечения по оси x положим y = 0. Тогда мы получим 0 = (x + 3) / (x — 1) ⇒ x + 3 = 0 ⇒ x = -3. Таким образом, x-перехват находится в (-3, 0).
- Для точки пересечения по оси y положим x = 0. Тогда мы получим y = (0 + 3) / (0 — 1) ⇒ y = -3. Таким образом, точка пересечения по оси y находится в точке (0, -3).
У нас есть VA при x = 1, а точка пересечения x при x = -3. Теперь давайте составим таблицу с этими двумя значениями в столбце x и некоторыми случайными числами по обе стороны от каждого из этих чисел -3 и 1.
| х | и |
|---|---|
| -5 | г = (-5 + 3) / (-5 — 1) = 0,33 |
| -4 | г = (-4 + 3) / (-4 — 1) = 0,2 |
| -3 | 0 (х-целое) |
| -2 | г = (-2 + 3) / (-2 — 1) = -0,33 |
| 0 | -3 (г-целое) |
| 1 | ВА |
| 2 | у = (2 + 3) / (2 — 1) = 5 |
| 3 | у = (3 + 3) / (3 — 1) = 3 |
Нанесем на график все эти точки вместе со всеми асимптотами, дырками и точками пересечения.
Обратная рациональная функция
Чтобы найти обратную рациональную функцию y = f(x):
- Заменить f(x) на y.
- Развязка x и y.
- Решите полученное уравнение относительно y.
- Результат будет обратным f -1 (x).
Пример: Найдите обратную рациональную функцию f(x) = (2x — 1) / (x + 3).
Решение:
Данную функцию можно записать в виде:
y = (2x — 1) / (x + 3)
Перестановка x и y:
x = (2y — 1) / (y + 3)
Теперь найдем у.
x(y + 3) = 2y — 1
xy + 3x = 2y — 1
3x + 1 = 2y — xy
3x + 1 = y (2 — x)
y = (3x + 1) ) / (2 — x) = f -1 (x)
Важные замечания по рациональной функции:
- Уравнение рациональной функции имеет форму f(x) = P(x) / Q(x ), где Q(x) ≠ 0,
- Каждая рациональная функция имеет хотя бы одну вертикальную асимптоту.
- Каждая рациональная функция имеет не более одной горизонтальной асимптоты.
- Каждая рациональная функция имеет не более одной наклонной асимптоты.
- Исключенные значения области определения рациональной функции помогают идентифицировать ВА.
- Исключенные значения диапазона рациональной функции помогают идентифицировать ГК.
- Линейные множители, которые сокращаются при упрощении рациональной функции, дают нам дыры.
☛ Связанные темы:
- Графические функции
- Калькулятор упрощения рациональных выражений
- Калькулятор асимптот
- Обратная функция
Часто задаваемые вопросы по Rational Functions
Что такое определение рациональной функции?
Рациональная функция — это функция, похожая на дробь, в которой и числитель, и знаменатель являются полиномами. Похоже, что f(x) = p(x)/q(x), где и p(x), и q(x) являются многочленами.
Каково конечное поведение рациональной функции?
Конечное поведение родительской рациональной функции f(x) = 1/x:
- f(x) → 0 при x → ∞ или -∞, и это соответствует горизонтальной асимптоте.
- f(x) → ∞ при x → 0 + и f(x) → -∞ при x → 0 — , и они соответствуют вертикальной асимптоте.
Как узнать, рациональна ли функция?
Всякий раз, когда функция имеет многочлены в числителе и знаменателе, она является рациональной функцией. Но помните:
- Числитель рациональной функции может быть константой. Например: 1/x 2 — рациональная функция.
- Знаменатель рациональной функции не может быть константой. Например: x 2 / 1 НЕ является рациональной функцией.
Как построить график рациональной функции?
Чтобы изобразить рациональную функцию, сначала начертите все асимптоты пунктирными линиями. Постройте точки пересечения x и y. Составьте таблицу с двумя столбцами, помеченными x и y.
Как найти область определения и область значений рациональной функции?
Чтобы найти область определения и область значений рациональной функции:
- Сначала упростим функцию.
- Для домена установите знаменатель не равным нулю и найдите x.
- Для диапазона решите упрощенное уравнение для x, установите знаменатель не равным нулю и решите для y.
Как найти дыры в рациональных функциях?
Чтобы найти дыры, сначала разложите на множители числитель и знаменатель. Если какие-либо линейные факторы отменяются, просто установите для каждого из них значение 0 и упростите. Они дадут x-координаты отверстий. Мы можем использовать функцию, чтобы найти соответствующие y-координаты отверстий.
Как найти асимптоты рациональных функций?
Чтобы найти асимптоты рациональной функции:
- Упростите функцию до наименьшей формы.
- Установите знаменатель = 0 и найдите вертикальные асимптоты.
- Решите уравнение для x, установите знаменатель = 0 и решите, чтобы найти горизонтальные асимптоты.
Как найти обратную рациональную функцию?
Чтобы найти обратную рациональную функцию y = f(x), просто сначала поменяйте местами x и y, а затем решите полученное уравнение относительно y. Это даст обратную функцию f(x), которая представлена как f -1 (х).
Каковы применения рациональной функции?
Рациональные функции используются для моделирования многих сценариев реальной жизни. В частности, они используются в сферах бизнеса, науки и медицины.
Рациональные функции
Рациональные функции
|
Содержание : Эта страница соответствует § 3.
3.6 (стр. 299) текста.
Предполагаемые проблемы из текста:
стр. 295 #1-12, 15-17, 21, 24, 37
стр. 304 #35, 37, 49, 52
Введение
Асимптоты
Заявка
Введение
Рациональная функция — это функция, которую можно записать в виде многочлена, деленного на многочлен. Поскольку многочлены
определены везде, областью определения рациональной функции является множество всех чисел кроме нули
знаменатель.
Пример 1 .
f(x) = x/(x — 3). В знаменателе есть только один нуль, x = 3. Таким образом, область определения f — это множество всех чисел, кроме
чем 3.Домен f: (-inf, 3) объединение (3, inf).
График f показан ниже.
Вернуться к содержанию
Асимптоты
Посмотрите еще раз на график f(x) = x / (x — 3), показанный выше.
на графике с первой координатой 3, поэтому в графике должен быть разрыв. В самом деле, мы видим, что функция
значения становятся неограниченными (уходят в бесконечность или отрицательную бесконечность) по мере того, как x приближается к 3. Следующие таблицы функций
значения иллюстрируют это поведение.
|
х |
4 |
3,5 |
3.1 |
3.01 |
3,001 |
|
f(x) = x / (x — 3) |
4 |
7 |
31 |
301 |
3001 |
Мы говорим, что f (x) стремится к бесконечности, когда x приближается к 3 справа , или
f(x) -> inf as x -> 3 + .
Фраза справа важна. Это означает, что мы используем значения для x, которые на 90 605 больше, чем 90 606.
3 и приближается к 3. В следующей таблице показано поведение f при приближении x к 3 слева.
|
х |
2 |
2,5 |
2,9 |
2,99 |
2,999 |
|
f(x) = x / (x — 3) |
-2 |
-5 |
-29 |
-299 |
-2999 |
Мы говорим, что f(x) стремится к отрицательной бесконечности, когда x приближается к 3 слева. Здесь мы будем использовать надстрочный индекс
— для обозначения приближения слева.
f(x) -> — inf as x -> 3 — .
В предыдущем разделе мы указывали, что полиномиальные графы либо возрастают вправо, либо падают вправо.
график рациональной функции f не делает ни того, ни другого. Из рисунка видно, что точки на графике
f приближаются к горизонтальной линии y = 1, когда x идет вправо, а x идет влево. В таблицах ниже приведены дополнительные доказательства
что это так.
|
х |
5 |
10 |
100 |
1000 |
10000 |
|
f(x) = x / (x — 3) |
2,5 |
1.4285715 |
1.0309278 |
1.0030091 |
1,0003 |
|
х |
-5 |
-10 |
-100 |
-1000 |
-10000 |
|
f(x) = x / (x — 3) |
0,625 |
0,76 |
0,9708738 |
0,997009 |
0,99970007 |
Пишем
f(x) -> 1 как x -> inf и f(x) -> 1 как x -> — inf,
или
f(x) -> 1 при x -> ± инф.
Вертикальная линия x = 3 и горизонтальная линия y = 1 являются примерами асимптот . Асимптота – это линия
что график 90 605 приближается к 90 606, когда x приближается к плюс или минус бесконечности или к определенному числу.
Определение горизонтальной и вертикальной асимптот
Линия x = a является вертикальной асимптотой графика f, если f(x) -> ± бесконечность при x -> a
слева или справа.Линия y = b является горизонтальной асимптотой графика f, если f(x) -> b при x -> ± бесконечности.
В общем случае график рациональной функции будет иметь вертикальную асимптоту в нуле знаменателя.
Исключением из этого правила является случай, когда числитель и знаменатель имеют общий ноль.
Пример 2 .
г(х) = (х 2 — 4) / (х — 2). g — рациональная функция, а g не определена в 2, потому что 2 — это ноль.
знаменателя. Однако 2 также является нулем числителя, и мы можем упростить частное.
(х 2 — 4) / (х — 2) = (х — 2)(х + 2)/(х — 2) = х + 2.
Однако функция g не равна функции h(x) = x + 2, потому что h определяется как 2, а g
не является! (Этот момент обычно упоминается на уроках алгебры в колледже, а затем тут же забывается.)График g не имеет вертикальной асимптоты через 2. График g представляет собой прямую y = x + 2 с отверстием
где будет точка (2, 4).
Обычно с помощью графической утилиты можно увидеть, имеет ли график рациональной функции горизонтальную
асимптота. Однако из рисунка, как правило, не ясно, через какое число проходит асимптота.
ось Y. Создание таблицы, как мы сделали выше, дает вам гораздо лучшее представление о том, где находится горизонтальная асимптота.
Пример 3 .
f(x) = x 2 / (x — 3). График f изображен ниже.
Из графика видно, что f(x) -> -inf при x -> 3 — и f(x) -> inf при x -> 3 + .
Также из рисунка видно, что график не имеет горизонтальной асимптоты . График поднимается вправо
и падает влево.Пунктирная линия наклонная асимптота графика f. Наклонные асимптоты обсуждаются на стр.
302 текста.
Можно сказать, имеет ли рациональная функция горизонтальную асимптоту, и если да, то где именно
это происходит путем анализа ведущих членов числителя и знаменателя. Эта процедура подробно описана на
стр. 291 текста.
Конечно, графом можно обмануться. Рассмотрим график, изображенный ниже.
Похоже, это график с вертикальной асимптотой по оси Y. На самом деле это график f(x) = 5x/
(x 2 + 0,01), как показано с помощью Java Grapher. Знаменатель не имеет (действительных) нулей, поэтому график имеет
нет вертикальных асимптот.
Упражнение 1 :
Используйте графическую утилиту для построения графика f(x) = 3x 2 / (x 2 — 16).
Найдите все асимптоты. Ответ
Вернуться к содержанию
Заявка
Пример 4 .
Мы собираемся окружить загон рядом с рекой, как показано на схеме ниже. На реке забор не нужен
сторона. Закрытая территория должна быть 800 квадратных метров. Найдите измерения x и y, которые требуют наименьшего количества
забора.Поскольку известно, что площадь должна быть 800 кв. ярдов, а площадь прямоугольника равна произведению двух измерений,
это дает нам уравнение, которому x и y должны удовлетворять.х у = 800.
Решение для y дает
у = 800/х.
Пусть F обозначает длину используемого забора в ярдах. Так как есть одна сторона длины х и две стороны длины
г, у нас естьF = х + 2у.
Замена y дает
F = х + 2 (800 / х).
Ф = х + 1600 / х.

F — рациональная функция. Его график имеет ось y (x = 0) как вертикальную асимптоту, потому что F не определено
в 0. График F не имеет горизонтальной асимптоты, но линия y = x является наклонной асимптотой.F = х + 1600 / х
Обратите внимание: поскольку переменная x в этой задаче обозначает длину, нас интересуют только значения x >
0, поэтому мы можем сосредоточиться на квадранте I графика F.Нам нужно найти первую координату точки относительного минимума в квадранте I, ибо это длина x, соответствующая
до наименьших значений F, и наша цель — использовать наименьшее возможное количество ограждений.Одним из оцениваемых заданий курса будет выполнение этой задачи с помощью графической утилиты для
аппроксимировать координаты точки относительного минимума и найти размеры загона по осям x и y, требующие
наименьшее количество забора.
Вернуться к содержанию
|
Нахождение области определения и диапазона радикальных и рациональных функций
Поиск
На этот раз мы займемся поиском домена и ряда более интересных функций, а именно радикальные функции и рациональные функции .
Если вы хотите повторить, у меня также есть отдельный урок о том, как найти область определения и диапазон линейных и квадратичных функций.
Пример 1: Найдите область определения и диапазон радикальной функции символ квадратного корня. Чтобы найти домен («хорошие значения x»), я знаю, что можно взять квадратный корень из нуля или любого положительного числа. Мой план состоит в том, чтобы найти все значения x, удовлетворяющие этому условию. Он станет самим доменом.
Я бы сделал выражение под радикалом x-2 больше или равным нулю; а потом решить неравенство. Посмотрите мой другой урок о том, как решать неравенства.
Область определения этой радикальной функции составляет x ≥ 2 . Мне нужно быть осторожным в поиске диапазона этой функции. График функции выглядит следующим образом.
Радикальная функция начинается с y = 0 и может достигать любого значения (положительная бесконечность). Вы можете подумать, что эта функция растет медленно (медленное увеличение значений y) и поэтому не может достигать очень больших значений. Однако вы должны учитывать, что подстановка достаточно большого значения x (то есть миллиардов триллионов) может привести к очень большому выходному значению y.
Следовательно, я буду утверждать, что диапазон этой функции равен y ≥ 0.
Это сводка домена и диапазона, записанная как в виде набора, так и в виде интервала.
Пример 2: Найдите область определения и диапазон радикальной функции
y = — sqrt {10 — 2x}
Под квадратным корнем допустимы нулевые и положительные числа. Поэтому я позволю «материалу» внутри радикала быть равным или больше нуля, а затем найду требуемое неравенство.
Теперь область определения функции x ≤ 5 . Как и в наших предыдущих примерах, я построю график функции для определения диапазона.
Радикальная функция начинается при y = 0, а затем медленно, но неуклонно уменьшается в значениях вплоть до отрицательной бесконечности. Это делает диапазон y ≤ 0. Ниже приводится сводка домена и диапазона.
Пример 3: Найдите область определения и область значений рациональной функции
Large{y = {5 over {x — 2}}}
Эта функция содержит знаменатель. Это говорит мне, что я должен найти значения x, которые могут сделать знаменатель равным нулю, чтобы предотвратить неопределенный случай .
Здесь наша область значений состоит из всех значений x, но не включает x = 2. Это имеет большой смысл, потому что я могу подставить в функцию любые значения x, за исключением x = 2, и функция будет иметь действительные выходы. На приведенном ниже графике показано, что x = 2 на самом деле является вертикальной асимптотой (см. пунктирную оранжевую линию 90 057 9).0058).
Найти диапазон немного сложно. Внимательно взглянув на график, я вижу, что он без ограничений идет вверх и вниз тоже без ограничений.
Проведение анализа «здравого смысла», чтобы показать, что y не может равняться нулю (y ≠ 0).
Возврат к исходной функции
Large{y = {5 over {x — 2}}}
Если я хочу, чтобы y равнялось нулю, мне нужно найти значения x, чтобы выполнить задание. Если подумать, нет значений x, которые могли бы заставить это произойти. Почему? Потому что для того, чтобы рациональное выражение стало нулем, ЧИСЛИТЕЛЬ ДОЛЖЕН БЫТЬ НУЛЕМ. Но числитель не ноль, на самом деле это 5! 93}} over {x — 2}}}
Область определения этой функции точно такая же, как в примере 7.
Чтобы найти диапазон, я буду сильно зависеть от самого графика. Можно нарисовать его вручную, используя более продвинутые графические техники, но я оставлю это для другого урока. В любом случае, график показывает, что он охватывает все возможные значения y: идет вверх и вниз без ограничений и без перерывов между ними. Следовательно, диапазон — это все значения y.
Область и область значений, записанные двумя способами:
Вас также могут заинтересовать:
Область определения и область значений линейных и квадратичных функций
Как найти область определения, область значений и корни полиномов и рациональных функций
Ключевые термины
- Полином
- Степень
- Линейная функция
- Склон у -перехват
- x -пересечение
- Корень
- Нуль (функции) Квадратичная функция
- Квадратичная формула
Рациональная функция
Цели
- Определение многочленов и их основных характеристик
- Определение рациональных функций
- Найдите область определения, область значений и корни простых многочленов и рациональных функций
Введение в многочлены
Многочлены — это тип функции, с которой вы будете регулярно сталкиваться при изучении математики.
Здесь коэффициенты c i являются постоянными, а n — это степень многочлена ( n должно быть целым числом, где 0 ≤ < n ). Обратите внимание, что линия, имеющая вид (или, возможно, более знакомо, y = m x + b ), является полиномом первой степени или полиномом первой степени. Квадратичная функция является многочленом второй степени.
Линейные функции
Линейные функции (за исключением констант или функций нулевой степени) являются простейшим видом многочленов. Учитывая форму , наклон линии равен c 1 , а точка пересечения y- равна c 0 .
В общем, многие функции имеют y — перехваты — опять же, для функции f ( x ), это просто f 01180 (). (Однако не все функции имеют y -intercept, так как не все определены в x = 0. Например, функция не определена при x = 0, поэтому она не имеет точки пересечения y . Поскольку функция должна пройти тест вертикальной линии, как мы отмечали ранее, функция может иметь не более одного y -intercept.
Некоторые функции могут также иметь x- точек пересечения: для функции g ( x ), это значения x , для которых x
g ( In) .
Корень этой функции показан графически ниже.
Квадратичные функции
Вы также можете быть знакомы с квадратичными функциями (многочленами второй степени), которые имеют вид 4. Квадратичные функции, как и все многочлены, имеют точку пересечения y c 0 . Они могут не иметь ни одного, одного или двух корней, что можно определить с помощью квадратичной формулы , которая выражена ниже.
Хотите узнать больше? Почему бы не пройти онлайн-курс Precalculus?
Обратите внимание, что многочлен первой степени (линейная функция) может иметь максимум один корень.
Практическая задача: Найдите корни, если они существуют, функции .
Решение: Вы можете использовать различные методы решения. Один из них заключается в вычислении квадратичной формулы:
t = 1, 4
В качестве альтернативы, вы можете разложить на множители, чтобы найти значения 91 10 179 x 18 118 равные нулю .
t = 1, 4 методы вообще. График для h ( t ) показано ниже с корнями, отмеченными точками.
Нахождение корней многочленов более высоких степеней является более сложной задачей.
Введение в рациональные функции
Рациональные функции представляют собой дроби, включающие многочлены.
Обратите внимание, что все многочлены являются рациональными функциями (полином — это рациональная функция, для которой q ( x ) = 1), но не все рациональные функции являются полиномами. Пример рациональной функции следующий.
Предостережение: хотя приведенное выше выражение можно упростить, результат может не совпадать с исходной функцией. Чтобы проиллюстрировать этот момент, давайте разложим числитель 91 179 g 91 180 ( 91 179 r 91 180 ).
Естественно, возникает соблазн вычесть один множитель r – 1 как из числителя, так и из знаменателя, оставив следующее выражение:
Таким образом, мы видим, что g ( r ) является линейным.
Практическая задача: Найдите область определения и диапазон функции и постройте график функции.
Решение: Область определения многочлена — это все множество действительных чисел. Ограничивающим фактором на области определения рациональной функции является знаменатель, который не может быть равен нулю. Значения, не входящие в домен t ( x ) — корни многочлена в знаменателе. Разложим и числитель, и знаменатель.
Из этого разложения мы можем видеть, что область значений t ( x ) состоит из всех действительных чисел, кроме x = –1. То есть область включает интервалы (-∞,-1) и (-1, ∞). Чтобы найти диапазон, построим график функции. Для этого мы можем упростить его, исключив одинаковые множители:
Поскольку ограничение, заключающееся в том, что x не может равняться –1, остается после упрощения, мы можем построить упрощенную функцию на графике, не беспокоясь о том, что можно пренебречь дырами.
Обратите внимание, что x никогда не может быть –1, потому что функция стремится к бесконечности (или отрицательной бесконечности) по мере приближения к этому значению. Также обратите внимание, что диапазон функции включает все действительные значения, кроме t = 1. Оно очень близко к t = 1, но никогда не достигает этого значения (числитель никогда не равен знаменателю!).
Как найти область определения и область значений рациональной функции?
1078 просмотров
Как найти область определения и область значений рациональной функции?
- домен
- диапазон
- рациональное
- функция
спросил
Устарело : strlen(): Передача null в параметр #1 ($string) строкового типа устарела в 9 160
Устарело строка типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 162
15 сентября 2020 г.
по математике
по
♦МатематикаГи
Платина
(136 794 балла)
|
1078 просмотров
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в 9 935
Устарело ) строки типа устарела в /home/customer/www/mathsgee.
1 ответ
1 лайк
0 не нравится
Лучший ответ
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-theme/Donut-theme/qa-donut-layer.php онлайн 1030
Чтобы определить область определения рациональной функции, найдите все действительные значения x, для которого y определено, исключая любое значение x, для которого y не определено.
Чтобы определить область определения рациональной функции, найдите все действительные значения y для заданной области.
Это можно легко сделать, нарисовав график рациональной функции, используя вертикальную асимптоту, горизонтальную асимптоту и таблицу значений. Затем график используется для идентификации домена и диапазона.
ответил
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
Устарело : strlen(): передача значения null параметру #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa -include/qa-theme-base.php онлайн 162
22 сентября 2020 г.
по
♦КТ
Алмаз
(49 174 балла)
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 935
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php в строке 935
Похожие вопросы
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
Устарело : strlen (): передача нуля параметру № 1 ($ string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/app /format.php в строке 576
Устарело : strlen(): Передача нулевого значения в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/app/format.php в строке 576
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ app/format.php онлайн 576
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/app/format.php в строке 576
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в 9 576
Устарело строка типа устарела в /home/customer/www/mathsgee.
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарел в /home/customer/www/mathsgee.com/public_html/qa-include/app/format.php в строке 576
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ app/format.php в строке 576
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html /qa-include/app/format.php онлайн 576
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/app/format.php on строка 576
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в 9 576
Устарело строка типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/app/format.php в строке 576
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарело в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 935
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php онлайн 935
Как найти область определения и область значений функции в интервальной записи?
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php на линии 162
15 сентября 2020 г.
по математике
по
♦МатематикаГи
Платина
(136 794 балла)
|
214 просмотров
- диапазон
- домен
- функция
- график
- функций
- интервал
- обозначение
Нарисуйте функцию $f(x)=left{begin{array}{cc}|x| & text { если }|x| leq 1 \ 1 & text { если }|x| geq 1end{array}right.$ и запишите его домен и диапазон.
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
10 мая 2021 г.
по математике
по
♦Гаусс
Алмаз
(64 437 баллов)
|
300 просмотров
- диапазон
- домен
- функция
- график
- перехватов
- синус
- цельный
Нарисуйте функцию $f(x)=-frac{1}{2} sqrt{x+1}$ и запишите ее область определения и область значений.
спросил
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen (): передача значения null в параметр № 1 ($ string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme -base.php на линии 162
10 мая 2021 г.
по математике
по
♦Гаусс
Алмаз
(64 437 баллов)
| 92-3$ ?
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php на линии 162
15 сентября 2020 г.
по математике
по
♦МатематикаГи
Платина
(136,794 балла)
|
242 просмотра
- функции
- домен
- диапазон
- график
- вычислить
- уравнение
Какова область определения линейной функции (y=2 x-5), если диапазон равен ((9 ; 7]) ?
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen(): передача значения null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
13 сентября 2021 г.
по математике
по
♦МатематикаГи
Платина
(136 794 балла)
|
233 просмотра
- диапазон
- домен
- график
- цельный
- перехватов
- функция
- синус
Каков диапазон линейной функции (f(x)=-1) для области ([-10 ; 10] ?)
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php 9(х+1) + 2
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php на линии 162
24 августа 2020 г.
по математике
по
Джошуа Мванза
Алмаз
(53 024 балла)
|
149 просмотров
- диапазон
- домен
- экспоненциальный
- функция
- график
Укажите домен и диапазон графа соответственно $ g(x)= -log_{0.5}(-x) +2$
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в сети 160
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php на линии 162
24 августа 2020 г.
по математике
по
Джошуа Мванза
Алмаз
(53 024 балла)
|
833 просмотра
- функция
- график
- диапазон
- домен
- вычислить
- уравнение
Пусть (g(x)=arcsin (sin x)). Нарисуйте график (g(x)) и укажите его область определения и область значений.
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php на линии 162
19 июня 2021 г.
по математике
по
♦МатематикаГи
Платина
(136,794 балла)
|
152 просмотра
- домен
- диапазон
- синус
- функция
- джи
- график
- цельный
Найдите область определения функции $f(x)=frac{ln (ln (ln x))}{x-3}+sin x$
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php на линии 162
24 августа 2020 г.
по математике
по
Джошуа Мванза
Алмаз
(53 024 балла)
| 92 — 1, помогите найти его домен.
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.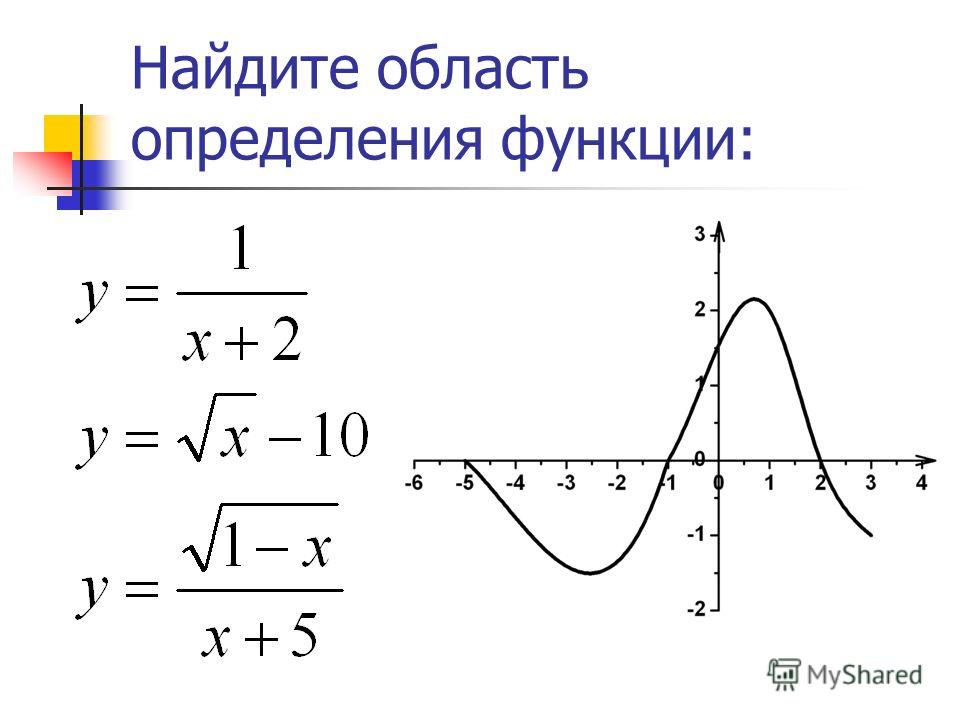
спросил
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 160
Устарело : strlen(): Передача null в параметр #1 ($string) строки типа устарела в /home/customer/www/mathsgee.com/public_html/qa-include/ qa-theme-base.php в строке 162
18 мая
по математике
по
♦МатематикаГи
Платина
(136 794 балла)
|
114 просмотров
- домен
- функция
- эквивалент
- диапазон
Устарело : strlen(): передача значения NULL в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.com/public_html/qa-include/qa-theme-base.php в строке 935
Устарело : strlen(): Передача null в параметр #1 ($string) типа string устарела в /home/customer/www/mathsgee.
Алгебраическое определение области определения функции
Функция выражается как
y=f(x) ,
, где x — независимая переменная, а y — зависимая переменная.
Сначала мы узнаем что такое область определения перед изучением Как найти область определения функции алгебраически
👉 Что такое домен функции?
Пусть f(x) — функция с действительным знаком. Тогда область функции — это набор всех возможных значений x, для которых определено f(x).
Область определения функции f(x) выражается как D(f).
Предлагаем вам сначала прочитать, как найти нули функции и нули квадратной функции.
👉 Правила, которые следует помнить при нахождении области определения функции
Мы всегда должны помнить следующие правила при нахождении области определения функции:
- Если функция полиномиальная, то x может быть положительным, нулевым или отрицательным, т.
е. x>0, x=0 или x<0,
- Если f(x)=frac{g(x)} {h(x)}, то всегда h(x)neq0,
- Если f(x)=sqrt{g(x)}, то всегда g(x)geq0,
- Если f(x)= frac{g(x)}{sqrt{h(x)}}, то всегда h(x)>0,
- Если f(x)=frac{sqrt{g(x)}}{h (x)}, то всегда g(x)geq 0 и h(x)neq 0,
- Если f(x)=sqrt{frac{g(x)}{h(x)}}, тогда всегда g(x)geq0 и h(x)>0,
- Если f(x)=ln left ( g(x) right ), то всегда g(x)>0.
7 правил, упомянутых выше, облегчат нашу работу, когда мы найдем область определения функции.
Есть еще 2 правила. Их мы узнаем во время обсуждения.
Содержание — Чему вы научитесь
👉 Как найти область определения функции алгебраически
Существуют различные способы найти область определения функции .
Здесь мы обсудим 9лучшие способы для различных функций.
№1. Найдите область определения полиномиальной функции
Существуют различные типы полиномиальной функции в зависимости от степени.
Some of them are
| Degree of polynomial Function | Polynomial Function | Name of Polynomial Function | Domain |
|---|---|---|---|
| 1 | 3x+5 | Linear Function | mathbb{R }=(-infty,infty) |
| 2 | x 2 +1 | Quadratic Function | mathbb{R}=(-infty,infty) |
| 3 | 2x 3 +x 2 +3 | Кубическая функция | mathbb{R}=(-infty,infty) |
| 4 | 7x 4 +2 | Функция четвертой степени | } infty) |
| 5 | 6x 5 +2x 2 -3 | Функция Quintic | mathbb{R}=(-infty,infty) |
Область определения полиномиальной функции
Обратите внимание, что все полиномиальные функции определены для всех xepsilonmathbb{R}.
поэтому областью определения любой полиномиальной функции является mathbb{R}=(-infty,infty).
#2. Найдите область определения рациональной функции
Рациональная функция — это дробь функций, обозначенная
f(x)=frac{g(x)}{h(x)}, h(x)neq 0
Рациональная функция также называется факторной функцией. 9{2}+2} равно
D(f)=mathbb{R}=(-infty,infty).
№3. Нахождение области определения функции с квадратным корнем
Пример:
Нахождение области определения
f(x)=sqrt{x+2}
Решение:
Из правила 3 мы знаем, что функция вида f (x)=sqrt{g(x)} определяется, когда g(x)geq 0
, т. е.
f(x)=sqrt{x+2} определяется, когда
x+2geq 0
или, xgeq -2
Положив этот результат на прямую, получим
9{2}+3x+2geq 0
т. е. (x+2)(x+1)geq 0
т. е. либо x+2leq 0, либо x+1geq 0
т. е. либо xleq -2, либо xgeq — 1
Почему мы пишем xleq -2 и xgeq -1?
См.
т. е. xepsilon (-infty,-2) -VE -VE > 0
, то есть, +VE ✅ x = -2 0 -VE = 0 ✅ = 0 ✅ = 0 ✅ = 0 ✅ = 0 ✅ -V = 0 = 0 .
i.e., xepsilon (-2,-1) +ve -ve <0
i.
т. е. xepsilon (-1,infty) +ve 9{2}+3x+2} равно
D(f) = : x : epsilon : (-infty,-2] cup [-1,infty)
: : : : : : : : : : = {x : epsilon : mathbb{R}:xleq -2,xgeq -1}
#4. Нахождение области определения функции с квадратным корнем в знаменателе
Из правила 4 мы знаем, что функция вида f(x)=frac{g(x)}{sqrt{h(x)}} определена когда h(x)>0.
Пример:
Как найти область определения функции, указанной ниже
f(x)=frac{1}{sqrt{1-x}} 9{2}-4} в интервальной записи равно [-1,2)cup (2,infty).
#6. Нахождение области определения функции с квадратным корнем в числителе и знаменателе
Из правила 6 мы знаем, что функция вида f(x)=sqrt{frac{g(x)}{h(x)}} определяется, когда g(x)geq0 и h(x)>0.
Пример:
Найдите область значений
f(x)=sqrt{frac{x-2}{3-x}}
Решение:
Для определения f(x)
3-xneq 0
т. е. 3neq x
т. е. xneq 3 9{2}}geq 0
т. е. (x-2)(3-x)geq 0
Далее нам нужно найти значения x так, чтобы (x-2)(3-x)geq 0
Теперь см. таблицу ниже:
| Значение x | Знак (x-2) | Знак (3-x) | Знак (x-2)(3-x) | (x-2)(3-x)geq 0 удовлетворено или нет | |
|---|---|---|---|---|---|
| x=0 т.е. 0 т. е. -ve |
❌ | ||||
| x=2 | 0 | +ve | 0 | ✅ | |
| x=2.5 i.e., xepsilon (2,3) |
+ve | +ve | >0 , т.е., +VE |
✅ | |
| x = 4 , т.е., x epsilon (3, infty) |
+VE | -V | <0 , т.  е., -в е., -в |
2 ❌ | <0 , т.е. |
Теперь расставив знаки на вещественной оси для каждого интервала и значения x, получим
поэтому область определения функции f(x)=sqrt{frac{x-2}{3-x}} равна D(f) = [2,3)
#7. Найти область определения логарифмической функции
Из правила 7 мы знаем, что логарифмическая функция вида f(x)=ln left ( g(x) right ) определяется, когда g(x)>0.
Пример:
Найдите область определения
f(x)= ln (x-2)
Решение:
Функция f(x)= ln (x-2) определена, когда
x -2>0
т. е. x>2
Следовательно, f(x)= ln (x-2) определено для всех x>2. 9{2}-3x+2>0
т. е. (x-1)(x-2)>0
222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 ✅
| Значение x | Знак (x-1) | Знак (x-2 ) | Знак (x-1)(x-2) | (x-1)(x-2)>0 выполняется или нет | |
|---|---|---|---|---|---|
| x=.5<1 т. е. x epsilon (-infty,1) |
-ve | -ve | +ve i.  e., >0 e., >0 |
✅ | |
| x=1 | 0 | -ve | =0 | ❌ | |
| x = 1,5 , т.е., x epsilon (1,2) |
+VE | -V | -V , т.е., <0 |
❌ | |
| X = 2 | +VE | ||||
| X = 2 | +VE | ||||
| X = 2 | +VE | ||||
| X = 2 | +VE | ||||
| x = 2 | ❌ | ||||
| x = 2 | . | 0 | = 0 | ❌ | |
| x = 3>> 2 , т.е., x epsilon (2, infty) |
+VE | +VE | +VE I.E.,> 0 |
+VE | +VE I.E.,> 0 |
т.
D(f) = {xepsilon mathbb{R}:x<1,x>2} = (-infty,1)cup (2,infty)
#8. Нахождение области определения функции с помощью отношения
Правила:
- Прежде чем находить область определения функции с помощью отношения, сначала мы должны проверить, является ли данное отношение функцией или нет,
- Отношение представляет собой множество упорядоченных пары, т. е. набор (x, y) и домен отношения — это набор всех x-координат, т. е. набор {x}.
Пример:
Находим область определения отношения
{(2,5), (3,6), (4,17), (11,8)}
Решение:
Сначала проверяем отношение {(2, 5), (3,6), (4,17), (11,8)} является функцией или нет.
Диаграмма отношения
Обратите внимание, что каждый элемент множества {2, 3, 4, 11} связан с уникальным элементом множества {5, 6, 8, 17}.
Следовательно, отношение является функцией.
В отношении
{(2,5), (3,6), (4,17), (11,8)}
набор координат x равен {2, 3, 4, 11} и набор y-координат {5, 6, 17, 8}.
поэтому домен отношения {2, 3, 4, 11}
Подробнее: Какое отношение является функцией?
Пример:
Найти домен отношения
{(2, 3), (5, 8), (6, 7), (6, 15), (11,17)}
Решение:
Диаграмма данного отношения
Видим, что элемент 6 связан с двумя разными элементами 7 и 15
, т. е. 6 не связан с уникальным элементом.
Следовательно, данное отношение не является функцией.
Дополнительное чтение: Какие отношения не являются функцией?
#9. Поиск домена функции на графике
Поиск домена функции с помощью графика — самый простой способ найти домен.
Правило:
Область определения функции на графике — это набор всех возможных значений x на оси x.
Для домена мы должны найти, где начинается значение x и где значение x заканчивается, т. е. часть оси x, где определяется f(x). 9{2}=2(x-2)
Решение:
Шаг 1: график данной параболы равен
Шаг 2:
Обратите внимание, что значение x начинается с 2 и простирается до бесконечности (т.
Загрузить PDF
Загрузить PDF
В каждой функции есть две переменные – независимая переменная и зависимая переменная, значения которой зависят от значений независимой переменной. Например, в функции y = f(x) = 2x + y независимой переменной является «х», а зависимой – «у» (другими словами, «у» – это функция от «х»). Допустимые значения независимой переменной «х» называются областью определения функции, а допустимые значения зависимой переменной «у» называются областью значений функции.[1]
-
1
Определите тип данной вам функции. Областью значений функции являются все допустимые значения «х» (откладываются по горизонтальной оси), которым соответствуют допустимые значения «у». Функция может быть квадратичной или содержать дроби или корни. Для нахождения области определения функции сначала необходимо определить тип функции.
- Квадратичная функция имеет вид: ax2 + bx + c:[2]
f(x) = 2x2 + 3x + 4 - Функция, содержащая дробь: f(x) = (1/x), f(x) = (x + 1)/(x — 1) (и так далее).
- Функция, содержащая корень: f(x) = √x, f(x) = √(x2 + 1), f(x) = √-x (и так далее).
- Квадратичная функция имеет вид: ax2 + bx + c:[2]
-
2
Выберите соответствующую запись для области определения функции. Область определения записывается в квадратных и/или круглых скобках. Квадратная скобка применяется в том случае, когда значение входит в область определения функции; если значение не входит в область определения, используется круглая скобка. Если у функции несколько несмежных областей определения, между ними ставится символ «U».[3]
- Например, область определения [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
-
3
Постройте график квадратичной функции. График такой функции представляет собой параболу, ветви которой направлены либо вверх, либо вниз. Так как парабола возрастает или убывает на всей оси Х, то областью определения квадратичной функции являются все действительные числа. Другими словами, областью определения такой функции является множество R (R обозначает все действительные числа).[4]
- Для лучшего уяснения понятия функции выберите любое значение «х», подставьте его в функцию и найдите значение «у». Пара значений «х» и «у» представляют собой точку с координатами (х,у), которая лежит на графике функции.
- Нанесите эту точку на плоскость координат и проделайте описанный процесс с другим значением «х».
- Нанеся на плоскость координат несколько точек, вы получите общее представление о форме графика функции.
-
4
Если функция содержит дробь, приравняйте ее знаменатель к нулю. Помните, что делить на нуль нельзя. Поэтому, приравняв знаменатель к нулю, вы найдете значения «х», которые не входят в область определения функции.[5]
- Например, найдите область определения функции f(x) = (x + 1)/(x — 1).
- Здесь знаменатель: (х — 1).
- Приравняйте знаменатель к нулю и найдите «х»: х — 1 = 0; х = 1.
- Запишите область определения функции. Область определения не включает 1, то есть включает все действительные числа за исключением 1. Таким образом, область определения функции: (-∞,1) U (1,∞).
- Запись (-∞,1) U (1,∞) читается так: множество всех действительных чисел за исключением 1. Символ бесконечности ∞ означает все действительные числа. В нашем примере все действительные числа, которые больше 1 и меньше 1, включены в область определения.
-
5
Если функция содержит квадратный корень, то подкоренное выражение должно быть больше или равно нулю. Помните, что квадратный корень из отрицательных чисел не извлекается. Поэтому любое значение «х», при котором подкоренное выражение становится отрицательным, нужно исключить из области определения функции.[6]
- Например, найдите область определения функции f(x) = √(x + 3).
- Подкоренное выражение: (х + 3).
- Подкоренное выражение должно быть больше или равно нулю: (х + 3) ≥ 0.
- Найдите «х»: х ≥ -3.
- Область определения этой функции включает множество всех действительных чисел, которые больше или равны -3. Таким образом, область определения: [-3,∞).
Реклама
-
1
Убедитесь, что вам дана квадратичная функция. Квадратичная функция имеет вид: ax2 + bx + c: f(x) = 2x2 + 3x + 4. График такой функции представляет собой параболу, ветви которой направлены либо вверх, либо вниз. Существуют различные методы нахождения области значений квадратичной функции.[7]
- Самый простой способ найти область значений функции, содержащей корень или дробь, – это построить график такой функции при помощи графического калькулятора.
-
2
Найдите координату «х» вершины графика функции. В случае квадратичной функции найдите координату «х» вершины параболы. Помните, что квадратичная функция имеет вид: ax2 + bx + c. Для вычисления координаты «х» воспользуйтесь следующим уравнением: х = -b/2a. Это уравнение является производной от основной квадратичной функции и описывает касательную, угловой коэффициент которой равен нулю (касательная к вершине параболы параллельна оси Х).[8]
- Например, найдите область значений функции 3x2 + 6x -2.
- Вычислите координату «х» вершины параболы: х = -b/2a = -6/(2*3) = -1
-
3
Найдите координату «у» вершины графика функции. Для этого в функцию подставьте найденную координату «х». Искомая координата «у» представляет собой предельное значение области значений функции.
- Вычислите координату «у»: y = 3x2 + 6x – 2 = 3(-1)2 + 6(-1) -2 = -5
- Координаты вершины параболы этой функции: (-1,-5).
-
4
Определите направление параболы, подставив в функцию по крайней мере одно значение «х». Выберите любое другое значение «х» и подставьте его в функцию, чтобы вычислить соответствующее значение «у». Если найденное значение «у» больше координаты «у» вершины параболы, то парабола направлена вверх. Если же найденное значение «у» меньше координаты «у» вершины параболы, то парабола направлена вниз.
- Подставьте в функцию х = -2: y = 3x2 + 6x – 2 = y = 3(-2)2 + 6(-2) – 2 = 12 -12 -2 = -2.
- Координаты точки, лежащей на параболе: (-2,-2).
- Найденные координаты свидетельствуют о том, что ветки параболы направлены вверх. Таким образом, область значений функции включает все значения «у», которые больше или равны -5.
- Область значений этой функции: [-5, ∞)
-
5
Область значений функции записывается аналогично области определения функции. Квадратная скобка применяется в том случае, когда значение входит в область значений функции; если значение не входит в область значений, используется круглая скобка. Если у функции несколько несмежных областей значений, между ними ставится символ «U».[9]
- Например, область значений [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
Реклама
-
1
Постройте график функции. Во многих случаях проще найти область значений функции, построив ее график. Областью значений многих функций с корнями является (-∞,0] или [0,+∞), так как вершина параболы, направленной вправо или влево, лежит на оси Х. В этом случае область значений включает все положительные значения «у», если парабола возрастает, или все отрицательные значения «у», если парабола убывает. Функции с дробями имеют асимптоты, которые определяют область значений.[10]
- Вершины графиков некоторых функций с корнями лежат выше или ниже оси Х. В этом случае область значений определяется координатой «у» вершины параболы. Если, например, координата «у» вершины параболы равна -4 (у = -4), а парабола возрастает, то область значений равна [-4,+∞).
- Самый простой способ построить график функции – это воспользоваться графическим калькулятором или специальным программным обеспечением.
- Если у вас нет графического калькулятора, постройте приблизительный график, подставив в функцию несколько значений «х» и вычислив соответствующие значения «у». Нанесите найденные точки на координатную плоскость, чтобы получить общее представление о форме графика.
-
2
Найдите минимум функции. Построив график функции, вы увидите на нем точку, в которой функция имеет минимальное значение. Если наглядного минимума нет, то он не существует, а график функции уходит в -∞.
- Область значений функции включает все значения «у» за исключением значений асимптот. Зачастую, области значений таких функций записываются так: (-∞, 6) U (6, ∞).
-
3
Определите максимум функции. Построив график функции, вы увидите на нем точку, в которой функция имеет максимальное значение. Если наглядного максимума нет, то он не существует, а график функции уходит в +∞.
-
4
Область значений функции записывается аналогично области определения функции. Квадратная скобка применяется в том случае, когда значение входит в область значений функции; если значение не входит в область значений, используется круглая скобка. Если у функции несколько несмежных областей значений, между ними ставится символ «U».[11]
- Например, область значений [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
Реклама
Об этой статье
Эту страницу просматривали 352 307 раз.
Была ли эта статья полезной?
Дробно-рациональная функция — это функция вида , где f(x) и g(x) — некоторые функции.
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты
Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x — нечетная
Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная
Пример1 . Построим график функции , т.е. представим ее в виде
: выделим целую часть дроби, разделив числитель на знаменатель, мы получим:
.
Итак, . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы
вверх на 2 единицы.
При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.
Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3. Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):
|
x |
-7 |
-2 |
-1 |
0 |
1 |
2 |
2,5 |
|
y |
1,5 |
1 |
0,75 |
0,33 |
-0,5 |
-3 |
-8 |
|
x |
3,5 |
4 |
5 |
6 |
7 |
8 |
13 |
|
y |
12 |
7 |
4,5 |
3,33 |
3,25 |
3 |
2,52 |
Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы. Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции изображен на рисунке 3.
Любую дробь можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.
Пример 2.
Построим график функции .
Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.
Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.
Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби относительно малы. Поэтому
.
Стало быть, горизонтальная асимптота – прямая у=3/2.
Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.
Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).
Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.
Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.
-
Найти область определения функции.
-
Разложить на множители квадратный трехчлен.
-
Сократить дробь.
-
Построить график (параболу, гиперболу, кубическую параболу).
-
Исключить из графика точки, не входящие в область определения («выколотые» точки).
-
Найти значение функции в «выколотых» точках.
-
Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.
ЗАДАНИЕ
Построить график функции (D(y), на графике – выколотые точки):

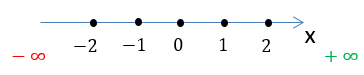
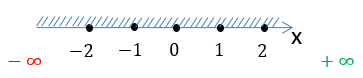
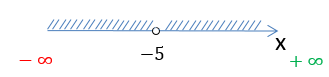
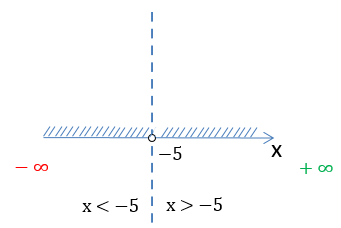
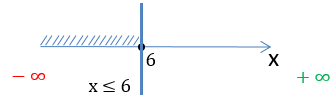
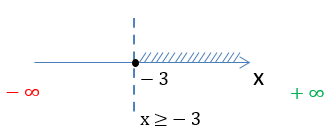
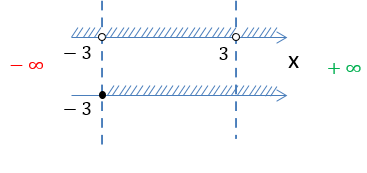
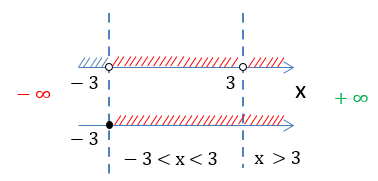
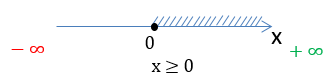
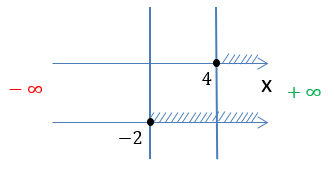
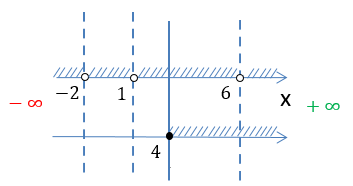

























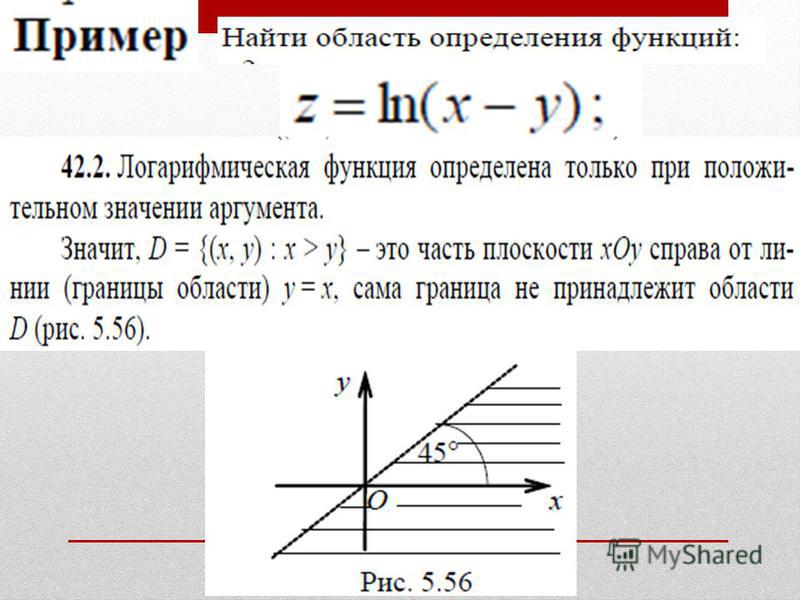 Додавання і віднімання дробів
Додавання і віднімання дробів Нахождение дробной степени числа
Нахождение дробной степени числа Рiвнiсть векторiв
Рiвнiсть векторiв






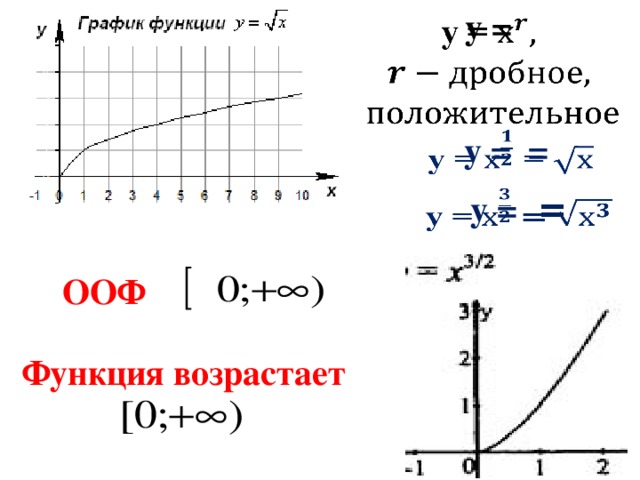

 Найдите все асимптоты. Ответ
Найдите все асимптоты. Ответ 
 е. x>0, x=0 или x<0,
е. x>0, x=0 или x<0,