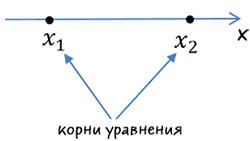
Неравенством с одной переменной называют каждое из выражений вида:
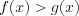


где знаки 



Например, 




Решением неравенства называют значение переменной, при котором данное неравенство обращается в верное числовое неравенство.
Решить неравенство – значит найти множество всех его решений или доказать, что неравенство не имеет решений.
Областью определения (областью допустимых значений) неравенства 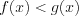


Равносильные неравенства
Два неравенства называют равносильными, если множества их решений совпадают или оба неравенства не имеют решений.
Например: 1) неравенства 

2) неравенства 

Решая неравенство, как правило, его заменяют более простым, но равносильным ему неравенством. Такие замены осуществляют на основании следующих утверждений:
1. Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получим неравенство, равносильное данному неравенству.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число или на одну и ту же функцию, положительную на области определения неравенства, то получим неравенство, равносильное данному неравенству.
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число или на одну и ту же функцию, отрицательную на области определения неравенства, изменив при этом смысловой знак неравенства, то получим неравенство, равносильное данному.
4. Неравенства 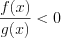



5. Неравенства 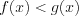




6. Неравенства 


7. Неравенства ![sqrt[2n+1]{f(x)}< sqrt[2n+1]{g(x)} LaTeX formula: sqrt[2n+1]{f(x)}< sqrt[2n+1]{g(x)}](https://helpy.quali.me/uploads/formulas/fba645ad1ebd71ce03c560c56e25ab36b08ec1bc.1.1.png)
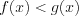

Системы и совокупности неравенств с одной переменной
Рассмотрим два неравенства 

Систему двух неравенств записывают в виде: 
Совокупность неравенств записывают в виде:
Чтобы решить систему неравенств, необходимо найти множества решений каждого неравенства системы, тогда общая часть (пересечение) этих множеств и будет решением системы.
Чтобы решить совокупность неравенств, необходимо найти множества решений каждого неравенства совокупности, тогда объединение этих множеств и будет решением совокупности.
Метод интервалов
Метод интервалов основан на следующем свойстве двучлена: если отметить на координатной оси 







Рассмотрим дробно-рациональную функцию 

Если 









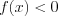
Число 



В процессе решения неравенств методом интервалов для удобства корни четной кратности будем наносить на координатную прямую дважды, а нечетной кратности – один раз. При переходе через корень четной кратности знаки значений функции не изменятся, а при переходе через корень нечетной кратности – изменятся.
При решении неравенств вида 


Наряду с алгебраическим подходом к решению неравенств можно использовать также и функциональный подход.
Приведем алгоритм решения методом интервалов неравенства вида 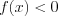




1) запишем функцию 
2) найдем область определения функции;
3) найдем нули функции, решая уравнение 
4) нанесем нули функции на ее область определения;
5) определим знаки значений функции на одном из полученных промежутков;
6) определим знаки значений функции на остальных промежутках по правилу: при переходе через каждый нуль функции знаки значений функции изменяются (учитываем кратность нулей);
7) запишем решение неравенства, учитывая его смысловой знак.
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.


9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 





20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
Прежде чем разбираться, как решать квадратное неравенство,
давайте рассмотрим, какое неравенство называют квадратным.
Запомните!
Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного «x»
равна двум.
Потренируемся определять тип неравенства на примерах.
| Неравенство | Тип |
|---|---|
| x − 7 < 0 | линейное |
| x2 + 5x ≥ 0 | квадратное |
| 2x − 7 > 5 | линейное |
| x2 + x − 12 ≤ 0 | квадратное |
Как решить квадратное неравенство
В предыдущих уроках мы разбирали, как решать
линейные неравенства.
Но в отличие от линейных неравенств квадратные решаются совсем иным образом.
Важно!
Решать квадратное неравенство таким же образом как и линейное нельзя!
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Что такое метод интервалов
Методом интервалов называют специальный способ решения квадратных неравенств. Ниже мы объясним, как использовать
этот метод и почему он получил такое название.
Запомните!
Чтобы решить квадратное неравенство методом интервалов нужно:
- перенести все члены неравенства в левую часть, так чтобы в правой остался только ноль;
- сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент;
- приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение;
- полученные корни уравнения разместить на числовой оси в порядке возрастания;
- нарисовать «арки» для интервалов. Справа налево,
начиная с «+», проставить чередуя знаки «+»
и «−»; - выбрать необходимые интервалы и записать их в ответ.
Мы понимаем, что правила, описанные выше, трудно воспринимать только в теории, поэтому сразу рассмотрим пример решения
квадратного неравенства по алгоритму выше.
Требуется решить квадратное неравенство.
x2 + x − 12 < 0
Итак, согласно п.1 мы должны перенести
все члены неравенства в левую часть, так чтобы в правой остался только ноль.
В заданном неравенстве
«x2 + x − 12 < 0» ничего дополнительно делать не требуется,
так как в правой части и так уже стоит ноль.
Переходим к п.2. Необходимо сделать так, чтобы перед «x2»
стоял положительный коэффициент. В неравенстве
«x2 + x − 12 < 0»
при «x2» стоит положительный коэффициент «1»,
значит, снова нам ничего делать не требуется.
Согласно п.3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x1 = |
x2 = |
|
x1 = |
x2 = |
|
x1 = −4 |
x2 = 3 |
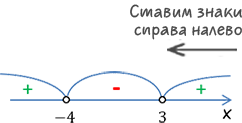
Теперь по п.4 отметим полученные корни на числовой оси в порядке возрастания.
Помните, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси
разным образом.
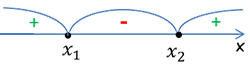
Теперь, как сказано в п.5, нарисуем «арки» над интервалами между отмеченными точками.
Проставим знаки внутри интервалов.
Справа налево чередуя, начиная с «+», отметим знаки.
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ.
Вернемся к нашему неравенству.
Так как в нашем неравенстве
«x2 + x − 12 < 0»,
значит, нам требуются отрицательные интервалы.
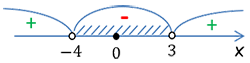
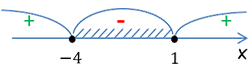
Заштрихуем все отрицательные области на числовой оси и выпишем их в ответ.
Отрицательным интервалом оказался лишь один, который находится между числами
«−4» и «3», поэтому
запишем его в ответ в виде двойного неравенства
−4 < x < 3.
Запишем полученный ответ квадратного неравенства.
Ответ: −4 < x < 3
Именно из-за того, что при решении квадратного неравенства мы рассматриваем интервалы между числами,
метод интервалов и получил свое название.
После получения ответа имеет смысл сделать его проверку, чтобы убедиться в правильности решения.
Выберем любое число, которое находится в заштрихованной области полученного ответа −4 < x < 3
и подставим его вместо «x» в исходное неравенство.
Если мы получим верное неравенство,
значит мы нашли ответ квадратного неравенства верно.
Возьмем, например, из интервала число «0». Подставим его в исходное неравенство
«x2 + x − 12 < 0».
x2 + x − 12 < 0
02 + 0 − 12 < 0
−12 < 0
(верно)
Мы получили верное неравенство при подстановке числа из области решений, значит ответ найден правильно.
Краткая запись решения методом интервалов
Сокращенно запись решения квадратного неравенства
«x2 + x − 12 < 0»
методом интервалов будет выглядеть так:
x2 + x − 12 < 0
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x1 = |
x2 = |
|
x1 = |
x2 = |
|
x1 = −4 |
x2 = 3 |
Ответ: −4 < x < 3
Другие примеры решения квадратных неравенств
Рассмотрим решение других примеров квадратных неравенств. Требуется решить квадратное неравенство:
2x2 − x ≥ 0
В правой части неравенство уже стоит ноль. При «x2»
стоит «2» (положительный коэффициент), значит можно сразу переходить
к поиску корней.
2x2 − x ≥ 0
2x2 − x = 0
x1;2 =
| −(−1) ± √(−12) − 4 · 2 · 0 |
| 2 · 2 |
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = |
x2 = 0 |
Ответ: x ≤ 0; x ≥
Рассмотрим пример, где перед «x2» в квадратном неравенстве стоит
отрицательный коэффициент.
−x2 − 3x + 4 ≥ 0
По п.2 общих правил решения методом интервалов нам нужно сделать так, чтобы
перед «x2» стоял положительный
коэффициент. Для этого умножим все неравенство на «−1».
−x2 − 3x + 4 ≥ 0 | ·(−1)
x2 + 3x − 4 ≤ 0
Можно переходить к п.4 и п.5. Приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
Затем расположим полученные корни на числовой оси и проведем между ними «арки».
x2 + 3x − 4 ≤ 0
x2 + 3x − 4 = 0
x1;2 =
| −3 ± √32 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x2 = |
x1 = |
|
x2 = |
x1 = |
| x2 = −4 | x1 = 1 |
Важно!
При определении того какие интервалы нам нужно брать в ответ, исходить нужно из самого последнего изменения неравенства
перед нахождением его корней.
В нашем случае самая последняя версия неравенства перед поиском корней уравнения это
«x2 + 3x − 4 ≤ 0».
Значит для ответа нужно выбирать интервалы со знаком «−».
Ответ: −4 ≤ x ≤ 1
К сожалению, при решении квадратного неравенства не всегда получаются два корня и все идет по общему плану выше.
Возможны случаи, когда получается один корень или даже ни одного корня.
Как решить квадратные неравенства в таких случаях, мы разберем в следующем уроке
«Квадратные неравенства
с одним корнем или без корней».
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
5 апреля 2019 в 8:15
Gulnara Muslimova
Профиль
Благодарили: 0
Сообщений: 1
Gulnara Muslimova
Профиль
Благодарили: 0
Сообщений: 1
Помогите решить неравенство (желательно подробно и с пояснениями):
(x2+3x+3)x^2 -1<(8x-3)x^2 -1
0
Спасибо
Ответить
6 апреля 2019 в 16:12
Ответ для Gulnara Muslimova
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Логарифмируем
ac < bc <=> c·ln(a/b) < 0
и метод интервалов.
0
Спасибо
Ответить
15 сентября 2018 в 22:11
Vlad Lukashenok
Профиль
Благодарили: 0
Сообщений: 1
Vlad Lukashenok
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство:
x · sin2(πx)>=0
0
Спасибо
Ответить
17 сентября 2018 в 23:05
Ответ для Vlad Lukashenok
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x = k ∈ Ζ; x > 0.
0
Спасибо
Ответить
Квадратные неравенства
Ключевые слова: квадратные неравенства, решение квадратных неравенств, примеры решения задач. Раздел ОГЭ по математике: 3.2.5. Квадратные неравенства.
☑ ОПРЕДЕЛЕНИЕ. Неравенство вида ах2 + bх + с > 0, где а ≠ 0, называют квадратным неравенством.
Примечание к определению: вместо знака > могут стоять и другие знаки неравенства: <, ≥, ≤.
Множество решений квадратного неравенства легко найти, используя график функции у = ах2 + bх + с.
На рисунке изображён график функции у = х2 – 2х – 3. График пересекает ось х в двух точках, абсциссы которых равны –1 и 3, т. е. при х = –1 и х = 3 значения функции у = х2 – 2х – 3 равны нулю.
- При –1 < х < 3 график расположен ниже оси х, т. е. значения функции на этом промежутке отрицательны. Иными словами, множеством решений неравенства у < 0 является промежуток –1 < х < 3.
- При x < –1 и x > 3 график расположен выше оси х, т. е. значения функции положительны. Иными словами, неравенство х2 – 2х – 3 > 0 выполняется при х < –1 и х > 3.
При решении квадратных неравенств можно ограничиться схематическим рисунком, показывающим положение графика относительно оси х, так как координаты вершины в данном вопросе значения не имеют; можно также не изображать ось у.
Если требуется решить квадратное неравенство с отрицательным коэффициентом а, то всегда целесообразно перейти к равносильному неравенству с положительным первым коэффициентом, умножив обе части неравенства на –1. Например, вместо неравенства 5 + 4х – х2 ≤ 0 решать неравенство х2 – 4х – 5 ≥ 0.
Примеры решения задач
Пример 1. Решим неравенство х2 – x – 6 > 0.
Выясним, пересекает ли график функции у = х2 – х – 6 ось х. Для этого решим уравнение х2 – x – 6 = 0. Его корни x1 = –2 и х2 = 3. Следовательно, парабола (график функции) пересекает ось х в точках с абсциссами –2 и 3, её ветви направлены вверх. Покажем схематически расположение параболы относительно оси х.
Из рисунка видно, что парабола расположена выше оси x при х < –2 и х > 3. Объединение этих промежутков и составляет множество решений неравенства x2 – x – 6 > 0.
Ответ можно записать по–разному:
1) x < –2; х > 3;
2) (–оо; –2) U (3; +оо).
Пример 2. Решим неравенство х(3 – 2х) > 2.
Раскроем скобки и перенесём все слагаемые в левую часть, получим: –2x2 + 3x – 2 > 0. Теперь заменим неравенство равносильным неравенством с положительным первым коэффициентом (для этого умножим обе части неравенства на –1 и заменим знак неравенства на противоположный): 2х2 – 3х + 2 < 0.
Выясним, пересекает ли парабола – график функции у = 2х2 – 3х + 2 – ось х. Найдём дискриминант квадратного трёхчлена 2х2 – 3х + 2, a именно: D = 9 – 4·2·2 = 9 – 16 < 0. Так как дискриминант отрицательный, то квадратный трёхчлен не имеет корней и парабола не пересекает ось х. Изобразим эту параболу схематически:
При всех значениях х парабола расположена выше оси х, это означает, что нет таких значений х, при которых функция у = 2х2 – 3х + 2 принимает отрицательные значения, значит, неравенство 2х2–Зх + 2 < 0 решений не имеет.
Ответ можно записать по–разному:
1) неравенство решений не имеет;
2) ∅.
Пример 3. Воспользуемся этим же рисунком, чтобы решить неравенство –2х2 + 3х – 2 < 0. Заменим его равносильным неравенством 2х2 – 3х + 2 > 0. В этом случае любое число является решением неравенства, так как при всех значениях х функция у – 2х2 – 3х + 2 принимает положительные значения.
Ответ можно записать по–разному:
1) х – любое число;
2) (–оо; +оо).
Если неравенство нестрогое, то не надо забывать включить в множество решений значения переменной, при которых квадратный трёхчлен обращается в нуль.
Пример 4. Найдём область определения выражения:
Область определения выражения задаётся условиями:
Решив каждое из неравенств, получим:
Сделаем схематический рисунок:
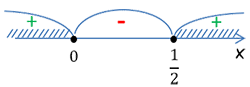
Из рисунка видно, что множеством решений системы неравенств является промежуток от 2/3 до 2 (включая эти числа) без числа 1. Ответ можно записать по–разному:
Это конспект по алгебре на тему «Квадратные неравенства». Выберите дальнейшие действия:
- Перейти к следующему конспекту:
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
В данной публикации мы рассмотрим, что такое квадратное неравенство, и как оно решается методом интервалов в зависимости от количества корней. Также разберем практические примеры по этой теме.
- Определение квадратного неравенства
-
Решение квадратных неравенств
- С двумя корнями
- С одним корнем
- Без корней
Определение квадратного неравенства
Если старшая степень неизвестной переменной (чаще всего это x) равняется двум, то неравенство называется квадратным.
Например:
- x2 – 3x + 4 > 0
- 2x2 + 7x – 5 < 0
- x2 + 12x + 2 ≥ 0
- 3x2 – 4 ≤ 0
Решение квадратных неравенств
С двумя корнями
Квадратные уравнения решаются с помощью так называемого метода интервалов, принцип которого заключается в следующем:
1. Все элементы неравенства собираем в левой части, в правой должен остаться только ноль. Помним, что при переносе элемента из одной части в другую его знак меняется на противоположный.
2. Если перед неизвестной переменной во второй степени стоит отрицательный коэффициент, умножаем все элементы неравенства на число -1, изменив знак сравнения на противоположный.
3. Заменив знак сравнения на “равно” решаем полученное квадратное уравнение.
4. Найденные корни отмечаем на числовой оси.
При этом, если знак сравнения строгий (“больше” или “меньше”), то отметкой обычно является незакрашенный внутри кружок, если нестрогий (“больше или равно”, “меньше или равно”) – закрашенный.
5. Рисуем интервалы, и справа-налево присваиваем им знаки “плюс” и “минус” (начинаем с “+”, затем чередуем).
6. Если в неравенстве стоят знаки “>“ или “≥“, нам нужны положительные интервалы, если “<“ или “≤“ – отрицательные.
Пример 1
Решим квадратное неравенство x2 + 4x > -3.
Решение:
1. Т.к. правая часть должны быть нулевой, перенесем число -3 в левую, заменив его знак на “плюс”:
x2 + 4x + 3 > 0
2. Теперь найдем корни квадратного уравнения x2 + 4x + 3 = 0.
Мы подробно рассматривали данный вопрос в отдельной публикации, поэтому здесь отдельно на этом останавливаться не будем.
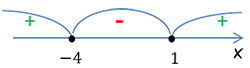
Итак, корни заданного уравнения: x1 = -1, x2 = -3. Отмечаем их на числовой оси (незакрашенные кружки, т.к. неравенство является строгим).
Рисуем интервалы, отметив знаками “плюс” и “минус”.
Нам нужные только положительные области, т.к. в неравенстве стоит знак “больше”.
Таким образом, решение неравенства следующее:
x > -1 и x < -3.
Примечание: если бы в рассматриваемом нами неравенстве стояли другие знаки, область решения была бы следующей:
- знак “<“, тогда -3 < x < -1
- знак “≥”, тогда x ≥ -1 и x ≤ -3
- знак “≤”, тогда -3 ≤ x ≤ -1
С одним корнем
Квадратные уравнения не всегда имеют два корня, иногда он может быть один.
Пример 2
Давайте решим x2 – 4x + 4 < 0.
Решение:
Корень у соответствующего квадратного уравнения всего один: x1 = x2 = 2, т.е. его значение повторяется дважды.
Отмечаем точку в виде незаполненного кружка на числовой оси и рисуем два исходящих от нее интервала.
Теперь нужно присвоить знаки интервалам, и здесь эта процедура отличается от описанного выше (когда у уравнения два корня): если значение корня в уравнении повторяется четное количество раз, то при смене интервалов знак не меняется. Проставляем их, также, справа-налево, начав с “плюса”.
В нашем случае значение повторяется два раза, т.е. получаем:
Нам нужны только отрицательные интервалы, а их здесь нет. К тому же, неравенство строгое. Следовательно, решений у него нет.
Примечание: если бы этом неравенстве стояли другие знаки, область решения была бы следующей:
- знак “>”, тогда x > 2 и x < 2
- знак “≥”, тогда x ≥ 2 и x ≤ 2, т.е. все действительные числа.
- знак “≤”, единственное решение – это x = 2
Без корней
В некоторых случаях квадратные уравнения могут и вовсе не иметь действительных корней.
В этом случае у соответствующее неравенства, также, не будет действительных решений. Это и будет ответом.
Пример 3
x2 + 3x + 5 > 0
Решение:
Уравнение не имеет корней, следовательно, у неравенства нет действительных решений.