Загрузить PDF
Загрузить PDF
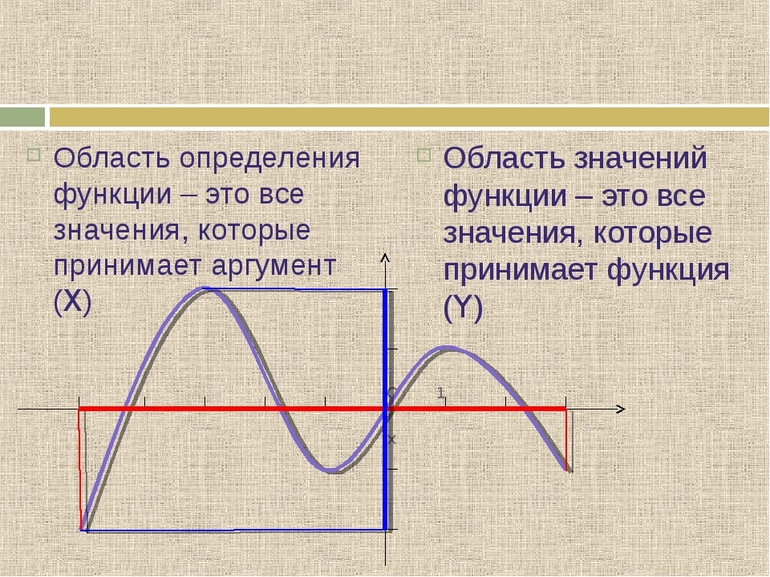
Область определения функции — это множество чисел, на котором задается функция. Другими словами, это те значения х, которые можно подставить в данное уравнение. Возможные значения у называются областью значений функции. Если вы хотите найти область определения функции в различных ситуациях, выполните следующие действия.
-
1
Запомните, что такое область определения. Область определения — это множество значений х, при подставлении которых в уравнение мы получаем область значений у.
-
2
Научитесь находить область определения различных функций. Тип функции определяет метод нахождения области определения. Вот основные моменты, которые вы должны знать о каждом типе функции, о которых пойдет речь в следующем разделе:
- Полиномиальная функция без корней или переменных в знаменателе. Для этого типа функции областью определения являются все действительные числа.
- Дробная функция с переменной в знаменателе. Чтобы найти область определения данного типа функции, знаменатель приравняйте к нулю и исключите найденные значения х.
- Функция с переменной внутри корня. Чтобы найти область определения данного типа функции, задайте подкоренное выражение больше или равно 0 и найдите значения х.
- Функция с натуральным логарифмом (ln). Задайте выражение под логарифмом > 0 и решите.
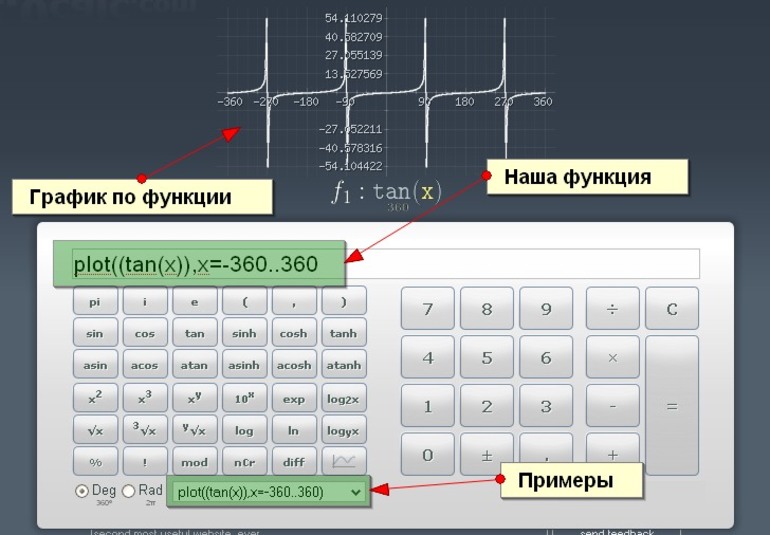
- График. Нарисуйте график для нахождения х.
- Множество. Это будет список координат х и у. Область определения — список координат х.
-
3
Правильно обозначайте область определения. Легко научиться правильному обозначению области определения, но важно, чтобы вы правильно записывали ответ и получали высокую оценку. Вот несколько вещей, которые вы должны знать о написании области определения:
- Один из форматов написания области определения: квадратная скобка, 2 конечных значения области, круглая скобка.
- Например, [-1; 5). Это означает область определения от -1 до 5.
-
Используйте квадратные скобки [ и ] , чтобы указать, что значение принадлежит области определения.
- Таким образом, в примере [-1; 5) область включает -1.
-
Используйте круглые скобки ( и ) , чтобы указать, что значение не принадлежит области определения.
- Таким образом, в примере [-1; 5) 5 не принадлежит области. Область включает только значения, бесконечно близкие к 5, то есть 4,999(9).
-
Используйте знак U для объединения областей, разделенных промежутком.
- Например, [-1; 5 ) U (5; 10]. Это означает, что область проходит от -1 до 10 включительно, но не включает 5. Это может быть у функции, где в знаменателе стоит «х — 5».
- Вы можете использовать несколько U по мере необходимости, если область имеет несколько разрывов/промежутков.
-
Используйте знаки «плюс бесконечность» и «минус бесконечность», чтобы выразить, что область бесконечна в любом направлении.
- Со знаком бесконечности всегда используйте ( ), а не [ ].
Реклама
- Один из форматов написания области определения: квадратная скобка, 2 конечных значения области, круглая скобка.
-
1
Запишите пример. Например, вам дана следующая функция:
- f(x) = 2x/(x2 — 4)
-
2
Для дробных функций с переменной в знаменателе надо приравнять знаменатель к нулю. При нахождении области определения дробной функции необходимо исключить все значения х, при которых знаменатель равен нулю, потому что нельзя делить на ноль. Запишите знаменатель как уравнение и приравняйте его к 0. Вот как это делается:
- f(x) = 2x/(x2 — 4)
- x2 — 4 = 0
- (x — 2 )(x + 2) = 0
- x ≠ 2; — 2
-
3
Запишите область определения:
- х = все действительные числа, кроме 2 и -2
Реклама
-
1
Запишите пример. Дана функция y =√(x-7)
-
2
Задайте подкоренное выражение больше или равным 0. Вы не можете извлечь квадратный корень из отрицательного числа, хотя вы можете извлечь квадратный корень 0. Таким образом, задайте подкоренное выражение больше или равным 0. Заметим, что это относится не только к квадратным корням, но и ко всем корням с четной степенью. Тем не менее, это не относится к корням с нечетной степенью, так как отрицательное число может стоять под корнем нечетной степени.
- х — 7 ≧ 0
-
3
Выделите переменную. Для этого перенесите 7 в правую часть неравенства:
- x ≧ 7
-
4
Запишите область определения. Вот она:
- D = [7; +∞)
-
5
Найдите область определения функции с корнем, когда есть несколько решений. Дано: y = 1/√( ̅x2 -4). Приравняв знаменатель к нулю и решив это уравнение, вы получите х ≠ (2; -2). Вот как вы действуете далее:
- Проверьте область за -2 (например, подставив -3), чтобы удостовериться, что подстановка в знаменатель чисел меньше -2 в результате дает число больше 0. И это так:
- (-3)2 — 4 = 5
- Теперь проверьте область между -2 и +2. Подставьте, например, 0.
- 02 — 4 = -4, так что числа между -2 и 2 не подходят.
- Теперь попробуйте числа больше 2, например 3.
- 32 — 4 = 5, так что числа больше 2 подходят.
- Запишите область определения. Вот как записывается эта область:
- D = (-∞; -2) U (2; +∞)
Реклама
- Проверьте область за -2 (например, подставив -3), чтобы удостовериться, что подстановка в знаменатель чисел меньше -2 в результате дает число больше 0. И это так:
-
1
Запишите пример. Допустим, дана функция:
- f(x) = ln(x —
- f(x) = ln(x —
-
2
Задайте выражение под логарифмом больше нуля. Натуральный логарифм должен быть положительным числом, поэтому задаем выражение внутри скобок больше нуля.
- x — 8 > 0
-
3
Решите. Для этого обособьте переменную х, прибавив к обеим частям неравенства 8.
- x — 8 + 8 > 0 + 8
- x > 8
-
4
Запишите область определения. Область определения этой функции есть любое число больше 8. Вот так:
- D = (8; +∞)
Реклама
-
1
Посмотрите на график.
-
2
Проверьте значения х, которые отображены на графике. Это может быть легче сказать, чем сделать, но вот несколько советов:
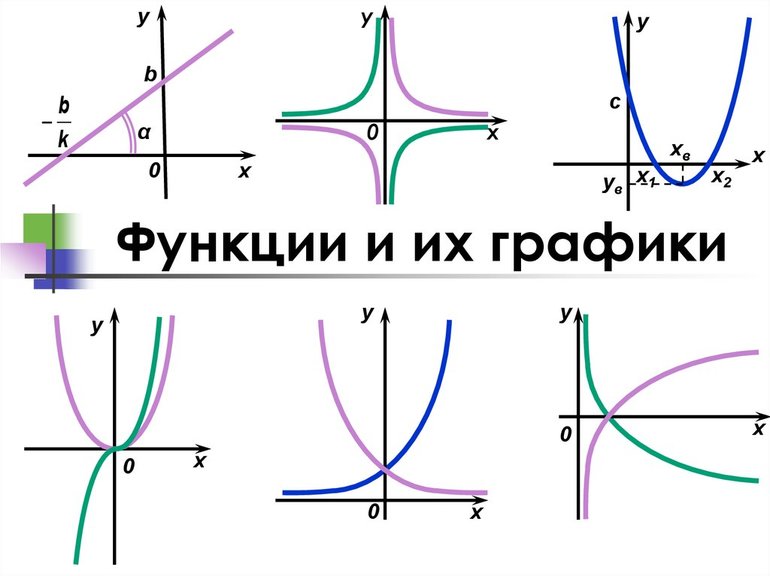
- Линия. Если на графике вы видите линию, которая уходит в бесконечность, то все значения х верны, и область определения включает все действительные числа.
- Обычная парабола. Если вы видите параболу, которая смотрит вверх или вниз, то область определения — все действительные числа, потому что подходят все числа на оси х.
- Лежачая парабола. Теперь, если у вас есть парабола с вершиной в точке (4; 0), которая простирается бесконечно вправо, то область определения D = [4; +∞)
-
3
Запишите область определения. Запишите область определения в зависимости от типа графика, с которым вы работаете. Если вы не уверены в типе графика и знаете функцию, описывающую его, для проверки подставьте координаты х в функцию.
Реклама
-
1
Запишите множество. Множество — это набор координат х и у. Например, вы работаете со следующими координатами: {(1; 3), (2; 4), (5; 7)}
-
2
Запишите координаты х. Это 1; 2; 5.
-
3
Область определения: D = {1; 2; 5}
-
4
Убедитесь, что множество является функцией. Для этого необходимо, чтобы каждый раз, когда вы подставляете значение х, вы получали одно и то же значение y. Например, подставляя х = 3, вы должны получить у = 6, и так далее. Приведенное в примере множество не является функцией, потому что дано два разных значения у: {(1; 4), (3; 5), (1; 5)}.
Реклама
Об этой статье
Эту страницу просматривали 854 199 раз.
Была ли эта статья полезной?
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
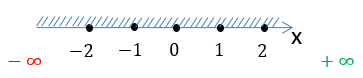
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
Запишем результат по правилам записи неравенств.
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
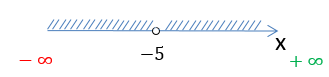
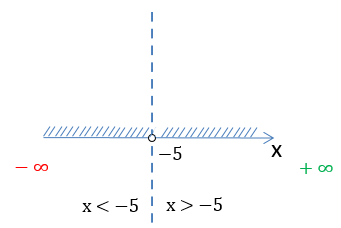
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
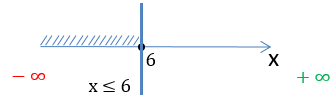
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
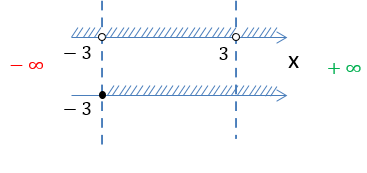
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
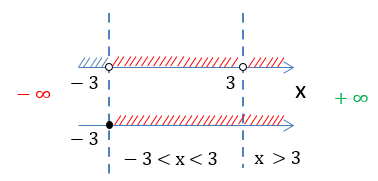
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
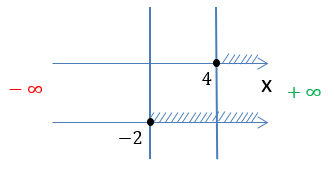
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
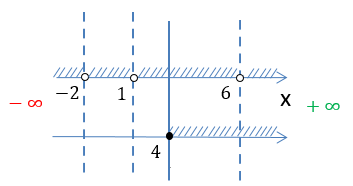
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
Нахождение области определения сложной функции — Студопедия
Поделись
Рассмотрим для начала сложную функцию f, которой соответствует формула . Какова же область определения сложной функции f ? Это множество всех x из области определения функции f2, для которых f2(x) входит в область определения функции f1.
Таким образом, область определения сложной функции — это пересечение двух множеств: множества всех таких x, что , и множества всех таких x, для которых . То есть, областью определения сложной функции f является множество всех x, удовлетворяющих условию .
Записанная система представляет собой систему неравенств, решением которой является искомая область определения сложной функции .
Таким образом, нахождение областей определения сложных функций сводится к решению систем неравенств различного вида.
Давайте рассмотрим решения нескольких примеров, в которых находятся области определения сложных функций.
Мы не будем подробно описывать решения систем неравенств, так как это выходит за рамки этой статьи.
Пример.
Найдите область определения сложной функции .
Решение.
Исходную сложную функцию можно записать в виде , то есть, f1 – логарифмическая функция с основанием e, а f2 – степенная функция с показателем 2.
Обратившись к известным областям определения основных элементарных функций, имеем и .
Тогда
Следовательно, областью определения заданной сложной функции является множество всех действительных чисел, кроме нуля.
Ответ:
.
Пример.
Какова область определения функции ?
Решение.
Перепишем данную функцию в виде . Теперь стало видно, что нам требуется найти область определения сложной функции f=f1(f2), где f1 – степенная функция с показателем , а f
2 – функция арксинус.
Нам известны области определения основных элементарных функций, откуда мы и заключаем, что и .
Осталось решить систему неравенств: .
Для решения неравенства вспомним свойства функции арксинус. Арксинус возрастает на всей области определения и обращается в ноль при x=0, следовательно, .
Вернемся к системе неравенств: .
Таким образом, областью определения исходной сложной функции является интервал .
Ответ:
.
Теперь давайте рассмотрим сложную функцию вида . Область определения функции f находится как решение системы вида
Пример.
Найдите область определения сложной функции .
Решение.
Заданную сложную функцию можно представить в виде , где f1 – функция синус, f2 – функция корень четвертой степени, f
3 – логарифмическая функция с основанием 10.
Нам известно, что .
Тогда область определения сложной функции f найдем, решив систему неравенств:
Условие равносильно условию , следовательно,
Ответ:
.
Замечание. В разобранных выше примерах мы специально брали сложные функции, составленные только из основных элементарных функций, чтобы лучше донести принцип нахождения области определения сложных функций. В следующих пунктах этой статьи мы разберем примеры нахождения областей определения сложных функций, составленных не только из основных элементарных функций, но и из элементарных функций.
К началу страницы
Домен и диапазон функции
Содержание:
- Что такое домен и диапазон функции?
- Как найти домен и диапазон функции
- Диапазон (статистика)
- Закрытый домен
- Кодовый домен
- Частотный диапазон
- Домен интеграции
- Интервальный домен
- Домен — это набор значений x, которые можно поместить в функцию. Другими словами, это набор всех возможных значений независимой переменной.
- Диапазон — это набор значений y, которые выводятся для домена.
- Кодовый домен подобен диапазону, но с одним большим отличием: кодовый домен может содержать все возможных выходных данных
, а не только те, которые действительно появляются.
Посмотрите видео для краткого обзора:
Домен и область действия
Посмотрите это видео на YouTube.
- Проверить известные домены/диапазоны,
- Угадай и проверь,
- Графики,
- Таблица значений.
Сначала посмотрите, сможете ли вы выяснить, какой тип функции у вас есть (это не всегда ясно).
Многие функции имеют бесконечный набор для домена. «Бесконечное множество» — это просто множество всех возможных чисел. Например, вы можете ввести любое число в функцию y = x 2 , и она все равно выдаст вам результат. Но как насчет диапазона? Отрицательное число никогда не будет отображаться для этой функции; отрицательный раз отрицательный всегда будет положительным.
y = -10 2 = -10 * -10 = 100.
Имеет смысл, что диапазон для x 2 равен 0 > ∞.
Некоторые функции имеют определенные домены и диапазоны. Краткое описание приведено ниже или просмотрите наш плейлист на YouTube, в котором есть серия очень коротких видеороликов о поиске доменов и диапазонов для различных функций.
- Линейные функции обычно имеют область определения и диапазон всех действительных чисел. См.: Линейные функции (видео).
- Полиномиальные функции имеют область определения всех действительных чисел. Диапазон зависит от степени и старшего коэффициента. См.: Полиномиальные функции.
- Квадратичные (квадратичные) функции имеют область определения всех действительных чисел. Диапазон зависит от знака старшего коэффициента: y ≥ min (+) или y ≥ max, (-). См.: Квадратичные функции.
- Функции абсолютного значения имеют область определения всех действительных чисел.
Диапазон зависит от вершины и знака выражения абсолютного значения. См.: Функция абсолютного значения.
- Функция квадратного корня имеет область определения x ≥ 0 и диапазон y ≥ 0. Другие функции квадратного корня, такие как √(x – 5), см.: Квадратный корень и радикальные функции.
- Рациональные функции f(x) = 1/x имеют область определения x ≠ 0 и диапазон значений x ≠ 0. Если у вас более сложная форма, например f(x) = 1 / (x – 5), вы можете найти домен и диапазон с помощью обратной функции или графика. См. Рациональные функции.
- Синусоидальные функции и функции косинуса имеют область определения всех действительных чисел и диапазон -1 ≤ y ≤ 1.
Совет: Ознакомьтесь с формами основных функций, таких как синус/косинус и многочлены. Таким образом, вы сможете разумно найти область определения и диапазон функции, просто взглянув на уравнение.
Если у вас нет сильных навыков алгебры, вы можете пропустить этот метод и вместо этого попробовать графические или табличные методы.
По сути, используйте свои навыки алгебры, чтобы найти домен и диапазон для функции, угадывая и проверяя! Несколько общих советов:
- Деление на ноль запрещено ). В качестве примера предположим, что у вас есть функция:
f(x) = 1/(x 2 – 9).
Вы можете исключить любые значения x (домен), которые делают знаменатель равным нулю. - Для домена число под знаком квадратного корня не может быть отрицательным . Например, вы не можете найти домен для √-10, потому что решение — мнимое число.
- Попробуйте ввести в функцию разные x-значения
для y, чтобы посмотреть, что произойдет. Ищите такие тенденции, как: всегда положительные, всегда отрицательные или наборы чисел, которые не работают. Попробуйте ввести очень большое (например, миллион) или очень маленькое (например, отрицательное значение миллиона) и посмотрите, сработает ли это.
Пример : Найти область определения и диапазон функции с помощью алгебры
Найти область определения и диапазон для:
Область определения:
- Числитель имеет квадратный корень; числа под этим не могут быть отрицательными (см.
№ 2 выше). Таким образом, у вас могут быть только числа для x, большие или равные -2.
- Знаменатель : Вы не можете разделить на ноль, вы не можете получить -3 + 3, так как это даст ноль. Например, 3 2 – 9 = 0,
.
Домен для этой конкретной функции: x >
-2, x ≠ 3.
Диапазон
Диапазон для этой функции — это набор всех значений f(x), исключая F(x) = 0. Здесь навыки алгебры получить тренировку!
- Числитель : Глядя на функцию, вы должны сразу увидеть, что числитель становится равным 0, когда x = -2:
√(2 + 2) = √0 = 0, - Знаменатель:
- Работая с -2, знаменатель становится: (-2) 2 – 9 = 5. Таким образом, f(-2) = 0/-5 = 0,
- Если вы вставите несколько значений x между 2 и 3 в (x 2 – 9), вы увидите, что функция приближается к отрицательной бесконечности.
- Вставьте еще несколько значений x, превышающих x = 3, обратите внимание, что функция стремится к положительной бесконечности.
- Чем больше становятся значения x, тем меньше становятся значения функции (но на самом деле они никогда не достигают нуля).
Постройте график функции и посмотрите, где находятся ваши значения x и y. Большинство графических калькуляторов помогут вам увидеть домен функции (или указать, какие значения могут быть недопустимы). Например, если вы нарисуете x 2 , будет ясно, что домен не может включать отрицательные числа. Если у вас нет графического калькулятора, попробуйте этот бесплатный онлайн-калькулятор. Всегда увеличивайте и уменьшайте масштаб графика, чтобы проверить непрерывность или отсутствующие области.
График для x 2 и 4x 2 +25 (используя онлайн-калькулятор HRW.
Из приведенного выше графика видно, что диапазон для x 2 (зеленый) и 4x 2 +25 (красный график) является положительным; На этом этапе вы можете предположить, что это набор из всех положительных действительных чисел, основываясь на графике
Составьте таблицу значений на вашем графическом калькуляторе ( См.
Включите ввод x от -10 до 10, затем несколько больших чисел (например, один миллион). Используйте калькулятор, чтобы найти значения y для значений x. Если калькулятор говорит вам, что значения или не определены, или что значения могут достигать предела (число, к которому функция приближается, но никогда не достигает), это должно помочь вам определить диапазон.
В статистике диапазон является мерой разброса: это разница между самым высоким и самым низким значением в наборе данных. Чтобы найти его, вычтите наименьшее число из наибольшего.
Несколько конкретных примеров поиска статистических диапазонов см. в разделе Как найти диапазон в статистике.
Другие значения «диапазона»
В исчислении диапазон равен всем выходным значениям функции . В некоторых областях математики диапазон может — что может сбивать с толку — также означать просто весь диапазон чисел — например, диапазон цен на мобильные телефоны может составлять от 40 до 550 долларов.
Закрытый домен — это домен, содержащий все его граничные точки. Если домен содержит набор всех внутренних точек (исключая границу), домен является открытым доменом . Незакрытый домен (это не то же самое, что открытый домен) содержит некоторые граничные точки, но не все.
Если домен содержит все точки в пределах ограниченного расстояния от начала координат, он называется ограниченным доменом . Неограниченная область имеет точки, не находящиеся внутри границы; Другими словами, они находятся на произвольном расстоянии от начала координат.
Непрерывная функция в ограниченной закрытой области D будет иметь максимальное значение и минимальное значение в D.
Закрытая область в других контекстах
конкретная система ответа на вопрос (QA). Например, система под названием САМОЛЕТ может хорошо отвечать на вопросы о воздушной скорости, ускорении и грузоподъемности конкретного самолета, но не очень хороша за пределами этой конкретной области.
В разработка программного обеспечения закрытый домен — это просто домен, все границы которого закрыты. Открытый домен — это домен, в котором открыты все границы.
Целостно замкнутые области находятся в коммутативной алгебре. Целостно замкнутая область A — это область целостности (ненулевое коммутативное кольцо, в котором произведение любых двух ненулевых элементов также не равно нулю), интегральное замыкание которой в своем поле частных есть само A.
Кодовый домен A (или целевой набор) содержит все значения (выходные данные) функции.
Когда мы говорим, что функция f: X → Y (что означает «набор значений X выводит набор значений Y»), кодовый домен — это Y . Другими словами, выходные данные функции ограничены доменом кода.
Диапазон аналогичен, но разница в том, что диапазон представляет собой набор фактических значений функции (фактических выходов).
Графическое представление кода домена
На приведенном ниже изображении показана взаимосвязь между доменом, совместным доменом и диапазоном.
- Красный овал — домен . Каждый вход для функции f является членом этой области и может быть представлен x.
- Синий овал (рассматриваемый в целом, включая желтый подраздел) — это кодовый домен . Это представляет все возможные числа, которые могут быть получены на выходе. Каждый экземпляр домена отображается функцией f в этот кодовый домен.
- Желтый овал, — подмножество этого целевого домена, — диапазон , содержащий все фактические экземпляры f(x).
Примеры кода домена
Возьмем функцию f(x) = x 2 , ограниченную вещественными числами, поэтому f: ℝ → ℝ.
Здесь целевым набором f являются все действительные числа (ℝ), но поскольку все значения x 2 положительны*, фактическое изображение или диапазон f равен ℝ + 0 .
*Любой отрицательный ввод приведет к положительному результату (например, -2 * -2 = +4).
Целевые наборы и композиция
Целевые наборы приобретают решающее значение, когда мы начинаем обсуждать композиции функций. Композиция «f∘g» читается как «f из g» или «f после g» и представляет собой составную функцию, которая включает в себя взятие члена домена g, отправку его через функцию g и передачу этого вывода через f. .
Композиция действительна тогда и только тогда, когда область определения второй функции совпадает с областью определения первой функции. В нашем примере композиция действительна только в том случае, если кодовый домен g совпадает с доменом f.
Анализ частотной области — это когда сигнал изучается относительно частоты , а не относительно времени . Исследуемые данные нанесены с частотой по оси x и амплитудой по оси y; это показывает, как энергия сигнала распределяется в зависимости от частоты.
Функция может быть представлена либо временной областью либо частотной областью; каждый полезен для разных целей. Представление сигнала во временной области может быть преобразовано в частотное представление с использованием преобразования Фурье или аналогичных манипуляций.
Преобразование Фурье преобразует представление во временной области (красный) в частотную область (синий). Пики в области представляют частоты компонентов.
Важность и использование анализа в частотной области
Термин впервые появился в 1953 году в технике связи. Однако сегодня этот анализ используется во многих различных областях, в том числе:
- Геология,
- Химия,
- Дистанционное зондирование,
- Обработка изображений,
- Электротехника,
- Связь.
Анализ в частотной области называют краеугольным камнем системной инженерии и важной частью набора инструментов почти любого ученого, инженера или статистика.
Это представление часто позволяет охарактеризовать сигнал или серию сигналов с помощью простой алгебры, в отличие от сложных дифференциальных уравнений, которые используются для представления сигнала во временной области. Простые вычисления, связанные с обработкой этих сигналов, делают его особенно полезным для инженеров. Возможно, что более важно, частотный анализ позволяет вам увидеть циклическое поведение, которое могло бы быть не сразу очевидным в представлении во временной области.
При интегрировании некоторой функции по замкнутому интервалу [a, b] этот интервал называется областью интегрирования . Например:
Областью интегрирования для этой функции является закрытый интервал [1, 3].
Область интегрирования может быть бесконечной (т. е. от -∞ до ∞), как показывает следующий несобственный интеграл:
Пример несобственного интеграла с бесконечной областью интегрирования.
Несобственные интегралы нельзя вычислить напрямую; Они вычисляются как пределы обычных интегралов.
В трех измерениях все становится немного сложнее, но в большинстве случаев область у основания объекта является областью интеграции.
Область интегрирования на 3D-форме обычно является базой (показана красными линиями на этом изображении).
Как нарисовать область интегрирования
Начертить область для любого интеграла легко, если у вас есть только один интеграл (см. пример в шаге 1 ниже). Для нескольких интегралов, если вы разбиваете их на шаги, это становится намного менее сложным.
Пример задачи: Нарисуйте область интегрирования для следующего повторного интеграла:
Решение:
Шаг 1: Нарисуйте границы интегрирования для первого интеграла. Границы даны как x = от 0 до 1, поэтому:
Шаг 2: Нарисуйте границы второго интеграла на том же графике из шага 1. Примечание: Если границы интегрирования не являются целыми числами (второй интеграл здесь есть e, число Эйлера), вы можете использовать графический калькулятор (я использовал калькулятор на Desmos.
Шаг 3: Найдите заштрихованную область, соответствующую определению обоих интегралов. В этом примере вы затеняете только область от 0 до 1, которая также находится в пределах [e, e x ].
Вот и все!
Вообще говоря, интервальный домен — это домен, ограниченный интервалом [1]. Например, входные данные (например, значения x) для конкретной функции могут быть ограничены интервалом [0, 1]. Интервалы могут быть закрытыми, открытыми или полузакрытыми/полуоткрытыми.
Функция, определенная на полуоткрытом интервале «область интервала» из [5.5, 10).
Интервальная область в теории областей
В теории областей термин «интервальная область», впервые предложенный Д. С. Скоттом в 1972 г. [2], представляет собой способ аппроксимации действительных чисел. Он получил свое название, потому что реалы разделены на интервалы для вычислений.
Аппроксимации иногда необходимы для вычислений над несчетными пространствами, такими как вещественные числа (ℝ) или некоторые функциональные пространства. Области интервалов не так просто определить, как «интервалы», с которыми вы сталкиваетесь в исчислении; Алгебраические структуры, состоящие из набора плюс одна или несколько бинарных операций, удовлетворяющих определенным аксиомам, необходимы для демонстрации различий между многими эквивалентными (и неэквивалентными) версиями интервальной области [3].
Теоретическая основа Скотта для дифференциального исчисления изначально была разработана для функций с одной переменной. Недавно он был распространен на функции нескольких переменных [3]. Это расширение переводит интервальную область в аппроксимации кривых и поверхностей [4].
Теория доменов и алгебраические структуры выходят за рамки этой статьи, но если вам интересно, прочитайте статью Джесс Бланк в Computer Journal Интервальные домены и вычислимые последовательности: пример редукции доменов [5].
Область интервалов: ссылки
[1] Klippert, J. (1989). Расширенное расширенное исчисление: подсчет разрывов функции с действительным знаком с интервальной областью. Журнал «Математика»
Том. 62, № 1 (февраль 1989 г.), стр. 43-48 (6 страниц)
[2] Скотт, Д. С. (1972) Теория решеток, типы данных и семантика. В
Растин, Р. (редактор), Формальная семантика языков программирования,
стр. 65
[3] Эдалат, А. (1995a) Теория предметной области и интеграция. Теоретическая информатика 151 163–193.
[4] Edalat, A. & Lieutier, A. (2004). Теория доменов и дифференциальное исчисление (функции одной переменной). Мат. Структура в Комп. Наука, том. 14, стр. 771–802. c2004 Cambridge University PressDOI: 10.1017/S0960129504004359 Напечатано в Соединенном Королевстве
[5] Blanck, J. (2012). Интервальные домены и вычислимые последовательности: пример сокращения доменов. Компьютерный журнал (5 сентября).
Домен и диапазон: другие ссылки
Кэссиди, Стив.
Кулкарни. Частота Дом. и преобразования Фурье. Получено с https://www.princeton.edu/~cuff/ele201/kulkarni_text/frequency.pdf 16 июня 2018 г.
Лю, Г. Исчисление нескольких переменных. Получено 31 августа 2020 г. с: https://www.math.ucla.edu/~azhou/teaching/18W/hw-solutions.pdf
MIT Department of Machine Engineering. 2.14 Раздаточный материал; Введение в частоту. Обработка домена. Получено с http://web.mit.edu/2.14/www/Handouts/FreqDom.pdf 16 июня 2018 г.
Ци, П. (2019). Ответы на сложные открытые вопросы в масштабе. Получено 7 января 2020 г. с: http://ai.stanford.edu/blog/answering-complex-questions/
Rogawski, J. (2007). Многомерное исчисление. WH Freeman.
Тиан, Дж. Инженерия качества программного обеспечения: тестирование, обеспечение качества и количественное улучшение.
Чжоу, А. Проблема.
ЦИФРОВАТЬ ЭТО КАК:
Stephanie Glen . «Домен и диапазон функции» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/types-of-functions/domain-and-range-of-a-function/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Как найти область определения функции
Обновлено 7 декабря 2020 г.
Автор Lisa Maloney
Когда вы впервые начинаете изучать функции, вам, возможно, придется рассматривать их как машину: вы вводите значение, x в функцию, и как только оно будет обработано машиной, другое значение — назовем его y — выскакивает из дальнего конца.
Стратегия поиска домена
Если вы только изучаете функции и домены, обычно предполагается, что доменом функции являются «все действительные числа». Поэтому, когда вы приступаете к определению домена, часто проще всего использовать свои знания математики, особенно алгебры, чтобы определить, какие числа не являются действительными членами домена. Поэтому, когда вы видите инструкции «найти домен», часто проще всего прочесть их в голове как «найти и исключить любые числа, которые не могут быть в домене».
В большинстве случаев это сводится к проверке (и устранению) потенциальных входных данных, которые могут привести к тому, что дроби станут неопределенными или будут иметь 0 в знаменателе, и поиску потенциальных входных данных, которые дадут вам отрицательные числа под знаком квадратного корня.
Пример нахождения домена
Рассмотрим функцию
f(x) = frac{3}{x — 2}
, которая на самом деле означает, что любое введенное вами число будет плюхаться вместо x в правой части уравнения. Например, если вы вычислили f (4), вы получили бы
f(4) = frac{3}{4 — 2}
, что дает 3/2.
А что, если вы вычислили f (2) или, другими словами, вместо 9 ввели 20039 х ? Тогда у вас будет
f(2) = frac{3}{2 — 2}
, что упрощается до 3/0, что является неопределенной дробью.
Здесь показан один из двух распространенных случаев, когда число может быть исключено из домена функции. Если задействована дробь, и входные данные приведут к тому, что знаменатель этой дроби будет равен нулю, то входные данные должны быть исключены из области определения функции.
Небольшое исследование покажет вам, что абсолютно любое число , кроме 2 вернет действительный (хотя иногда и беспорядочный) результат для рассматриваемой функции, поэтому областью применения этой функции являются все числа, кроме 2.
Другой пример поиска области
исключить возможные члены области определения функции: иметь отрицательную величину под знаком квадратного корня или любой радикал с четным индексом. Рассмотрим пример функции
f(x) = sqrt{5 — x}
Если x ≤ 5, то количество под радикальным знаком будет либо 0, либо положительным, и возвратит действительный результат. Например, если x = 4,5, у вас будет
f(4,5) = sqrt{5 — 4,5} = sqrt{0,5}
, что, несмотря на беспорядок, все же возвращает правильный результат. И если x = −10, у вас будет
f(-10) = sqrt{5 — (-10)} = sqrt{5 + 10} = sqrt{15}
, что, снова возвращает допустимый, если запутанный результат.
Но представьте, что х = 5,1. В тот момент, когда вы на цыпочках перейдете разделительную линию между 5 и любыми числами, превышающими ее, вы получите отрицательное число под корнем:
f(5.
В этом вопросе следует разбираться, поскольку понятие не только встречается в школьной и университетской программах, но и широко применяется в науке и программировании (разработке программного обеспечения и прошивки контроллеров).
Общие сведения
Областью определения произвольной функции является множество значений переменных, от которых она зависит и принимает определенное значение. Встречаются функции с одной или несколькими переменными. Для простоты исследования нужно рассмотреть первый тип. Для того чтобы найти область определения и множество значений функции, необходимо использовать простые примеры. Специалисты рекомендуют применять метод изучения «от простого к сложному».
Первый раз этот термин упоминается в школьной программе. Книга «Алгебра и начало анализа» дает базовые знания в этой области. Однако она написана не для всех понятным языком.
Обучаемый часто ищет информацию в интернете. В некоторых случаях ученики занимаются поиском готовых решений, а это не совсем правильно, поскольку математические дисциплины пригодятся при поступлении в высшие учебные заведения. Исследование функции — естественный процесс, который встречается в различных дисциплинах.
Программирование на разных языках пользуется огромной популярностью. В нем нужны математические знания для написания некоторых программ и игр. В последних следует производить точные расчеты и описывать некоторые функции героя. Например, удар мечом подчиняется определенному математическому закону или функции. Для корректной ее работы и тестирования следует находить грамотно ее область определения.
Основные понятия
Область определения функции обозначается буквой «D». Кроме того, указывается ее имя D (f). Допускается также следующее обозначение «D (y)». Если необходимо ее найти для нескольких функций, можно изменить обозначение. Для сложного типа функций z = f (a, b, x, y) эта величина обозначается таким образом: D (z). Аргумент — независимая переменная, принимающая определенные значения.
Существуют также сложные функции, которые включают в число своих переменных и другие функции. Пример, z = f (x, k, l, w, y). В нем величины x, k, l являются переменными, а w и y — следующими функциями: w = 2 * x1 + 5 и y = 2 / (x2 — 6). Для каждого типа функции существует определенный алгоритм, по которому следует находить D (f). Он основывается на многолетнем опыте специалистов и придуман для оптимизации вычислений.
Важно уметь правильно определять тип функции, поскольку от этого зависит процесс выбора алгоритма. Для одних можно сразу определить D (f), для других — решить уравнение или неравенство, для третьих следует решить систему уравнений и т. д.
Можно воспользоваться специальными программными модулями. Простым примером программы является онлайн-калькулятор, позволяющий не только вычислить D (f), но и начертить ее график. Кроме того, D (f) записывается в виде множества значений.
Например, D (y) = [0, 157). Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[«) до 157 не включительно.
Типы функций
Функций существует огромное разнообразие. Они бывают простыми и сложными. Первые в математических дисциплинах классифицируются на несколько типов: алгебраические, тригонометрические и трансцендентные. Алгебраические классифицируются на рациональные и иррациональные. Рациональные бывают целыми и дробными. Тригонометрические включают в свой состав все функции с sin, cos, tg, ctg и т. д. Трансцендентные делятся на степенные, показательные и логарифмические.
Рациональные целые — выражения полиномиального типа (линейные). Они без корней и степеней, дробей и логарифмов, а также без тригонометрических функций. Областью их определения является множество всех действительных чисел (Z) от бесконечно малого до бесконечно большого числа.
Дробный тип — функции, в числителе и знаменателе которых находится переменная. Для нахождения D (f) нужно исключить все значения переменных в нем, приводящие к 0. Если встречается тригонометрические функции, то нужно вычислить все значения, приводящие к отсутствию D (f) на определенном интервале. Этот тип функций может быть иррациональным, дробным, линейным, а также использоваться вместе со степенью и логарифмом.
К иррациональным функциям относят выражения, которые содержат переменную величину под корнем. Значение D (f) — все Z, кроме переменных, приводящих к отрицательным значениям выражений с четными степенями корней. D (f) степенной функции являются все действительные числа. Однако если степень представлена дробным выражением, то значения переменных не должны приводить к неопределенности (например, 4/0, т. к. на 0 делить нельзя). Для функций с натуральным логарифмом выражение, находящееся под ним, должно быть больше 0.
Правильное обозначение
Очень важно правильно обозначать D (f), поскольку это существенно влияет на результат. Это позволит избежать многих ошибок в любой сфере.
Следует руководствоваться такими правилами:
- Использовать скобку «[» и/или «]», когда нужно указать принадлежность к множеству.
- Круглые скобки используются в двух случаях: указывание границы бесконечности и значения, которое не входит в интервал.
- Для объединения нескольких множеств нужно применять специальный символ «U».
- Допускается использование круглых и квадратных скобок в одном множестве.
Примером в первом случае является множество [0, 100]: от 0 включительно и до 100 не включительно. Во втором случае — (8, 10): значение, равное 9, поскольку 8 и 10 — нижняя и верхняя границы, не принадлежащие множеству.
Два предыдущих множества можно объединить: [0, 100] U (8, 10). Пример записи последнего случая следующий: (20, 50].
Алгоритмы определения
Для удобства определения D (f) необходимо применять специальные алгоритмы, которые упрощают операцию. Целая рациональная функция, как уже было описано ранее, имеет D (f), принадлежащую множеству Z (весь ряд действительных чисел). Кроме того, степенная функция также имеет D (f), которая соответствует Z.
Если функция является дробной, то следует использовать следующий алгоритм:
- Обратить внимание на знаменатель, который не должен быть равен 0.
- Выписать выражение знаменателя и решить его, приравнивая к 0.
- Записать интервал.
Если она представлена в виде четного корня, следует решить неравенство. Значение подкоренного выражения должно быть больше 0. В противном случае область определения под корнем не будет существовать (неопределенность).
Однако если корень нечетный, то D (f) — множество действительных чисел. Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.
Для тригонометрических выражений синуса sin (x) и косинуса cos (x) множество всех Z является D (f). Однако для тангенса tg (x) и котангенса ctg (x) необходимо исключить значения переменной x = (Pi / 2) + Pi * k и x = Pi * k соответственно. В этих выражениях k является множеством действительных чисел.
Другие методы
Существуют также и другие методы определения D (f). Ее можно выяснить при помощи следующих инструментов: онлайн-калькулятора, специальных программ и построения графика. Первый способ позволяет довольно быстро найти необходимую величину. Но это не все его возможности. Можно с его помощью строить графики и находить все свойства функции.
Однако первый метод уступает второму, суть которого сводится к использованию специализированного программного обеспечения. В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.
В некоторых случаях можно найти D (f), построив ее график. Для этого следует подставить значение аргумента функции и получить ее значение. Построение таблицы зависимости значения функции от ее аргумента позволяет правильно построить графическое представление. Чтобы быстро строить графики, нужно знать их базовые виды: линейный, степенной (квадратичный, кубический и т. д. ), а также другие. Чем точнее графическая иллюстрация, тем легче определить D (f).
После заполнения таблицы значений следует приступать к построению графика. Для этого берутся точки с координатами из таблицы (x, y), и отмечаются на декартовой системе координат.
Затем их следует соединить. Получится график заданной функции, по которому не составит труда сделать определенные выводы.
Примеры решения
Теоретические знания необходимы, но некоторые люди делают огромную ошибку. Они не закрепляют их при помощи практики. Необходимо регулярно решать задачи на нахождения D (f), поскольку в этом случае набирается опыт. Наиболее простыми задачами считаются следующие: нахождения D (f) линейной, степенной, показательной и тригонометрической функций. Важным аспектом считается упрощение выражения. Для этого следует вспомнить также и формулы сокращенного умножения.
С дробными и иррациональными функциями могут возникнуть некоторые сложности, поскольку нужно решить уравнение или неравенство. Однако в последнем случае нельзя путать знак неравенства.
Для линейного вида
Нужно найти D (f) для y = 2*x — 3 * (x — 5). Для решения следует применить такой алгоритм:
- Упростить выражение.
- Определить D (f).
Для упрощения выражения следует раскрыть скобки. Конечно, это делать необязательно, поскольку ответ очевиден D (y) = (-бесконечность, +бесконечность). Но по правилам «хорошего тона» любое математическое выражение следует упрощать: y = 2 * x — 3 * x + 15 = — x + 15 = 15 — x. При решении следует правильно раскрывать скобки, а также следить за знаками. Малейшая ошибка может привести к значительному искажению графика.
В некоторых задачах следует также построить график функции. Для конкретного случая создается таблица зависимости значения «y» от аргумента. Не имеет смысла брать много значений «х», поскольку графиком является прямая. Известно, что необходимы только две точки для ее проведения. Подстановка количества значений «х», превышающих двух, является грубой и распространенной ошибкой.
Дробные и иррациональные
Пусть существует выражение вида y = 1 / [(x — 4) * (x + 4)]. Нужно определить D (f).
Решается задача таким способом:
- Приравнивается знаменатель к 0.
- Решается уравнение.
- Определяется интервал допустимых значений.
Нужно решить уравнение (x — 4) * (x + 4) = 0. Из него видно, что x1 = 4 и x2 = -4, поскольку эти значения «превращают» знаменатель в неопределенность. Следовательно, D (y) = (-бесконечность, -4) U (4, +бесконечность).
В случае с иррациональным выражением: y = sqrt[4 * sqr (x) — 12 * x + 9], нужно решить уравнение подкоренного выражения.
Для решения квадратного уравнения следует применить такой алгоритм:
- Записать неравенство: 4 * sqr (x) — 12 * x + 9 >= 0.
- Дискриминант: D = [(- b)^2] — (4 * a * c) = [(-12)^2] — (4 * 4 * 9) = 144 — 144 = 0.
- D = 0 — только одно решение.
- x = (-b) / (2 * a) >= 12 / (2 * 4) >= 12 / 8 >= 6 / 4 >= 1,5.
Множество чисел D (y) ограничивается следующим интервалом (-бесконечность, 1.5) U (1.5, +бесконечность).
Таким образом, для нахождения множества значений D (f) для конкретного выражения следует воспользоваться специальными алгоритмами. На первоначальном этапе исследования функции следует определить ее тип, поскольку это поможет избежать многих сложностей в процессе решения.
























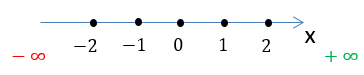
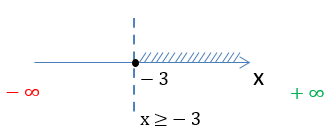
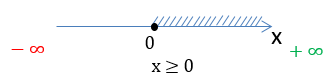











 Диапазон зависит от вершины и знака выражения абсолютного значения. См.: Функция абсолютного значения.
Диапазон зависит от вершины и знака выражения абсолютного значения. См.: Функция абсолютного значения.  № 2 выше). Таким образом, у вас могут быть только числа для x, большие или равные -2.
№ 2 выше). Таким образом, у вас могут быть только числа для x, большие или равные -2.