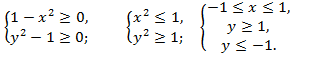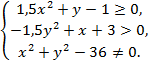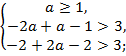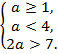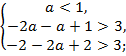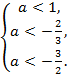Неявные функции
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Неявные функции, определяемые одним уравнением.
Начать изучение
-
Неявные функции, определяемые системой уравнений.
Начать изучение
-
Локальная обратимость регулярного отображения.
Начать изучение
Неявные функции, определяемые одним уравнением.
Пусть функция (F(x,y)) определена в (R^2). Рассмотрим уравнение
$$
F(x,y)=0.label{ref1}
$$
Множество (G_F) точек плоскости, координаты которых удовлетворяют уравнению eqref{ref1}, было названо графиком уравнения. Через (A_F) будем обозначать проекцию графика (G_F) на ось (x). Будем рассматривать такие уравнения eqref{ref1}, графики которых не есть пустые множества.
Так, график уравнения (x^2 + y^2 — 1 = 0) есть окружность, график уравнения ((x-1)(x+y-1)=0) есть пара прямых (x = 1) и (x+y-1=0) (рис. 28.1).
Если график (G_F) уравнения eqref{ref1} взаимно однозначно проектируется на (A_F), то существует единственная функция (f: ; A_Frightarrow R), график которой совпадает с графиком уравнения. Эта функция каждому (xin A_F) ставит в соответствие тот единственный (y), для которого (F(x,y)=0). Говорят, что уравнение eqref{ref1} определяет (y) как неявную функцию (x).
Но, как правило, график уравнения eqref{ref1} не проектируется взаимно однозначно на (A_F). Тогда на (A_F) в общем случае определено бесконечное множество функций, графики которых совпадают с некоторым подмножеством графика (G_F) уравнения eqref{ref1}. Так, разбивая отрезок ([-1,1]) точками (x_0= -1 < x_1 < ldots < x_n=1) и полагая на каждом из отрезков ([x_{i-1},x_i]) функцию (f(x)) равной (displaystylesqrt{1-x^2}) или (displaystyle -sqrt{1-x^2}), получим, что график (f) есть некоторое подмножество графика уравнения (x^2+y^2-1=0), так что (x^2+(f(x))^2 — 1 = 0).
Пусть график уравнения (G_F) не проектируется взаимно однозначно на (A_F), но существует такой прямоугольник
$$
K = {(x,y): ; aleq xleq b, ; cleq yleq d},nonumber
$$
что та часть графика (G_F), которая лежит внутри (K), взаимно однозначно проектируется на отрезок ([a,b]). Тогда определена функция (f: ; [a,b]rightarrow R), которая каждому (xin [a,b]) ставит в соответствие единственный (yin [c,d]) такой, что ((x,y)in G_F). Очевидно, что (F(x,f(x))=0). Говорят, что функция (f(x)) неявно определяется уравнением eqref{ref1} в прямоугольнике (K), или что уравнение eqref{ref1} определяет в прямоугольнике (K) переменную (y) как неявную функцию переменной (x).
Например, уравнение (x^2+y^2-1=0) неявно определяет функцию (y=sqrt{1-x^2}) в прямоугольнике (-1leq xleq 1, ; 0leq yleq 1) и функцию (y=-sqrt{1-x^2}) в прямоугольнике (-1leq xleq 1, ; -1leq yleq 0).
Меняя местами переменные (x) и (y), можно говорить о том, что уравнение eqref{ref1} определяет в некотором прямоугольнике переменную (x) как неявную функцию переменной (y).
Докажем теорему, дающую достаточные условия существования, непрерывности и дифференцируемости неявной функции, определяемой уравнением eqref{ref1} в некотором прямоугольнике.
Теорема 1.
Пусть:
- функция (F(x,y)) имеет в окрестности точки ((x_0,y_0)) непрерывные частные производные (F_x(x,y)) и (F_y(x,y));
- (F(x_0,y_0)=0);
- (F_y(x_0,y_0)neq 0).
Тогда существует прямоугольник
$$
K = {(x,y): ; x_0-aleq xleq x_0+a, ; y_0-bleq yleq y_0+b},nonumber
$$
в котором уравнение (F(x,y) = 0) определяет (y) как неявную функцию (x). Функция (y=f(x)) непрерывно дифференцируема на интервале ((x_0-a,x_0+a)) и
$$
f'(x)=-frac{F_x(x,f(x))}{F_y(x,f(x))}.label{ref2}
$$
Доказательство.
(circ) Разобьем доказательство на два пункта.
Доказательство существования неявной функции. Из условия (F_y(x_0,y_0)neq 0) следует, что либо (F_y(x_0,y_0) > 0), либо (F_y(x_0,y_0) < 0). Без ограничения общности можно считать, что
$$
F_y(x_0,y_0) > 0.label{ref3}
$$
Если (F_y(x_0,y_0) < 0), то вместо уравнения (F(x,y)=0) можно было бы рассмотреть эквивалентное уравнение (widetilde{F}(x,y)=-F(x,y) = 0). Тогда (widetilde{F}(x_0,y_0)=-F(x_0,y_0) > 0).
Так как функция (F_y(x,y)) в точке ((x_0,y_0)) непрерывна и в силу условия eqref{ref3} принимает в этой точке положительное значение, то найдется такой прямоугольник (рис. 28.3)
$$
K_1={(x,y): ; |x-x_0|leq a_1, ; |y-y_0|leq b},nonumber
$$
в котором функция (F_y(x,y) > 0).
Рассмотрим функцию одной переменной
$$
psi (y)=F(x_0,y),quad y_0-bleq yleq y_0+b.nonumber
$$
Функция (psi (y)) строго возрастает на отрезке ([y_0-b,y_0+b]), так как
$$
psi'(y)=F_y(x_0,y) > 0.nonumber
$$
Кроме того, в силу условия (F(x_0,y_0)=0)
$$
psi (y_0) = F(x_0,y_0) = 0.nonumber
$$
Поэтому
$$
psi (y_0-b)= F(x_0,y_0-b) < 0,quad psi(y_0+b)=F(x_0,y_0+b) > 0.label{ref4}
$$
Неравенства eqref{ref4} в силу непрерывности функции (F(x,y)) должны сохраняться в некоторых окрестностях точек ((x_0,y_0-b)) и ((x_0,y_0+b)). Поэтому существует такое (ain (0,a_1)), что для всех (xin [x_0-a,x_0+a]) выполнены неравенства
$$
F(x,y_0-b) < 0,quad F(x,y_0+b) > 0.label{ref5}
$$
Покажем, что в прямоугольнике
$$
K={(x,y): ; |x-x_0|leq a, ; |y-y_0|leq b},nonumber
$$
уравнение (F(x,y) = 0) определяет (y) как неявную функцию (x).
Возьмем любую точку (x^*in [x_0-a,x_0+a]) и рассмотрим непрерывную на отрезке ([y_0-b,y_0+b]) функцию одной переменной (varphi (y)=F(x^*,y)). В силу условия eqref{ref5} эта функция принимает на концах отрезка значения разных знаков:
$$
varphi(y_0-b)= F(x^*,y_0-b) < 0,quad varphi(y_0+b)=F(x^*,y_0+b) > 0.nonumber
$$
По теореме Коши о промежуточных значениях найдется такая точка (y^*in [y_0-b,y_0+b]), что
$$
varphi(y^*) = F(x^*,y^*)=0.nonumber
$$
Так как (varphi'(y) = F_y(x^*,y) > 0), то функция (varphi(y)) строго возрастает на отрезке ([y_0-b,y_0+b]) и не может обратиться на этом отрезке в нуль более одного раза.
Таким образом, для любого (xin [x_0-a,x_0+a]) найдется единственный (yin [y_0-b,y_0+b]) такой, что (F(x,y) = 0). Это означает, что в прямоугольнике (K) уравнение (F(x,y) = 0) определяет (y) как неявную функцию (x).
Доказательство непрерывной дифференцируемости неявной функции. Непрерывная на замкнутом прямоугольнике (K) функция (F_y(x,y)) по теореме Вейерштрасса принимает на этом прямоугольнике свое наименьшее значение (alpha). Так как (F_y(x,y) > 0) на (K), то
$$
F_y(x,y)geq a > 0,qquad (x,y)in K.label{ref6}
$$
Непрерывная на (K) функция (F_x(x,y)) ограничена на (K). Поэтому
$$
|F_x(x,y)| < beta,qquad (x,y)in K.label{ref7}
$$
Пусть (y=f(x)) есть неявная функция, определяемая в прямоугольнике (K) уравнением (F(x,y)=0). Возьмем две точки ((x,y)) и ((x + Delta x,y+Delta y)), лежащие на графике функции (f(x)). Тогда
$$
F(x,y)=0,qquad F(x+Delta x,y+Delta y)=0.nonumber
$$
Применяя формулу конечных приращений Лагранжа, получаем
$$
begin{array}{c}
F_x(x+thetaDelta x, y +thetaDelta y)Delta x+ F_y(x+thetaDelta x, y +thetaDelta y)Delta y = 0,\
Delta y=displaystyle-frac{F_x(x+thetaDelta x,y+thetaDelta y)}{F_y(x+thetaDelta x,y+thetaDelta y)}Delta x,quad 0 < theta < 1end{array}label{ref8}
$$
Если воспользоваться неравенствами eqref{ref6} и eqref{ref7}, то из eqref{ref8} получаем
$$
|Delta y|leq frac{beta}{alpha}|Delta x|.label{ref9}
$$
Следовательно, (Delta yrightarrow 0) при (Delta xrightarrow 0) и неявная функция (f(x)) непрерывна в любой точке (xin[x_0-a,x_0+a]).
Если теперь воспользоваться непрерывностью частных производных, то, деля второе из равенств eqref{ref8} на (Delta x) и переходя к пределу при (Delta xrightarrow 0), получаем, что существует предел отношения (Delta y/Delta x) при (Delta xrightarrow 0) и (f'(x)) вычисляется при помощи формулы eqref{ref2}. Из этой формулы следует, что (f'(x)) будет непрерывной функцией на отрезке ([x_0-a,x_0+a]) как суперпозиция непрерывных функций. (bullet)
Замечание 1.
Если известно, что уравнение (F(x,y)=0) определяет в прямоугольнике (aleq xleq b, ; cleq yleq d) переменную (y) как неявную функцию (x), то связь между (dy) и (dx) можно установить, формально дифференцируя тождество (F(x,y(x)) = 0). Воспользовавшись инвариантностью формы дифференциала, получаем
$$
F_x(x,y)dx + F_y(x,y)dy = 0.nonumber
$$
Дифференцируя последнее тождество еще раз, можем найти второй дифференциал (d^2y)
$$
F_{xx} dx^2 + 2F_{xy} dx dy + F_{yy} dy^2 + F_y d^2y = 0.nonumber
$$
Неявные функции, определяемые системой уравнений.
Рассмотрим систему (m) уравнений с (n+m) неизвестными
$$
left{begin{array}{l}F_1(x_1,ldots,x_n,x_{n+1},ldots,x_{n+m})=0,\…..\F_m(x_1,ldots,x_n,x_{n+1},ldots,x_{n+m})=0end{array}right.label{ref10}
$$
При формулировке общей теоремы о неявных функциях удобно пользоваться понятием декартова произведения множеств. Если (A) и (B) — произвольные множества, то их декартово произведение (Atimes B) есть множество пар ((x,y)), где (xin A), (yin B). Так, декартово произведение ([a,b]times [c,d]) есть множество пар вещественных чисел таких, что (aleq xleq b,) и (cleq yleq d), то есть прямоугольник в (R^2).
Клеточной окрестностью точки (x^0 =(x_1^0,ldots,x_n^0)) будем называть следующее множество:
$$
K(x^0)={x: ; xin R^n, ; -varepsilon_ileq x_i-x_i^0leq varepsilon_i, ; i=overline{1,n}},nonumber
$$
где (varepsilon_i, ; i =overline{1,n}) — положительные числа, (x = (x_1,…,x_n)).
Легко видеть, что в том случае, когда (K_1(x^0)subset R^n) и (K_2(y^0)subset R^m) — клеточные окрестности, их декартово произведение (K_1(x^0)times K_2(y^0)) есть клеточная окрестность точки ((x^0,y^0)=(x_1^0,…,x_n^0,y_1^0,…,y_m^0) в пространстве (R^{n+m}).
Для дальнейшего удобно преобразовать переменные, полагая (x=(x_1,…,x_n), ; y=(y_1,…,y_m)), где (y_1=x_{n+1},…,y_m=x_{n+m}).
Тогда систему уравнений eqref{ref10} можно записать в более кратком виде:
$$
F_i(x,y) = 0, ; i=overline{1,m}.label{ref11}
$$
Функции (F_i(x,y) = 0) будем считать определенными в некоторой клеточной окрестности точки ((x^0,y^0)).
Определение.
Пусть (K(x^0)subset R^n) и (Q(y_0)subset R^m) есть клеточные окрестности. Будем говорить, что система уравнений (F_i(x,y)=0, ; i=overline{1,m}), определяет в (K(x^0)times Q(y_0)) переменные (y_1,…,y_m) как неявные функции переменных (x_1,…,x_n), если для любого (xin K(x^0)) найдется единственный (yin Q(y^0)) такой, что (F_i(x,y) = 0, ; i=overline{1,m}).
Теорема 2.
Пусть выполнены следующие условия:
- функции (F_i(x,y)=0, ; i=overline{1,m}), непрерывно дифференцируемы в клеточной окрестности точки ((x^0,y^0));
- (F_i(x^0,y^0) = 0, ; i =overline{1,m};)
- $$
{begin{vmatrix}displaystylefrac{partial F_1}{partial y_1}&…&displaystylefrac{partial F_1}{partial y_m}\…&…&…\displaystylefrac{partial F_m}{partial y_1}&…&displaystylefrac{partial F_m}{partial y_m}end{vmatrix}}_{(x^0,y^0)}neq0label{ref12}
$$
Тогда найдутся клеточные окрестности (K(x^0) subset R^n) и (Q(y^0) subset R^m) такие, что в (K(x^0)times Q(y^0)) система уравнений eqref{ref11} определяет переменные (y_1,…,y_m) как неявные функции переменных (x_1,…,x_n). Неявные функции (y_j =varphi_j(x)) непрерывно дифференцируемы в (K(x^0)) и (y_j^0=varphi_j(x^0), ; j=overline{1,m}).
Доказательство.
(circ) Воспользуемся методом индукции по числу уравнений (m). При (m=1) доказательство теоремы 2 не отличается от доказательства теоремы 1 (в дальнейшем будем ссылаться на этот частный случай теоремы 2 как на теорему 1).
Предположим, что утверждение теоремы верно в том случае, когда система eqref{ref11} содержит (m-1) уравнение. Докажем, что тогда теорема верна и для системы eqref{ref11} из (m) уравнений.
Так как определитель eqref{ref12} отличен от нуля, то, раскладывая его по элементам последней строки, получаем, что хотя бы один из соответствующих миноров (m-1)-го порядка отличен от нуля. Пусть, например
$$
{begin{vmatrix}displaystylefrac{partial F_1}{partial y_1}&…&displaystylefrac{partial F_1}{partial y_{m-1}}\…&…&…\displaystylefrac{partial F_{m-1}}{partial y_1}&…&displaystylefrac{partial F_{m-1}}{partial y_{m-1}}end{vmatrix}}_{(x^0,y^0)}neq0nonumber
$$
(Здесь и в дальнейшем символ (0) означает, что значение соответствующей функции берется для аргументов с верхним индексом (0)).
Тогда в силу индукции найдутся такие клеточные окрестности
$$
begin{array}{c}K_1=displaystyleleft{(x,y_m): ; vert x_i-x_i^0vertleqvarepsilon_i’, ; i=overline{1,n}, ; vert y_m-y_m^0vert < delta_m’right},\Q_1=displaystyleleft{(y_1,…,y_{m-1}), ; vert y_j-y_j^0vertleqdelta_j’, ; j=overline{1,m-1}right},end{array}label{ref13}
$$
в которых система первых (m-1) уравнений eqref{ref11} определяет (y_1,…,y_{m-1}) как неявные функции переменных (x_1,…,x_n,y_m), то есть
$$
y_j=psi_j(x,y_m),quad j=overline{1,m-1}.label{ref14}
$$
Функции (psi_j(x,y_m)) непрерывно дифференцируемы и
$$
psi_j(x^0,y_m^0)=y_j^0,quad j=overline{1,m-1};quad (x,y_m)in K_1,label{ref15}
$$
$$
F_j(x,psi_1(x,y_m),ldots,psi_{m-1}(x,y_m),y_m)equiv 0.label{ref16}
$$
Если
$$
begin{array}{c}K_2=left{(x_1,…,x_n): ; vert x_i-x_i^0vert < varepsilon_i’, ; i=overline{1,n}right},\Q_2=left{(y_1,…,y_m): ; vert y_j-y_j^0vert < delta_j’, ; j=overline{1,m}right},end{array}nonumber
$$
то при (xin K_2, ; yin Q_2) система уравнений eqref{ref11} эквивалентна следующей системе:
$$
begin{array}{c}y_1-psi_1(x,y_m)=0, ; y_{m-1}-psi_{m-1}(x,y_m)=0,\{widetilde F}_m(x,y_m)=F_m(x, ; psi_1(x,y_m), ; …, ; psi_{m-1}(x,y_m), ; y_m)=0.end{array}label{ref17}
$$
Покажем, что последнее уравнение системы eqref{ref17} (widetilde{F}_m(x,y_m)=0) может быть разрешено относительно (y_m). Для него выполнены все условия теоремы 1. Из формулы eqref{ref17} следует, что (widetilde{F}_m(x,y_m)) непрерывно дифференцируема как суперпозиция непрерывно дифференцируемых функций. Вследствие равенств eqref{ref15} получаем, что
$$
{widetilde F}_m(x^0,y_m^0)=\=F_m(x^0, ; psi_1(x^0,y_m^0), ; …, ; psi_{m-1}(x^0,y_m^0), ; y_m^0)=F_m(x^0,y_1^0,…,y_m^0)=0.nonumber
$$
Осталось проверить условие (displaystyle{left.frac{partial{widetilde F}_m}{partial y_m}right|}_0neq 0).
Если оно не выполнено, то
$$
{left.frac{partial{widetilde F}_m}{partial y_m}right|}_0=sum_{p=1}^{m-1}{left.frac{partial F_m}{partial y_p}right|}_0 ; {left.frac{partialpsi_p}{partial y_m}right|}_0+{left.frac{partial F_m}{partial y_m}right|}_0=0.label{ref18}
$$
С другой стороны, дифференцируя по (y_m) тождества eqref{ref16} в точке ((x^0,y^0)), получаем
$$
sum_{p=1}^{m-1}{left.frac{partial F_j}{partial y_p}right|}_0 ; {left.frac{partialpsi_p}{partial y_m}right|}_0+{left.frac{partial F_j}{partial y_m}right|}_0=0.,quad j=overline{1,m-1}.label{ref19}
$$
Из eqref{ref18} и eqref{ref19} следует, что последний столбец определителя eqref{ref12} есть линейная комбинация остальных его столбцов, поэтому определитель eqref{ref12} равен нулю, что противоречит условию теоремы. Так как выполнены все условия теоремы 1, то найдется окрестность
$$
K = {(x,y_m): ; |x_i-x_i^0| < varepsilon_i < varepsilon_i’, ; i=overline{1,n}; ; |y_m-y_m^0| < delta_m < delta_m’},nonumber
$$
в которой уравнение (widetilde{F}_m(x,y_m)=0) определяет (y_m) как неявную непрерывно дифференцируемую функцию (y_m = varphi_m(x)), причем (y_m^0=varphi_m(x^0)).
В окрестности (K) система уравнений eqref{ref17} эквивалентна и системе eqref{ref11}, и системе
$$
begin{array}{c}y_1-psi_1(x,y_m)=0, ; …, ; y_{m-1}-psi_{m-1}(x,y_m)=0,\y_m-varphi_m(x)=0.end{array}label{ref20}
$$
В свою очередь система eqref{ref20} эквивалентна следующей системе:
$$
y_1=varphi(x),quadldots,quad y_m=varphi(x),label{ref21}
$$
где (varphi_1(x)=psi_1(x,varphi_m(x)), ; ldots, ; varphi_{m-1}(x)=psi_{m-1}(x,varphi_m(x))), причем
$$
varphi_1(x^0)=y_1,quadldots,quad varphi_m(x^0)=y_m^0.label{ref22}
$$
Система функций (varphi_1(x),ldots,varphi_m(x)) неявно определяется уравнениями eqref{ref11} в окрестности (Ktimes Q) точки ((x^0,y^0)), где
$$
begin{array}{c}K={x: ; vert x_i-x_i^0vert < varepsilon_i, ; i=overline{1,n}}\Q=left{y: ; vert y_j-y_j^0vert < delta_j, ; j=overline{1,m}right}, ; delta_j=delta_j’ ; при ; j=overline{1,m-1}.qquadbulletend{array}label{ref23}
$$
Замечание 2.
Существует несколько способов доказательства теоремы о неявных функциях. Предложенный способ является, по-видимому, наиболее простым, но обладает двумя недостатками: не дает алгоритма для вычисления неявной функции и не обобщается на бесконечномерный случай.
Локальная обратимость регулярного отображения.
Пусть на множестве (Esubset R^n) заданы (n) функций
$$
f_1(x),…,f_n(x).nonumber
$$
Они задают отображение (f: ; Erightarrow R^n), которое каждой точке (xin E) ставит в соответствие точку (y=f(x)), где
$$
y_1=f_1(x),quad,…,quad y_n=f_n(x).nonumber
$$
Точка (y=f(x)) называется образом точки (x) при отображении (f). Точка (x) называется прообразом точки (y).
Если (Omegasubset E), то множество
$$
f(Omega)={y: ; y=f(x), ; xin Q}nonumber
$$
называется образом множества (Omega) при отображении (f). Если (omegasubset f(E)), то множество
$$
f^{-1}(omega)={x: ; f(x)in omega}nonumber
$$
называется прообразом множества (omega).
Пусть (G subset R^n) есть открытое множество. Отображение (f: ; Grightarrow R^n) называется непрерывным в точке (x^0), если (forall varepsilon > 0 ; existsdelta > 0) такое, что (forall x) таких, что (rho(x,x^0) < delta), выполнено неравенство (rho(f(x),f(x^0)) < varepsilon).
На языке окрестностей непрерывность отображения в точке (x^0) означает, что для любой шаровой окрестности (S_{varepsilon}(y^0), ; y^0 = f(x^0)), найдется такая шаровая окрестность (S_{delta}(x^0)), что
$$
f(S_{delta}(x^0)) subset S_{varepsilon}(y^0).label{ref24}
$$
Отображение (f: ; Grightarrow R^n) называется непрерывным, если оно непрерывно в каждой точке множества (G).
Лемма 1.
Если (G) есть открытое множество, а (f: ; Grightarrow R^n) — непрерывное отображение, то прообраз каждого открытого множества (omegain f(G)) есть открытое множество.
Доказательство.
(circ) Пусть (Omega= f^{-1}(omega)). Возьмем любую точку (x^0inOmega). Тогда (f(x^0)=y^0in omega). Так как множество (omega) открыто, то найдется окрестность (S_{varepsilon}(y^0)in omega). В силу непрерывности отображения (f) в точке (x^0) найдется шаровая окрестность (S_{delta}(x^0)), для которой выполнено условие eqref{ref24}.
Следовательно,
$$
S_{delta}(x^0)subset f^{-1}(omega)subsetOmega,nonumber
$$
и (Omega) — открытое множество. (bullet)
Как обычно, под окрестностью (A(x^0)) точки (x^0) будем понимать любое множество (A), для которого точка (x^0) внутренняя.
Пусть (G subset R^n) — открытое множество. Отображение (f: ; Grightarrow R^n) будем называть непрерывно дифференцируемым, если функции (f_1(x),…,f_n(x)), задающие это отображение, непрерывно дифференцируемы в (G). Непрерывно дифференцируемое отображение (f: ; Grightarrow R^n) будем называть регулярным, если в области (G) якобиан отображения (j_f(x)neq 0). Якобианом отображения (j_f(x)) называется следующий функциональный определитель:
$$
j_f(x)=begin{vmatrix}frac{partial f_1(x)}{partial x_1}&…&frac{partial f_1(x)}{partial x_n}\…&…&…\frac{partial f_n(x)}{partial x_1}&…&frac{partial f_n(x)}{partial x_n}end{vmatrix}.nonumber
$$
Теорема 3.
Пусть (G) — открытое множество в (R^n), а отображение (f: ; Grightarrow R^n) регулярно. Тогда в каждой точке (x^0in G) оно локально регулярно обратимо, то есть (forall x^0in G) найдутся такие окрестности (A(x^0) subset G) и (B(y^0)subset f(G)), где (y^0= f(x^0)), что отображение (f: ; A(x^0)rightarrow B(y^0)) будет взаимно однозначным, причем обратное отображение (f^{-1}: ; B(y^0)rightarrow A(x^0)) регулярно.
Доказательство.
(circ) Рассмотрим в (Gtimes R^n) систему уравнений
$$
F_i(x,y)equiv y_i-f_i(x)=0,quad i=overline{1,n}.label{ref25}
$$
Пусть (x^0) — произвольная точка множества G и (y^0=f(x^0)). Тогда функции (F_i(x,y)) непрерывно дифференцируемы в (Gtimes R^n) и (y_i^0= f_i(x^0), ; i=overline{1,n}). Так как отображение (f) регулярно, то
$$
{begin{vmatrix}frac{partial F_1}{partial x_1}&…&frac{partial F_1}{partial x_n}\…&…&…\frac{partial F_n}{partial x_1}&…&frac{partial F_n}{partial x_n}end{vmatrix}}_{(x^0,y^0)}=(-1)^nj_f(x^0)neq0.nonumber
$$
Для системы уравнений eqref{ref25} выполнены все условия теоремы 2 о неявных функциях. Поэтому найдутся такие клеточные окрестности
$$
begin{array}{c}K(x^0)=left{x: ; vert x_i-x_i^0vertleqvarepsilon_i, ; i=overline{1,n}right},quad K(x^0)subset G,\Q(y^0)=left{y: ; vert y_i-y_i^0vertleqdelta_i, ; i=overline{1,n}right},quad Q(y^0)subset f(G),end{array}nonumber
$$
что в (K(x^0)times Q(y^0)) система уравнений eqref{ref25} определяет переменные (x_1,…,x_n) как неявные непрерывно дифференцируемые функции переменных (y_1,…,y_n):
$$
begin{array}{c}x_1=varphi_1(y),quad …,quad x_n=varphi_n(y),\xin K(x^0),quad yin Q(y^0),quad x_i^0=varphi_i(y^0),quad i=overline{1,n}.end{array}label{ref26}
$$
Пусть (B(y^0)) есть внутренность (Q(y^0)):
$$
B(y^0) = left{y: ; |y_i-y_i^0| < delta_i,quad i=overline{1,n}right}.nonumber
$$
Вследствие леммы 1 прообраз открытого множества (B(y^0)) при непрерывном отображении (f) есть открытое множество, причем в силу условий eqref{ref26} это множество содержит точку (x^0). Обозначим прообраз (f^{-1}(B)) через (A(x^0)). Отображение окрестности (A(x^0)) на окрестность (B(y^0)) будет взаимно однозначным, и обратное отображение (f^{-1}: ; B(y^0)rightarrow A(x^0)), определяемое формулами eqref{ref26}, будет непрерывно дифференцируемым.
Докажем регулярность обратного отображения (f^{-1}). Так как
$$
y_i-f_i(varphi_1(y),ldots,varphi_n(y))equiv 0,quad i=overline{1,n},nonumber
$$
то, дифференцируя эти тождества по переменным (y_j), получаем
$$
sum_{k=1}^nfrac{partial f_i}{partial x_k}frac{partialvarphi_k}{partial y_j}=frac{partial y_i}{partial y_j}=delta_{ij}=left{begin{array}{lc}1,&i=j,\0,&ineq j.end{array}right.label{ref27}
$$
Из равенств eqref{ref27} и из теоремы об умножении определителей следует, что
$$
j_f(x)j_{f^{-1}}(y)=1,quad y=f(x),quad xin A(x^0).quadbulletlabel{ref28}
$$
Следствие.
Если (f: ; Grightarrow R^n) есть регулярное отображение, то образ любого открытого множества (Omegasubset G) есть открытое множество.
(circ) Пусть (omega=f(Omega)). Возьмем произвольную точку (y^0inomega) и пусть (x^0) есть какой-то ее прообраз. Тогда, вследствие теоремы 3, найдутся такие окрестности (A(x^0) subset Omega) и (B(y^0) subset omega); что отображение (f: ; A(x^0)rightarrow B(y^0)) регулярно обратимо. Поэтому каждая точка (y^0inomega) принадлежит (omega) вместе с некоторой окрестностью (B(y^0)). Множество (omega=f(Omega)) открыто. (bullet)
Определение.
Неявная функция, заданная уравнением
F(x1,x2,…,xn,y)=0
(или кратко F(x,y)=0)
определяется, как функция y=f(x)=f(x1,x2,…,xn)
при подстановке которой в уравнение,
оно превращается в тождество на некотором
множестве, т. е.
F(x1,x2,…,xn,
f(x1,x2,…,xn))=0
, или кратко, F(x,f(x))=0
при xD.
Теорема 2.
Пусть
-
F(x,y)
имеет непрерывные частные производные
первого порядка в окрестности U(M0)
точки M0=(x0,y0)=
,
x0= -
F(M0)=0,
-
.
Тогда существует
окрестность U(x0)
и единственная функция, определенная
в этой окрестности y
= f(x),
такая, что
x
U(x0)
: F(x,f(x))=0
и y0
= f(x0).
Эта функция
дифференцируема в точке x0
и ее производные определяется по формуле

Доказательство.
Для
определенности будем считать, что
.Пусть в
U(M0)
выполнены
условия теоремы и
,
положим
= /2.
Тогда цилиндр
B={(x,y):(x,x0)
< ,|y
— y0|<
} содержится
в U(M0)
так как
(M,M0)=<
.
Так как в этом
цилиндре
,то функция
F(x0,y)
строго
возрастает на
[y0
— ,
y0
+ ].
В центре этого отрезка функция равна
нулю, поэтому F(x0,
y0
— )
< 0 , F(x0,
y0
+ )
> 0. Функции
F(x,
y0
— )
, F(x,
y0
+ )
непрерывны
по x
и поэтому
сохраняют знак в окрестности точки x0
. таким
образом, существует
<
x
U(
x0)
: F(x,
y0
— )
< 0 , F(x,
y0
+ )
> 0 . Тогда
для
U(
x0)
функция
F(,y)
имеет на [y0
—
, y0
+ ]
единственный
ноль
,F(
,
) = 0 (промежуточное
значение строго монотонной функции).
Функция f
:
,
действующая наU(
x0)
является
искомой. В силу единственности нуля
f(x0)
= y0.
Построенная
функция является функцией неявно
заданной уравнение F(x,y)=0
в окрестности
U(
x0).
Докажем
дифференцируемость этой функции. В
окрестности точки M0
справедливо
равенство
F=.
Если в этом равенстве
положить y=f=f(x)
– f(x0),
где x=
то F
= 0 и все xk=0
кроме одного
при k=j
Откуда

Переходя к пределу
при M
M0
получим
требуемое равенство.
Замечание. При
выполнении условий теоремы построенная
функция будет принадлежать классу C1
в некоторой окрестности точки x0
.
Действительно,
условия теоремы будут выполнены, если
в качестве точки (x0,y0)
взять любую
точку (x,
f(x)),
x.
Для таких
точек будут выполнено равенство

где правая часть
является непрерывной функцией.
3 Касательная к поверхности, заданной неявно
Рассмотрим
поверхность заданную неявно уравнением
F(x, y, z) = 0.
Будем предполагать
выполненными условия теоремы существования
неявной функции z
= f(x,y)
в окрестности
точки P0=(x0,
y0)
(,M0=(x0,
y0,
z0),
z0=f(x0,
y0)).
Уравнение
касательной плоскости к поверхности в
точке M0,
будет иметь
вид
. (1)
С другой стороны,
для неявно заданной функции


Подставляя эти
выражения в (1)
получим
или
. (2)
Отсюда следует
следующее правило для построения
касательной плоскости к поверхности,
заданной неявно.
Нужно взять
дифференциал левой и правой части
уравнения (1)
dF=0
и в полученном
выражении частные производные вычислить
в интересующей нас точке поверхности
M0
, а дифференциалы
dx,
dy,
dz
нужно заменить
на (x—x0),
(y—y0),
(z—z0)
соответственно.
Замечание. Формула
(2) будет справедлива и в случаях, когда
уравнение (1) можно разрешить относительно
y
(в случае выполнения условия
) или относительно x
(при выполнении условия
).
Цели работы:
- повторить и систематизировать нахождение
области определения функции, закрепить это
понятие и наглядно представить в координатной
плоскости и в пространстве; - рассмотреть аналитические и геометрические
методы не изолированно друг от друга, а в тесной
взаимосвязи. Это позволит облегчить переход от
стандартных решений конкретных математических
задач к нестандартным; - воспитание интереса к математике и мультимедиа,
активности, мобильности; восприятие компьютера,
как инструмента обучения; - использование компьютера для нахождения
области определения и построения графиков с
помощью графического редактора 3D Grapher 1.2, Copyright ©
2000-2002 RomanLab Software и формирование информационной
компетентности учащихся.
Определение функции двух переменных
Если каждой паре ( x;y) значений двух
независимых друг от друга переменных величин х и
у из некоторого множества D соответствует
единственное значение величины, то говорят,
что z есть функция двух независимых
переменных x и y, определенная на
множестве D.
Обозначается: z=f(x;y) или z=z(x;y).
Например, S=ab, S=S(a;b)- функции двух переменных; V=abc,
V=V(a,b.c) – функция трех переменных;
A= –
функция трех переменных.
Способы задания функций нескольких
переменных
Чтобы задать функцию двух (трех) переменных,
нужно указать способ, с помощью которого для
каждой пары (тройки) значений аргументов можно
найти соответствующее значение функции.
Наиболее часто функция задается аналитически — это
явное задание функции или неявное задание
Например, — это явно заданная функция двух
переменных; уравнение задает неявно две функции двух
переменных.
Область определения функции
Непрерывное множество пар значений независимых
переменных , при которых функция
определена,
называется областью определения функции.
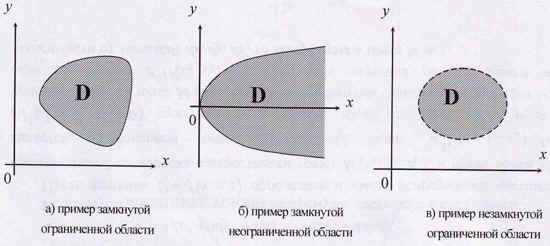
Область определения называется замкнутой
областью, если она включает в себя свою границу;
открытой областью, если она не включает в себя
свою границу; ограниченной областью, если может
быть помещена в круг конечного радиуса.
Геометрически изобразить область определения
функции можно только для функций:
Геометрическое изображение самой функции
возможно только для функции двух переменных.
Графиком функции двух переменных является
поверхность, проектирующаяся на плоскость в область
D, которая является областью определения
функции.
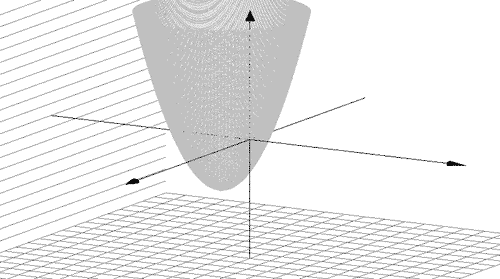
На рис. изображена поверхность графика функции и ее область определения.
В курсе учебного материала 9-го класса мы
рассматриваем следующие задания на нахождение и
построение области определения функции.
ПРИМЕРЫ
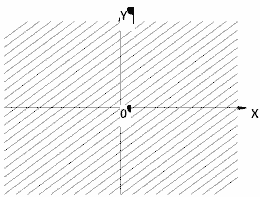
Найти область определения функции
Решение. Областью определения данной функции
является вся плоскость, т.к. нет ограничений на
переменные x и y.
2. Найти область определения функции .
Решение. Данная функция определена, когда xy
> 0, т.е. в тех точках координатной плоскости, в
которых знаки координат x и y —
одинаковы. Это будут точки, лежащие в I и III
координатных четвертях, т.е. множество точек,
удовлетворяющих условиям:
и
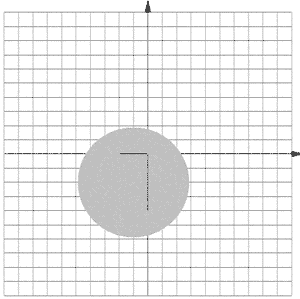
3. Найти область определения функции .
Решение. Данная функция определена при
условии, когда
т.е. .
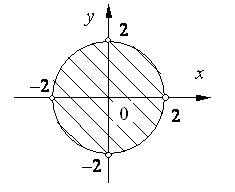
Это множество точек, лежащих внутри круга с
центром в начале координат, радиус которого
равен 2.
Изобразить на координатной плоскости Оху
область определения функции .
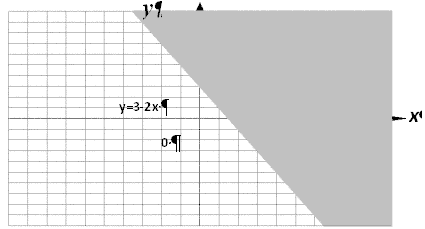
Решение. Подкоренное выражение должно быть
неотрицательно, т.е. следовательно,
. Геометрическим
решением неравенства служит полуплоскость,
расположенная выше прямой и сама прямая.
5. Найти область определения функции и
изобразить её графически.
.
Решение. Областью определения функции является
множество точек плоскости, координаты которых
удовлетворяют системе неравенств:
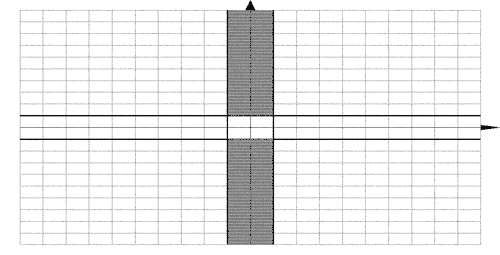
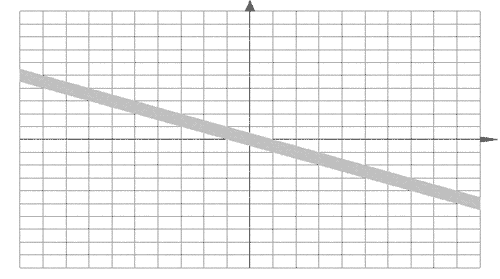
6. Изобразить на координатной плоскости
Оху область определения функции
Решение. Эта функция определена, когда
подкоренное выражение неотрицательно, т.е. Данным
соотношениям удовлетворяют координаты всех
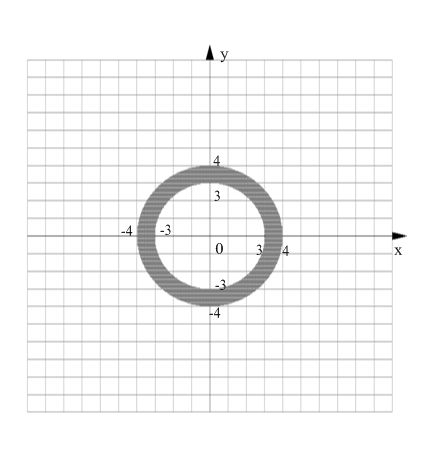
точек, находящихся внутри кольца, образованного
двумя окружностями с центрами в начале координат
и радиусами R=3, R=4.
7. Изобразить на координатной плоскости Оху
область определения функции
.
Решение. Учащиеся не могут найти область
определения данной функции аналитически, но с
помощью графического редактора 3D Grapher 1.2 это
выполняется легко.
В Приложении приведено ещё несколько примеров,
с решениями, для учащихся девятых классов.
Для учащихся 10-11 классов мы предлагаем систему
упражнений по нахождению и построению области
определения функции двух переменных. При этом
отрабатываются свойства логарифмических,
тригонометрических и обратных
тригонометрических функций. Данные упражнения
можно использовать при изучении нового
материала, при повторении, при решении уравнений
и неравенств.
Найти и изобразить на плоскости область
определения функции
Решение. Область определения функции есть
пересечение областей определения слагаемых
функции. Для первой функции подкоренное
выражение должно быть неотрицательным, т.е. Если
значение логарифмической функции
неотрицательно, то выражение, стоящее под знаком
логарифма, должно быть больше или равно единице,
т.е.
отсюда .
Это неравенство задает нам множество точек
плоскости, лежащих вне окружности с центром в
начале координат, радиуса 2, включая и точки
данной окружности. Вторая функция определена при
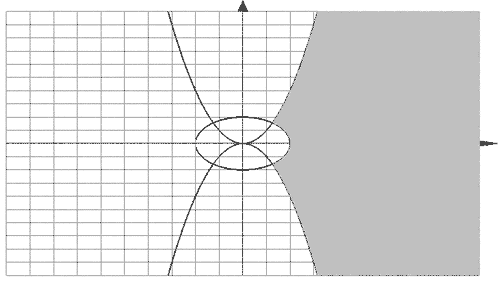
Следовательно, Имеем две параболы с вершиной в начале
координат . Поэтому полученное неравенство
задает нам часть плоскости, заключенную между
этими параболами, включая границы без начала
координат. Третья функция определена при
Областью определения данной функции является
общая часть найденных областей определения
слагаемых.
Покажите на координатной плоскости xOy область
определения функции
.
Решение. Ограничения для функции имеют вид:
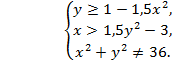
3. Изобразить область определения функции
Решение. Эта функция определена при , т.е.
Областью определения является часть плоскости,
расположенная между двумя прямыми.
4. Найти область определения функции .
Решение. Областью определения функции является
решение неравенства. Поэтому нужно решить
неравенство
Решая данное неравенство, получим Это область,
заключенная между двумя параболами и
.
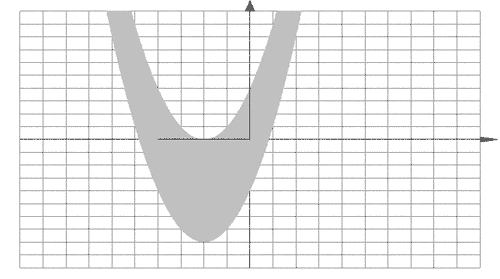
5. Построить область определения функции
Решение. Область определения данной функции
определяется системой неравенств:
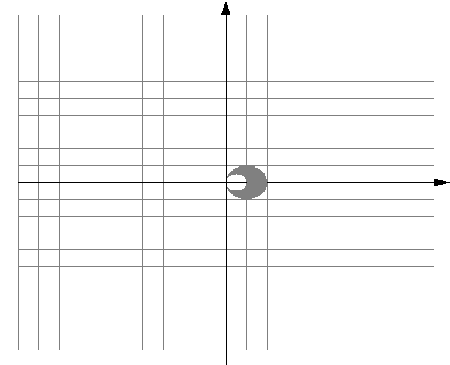
Первое неравенство определяет круг с центром в
точке (-2;0) и радиусом равным 2 за исключением его
границы:
Второе неравенство определяет I и III
координатные четверти, за исключением осей.
В Приложении приведено ещё несколько примеров,
с решениями, для учащихся десятых и одиннадцатых
классов.
Рассмотрим задание С5, используя функцию двух
переменных.
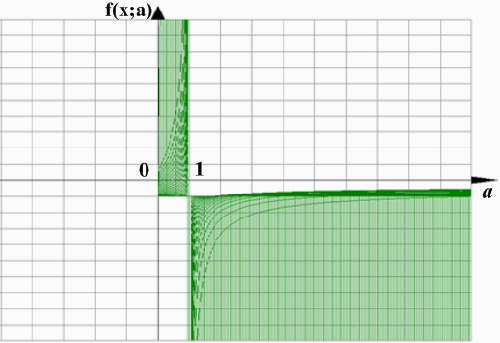
Найдите все значения параметра а, при
которых система , имеет ровно два решения.
Решение. Из второго уравнения находим y =. Первое
уравнение принимает вид .
Пусть .
В этом случае уравнение имеет единственное
решение .
Запишем второе уравнение в виде
= 0. Его дискриминант равен
4
, и он
положителен, поскольку . Уравнение имеет два различных
корня
и Значит,
в этом случае система имеет ровно два решения и
.
Пусть теперь 1. В этом случае уравнение
если и имеет корни,
то только больше единицы Но тогда дискриминант
уравнения
= 0
отрицателен. Решений нет.
Ответ: .
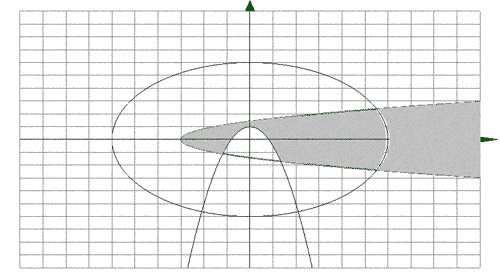
С помощью графического редактора задаем
функцию двух переменных ,
Находим значения а, при которых
функция обращается в ноль.
На рисунке видно, что решением является
интервал от 0 до 1.
При подготовке учащихся к итоговой аттестации
мы сталкиваемся с тем, что задания уровня С5
решаются тяжело и не сразу. А ведь это функция
двух переменных! Оперирование геометрическими
образами упрощает решение задач с параметрами, а
в некоторых случаях геометрический подход часто
является единственно возможным методом решения.
В сборнике ЕГЭ-2011 предложено задание.
Найдите все значения а, такие, что для любого х
выполняется неравенство.
Решение. Рассмотрим функцию
Если
то
убывает.
Если
то
возрастает.
Значит, наименьшее значение функции равно или
, или
. Поэтому
решение задачи получаем из решения системы
Решений нет.
Ответ: .
C помощью графического редактора мы построили
график функции и определили значение параметра а
при .
График функции в системе координат выглядит
следующим образом.
Приложение 1
Приложение 2
Приложение 3
Список источников и литературы.
- Математика (математический анализ):
учебно-методическое пособие для студентов
нематематических специальностей / О.Ю. Ватюкова,
Е.Е.Зайцева, Ю.В.Зайцева и др.; ВолГУ.-4-е изд.,
Волгоград: Волгоградское научное издательство,
2009. – 238с. - Дифференциальное исчисление функций
нескольких переменных: типовой расчет по высшей
математике / Сост.: А. В. Анкилов, Н. Я. Горячева, Т.
Б. Распутько.- Ульяновск: УлГТУ, 2004.-32 с. - ЕГЭ 2011. Математика. Типовые тестовые задания /
И.Р. Высоцкий, Д.Д. Гущин, П.И.Захаров, В.С. Панферов,
и др.; под ред. А.Л. Семенова, И.В. Ященко. -М.:
Издательство “Экзамен”, 2011.-63с. - Самое полное издание типовых вариантов
реальных заданий ЕГЭ: 2010: Математика/авт.- сост.
И.Р.Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред.
А.Л. Семенова, И.В. Ященко. -М.: АСТ: Астрель, 2010.-93с. - Мордкович А.Г. Алгебра . 9 класс. В 2 ч. Ч.1. Учебник
для учащихся общеобразовательных учреждений /
А.Г.Мордкович, П.В.Семенов .—11-е изд., стер. -М.:
Мнемозина, 2009.-224 с. - Смирнова И.М. Геометрия. 10-11 кл.: Учеб. для
общеобразоват. учреждений (гуманитарный
профиль).- М.: Мнемозина,2004. -223с.