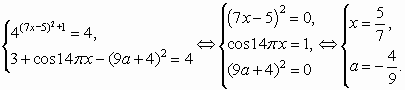Область определения в уравнениях и неравенствах
Среди множества уравнений и неравенств выделить те , которые решаются с помощью нахождения ОДЗ
Скачать:
| Вложение | Размер |
|---|---|
| метод решения уравнений и неравенств | 67.88 КБ |
Предварительный просмотр:
§1.Нахождение области определения функции………………..…………………………….………5
§2. Область определения в уравнениях.………………………………………….…………………. 6
Тема: «Область определения в уравнениях и неравенствах».
Максакова Д.В., Забайкальский край, п.Карымское, МОУ «СОШ №5
п. Карымское с пришкольным интернатом»,11 класс.
Тема моей исследовательской работы «Область определения в уравнениях и неравенствах». На уроках алгебры область определения рассматривается при решении стандартных задач, но при конкурсном отборе и при подготовке к конкурсным экзаменам в ВУЗы, а также на олимпиадах встречаются задания, связанные с ограничением условий, которые требуют нестандартных приемов и подходов к решению. Кроме того, в части C тестов ЕГЭ часто встречаются задания, построенные на исследовании ОДЗ. Поэтому в настоящее время эта тема является актуальной.
Цель моей работы : найти среди множества уравнений и неравенств те, которые сводятся к изучению области определения, установить связь между уравнениями, неравенствами и системами уравнений и неравенств.
1) Просмотреть и изучить задания, связанные с ОДЗ.
2) Разбить их на группы, систематизировать знания о решении систем уравнений и неравенств.
При выполнении работы мне пришлось сравнивать различные методы, переходить от общих методов к частным, и наоборот. Также я обобщила информацию, собранную из различных источников. В связи с этим можно выделить следующие методы исследовательской деятельности: пошаговые, репродуктивные, логическое исследование.
В результате мной получены следующие результаты и выводы :
1) Во многих уравнениях и неравенствах область определения играет определяющую роль.
2) Чтобы найти ОДЗ, необходимо знать множество ограничений и свойств.
3) Нахождение ОДЗ не всегда необходимо.
Тема: «Область определения в уравнениях и неравенствах».
Максакова Д.В., Забайкальский край, п.Карымское, МОУ «СОШ №5 п. Карымское
с пришкольным интернатом»,11 класс.
Объектная область , в которой я проводила исследование, — алгебра.
Объект моего исследования — исследование ограничений в уравнениях и неравенствах.
Среди всех уравнений и неравенств я выбрала те, которые требуют изучение ОДЗ – предмет моего исследования .
Гипотеза : если правильно исследовать ОДЗ в уравнениях и неравенствах, то их решение значительно упростится.
Значит, если громоздкие выражения с помощью ограничений можно заменить несложными системами уравнений и неравенств, то можно сказать, что выбранная мною тема нужная и важная.
Свою работу я разбила на три параграфа. В первом параграфе я обобщила различные условия, при которых функция имеет ограничения, проиллюстрировала примерами процесс нахождения области определения функции.
Второй параграф был посвящен уравнениям, при решении которых ОДЗ играет ключевую роль. В этом же параграфе я рассмотрела ошибки при решении логарифмических уравнений, связанные с изменением ОДЗ, и случаи, когда задача определения ОДЗ оказывается сложной и абсолютно ненужной.
Свойства неравенств, которыми обусловлена их область определения, и промежутки возрастания и убывания функции были изучены в третьем параграфе.
Тема: «Область определения в уравнениях и неравенствах».
Максакова Д.В., Забайкальский край, п.Карымское, МОУ «СОШ №5п. Карымское
с пришкольным интернатом»,11 класс.
§1.Нахождение области определения функции
Процесс нахождения области определения функции состоит из двух этапов: составление системы ограничений и решение этой системы.
Чтобы составить систему ограничений нужно знать, чем вызваны ограничения:
При этом необходимо помнить, что выполнение преобразований заданной функции порой неправомерно. Разберем это на примере 1.
Найдите ОДЗ функций и
Решением является промежуток
При решении системы, составленной из ограничений, последовательно находят пересечения различных множеств, приближаясь к ответу. Пронаблюдаем это на примере.
Составим систему ограничений:
Рассмотрим еще несколько примеров.
§2.Область определения в уравнениях
Областью определения уравнения или областью допустимых значений (ОДЗ) уравнения называют множество тех значений неизвестного, при котором имеют смысл его левая и правая часть.
При решении уравнений, содержащих тригонометрические и логарифмические функции, ОДЗ играет ключевую роль. Покажем это на примерах.
На первый взгляд, в данном уравнении нет ограничений , но
при любых , значит 0 , тогда , то есть , ,
Найдите все значения , где , при котором уравнение имеет хотя бы одно решение, удовлетворяющее условию
Учитывая ограниченность функции , имеем:
Так как функция убывающая, получим
Тогда левая часть тоже имеет ограничения
Равенство , выполняется при ,
Учтем условие : , значит .
То есть , , так как , то ,
Часто при решении логарифмических уравнений используют прием логарифмирования обеих частей.
Найдем косинус от обеих частей уравнения:
Введем новую переменную: , , тогда
корней нет, значит .
Корень включает решение первого уравнения, то есть
Поскольку , , то левая часть равна 3, если
, только для четных , значит
Если , то функция убывает с ростом , следовательно, . Сложив почленно эти неравенства, будем иметь:
Следовательно, левая часть данного уравнения равна 1 тогда и только тогда, когда
То есть может принимать значения, а может принимать значения -1, 0. Тогда
то есть (3 и 4 четверть).
или – решения нет, так как , тогда , но учитывая то, что ,
Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y = x + x — 2 или y = 5 · x 2 + 1 · x 3 , y = x x — 5 или y = x — 1 5 — 3 . Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y = f ( x ) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть ( 0 , + ∞ ) или такой [ − 3 , 1 ) ∪ [ 5 , 7 ) . Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y = x + 2 · x x 4 — 1 ;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y = x + 1 или y = 2 3 · x + 3 x ;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y = 5 · ( x + 1 ) — 3 , y = — 1 + x 1 1 3 , y = ( x 3 — x + 1 ) 2 , которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y = ln x 2 + x 4 или y = 1 + log x — 1 ( x + 1 ) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y = x 3 + t g 2 · x + 5 или y = c t g ( 3 · x 3 — 1 ) , так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y = a r c sin ( x + 2 ) + 2 · x 2 , y = a r c cos x — 1 + x , область определения которых определяется ни интервале от — 1 до 1 .
При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y = x 4 + 2 · x 2 — x + 1 2 + 2 2 3 · x . Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y = 2 · x + 1 . Для вычисления ее значения можем определить x . Из выражения 2 · x + 1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y = 3 x — 1 , а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3 x — 1 знаменатель равняется нулю при х = 1 , поэтому искомая область определения данной функции примет вид ( − ∞ , 1 ) ∪ ( 1 , + ∞ ) и считается числовым множеством.
На рассмотрении примера y = x 2 — 5 · x + 6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x 2 − 5 · x + 6 ≥ 0 . После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как ( − ∞ , 2 ] ∪ [ 3 , + ∞ ) .
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция f f считается суммой n функций f 1 , f 2 , … , f n , иначе говоря, эта функция задается при помощи формулы y = f 1 ( x ) + f 2 ( x ) + … + f n ( x ) , тогда ее область определения считается пересечением областей определения функций f 1 , f 2 , … , f n . Данное утверждение можно записать как:
D ( f ) = D ( f 1 ) D ( f 2 ) . . . D ( f n )
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y = x 7 + x + 5 + t g x .
Заданная функция представляется как сумма четырех: степенной с показателем 7 ,степенной с показателем 1 , постоянной, функции тангенса.
По таблице определения видим, что D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = ( − ∞ , + ∞ ) , D ( f 3 ) = ( − ∞ , + ∞ ) , причем область определения тангенса включает в себя все действительные числа, кроме π 2 + π · k , k ∈ Z .
Областью определения заданной функции f является пересечение областей определения f 1 , f 2 , f 3 и f 4 . То есть для функции существует такое количество действительных чисел, куда не входит π 2 + π · k , k ∈ Z .
Ответ: все действительные числа кроме π 2 + π · k , k ∈ Z .
Для нахождения области определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f 1 , f 2 , f 3 и f n , тогда существует такая функция f , которую можно задать при помощи формулы y = f 1 ( x ) · f 2 ( x ) · … · f n ( x ) , тогда ее область определения считается областью определения для всех функций.
Запишется D ( f ) = D ( f 1 ) D ( f 2 ) . . . D ( f n )
Найти область определения функции y = 3 · a r c t g x · ln x .
Правая часть формулы рассматривается как f 1 ( x ) · f 2 ( x ) · f 3 ( x ) , где за f 1 является постоянной функцией, f 2 является арктангенсом, f 3 – логарифмической функцией с основанием e . По условию имеем, что D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = ( − ∞ , + ∞ ) и D ( f 3 ) = ( 0 , + ∞ ) . Мы получаем, что
D ( f ) = D ( f 1 ) D ( f 2 ) D ( f n ) = ( — ∞ , + ∞ ) ( — ∞ , + ∞ ) D ( 0 , + ∞ ) = ( 0 , + ∞ )
Ответ: область определения y = 3 · a r c t g x · ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y = C · f ( x ) , где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y = C · f ( x ) – произведение постоянной функции и f . Область определения – это все действительные числа области определения D ( f ) . Отсюда видим, что область определения функции y = C · f ( x ) является — ∞ , + ∞ D ( f ) = D ( f ) .
Получили, что область определения y = f ( x ) и y = C · f ( x ) , где C является некоторое действительное число, совпадают. Это видно на примере определения корня y = x считается [ 0 , + ∞ ) , потому как область определения функции y = — 5 · x — [ 0 , + ∞ ) .
Области определения y = f ( x ) и y = − f ( x ) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y = log 3 x − 3 · 2 x .
Необходимо рассмотреть как разность двух функций f 1 и f 2 .
f 1 ( x ) = log 3 x и f 2 ( x ) = 3 · 2 x . Тогда получим, что D ( f ) = D ( f 1 ) D ( f 2 ) .
Область определения записывается как D ( f 1 ) = ( 0 , + ∞ ) . Приступим к области определения f 2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D ( f 2 ) = ( − ∞ , + ∞ ) .
Для нахождения области определения функции y = log 3 x − 3 · 2 x получим, что
D ( f ) = D ( f 1 ) D ( f 2 ) = ( 0 , + ∞ ) — ∞ , + ∞
Необходимо озвучить утверждение о том, что областью определения y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 является множество действительных чисел.
Рассмотрим y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 , где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы ( n + 1 ) -ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R .
Найти область определения f 1 ( x ) = x 5 + 7 x 3 — 2 x 2 + 1 2 .
Примем обозначение f за разность двух функций, тогда получим, что f 1 ( x ) = x 5 + 7 x 3 — 2 x 2 + 1 2 и f 2 ( x ) = 3 · x — ln 5 . Выше было показано, что D ( f 1 ) = R . Область определения для f 2 является совпадающей со степенной при показателе – ln 5 , иначе говоря, что D ( f 2 ) = ( 0 , + ∞ ) .
Получаем, что D ( f ) = D ( f 1 ) D ( f 2 ) = — ∞ , + ∞ ( 0 , + ∞ ) = ( 0 , + ∞ ) .
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y = f 1 ( f 2 ( x ) ) . Известно, что D ( f ) является множеством всех x из определения функции f 2 , где область определения f 2 ( x ) принадлежит области определения f 1 .
Видно, что область определения сложной функции вида y = f 1 ( f 2 ( x ) ) находится на пересечении двух множеств таких, где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . В стандартном обозначении это примет вид
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 )
Рассмотрим решение нескольких примеров.
Найти область определения y = ln x 2 .
Данную функцию представляем в виде y = f 1 ( f 2 ( x ) ) , где имеем, что f 1 является логарифмом с основанием e , а f 2 – степенная функция с показателем 2 .
Для решения необходимо использовать известные области определения D ( f 1 ) = ( 0 , + ∞ ) и D ( f 2 ) = ( − ∞ , + ∞ ) .
Тогда получим систему неравенств вида
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 ) ⇔ x ∈ — ∞ , + ∞ x 2 ∈ ( 0 , + ∞ ) ⇔ ⇔ x ∈ ( — ∞ , + ∞ ) x 2 > 0 ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ ⇔ x ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ )
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Найти область определения функции y = ( a r c sin x ) — 1 2 .
Так как дана сложная функция, необходимо рассматривать ее как y = f 1 ( f 2 ( x ) ) , где f 1 является степенной функцией с показателем — 1 2 , а f 2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D ( f 1 ) = ( 0 , + ∞ ) и D ( f 2 ) = [ − 1 , 1 ] . Теперь найдем все множества значений x , где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . Получаем систему неравенств вида
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 ) ⇔ x ∈ — 1 , 1 a r c sin x ∈ ( 0 , + ∞ ) ⇔ ⇔ x ∈ — 1 , 1 a r c sin x > 0
Для решения a r c sin x > 0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [ − 1 , 1 ] , причем обращается в ноль при х = 0 , значит, что a r c sin x > 0 из определения x принадлежит промежутку ( 0 , 1 ] .
Преобразуем систему вида
x ∈ — 1 , 1 a r c sin x > 0 ⇔ x ∈ — 1 , 1 x ∈ ( 0 , 1 ] ⇔ x ∈ ( 0 , 1 ]
Область определения искомой функции имеет интервал равный ( 0 , 1 ] .
Ответ: ( 0 , 1 ] .
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y = f 1 ( f 2 ( … f n ( x ) ) ) ) . Область определения такой функции ищется из x ∈ D ( f n ) f n ( x ) ∈ D ( f n — 1 ) f n — 1 ( f n ( x ) ) ∈ D ( f n — 2 ) . . . f 2 ( f 3 ( . . . ( f n ( x ) ) ) ∈ D ( f 1 ) .
Найти область определения y = sin ( l g x 4 ) .
Заданная функция может быть расписана, как y = f 1 ( f 2 ( f 3 ( x ) ) ) , где имеем f 1 – функция синуса, f 2 – функция с корнем 4 степени, f 3 – логарифмическая функция.
Имеем, что по условию D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = [ 0 , + ∞ ) , D ( f 3 ) = ( 0 , + ∞ ) . Тогда областью определения функции – это пересечение множеств таких значений, где x ∈ D ( f 3 ) , f 3 ( x ) ∈ D ( f 2 ) , f 2 ( f 3 ( x ) ) ∈ D ( f 1 ) . Получаем, что
x ∈ D ( f 3 ) f 3 ( x ) ∈ D ( f 2 ) f 2 ( f 3 ( x ) ) ∈ D ( f 1 ) ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x 4 ∈ — ∞ , + ∞
Условие lg x 4 ∈ — ∞ , + ∞ аналогично условию l g x ∈ [ 0 , + ∞ ) , значит
x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x 4 ∈ — ∞ , + ∞ ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) ⇔ ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) ⇔ x ∈ ( 0 , + ∞ ) lg x ≥ 0 ⇔ ⇔ x ∈ ( 0 , + ∞ ) lg x ≥ lg 1 ⇔ x ∈ ( 0 , + ∞ ) x ≥ 1 ⇔ ⇔ x ∈ [ 1 , + ∞ )
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f 1 ( x ) f 2 ( x ) . Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f 2 ( х ) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Запишем функцию y = f 1 ( x ) f 2 ( x ) в виде y = f 1 ( x ) · ( f 2 ( x ) ) — 1 . Тогда получим произведение функций вида y = f 1 ( x ) с y = ( f 2 ( x ) ) — 1 . Областью определения функции y = f 1 ( x ) является множество D ( f 1 ) , а для сложной y = ( f 2 ( x ) ) — 1 определим из системы вида x ∈ D ( f 2 ) f 2 ( x ) ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Значит, x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Найти область определения y = t g ( 2 · x + 1 ) x 2 — x — 6 .
Заданная функция дробная, поэтому f 1 – сложная функция, где y = t g ( 2 · x + 1 ) и f 2 – целая рациональная функция, где y = x 2 − x − 6 , а область определения считается множеством всех чисел. Можно записать это в виде
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0
Представление сложной функции y = f 3 ( f 4 ( x ) ) , где f 3 –это функция тангенс, где в область определения включены все числа, кроме π 2 + π · k , k ∈ Z , а f 4 – это целая рациональная функция y = 2 · x + 1 с областью определения D ( f 4 ) = ( − ∞ , + ∞ ) . После чего приступаем к нахождению области определения f 1 :
x ∈ D ( f 4 ) 2 · x + 1 ∈ D ( f 3 ) ⇔ x ∈ ( — ∞ , + ∞ ) 2 x + 1 ≠ π 2 + π · k , k ∈ Z ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z
Еще необходимо рассмотреть нижнюю область определения y = t g ( 2 · x + 1 ) x 2 — x — 6 . Тогда получаем, что
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z x ∈ — ∞ , + ∞ x 2 — x — 6 ≠ 0 ⇔ ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z x ≠ — 2 x ≠ 3
Ответ: множество действительных чисел, кроме — 2 , 3 и π 4 — 1 2 + π 2 · k , k ∈ Z .
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1 . Отсюда видно, что функция y = log f 2 ( x ) f 1 ( x ) имеет область определения, которая выглядит так:
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y = log a f 1 ( x ) log a f 2 ( x ) , a > 0 , a ≠ 1 . После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y = log a f 1 ( x ) и y = log a f 2 ( x ) можно определить из получившейся системы вида x ∈ D ( f 1 ) f 1 ( x ) > 0 и x ∈ D ( f 2 ) f 2 ( x ) > 0 . Иначе эту область можно записать в виде y = log a f 1 ( x ) log a f 2 ( x ) , a > 0 , a ≠ 1 , что означает нахождение y = log f 2 ( x ) f 1 ( x ) из самой системы вида
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 log a f 2 ( x ) ≠ 0 = x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
Обозначить область определения функции y = log 2 · x ( x 2 — 6 x + 5 ) .
Следует принять обозначения f 1 ( x ) = x 2 − 6 · x + 5 и f 2 ( x ) = 2 · x , отсюда D ( f 1 ) = ( − ∞ , + ∞ ) и D ( f 2 ) = ( − ∞ , + ∞ ) . Необходимо приступить к поиску множества x , где выполняется условие x ∈ D ( f 1 ) , f 1 ( x ) > 0 , x ∈ D ( f 2 ) , f 2 ( x ) > 0 , f 2 ( x ) ≠ 1 . Тогда получаем систему вида
x ∈ ( — ∞ , + ∞ ) x 2 — 6 x + 5 > 0 x ∈ ( — ∞ , + ∞ ) 2 · x > 0 2 · x ≠ 1 ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ ( — ∞ , 1 ) ∪ ( 5 , + ∞ ) x ∈ ( — ∞ , + ∞ ) x > 0 x ≠ 1 2 ⇔ ⇔ x ∈ 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ )
Отсюда видим, что искомой областью функции y = log 2 · x ( x 2 — 6 x + 5 ) считается множнство, удовлетворяющее условию 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ ) .
Ответ: 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ ) .
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y = ( f 1 ( x ) ) f 2 ( x ) . Ее область определения включает в себя такие значения x , которые удовлетворяют системе x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 1 ( x ) > 0 .
Эта область позволяет переходить от показательно-степенной к сложной вида y = a log a ( f 1 ( x ) ) f 2 ( x ) = a f 2 ( x ) · log a f 1 ( x ) , где где a > 0 , a ≠ 1 .
Найти область определения показательно-степенной функции y = ( x 2 — 1 ) x 3 — 9 · x .
Примем за обозначение f 1 ( x ) = x 2 − 1 и f 2 ( x ) = x 3 — 9 · x .
Функция f 1 определена на множестве действительных чисел, тогда получаем область определения вида D ( f 1 ) = ( − ∞ , + ∞ ) . Функция f 2 является сложной, поэтому ее представление примет вид y = f 3 ( f 4 ( x ) ) , а f 3 – квадратным корнем с областью определения D ( f 3 ) = [ 0 , + ∞ ) , а функция f 4 – целой рациональной, D ( f 4 ) = ( − ∞ , + ∞ ) . Получаем систему вида
x ∈ D ( f 4 ) f 4 ( x ) ∈ D ( f 3 ) ⇔ x ∈ ( — ∞ , + ∞ ) x 3 — 9 · x ≥ 0 ⇔ ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) ⇔ x ∈ — 3 , 0 ∪ [ 3 , + ∞ )
Значит, область определения для функции f 2 имеет вид D ( f 2 ) = [ − 3 , 0 ] ∪ [ 3 , + ∞ ) . После чего необходимо найти область определения показательно-степенной функции по условию x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 1 ( x ) > 0 .
Получаем систему вида x ∈ — ∞ , + ∞ x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) x 2 — 1 > 0 ⇔ x ∈ — ∞ , + ∞ x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) x ∈ ( — ∞ , — 1 ) ∪ ( 1 , + ∞ ) ⇔ ⇔ x ∈ — 3 , — 1 ∪ [ 3 , + ∞ )
Ответ: [ − 3 , − 1 ) ∪ [ 3 , + ∞ )
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
Сумма, разность, произведение функций
f 1 , f 2 , . . . , f n
D ( f 1 ) , D ( f 2 ) , . . . , D ( f n )
y = f 1 ( f 2 ( f 3 ( . . . f n ( x ) ) ) )
Множество всех x , одновременно удовлетворяющих условиям
x ∈ D ( f n ) , f n ( x ) ∈ D ( f n — 1 ) , f n — 1 ( f n ( x ) ) ∈ D ( f n — 2 ) , . . . , f 2 ( f 3 ( . . . f n ( x ) ) ) ∈ D ( f 1 )
x ∈ D ( f 2 ) , f 2 ( x ) ∈ D ( f 1 )
Расположим функции и их области определения.
| Функция | Ее область определения |
Прямая пропорциональность y = k · x
Обратная пропорциональность y = k x
Дробная y = f 1 ( x ) f 2 ( x )
В частности, если f 1 ( x ) , f 2 ( x ) — многочлены
Множество всех x , которые одновременно удовлетворяют условиям
x ∈ D ( f 1 ) , x ∈ D ( f 2 ) , f 2 ( x ) ≠ 0
y = log f 2 ( x ) f 1 ( x )
В частности, y = log a f 1 ( x )
В частности, y = log f 2 ( x ) a
x ∈ D ( f 1 ) , f 1 ( x ) > 0 , x ∈ D ( f 2 ) , f 2 ( x ) > 0 , f 2 ( x ) ≠ 1
x ∈ D ( f 1 ) , f 1 ( x ) > 0
x ∈ D ( f 2 ) , f 2 > 0 , f 2 ( x ) ≠ 1
| Функция | Ее область определения |
| R | |
| Линейная y = k · x + b | R |
| — ∞ , 0 ∪ 0 , + ∞ | |
| Квадратичная y = a · x 2 + b · x + c | R |
| y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 | R |
| Целая рациональная | R |
| y = C · f ( x ) , где C — число | D ( f ) |
| y = f ( x ) n , где n — четное | x ∈ D ( f 1 ) , f ( x ) ≥ 0 |
| Показательно-степенная y = ( f 1 ( x ) ) f 2 ( x ) | x ∈ D ( f 1 ) , x ∈ D ( f 2 ) , f 1 ( x ) > 0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y = x 2 — 4 x — 2 и y = x + 2 являются разными функциями, так как первая определяется на ( − ∞ , 2 ) ∪ ( 2 , + ∞ ) , а вторая из множества действительных чисел. Из преобразования y = x 2 — 4 x — 2 = x — 2 x + 2 x — 2 = x + 2 видно, что функция имеет смысл при x ≠ 2 .
Область допустимых значений: теория и практика
Конкурс исследовательских и проектных работ учащихся
«ИНТЕЛЛЕКТУАЛЬНОЕ БУДУЩЕЕ МОРДОВИИ»
ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ:
ТЕОРИЯ И ПРАКТИКА
Автор: Малышева Оксана
2. Исторический очерк 4
3. «Место» ОДЗ при решении уравнений и неравенств 5-6
4. Особенности и опасность ОДЗ 7
5. ОДЗ – есть решение 8-9
6. Нахождение ОДЗ – лишняя работа.
Равносильность переходов 10-13
7. ОДЗ в ЕГЭ 14-15
8. Заключение 16
9. Литература 17
Уравнения и неравенства, в которых нужно находить область допустимых значений, не нашли места в курсе алгебры систематического изложения, возможно поэтому мои сверстники часто делают ошибки при решении таких примеров, уделив много времени их решению, забыв при этом об области допустимых значений. Это и определило проблему данной работы.
В настоящей работе предполагается исследовать явление существования области допустимых значений при решении уравнений и неравенств разных типов; проанализировать данную ситуацию, сделать логически корректные выводы в примерах, где нужно учитывать область допустимых значений.
-
Опираясь на имеющийся опыт и теоретическую базу, собрать основные сведения об области допустимых значений и её использовании в школьной практике; Проанализировать решения разнообразных типов уравнений и неравенств (дробно-рациональных, иррациональных, логарифмических, содержащих обратные тригонометрические функции); Проверить ранее полученные при решении различных уравнений и неравенств результаты, убедиться в надёжности способов и методов их решения; Определить «место» области допустимых значений при решении уравнений и неравенств; Применить полученные материалы исследования в ситуации, которая отличается от стандартной, и использовать их при подготовке к ЕГЭ.
При решении этих задач использованы следующие методы исследования: анализ, статистический анализ, дедукция, классификация, прогнозирование.
Исследование начато с повторения известных функций, изучаемых в школьной программе. Область определения многих из них имеет ограничения.
Область допустимых значений встречается при решении: дробно-рациональных уравнений и неравенств; иррациональных уравнений и неравенств; логарифмических уравнений и неравенств; уравнений и неравенств, содержащих обратные тригонометрические функции.
Прорешав множество примеров из различных источников (пособий по ЕГЭ, учебников, справочников), выделили решение примеров по следующим принципам:
· можно решить пример и учесть ОДЗ (самый распространённый способ)
· можно решить пример, не учитывая ОДЗ
· можно только учитывая ОДЗ прийти к правильному решению.
Изучен анализ результатов ЕГЭ за прошедшие годы. Много ошибок было допущено в примерах, в которых нужно учитывать ОДЗ. Практическое значение работы заключается в том, что ее содержание, оценки и выводы могут быть использованы в преподавании математики в школе, при подготовке к итоговой аттестации школьников 9 и 11 классов.
2. Исторический очерк
Как и остальные понятия математики, понятие функции сложилось не сразу, а прошло долгий путь развития. В работе П. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. 1679) говорится: «Всякий раз, когда в заключительном уравнении имеются две неизвестные величины, налицо имеется место». По существу здесь идёт речь о функциональной зависимости и её графическом изображении («место» у Ферма означает линию). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У И. Барроу («Лекции по геометрии», 1670) в геометрической форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует уже о совершенно отчётливом владении понятием функции. В геометрическом и механическом виде это понятие мы находим и у И. Ньютона. Однако термин «функция» впервые появляется лишь в 1692 у Г. Лейбница и притом не совсем в современном его понимании. Г. Лейбниц называет функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.
Первое определение функции в смысле, близком к современному, встречается у И. Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Л. Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств». Впрочем, уже Л. Эйлеру не чуждо и современное понимание функции, которое не связывает понятие функции с каким-либо аналитическим её выражением. В его «Дифференциальном исчислении» (1755) говорится: «Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функциями вторых».
С начала XIX века уже всё чаще и чаще определяют понятие функции без упоминания об её аналитическом изображении. В «Трактате по дифференциальному и интегральному исчислению» (1797—1802) С. Лакруа говорится: «Всякая величина, значение которой зависит от одной или многих других величин, называется функцией этих последних». В «Аналитической теории тепла» Ж. Фурье (1822) имеется фраза: «Функция f(x) обозначает функцию совершенно произвольную, то есть последовательность данных значений, подчинённых или нет общему закону и соответствующих всем значениям x, содержащимся между 0 и какой-либо величиной x». Близко к современному и определение Н. И. Лобачевского: «…Общее понятие функции требует, чтобы функцией от x называть число, которое даётся для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной». Там же немного ниже сказано: «Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе». Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое П. Дирихле (1837), неоднократно предлагалось и до него:
у есть функция переменной х (на отрезке 
3. «Место» области допустимых значений при решении уравнений и неравенств
При решении уравнений и неравенств часто возникает дилемма: находить область допустимых значений или нет, выбрать традиционный способ решения или воспользоваться нерациональным, объёмным, чтобы рассмотреть все варианты, не совершить ошибку и прийти, наконец, к верному решению.
Для начала вспомним методы решения уравнений и неравенств разных видов и уровней сложности, рассмотрим частные случаи.
1. При решении дробно-рациональных уравнений и неравенств знаменатель не должен равняться нулю.
2. Решение иррациональных уравнений и неравенств.
2.1. Простейшие иррациональные уравнения имеют вид 

В данном случае нет необходимости находить ОДЗ: из первого уравнения следует, что при полученных значения х выполняется неравенство: 
2.2. Решением уравнения вида 





2.3. Схемы решения основных иррациональных неравенств:

3. Решение логарифмических уравнений и неравенств.
3.1. Схема решения логарифмического уравнения
Но проверить достаточно только одно условие ОДЗ.
3.2. Схема решения логарифмического неравенства вида 

4. Тригонометрические уравнения вида 



Уравнения 
4. Особенности и опасность области допустимых значений
На уроках математики от нас требуют нахождения ОДЗ в каждом примере. В то же время по математической сути дела нахождение ОДЗ вовсе не является обязательным, часто не нужно, а иногда и невозможно — и все это без какого бы то ни было ущерба для решения примера. С другой стороны, часто случается такое, что решив пример, школьники забывают учесть ОДЗ, записывают её как конечный ответ, учитывают лишь некоторые условия. Обстоятельство это хорошо известно, но «война» продолжается каждый год и, похоже, будет идти еще долго.
Рассмотрим, к примеру, такое неравенство:

Здесь ищется ОДЗ, и неравенство решается. Однако при решении этого неравенства школьники иногда считают, что вполне можно обойтись без поиска ОДЗ, точнее, можно обойтись и без условия
В самом деле, для получения верного ответа необходимо учесть и неравенство 

А вот, например, решение уравнения:
Решают его, естественно, избавляясь от логарифмов, но затем найденные значения нередко проверяются на выполнение системы трех таких неравенств:
что равносильно работе с ОДЗ. Однако и в этом примере такая работа излишняя — достаточно проверить выполнение только двух из этих неравенств, причем любых двух.
Напомним, что всякое уравнение (неравенство) может быть сведено к виду 




5. Область допустимых значений – есть решение
И наконец, в массе примеров нахождение ОДЗ позволяет получить ответ без громоздких выкладок, а то и вовсе устно.
1. ОД3 представляет собой пустое множество, а значит, исходный пример не имеет решений.
1) 

2. В ОДЗ находится одно или несколько чисел, и несложная подстановка быстро определяет корни.
1) 
2) 
3) 
4) 

Эффективно может использоваться ОДЗ в сочетании с анализом самого выражения.
5) 


А теперь приведём пример, который был предложен учителем на уроке алгебры. Решить его сразу нам не удалось, но когда мы нашли ОДЗ, всё стало ясно.
Найдите целочисленный корень уравнения 


Целочисленное решение возможно лишь при х=3 и х=5. Проверкой находим, что корень х=3 не подходит, а значит ответ: х=5.
6. Нахождение области допустимых значений – лишняя работа. Равносильность переходов.
Можно привести примеры, где ситуация ясна и без нахождения ОДЗ.
1.
Равенство невозможно, ибо при вычитании из меньшего выражения большее должно получатся отрицательное число.
2. 
Сумма двух неотрицательных функций не может быть отрицательной.
Приведу также примеры, где нахождение ОДЗ затруднено, а иногда просто невозможно.
И, наконец, поиски ОДЗ являются очень часто просто лишней работой, без которой прекрасно можно обойтись, доказав тем самым понимание происходящего. Тут можно привести громадное число примеров, поэтому выберем только наиболее типичные. Главным приемом решения являются в этом случае равносильные преобразования при переходе от одного уравнения (неравенства, системы) к другому.
1.
2. 
3. 
4.
ОДЗ не нужна, ибо подкоренное выражение равно квадрату некоторой функции, а потому не может быть отрицательным.
5. 
6. 

7. 
8. 
9. 
10. 

11. 
Стоит, однако, заметить, что при решении способом равносильных преобразований помогает знание ОДЗ (и свойств функций).
Вот несколько примеров.
1. 


2. 


3. 


В целом эффективность способа равносильных преобразований вроде бы ясна. С их помощью мы добираемся до ответа и без поисков ОДЗ. Значит ли это, что имеется некий универсальный способ и осталось только научиться им пользоваться? Но это не совсем так. Тому несколько причин. Теорем о равносильных преобразованиях довольно много, они непросты для запоминания, и уверенное владение ими – дело не простое. Часто, пользуясь равносильными преобразованиями, начинаешь ставить этот знак при любых переходах от одного уравнения к другому, как действительно равносильных, так и не являющихся таковыми. Теоремы же эти быстро забываются.
Еще одна сложность — при записи равносильности можно забыть выписать все условия, ее гарантирующие, но на ответе это может никак не отразиться. Вот два таких примера:
1. 
В данном примере выражение под знаком логарифма, стоящего справа, всегда положительно. Поэтому применительно к этому примеру та часть условий равносильности, которая записана в виде совокупности, ничего не добавляет. Но дав такое решение, можно просто забыть об этой совокупности.
2.
Возможны два случая: 0 1.
Значит, исходное неравенство равносильно следующей совокупности систем неравенств:
Первая система не имеет решений, а из второй получаем: x 1, откуда следует x 

http://zaochnik.com/spravochnik/matematika/funktsii/kak-najti-oblast-opredelenija-funktsii/
http://pandia.ru/text/78/093/15148.php
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
Запишем результат по правилам записи неравенств.
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
Содержание:
Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
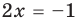
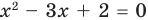
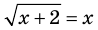
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
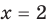
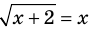
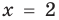
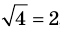
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 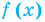
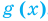
Для уравнения 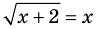
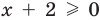
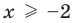
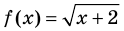

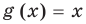
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 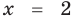
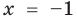
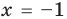
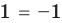
Ответ: 2.
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
5. Схема поиска плана решения уравнений



Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 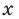
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 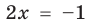
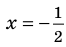
а уравнение 
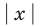
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 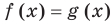
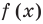
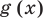
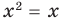
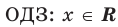
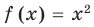
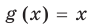
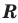
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 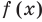
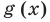
Например, в уравнении 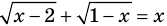
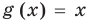
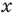
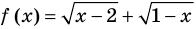
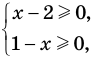
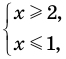
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 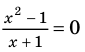
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 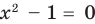
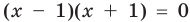
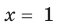
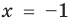
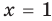
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
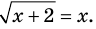
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
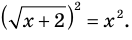
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 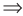
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 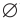
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 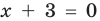
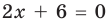
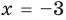
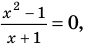
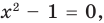
то, как было показано выше, уравнение (3) имеет единственный корень 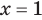
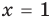
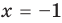
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 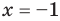
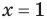
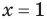
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 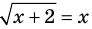
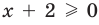

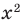
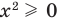
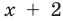


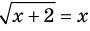
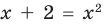
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 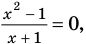
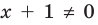
Запись решения в этом случае может быть такой:
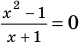
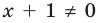
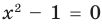
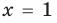
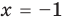
Ответ: 1.
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Ответ: 1.
Пример №423
Решите уравнение 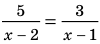
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 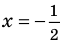
Ответ:
Комментарий:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
- Заказать решение задач по высшей математике
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Ориентир
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
Проверка.
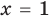
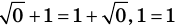
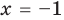
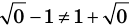
Ответ: 1.
2. Оценка левой и правой частей уравнения
Если надо решить уравнение вида 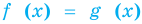


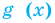
Пример:
►
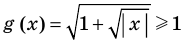
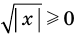
Итак, заданное уравнение равносильно системе
Ответ: 0.
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 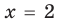
Ответ: 2.
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 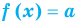
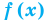
Пример:
Уравнение 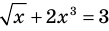
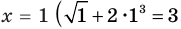
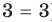
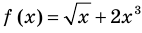
Если в уравнении 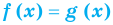
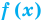
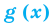
Пример:
Уравнение 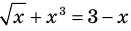
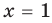
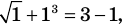
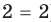
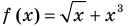

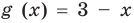
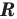
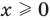
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 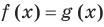
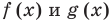
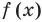
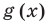
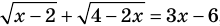
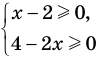
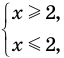


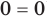


Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 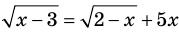
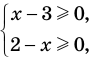
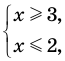
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 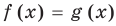
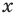
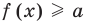
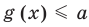
Рассмотрим два случая:
Если 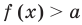
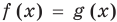
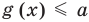
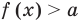
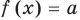
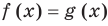
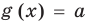
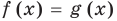
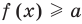
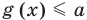
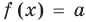
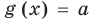
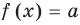
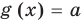
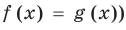
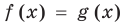
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 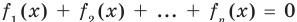
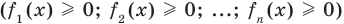
Если предположить, что 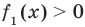

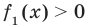
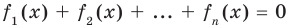
Например, чтобы решить уравнение 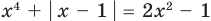
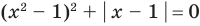
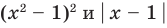
Из второго уравнения получаем 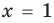
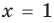
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
Теорема 1. Если в уравнении 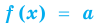
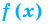
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 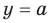
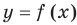
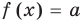
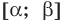
• Если на промежутке 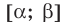
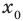
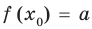
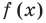
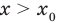
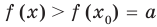
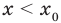
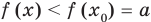
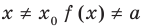
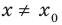
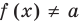
Теорема 2. Если в уравнении 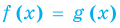
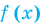
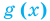
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 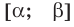
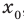
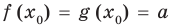
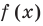
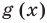
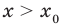
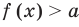
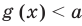
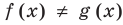
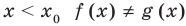
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 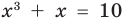
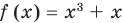

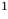
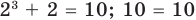
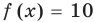
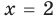
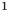

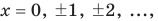
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 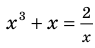
► Сначала следует учесть его ОДЗ: 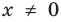
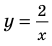
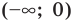
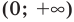
1) При 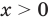
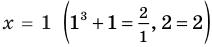
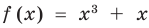

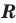
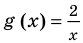

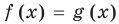
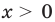
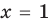
2) При 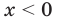
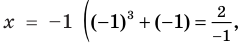
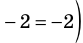
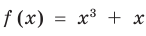
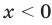
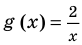
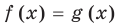
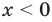
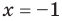
Примеры решения задач:
Пример №424
Решите уравнение 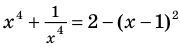
Решение:
► ОДЗ: 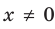
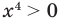
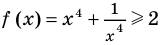
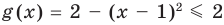
Таким образом, данное уравнение равносильно системе 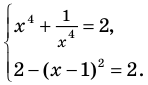


Ответ: 1.
Комментарий:
Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 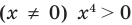
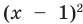
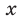
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: 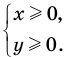
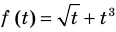
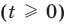
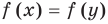
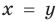
Подставляя 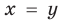
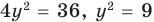
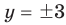

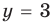
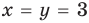
Ответ: (3; 3).
Комментарий:
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 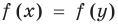
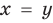
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 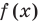
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
Уравнения с одной переменной
Равенство, содержащее переменную, называют уравнением и записывают
Областью определения (или областью допустимых значений) уравнения 

Значение переменной, при подстановке которого в уравнение получаем верное равенство, называют корнем (решением) уравнения.
Решить уравнение – значит найти все его корни или доказать, что их нет.
Число 







Равносильные и неравносильные уравнения
Уравнения 

Например: 1) уравнения 




Уравнение 


Например, уравнение 




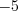

Если выполняются условия 

Равносильные уравнения получают в результате следующих преобразований:
1. При переносе слагаемых из одной части уравнения в другую с противоположным знаком.
2. При умножении или делении обеих частей уравнения на одно и то же отличное от нуля число.
3. При замене уравнения 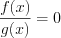
Существует ряд преобразований уравнений, которые могут привести к уравнению, неравносильному данному:
1. Возведение обеих частей уравнения в четную степень (в результате могут появиться посторонние корни).
Например,уравнения 



2. Умножение обеих частей уравнения на выражение, содержащее переменную (могут появиться посторонние корни).
Например, уравнения 





3. Деление обеих частей уравнения на выражение, содержащее переменную (может произойти потеря корней).
Например, 1) уравнения 





Пример 1. Найдите область определения уравнения
Решение. Так как функция 
![g(x)=sqrt[3]{6+x}. LaTeX formula: g(x)=sqrt[3]{6+x}.](https://helpy.quali.me/uploads/formulas/63e15ff02c3736b98a64dbece0d278c396c410a8.1.1.png)
Цели: систематизировать, обобщать знания
учащихся, проверить уровень знаний по теме.
Развивать целеустремленность в достижении
поставленной задачи, честность в оценке своих
знаний и знаний товарищей, умения объяснять и
доступно рассказывать подготовленный материал.
Воспитывать познавательную активность,
культуру общения.
Цитата занятия: “Пока законы математики
остаются определенными, они не имеют ничего
общего с реальностью; как только у них появляется
нечто общее с реальностью, они перестают быть
определенными”.
Альберт Эйнштейн.
Ход занятия
1. Орг. момент. Проверить готовность учащихся
к занятию.
2. Теоретическая часть вопроса. Материал
подготовил и отвечал ученик.
Я хотел бы напомнить общие сведения о понятии
области определения функции.
– Рассмотрим числовое множество Х и
правило f, позволяющее поставить в
соответствие каждому элементу х на множестве
Х определенное число у, то говорят, что
задана функция у = f(x) с областью определения Х.
Пишут
у = f(x), х Х.
Областью определения функции, заданной
некоторым выражением, называется множество
значений аргумента, при которых можно выполнить
все действия в записи функции. Значения
аргумента, принадлежащие области определения
функции, называются допустимыми значениями.
Для области определения функции используют
обозначение D(y).
Если f(x) – алгебраическое выражение и
область определения функции у = f(x) совпадает
с областью определения этого выражения (такую
область определения называют естественной), то
вместо записи у = f(x), х Х используют более короткую
запись: у = f(x).
Для нахождения области определения функции
следует исключить те значения аргумента, при
которых указанные действия невозможно
выполнить. Невозможно, например, делить на нуль;
извлекать корень четной степени из
отрицательного числа; вычислять логарифм
отрицательного числа и нуля; вычислять логарифм
по отрицательному основанию и основанию, равному
нулю и единице; возводить нуль в степень нуля;
возводить отрицательное число в иррациональную
степень; вычислять arcsin x, arсcos x, если |x|>1.
3. Рассмотрение вопроса на примерах. Материал
подготовил и рассказывал ученик.
Я хотел бы рассмотреть некоторые важные
моменты при нахождении области определения:
1) знаменатель дробного выражения не должен
обращаться в нуль. Например: у = 1/х,
область определения состоит из всех х 0;
у = sin x/cos x, область определения
состоит из всех х, для которых cos x 0, т.е. из
(n = 0,
1,
2, …):
2) выражение, находящееся под знаком корня
четной степени, должно быть неотрицательным.
Например: у = , область определения x-5
0, x
5;
у = ,
область определения + 2х – 3
0, т.е. х
-3 и х
1;
3) выражение, находящееся под знаком логарифма
должно быть положительным. Например: у = lg(2-х),
область определения 2-х >0, т.е. х < 2.
4) основание логарифма должно быть больше нуля и
не равным единице. Например: у = logх+27,
область определения х + 2 > 0 и х + 2 1, т.е. х > -2 и х
– 1;
5) выражение, возводимое в иррациональную
степень, должно быть неотрицательным. Например: у
= ,
область определения х 0;
6) выражение стоящее под знаком функций arcsin и
arсcos, по абсолютной величине не должно быть
больше единицы. Например: у = arcsin(lg х),
область определения |lg x| 1 т.е. 0,1
х
10;
7) выражение, стоящее под знаком тангенса и
секанса, не должно равняться , где k = 0,
1,
2,
3, …;
8)выражение, находящееся под знаком котангенса
или косеканса, не должно равняться , где k =0,
1,
2,
3, …;
9)степенно-показательная функция считается
определенной, когда основание положительно.
Точки, в которых основание равно нулю, включаются
в область определения, если показатель в этих
точках отличен от нуля.
Этот вопрос я подготовил пользуясь пособием по
математике (авторы: М.Н.Горейко, А.Б. Антоневич)
4. Примеры нахождения D(y). Материал
подготовил и рассмотрел перед классом ученик.
Найти области определения функций:
- у = (
.
- у =
.
- у = logх – 1(х2 + х – 2).
Решение. Так как sin x принимает и
иррациональные значения, то x + 0, т.е. х
. Кроме того, х не
должен обращаться в , так как при х =
и основание, и показатель
степени обращаются в нуль. Область определения
функции
у = (
есть х > .
Решение. Области определения этой функции
принадлежат те х, при которых определен и
0. Для этого
нужно, чтобы
1.
Но последнее неравенство справедливо лишь в
точках х = 0, 1,
2, … . Таким образом,
только в этих точках можно выполнить все
действия в записи функции и, значит, область
определения этой функции состоит только из целых
чисел.
Решение. Логарифм определен только для
положительных оснований, не равных единице.
Выражение, стоящее под знаком логарифма, должно
дыть положительным. Поэтому получаем систему:
х -1 > 0;
х2 – х – 2 > 0;
х – 1
1.
Решая эту систему, находим область определения:
х > 1, х
2.
5. Метод Мажорант (метод оценки). Решение
уравнений.
Материал рассмотрен учителем вместе с
учениками.
Метод, который имел место быть во всех ЕГЭ по
математике. Отметим этот метод, как начальный
олимпиадный.
Основная идея метода мажорант состоит в
следующем:
Пусть мы имеем уравнение и существует такое число М,
что для любого х из области определения имеем
. Тогда уравнение
равносильно
системе
Пример 1 Решите уравнение .
Решение. Оценим обе части уравнения.
При всех значениях х верны неравенства . Следовательно,
данное уравнение равносильно системе 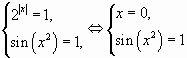
система не имеет решений, так как не удовлетворяет второму
уравнению.
Ответ: нет решений.
Пример 2. Решить уравнение .
Решение. Оценим обе части уравнения.
Поскольку ,
равенство
выполняется тогда и только тогда, когда 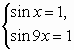
первого уравнения системы являются значения . При этих х
найдем .
Следовательно, решение системы.
Ответ: .
Пример 3 Решить уравнение .
Решение.
Пусть , тогда
уравнение примет вид . Поскольку
и
,
неравенство выполняется тогда и только тогда,
когда 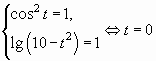
Обратная замена: х + 1 = 0 .
Ответ: – 1.
Пример 4. Найти все значения параметра а,
при каждом из которых уравнение имеет решения. Найдите эти
решения.
Решение.
Перепишем уравнение в виде . При всех значениях х
выражение
поэтому .
При всех значения х выражения и
. Поэтому
.
Следовательно, левая часть уравнения не меньше
4, а правая часть – не больше 4.
Получаем систему:
Ответ: при
.
Разновидностью метода мажорант являются
задачи (“встреча на краю”) в которых множества
значений левой и правой частей уравнения или
неравенства имеют единственную общую точку,
являющуюся наибольшим значением для одной части
и наименьшим для другой.
Прежде всего – привести заданные уравнения или
неравенства к более простому виду: путем
разложения на множители, избавлением от модулей,
логарифмов и т.д. Затем необходимо ещё раз
внимательно прочитать задание, попробовать
нарисовать графический образ функций входящих в
задачу.
Пример 1. Решить уравнение .
1 способ.
Решение: Заметим, что левая часть уравнения
не превосходит единицы, в то время как правая
часть не меньше единицы. Следовательно, исходное
уравнение имеет решение, только если обе его
части равны единицы. Это возможно только при .
Ответ: .
2 способ. Данное уравнение можно решить
графически. Для этого построим в одной системе
координат графики правой и левой частей
уравнения, т.е график функции и график функции
. Из рисунка видно, что
исходное уравнение имеет решение, только при .
Пример 2. Решить уравнение .
Решение.
Так как при любом значении х: то данное уравнение
выполняется только в том случае, если
выполняется система 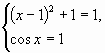
единственный корень х = 1, но этот корень не
удовлетворяет второму уравнению. Поэтому
система решений не имеет.
Ответ: .
Пример 3. Решить уравнение .
Решение:
Так как , то
левая часть уравнения принимает значение от до 2. Для правой
части (в силу неравенства для суммы двух взаимно
обратных чисел) выполнено 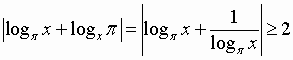
Поэтому уравнение имеет решения, если и только
если одновременно выполнены два условия 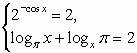
систему, получаем
Ответ:
Пример 4. Решить уравнение .
Решение.
Левая часть уравнения не больше 2, так как , значит
. Равенство
возможно при условии .
Правая часть должна быть положительна, так как , а значит
.
Кроме того, .
Тогда равенство обеих частей уравнения
возможно лишь при условии .
Отсюда находим, что .
Ответ: .
Пример 5. Решите уравнение .
Решение.
Для решения уравнения оценим его части:
и
. Поэтому равенство
возможно только при условии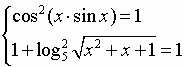
Сначала решим второе уравнение.
Получаем: ,
,
,
или
. Корни этого уравнения
и
.
Проверим справедливость первого
равенства, подставив эти корни.
При
получаем:
(верное равенство).
Для
имеем: (неверное
равенство).
Итак, данное уравнение имеет
единственный корень .
Ответ: 0.
6. Подведем итоги занятия. Оценим выступление
учащихся.




























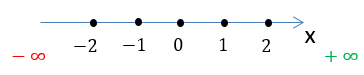
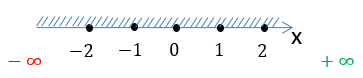
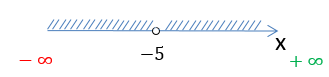
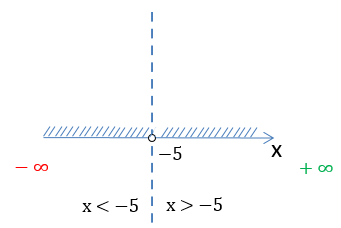
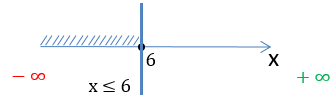
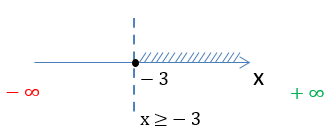
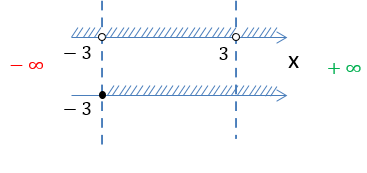
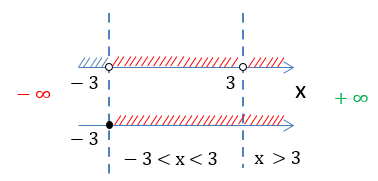
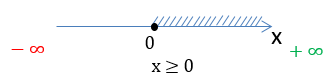
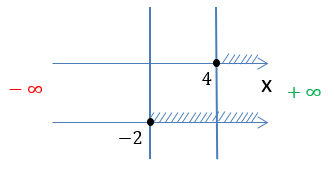
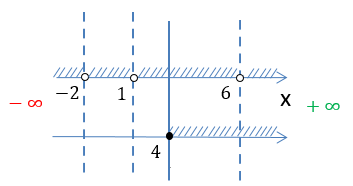










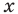
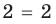
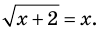
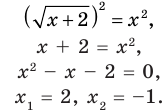
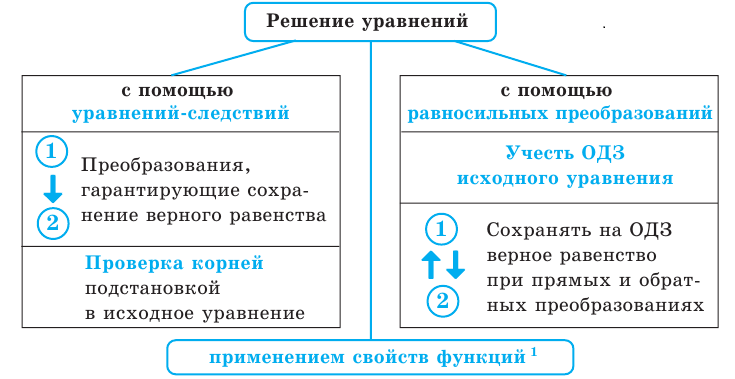
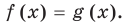
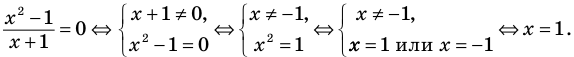
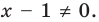
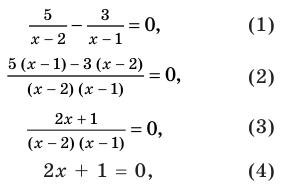
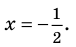
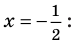
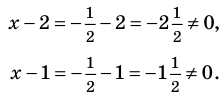
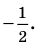




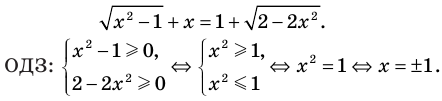

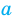
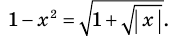
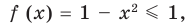
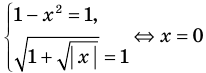
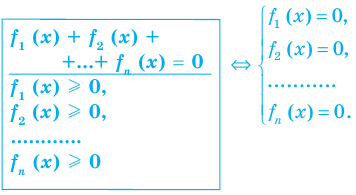
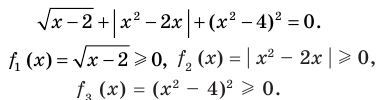
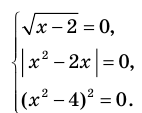
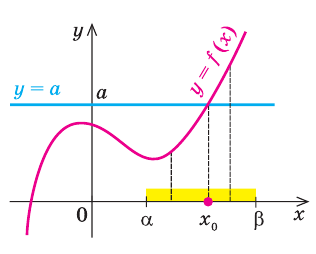
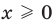
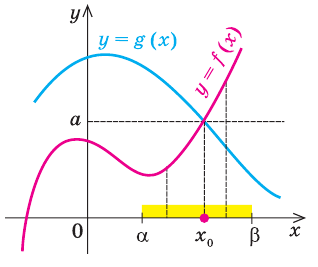
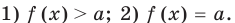
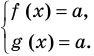
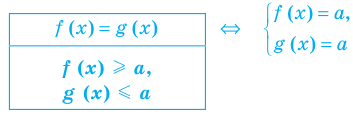
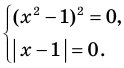
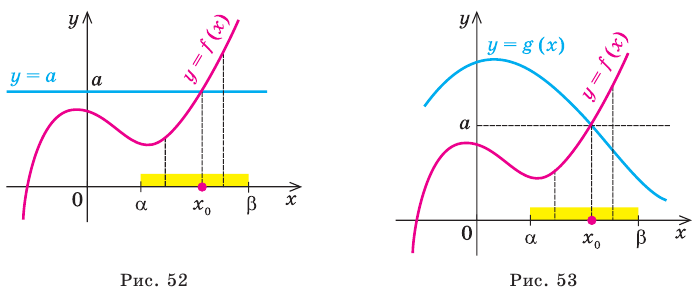
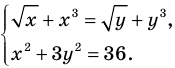
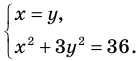
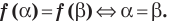

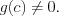






![frac{x-5}{21x}=sqrt[3]{6+x}. LaTeX formula: frac{x-5}{21x}=sqrt[3]{6+x}.](https://helpy.quali.me/uploads/formulas/7bba61303c94aa13d9a3b3e43e6c78c6c5ef8a5d.1.1.png)