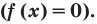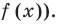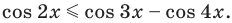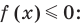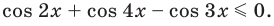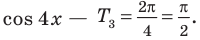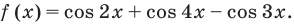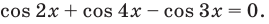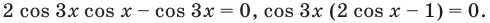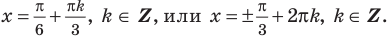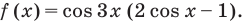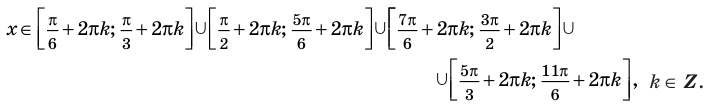Содержание:
Для решение простейших тригонометрических неравенств можно использовать как единичную окружность, так и графики тригонометрических функций.
Пример 1.
Решим неравенство
Решение:
Запишем решение в общем виде.
Решить данное неравенство значит, найти абсциссы множества точек графика функции 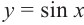
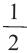
1.Построим график функции 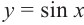
2.В одной системе координат построим график функции 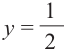
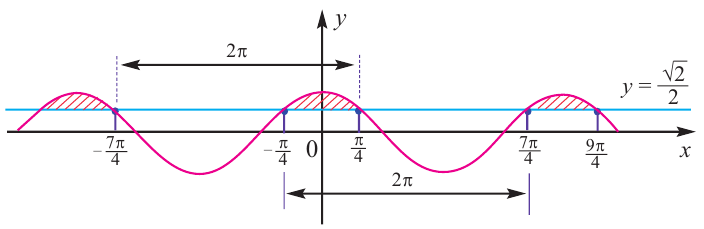
3.Отметим точки пересечения графиков.
4. Как видно, прямая 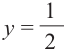
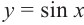
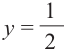
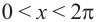
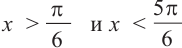
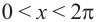
Также решения тригонометрических неравенств можно ясно увидеть на единичной окружности. Все остальные интервалы, удовлетворяющие решению неравенства получаются смещением интервала 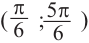
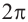
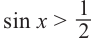
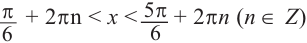
Пример 2.
Решим неравенство
Решение:
Решения уравнения 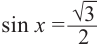
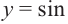
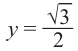
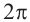
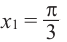
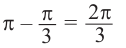
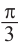
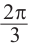
От каждой из них, по обе стороны, отметим ещё две точки — вправо от
точки 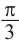
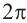
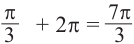
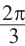
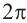
Они также являются абсциссами точек пересечения графиков.
На промежутке (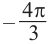
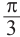
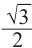
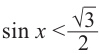
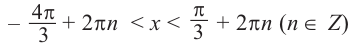
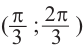
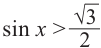
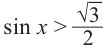
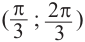
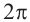
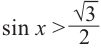
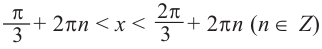
Пример 3.
Решим неравенство
Решение:
Найдём абсциссы точек пересечения графиков функций
и 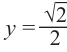
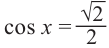
Получим: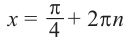
При 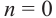
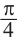
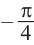
Отметим от точки 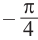
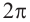
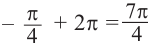
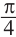
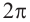
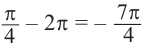
Один из промежутков, удовлетворяющих неравенству, расположен между наименьших но абсолютному значению корней соответствующего уравнения, т.е. между точками 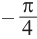
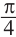
Приняв во внимание периодичность 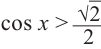
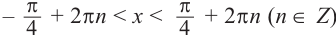
По графику решение неравенства 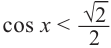
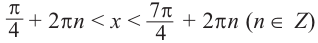
Пример 4.
Решим неравенства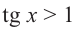
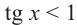
Решение:
В одной системе координат построим графики функций 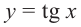
Найдём абсциссу точки пересечения , расположенной в интервале 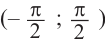
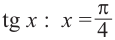
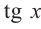
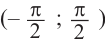
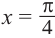
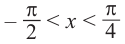
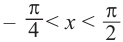
Так как функция 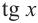
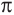
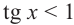
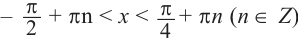
tg х > 1 будет 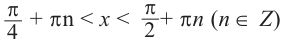
Пример 5.
Решим неравенства 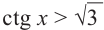
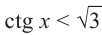
Решение:
На одной координатной плоскости построим графики функций 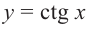
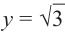
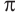
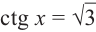
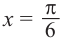
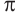
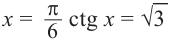
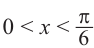
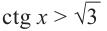
если 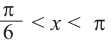
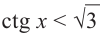
Это говорит о том , что условию неравенства 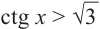
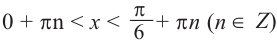
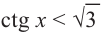
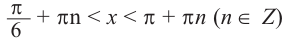
Для решения тригонометрических неравенств:
1) В одной системе координат постройте графики функций из левой и правой частей неравенства;
2) Решите соответствующие уравнения. Найдите абсциссы для нескольких точек пересечения, расположенных близко к началу координат и отметьте их на графике;
3) Определите какой-либо интервал, удовлетворяющий неравенству;
4) Принимая во внимание периодичность функции, запишите все решения.
Пример 6.
Решите неравенство 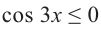
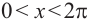
Решение:
1.Построим график функции 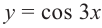
Как видно из графика, значения 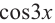
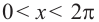
Пример 7.
Решим неравенство 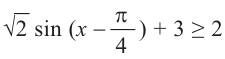
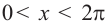
Решение:
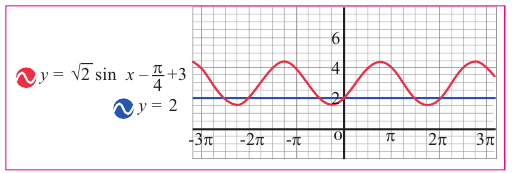
1. Построим графики функций 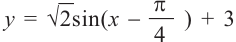
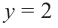
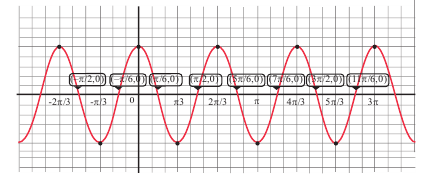
Решением неравенства являются абсциссы всех точек, которые расположены на прямой у = 2 и выше неё. Это точки 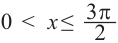
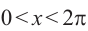
А общее решение неравенства имеет вид 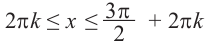
Проверка: На интервале решения для проверки выберем одну точку, напри-л
мер 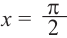
Пример 8.
Решение:
Пусть 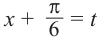
Пример решении задачи:
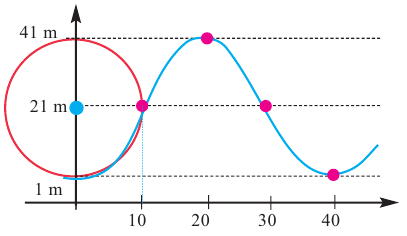
Карусель, радиусом 20 м за каждые 40 секунд совершает один оборот. Самое низкое сиденье находится на высоте 1 м.
а)Изобразите график, соответствующий задаче.
б)Запишите функцию зависимости движения человека, находящегося на сиденье карусели в виде 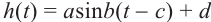
в)В какие секунды за один полный оборот человек на карусели, окажется на высоте выше 21 м?
Решение:
а) Изобразим схематично решение задачи. Отметим на окружности точки, соответствующие каждой четвёртой части оборота при движении карусели. Соединим эти точки и получим график, в виде синусоиды, движения карусели за один оборот (360°).
б)Из графика видно, что с 10 но 30 секунду человек на карусели, будет находится на высоте от 21 ми более.
в)По данным задачи и графику запишем формулу функции.
Зная период, найдём частоту b:
Найдём амплитуду и среднюю линию, зная максимальное и минимальное значения. 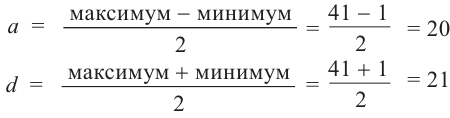
Формула имеет вид 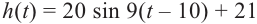
Решение неравенств
Понятия неравенства с одной переменной и его способы решения:
Определение:
Если два выражения с переменной соединить одним из знаков 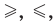
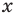
Решением неравенства с переменной называется значение переменной, которое обращает заданное неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет.
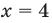
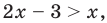
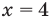
Область допустимых значений (ОДЗ):
Областью допустимых значений (или областью определения) неравенства называется общая область определения для функций 
Для неравенства 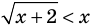
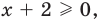
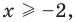
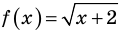
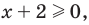
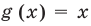
Два неравенства называется равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго и наоборот, каждое решение второго неравенства является решением первого.
- Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
- Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не меняя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного неравенства).
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное задан ному (на ОДЗ заданного неравенства).
- Метод интервалов (решения неравенств вида
Решите неравенство
Пусть
ОДЗ:
Нули функции
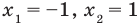
Ответ:
Схема поиска плана решения неравенства
Объяснение и обоснование:
Понятия неравенства с переменной и его решение
Если два выражения с переменной соединить одним из знаков 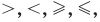
Аналогично уравнению, неравенство с переменной (например, со знаком 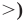
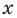
Напомним, что решением неравенства называется значение переменной, которое обращает это неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет.
Например, решениями неравенства 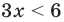
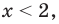

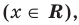
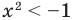
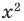
Область допустимых значений (ОДЗ) неравенства
Область допустимых значений (ОДЗ) неравенства определяется аналогично ОДЗ уравнения. Если задано неравенство 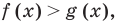
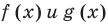
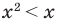
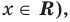
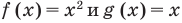
Понятно, что каждое решение заданного неравенства входит как в область определения функции 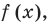
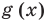
Например, в неравенстве 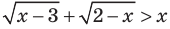
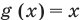
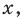
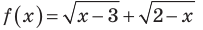
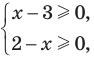
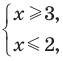
В основном при решении неравенств различных видов приходится применять один из двух методов решения: равносильные преобразования неравенств или так называемый метод интервалов.
Равносильные неравенства
С понятием равносильности неравенств вы знакомы еще из курса алгебры 9 класса. Как и для случая равносильных уравнений, равносильность неравенств мы будем рассматривать на определенном множестве.
Два неравенства называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго, и наоборот, каждое решение второго неравенства является решением первого.
Договоримся, что в дальнейшем все равносильные преобразования неравенств будем выполнять на ОДЗ заданного неравенства. Укажем, что в том случае, когда ОДЗ заданного неравенства является множество всех действительных чисел, мы не всегда будем его записывать (как не записывали ОДЗ при решении линейных или квадратных неравенств). И в других случаях главное — не записать ОДЗ при решении неравенства, а действительно учесть ее при выполнении равносильных преобразований заданного неравенства.
Общие ориентиры выполнения равносильных преобразований неравенств аналогичны соответствующим ориентирам выполнения равносильных преобразований уравнений.
Как указывалось выше, выполняя равносильные преобразования неравенств, необходимо учитывать ОДЗ заданного неравенства — это и есть первый ориентир для выполнения равносильных преобразований неравенств.
По определению равносильности неравенств необходимо обеспечить, чтобы каждое решение первого неравенства было решением второго, и наоборот, каждое решение второго неравенства было решением первого. Для этого достаточно обеспечить сохранение верного неравенства на каждом шаге решения не только при прямых, а и при обратных преобразованиях. Это и есть второй ориентир для решения неравенств с помощью равносильных преобразований. Действительно, каждое решение неравенства обращает его в верное числовое неравенство, и если верное неравенство сохраняется, то решение каждого из неравенств будет также и решением другого, таким образом, неравенства будут равносильны (соответствующие ориентиры схематически представлены в пункте 5 табл. 38).
Например, чтобы решить с помощью равносильных преобразований неравенство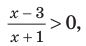
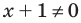
Решение:
Данное неравенство равносильно совокупности двух систем:
Тогда получаем
Таким образом,
Ответ:
Комментарий:
Заметим, что при записи условия положительности дроби — совокупности систем (2) — мы неявно учли ОДЗ неравенства (1). Действительно, если 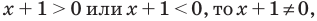
- Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
- Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не изменяя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного).
- Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований заданного неравенства.
Замечание. Для обозначения перехода от заданного неравенства к неравенству, равносильному ему, можно применять специальный значок 
Метод интервалов
Решение неравенств методом интервалов опирается на свойства функций, связанные с изменением знаков функции. Объясним эти свойства, используя графики известных нам функций, например функций 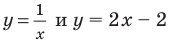
Рассматривая эти графики, замечаем, что функция может изменить свой знак только в двух случаях:
- если график разрывается (как в случае функции
(рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);
- если график без разрыва переходит из нижней полуплоскости в верхнюю (или наоборот). Но тогда график пересекает ось
(как в случае функции
(рис. 100,6).
На оси 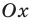
Точки, в которых разрывается график функции 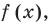
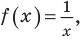
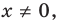
В таблице 39 приведено решение дробно-рационального неравенства 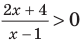
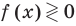
Пример №1
Решение:
1. ОДЗ: 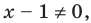
Рассмотрим функцию, стоящую в левой части этого неравенства, и обозначим ее через 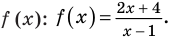
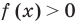
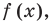
1. Найти ОДЗ неравенства.
2. Нули
тогда
Нас интересуют те промежутки области определения функции 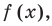
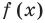
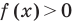
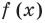
2. Найти нули
Если теперь отметить нули на области определения функции 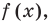
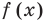
3. Отметить нули на ОДЗ и найти знак функции в каждом промежутке, на которые разбивается ОДЗ.
4 Ответ:
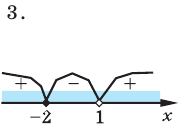
Из рисунка видно, что решением неравенства является объединение промежутков
4. Записать ответ, учитывая знак неравенства.
Приведем пример решения более сложного дробно-рационального неравенства методом интервалов и с помощью равносильных преобразований.
Пример №2
Решите неравенство
1 способ (метод интервалов)
Решение:
Пусть
1 ОДЗ:
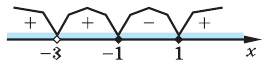
2. Нули
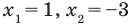
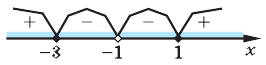
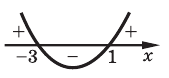
3. Отмечаем нули функции на ОДЗ и находим знак 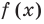
Ответ:
Комментарий:
Данное неравенство имеет вид 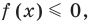
При нахождении нулей 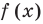
Записывая ответ к нестрогому неравенству, следует учесть, что все нули функции должны войти в ответ (в данном случае — числа -3 и 1).
2 способ (с помощью равносильных преобразований)
Комментарий:
Выберем для решения метод равносильных преобразований неравенства. При выполнении равносильных преобразований мы должны учесть ОДЗ данного неравенства, то есть учесть ограничение
Но если 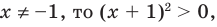
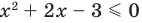
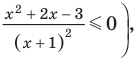
Чтобы решить полученное квадратное неравенство, найдем корни квадратного трехчлена 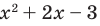
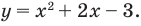
Поскольку все преобразования были равносильными только на ОДЗ, то мы должны выбрать те решения квадратного неравенства, которые удовлетворяют ограничению ОДЗ.
Решение:
ОДЗ:
Тогда 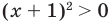
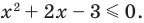
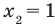
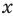
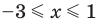
Учитывая ОДЗ, получаем ответ.
Ответ:
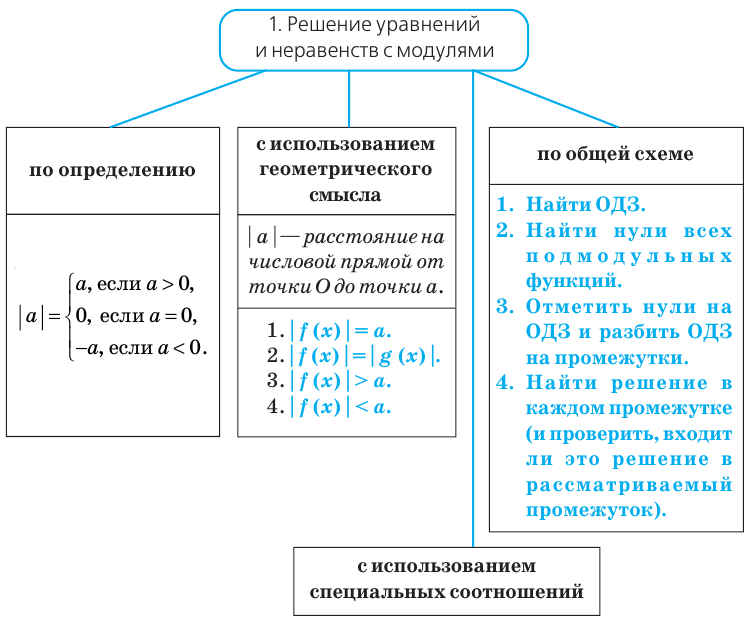
Уравнения и неравенства с модулями
Использование геометрического смысла модуля ( при
Обобщение:
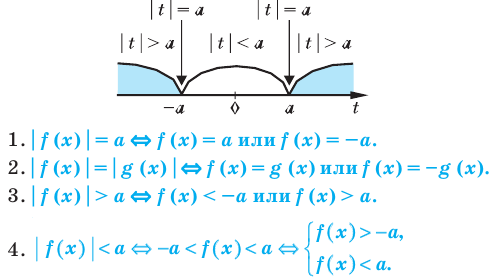
Использование специальных соотношений:
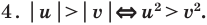
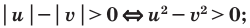
Объяснение и обоснование:
Решение любых уравнений или неравенств с модулем
Решать любое уравнение или неравенство с модулем можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства с модулем могут быть также решены с использованием специальных соотношений (табл. 40).
В зависимости от выбранного способа решения получаем разные записи решения.
Пример №3
Решите уравнение
1 способ (по определению модуля)
Решение:
- Если
то получаем уравнение
Тогда
что удовлетворяет и условию (1).
- Если
то получаем уравнение
Тогда
что удовлетворяет и условию (2).
Ответ:
Комментарий:
Чтобы раскрыть знак модуля по определению, рассмотрим два случая: 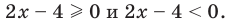
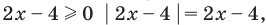
В каждом случае решаем полученное уравнение и выясняем, удовлетворяет ли каждый из найденных корней тому условию, при котором мы его находили.
2 способ (использование геометрического смысла модуля)
Решение:
Ответ: 5; -1.
Комментарий:
С геометрической точки зрения 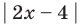
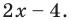
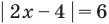
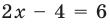
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств с модулями — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции 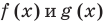
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции 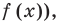
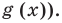
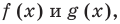
Чтобы продолжить решение неравенств 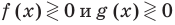
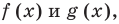
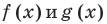
Обоснование возможности применения приведенной схемы к решению неравенств с модулями проводится аналогично.
Примеры решения задач:
Пример №4
Решите уравнение
Решение:
1. ОДЗ:
2. Нули подмодульных функций:
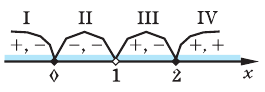
3. Нули 0 и 2 разбивают ОДЗ на четыре промежутка, в которых подмодульные функции имеют знаки*, показанные на рисунке.
4. Находим решения данного уравнения в каждом из промежутков (поскольку знаки подмодульных функций одинаковы на промежутках 1 и 3, удобно для решения объединить эти промежутки).
Промежутки 1 и 3 : 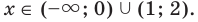
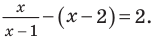
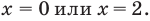
Промежуток 2: 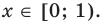
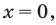
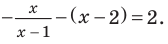
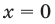
Промежуток 4: 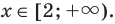
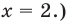
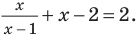
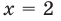
Ответ: 0; 2.
Проиллюстрируем также получение и использование специальных соотношений, приведенных в таблице 40. Обоснуем, например, соотношение
Запишем заданное равенство в виде 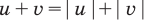
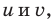
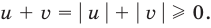
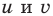
неотрицательные. Наоборот, если 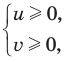
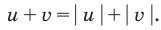
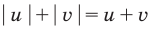
- Заказать решение задач по высшей математике
Пример №5
Решите уравнение
Решение:
Поскольку 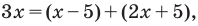
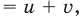
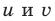
Таким образом,
Ответ:
Комментарий:
Если обозначить 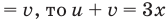
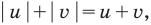
Заметим, что данное уравнение можно решать и по общей схеме, но тогда решение будет более громоздким но системе
При решении неравенств с модулями рассуждения, связанные с раскрытием знаков модулей, полностью аналогичны рассуждениям, которые использовались при решении уравнений с модулями.
Пример №6
Решите неравенство
Решение:
Учитывая геометрический смысл модуля, получаем, что заданное неравенство равносильно неравенству 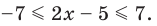
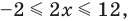
Ответ:
Комментарий:
Неравенство вида 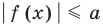
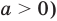
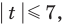
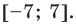
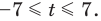
Пример №7
Решите неравенство
Решение:
1. ОДЗ: 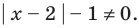
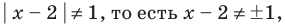
2. Нули подмодульных функций: 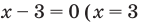
3. Нуль 2 разбивает ОДЗ на четыре промежутка, на которых подмодульные функции имеют знаки, показанные на рисунке (на каждом из промежутков первый знак — это знак функции 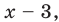
4. Находим решения заданного неравенства в каждом из промежутков (поскольку знаки подмодульных функций являются одинаковыми на промежутках I и II, удобно для решения объединить эти промежутки). Промежутки I и II: 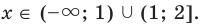
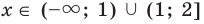
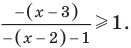
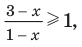
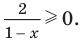
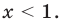
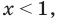
Промежуток III: 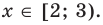
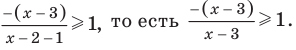
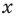
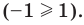
Промежуток IV: 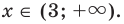
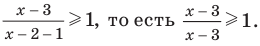
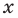
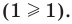
Объединяя все решения, полученные в каждом из промежутков, имеем решение данного неравенства на всей ОДЗ:
Ответ:
Укажем, что для решения некоторых неравенств с модулями удобно применять также специальные соотношения, приведенные в таблице 40.
Пример №8
Решите неравенство
Решение:
Поскольку 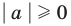
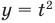
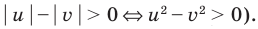
Раскладывая на множители все разности квадратов, имеем:
Далее методом интервалов (см. рисунок)получаем
Ответ:
Общая схема, предложенная в таблице 40, может быть использована не только при решении уравнений или неравенств с модулями, но и при выполнении преобразований выражений с модулями.
Например, для построения графика функции 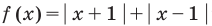
Оформление решения подобного примера может быть таким.
Пример №9
Постройте график функции
Решение:
1. Область определения функции:
2. Нули подмодульных функций:
3. Отмечаем нули на области определения и разбиваем область определения на промежутки (на рисунке также указаны знаки подмодульных функций в каждом из промежутков). 4. Тогда
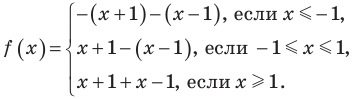
Строим график этой функции (см. рисунок).
Решение тригонометрических неравенств
Примеры решения простейших тригонометрических неравенств:
Способы решения более сложных тригонометрических неравенств:
а) Использование равносильных преобразований и, в частности, сведение тригонометрического неравенства к алгебраичкому неравенству по схеме: 1) к одному аргументу, 2) к одной функции, 3) замена переменной (аналогично схеме решения тригонометрических уравнений, приведенной на с. 170) и последующее решение полученных простейших тригонометрических неравенств.
б) Использование метода интервалов (после сведения неравенства к виду 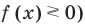
- Найти ОДЗ неравенства.
- Найти общий период (если он существует) для всех функций, входящих в неравенство, то есть период функции
- Найти нули функции:
- Отметить нули функции на ОДЗ на одном периоде и найти знак функции
в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).
- Записать ответ, учитывая знак заданного неравенства и период функции
Объяснение и обоснование:
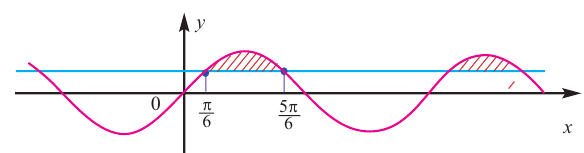
Решение простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами считают неравенства вида 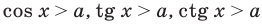
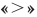
Чтобы рассуждения по нахождению решений этих неравенств были более наглядными, используют единичную окружность или графики соответствующих функций, как это показано в первом пункте таблицы 41.
Пример №10
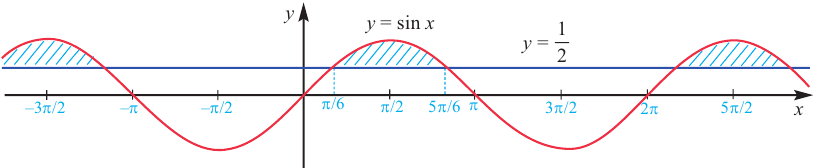
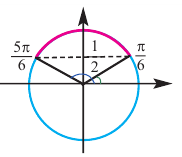
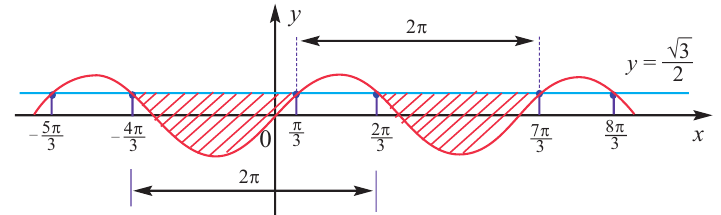
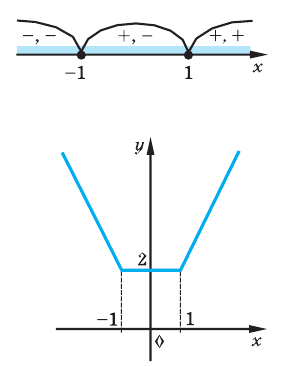
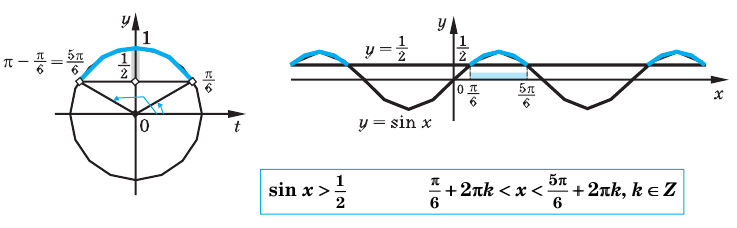
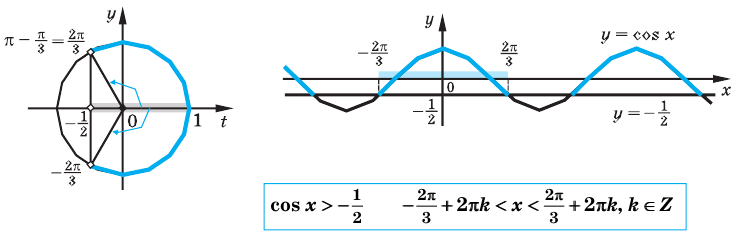
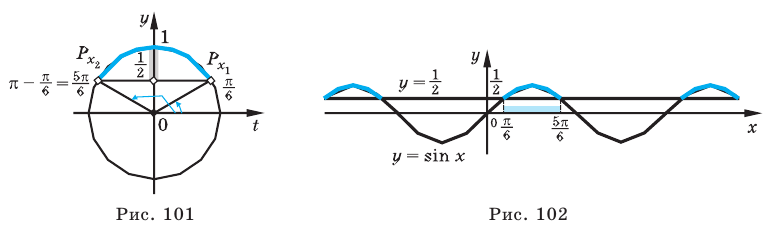
Объясним более детально решение неравенства 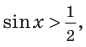
Решение:
Поскольку 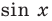
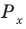
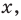
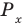
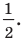
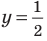
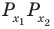
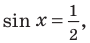
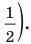
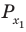
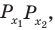
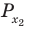
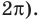
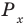
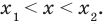
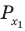
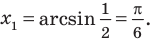
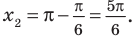
Через период 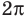
Ответ:
Для решения неравенства 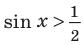
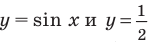
Решениями неравенства 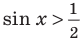
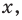
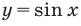
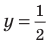
Достаточно решить уравнение 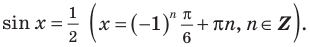
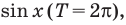
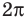
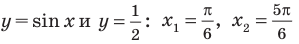
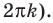
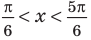
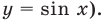
Ответ:
Аналогично можно получить и решения других видов простейших неравенств, приведенных в пункте 1 таблицы 41.
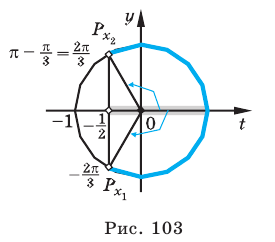
Пример №11
Решите неравенство
Решение:
Поскольку 
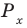
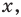
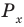
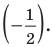
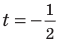
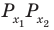
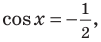
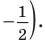
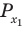
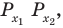
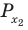
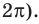
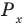
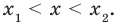
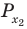
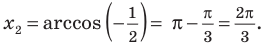
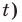
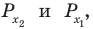
Таким образом, на одном 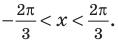
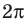
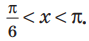
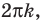
Ответ:
Рассуждения при использовании графической иллюстрации решения неравенства 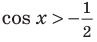
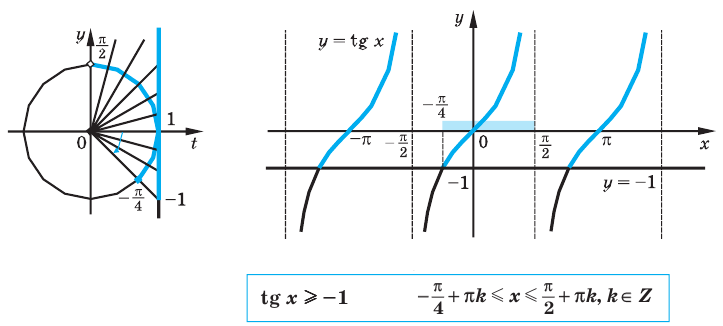
Пример №12
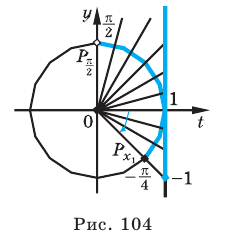
Решите неравенство
Решение:
Период тангенса равен 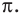
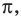
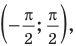
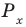
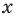
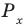
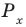
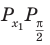
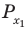
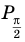
Поскольку точка 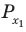
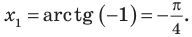
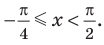
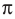
Ответ:
Заметим, что при решении данного неравенства с использованием графиков достаточно, как и в предыдущих случаях, на одном периоде (например, на промежутке 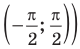
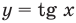
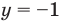
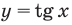
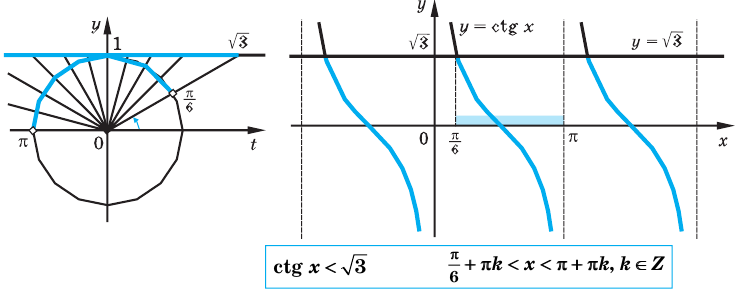
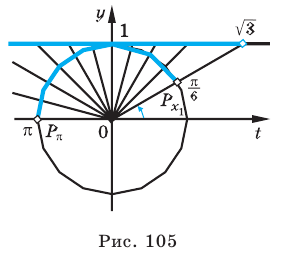
Пример №13
Решите неравенство
Решение:
Период котангенса равен 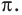
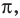
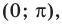
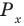
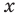
Сначала выделим на линии котангенсов значения котангенсов, меньшие, чем 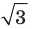
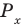
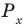
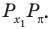
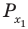
Таким образом, на одном периоде решениями данного неравенства являются
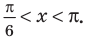
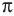
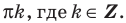
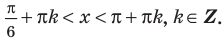
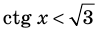
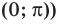
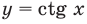
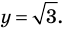
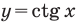
Способы решения более сложных тригонометрических неравенств
Способы решения более сложных тригонометрических неравенств также проиллюстрируем на примерах.
Пример №14
Решите неравенство:
Решение:
Тогда 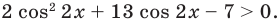
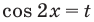
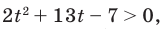
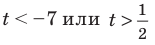
Обратная замена дает: 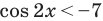
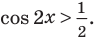
Таким образом,
Комментарий:
Используем равносильные преобразования данного неравенства. Для этого приведем его к алгебраическому по схеме, аналогичной схеме решения
- к одному аргументу
- к одной функции
- проведем замену переменной
После обратной замены решим полученные простейшие тригонометрические неравенства.
Решая более сложные тригонометрические неравенства, можно также применить метод интервалов, немного изменив его. Необходимость коррекции известной схемы решения неравенств 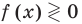
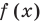
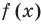
Таким образом, метод интервалов для решения тригонометрических неравенств 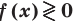
- Найти ОДЗ неравенства.
- Найти период функции
(если он существует).
- Найти нули функции
- Отметить нули на ОДЗ внутри одного периода и найти знак функции в каждом из промежутков, на которые разбивается ОДЗ (внутри одного периода).
- Записать ответ (учитывая знак заданного неравенства и период функции
Пример №15
Решите неравенство
Решение:
Решим данное неравенство методом интервалов. Для этого приведем его к виду
1. ОДЗ: 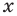
2. Как мы знаем, период функции 
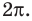
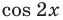
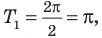
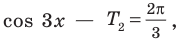
На отрезке длиной 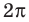
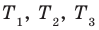
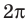
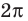
3.Найдем нули этой функции:
Тогда
Отсюда 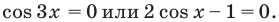
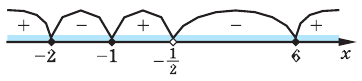
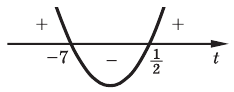
4. Отметим все нули на периоде длиной 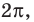
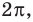
Находим знаки функции 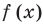
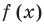
Ответ (записывается с учетом периода):
Замечание. При решении тригонометрических неравенств методом интервалов часто приходится находить знак функции в большом количестве промежутков. Для того чтобы уменьшить объем работы, можно предложить такой способ: следить за тем, через какой нуль мы проходим при переходе от одного интервала к другому и изменяется ли знак заданной функции в этом нуле.
В случае, когда функция 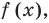
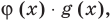
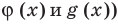
Практически для использования этого свойства в случае, если левая часть неравенства записана как произведение нескольких функций, нули каждого множителя отмечают на промежутке разным цветом (так, как это сделано на рисунке к задаче 6), или, если множителей только два, нули первого множителя обозначают под осью, а нули второго — над осью.
Если у функций-множителей нет одинаковых нулей, то знак функции 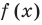
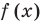
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
Алгебраические неравенства: понятие, ОДЗ, равносильность (Автор Колчанов А.В.)
Алгебраические неравенства. Подготовка к ЕГЭ.
Универсальный метод решения алгебраических неравенств заключается в приведении их с помощью равносильных преобразований к системам или совокупностям легко решаемых рациональных неравенств или уравнений. Этот метод школьники осваивают, начиная с 9-го класса. В 10 – 11 классах средней школы, рассматривая кроме алгебраических еще тригонометрические, показательные и логарифмические уравнения и неравенства, как правило, с помощью замен или других рассуждений удается решение свести к исследованию равносильных систем или совокупностей простейших уравнений и неравенств.
Понятия неравенства с переменной и его решений
Если два выражения с переменной соединить одним из знаков >, <, <, то получаем неравенство с переменной.
Аналогично уравнению, неравенство с переменной (например, со знаком >) чаще всего понимают как аналитическую запись задачи о нахождении тех значений аргументов, при которых значение одной из заданных функций больше, чем значение другой заданной функции. Поэтому в общем виде неравенство с одной переменной х (например, для случаев «больше») записывают так: f(x)>g (*).
Напомним, что решением неравенства называется значение переменной, которое обращает это неравенство в верное числовое неравенство.
Решить неравенство — значит найти все его решения (и обосновать, что других решений нет) или доказать, что решений нет.
Например, решениями неравенства Зх < 6 являются все значения х < 2, для неравенства х2 > -1 решениями являются все действительные числа (R), а неравенство х2 <-1 не имеет решений, поскольку значение х2 не может быть отрицательным числом.
Область допустимых значений (ОДЗ)
Область допустимых значений (ОДЗ) неравенства определяется аналогично ОДЗ уравнения. Если задано неравенство f (х) > g(x), то общая область определения функций f(x) и g(x) называется областью допустимых значений этого неравенства (иногда используются также термины «область определения неравенства* или «множество допустимых значений неравенства*).
Например, для неравенства х2 < х областью допустимых значений являются все действительные числа (это можно записать, например, так: ОДЗ: R), поскольку функции f(x) = х2 и g(x) = х имеют области определения R.
Понятно, что каждое решение заданного неравенства входит как в область определения функции f(x), так и в область определения функции g(x) (иначе мы не сможем получить верное числовое неравенство). Таким образом, каждое решение неравенства обязательно входит в ОДЗ этого неравенства. Это позволяет в некоторых случаях применить анализ ОДЗ неравенства для его решения.
Равносильные неравенства
С понятием равносильности неравенств вы знакомы еще из курса алгебры 9 класса. Как и для случая равносильных уравнений, равносильность неравенств мы будем рассматривать на определенном множестве.
Два неравенства называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго и, наоборот, каждое решение второго неравенства является решением первого.
Договоримся, что в дальнейшем все равносильные преобразования неравенств будем выполнять на ОДЗ заданного неравенства. Укажем, что в том случае, когда ОДЗ заданного неравенства является множество всех действительных чисел, мы не всегда будем его записывать (как не записывали ОДЗ при решении линейных или квадратных неравенств). И в других случаях главное — не записать ОДЗ при решении неравенства, а действительно учесть ее при выполнении равносильных преобразований заданного неравенства.
Общие ориентиры выполнения равносильных преобразований неравенств аналогичны соответствующим ориентирам выполнения равносильных преобразований уравнений.
Как указывалось выше, выполняя равносильные преобразования неравенств, необходимо учитывать ОДЗ заданного неравенства — это и есть первый ориентир для выполнения равносильных преобразований неравенств.
По определению равносильности неравенств необходимо обеспечить, чтобы каждое решение первого неравенства было решением второго, и наоборот, каждое решение второго неравенства было решением первого. Для этого достаточно обеспечить сохранение верного неравенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях. Это и есть второй ориентир для решения неравенств с помощью равносильных преобразований. Действительно, каждое решение неравенства обращает его в верное числовое неравенство, и если верное неравенство сохраняется, то решение каждого из неравенств будет также и решением другого, таким образом, неравенства будут равносильны.
Например, чтобы решить с помощью равносильных преобразований неравенство
достаточно учесть его ОДЗ: х + 1 не не равно 0 и условие положительности дроби (дробь будет положительной тогда и только тогда, когда числитель и знаменатель дроби имеют одинаковые знаки), а также учесть, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлении с сохранением верного неравенства.
Кроме выделенных общих ориентиров, для выполнения равносильных преобразований неравенств можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности неравенств обобщим также формулировки простейших теорем о равносильности неравенств, известных из курса алгебры 9 класса.
1. Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
2. Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не изменяя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного).
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем проводится с использованием основных свойств числовых неравенств и полностью аналогично обоснованию ориентиров для равносильных преобразований заданного неравенства.
Замечание. Для обозначения перехода от заданного неравенства к неравенству, равносильному ему, можно применять специальный значок <=>, но его использование при оформлении решений не является обязательным.
Графический метод решения задач линейного программирования
1. Область решений линейных неравенств.
Пусть
задано линейное неравенство с двумя
переменными
и
(1)
Если
величины
и
рассматривать как координаты точки
плоскости, то совокупность точек
плоскости, координаты которых удовлетворяют
неравенству (1), называется областью
решений данного неравенства. Следовательно,
областью решений неравенства (1) является
полуплоскость с граничной прямой линией.
Пример
1.
Найти полуплоскость, определяемую
неравенством
.
Решение.
Строим прямую
по двум точкам, например, по точкам
пересечения с осями координат (0; 4) и (6;
0). Эта линия делит плоскость на две
части, т.е. на две полуплоскости. Берем
любую точку плоскости, не лежащую на
построенной прямой. Если координаты
точки удовлетворяют заданному неравенству,
то областью решений является та
полуплоскость, в которой находится эта
точка. Если же получаем неверное числовое
неравенство, то областью решений является
та полуплоскость, которой эта точка не
принадлежит. Обычно для контроля берут
точку (0; 0).
Подставим
и
в заданное неравенство. Получим
.
Следовательно, полуплоскость «к нулю»
является областью решений данного
неравенства (заштрихованная часть
рис. 1).
Пример
2.
Найти полуплоскость, определяемую
неравенством
.
Решение.
Строим прямую
,
например, по точкам (0; 0) и (1; 3). Т.к. прямая
проходит через начало координат, точку
(0; 0), то нельзя брать ее для контроля.
Возьмем, например, точку (– 2; 0) и подставим
ее координаты в заданное неравенство.
Получим.
Это неверно. Значит, областью решений
данного неравенства будет та полуплоскость,
которой не принадлежит контрольная
точка (заштрихованная часть рис. 2).
2. Область решений системы линейных неравенств.
Пример.
Найти область решений системы неравенств:
Решение.
Находим область решений I-го
неравенства (рис. 1) и II-го
неравенства (рис. 2).
Все
точки части плоскости, где штриховка
наложилась, будут удовлетворять и
первому и второму неравенству. Таким
образом, получена область решений
заданной системы неравенств (рис. 3).
Если
к заданной системе неравенств добавить
условия
и
,
то область решений системы неравенств
координатной четверти (рис. 4).
Принцип
нахождения решения системы линейных
неравенств не зависит от количества
неравенств, входящих в систему.
Примечание:
Область допустимых решений (ОДР) если
существует, то представляет собой
замкнутый или незамкнутый выпуклый
многоугольник.
3. Алгоритм графического метода решения злп
Если задача
линейного программирования содержит
только две переменные, то ее можно решить
графическим методом, выполняя следующие
операции:
-
Строим все
полуплоскости, соответствующие
ограничениям системы. -
Находим
область допустимых решений (ОДР), как
множество точек, в котором пересекаются
все построенные полуплоскости. -
Строим
вектор
,
выходящий из начала координат, гдеи
– это коэффициенты при неизвестных в
целевой функции.
Этот вектор указывает направление
возрастания целевой функции. -
Перпендикулярно
вектору
проводим так называемую линию уровня
(т.е. прямую
,
проходящую через начало координат). -
Перемещаем
линию уровня
параллельно самой себе в направлении
вектора(если задача на максимум (max))
или в противоположном направлении
(если задача на минимум (min))
до тех пор, пока линия уровня имеет хотя
бы одну общую точку с ОДР. -
Находим
координаты
этой общей крайней точки, решая систему
уравнений прямых, на пересечении которых
она находится. -
Подставляем
эти координаты в целевую функцию и
находим ее max
(или
min).
Пример.
Решить задачу линейного программирования
графическим методом
max
Решение.
Третье и четвертое ограничения системы
– двойные неравенства, преобразуем их
к более привычному для подобных задач
виду
,
этои
,
т.о. первое из полученных неравенств(или
)
относится к условию неотрицательности,
а второек системе ограничений. Аналогично,
это
и
.
Т.о. задача примет
вид
max
,
Заменив знаки
неравенств на знаки точных равенств,
построим область допустимых решений
по уравнениям прямых:

;
;
.
Областью
решений неравенств является пятиугольник
ABCDE.
Построим
вектор
.
Через
начало координат перпендикулярно
вектору
проведем линию уровня
.
И затем будем перемещать ее параллельно
самой себе в направлении векторадо точки выхода из области допустимых
решений. Это будет точкаС.
Найдем координаты этой точки, решив
систему, состоящую из уравнений первой
и четвертой прямых:
.
Подставим
координаты точки С
в целевую функцию и найдем ее максимальное
значение
Пример.
Построить линии уровня
и
для задачи линейного программирования:
max
(min)
Решение.
Область допустимых решений – открытая
область (рис. 6). Линия уровня
проходит через точкуВ.
Функция Z
имеет минимум в этой точке. Линию уровня
построить нельзя, так как нет точки
выхода из области допустимых решений,
это значит, что.
Задания
для самостоятельной работы.
-
Найти область
решений системы неравенств:
а)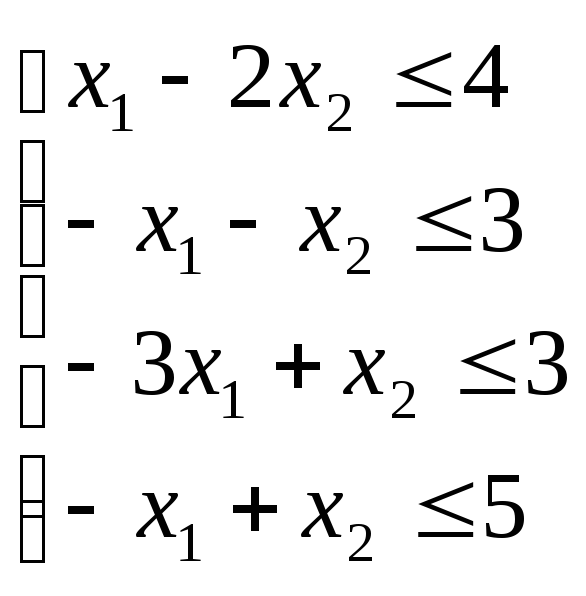
-
Решить графически
задачу линейного программирования
min
-
Составить
экономико-математическую модель и
решить графически задачу линейного
программирования
Фирма
выпускает изделия двух видов А и
В. Изделия каждого вида обрабатывают
на двух станках (I
и II).
Время обработки одного изделия каждого
вида на станках, время работы станков
за рабочую смену, прибыль фирмы от
реализации одного изделия вида А и вида
В занесены в таблицу:
|
Станки |
Время |
Время |
|
|
А |
В |
||
|
I |
10 |
20 |
1300 |
|
II |
4 |
13 |
720 |
|
Прибыль |
0,3 |
0,9 |
Изучение рынка
сбыта показало, что ежедневный спрос
на изделия вида В никогда не превышает
спрос на изделия вида А более чем на 40
единиц, а спрос на изделия вида А не
превышает 90 единиц в день.
Определить план
производства изделий, обеспечивающий
наибольшую прибыль.
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.


9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 





20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
Справочник ОГЭ по математике. 3.2. Неравенства.
3.2.1. Числовые неравенства и их свойства.
3.2.2. Неравенство (линейное) с одной переменной. Решение неравенства.
3.2.3. Линейные неравенства с одной переменной и сводящиеся к ним.
3.2.4. Системы линейных неравенств. Совокупности неравенств.
3.2.5. Квадратные неравенства. Метод интервалов.
Вы смотрели конспект по математике «3.2. Неравенства (справочник ОГЭ)».
OСR-текст раздела (только текст)

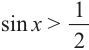
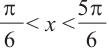
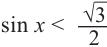
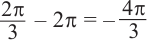
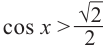
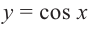
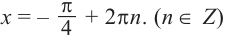
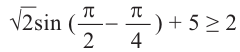
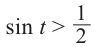
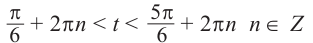
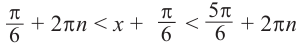
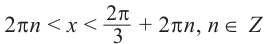


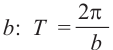
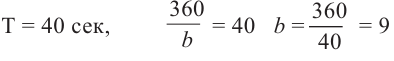
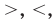
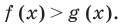
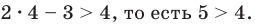
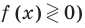
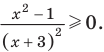
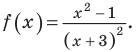
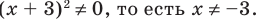
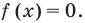
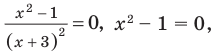
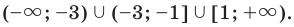

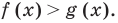
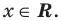
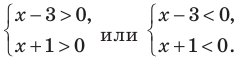
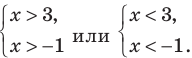
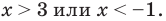
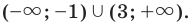
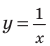 (рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);
(рис. 100, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);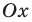 (как в случае функции
(как в случае функции 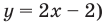 (рис. 100,6).
(рис. 100,6).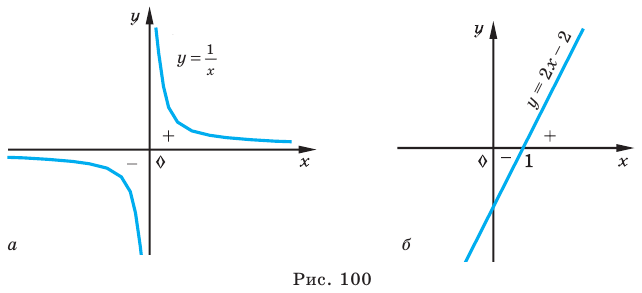
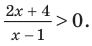
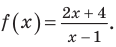
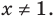
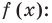
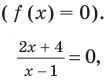
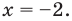
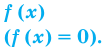
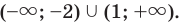

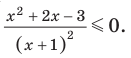
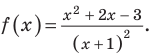
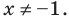
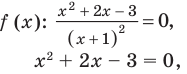
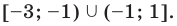
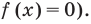
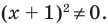
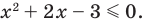
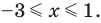
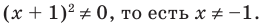
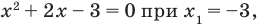
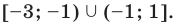
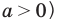
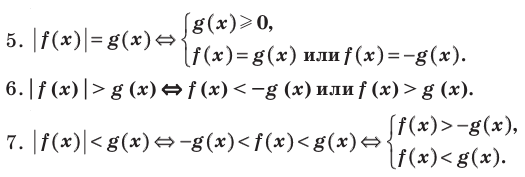
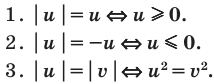
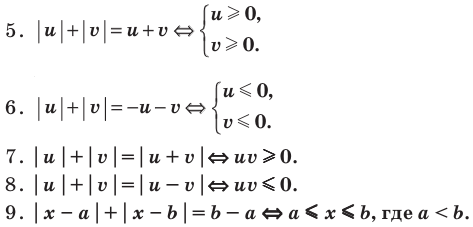
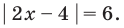
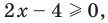 то получаем уравнение
то получаем уравнение 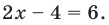 Тогда
Тогда 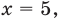 что удовлетворяет и условию (1).
что удовлетворяет и условию (1).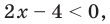 то получаем уравнение
то получаем уравнение 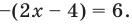 Тогда
Тогда 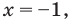 что удовлетворяет и условию (2).
что удовлетворяет и условию (2).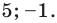
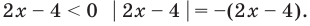
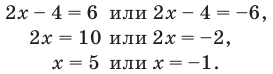
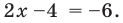
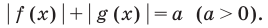
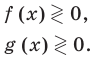
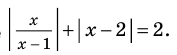
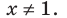
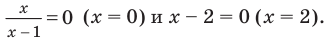
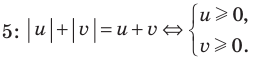
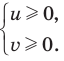
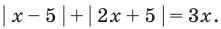
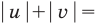
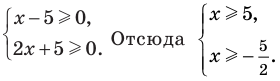
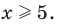
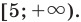
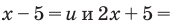
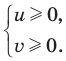
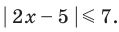
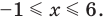
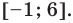
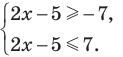
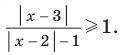
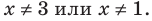
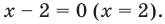
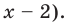
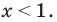
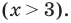
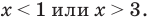
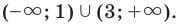
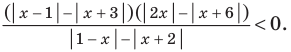
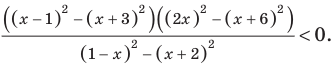
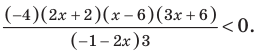
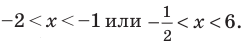
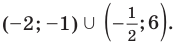
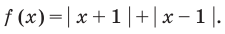
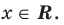
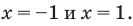

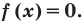
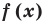 в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).
в каждом из промежутков, на которые разбивается ОДЗ (на одном периоде).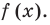
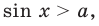

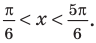
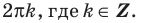
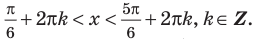
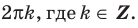
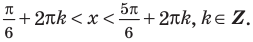
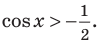
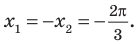
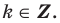
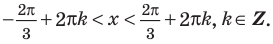
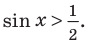
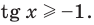
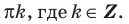
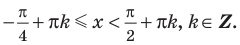
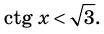
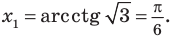
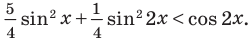
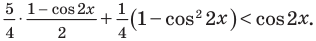
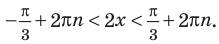
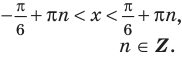
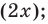
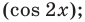
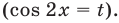 После обратной замены решим полученные простейшие тригонометрические неравенства.
После обратной замены решим полученные простейшие тригонометрические неравенства.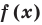 (если он существует).
(если он существует).