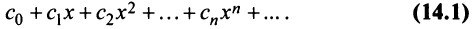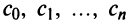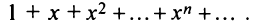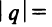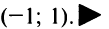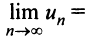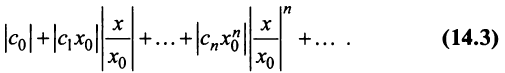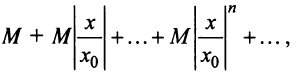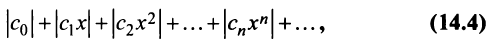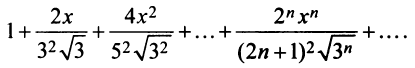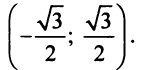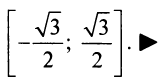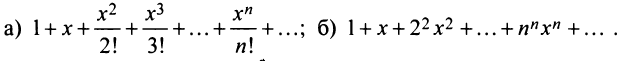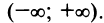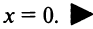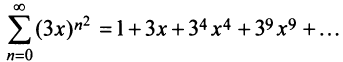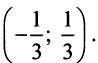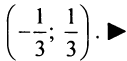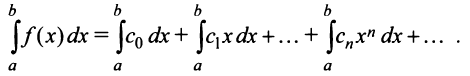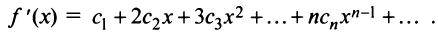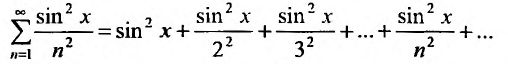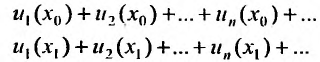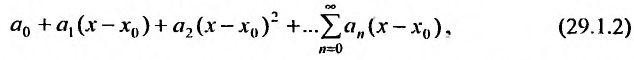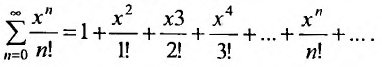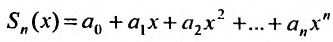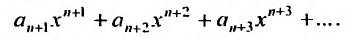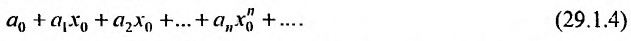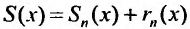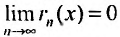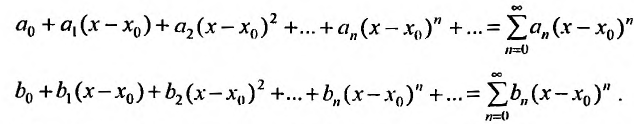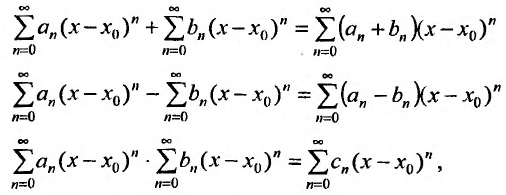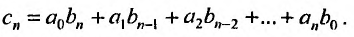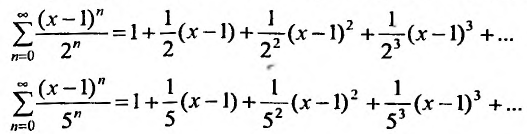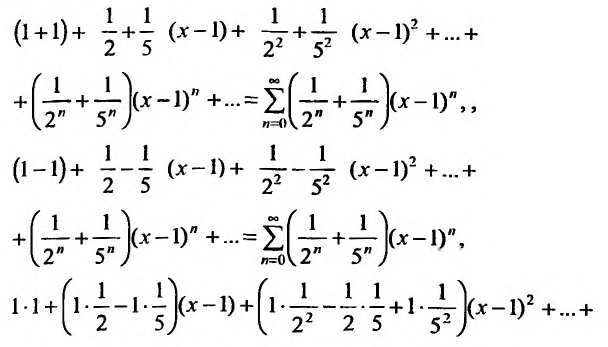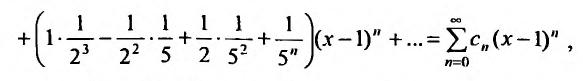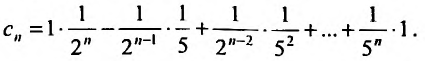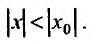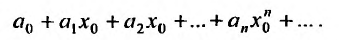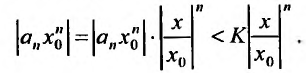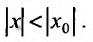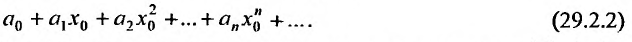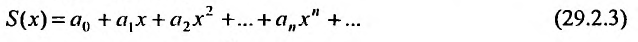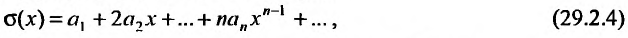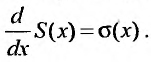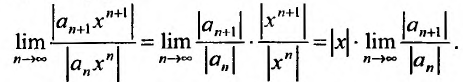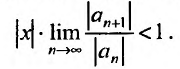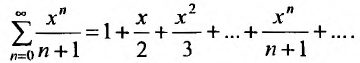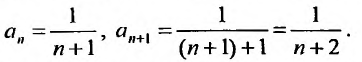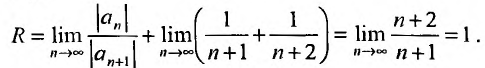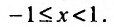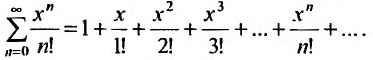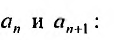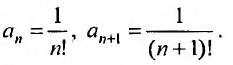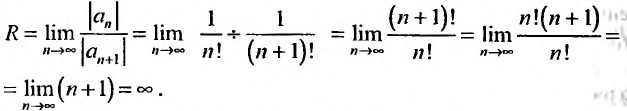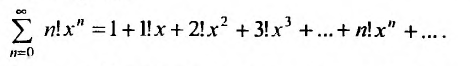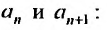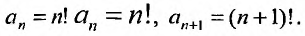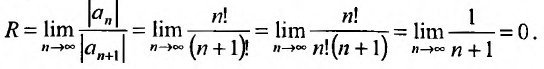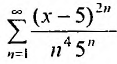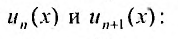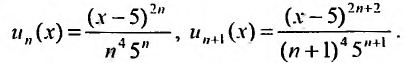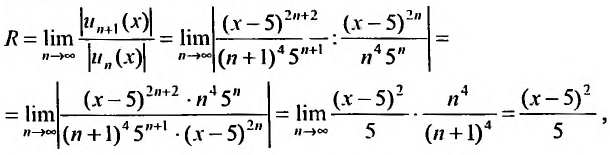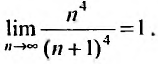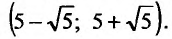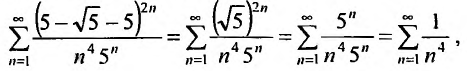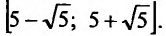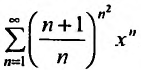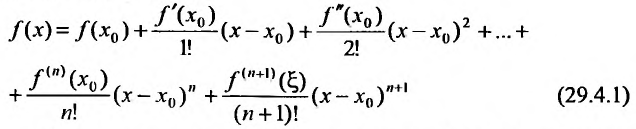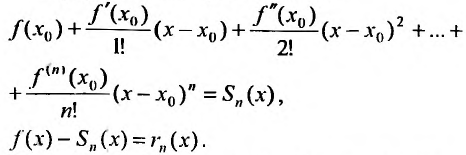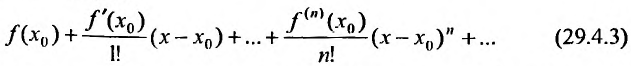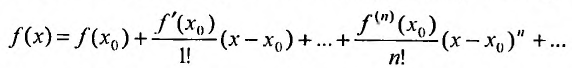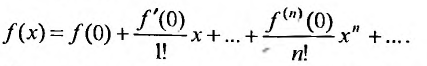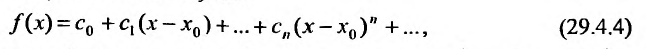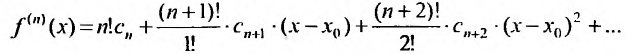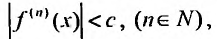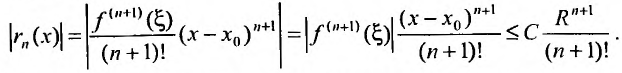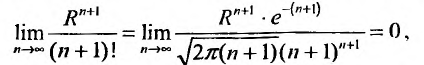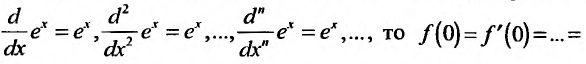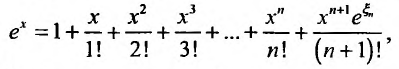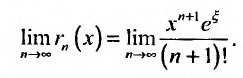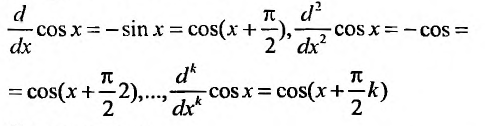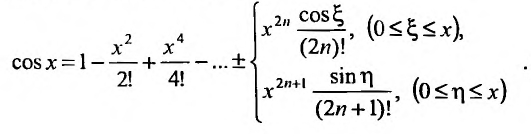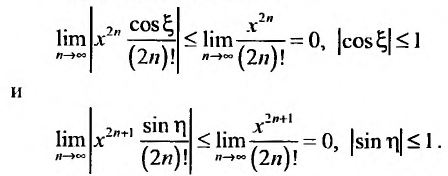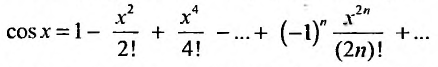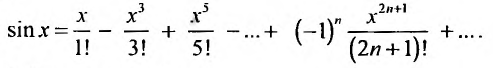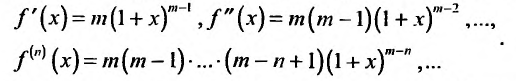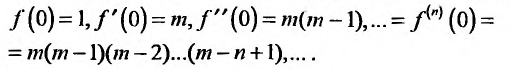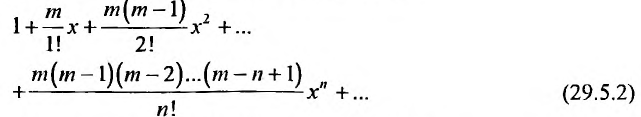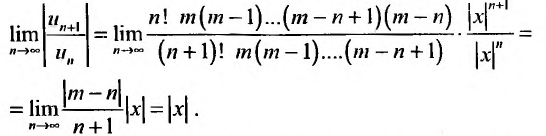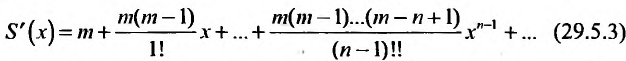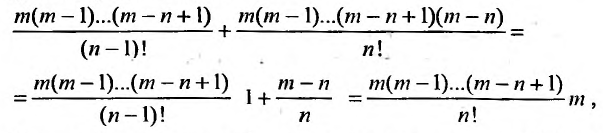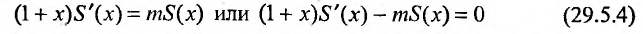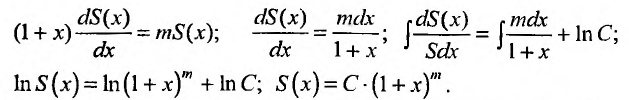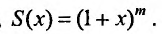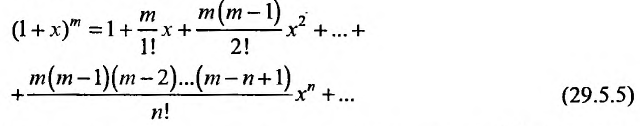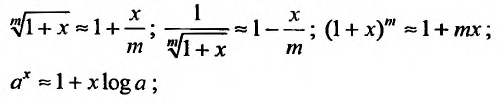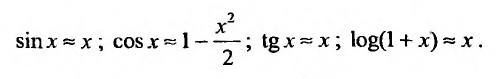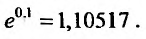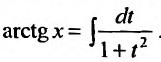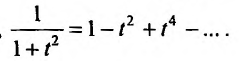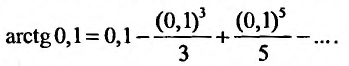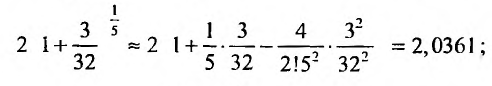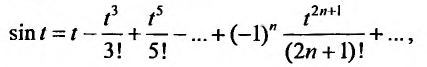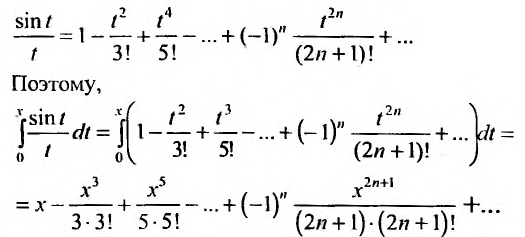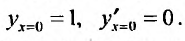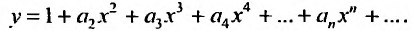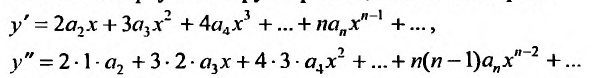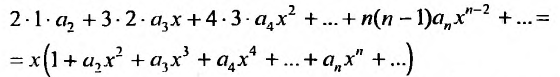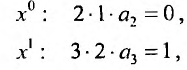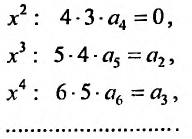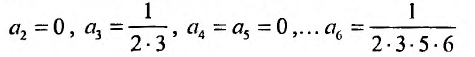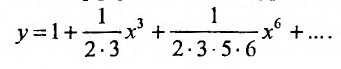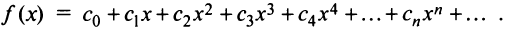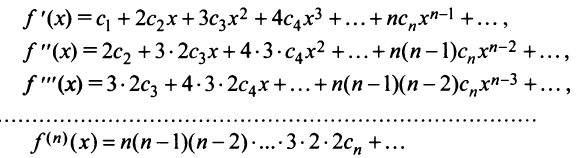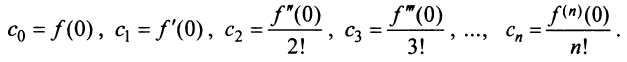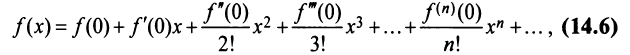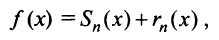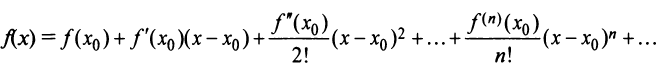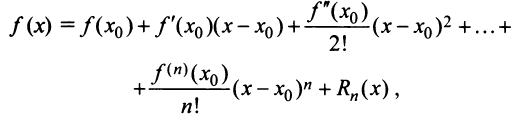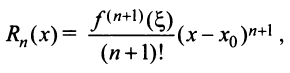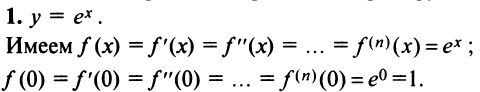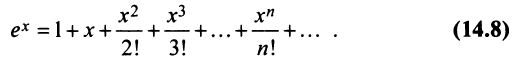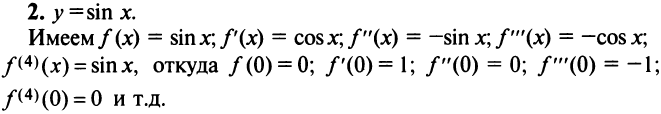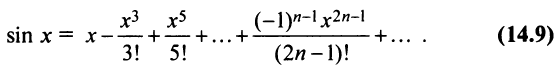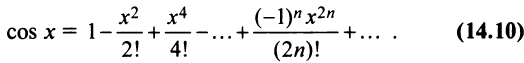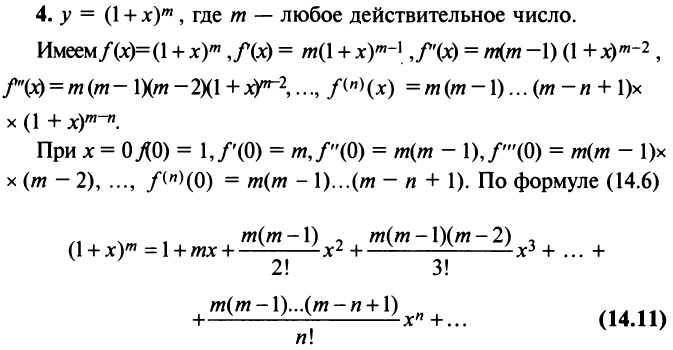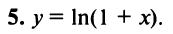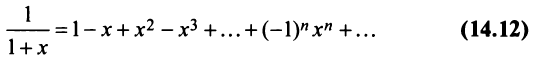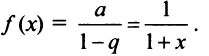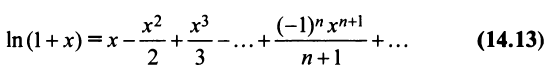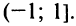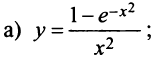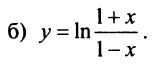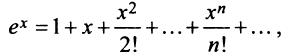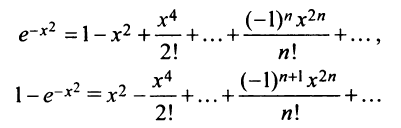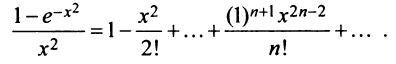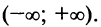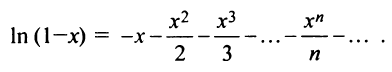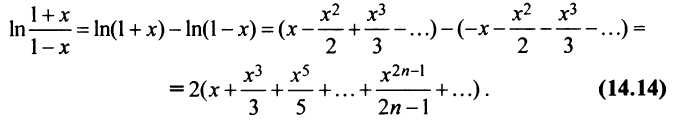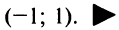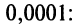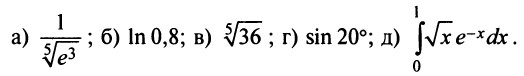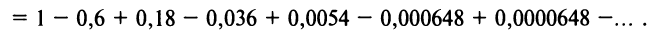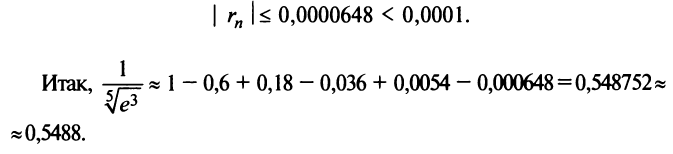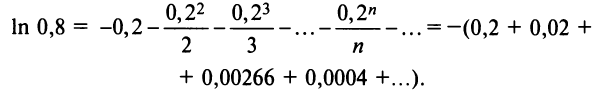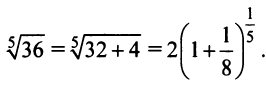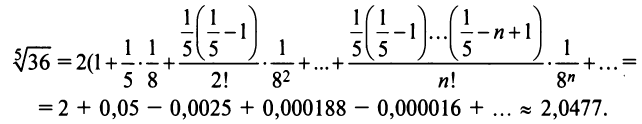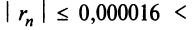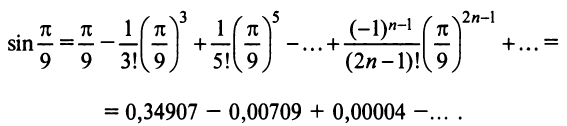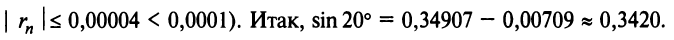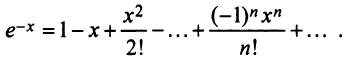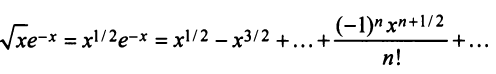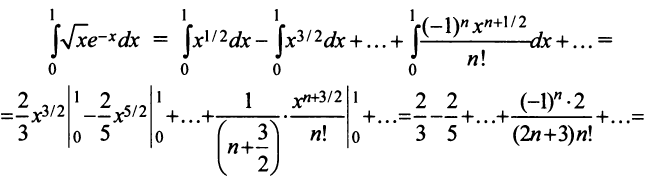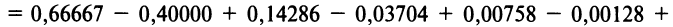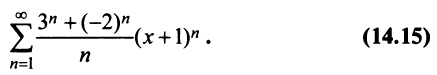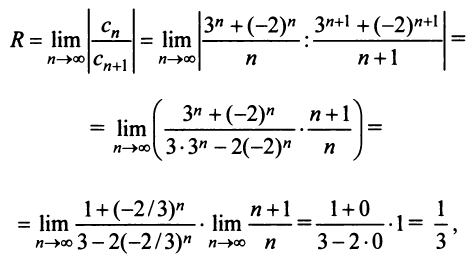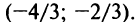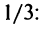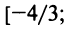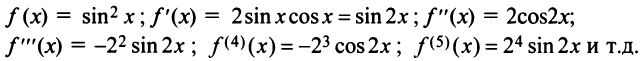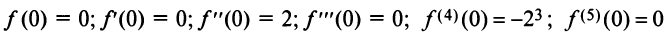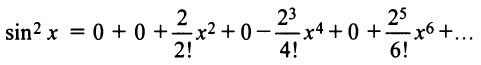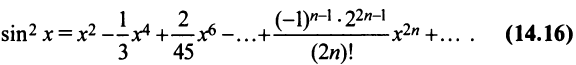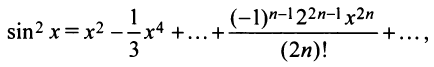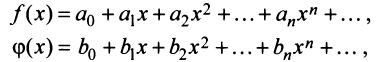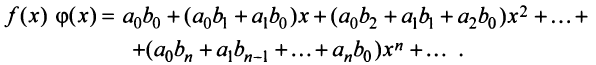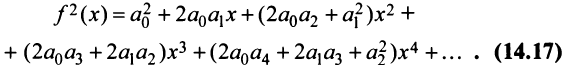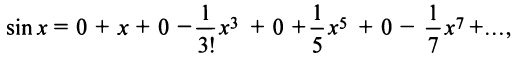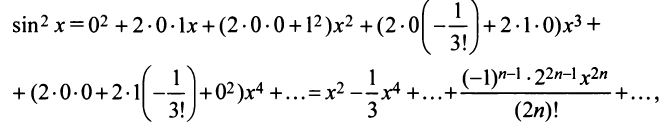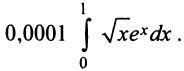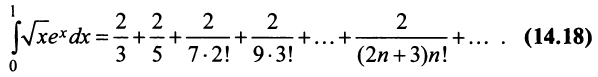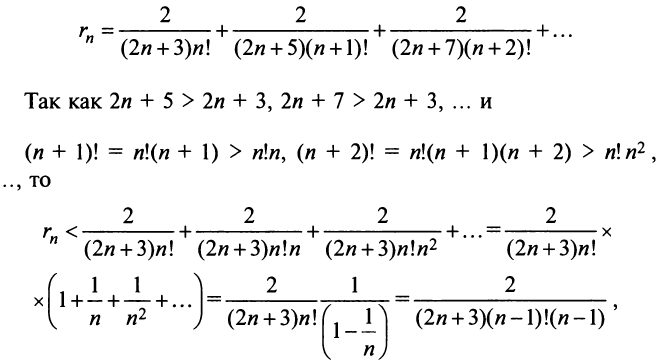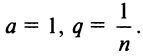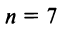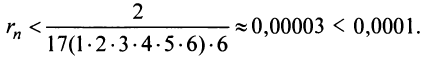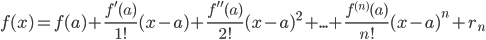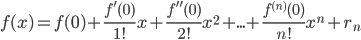Содержание:
Степенные ряды:
До сих пор мы рассматривали ряды, членами которых были числа, т.е. числовые ряды. Теперь перейдем к рассмотрению рядов, членами которых являются функции, в частности степенные функции
Такие ряды называются степенными, а числа
Область сходимости степенного ряда
Совокупность тех значений 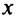
Пример:
Найти область сходимости степенного ряда
Решение:
Данный ряд можно рассматривать как геометрический ряд со знаменателем 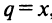
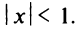
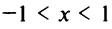
Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.
Теорема Абеля. 1) Если степенной ряд сходится при значении 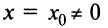
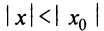
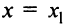
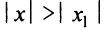
1) По условию ряд (14.1) сходится при 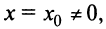
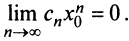
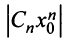
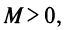
Рассмотрим ряд, составленный из абсолютных величин членов ряда (14.1) 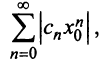
Члены ряда (14.3) согласно неравенству (14.2) меньше соответствующих членов ряда
представляющего геометрический ряд, который сходится, когда его знаменатель 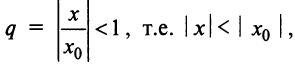
2) По условию ряд (14.1) расходится при 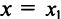
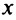
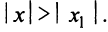
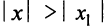
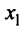
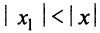
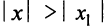
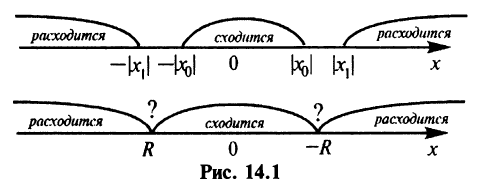
Из теоремы Абеля (см. рис. 14.1) следует, что существует такое число 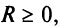
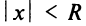
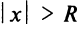
Число 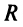
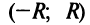
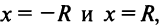
Найдем выражение радиуса сходимости степенного ряда (14.1) через его коэффициенты. Рассмотрим ряд, составленный из абсолютных величин его членов
в котором все коэффициенты 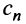
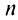
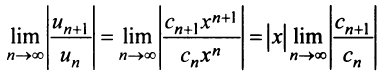
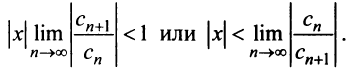
Замечание. Следует отметить, что у некоторых рядов интервал сходимости вырождается в точку 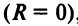
Пример:
Найти область сходимости степенного ряда
Решение:
Найдем радиус сходимости ряда по формуле (14.5) 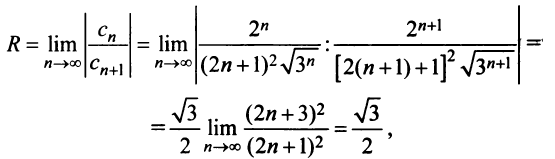
Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при 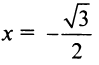
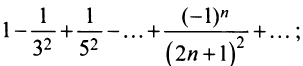
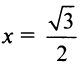
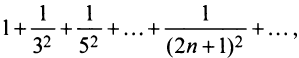
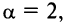
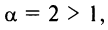
Следует отметить, что сходимость ряда на левом конце ин-тервала сходимости при 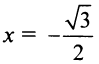
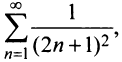
Итак, область сходимости данного ряда
Замечание. При исследовании сходимости на концах интервала сходимости для получающегося ряда с положительными членами применять признак Даламбера не имеет смысла, так как в этом случае всегда будем получать 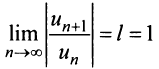
Пример:
Найти области сходимости степенных рядов:
Решение:
а) Радиус сходимости ряда по (14.5)
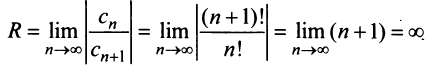
б) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что 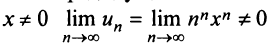
Итак, область сходимости ряда состоит из одной точки
Пример:
Найти область сходимости ряда
Решение:
Найти радиус сходимости по формуле (14.5) в данном случае не представляется возможным, так как коэффициенты ряда 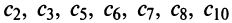

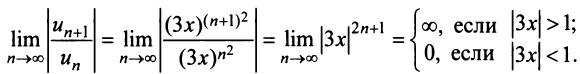
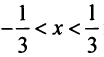
Исследуем сходимость на концах интервала сходимости: при 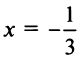
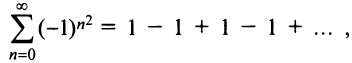
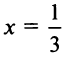
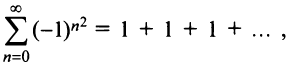
Итак, область сходимости ряда
Свойства степенных рядов. Пусть функция 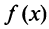
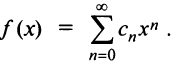
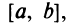
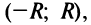
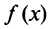
Кроме того, в интервале сходимости степенной ряд можно почленно дифференцировать:
При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости
Определение степенного ряда и его сходимости
Понятое функциональной зависимости является одним из важнейших в математике. Всякая функция осуществляет некоторое соответствие между объектами, составляющими область задания этой функции, и объектами, составляющими область её значений. Так можно рассматривать функции, которые ставят в соответствие числам — ряды. Эти функции называются функциональными рядами, т.е. функциональный ряд это выражение
членами которого являются некоторые функции переменной х. Например, ряд
является функциональным рядом.
Придавая в выражении (29.1.1) переменной х некоторые значения 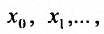
которые могут оказаться, как сходящимися, так и расходящимися.
В простейших случаях для определения сходимости ряда (29.1.1) можно применять к нему известные признаки сходимости числовых рядов, считая х фиксированным.
Определение 29.1.1. Совокупность всех значений переменной х, для которых соответствующие числовые ряды сходятся, называется областью сходимости функционального ряда (29.1.1). Определение 29.1.2. Функциональный ряд вида
где 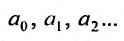
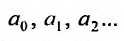
Если в ряде (29.1.2) сделать замену переменного, положив
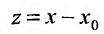
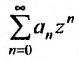
Очевидно, что исследование сходимости ряда (29.1.2) эквивалентно исследованию сходимости ряда (29.1.3). Примером степенного ряда может служить ряд
Сумма п первых членов ряда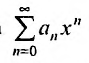
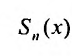
Для степенного ряда можно составить последовательность частичных сумм 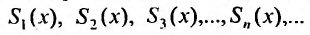
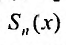
Остатком степенного ряда после n -го его члена (или n -ым остатком) называется ряд, полученный из заданного исключением n его первых членов:
Определение 29.1.3. Степенной ряд называется сходящимся на некотором множестве, если он сходится в любой точке этого множества.
Степенной ряд называется абсолютно сходящимся на некотором множестве, если в каждой точке этого множества сходится ряд из модулей его членов:
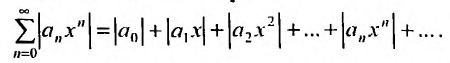
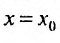
Соответствующий числовой ряд а0 +о,л:0 +… сходится абсолютно, если сходится ряд 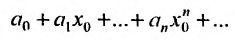
Так как каждой точке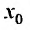
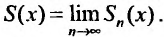
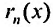
Для сходящегося степенного ряда предел остатка равен нулю:
Степенные ряды можно складывать, вычитать, умножать. Пусть заданы два степенных ряда:
Сумма, разность и произведение заданных степенных рядов определяется формулами:
где
Например, сумма, разность и произведение степенных рядов:
имеет вид:
где
Радиус сходимости, интервал сходимости
Области сходимости степенных рядов устроены довольно просто. Они описываются следующей теоремой.
Теорема 29.2.1 (теорема Абеля). Если степенной ряд
сходится при некотором 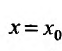
Если же степенной ряд (29.2.1) расходится при 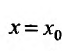
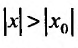
Доказательство. Предположим сначала, что степенной ряд (29.2.1) сходится в точке 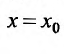
Тогда, в силу необходимого признака сходимости, 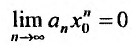
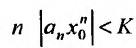
Если 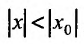
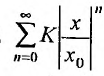
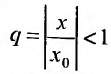
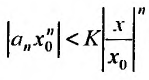
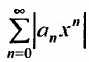
Предположим теперь, что степенной ряд (29.2.1) расходится, при 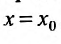
Возьмём тогда некоторое значение х, для которого 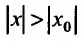
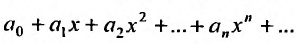
сходится. Но тогда из сходимости этого ряда, в силу первой части доказательства теоремы, вытекает сходимость ряда (29.2.2), что противоречит предположению, о его расходимости. Полученное противоречие означает, что для всех 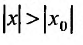
Если ряд (29.2.1) имеет вещественные коэффициенты и переменная х принимает только вещественные значения, то справедливо следующее определение, вытекающее из теоремы Абеля.
Определение 29.2.1. Величина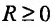
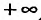
такая, что при всех х, у которых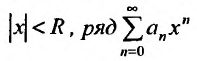
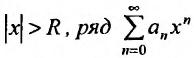
Множество точек х удовлетворяющих соотношению 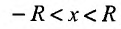
Итак, из определения 29.2.1 и теоремы Абеля следует, что областью сходимости степенного ряда — является интервал сходимости. И если значение 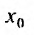
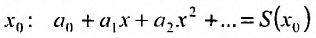
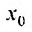
Свойства степенных рядов
Для степенных рядов справедливы следующие свойства:
1) Степенной ряд сходится равномерно внутри интервала сходимости.
2) Внутри интервала сходимости ряда сумма его является непрерывной функцией.
3) Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
4) Если степенной ряд
имеет радиус сходимости R , то и ряд
получаемый в результате почленного дифференцирования ряда (29.2.3) также имеет радиус сходимости R. Производная суммы ряда (29.2.3) равна сумме ряда (29.2.4), т.е.
Вычисление интервала сходимости
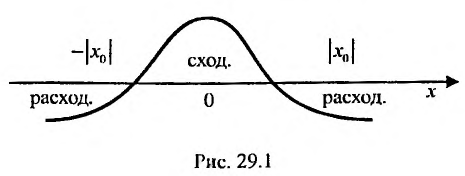
Как уже было сказано в и. 2 областью сходимости степенного ряда является интервал сходимости. Более того, из теоремы Абеля следует, что областью сходимости степенного ряда является интервал с центром в начале координат (рис 29.1).
Действительно, если 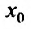
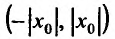
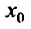
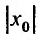
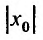
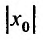
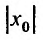
Заметим, что на концах интервала вопрос о сходимости или расходимости решается индивидуально в каждом конкретном случае. У некоторых рядов интервал сходимости может вырождаться в точку, у других охватывать всю ось Ох.
Укажем теперь способ вычисления радиуса сходимости степенного ряда.
Пусть задан степенной ряд 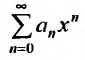
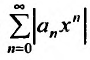
вычислим предел
Если этот предел меньше единицы, то, как следует из признака Д’Аламбера, ряд, составленный из модулей членов ряда (29.2.1) сходится, т.е. ряд сходится если
Если же 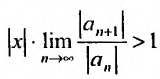
А это означает, что если 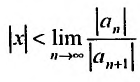
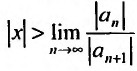
Учитывая определение радиуса сходимости степенного ряда, получим, что радиус сходимости можно вычислить по формуле:
Рассуждая аналогичным образом можно получить еще одну формулу для определения радиуса сходимости:
Если степенной ряд содержит только четные или нечетные степени х, то применяем признак Д’Аламбсра или Коши к ряду, составленному из модулей членов данного ряда.
Пример №1
Найти радиус и интервал сходимости степенного ряда:
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
Итак, степенной ряд сходится для |х| 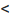
Исследуем сходимость ряда на концах интервала сходимости.
Пусть х =—1. Тогда получим знакочередующийся ряд 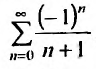
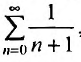
Суммируя вышесказанное, получим интервал сходимости
Пример №2
Найти радиус и интервал сходимости степенного ряда
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.2):
Так как 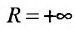
Пример №3
Найти радиус и интервал сходимости степенного ряда:
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
Так как радиус сходимости равен нулю, то ряд сходится только в одной точке x= 0.
Пример №4
Найти радиус и интервал сходимости степенного ряда
Решение:
Данный ряд содержит только четные степени (а- — 5), коэффициенты при нечетных степенях равны нулю. Поэтому воспользоваться формулами (29.3.1) и (29.3.2) не представляется возможным.
Считая х фиксированным, применим признак Д’Аламбера к ряду, составленному из модулей членов данного ряда. Выпишем значения
Тогда
так как
Ряд сходится, если 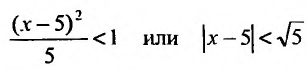
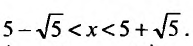
Исследуем сходимость ряда на концах интервала сходимости. Пусть 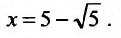
который сходится, как ряд Дирихле, для которого а = 4. При 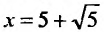
Пример №5
Найти радиус и интервал сходимости степенного ряда
Решение:
Выпишем значение 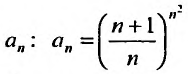
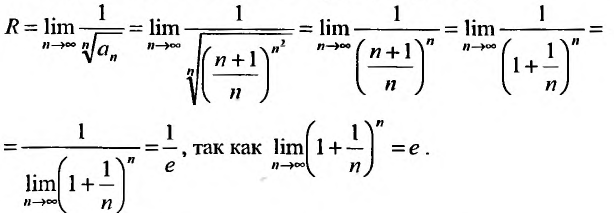
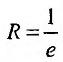
Исследуем его сходимость на концах интервала.
Пусть 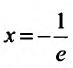
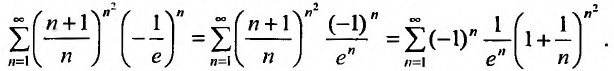
Следовательно, данный ряд расходится. И при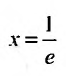
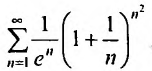
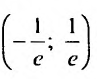
Ряды Тейлора и Маклорена
Как уже отмечалось, сумма сходящегося степенного ряда является некоторой функцией, определенной внутри интервала сходимости. В связи с этим мы рассмотрим задачу разложения некоторой функции в ряд, т.е. будем по заданной функции искать сходящийся ряд того или иного типа, сумма которого в интервале сходимости равнялась бы заданной функции.
Известно, что если функция f имеет на некотором отрезке производные всех порядков, то можно написать формулу Тейлора для любого значения n:
где 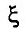
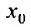
В формуле Тейлора обозначим:
пункта 27.2 (теорема 27.2.1) следует, что если
то степенной ряд
сходится и его суммой будет функция f(х), так как 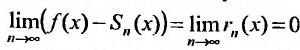
Справедливо и обратное утверждение, что если степенной ряд (29.4.3) сходится, то выполняется (29.4.2).
Определение 29.4.1. Представление функции f в виде ряда
называется разложением этой функции в ряд Тейлора. Если же 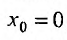
Следует заметить, что остаточный член в формуле Тейлора для функции J не обязательно является остатком ряда Тейлора для этой функции. Поэтому из сходимости ряда Тейлора для функции f , еще не следует сходимость именно к этой функции. При разложении функции в ряд Тейлора необходимо проверять условие (29.4.2). Однако сели разложение функции в какой-либо степенной ряд вообще возможно, то оно является разложением в ряд Тейлора, т.е. справедлива следующая теорема.
Теорема 29.4.1. Пусть
и стоящий справа ряд сходится в интервале 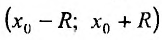
Доказательство. Так как степенной ряд в интервале сходимости можно почленно дифференцировать, то n-ую производную функции (29.4.4) можно представить в виде:
Полагая в последнем тождестве 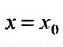
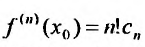
Из доказанной теоремы вытекает, что в одной и той же области, для одной и той же функции существует единственное разложение.
На практике, для разложения функции в ряд Тейлора, удобно пользоваться следующей теоремой.
Теорема 29.4.2. Если при любых х, удовлетворяющих неравенству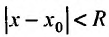
то ряд Тейлора, для этой функции, сходится в интервале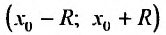
Доказательство. Из условия теоремы следует, что функцию f можно представить формулой Тейлора с остаточным членом в форме Лагранжа, т.е.
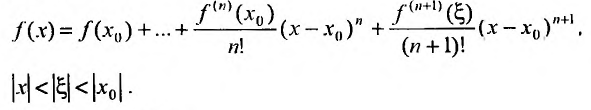
Переходя к пределу при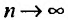
Воспользовавшись асимптотической формулой Стерлинга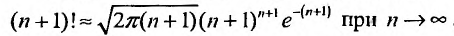
так как стспснно-показательная функция 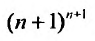
Тогда из неравенства (29.4.6) получим: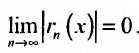
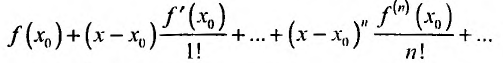
Разложение некоторых элементарных функций в ряд Маклорена
Из пункта 29.4 следует, что для того чтобы некоторая функция разлагалась в ряд Тейлора нужно, чтобы она имела производные любого порядка и чтобы либо 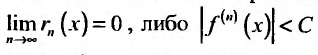
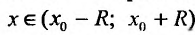
1. Разложение функции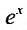
Находим производные данной функции и их значения при х=0. Так как
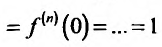
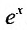
где 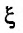
Вычислим предел остаточного члена, для любого х:
Выражение 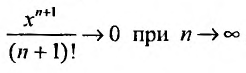
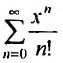
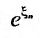
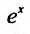
Следовательно, ряд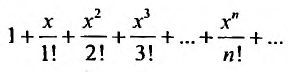
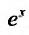
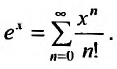
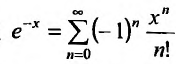
2. Разложение функций cos х и sin х. Для функции cos x имеем:
Следовательно,
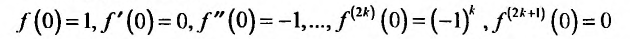
Маклорена с остаточным членом в форме Лагранжа для функции cosx имеет вид:
Ясно, что для любого X
Поэтому, функция cos л- разлагается в ряд Маклорена вида:
Аналогично получается разложение в ряд Маклорена функции sinx:
3. Биномиальный ряд.
Найдем разложение в степенной ряд функции
где m -произвольное действительное число.
Дифференцируя равенство (29.5.1) n раз, получим:
Значения функции и се производных при х = 0 равны:
Следовательно, ряд Маклорена имеет вид:
Если m- целое, то выражение (29.5.2) содержит конечное число членов. Если же m- нецелое, то выражение (29.5.2)- бесконечный ряд, называемый биномиальным.
Определим вначале радиус сходимости этого ряда, для чего применим признак Д’Аламбсра к ряду, составленному из модулей его членов:
Следовательно, при |х| 
Покажем теперь, что ряд (29.5.2) сходится к функции 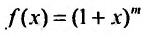
Умножим обе части (29.5.3) на 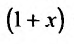
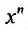
Эта сумма, как показано, равна произведению коэффициента при 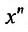
С другой стороны, вычисляя производную отношения
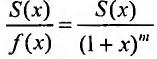
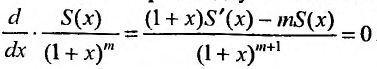
Решая дифференциальное уравнение 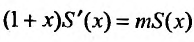
Пусть x = 0, тогда S(0) = С. Из (29.5.2) следует, что S(0) = 1, тогда С = 1.
Следовательно,
Итак, разложение
имеет место при всех х, удовлетворяющих условию 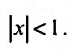
Применение рядов в приближенных вычислениях
Разложения функций в ряд Маклорена позволяют во многих случаях вычислить с большой степенью точности значения этих функций, заменяя ее конечным числом членов разложения. Чем меньше х, тем меньше членов можно брать в этом разложении для вычисления f(х) с желаемой точностью. Если х весьма мало, то достаточно ограничится первыми двумя членами, отбросив все остальные. Например, при х близких к нулю можно пользоваться следующими приближенными формулами:
Например, вычислим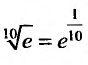
Имеем, 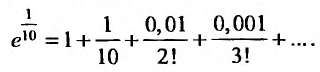
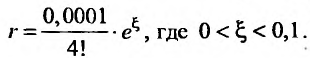
Иногда при вычислении значений функций удобно пользоваться почленным дифференцированием или интегрированием рядов.
Например, известно, что
С другой стороны,
Следовательно,
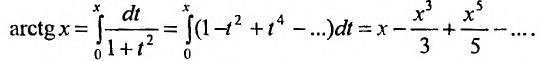
Этот ряд знакочередующийся. Поэтому, его остаток не превосходит первого «отброшенного» члена. Удерживая в разложении первых два слагаемых, получим значение arctg 0,1 = 0,09967 с пятью верными знаками.
При помощи биномиальною ряда можно быстро и довольно точно вычислять значение корней из чисел.
Пример №6
Вычислить 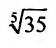
Решение:
Представим, этот корень в виде
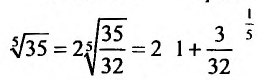
следующим член 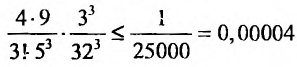
В общем случае можно записать:
где 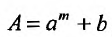
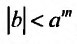
Кроме того, биномиальный ряд является основой многих дальнейших разложений функций в ряды. Например, можно найти разложение в ряд Маклорена функции:
При помощи рядов можно вычислять определенные интегралы.
Например, вычислим интегральный синус:
Имеем
тогда
Подставляя вместо x, те или иные конкретные значения переменной, мы можем вычислять интересующие нас значения интегрального синуса.
При помощи разложении в степенные ряды можно приближенно интегрировать разнообразные дифференциальные уравнения.
Например, найдем решение уравнения 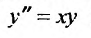
Будем искать решение этого уравнения в виде степенного ряда: 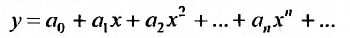
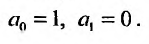
Вычислим первую и вторую производные от этого ряда:
и подставив у, 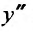
приравняем коэффициенты при равных степенях .г, предварительно умножив правую часть на х:
Получаем систему уравнений, из которой находим:
Замечаем, что отличными от нуля будут лишь те коэффициенты, у которых индекс и степень делятся на 3. Получим решение заданного дифференциального уравнения в виде:
- Заказать решение задач по высшей математике
Ряд Маклорена
Предположим, что функция 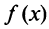
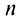
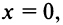
Выразим коэффициенты ряда через 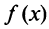
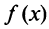
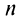
Полагая в полученных равенствах 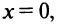
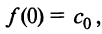
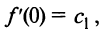
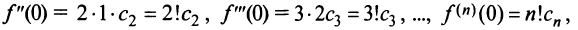
Подставляя значения коэффициентов 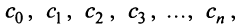
называемый рядом Маклорена.
Следует отметить, что не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд Маклорена, составленный формально для функции 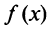
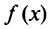
Так же как и для числовых рядов, сумму 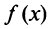
где 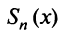
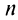
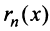
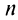
Тогда на основании свойства 4 сходящихся рядов (см. §13.1) можно сформулировать теорему.
Теорема. Для того чтобы ряд Маклорена сходился к функции 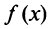
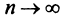
для всех значений 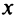
Можно доказать, что если функция 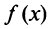
Замечание. Ряд Маклорена является частным случаем ряда Тейлора:
при
Ряд Тейлора тесно связан с формулой Тейлора.
где 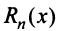
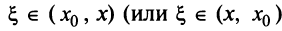
Очевидно, что при выполнении условия (14.7) остаток 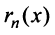
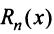
Разложение в ряд Маклорена некоторых функций
По формуле (13.6)
Область сходимости ряда 
Очевидно, что производные четного порядка 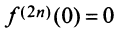
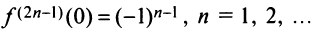
Область сходимости ряда
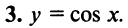
Область сходимости ряда
Интервал сходимости ряда 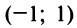
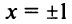
Ряд (14.11) называется биномиальным. Если 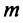
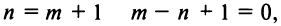
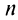
Получить разложение для этой функции можно проще, не вычисляя непосредственно коэффициенты ряда (14.6) с помощью производных.
Рассмотрим геометрический ряд
со знаменателем 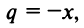
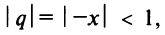
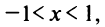
Интегрируя почленно равенство (14.12) в интервале 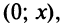
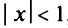
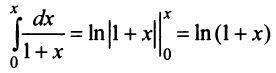
Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть
Можно доказать, что ряды, приведенные в формулах (14.8) — (14.13), сходятся к функциям, для которых они составлены.
При разложении более сложных функций используют непосредственно формулу (14.6) либо таблицу простейших разложений (14.8) — (14.13).
Пример №7
Разложить в ряд функции:
Решение:
а) Так как по (14.8)
то, заменяя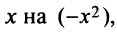
и, наконец,
Область сходимости ряда
б) В разложении 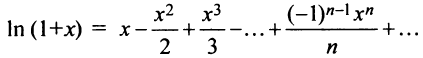
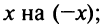
Теперь
Область сходимости ряда
Применение рядов в приближенных вычислениях
Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «неберущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.
Пример №8
Вычислить приближенно с точностью до
Решение:
а) Для вычисления 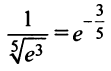
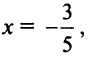
Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница (см. § 13.4) для сходящегося знакочередующегося ряда мы допустим погрешность 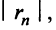
б) Для вычисления 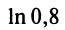
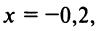
Если в качестве 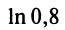
(Мы учли, что сумма сходящегося геометрического ряда в
скобках равна 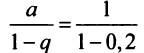
Следует отметить, что для вычисления логарифмов более удобным является ряд (14.14), который сходится быстрее ряда (14.13). Действительно, пусть 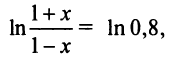
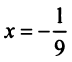
т.е. для вычисления 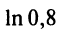
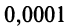
в) Представим 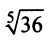
Так как 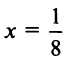
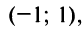
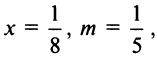
(Для обеспечения данной точности расчета необходимо взять 4 члена, так как по следствию из признака Лейбница для сходящегося знакочередующегося ряда погрешность 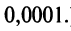
г) Для вычисления 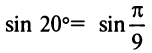
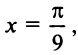
(Необходимо взять два члена, так как при этом погрешность
д)«Точное» интегрирование здесь невозможно, так как интеграл «неберущийся». Заменив 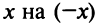
Умножая полученный ряд на
и почленно интегрируя в интервале 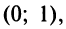
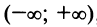
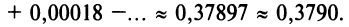
Пример №9
Исследовать сходимость ряда
Решение:
Радиус сходимости ряда (14.15), заданного по степеням 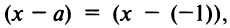
т.е. 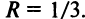
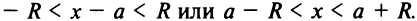
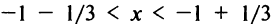
Исследуем сходимость ряда (14.15) на концах этого интервала. При 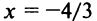
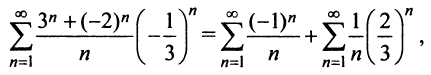
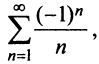
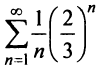
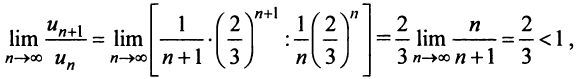
При 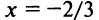
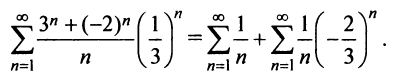
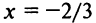
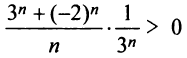
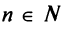
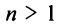
Итак, область сходимости степенного ряда (14.15)
Пример №10
Разложить в ряд Маклорена функцию
Решение:
Первый способ. Применим метод непосредственного разложения по формуле (14.6).
Вначале найдем производные до «-го порядка и вычислим их значения при
При 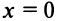
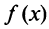
и т.д. Теперь по формуле (14.6) запишем ряд
или
Второй способ. Учитывая, что 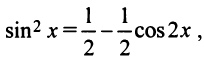
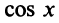
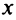
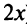
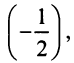
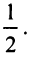
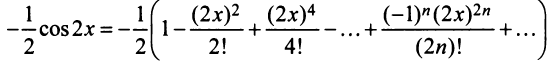
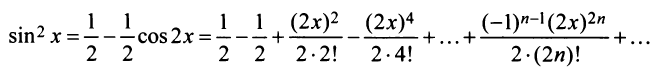
т.е. то же разложение (14.16).
Третий способ. Разложение функции 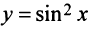
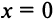
то произведение функций разлагается в той же окрестности в степенной ряд
В частности, при 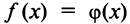
Для функции 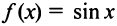
находим по формуле (14.17)
т.е. получили то же разложение (14.16).
Область сходимости ряда, как нетрудно убедиться, есть 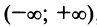
Пример №11
Вычислить с точностью до
Решение:
Выражение данного интеграла в виде числового ряда находится
Вычисление интеграла свелось не к нахождению суммы сходящегося знакочередующегося ряда, при вычислении которой погрешность оценивается с помощью следствия из теоремы Лейбница, а к определению суммы ряда с положительными членами с неизвестной оценкой погрешности.
Поступим следующим образом. Предположим, что для оценки суммы ряда мы взяли 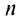
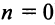
ибо выражение в круглых скобках представляет сумму сходящегося геометрического ряда (13.5) при
При
(Легко вычислить, что при любых 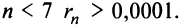
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
Степенные ряды и их сходимость
Степенной ряд в общем виде записывается как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k,
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots – постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости.
Ряд называют сходящимся, когда для частичных сумм Sn(x)S_n(x):
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)nS_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n
существует предел, сумма ряда S(x)S(x):
limn→∞Sn(x)=S(x)limlimits_{n to infty } S_n (x) = S (x)
Интервал сходимости степенного ряда определяется радиусом сходимости:
∣x−x0∣<R|x-x_0|<R
Сходимость на границе области ∣x−x0∣=R|x-x_0|=R, обычно исследуется дополнительно. Степенной ряд вида:
∑k=1∞ak(x−x0)ksumlimits_{k=1}^{infty} a_k(x-x_0)^k
сходится равномерно в любом круге вида ∣x−x0∣≤r|x-x_0| le{r}, целиком лежащем внутри круга сходимости.
Примеры степенных рядов
2!(x−2)2+3!(x−5)24+…+(n+1)!(x−2)n2n+…=∑k=1∞(k+1)!(x−2)k2kfrac{2!(x-2)}{2}+frac{3!(x-5)^2}{4}+ldots +frac{(n+1)!(x-2)^n}{2^{n}} +ldots =sum limits_{k=1} ^{infty} frac{(k+1)!(x-2)^k}{2^{k}}
x28ln22−x316ln32+x432ln42−…+(−1)nxn2n+1lnn2+…=∑k=2∞(−1)kxk2k+1lnk2frac{x^{2}}{8ln^{2}{2}}-frac{x^{3}}{16ln^{3}{2}}+ frac{x^{4}} {32ln^{4}{2}}-ldots+(-1)^nfrac{ x^{n}}{2^{n+1}ln^{n}{2}}+ldots = sumlimits_{k=2}^{infty} (-1)^k frac{x^{k}}{2^{k+1}ln^{k}{2}}
Разложение функций в ряд Тейлора и Маклорена
Возьмем функцию f(x)f(x), которая является бесконечно дифференцируемой в точке x0x_0. Такую функцию можно разложить в степенной ряд следующего вида:
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{»}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд по степеням двучлена (x−x0)(x-x_0 ) называют рядом Тейлора.
В случае x0=0x_0=0 полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{»}(0)}{2!}(x-x_0)^2 +ldots+ dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Ряд Тейлора можно свести к ряду Маклорена, используя замену переменных:
x−x0=t,f(x)=f(x0+t)=g(t)x-x_0=t, quad f(x)=f(x_0+t)=g(t)
Подставив:
f(x)=f(x0+t)=f(0)+f′(x0)1!t+f′′(x0)2!t2+…+f(n)(x0)n!tn+…=∑k=0∞f(k)(x0)k!tkf(x)=f(x_0+t)=f(0)+dfrac{f{‘}(x_ 0)}{1!} t +dfrac{f{»}(x_0)}{2!}t^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}t^k
получаем ряд Маклорена:
g(t)=g(0)+g′(0)1!t+…+g(n)(0)n!tn+…=∑k=0∞g(k)(0)k!tkg(t)=g(0)+dfrac{g{‘}( 0)}{1!}t +ldots+dfrac{g^{(n)}(0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{g^{(k)}(0)}{k!}t^k
Ряды Тейлора и Маклорена, как и любые степенные ряды, имеют соответствующий интервал сходимости.
Пример
Разложим в ряд Тейлора функцию:
f(x)=1x−1f(x)=dfrac{1}{x-1} в окрестности точки x0=2x_0=2.
С помощью замены:
x−x0=x−2=tx-x_0=x-2=t
функция сводится к виду:
f(x)=f(t+2)=11+tf(x)=f(t+2)=dfrac{1}{1+t}
Полученное выражение при ∣t∣<1|t|<1 является суммой бесконечно убывающей геометрической прогрессии знаменателем (−t)(-t), и ряд записывается в виде:
11+t=1−t+t2−t3+…+(−1)ntn+…=∑k=0∞(−1)ktkdfrac {1}{1+t}=1-t+t^2-t^3+ldots+(-1)^{n}t^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}t^{k}
Возвращаясь к переменной xx, получаем разложение по степеням двучлена (x−2)(x-2):
1x−2=1−(x−2)+(x−2)2−(x−2)3+…+(−1)n(x−2)n+…=∑k=0∞(−1)k(x−2)k,∣x−2∣<1dfrac {1}{x-2}=1-(x-2)+ (x-2)^2-(x-2)^3+ldots+(-1)^{n}(x-2)^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}(x-2)^{k}, quad |x-2|<1
Разложение основных элементарных функций в степенной ряд
Разложение в степенной ряд многих функций проще осуществлять путем сведения задач к разложениям элементарных функций. Запишем разложения основных элементарных функций в ряд Маклорена, укажем соответствующие интервалы сходимости:
ex=1+x1!+x22!+x33!+…+xnn!+…=∑k=1∞xnn!,∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+ldots=sumlimits_{k=1}^{infty} dfrac{x^n}{n!},quad |x|<infty
ax=1+xlna1!+(xlna)22!+(xlna)33!+…+(xlna)nn!+…=∑k=1∞(xlna)nn!,∣x∣<∞{a^x} = 1 + largefrac{{xln a}}{{1!}}normalsize + largefrac{{{{left( {xln a} right)}^2}}}{{2!}}normalsize + largefrac{{{{left( {xln a} right)}^3}}}{{3!}}normalsize + ldots + largefrac{{{{left( {xln a} right)}^n}}}{{n!}}normalsize + ldots=sumlimits_{k=1}^{infty} dfrac{{(xln{a})}^n}{n!},quad |x|<infty
ln(1+x)=x−x22+x33−x44+…+(−1)nxn+1n+1+…=∑k=1∞(−1)k+1xkk!, −1<x≤1ln left( {1 + x} right) = x — largefrac{{{x^2}}}{2}normalsize + largefrac{{{x^3}}}{3}normalsize — largefrac{{{x^4}}}{4}normalsize + ldots + largefrac{{{{left( { — 1} right)}^n}{x^{n + 1}}}}{{n + 1}}normalsize + ldots= sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}x^{ k }}{ k!} ,;; — 1 < x le 1
lnx=2[x−1x+1+13(x−1x+1)3+15(x−1x+1)5+…], x>0ln x = 2left[ {largefrac{{x — 1}}{{x + 1}}normalsize + largefrac{1}{3}normalsize {{left( {largefrac{{x — 1}}{{x + 1}}normalsize} right)}^3} + largefrac{1}{5}normalsize{{left( {largefrac{{x — 1}}{{x + 1}}normalsize} right)}^5} + ldots } right],;;x > 0
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+…=∑k=1∞(−1)k+1x2k−1(2k−1)!,∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ldots=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}x^{2 k -1}}{(2 k -1)!},quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+…=∑k=0∞(−1)kx2k(2k)!,∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ldots=sumlimits_{ k =0}^{infty} dfrac{(-1)^{k}x^{2 k }}{(2 k)!},quad |x|<infty
tgx=x+x33+2×515+17×7315+62×92835+…, ∣x∣<π2tg x = x + largefrac{{{x^3}}}{3}normalsize + largefrac{{2{x^5}}}{{15}} normalsize + largefrac{{17{x^7}}}{{315}}normalsize + largefrac {{62{x^9}}}{{2835}}normalsize + ldots ,;;left| x right| < largefrac{pi }{2} normalsize
ctgx=1x−(x3+x345+2×5945+2×74725+…), ∣x∣<πctg x = largefrac{1}{x}normalsize — left({largefrac{x}{3}normalsize+ large frac{{{x^3}}}{{45}}normalsize + largefrac{{2{x^5}}}{{945}} normalsize + largefrac{{2{x^7}}}{{4725}}normalsize + ldots } right),;;left| x right| < pi
arcsinx=x+x32⋅3+1⋅3×52⋅4⋅5+…+1⋅3⋅5…(2n−1)x2n+12⋅4⋅6…(2n)(2n+1)+…, ∣x∣<1arcsin x = x + largefrac{{{x^3}}}{{2 cdot 3}}normalsize + largefrac{{1 cdot 3{x^5}}}{{2 cdot 4 cdot 5}}normalsize + ldots + largefrac{{1 cdot 3 cdot 5 ldots left( {2n — 1} right){x^{2n + 1}}}}{{2 cdot 4 cdot 6 ldots left( {2n} right)left( {2n + 1} right)}}normalsize + ldots ,;;left| x right| < 1
arccosx=π2−(x+x32⋅3+1⋅3×52⋅4⋅5+…+1⋅3⋅5…(2n−1)x2n+12⋅4⋅6…(2n)(2n+1)+…), ∣x∣<1arccos x = largefrac{pi }{2}normalsize — left( {x + largefrac{{{x^3}}}{{2 cdot 3}}normalsize + largefrac{{1 cdot 3{x^5}}}{{2 cdot 4 cdot 5}}normalsize + ldots + largefrac{{1 cdot 3 cdot 5 ldots left( {2n — 1} right){x^{2n + 1}}}}{{2 cdot 4 cdot 6 ldots left( {2n} right)left( {2n + 1} right)}}normalsize + ldots} right) ,;;left| x right| < 1
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1±…, ∣x∣≤1arctg x = x — largefrac{{{x^3}}}{3}normalsize + largefrac{{{x^5}}}{5} normalsize — largefrac{{{x^7}}}{7}normalsize + ldots +largefrac{{{{left({-1} right)}^n}{x^{2n + 1}}}}{{2n + 1}}normalsize pm ldots ,;;left| x right| le1
chx=1+x22!+x44!+x66!+…+x2n(2n)!+…=∑k=0∞x2k(2k)!ch x = 1 + largefrac{{{x^2}}}{{2!}}normalsize + largefrac{{{x^4}}} {{4!}}normalsize + largefrac{{{x^6}}}{{6!}}normalsize + ldots + largefrac {{{x^{2n}}}}{{left( {2n} right)!}}normalsize + ldots=sumlimits_{ k =0}^{infty} dfrac{x^{2k}}{(2k)!}
shx=x+x33!+x55!+x77!+…+x2n+1(2n+1)!+…=∑k=0∞x2k+1(2k+1)!sh x = x + largefrac{{{x^3}}}{{3!}}normalsize + largefrac{{{x^5}}}{{5!}} normalsize + largefrac{{{x^7}}}{{7!}}normalsize + ldots + largefrac {{{x^{2n + 1}}}}{{left( {2n + 1} right)!}}normalsize + ldots =sumlimits_{ k =0}^{infty} dfrac{x^{2 k+1 }}{(2k+1)!}
Примеры разложения функций в степенной ряд
Пример 1
Разложим в ряд Тейлора, функцию
f(x)=(x−1)ln(x2−2x+2)f(x)=(x-1)ln (x^2-2x+2)
в окрестности точки x0=1x_0=1. Выполнив замену переменной
x−x0=x−1=tx-x_0=x-1=t
записываем функцию в виде:
g(t)=tln(1+t2)g(t)=t ln(1+t^2)
Используя далее разложение логарифмической функции:
ln(1+t2)=∑k=1∞(−1)k+1(t2)kk!=∑k=1∞(−1)k+1t2kk!ln{(1+t^2)}=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}{(t^2)}^{ k }}{ k!}= sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}t^{2 k}}{ k!}
получаем
g(t)=t∑k=1∞(−1)k+1t2kk!=∑k=1∞(−1)k+1t2k+1k!g(t)=tsumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}t^{2 k}}{ k!}=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}t^{2 k+1}}{ k!}
Выполняем далее обратную замену переменной:
f(x)=∑k=1∞(−1)k+1(x−1)2k+1k!=(x−1)3−(x−1)52+(x−1)76−…f(x)=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}{(x-1)}^{2 k+1}}{ k!}={(x-1)}^{3}-dfrac{(x-1)^{5}}{2}+dfrac{(x-1)^{7}}{6}-ldots
Пример 2
Разложим в ряд Маклорена функцию
f(x)=(x−1)cos2x+sin(x2)f(x)=(x-1) cos{2x} + sin{(x^2)}
Используем разложение в ряд Маклорена тригонометрических функций:
sin(x2)=∑k=1∞(−1)k+1(x2)2k−1(2k−1)!==∑k=1∞(−1)k+1x4k−2(2k−1)!sin{(x^2)}=sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}{(x^2)}^{2 k -1}}{(2 k -1)!}= =sumlimits_{ k =1}^{infty} dfrac{(-1)^{ k +1}{x}^{4 k -2}}{(2 k -1)!}
cos2x=∑k=0∞(−1)k4kx2k(2k)!=1+∑k=1∞(−1)k4kx2k(2k)!cos{2x}=sumlimits_{ k =0}^{infty} dfrac{(-1)^{k}4^{k}x^{2 k }}{(2 k)!}=1+sumlimits_{ k =1}^{infty} dfrac{(-1)^{k}4^{k}x^{2 k }}{(2 k)!}
В результате получаем:
f(x)=(x−1)cos2x+sin(x2)=x−1+∑k=1∞((−1)k4k(x2k+1−x2k)(2k)!+(−1)k+1x4k−2(2k−1)!)f(x)=(x-1) cos{2x} + sin{(x^2)}=x-1+sumlimits_{ k =1}^{infty}left(dfrac{(-1)^{k}4^{k}(x^{2 k+1 }-x^{2k})}{(2 k)!}+ dfrac{(-1)^{ k +1}{x}^{4 k -2}}{(2 k -1)!}right)
f(x)=x−1+∑k=1∞(−1)k(4kx2k+1−4kx2k−2kx4k−2)(2k)!f(x)=x-1+sumlimits_{ k =1}^{infty} dfrac{(-1)^{k}(4^{k}x^{2 k+1 }-4^{k}x^{2k}-2k x^{4k-2})}{(2 k)!}
Разложение функции в ряд x→∞xrightarrowinfty
При необходимости разложить функцию в ряд Тейлора при x→+∞x to +infty необходимо последовательно выполнить следующие действия:
- выполняем замену переменной t=1xt=dfrac{1}{x},
- полученную функцию g(t)g(t) разложить в ряд Тейлора,
- с помощью обратной замены переменных записать искомое выражение для f(x)f(x).
Пример
Разложим в ряд Тейлора, функцию
f(x)=x−x2+1f(x)=x-sqrt{x^2+1}
при x→+∞x to +infty. Выполнив замену переменной
t=1x,x=1tt=dfrac{1}{x}, quad x=dfrac{1}{t}
получаем:
g(t)=1t−1t2+1=1−(1+t2)1/2tg(t)=dfrac {1}{t}-sqrt {dfrac{1}{t^2}+1}=dfrac{1-(1+t^2)^{1/2}}{t}
Используем разложение степенной функции в ряд Тейлора:
(1+t2)1/2=1+∑k=1∞(−1)k+1⋅1⋅2⋅3⋅5⋯(2k−3)⋅tk2kk!(1+t^2)^{1/2}=1+sumlimits_{ k =1}^{infty}dfrac{(-1)^{k+1}cdot1cdot2cdot3cdot5cdots(2k-3)cdot{t}^k}{2^kk!}
Далее:
g(t)=1t(1−(1+∑k=1∞(−1)k⋅1⋅2⋅3⋅5⋯(2k−3)⋅tk2kk!))g(t)=dfrac{1}{t}left(1-left(1+sumlimits_{ k =1}^{infty}dfrac{(-1)^{k}cdot1cdot2 cdot3cdot5cdots(2k-3)cdot{t}^{k}}{2^kk!}right)right)
g(t)=∑k=1∞(−1)k⋅1⋅2⋅3⋅5⋯(2k−3)⋅tk−12kk!g(t)=sumlimits_{ k =1}^{infty}dfrac{(-1)^{k}cdot1cdot2 cdot3cdot5cdots(2k-3)cdot{t}{k-1}}{2^kk!}
Выполняя обратную замену переменной, находим:
f(x)=∑k=1∞(−1)k⋅1⋅2⋅3⋅5⋯(2k−3)2kk!⋅xk−1f(x)=sumlimits_{ k =1}^{infty}dfrac{(-1)^{k}cdot1cdot2cdot3cdot5cdots(2k-3)}{2^kk!cdot{x}^{k-1}}
Тест по теме «Разложение функций в степенные ряды»
Разложение в ряд Тейлора
Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:
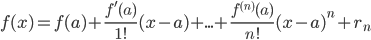
где rn – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
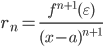
- Решение онлайн
- Видеоинструкция
Если для некоторого значения х rn→0 при n→∞, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:
- она имеет производные всех порядков;
- построенный ряд сходится в этой точке.
При а=0 получаем ряд, называемый рядом Маклорена:
Разложение простейших (элементарных) функций в ряд Маклорена:
Пример №1. Разложить в степенной ряд функцию f(x)=2x.
Решение. Найдем значения функции и ее производных при х=0
f(x) = 2x, f(0) = 20=1;
f'(x) = 2xln2, f'(0) = 20 ln2= ln2;
f»(x) = 2x ln22, f»(0) = 20 ln22= ln22;
…
f(n)(x) = 2x lnn2, f(n)(0) = 20 lnn2= lnn2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:
Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -∞<x<+∞.
Пример №2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=ex.
Решение. Находим производные функции ex и их значения в точке х=-4.
f(x) = еx, f(-4) = е-4;
f'(x) = еx, f'(-4) = е-4;
f»(x) = еx, f»(-4) = е-4;
…
f(n)(x) = еx, f(n)( -4) = е-4.
Следовательно, искомый ряд Тейлора функции имеет вид:
Данное разложение также справедливо для -∞<x<+∞.
Пример №3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),
( т.е. в ряд Тейлора в окрестности точки х=1).
Решение. Находим производные данной функции.
f(x)=lnx, 


f(1)=ln1=0, f'(1)=1, f»(1)=-1, f»'(1)=1*2,…, f(n)=(-1)n-1(n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:
С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1. Действительно,
Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].
Пример №4. Разложить в степенной ряд функцию 
Решение. В разложении (1) заменяем х на -х2, получаем:

Пример №5. Разложить в ряд Маклорена функцию 
Решение. Имеем
Пользуясь формулой (4), можем записать:
подставляя вместо х в формулу –х, получим:
Отсюда находим: ln(1+x)-ln(1-x) = 
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим

Замечание.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример №5а. Разложить в ряд Маклорена функцию 
Решение. Сначала найдем 1-x-6x2=(1-3x)(1+2x), далее разложим дробь с помощью сервиса.


Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
с областью сходимости |x| < 1/3.
Пример №6. Разложить функцию 
Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):

Полученный ряд сходится при 
Пример №7. Написать ряд Тейлора по степеням (х-1) функции ln(x+2).
Решение.

Ряд сходится при 
Пример №8. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x=2.
Решение. Сделаем замену t=х-2:
Воспользовавшись разложением (3), в котором на место х подставим π/4t, получим:
Полученный ряд сходится к заданной функции при -∞<π/4t<+∞, т.е. при (-∞<x<+∞).
Таким образом,

Приближенные вычисления с помощью степенных рядов
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
Рассмотрим разложение функции в степенной ряд:
Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:
Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток rn(x). Для этого применяют следующие приемы:
- если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
- если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
- в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или x<c<a).
Пример №1. Вычислить ln(3) с точностью до 0,01.
Решение. Воспользуемся разложением 
Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
Таким образом, мы можем отбросить этот остаток и получаем
Пример №2. Вычислить 
Решение. Воспользуемся биномиальным рядом. Так как 53 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=53+5.

так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:

Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Пример №3. Вычислить интеграл ∫014sin(x)x с точностью до 10-5.
Решение. Соответствующий неопределенный интеграл 
Разделив почленно ряд для sinx на x , получим:
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:
Так как полученный ряд удовлетворяет условиям Лейбница и 
Таким образом, находим
Пример №4. Вычислить интеграл ∫014ex2 с точностью до 0,001.
Решение.
Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.

Следовательно, 
Лекция
5
Лекция
5 1
5.1.
Ряды Тейлора и Маклорена. Условия
сходимости рядов Тейлора к исходной
функции 1
5.2.
Разложение основных элементарных
функций в степенные ряды 3
5.1.
Ряды Тейлора и Маклорена. Условия
сходимости рядов Тейлора к исходной
функции
Пусть
функция
определена в некоторой окрестности
точки х0:
и имеет производные любого порядка,
тогда для этой функции формально можно
составить ряд по степеням
:
,
где
Определение
1.
Обобщенный степенной ряд вида
называется рядом
Тейлора
для функции
по степеням
.
Если положить
,
то получим ряд
,
который носит название ряда
Маклорена
для функции
по
степеням х.
Задача.
Пусть задана функция
,
бесконечно дифференцируемая в окрестности
точки х0:
,
и пусть для этой функции составлен ряд
Тейлора по степеням
:
и его сумма равна
.
Если интервал
,
является интервалом сходимости данного
ряда с радиусом сходимости R,
то можно записать равенство:
при всех
.
Выясним, при каких условиях такой
степенной ряд имеет своей суммой функцию
,
т.е. когда
,
поскольку существуют функции, для
которых сумма ряда Тейлора не совпадает
с данной функцией.
Рассмотрим
такой пример. Дана функция

которая является бесконечно дифференцируемой
.
Вычислим производные этой функции в
точке
:

т.е. все коэффициенты ряда Тейлора-Маклорена
для этой функции равны 0, тогда этот ряд
сходится на всей оси, его сумма тождественно
равна 0:
,
однако
при
(
только в начале координат).
Пусть
ряд Тейлора
имеет интервал сходимости
,
где R – радиус
сходимости. Тогда, если
− частичная сумма этого ряда, то
существует
.
Рассмотрим теорему, которая дает условия
того, что
.
Теорема
1 (необходимый и достаточный признак
сходимости ряда Тейлора к функции
).
Для
того чтобы ряд Тейлора
,
,
имел своей суммой функцию
,
т.е.
,
необходимо и достаточно, чтобы для всех
существовал предел
,
где
− остаток ряда Тейлора.
Доказательство.
1) Необходимость.
Пусть функция
есть сумма ряда Тейлора на указанном
промежутке:
,
или
,
где
− частичная сумма ряда Тейлора,
−
остаток ряда. Тогда при всех
существует предел
,
и т.к.
,
то существует предел
,
т.е.
.
Необходимость доказана.
2) Достаточность.
Пусть существует
;
т.к. функция
бесконечно дифференцируема при всех
,
то для нее имеет место формула Тейлора:
,
,
где
− остаточный член формулы Тейлора,
который совпадает с остатком ряда. Тогда
частичная сумма соответствующего ряда
Тейлора имеет вид:
.
Рассмотрим предел
,
который обозначим через
,
учитывая, что
:
,
т.е.
.
Достаточность доказана.
Замечание.
Если
,
то сумма ряда Тейлора может не совпадать
с данной функцией (),
хотя сам ряд может сходиться к другой
функции.
Необходимое
и достаточное условие сходимости ряда
Тейлора к исходной функции не удобно
для проверки на практике конкретных
рядов; существуют более простые, хотя
и более жесткие, достаточные условия
разложения функции
в ряды Тейлора−Маклорена. Сначала
сформулируем лемму.
Лемма.
Для любого
существует следующий предел:.
Доказательство.
Рассмотрим степенной ряд
,
общий член которого
.
Найдем радиус и область сходимости
этого ряда, используя признак Даламбера:
;
вычисляем предел
,
т.е. радиус сходимости ряда
.
Следовательно, рассмотренный ряд
сходится для всех
,
тогда по необходимому признаку сходимости
общий член ряда
,
,
т.е.
для любого
.
Теорема
2 (достаточные условия разложимости
функции
в ряд Маклорена)
Пусть
функция
определена и бесконечно дифференцируема
на интервале
.
Если существует такое число
,
что для каждого натурального
и всех
выполняется неравенство:
(это означает, что производные любого
порядка ограничены одним и тем же
числом), тогда остаток ряда Маклорена
при
,
а значит,
.
Доказательство.
Покажем, что остаток ряда Маклорена
стремится к нулю при
.
Запишем для функции
формулу Маклорена с остаточным членом
в форме Лагранжа:
,
где
− многочлен Маклорена, а
.
Отметим, что частичная сумма ряда
Маклорена
является этим многочленом
,
а остаток ряда есть
.
Выполним его оценку, используя условия
данной теоремы и учитывая, что
для
всех
:
.
По лемме
при
,
тогда
,
.
Следовательно, по теореме 1 о необходимом
и достаточном признаке сходимости ряда
Тейлора−Маклорена к исходной функции
получаем
.
Теорема доказана.
5.2.
Разложение основных элементарных
функций в степенные ряды
Используем
изложенную выше теорию для разложения
основных элементарных функций в степенные
ряды. Для разложения функции
в степенной ряд по степеням
можно рекомендовать следующий порядок
действий:
1)
Находим производные функции
в точке
:
.
2)
Составляем ряд Тейлора
.
3)
Находим интервал сходимости данного
ряда:
,
где R
− радиус сходимости.
4)
Исследуем поведение остатка ряда
для всех
.
Если окажется, что
,
то на основании теорем 1 и 2 делаем вывод,
что
при всех
.
В результате получаем формулу разложения
функции в степенной ряд.
Разложение
в степенной ряд функции
имеет вид:
(1)
Вывод.
Рассмотрим ряд геометрической прогрессии
,
знаменатель которой
и
.
Можно показать, что интервал сходимости
этого ряда
,
и сумма этого ряда
(сумма ряда бесконечно убывающей
геометрической прогрессии вычисляется
по формуле
).
Оценим остаток ряда:
;
при
при
,
тогда на основании теоремы 1 рассмотренный
ряд имеет своей суммой функцию
.
Разложение (1) имеет место.
Разложение
в степенной ряд функции
имеет вид:
(2)
Вывод.
Для данной функции
запишем ряд Маклорена:
;
т.к.
− бесконечно дифференцируема, то все
производные существуют и имеют вид:
.
Находим эти производные в точке
,
получаем
,
для всех
,
тогда ряд Маклорена приобретает вид
.
Этот ряд сходится для всех
.
Фиксируем
некоторое число
и рассмотрим некоторый отрезок [−a,
a],
на котором
для любого
.
В этом случае по теореме 2 данный ряд
Маклорена будет сходиться на указанном
отрезке к исходной функции
.
Отметим, что это верно для любого
фиксированного числа
.
Разложение (2) имеет место при всех
.
Разложение
в степенной ряд функции
имеет вид:
,
(3)
Вывод.
Для функции
запишем ряд Маклорена
.
Находим все производные:
,
,
,
,
…,
.
В
точке х
= 0 получаем:
.
Подставив эти значения в ряд Маклорена,
получаем ряд:
.
Данный ряд сходится при любом
.
В
силу теоремы 2 (поскольку
,
т.е. все производные ограничены одним
и тем же числом) данный ряд Маклорена
будет сходиться к исходной функции
при всех
.
Таким образом, имеет место разложение
(3).
Разложение
в степенной ряд функции
имеет вид:
,
(4)
Вывод.
Рассмотрим разложение (3)
,
.
Продифференцируем данный ряд; получившийся
новый ряд будет также сходиться при
всех
к функции, которая равна производной
от
(свойство 3, лекция 4), т.е.
.
Таким образом, разложение (4) имеет место.
Разложение
в степенной ряд функции
имеет вид:
(5)
Приведем
это разложение без вывода; отметим, что
оно верно при фиксированном
и называется биномиальным
рядом.
При натуральном
этот ряд представляет собой конечную
сумму, известную как бином
Ньютона:
.
Для
нецелых m
имеет место формула Тейлора:
.
При
из этой формулы получаем бесконечный
степенной ряд (5). Найдем радиус его
сходимости, применяя признак Даламбера.
,
;
вычисляем предел:
,
тогда при
биномиальный ряд сходится и его радиус
сходимости
,
а интервал сходимости − (−1;1) (можно
показать, что
).
Итак,
разложение (5) верно для всех
.
В частном случае, когда
,
из разложения (5) получаем ряд
,
который при
абсолютно сходится. Если в каждом члене
ряда заменить х
на (− х),
то получим разложение (1):
.
Разложение
в степенной ряд функции
имеет вид:
(6)
Вывод.
Из разложения (5) биномиального ряда при
получаем ряд
,
который является рядом геометрической
прогрессии с
,
который сходится при
,
т.е. этот ряд имеет радиус сходимости
и интервал сходимости − (−1;1). Полученный
ряд почленно интегрируем на отрезке
,
используя свойство 3 (лекция 4), при этом
интервал сходимости сохранится:

Сумма
полученного ряда равна
(или
,
т.к.
).
Таким образом,
,
т.е. имеет место разложение (6) при
.
Исследуя сходимость данного ряда в
точке
,
получаем числовой ряд
,
который условно сходится. В итоге,
область сходимости ряда в разложении
(6) имеет вид
,
а радиус сходимости
.
Разложение
в степенной ряд функции
имеет вид:
(7)
Вывод.
Из разложения (5) биномиального ряда при
получаем разложение
,
из которого заменой
на
вытекает следующий ряд:
,
который сходится при
,
а именно, при
.
Полученный ряд почленно интегрируем
на отрезке
,
используя свойство 3 (лекция 4), при этом
интервал сходимости сохранится:
.
Сумма
полученного ряда
.
Таким образом,
,
т.е. разложение (7) имеет место при
.
Исследуя полученный ряд в точках
и
,
получаем два условно сходящихся числовых
ряда
и
соответственно. В итоге, область
сходимости ряда в разложении (7) является
отрезком
,
а радиус сходимости R
равен 1.
Разложение
в степенной ряд функции
имеет вид:
(8)
Вывод.
Из разложения (5) биномиального ряда при
и при замене
на
получаем разложение
.
Получившийся ряд сходится при
.
Этот ряд почленно проинтегрируем на
отрезке
,
используя свойство 3 (лекция 4), при этом
интервал сходимости сохранится:

Сумма полученного ряда
.
Таким образом,
,
т.е. имеет место разложение (8) на интервале
сходимости
.
В
заключение добавим, что разложения −
называют основными
разложениями элементарных
функций в степенной ряд, которые
используются как эталонные для разложения
других функций.
7
Разложение функций в степенные ряды. Ряд Тейлора
Общая постановка задачи разложения функции в ряд в комплексной области формулируется так же, как и в действительной области. А именно, для заданной функции , определенной в области
и удовлетворяющий в ней него которым дополнительным условиям, требуется найти ряд вида
который бы сходился в области
и его сумма в этой области совпадала с
.
Постановка задачи разложения функции в степенной ряд
Для функции , аналитической в области
, найти ряд
, сходящийся к
в круге
, принадлежащем области
, то есть
(3.15)
Равенство (3.15) означает, что является суммой ряда в круге
.
Для решения задачи нужно, очевидно, найти коэффициенты ряда по заданной функции ; найти круг сходимости ряда и установить сходимость ряда именно к
. Последнее, напомним, означает, что для точек круга выполняется неравенство
для любого
и
.
Все поставленные вопросы решаются с помощью следующей теоремы.
Теорема Тейлора о разложении функции в степенной ряд
Теорема 3.4. Функция, аналитическая в области , в окрестности каждой точки
этой области представляется в виде степенного ряда (3.15), радиус сходимости
которого не меньше, чем расстояние от точки
до границы области
. Коэффициенты ряда вычисляются по формуле
(3.16)
где — произвольный контур, принадлежащий области
и охватывающий точку
, в частности,
— окружность
или по формуле
(3.17)
На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.
Алгоритм разложения аналитической функции в степенной ряд
1. Найти производные от данной функции: .
2. Вычислить значения производных в точке ; записать коэффициенты по формуле (3.17). Составить ряд по степеням
с этими коэффициентами, который соответствует данной функции
3. Найти область сходимости полученного ряда и записать разложение (3.15).
Если функция не имеет конечных особых точек, то ряд сходится к ней во всей плоскости, .
Утверждение 3.3
1. Функция, аналитическая в точке , раскладывается в окрестности этой точки в степенной ряд.
2. На границе круга сходимости ряда есть хотя бы одна особая точка функции, т.е. радиус сходимости круга равен расстоянию от центра разложения до ближайшей особой точки функции.
3. Степенной ряд в круге сходимости является рядом Тейлора для своей суммы, т.е. коэффициенты ряда вычисляются по формулам (3.16), (3.17).
Примеры разложения функций по степеням z
Пример 3.13. Записать разложения по степеням функций
.
Решение
Задачу решаем по вышеприведенному алгоритму.
1. Найдем производные:
В поставленной задаче . По формуле (3.17) имеем
3. Нетрудно убедиться, что все составленные ряды сходятся во всей комплексной плоскости, . В результате получаем формулы, которые ранее были приняты за определения соответствующих функций:
В результате получены так называемые основные разложения.
Пример 3.14. Записать разложения по степеням функций: а)
; б)
.
Решение
Задачу можно решать, пользуясь алгоритмом, а можно использовать формулы (3.13) для суммы членов геометрической профессии. Заданные функции являются аналитическими во всей комплексной плоскости за исключением одной точки . Для каждого случая получаем:
заметим, что здесь
для
.
Пример 3.15. Записать разложения по степеням функций: а)
; б)
.
Решение
Разложения записываются для однозначных ветвей многозначного выражения. Выбор ветви определяется заданием функции в точке .
a) Функция определена во всей комплексной плоскости за исключением , т.е. в двусвязной области
. Чтобы получить односвязную область из
, проведем разрез, соединяющий точки
и
. Из условия
следует, что точка
должна быть внутренней точкой области. Поэтому выбираем разрез, не проходящий через
. например по лучу
. В полученной односвязной области, где
, функция
является однозначной аналитической функцией. Далее решаем задачу по алгоритму.
1. Находим производные (формулу устанавливаем по индукции):
2. По формуле (3.17):
3. Находим радиус сходимости ряда: , где
. В результате получаем
б) Функция определена всюду в
за исключением
, т.е. в двусвязной области. В односвязной области, полученной из
путем разреза по лучу
, функция является однозначной , аналитической. Задачу можно решать, как и выше, т.е. по алгоритму, а можно использовать полученный выше результат, введя обозначение
. Для
, удовлетворяющих неравенству
имеем разложение
. Заменяя
на
, получаем результат
Разложения основных функция в степенной ряд
Разложения, полученные в результате решения примеров 3.13-3.15, носят название основных (табличных) разложений. Выпишем их:
Основные разложения позволяют при решении примеров на разложение функции в ряд Тейлора не пользоваться сформулированным выше алгоритмом, сложность которого связана с техникой дифференцирования и составления формулы общего члена.
Утверждение 3.4. При разложении функции в ряд Тейлора используются основные (табличные) разложения и действия над рядами. Радиус сходимости ряда может быть получен по виду раскладываемой функции без использования формулы общего члена ряда и формул для нахождения радиуса. Радиус сходимости ряда, полученного при разложении данной функции в окрестности точки , равен расстоянию от центра разложения — точки
до ближайшей особой точки функции. Если функция является аналитической всюду, то
.
Пример 3.16. Разложить по степеням функции комплексного переменного:
Решение
а) Обозначим через
и, используя табличное разложение для функции
, получим ответ:
, то есть
.
б) Запишем функцию в виде произведения и, используя разложение для
, получим ответ:
, то есть
.
в) Чтобы воспользоваться одним из основных разложений, применим тригонометрическую формулу — формулу «понижения». Получим:
Заметим, что свободный член разложения в этой записи встречается дважды, поэтому нужно привести подобные члены. Для этого в записи рада отделим слагаемое при — свободный член:
В результате имеем .
Из этого разложения можно найти значение производной любого порядка функции в точке
, так как эти значения связаны формулой (3.17) с коэффициентами разложения:
. Поэтому, учитывая, что в разложении присутствуют только четные степени, заключаем, что все производные нечетных порядков от
в точке
равны нулю, а производная, например, десятого порядка не равна нулю. Найдем ее, используя равенство
, где
— коэффициент в разложении
при
, т.е. в записанном выше разложении нужно взять
. Получим
г) Функция определена всюду, кроме . В односвязной области, например в плоскости с разрезом по лучу
, где
, возможно выделение однозначных ветвей многозначного выражения
(рис. 3.1). Выбираем ту ветвь, для которой
, то есть из
получаем
. Разложим аналитическую функцию
по степеням
в круге
; радиус круга
— расстояние от центра разложения
до граничной точки
.
Чтобы воспользоваться основным разложением, преобразуем функцию следующим образом:
Тогда, обозначая через
и используя основное разложение для
, получаем
при условии
, т.е. в круге
.
Пример 3.17. Разложить в окрестности точки ветвь функции
, для которой
.
Решение
Функция определена всюду в
, кроме точек
, т.е. в трехсвязной области — плоскости с выколотыми точками
и
. Чтобы получить односвязную область, проведем разрезы по лучам, выходящим из этих точек. Например, луч из точки
выберем параллельным мнимой оси,
, а луч из точки
— по действительной оси:
. В полученной односвязной области (рис. 3.2) каждая ветвь является аналитической функцией и раскладывается в ряд в круге
(
— расстояние от
до границы). Здесь ветвь задается условием:
, то есть из
при
.
Далее, чтобы использовать основное разложение, преобразуем функцию:
Для числа в силу выбора ветви берем
, а функции
и
раскладываем в ряды, как в предыдущем примере:
В области , принадлежащей выбранной односвязной области, сходятся оба ряда. Используя свойство сложения рядов, получаем окончательный результат:
При разложении функции в ряд в окрестности точки , т.е. по степеням
, удобно использовать замену
и полученную после замены функцию раскладывать по степеням
.
Пример 3.18. Разложить по степеням функции: a)
; б)
в)
.
Решение
а) Обозначим через
, и, используя тригонометрическую формулу для функции
, получим:
. Здесь
и
— постоянные величины, а для функций
и
используем основные разложения. В результате получим
то есть ряд вида , где коэффициент
определяется следующим образом:
для
и
для
.
б) Можно, как и выше, использовать вспомогательную переменную, а можно сделать то же самое, применив простое преобразование: . Здесь
— постоянная величина, функция
раскладывается в ряд как функция
по степеням
. Получаем ответ:
, или
.
в) Обозначая через
, получаем функцию
. Разложение этой функции по степеням
найдено в примере 3.16:
Возвращаясь к исходной переменной, получаем разложение исходной функции в круге (рис. 3.3):
Пример 3.19. Разложить по степеням функции:
.
Решение
Данные функции являются простейшими рациональными (элементарными) дробями. Для их разложения используется формула суммы членов бесконечно убывающей геометрической прогрессии . В первом случае формула используется непосредственно, при
, во втором — после преобразования
получаем
. Разложение заданных функций имеет вид
(3.18)
(3.19)
Соотношения (3.18),(3.19) обобщают формулу , которая получается из них при
.
При разложении дроби замечаем, что она является производной от
, то есть
, поэтому ее разложение можно получить, используя дифференцирование ряда:
Ответ удобнее записать в виде .
Очевидно, повторяя процедуру дифференцирования, можно получить разложение элементарных дробей вида при любом натуральном
.
Алгоритм разложения рациональных дробей в ряд Тейлора
Рассмотрим примеры на разложение в ряд Тейлора рациональных дробей
где и
— многочлены. Первые этапы решения задачи аналогичны этапам интегрирования этих дробей. Приведем полный алгоритм.
1. Если дробь неправильная , следует выделить целую часть дроби многочлен.
2. Правильную рациональную дробь разложить на элементарные дроби:
а) записать дробь в виде суммы элементарных дробей вида с неопределенными коэффициентами
, где
— корень знаменателя,
— его кратность;
б) найти неопределенные коэффициенты.
3. Разложить элементарные дроби в степенные ряды. Основными приемами при этом являются применение формул (3.13),(3.18),(3.19) и правила дифференцирования ряда (см. пример 3.19)).
При разложении по степеням можно предварительно ввести вспомогательную переменную
.
Пример 3.20. Разложить по степеням функции: а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь неправильная, поэтому выделяем целую часть: .
2. Полученная правильная дробь является элементарной дробью.
3. Записываем разложение элементарной дроби и получаем:
Для разложения дроби можно было использовать формулу (3.19) при
.
Для нахождения окончательного ответа нужно сделать преобразование приведения подобных членов, так как в полученном выражении свободный член встречается дважды. Имеем
, то есть
.
б) Воспользуемся алгоритмом.
1. Дробь неправильная, выделяем целую часть. Можно, как и выше, применить преобразование дроби:
Можно для выделения целой части применить метод деления «углом», или, обозначая i + 2 = t, произвести почленное деление на одночлен
2,3. Записываем разложение заданной функции, используя формулу (3.19) для правильной дроби:
Окончательный ответ: .
Получен ряд вида , где
. Нетрудно проверить равенство:
.
Пример 3.21. Функцию разложить в ряд Тейлора в окрестности точки
, если а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем ее на элементарные дроби. Для этого представим дробь в виде
где и
— неопределенные коэффициенты, которые находим из тождества
Полагая последовательно и
, получаем
.
Записываем дробь в виде суммы дробей: .
3. Раскладываем по степеням г каждую элементарную дробь:
В общей области сходимости — круге — записываем сумму рядов разложение исходной дроби:
б) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Разложение дроби на элементарные получено в предыдущем пункте:
3. Раскладываем по степеням каждую элементарную дробь:
Записываем разложение исходной дроби в круге
При разложении по степеням, можно было сделать замену
в исходной дроби.
Радиусы сходимости в обоих случаях можно определить заранее, до записи» разложения — по виду функции. Ее особыми точками являются точки и
. В первом случае ближайшей к точке
является точка
, расстояние между точками равно единице и, следовательно,
; во втором — обе особые точки удалены от
на расстояние, равное двум, и
.
Пример 3.22. Разложить по степеням функции (рациональные дроби): а)
; б)
.
Решение
а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем правильную дробь на элементарные дроби, предварительно разложив знаменатель на множители:
, где
и
.
Представим дробь в виде . Находим коэффициенты
и
из тождества
, т.е. из системы
Дробь представлена в виде суммы: .
3. Раскладываем элементарные дроби по степеням
Записываем ответ:
б) Воспользуемся алгоритмом.
1,2. Раскладываем дробь на элементарные:
, где
— неопределенные коэффициенты.
Находим коэффициенты из тождества .
Приравнивая коэффициенты при одинаковых степенях , имеем
3. Раскладываем элементарные дроби по степеням
Для исходной дроби получаем разложение:
или, складывая ряды: .
Окончательный ответ: .
Пример 3.23. Разложить по степеням функции: а)
; б)
.
Решение
Обе дроби правильные; раскладывать на более простые нет необходимости. Используя основные разложения, получаем ответы:
а) ;
б) или
.
Пример 3.24. Используя разложение функции по степеням
, найти значение производной седьмого порядка в точке
.
Решение
Пример 3.25. Записать разложение функций a) и б)
по степеням
до члена, содержащего
.
Решение
а) Применим метод подстановки ряда в ряд, используя основные разложения для функций и
. Имеем
, или, подставляя:
где . Записывать большее число слагаемых нет необходимости, так как уже у следующего (первого отброшенного) младшая степень равна
.
Возведение в степень рядов, как и перемножение рядов, производится по правилам действий с многочленами, в частности применяется формула бинома Ньютона:
Так как младшая степень выражения
равна трем, следовательно,
— шести, то для записи результата следует взять из первых двух скобок по два слагаемых, а из остальных по одному, т.е.
Приводя подобные члены, получим окончательный ответ:
или .
Разложение, очевидно, можно получить, вычисляя коэффициенты разложения по формуле (3.17), что более громоздко.
б) Разложение можно получить, используя формулу (3.17) для коэффициентов либо произведя деление ряда
на ряд
методом деления «утлом» или методом неопределенных коэффициентов.
Применим последний прием. Разложение по степеням
ищем в виде
По определению деления имеем тождество
Перемножаем ряды справа и приравниваем коэффициенты полученного ряда известным коэффициентам при соответствующих степенях ряда, записанного слева. Получаем систему уравнений
из которой находим коэффициенты .
Ответ получаем в виде . Это разложение справедливо в круге
, так как
— ближайшая к
особая точка функции тангенса
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.