Как найти область треугольника по вершинам - Исправление недочетов и поиск решений вместе с Examum.ru

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Определение принадлежности точки треугольнику

Дано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты.

Что нужно узнать: нужно установить принадлежность точки треугольнику.

В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику.

Метод сравнения площадей

В данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно.

Затем находится площадь самого треугольника ABC.

Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность.

Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий.

Простейшая реализация алгоритма:

Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить.

Метод относительности

Данный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.

На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику.

Всё относительно!

Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой.

Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику.

Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции!

Векторный метод

Третий метод который я освещаю для меня самый интересный.

Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма…

Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :]

1) одну вершину треугольника помещаем в координаты (0;0);

2) две стороны, выходящие из этой вершины, представляем как вектора.

Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)

Рис. 4.

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

источники:

Определение принадлежности точки треугольнику

http://www-formula.ru/2011-10-09-11-08-41

Источник

Как найти площадь треугольника по координатам его вершин?

1способ:

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

2 способ:

вывести формулу для нахождения площади и использовать её для вычисления.

Утверждение

Площадь треугольника ABC с вершинами в точках A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) можно вычислить с помощью формулы

$[S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|.]$

Доказательство:

Рассмотрим треугольник ABC,

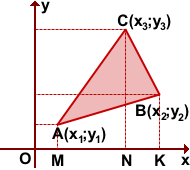
A(x₁;y₁), B(x₂;y₂), C(x₃;y₃)

Опустим перпендикуляры из вершин треугольника на координатные оси.

$[S_{Delta ABC} = S_{MACN} + S_{NCBK} - S_{MABK} ]$

$[S_{MACN} = frac{{MA + CN}}{2} cdot MN = frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ),]$

$[S_{NCBK} = frac{{NC + BK}}{2} cdot NK = frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ),]$

$[S_{MABK} = frac{{MA + BK}}{2} cdot MK = frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ).]$

$[S_{Delta ABC} = ]$

$[= frac{{y_1 + y_3 }}{2} cdot (x_3 - x_1 ) + frac{{y_3 + y_2 }}{2} cdot (x_2 - x_3 ) - frac{{y_1 + y_2 }}{2} cdot (x_2 - x_1 ) = ]$

$[= frac{1}{2}[(y_1 + y_3 )(x_3 - x_1 ) + (y_3 + y_2 )(x_2 - x_3 ) - (y_1 + y_2 )(x_2 - x_1 )] = ]$

$[= frac{1}{2}[x_3 y_1 - x_1 y_1 underline { + x_3 y_3 } - x_1 y_3 + x_2 y_3 underline { - x_3 y_3 } + x_2 y_2 - x_3 y_2 - ]$

$[= frac{1}{2}[(x_2 y_3 - x_2 y_1 ) + ( - x_1 y_3 + x_1 y_1 ) + (x_1 y_2 - x_1 y_1 ) + ]$

$[= frac{1}{2}[x_2 (y_3 - y_1 ) - x_1 (y_3 - y_1 ) + x_1 (y_2 - y_1 ) - x_3 (y_2 - y_1 )] = ]$

$[= frac{1}{2}[(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )].]$

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

$[ S_{Delta ABC} = frac{1}{2}left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} right|. ]$

Что и требовалось доказать.

3 способ:

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

4 способ:

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

1 способ:

Находим длины сторон треугольника ABC.

$[AB = sqrt {(x_B - x_A )^2 + (y_B - y_A )^2 } ]$

$[ AB = sqrt {(3 - ( - 1))^2 + (4 - ( - 3))^2 } = sqrt {16 + 49} = sqrt {65} ;]$

$[AC = sqrt {(x_C - x_A )^2 + (y_C - y_A )^2 } ]$

$[AC = sqrt {(5 - ( - 1))^2 + ( - 5 - ( - 3))^2 } = sqrt {36 + 4} = sqrt {40} ;]$

$[BC = sqrt {(x_C - x_B )^2 + (y_C - y_B )^2 } ]$

$[BC = sqrt {(5 - 3)^2 + ( - 5 - 4)^2 } = sqrt {4 + 81} = sqrt {85} .]$

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

2 способ:

Подставляем в формулу x₁=-1, y₁=-3, x₂=3, y₂=4, x₃=5, y₃=-5:

$[S_{Delta ABC} = frac{1}{2}left| {(3 - ( - 1))( - 5 - ( - 3)) - (5 - ( - 1))(4 - ( - 3))} right| = ]$

$[= frac{1}{2}left| {4 cdot ( - 2) - 6 cdot 7} right| = frac{1}{2} cdot 50 = 25.]$

3 способ:

Угол A образован векторами AC и AB. Отсюда

$[ cos angle A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}} ]$

Находим координаты векторов:

$[overrightarrow {AB} (x_B - x_A ;y_B - y_A )]$

$[overrightarrow {AC} (x_C - x_A ;y_C - y_A )]$

Скалярное произведение

Длины AB и AC уже знаем:

$[cos angle A = frac{{10}}{{sqrt {65} cdot sqrt {40} }} = frac{{10}}{{sqrt {5 cdot 13} cdot sqrt {5 cdot 4 cdot 2} }} = ]$

$[= frac{{10}}{{5 cdot 2sqrt {26} }} = frac{1}{{sqrt {26} }}.]$

Синус и косинус одного угла связаны соотношением:

Синус угла от 0° до 180° является положительным числом, поэтому

$[sin angle A = sqrt {1 - cos ^2 angle A} ]$

$[sin angle A = sqrt {1 - frac{1}{{26}}} = sqrt {frac{{25}}{{26}}} = frac{5}{{sqrt {26} }}.]$

Отсюда

$[S_{Delta ABC} = frac{1}{2} cdot AB cdot AC cdot sin angle A,]$

$[S_{Delta ABC} = frac{1}{2} cdot sqrt {65} cdot sqrt {40} cdot frac{5}{{sqrt {26} }} = 25.]$

4 способ:

Найдём уравнение прямой AB. Подставляем координаты A и B в уравнение y=kx+b:

$[left{ begin{array}{l} - 3 = k cdot ( - 1) + b \ 4 = k cdot 3 + b \ end{array} right.]$

Отсюда k=7/4, b=-5/4

$[y = frac{7}{4}x - frac{5}{4},4y = 7x - 5,]$

Найдём расстояние от точки C до прямой AB:

$[d = frac{{left| {7 cdot 5 - 4 cdot ( - 5) - 5} right|}}{{sqrt {7^2 + 4^4 } }} = frac{{50}}{{sqrt {65} }}.]$

Это расстояние равно высоте треугольника, проведённой из вершины C к стороне AB. Отсюда

$[S_{Delta ABC} = frac{1}{2} cdot AB cdot d = frac{1}{2} cdot sqrt {65} cdot frac{{50}}{{sqrt {65} }} = 25.]$

Источник

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

делящий противоположную углу сторону пополам — медиана;
разделяющий угол при вершине на два равных — биссектриса;
падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

A (x1; y1);
B (x2; y2);
C (x3; y3).

Тогда координаты его векторов AB- и AC- выразятся так:

AB- = (x2-x1; y2-y1);
AC- = (x3-x1; y3-y1).

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

h = AB*sin (α).

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

S = (p*(p-a)*(p-b)*(p-c))^0,5.

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

Необходимо определить координаты векторов, образующих стороны треугольника.
Затем, следует вычислить длины их сторон.
Посчитать полупериметр фигуры.
Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1² + y1²)^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

AB- = (2−1; 5-(-3)) = (1; 8);
BC- = (-2−2; -2−5) = (-4; -7).

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Источник

Данный онлайн калькулятор предназначен для нахождения площади треугольника по значениям координат 3-ех его вершин. Не вводите одинаковые
координаты точек, тогда точки не образуют треугольник и найти площадь треугольника
будет невозможно. Если Вам надо найти площадь треугольника в декартовой системе координат, то оставьте последнюю координату
каждой точки равной нулю.

Нахождение площади треугольника, образованного 3-мя точками.

Введите координаты 3-ех вершин треугольника:

Расчет площади прямоугольника
Расчет площади параллелограмма

Если после использования данного онлайн калькулятора
(Нахождение площади треугольника) у Вас возникли какие-то вопросы по работе сервиса или вопросы
образовательного характера, то Вы всегда можете задать их на нашем
форуме.

Вы поняли, как решать? Нет?

Рассчитайте цену решения ваших задач

Калькулятор
стоимости

Решение контрольной

от 300 рублей
^*

* Точная стоимость будет определена после загрузки задания для исполнителя

+Загрузить файл

Файлы doc, pdf, xls, jpg, png не более 5 МБ.

Источник

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Определение принадлежности точки треугольнику

Метод сравнения площадей

Метод относительности

Всё относительно!

Векторный метод

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

2. Как узнать сторону прямоугольного треугольника

3. Формулы сторон равнобедренного треугольника

4. Найти длину высоты треугольника

Самый простой многоугольник и вектор

Фигура на плоскости

Направленный отрезок

Методы вычисления площади по координатам

Универсальный подход

Использование формулы Герона

Другие способы

Решение задачи

Рассчитайте цену решения ваших задач

Калькуляторстоимости

Решение контрольной от 300 рублей *

Решить треугольник Онлайн по координатам

Калькулятор
стоимости

Решение контрольной

от 300 рублей
^*